Калькулятор балки на прогиб: Расчет балки на прогиб и прочность

Содержание

Статический прогиб свободно опертой балки с внецентренной точечной нагрузкой Калькулятор

✖Внецентренная точечная нагрузка в основном определяется как нагрузка, линия действия которой не проходит через ось колонны.ⓘ Внецентренная точечная нагрузка [we]

Ассарий (Библейская Roman)Масс-атомная единицаАттограммаЭвердюпуа драмБекан (Библейский иврит)КаратсантиграммДалтонДекаграммДециграммDenarius (Библейская Roman)Didrachma (Библейский греческий)Драхма (Библейский греческий)Масса электрона (Rest)ExagramFemtogramГаммаGerah (Библейский иврит)ГигаграммГигатонназернаграммГектограммЦентнер (Великобритания)Центнер (США)Масса ЮпитераКилограммКилограмм-сила в квадрате в секунду на метркилофунтКилотонна (метрическая)ЛЕПТОН (Библейская Roman)Масса ДейтронаМасса ЗемлиМасса нейтонаМасса протонаМасса СолнцамегаграммМегатоннамикрограммМиллиграммMina (Библейский греческий)Mina (Библейский иврит)масса мюонананограммунцияПеннивейтPetagramпикограммамасса ПланкафунтФунт (Troy или фармацевтическое)ПаундалФунт-сила в квадрате в секунду на футQuadrans (Библейская Roman)Четверть (Великобритания)Четверть (США)Квинтал (метрическая система)Скрупл (аптекарь)Шекель (библейский иврит)тихоходСолнечная массаСтоун (Великобритания)Камень (США)Талант (Библейский греческий)Талант (Библейский иврит)ТераграммаТетрадрахма (Библейский греческий)Тон (анализ) (Великобритания)Тон (анализ) (США)Тон (длинный)Тон (метрической размерности)Тон (короткометражный)Тонна

+10%

-10%

✖Расстояние нагрузки от одного конца — это численное измерение того, насколько далеко друг от друга находятся объекты или точки. ⓘ Расстояние нагрузки от одного конца [a]

створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр

+10%

-10%

✖Расстояние нагрузки от другого конца — это численное измерение того, насколько далеко друг от друга находятся объекты или точки.

ⓘ Расстояние нагрузки от другого конца [b]

створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр

+10%

-10%

✖Модуль Юнга — это механическое свойство линейно-упругих твердых тел. Он описывает взаимосвязь между продольным напряжением и продольной деформацией.ⓘ Модуль для младших [E]

Атмосфера ТехническийАттопаскальБармикробарСантиметр ртутного столба (0 °C)Сантиметр водяного столба (4 °C)сантипаскальдекапаскальдесятипаскальДина на квадратный сантиметрэкса паскаль Фемто паскаль Морская вода для ног (15 °C)Вода для ног (4 °C)Вода для ног (60 ° F)ГигапаскальГрамм-сила на квадратный сантиметргектопаскальДюйм ртутного столба (32 ° F)Дюйм ртутного столба (60 ° F)Дюйм водяного столба (4 °C)Дюйм воды (60 ° F)кгс / кв. смКилограмм-сила на квадратный метрКилограмм-сила / кв. миллиметрКилоньютон на квадратный метркилопаскальКило фунт на квадратный дюймКип-сила / квадратный дюймМегапаскальИзмеритель морской водыМетр воды (4 °C)МикробармикропаскальМиллибарМиллиметр ртутного столба (0 °C)Миллиметр воды (4 ° C)миллипаскальнанопаскальНьютон / кв.смНьютон / квадратный метрНьютон / квадратный миллиметрпаскальПета паскаль Пико паскаль пьезаФунт на квадратный дюймПаундаль / квадратный футФунт-сила на квадратный футФунт-сила на квадратный дюймФунты / квадратная ногаСтандартная атмосфераТерапаскальТонна-сила (длинная) на квадратный футТон-сила (длинный) / квадратный дюймТонна-сила (короткая) на квадратный футТонна-сила (короткая) на квадратный дюймторр

+10%

-10%

✖Момент инерции балки — это количественная мера инерции вращения тела. ⓘ Момент инерции балки [I]

Грамм квадратный сантиметрГрамм квадратный миллиметрКилограмм квадратный сантиметрКилограмм квадратный метрКилограмм квадратный миллиметрКилограмм-сила, метр в квадрате, секундаУнция квадратный дюймУнция-сила, дюйм в квадрате, секундаФунт квадратный футфунт квадратный дюймФунт-сила-фут-квадрат-секундаФунт-сила, дюйм в квадрате, секундаСлаг Квадратный фут

+10%

-10%

✖Длина балки между точками перегиба.ⓘ Длина балки [L]

створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр

+10%

-10%

✖Статическое отклонение — это расширение или сжатие ограничения. ⓘ Статический прогиб свободно опертой балки с внецентренной точечной нагрузкой [δ]

створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр

⎘ копия

👎

Формула

сбросить

👍

Статический прогиб свободно опертой балки с внецентренной точечной нагрузкой Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Внецентренная точечная нагрузка: 5.4 Килограмм —> 5.4 Килограмм Конверсия не требуется

Расстояние нагрузки от одного конца: 4 метр —> 4 метр Конверсия не требуется
Расстояние нагрузки от другого конца: 1.4 метр —> 1.4 метр Конверсия не требуется
Модуль для младших: 15 паскаль —> 15 паскаль Конверсия не требуется
Момент инерции балки: 6 Килограмм квадратный метр —> 6 Килограмм квадратный метр Конверсия не требуется
Длина балки: 5 метр —> 5 метр Конверсия не требуется

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

0.12544 метр —> Конверсия не требуется

< 8 Значения статического прогиба для различных типов балок и при различных условиях нагрузки Калькуляторы

Статический прогиб свободно опертой балки с внецентренной точечной нагрузкой формула

Статическое отклонение = (Внецентренная точечная нагрузка*(Расстояние нагрузки от одного конца^2)*(Расстояние нагрузки от другого конца^2))/(3*Модуль для младших*Момент инерции балки*Длина балки)
δ = (we*(a^2)*(b^2))/(3*E*I*L)

В чем разница между изгибом и прогибом?

Под «изгибом» вы действительно имеете в виду изгибающий момент. Изгибающий момент во внутреннем напряжении в элементе (обычно балке), который позволяет ему нести нагрузку. Прогиб измеряет фактическое изменение материала, которое можно назвать «изгибом». Он измеряет физическое смещение элемента под нагрузкой.

Share

Copied!

Расчет на прочность и прогиб балки при ударе в Excel

Опубликовано 12 Янв 2014
Рубрика: Механика | 4 комментария

Расчет на прочность при ударе в обычной работе инженера-конструктора встречается не очень часто. Поэтому возникновение такой задачи может поставить в тупик своей неожиданностью. Расчеты при ударных, то есть динамических нагрузках очень сложны и часто производятся…

…по эмпирическим – полученным из практических опытов — методикам и формулам. В этой статье мы рассмотрим расчет по приближенной теоретической формуле, которая, однако, позволяет быстро, просто, понятно и с достаточной для многих случаев жизни точностью учесть динамическую составляющую нагрузки!

Выполним расчет на прочность и определим прогиб балки при воздействии ударной нагрузки на примере консоли.

Общий подход к статическим расчетам на прочность при изгибе подробно изложен в статье «Расчет балки на изгиб – «вручную»!», где приведены уравнения общего вида, позволяющие произвести расчет на прочность балки с любыми опорами и при любых нагрузках.

Расчеты выполним в программе MS Excel. Вместо MS Excel можно воспользоваться программой OOo Calc из свободно распространяемого пакета Open Office.

С правилами форматирования ячеек листа Excel, которые применены в статьях этого блога, можно ознакомиться на странице «О блоге».

Расчет консольной балки при ударе.

Расчет на прочность, который мы будем выполнять, является приблизительным.

Во-первых, предполагаем, что вся потенциальная энергия груза, падающего с некоторой высоты, переходит в кинетическую энергию, которая при соприкосновении груза с балкой полностью переходит в потенциальную энергию деформации. В реальности часть энергии превращается в тепло.

Во-вторых, мы не будем учитывать в расчете массу балки. То есть прогиб балки под действием собственного веса примем равным нулю! (Чем меньше вес балки относительно веса груза, тем точнее результаты, полученные по рассматриваемой методике расчета!)

В-третьих, прогиб балки при ударе будем определять как прогиб от статического воздействия груза с весом больше реального веса груза на величину, определяемую коэффициентом динамичности. То есть силу при ударе найдем как сумму веса и силы инерции груза при торможении.

В-четвертых, считаем, что груз не отскакивает при ударе, а перемещается на величину динамического прогиба вместе с балкой. То есть удар абсолютно неупругий!

В-пятых, учтем ограничение, что ошибка расчета не превысит 8…12% только в случае, если рассчитанный коэффициент динамичности будет не более 12!

На рисунке, расположенном ниже, изображена  расчетная схема.

Составим в Excel программу и в качестве примера выполним расчет на прочность и определим прогиб балки круглого сечения. 3/32 =4580

Wx=π*d3/32

6. Допустимые напряжения материала балки (Ст3 сп5) при изгибе [σи] в Н/мм2 записываем

в ячейку D8: 235

7. Модуль упругости материала балки E в Н/мм2 вписываем

в ячейку D9: 215000

Результаты расчетов:

8. Максимальный изгибающий момент при статическом воздействии груза Mстx в Н*мм определяем

в ячейке D11: =D3*D5 =125000

Mстx=G*L

9. Максимальное напряжение при статическом воздействии груза σст в Н/мм2 вычисляем

в ячейке D12: =D11/D7 =27

σст=Mстx /Wx

10. Прогиб края консоли от статического воздействия груза Vстy в Н/мм2 рассчитываем

в ячейке D13: =D3*D5^3/3/D9/D6 =14,7

Vстy=G*L3/(3*E*Ix)

11. 0,5 =8,45

Kд=1+(1+2*h/Vстy)0,5

12. Максимальное напряжение при динамическом воздействии груза σд в Н/мм2 вычисляем

в ячейке D15: =D12*D14 =231

σд=σст*Kд

13. Прогиб балки в точке удара при динамическом воздействии груза Vдy в мм определяем

в ячейке D16: =D13*D14 =124,1

Vдy=Vстy*Kд

14. Коэффициент запаса прочности k вычисляем

в ячейке D17: =D8/D15 =1,02

k=[σи]/σд

Заключение.

Созданный расчет в Excel можно использовать для расчета на прочность при ударе консольных балок любого сечения. Для этого в исходных данных необходимо предварительно рассчитать  осевые моменты инерции и сопротивления соответствующего сечения.

Для балок с другими вариантами опор следует найти прогиб и напряжение от статического воздействия груза по соответствующим схеме опор формулам, затем по приведенной в п.11 формуле рассчитать коэффициент динамичности и определить прогиб балки в точке удара и максимальное напряжение в опасном сечении при ударе.

Опасное сечение – это сечение, в котором напряжение максимально и, соответственно, в котором начнется изгиб при достижении напряжением предельного значения. Определяется это сечение индивидуально для конкретных схем из эпюр и расчетов.

Коэффициент динамичности зависит – как следует из формулы – от высоты падения груза и величины прогиба при статическом приложении нагрузки. Чем больше высота падения, тем больше коэффициент динамичности. Это понятно, но почему этот коэффициент возрастает при уменьшении статического прогиба? Дело в том, что, чем меньше статический прогиб, тем жестче балка и тем быстрее остановится падающий груз после касания. Чем меньше время и путь торможения груза, тем больше ускорение (точнее торможение – ускорение с отрицательным знаком), а значит больше и сила инерции, которая по второму закону Ньютона, как известно, равна произведению массы тела на ускорение! Спрыгнуть на батут с высоты четырех метров можно легко, а вот на бетонный пол – чревато последствиями…

Ссылка на скачивание файла: raschet-na-prochnost-i-progib-balki-pri-udare (xls 20,0KB).

Другие статьи автора блога

На главную

Статьи с близкой тематикой

Отзывы

Формула прогиба балки — GeeksforGeeks

Прогиб балки определяется как явление, при котором некоторая нагрузка используется для отклонения тела. Другими словами, это отклонение балки в одном направлении при приложении к ней силы. Он оценивается путем интегрирования функции, описывающей наклон стержня под этой нагрузкой. Он прямо пропорционален приложенной силе и длине балки, но изменяется обратно пропорционально модулю Юнга и моменту инерции объекта. Обозначается символом D. Его единица измерения метры (м), а размерная формула дается [M 0 L 1 T 0 ].

Формула прогиба балки

D = WL 3 /3EI

Где,

  • Вт — приложенная сила, 90 025
  • L — длина балки,
  • E — модуль Юнга,
  • I – момент инерции.

Примеры задач

Задача 1. Рассчитать прогиб балки на длине 5 м, если к объекту, модуль Юнга которого равен 40 Н/м 9, приложена сила 250 Н.0003 2 и момент инерции 50 кг м 2 .

Решение:

Имеем,

W = 250

L = 5

E = 40

I = 50

Используя формулу, которую мы имеем,

D = WL 3 / 3EI

= (250 × 5 3 )/(3 × 40 × 50)

= 31250/6000

= 5,2 м

Задача 2: Рассчитайте прогиб балки на длине 4 м, если К объекту, модуль Юнга которого равен 60 Н/м 9 , приложена сила 200 Н.0003 2 и момент инерции 60 кг м 2 .

Решение:

Имеем,

W = 200

L = 4

E = 60

I = 60

Используя формулу, которую мы имеем,

D = WL 3 / 3EI

= (200 × 4 3 )/(3 × 60 × 60)

= 12800/10800

= 1,18 м

Задача 3 : Рассчитайте силу, приложенную при отклонении балки на длину 8 м составляет 0,78 м. Значение модуля Юнга 20 Н/м 2 , а момент инерции 45 кг·м 2 .

Решение:

Имеем,

D = 0,78

L = 8

E = 20

I = 45

Используя формулу, которую мы имеем,

D = WL 3 / 3EI

=> 0,78 = (Ш × 8 3 )/(3 × 20 × 45)

=> Ш = 2106/512

=> Ш = 4,11 Н

Задача 4: Рассчитать силу применяется, если прогиб балки на длине 2 м составляет 0,05 м. Значение модуля Юнга 30 Н/м 2 , а момент инерции 25 кг·м 2 .

Решение:

Имеем,

D = 0,05

L = 2

E = 30

I = 25

Используя формулу, которую мы имеем,

D = WL 3 / 3EI

=> 0,05 = (Ш × 2 3 )/(3 × 30 × 25)

=> Ш = 112,5/8

=> Ш = 14,06 Н

Задача 5. Вычислить модуль Юнга если прогиб балки на длине 2 м составляет 1,5 м при приложении силы 15 Н. Момент инерции 30 кг м 2 .

Решение:

Имеем,

D = 1,5

W = 15

L = 2

I = 30

Используя формулу, которую мы имеем,

D = WL 3 / 3EI

=> E = WL 3 /3ID

= (15 × 2 3 )/(3 × 30 × 1,5)

= 120/135

= 0 .88 Нм -2

Задача 6. Вычислить модуль Юнга, если прогиб балки на длине 6 м составляет 3 м при приложении силы 30 Н. Момент инерции 20 кг м 2 .

Решение:

Имеем,

D = 3

W = 30

L = 6

I = 20 90 009

Используя формулу, которую мы имеем,

D = WL 3 / 3EI

=> E = WL 3 /3ID

= (30 × 6 3 )/(3 × 20 × 3)

= 6480/180

= 36 Нм -2

Задача 7. Рассчитайте момент инерции, если прогиб балки на длине 8 м составляет 5 м при приложении силы 60 Н.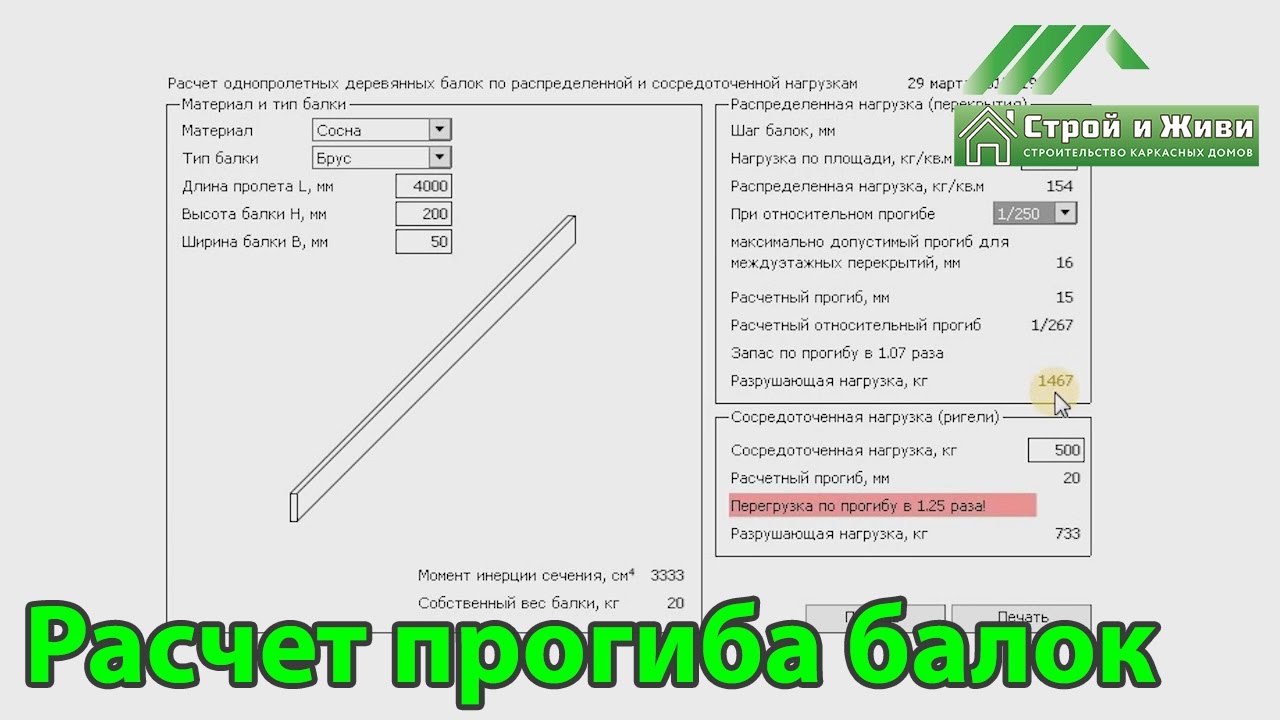 Значение модуля Юнга 12 Н/м 2 .

Решение:

Имеем,

D = 5

W = 60

L = 8

E = 12 90 009

Используя формулу, которую мы имеем,

D = WL 3 / 3EI

=> I = WL 3 /3ED

= (60 × 8 3 )/(3 × 12 × 5)

= 30720/180

= 1 70,67 кг м 2

Последнее обновление : 24 мая, 2022

Нравится статья

Сохранить статью

Матричные методы расчета прогибов консольных балок

Один из 4 107 отчетов в ряд: Технические примечания NACA доступны на этом сайте.

Показаны 1-4 из 59 страниц в этом отчете.

PDF-версия также доступна для скачивания.

Описание

Примечание, представляющее метод численного интегрирования для расчета прогиба балки в матричной форме, чтобы дать ему преимущества, присущие методу коэффициента влияния. Приведены примеры, показывающие, что использование взвешенных матриц сокращает время вычислений, необходимое для получения желаемой степени точности.

Физическое описание

58 стр. : больной.

Информация о создании

Бенскотер, Стэнли У. и Госсард, Майрон Л. Март 1949 года.

Контекст

Этот отчет входит в состав сборника под названием: Коллекция Национального консультативного комитета по аэронавтике и предоставлено отделом государственных документов библиотек ЕНТ к Электронная библиотека ЕНТ, цифровой репозиторий, размещенный на Библиотеки ЕНТ. Его просмотрели 1202 раза, из них 9в прошлом месяце. Более подробную информацию об этом отчете можно посмотреть ниже.


Поиск

ВОЗ

Люди и организации, связанные либо с созданием этого отчета, либо с его содержанием.

Авторы

  • Бенскотер, Стэнли У.
  • Госсард, Майрон Л.

Создатель

  • Авиационная лаборатория Лэнгли Национальный консультативный комитет по аэронавтике. Авиационная лаборатория Лэнгли

Предоставлено

Библиотеки ЕНТ Отдел государственных документов

Являясь одновременно федеральной и государственной депозитарной библиотекой, отдел государственных документов библиотек ЕНТ хранит миллионы единиц хранения в различных форматах.

Департамент является членом Программы партнерства по контенту FDLP и Аффилированного архива Национального архива.

О | Просмотрите этого партнера

Свяжитесь с нами

Исправления и проблемы Вопросы

Что

Описательная информация, помогающая идентифицировать этот отчет. Перейдите по ссылкам ниже, чтобы найти похожие элементы в электронной библиотеке.

Титулы

  • Основное название: Матричные методы расчета прогибов консольных балок
  • Название серии: Технические примечания НАКА

Описание

Примечание представляет метод численного интегрирования для расчета прогиба балки в матричной форме, чтобы дать ему преимущества, присущие методу коэффициента влияния. Приведены примеры, показывающие, что использование взвешенных матриц сокращает время вычислений, необходимое для получения желаемой степени точности.

Физическое описание

58 стр. : больной.

Предметы

Ключевые слова

  • прогибы консольной балки
  • матричные методы

Язык

  • Английский

Тип вещи

  • Отчет

Идентификатор

Уникальные идентификационные номера для этого отчета в электронной библиотеке или других системах.

  • Присоединение или местный контроль № : 93Р11802
  • URL-адрес : http://hdl.handle.net/2060/19930082512 Внешняя ссылка
  • Отчет № : НАКА-ТН-1827
  • Центр аэрокосмической информации, номер : 19930082512
  • Ключ архивного ресурса : ковчег:/67531/metadc55149

Сборники

Этот отчет является частью следующих сборников связанных материалов.

Коллекция Национального консультативного комитета по аэронавтике

Национальный консультативный комитет по аэронавтике (NACA) был федеральным агентством США, основанным 3 марта 1915 года для проведения, продвижения и институционализации авиационных исследований. 1 октября 1958 года агентство было распущено, а его активы и персонал переданы недавно созданному Национальному управлению по аэронавтике и исследованию космического пространства (НАСА).

О | Просмотрите эту коллекцию

Архив технических отчетов и библиотека изображений

Эта подборка материалов из Архива технических отчетов и библиотеки изображений (TRAIL) включает труднодоступные отчеты, опубликованные различными государственными учреждениями. Технические публикации содержат отчеты, изображения и технические описания исследований, выполненных для правительственных учреждений США. Темы варьируются от добычи полезных ископаемых, опреснения и радиации до более широких исследований в области физики, биологии и химии. Некоторые отчеты включают карты, раскладки, чертежи и другие материалы большого размера.

О | Просмотрите эту коллекцию

Какие обязанности у меня есть при использовании этого отчета?

Цифровые файлы

  • 59 файлы изображений доступны в нескольких размерах
  • 1 файл (. pdf)
  • API метаданных: описательные и загружаемые метаданные, доступные в других форматах

Когда

Даты и периоды времени, связанные с этим отчетом.

Дата создания

  • март 1949 г.

Добавлено в цифровую библиотеку ЕНТ

  • 14 ноября 2011 г., 22:26

Описание Последнее обновление

  • 3 декабря 2018 г. , 13:41

Статистика использования

Когда последний раз использовался этот отчет?

Вчера: 0

Последние 30 дней: 9

Всего использовано: 1 202

Дополнительная статистика

Взаимодействие с этим отчетом

Вот несколько советов, что делать дальше.

Поиск внутри

Поиск

Начать чтение

PDF-версия также доступна для скачивания.

  • Все форматы

Цитаты, права, повторное использование

  • Ссылаясь на этот отчет
  • Обязанности использования
  • Лицензирование и разрешения
  • Связывание и встраивание
  • Копии и репродукции

Международная структура взаимодействия изображений

Мы поддерживаем IIIF Презентация API

Распечатать/поделиться

Полезные ссылки в машиночитаемом формате.

Архивный ресурсный ключ (ARK)

  • ERC Запись: /ark:/67531/metadc55149/?
  • Заявление о стойкости: /ark:/67531/metadc55149/??

Международная структура совместимости изображений (IIIF)

  • IIIF Манифест: /арк:/67531/metadc55149/манифест/

Форматы метаданных

  • УНТЛ Формат: /ark:/67531/metadc55149/metadata. untl.xml
  • DC РДФ: /ark:/67531/metadc55149/metadata.dc.rdf
  • DC XML: /ark:/67531/metadc55149/metadata.dc.xml
  • OAI_DC : /oai/?verb=GetRecord&metadataPrefix=oai_dc&identifier=info:ark/67531/metadc55149
  • МЕТС : /ark:/67531/metadc55149/metadata. mets.xml
  • Документ OpenSearch: /арк:/67531/метадк55149/opensearch.xml

Изображений

  • Миниатюра: /ark:/67531/metadc55149/миниатюра/
  • Маленькое изображение: /арк:/67531/метадк55149/маленький/

URL-адреса

  • В текст: /ark:/67531/metadc55149/urls.