Как высчитать прямой угол в строительстве – Как проверить прямой угол без угольника

Содержание

Как проверить прямой угол без угольника

При отделочных работах и строительстве бывает нужна четкая геометрия: перпендикулярные стены и иные конструкции, требующие прямого угла в 90 градусов. Обыкновенный угольник не может позволить проверить или разметить углы со сторонами в несколько метров. Описываемый же метод превосходно подходит для разметки или проверки любых углов — длинна сторон не ограничена. Основной инструмент для измерений — рулетка.

Мы будем рассматривать точную разметку прямого угла, а также метод проверки уже размеченных углов на стенах и других объектах.

Теорема Пифагора

Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна квадрату длины гипотенузы. В виде формулы записывается это так:

a²+b²=c²

Стороны a и b — катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c — гипотенуза. Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем размечать прямые углы, а также проверять их.

Теорема Пифагора известна еще под названием «египетский треугольник». Это треугольник со сторонами 3, 4 и 5, причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 — ровно девяносто градусов. Проверим данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 — все сходится!

А теперь применим теорему на практике.

Проверка прямого угла

Начнем с самого простого — проверки прямого угла с помощью теоремы Пифагора. Самым частым примером в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены — это стены, расположенные друг к другу под прямым углом 90°.

Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно больше, но чтобы между отметками на стенах удобно было мерить диагональ. Например, мы отметили 2,5 метра (или 250 см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат (умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 — это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 — 3,9 метра должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали — проверяемый угол развернут и имеет отклонение от 90°.

Калькулятор расчета диагонали прямого угла

Извлечение квадратного корня никогда меня не привлекало — простому человеку не обойтись без калькулятора, к тому же, не на всех мобильных устройствах калькуляторы умеют извлекать его. Поэтому можно пользоваться упрощенным методом. Нужно лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у прямого угла со сторонами 2 м. — диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее. Хотя не стоит забывать о первоначальном способе совсем — в некоторых случаях он очень актуален.

Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см. в несколько миллиметров не даст отклонения в один целый градус.

Как проверить внешний угол? Проверка внешнего угла по сути не отличается, нужно лишь продлить линии каждой стены на полу (или земле, при помощи шнура) и получившийся внутренний угол измерить обычным способом.

Как разметить прямой угол рулеткой

Разметка может основываться как на общей теореме Пифагора, так и на принципе «египетского треугольника». Однако это только в теории линии просто чертятся на бумаге, «ловить» же все выбранные размеры растянутыми шнурами или линиями на полу — задача посложнее.

Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся последовательность разметки изображена на картинках ниже. Важно не забывать: диагональ 141,4 см. нужно умножать на количество метров в отрезке А-Б. Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах. Картинки увеличиваются по клику!

Как разметить острый угол

Гораздо реже возникает надобность в создании острых углов, в частности 45°. Для формирования подобных фигур формулы более сложные, однако это не самое проблематичное. Гораздо сложнее свести все линии, начерченные или натянутые шнурами — дело это непростое. Поэтому я предлагаю использовать упрощенный метод. Сначала размечается прямой угол 90°, а затем диагональ 141,4 делится на нужное количество равных частей. Например, чтобы получить 45°, диагональ нужно поделить пополам и от точки А провести линию через место деления. Таким образом мы получим два угла по 45 градусов. Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм вам понятен.

Собственно я рассказал все, что мог рассказать, надеюсь все изложил понятным языком и у вас больше не возникнет вопросов как размечать и проверять прямые углы. Стоит добавить, что уметь делать это должен любой отделочник или строитель, ведь полагаться на строительный угольник небольшого размера — непрофессионально.

Оцените публикацию:

Оценка: 4.5 (26 голосов)

Смотрите так же другие статьи

yserogo.ru

Самый простой способ как можно вычислить прямой угол подручными средствами

Каждый из нас учился в школе. Там человек получает огромное количество тех знаний, которые впоследствии могут понадобиться в жизни. Не все, конечно, могут в полной мере оценить значимость полученных знаний в школьной время, но сейчас речь не об этом.

Математика. Это страшное для многих слово, которое пугало достаточное количество школьников в своё время. Цифры, формулы и расчёты поддавались только самым пытливым. И с каждым годом этот сложный предмет становился всё сложнее и сложнее.

В старших классах появляется геометрия и всё становится ещё сложнее и непонятнее. Возможно, многие хоть раз в жизни, но в сердцах проклинали непонятную им науку и задавались вопросом, зачем это вообще нужно, и понадобится ли это в жизни.

Возможно, в повседневной жизни применить полученные в школе знания не удавалось. Вряд ли требовалось посреди белого дня высчитывать логарифмы и квадратные уравнения или доказывать, что две параллельные никогда не сойдутся. Но, где уж точно могут понадобиться знания геометрии и математике, так это в строительстве и при осуществлении ремонта.

В данной статье речь пойдёт о вычислении прямого угла, что требуется при строительстве зданий. Точность при возведении строений должна быть соблюдена в обязательном порядке, ведь только точные расчёты могут избавить от перекосов и нестабильности организации всего здания. Вычисление прямого угла при строительстве — не такой уж и трудный процесс, при котором потребуется знание и применение некоторых простых правил математики и геометрии. Подробнее об этом будет рассказано ниже.

Действительно ли прямой угол?

Возможно, некоторые читатели, ознакомившиеся с заголовком данной статьи, возразят, что прямой угол можно получить не всегда, и не всегда при строительстве используются именно ровные и точные прямые углы.

И, в принципе, они правы. Получить его весьма сложно, особенно если наблюдается неровность фундамента, на котором осуществляется строительство здания. Но, даже учитывая это обстоятельство, ни в коем случае нельзя делать вывод, что расчёт прямого угла можно делать просто «на глаз». В любом случае, если не представляется возможным вычислить идеальный прямой угол, то требуется достичь наиболее приближённого значения к идеальному углу в 90 градусов. И этого можно добиться, используя незатейливые инструменты и не самые сложные математические знания и познания в геометрии.

Что понадобится для определения прямого угла?

Итак, какие инструменты понадобится использовать для того, чтобы проверить прямой угол. Сразу стоит отметить, что никаких приборов и серьёзных инструментов для этого не потребуется. Нужно будет использовать весьма простые вещи, которые могут найтись практически в каждом хозяйстве. И даже если их не имеется под рукой, их с лёгкостью можно приобрести в магазине. С этим никаких трудностей не возникнет.

Для вычисления прямого угла нужно взять:

Карандаш;
Строительную рулетку.

И всё. Вот так вот всё просто.

Как можно вычислить прямой угол?

Итак, в этой статье будет описан принцип 3-4-5 при определении угла в 90 градусов. Ничего сложного в этом нет. Потребуется просто лишь чуть пораскинуть мозгами и вникнуть во все расчёты, которые смогут помочь в проверке угла.

Итак, нужно обозначить следующие шаги:

Для начала стоит разобраться в том, почему принцип так обозначен — 3-4-5. Это не просто набор цифр, это величина сторон прямоугольного треугольника. Теорема Пифагора гласит: квадрат гипотенузы равен сумме квадратов катетов. Цифры 3-4-5 очень подходят для проверки этого простого правила геометрии: 3*3+4*4=5*5, то есть 9+16=25. Именно эти цифры и будут использоваться в дальнейших вычислениях;
Итак, потребуется для начала отмерить 3 метра от угла вдоль одной из стен. Тут следует отметить, что 3 метра — предпочтительная длина замера, но в том случае, если комната маленькая, можно отметить всего 30 сантиметров. В месте замера нужно сделать отметку;
В принципе, можно использовать и другие цифры, но рекомендуется в любом случае использовать пропорционально увеличенные числа, например: 9-12-15 или же 30-40-50;
После проделанного предварительного замера нужно отмерить 4 метра вдоль другой стены, тоже от угла. Ну или соответственно 40 сантиметров, если комната маленькая. Нужно сделать отметку;
Теперь остаётся сделать последнее действие, по которому уже можно судить прямой угол или нет. От измеряющего потребуется измерить расстояние между сделанными отметками. По полученным данным можно будет сделать определённые выводы:
- Если расстояние между отметками будет равняться 5 метрам ровно, это будет означать, что угол является прямым;
- В том случае, если измеренное расстояние будет равняться меньше 5 метров, угол будет меньше, чем 90 градусов;
- Ну и, наконец, величина угла будет составлять больше 90 градусов, если полученная величина замера будет равняться больше 5 метров.

Вывод

Вот, как просто можно вычислить прямой угол без использования каких-либо строительных инструментов и приборов. Использовать можно самое простое, но в то же время весьма действенное средство, которое вкупе с использованием имеющихся знаний и бесхитростных расчётов, может помочь произвести измерение.

При использовании предложенных величин, ключевым становится финальный замер между двумя отметками, которые были сделаны ранее. Расстояние, которое будет равняться точно 5 метрам, покажется, что он прямой. Если же величина будет больше или меньше 5 метров, это будет означать, что он прямым не является.

bane.guru

Полезная геометрия | Наука и жизнь

В школе мы несколько лет подряд прилежно изучаем геометрию. Но не зря ли мы тратим время? Чем может помочь геометрия в жизни? Измерить расстояние от точки до точки, вычислить площадь или объём предмета и только? Нет, конечно. Законы геометрии применимы буквально на каждом шагу. Просто нужно знать, как ими воспользоваться.

Вешаем зеркало

Вы решили повесить в прихожей зеркало. Тут же возникает вопрос: какой минимальной высоты должно быть зеркало, чтобы человек среднего роста мог видеть себя в нём целиком? И ещё: имеет ли при этом значение размер помещения, где будет висеть зеркало? Решение. Предмет и его отражение симметричны относительно плоскости зеркала. Построим в нём изображение человека (рис. 1): АВ — человек, А₁В₁ — его изображение, точка С — глаз, DE — зеркало. Из рисунка видно, что минимальная высота зеркала приблизительно равна половине роста человека, считая от уровня глаз. При этом высота Е нижнего края зеркала от пола должна быть вдвое меньше расстояния от пола до глаз. Легко понять, что, на каком бы расстоянии от такого зеркала ни находился человек, он сможет увидеть себя в нём с головы до ног, значит, размер помещения значения не имеет.

Завариваем чай

Перед вами стеклянные чайники четырёх моделей одинаковой вместимости (рис. 2). В каком чайнике заваренный чай останется тёплым дольше? Решение. Из курса физики известно, что время охлаждения пропорционально площади поверхности тела. Значит, чем меньше поверхность чайника, тем дольше остывает чай. Самая маленькая площадь поверхности у четвёртого чайника, так как его форма близка к сфере (S = d²).

Выдерживаем прямые углы

Если вы решили склеить коробку, сделать шкатулку или выложить плитку, важно, чтобы все детали были точными прямоугольниками или квадратами. В противном случае всё пойдёт наперекосяк. Как проверить, имеет ли деталь нужную «геометрию»? Решение. Чтобы проверить, у всех ли деталей, с которыми вы работаете, прямые углы и одинаковые линейные размеры, можно использовать строи-тельный угольник (рис. 3), а можно применить знания по геометрии. Убедитесь в том, что противоположные стороны четырёхугольника равны и при этом диагонали тоже имеют одинаковую длину. Как вы и сами знаете, сделать это можно с помощью линейки. Но вот вопрос: обязательно ли проверять и стороны и диагонали? Геометрия утверждает, что да! Например, на рис. 4 диагонали в четырёхугольнике слева равны, но очевидно, что его углы совсем не прямые. А в четырёхугольнике справа противоположные стороны равны, но это тоже не прямоугольник. Для проверки прямоугольности геометрия ещё советует убедиться в равенстве всех четырёх отрезков, на которые разбиваются диагонали в точке их пересечения.

Строим прямой угол на земле

Известен старинный способ постро-ения прямого угла на поверхности земли. Его использовали ещё древние египтяне. Они строили прямой угол с помощью обычной верёвки, на которой через равные расстояния завязаны тринадцать узелков. Чтобы отрезки на верёвке были одинаковые, узелки завязывали вокруг колышков, вбитых в землю на равном расстоянии друг от друга. В чём состоит этот «верёвочный» способ? Решение. В древности при закладке храма такую верёвку с узелками использовали для определения направлений его стен. Концы верёвки на месте крайних узелков связывали, а затем натягивали её на три колышка так, как показано на рис. 5. Стороны при этом имели соотношение 3:4:5. В таком треугольнике один из углов получается прямым. Впоследствии этот факт был доказан в теореме Пифагора. Поэтому первых геометров называли ещё «натягивателями верёвок». Нужно отметить, что таким способом построения прямого угла на местности пользуются и сегодня, например при закладке фундамента небольшого строения.

Проверяем перпендикулярность стен

Как проверить, перпендикулярны ли друг другу соседние стены в комнате, воспользовавшись верёвкой с узелками из предыдущей задачи? Решение. Если предположить, что стены в комнате вертикальны, а пол горизонтален, то проверку проводят так. От точки на полу в углу между стенами откладывают отрезки длиной 3 и 4 единицы (рис. 6). Если стены перпендикулярны, то расстояние между концами отрезков будет равно 5 единицам, так как построенный тре-угольник со сторонами 3, 4, 5 — прямоугольный.

Отмеряем нужный объём

Часто в рецептуре того или иного блюда требуется взять четверть (или половину) стакана жидкости, муки либо какого-либо другого продукта. Как отмерить такой объём с наибольшей точностью, не прибегая к дополнительным измерительным средствам? Решение. Воспользуемся стаканом цилиндрической формы — это важно для точности измерений. Чтобы отмерить четверть стакана жидкости, надо из наполненного стакана вылить столько, чтобы оставшаяся в нём жидкость закрыла половину дна (рис. 7). Она займёт примерно четверть объёма стакана-цилиндра. Аналогично поступаем, если надо отмерить половину стакана. Наклоняем стакан так, чтобы оставшаяся в нём жидкость закрыла всё дно (рис. 8). А можно ли геометрическим способом узнать объём бутылки? Конечно! Для этого надо заполнить бутылку водой чуть меньше чем наполовину (рис. 9, слева) и измерить объём воды, умножив площадь дна бутылки на высоту налитой в неё воды (напомним, что объём цилиндра вычисляется как произведение площади основания на высоту). Затем нужно перевернуть бутылку горлышком вниз так, чтобы вода не вытекла, и измерить объём верхней цилиндрической части бутылки, оставшейся пустой (рис. 9, справа). Полный объём бутылки равен сумме найденных объёмов. Для точности можно учесть толщину стенок бутылки.

Укрепляем калитку

Прямоугольная калитка (рис. 10, слева) со временем расшатывается и становится похожей на параллело-грамм. Этого можно избежать, прибив к ней ещё одну планку. Только надо знать, как это сделать. Решение. Выбор такого положения планки, как показано на рис. 10, справа, основан на свойстве жёсткости треугольника. Оно гласит: существует единственный треугольник с заданными длинами сторон. Планка и есть гипотенуза такого треугольника.

Выбираем табурет

Если вы решили предыдущую задачу, то без труда определите, на какой табурет (рис. 11) можно сесть без риска оказаться на полу. Решение. Безопасный табурет изображён на правой картинке, так как его сиденье и ножки образуют треугольник.

Исправляем ошибку кроя

Предположим, вам нужно вырезать для аппликации два разносторонних треугольника из цветной бумаги — «левый» и «правый». Вы случайно вырезали их одинаковыми — оба «левые». Можно ли, не используя новый кусок бумаги, исправить ошибку? Решение. Для исправления ошибки вы можете разрезать один из треугольников, например так, как показано на рис. 12, а затем сложить из него нужный треугольник.

Находим середину

Как без всяких измерений найти середину негнущегося прута, доски или металлического стержня? Решение. Можно отмерить размеры стержня на шнуре, затем сложить его пополам и отложить полученную длину. А можно воспользоваться геометрическим построением середины отрезка с помощью циркуля и линейки, если, конечно, размеры позволяют это сделать. Ещё более рациональное решение даёт физика. Середину однородного стержня легко найти, используя понятие центра тяжести (рис. 13).

Наука и жизнь // Иллюстрации

‹

›

www.nkj.ru

Как применять правило 3 4 5 при строительстве прямых углов Как? Так!

Содержимое:

1 метода:

Одна из проблем при построении угла или треугольника – сделать угол прямым. Конечно, угол не обязательно должен быть идеально прямым, но при проектировании нужно постараться сделать так, чтобы максимально приблизить угол к значению 90 градусов. Если не получится, есть вероятность, что ковровое покрытие будет положено неровно относительно какой-либо стены. Метод 3-4-5 полезен для небольших строительных проектов, чтобы все покрытия были ровными и совпадали друг с другом, как и планировалось.

Шаги

Как пользоваться правилом 3-4-5

1 Поймите, в чем суть правила 3-4-5. Если у треугольника есть три стороны со значениями 3, 4 и 5 см (или кратное им значение), это прямоугольный треугольник, угол между сторонами с меньшими значениями составляет 90 градусов. Если у вас получилось построить треугольник, исходя из значений угла, то можно точно сказать, что угол прямоугольный. Это правило основано на : A² + B² = C² (в прямоугольном треугольнике). Где С – самая длинная сторона (гипотенуза), А и В –остальные стороны (катеты).^{Правило 3-4-5 очень удобно проверить благодаря целым числам. Итак, опираясь на математические расчеты: 3² + 4² = 9 + 16 = 25 = 5².}
2 Отмерьте от угла 3 см (или 3 м) на одной стороне. Можно взять любую меру длины. Пометьте отмеренный участок точкой.
- Можно умножить каждое число на одно и то же число – и это правило все равно сработает. Например, это правило будет работать для треугольника со сторонами 30-40-50 сантиметров или метров. Если у вас большая комната, можно использовать следующие числа: 9-12-15, 6-8-10 метров.
3 Отмерьте четыре метра (или длину со значением, которое кратно четырем) на другой стороне. То же самое, если у вас получится сделать треугольник, то угол между этими двумя сторонами будет равен 90 градусам. Снова пометьте отмеренный участок точкой.
4 Теперь измерьте расстояние между этими двумя метками. Если расстояние кратно пяти, то можно точно сказать, что угол составляет 90 градусов.^{Если расстояние меньше, чем 5 единиц (метров), значит, угол острый (меньше 90 градусов). Если есть такая возможность, нужно немного раздвинуть стороны, образующие этот угол.
Если расстояние между метками составляет больше 5 единиц (метров), значит, угол тупой (то есть больше 90 градусов). Если есть такая возможность, нужно свести стороны, образующие угол, поближе друг к другу, чтобы угол получился прямым. Строя прямой угол, можно использовать прямой угол рамки.
Получив прямой угол в 90 градусов, можно проверить остальные углы комнаты, чтобы убедиться в том, что они прямые.}

Советы

Этот метод считается более точным, чем с использованием специального инструмента угольника, потому что этот инструмент может быть слишком мал для измерения на больших расстояниях и площадях.
Чем большую меру измерения вы возьмете, тем точнее будет результат.

Что вам понадобится

Рулетка
Карандаш

Прислал: Cr1stal . 2017-11-09 22:48:20

kak-otvet.imysite.ru

Разметка фундамента с помощью штанов и паутины — просто о сложном

Чтобы дом стоял прочно на фундаменте, необходимо произвести тщательную разметку котлована и обеспечить восстановление границ периметра по окончании рытья траншей. Особенно это важно при использовании землеройной техники. По линиям разметки будет установлена опалубка, уложена арматура и залит раствор. Исправление ошибок, когда бетон затвердел, сложный и затратный процесс, его лучше избежать. В распоряжении строителя есть геодезические приборы, но можно обойтись простейшими инструментами и традиционными методами построения прямоугольников на земельном участке.

Гладко было на бумаге: делаем чертёж разметки

На первый взгляд, перенести план фундамента с чертежа на участок — задача простая. Вбил первый колышек и отмеряй от него. Как показывает практика, построить идеальный прямоугольник не у всех получается с первого раза, потому что:

поверхность земли не является ровной;
на расстояниях более 5 метров отклонения в доли градусов приводят к значительным погрешностям.

Ошибки выявляют контрольным замером сторон и диагоналей, когда выясняется:

противоположные стороны равны, а диагонали нет — получился параллелограмм;
диагонали равны, две стороны равны, а две другие нет — это признак равнобокой трапеции.

Вроде бы на глаз всё верно, но ошибки разметки на 10–20 см повлекут дальнейшие искажения, ведь фундамент — основа строения. Пройдут земляные работы, во время которых не исключены незначительные отклонения, особенно при использовании экскаватора и другой тяжёлой техники.

Выручает прямой угол. В параллелограмме и в равнобокой трапеции нет прямых углов. Ни одного. Задача сводится к тому, чтобы линии разметки были перпендикулярны друг другу. Школьный транспортир и треугольник не годятся. Они для чертежей на бумаге. Для топографической разметки потребуются другие инструменты.

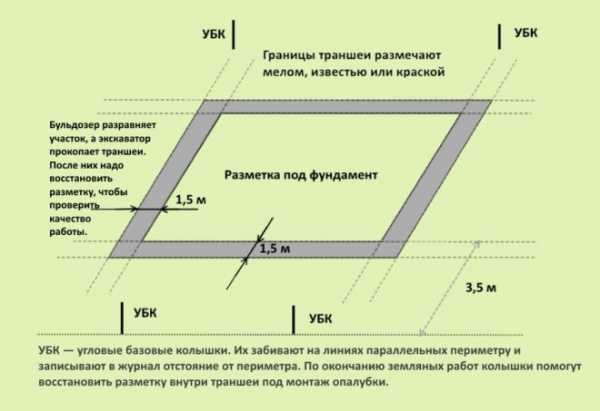
Разметку котлована необходимо произвести до начала земляных работ

Способы разметки

Геометрия зародилась в античные времена, как наука построения фигур на плоскости для вычисления площади и объёма. Тогда же разработали основные аксиомы, теоремы и правила. Одна из теорем принадлежит Пифагору. Не одно тысячелетие она служит для построения прямых углов.

Пифагоровы штаны

Пифагор доказал теорему, построив на каждой стороне прямоугольного треугольника квадрат. Фигура получила шуточное название «Пифагоровы штаны».

Квадрат гипотенузы равен сумме квадратов катетов.

Самая известная иллюстрация теоремы — цифровой ряд 3, 4, 5.

Действительно, 3² + 4² = 5². Если взять три отрезки длиной 3, 4, 5 или равно кратные этим значениям, то при соединении таких отрезков получится прямоугольный треугольник. Разумеется, можно подобрать и другие числа, но на практике именно 3, 4, 5 оказались самыми удобными для построений.

Когда концы трёх отрезков совпадут, получится прямоугольный треугольник

Построение легко выполнить с помощью реек, подбирая длину под соотношение 3 : 4 : 5. Например, три рейки: одна 60 см, вторая 80 см, третья 1 метр. Если закрепить их концы, то стороны 60 и 80 см будут катетами, вдоль которых натягивают леску или шнур, обозначая границы траншеи. А гипотенуза в 1 м обеспечит общую прочность инструмента. Для этой же цели можно использовать бечёвку или шнур, длиной более 12 м. На бечёвке вяжут узелки через 3, 4 и 5 м и соединяют начало первого отрезка с концом третьего. В каждый узелок пропускают тонкий штырь. Теперь, если, удерживая за штыри, равномерно натянуть стороны, получим треугольник, подобный тому, который делали и в примере с рейками.

Видео: контроль разметки теоремой Пифагора

Метод паутины

Применение верёвочного треугольника привело к развитию метода паутины. В этом случае вяжут сразу прямоугольник с диагоналями и растягивают его на участке. В идеале длины отрезков бечёвки (шнура, шпагата) должны совпадать с размерами сторон и диагоналей фундамента, что практически редко осуществимо. Лучше взять оптимальное соотношение 6 : 8 : 10 метров для построения прямоугольников 6 х 8 м.

Метод паутины один из самых простых

При использовании «паутины» очень важно правильно выбрать бечёвку. Она должна быть свита из прядей, не изменяющих длину при натяжении. Такими свойствами обладают лён, пенька, джут, копра. Многие синтетические волокна, например, нейлон и капрон вытягиваются наподобие резины. Такой материал не подходит. Для надёжности делают контрольные замеры отрезка, увеличивая натяжение, чтобы убедиться в приемлемости бечёвки для вязки «паутины».

Видео: разметка с помощью двух рулеток

Метод радиусов и засечек

Прямоугольник можно построить засечками, проводя окружности радиусами равными длинам катетов и диагоналей. Вместо циркуля берут строительную 10-метровую рулетку. У неё есть ушко в начале ленты, куда вставляют заострённый штырь. Работать лучше втроём. Один держит рулетку на угловом колышке, второй прочерчивает дуги, третий контролирует натяжение ленты.

Видео: радиусы и засечки

Разметка фундамента своими руками

Знание методов недостаточно для точного нанесения границ фундамента. От первого вбитого колышка должны отойти не просто две перпендикулярные линии. Их направление определяется границами участка с учётом других объектов. Например, СНиП 30–02–97 требует, чтобы крайняя точка возводимого строения была не ближе 3 м к забору. Если крыша будет нависать 1 м над фундаментом, соответственно от фундамента до забора должно быть более 4 м.

В самом начале разметки фундамента важно выставить прямой угол между предполагаемыми стенами. Если этого не сделать сразу, то упущение может привести к плачевным результатам.
Дятька
https://www.forumhouse.ru/articles/house/5698

Для выверки границ котлована необязательно применять геодезические приборы. Можно обойтись простыми самодельными инструментами: размеченной верёвкой, треугольником из реек, нивелиром с уровнем, лазерной указкой, рулеткой.

Фотогалерея: инструменты для разметки фундамента

: Стороны 0,6 х 0,8 х 1,0 м обеспечат прямой угол

: Уровень с лазерной указкой — нивелир готов к работе

: Узелки через 3, 4 и 5 м позволят построить прямоугольный треугольник

: Для корректной работы с визиром потребуется вешка — тонкая высокая рейка

Разметку выполняют в следующей последовательности:

Сверяясь со СНиП 30–02–97, отмеряют допустимые расстояния от забора, улицы и других строений и определяют границы участка под разметку.
Забивают первый колышек. Пользуясь одним из методов, строят прямой угол.
От вершины угла отмеряют линии на длину сторон прямоугольника. Вбивают колышки.
От каждого колышка чертят прямой угол. На пересечении сторон забивают четвёртый колышек. Вершины прямоугольника построены. Определены внешние границы периметра разметки.
Производят контрольный замер противоположных сторон и диагоналей. Если равенство нарушено, проверяют, какой из углов не является прямым. Исправляют ошибку.

На следующем этапе нужно обозначить внутренние и внешние границы траншеи, а при неодходимости — линии, по которым будет возводиться опалубка внутри траншей.

Потребуются тонкие шнуры (шпагат, леска, капроновая нить, стальная проволока) и мерная скамеечка. В обиходе скамеечку также называют доской, рамой, обноской.

Мерная скамеечка или обноска служит для крепления шнуров, отмечающих границы фундамента

Конструкция скамеечки может быть самой разной, чаще всего её выполняют в виде небольших козел. Как сколотить — это на усмотрение домашнего мастера. Главное, чтобы она прочно стояла на своём месте и выдерживала натяжение шнуров.

Последовательность второго этапа:

Устанавливают скамеечки на некотором расстоянии за пределами разметки, чтобы они не создавали помехи земляным работам.
Вдоль разметки выкладывают шнуры, крепят их на скамеечках и натягивают как струны.
Если внутри траншеи будет монтироваться опалубка, то соответственно на скамеечке закрепят дополнительные струны. Внутренними отметят линии опалубки, внешними — границы траншеи.

По внешним шнурам проведут земляные работы, по внутренним возведут опалубку

Когда рытьё траншеи производится вручную, шнуры располагают невысоко над землёй, чтобы они не мешали землекопам и в то же время позволяли контролировать работу. Дополнительно используют отвес, проверяя вертикальность профиля траншеи.

При использовании экскаватора поверх шнуров сыпят контрастный порошок — мел, известь, цемент, золу либо прочерчивают контур краской. Шнуры убирают, а мерные скамеечки метят флажками, чтобы водитель техники случайно не наехал. После того как экскаватор закончит рытьё, шнуры снова натягивают и проверяю корректность выполненных работ.

Видео: разметка своими руками

Арсенал разметчика можно пополнить другими инструментами. В комплекте столярных или токарных наборов найдётся угольник. Закрепить на нём уровень и две лазерные указки — точность будет не хуже, чем у теодолита. В школьных кабинетах математики есть транспортиры и треугольники таких размеров, с которыми можно работать непосредственно на участке для выверки прямых углов. Туристы, особенно те, кто увлекается водными походами, знакомы с азимутальным кругом и пеленгатором. Деревянная крестовина, на концах которой закреплены саморезы в качестве прицелов, станет отличным визиром, если тщательно контролировать уровнем и отвесом её положение в горизонтальной и вертикальной плоскостях.

Вдоль линий разметки натянуты шнуры, закрепленные на мерных скамеечках

Знание основ геометрии и методов нанесения разметки простейшими инструментами позволит без труда подготовить участок перед земляными работами. Однако следует помнить золотое правило — семь раз отмерь, а потом копай. Контрольная проверка сторон, диагоналей и углов — необходимое условие, при котором будет обеспечено точное соответствие границ фундамента с планом строения.

kakpostroit.su

как найти прямой угол при разметке земли под теплицу

По сути то же можно проделать рулеткой. Берете одну сторону, например 4м и из ее концов проводите дуги радиусом 3м и 5 м. Точка пересечения — угол прямоугольного треугольника.

Согласен с Андреем… редко когда прибегали при разметке простейших объектов к теодолиту.. . Обычно при помощи теоремы Пифагора и двух рулеток отмеряли прямой угол. 3м и 4м катеты и 5м гипотенуза. Сперва откладуешь один катет, забивая колы (к примеру 3м) в нужном направлении, затем от колов соединяешь две рулетки: на одной 4м должно совпадать с 5м другой.. . или методом «циркуля», как описал Андрей. так что школьных знаний геометрии вполне достаточно для таких простых вещей.

Все гениальное просто.

без всяких теорем! меряешь рулеткой, делаешь одинаковые диагонали и все! в прямоугольнике с одинаковыми диагонали будут углы 90 град. иначе быть н может!

Жаль, не умею пока здесь рисовать. Из построения угла в школьной геометрии. Проводите длинную линию, по углам вставьте палки, к каждой — веревку длины больше половины линии привяжите, к свободному концу палки другую палочку, и как циркулем делаете на земле дугу с каждой стороны до пересечения дуг. Соединяете пересечение с серединой нарисованной линии. вот Вам и два прямых угла. В вашем конкретном случае чтобы угол получился где надо, от угла будущей теплицы проведите прямую по обе его стороны на равном расстоянии в направлении будущей ее стены. Успеха!

Да че заморачиваться, у прямоугольника диагонали должны быть равны- от этого и пляшите, бечевка, колышки-вот Вам идеальные углы и стороны.

Одна сторона 80, другая 60, между ними метр, соответственно увеличиваешь стороны в 2 раза получаешь 2м….

теорема пифагора: квадрат гипотеузы (диагональ) равен сумме квадратов катета (длина и ширина теплицы)

touch.otvet.mail.ru

Как сделать прямой угол между стенами.

Обычно прямая линия вдоль одной из 2 самых широких стен принимается за основу, если нет каких либо других точек отсчета. В этом случае площадь помещения при дальнейшей отделке будет уменьшена минимально.

Отмерьте от одного из углов с помощью рулетки 1 м и поставьте отметку на линии. Сделайте то же самое на перпендикулярной (возможно, не совсем) линии.

Соедините полученные отметки так, чтобы получился треугольник.

Измерьте расстояние между полученными отметками.

Если стены перпендикулярные это расстояние должно равняться ~ 1.414 м более точно 1.41421356 м, но такая точность вам не понадобится.

Если расстояние (гипотенуза треугольника) больше, то у Вас вместо прямого угла между стенами тупой. Для того, чтобы получить прямой угол, приложите начало рулетки к точке пересечения линий в углу и нарисуйте небольшую дугу радиусом 1 м. Затем приложите начало рулетки к отметке на линии вдоль стены принятой за основу и нарисуйте небольшую дугу радиусом 1.414 м. Проведите через точку пересечения дуг и точку пересечения линий в углу прямую линию. Эта новая линия и будет контуром стены. Если это для Вас слишком сложно, то просто отмерьте на гипотенузе 1.414 м от отметки у той стены которую вы приняли за основу. Проведите прямую линию через полученную отметку и точку пересечения линий в углу. В этом случае Вы получите не прямой угол, но все же намного ближе к прямому, чем тот который был.

Если расстояние (гипотенуза треугольника) меньше, то у Вас вместо прямого угла между стенами острый. Для того, чтобы получить прямой угол, отступите от отметки на линии вдоль стены, принятой за основу, несколько сантиметров. Нарисуйте на полу небольшие дуги по принципу, изложенному в предыдущем пункте. Полученную линию можно перенести ближе к стене. Главное условие — отметки выпирающих участков стены должны остаться между новой линией и стеной.

Если Вы не совсем поняли этот текст, то рисунок поможет Вам лучше разобраться:

От полученных 2 сторон прямоугольника методом параллельного переноса определяются оставшиеся 2 стороны.

doctorlom.com