Построение эпюр поперечных сил и изгибающих моментов

Похожие презентации:

Грузоподъемные машины. (Лекция 4.1.2)

Зубчатые передачи

Гидравлический домкрат в быту

Детали машин и основы конструирования

Газораспределительный механизм

Свайные фундаменты. Классификация. (Лекция 6)

Ременные передачи

Редукторы

Техническая механика. Червячные передачи

Фрезерные станки. (Тема 6)

ТЕМА «ПОСТРОЕНИЕ ЭПЮР
ПОПЕРЕЧНЫХ СИЛ И ИЗГИБАЮЩИХ
МОМЕНТОВ»
Рассмотрим тело произвольной формы в “спокойном”, ненагруженном
состоянии. Между его частицами всегда существуют силы
взаимодействия,
которые стремятся сохранить его как единое целое, то есть препятствуют
изменению взаимного расположения частиц. При нагружении тела
произвольной внешней нагрузкой силы взаимодействия между
частицами
изменяются, появляются дополнительные силы взаимодействия, которые
приводят к изменению взаимного расположения частиц тела, то есть к

его
деформации.
Эти дополнительные силы взаимодействия называются внутренними
силами упругости (ВСУ) и являются предметом изучения сопротивления
материалов.
Анализ характера распределения внутренних сил упругости
осуществляется при помощи метода сечений.
Эпю́ра (фр. epure — чертёж) — особый вид
графика, показывающий распределение
величины нагрузки на объект.
Эпюру можно построить на основании
следующих параметров: внутренних сил
(продольных и поперечных), крутящих и
изгибающих моментов, напряжений
(нормальных и касательных) и перемещений.
АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ
1. Определение реакций опор балки и выполнение
проверки;
2. Определение поперечных сил (Q) и построение
эпюры;
3. Определение изгибающих моментов (Мизг) и
построение эпюры;
4. Проверка правильности построения эпюр.
ОПРЕДЕЛЕНИЕ РЕАКЦИЙ ОПОР БАЛКИ
ОСНОВНАЯ ОШИБКА
АССОЦИАЦИИ ПО СХОДСТВУ, ПО КОНТРАСТУ, ПО СМЕЖНОСТИ В
ПРОСТРАНСТВЕ И ВРЕМЕНИ, ПО ПРИЧИННО-СЛЕДСТВЕННЫМ СВЯЗЯМ.
НОГА + БОТИНОК
ОПОРА + РЕАКЦИЯ
АССОЦИАЦИЯ ПО СХОДСТВУ
ВЕРНО
НЕВЕРНО
УРАВНЕНИЯ РАВНОВЕСИЯ
∑Fix= 0
∑МА= 0
∑МВ= 0
ПРОВЕРКА
∑Fiу= 0
ПОПЕРЕЧНАЯ СИЛА (Q, кН)
Q
Q
ПРАВИЛЬНОСТЬ ПОСТРОЕНИЯ ЭПЮРЫ МОЖНО ПРОВЕРИТЬ ПО
СКАЧКАМ, КОТОРЫЕ ВОЗНИКАЮТ ТАМ, ГДЕ ПРИЛОЖЕНЫ
СОСРЕДОТОЧЕННЫЕ СИЛЫ.
СКАЧОК = ЗНАЧЕНИЮ F
ИЗГИБАЮЩИЙ МОМЕНТ (МИЗГ, КН*М)
На эпюре изгибающих моментов скачок
возникает там, где приложена пара сил
ПРОВЕРКА ПРАВИЛЬНОСТИ ПОСТРОЕНИЯ ЭПЮР
Сопоставление эпюр поперечных сил и
изгибающих моментов
Q>0
Q<0
Q=0
Мизг возрастает
Мизг убывает
Мизг постоянен
Переход
от Q>0 к Q<0
Мизг = max
Переход
от
Q<0 к Q>0
Мизг = min
ЗАДАЧА
НА ДВУХ ОПОРНУЮ БАЛКУ ДЕЙСТВУЕТ
СОСРЕДОТОЧЕННАЯ СИЛА F=30 Н. ПОСТРОИТЬ
ЭПЮРЫ ПОПЕРЕЧНЫХ СИЛ И ИЗГИБАЮЩИХ
МОМЕНТОВ ДЛЯ БАЛКИ, ИЗОБРАЖЕННОЙ НА
РИСУНКЕ. ДОПУСКАЕМОЕ НОРМАЛЬНОЕ
НАПРЯЖЕНИЕ [Σ]= 160 МПА.
Решение
1) Наносим оси координат;
2) Наносим реакции в опорах;
3) Определяем реакции в
опорах из
условия
равновесия плоских сил;
4) Проверка;
5) Строим эпюру поперечных
сил Qу;
6) Строим эпюру изгибающих
моментов Ми;
7) Определяем размер
двутавровой балки;
8) В соответствии с
сортаментом
принимаем размер
двутавра.
Положительные значения
откладываются (в выбранном
масштабе) над осью эпюры,
отрицательные — под осью.
2. Правила построения эпюр
:
При сосредоточенной
нагрузке эпюра
поперечных сил Qу
изображается прямой,
параллельно оси балки,
а эпюра изгибающих
моментов Ми наклонной
прямой
Правила построения эпюр
При
сосредоточенной
нагрузке эпюра
поперечных сил Q
образует скачок,
численно равный
значению самой
силы
:
Правила построения
эпюр
:
При равномернораспределенной
нагрузке эпюра
поперечных сил Q
изображается
наклонной прямой, а
эпюра изгибающих
моментов М параболой
Правила построения
эпюр:
Если на участках Qу<0,
то изгибающий момент
убывает;
если на участках Qу>0,
то изгибающий момент
возрастает;
если на участках Qу=0,
то изгибающий момент
постоянен.
Правила построения эпюр
:
Сосредоточенный
внешний момент M
никак не отражается на
эпюре поперечных сил
Q.
На эпюре изгибающих
моментов М, в месте
приложения
этого
момента,
образуется
скачок, равный его
величине.
Решите задачу
НА ДВУХ ОПОРНУЮ БАЛКУ ДЕЙСТВУЮТ
СОСРЕДОТОЧЕННЫЕ СИЛЫ F1=40 Н И F2=20 Н . ПОСТРОИТЬ
ЭПЮРЫ ПОПЕРЕЧНЫХ СИЛ И ИЗГИБАЮЩИХ МОМЕНТОВ
ДЛЯ БАЛКИ, ИЗОБРАЖЕННОЙ НА РИСУНКЕ.
ДОПУСКАЕМОЕ НОРМАЛЬНОЕ НАПРЯЖЕНИЕ [Σ]=160 МПА.
Решите задачу
НА ДВУХ ОПОРНУЮ БАЛКУ ДЕЙСТВУЕТ СОСРЕДОТОЧЕННАЯ СИЛА F=22 Н .
ПОСТРОИТЬ ЭПЮРЫ ПОПЕРЕЧНЫХ СИЛ И ИЗГИБАЮЩИХ МОМЕНТОВ ДЛЯ
БАЛКИ, ИЗОБРАЖЕННОЙ НА РИСУНКЕ. ДОПУСКАЕМОЕ НОРМАЛЬНОЕ
НАПРЯЖЕНИЕ [Σ]=160 МПА.

English     Русский Правила

Построение окончательной эпюры изгибающих моментов. — Студопедия

Поделись с друзьями: 

После вычисления единичных коэффициентов и грузовых членов канонических уравнений эти уравнения решают.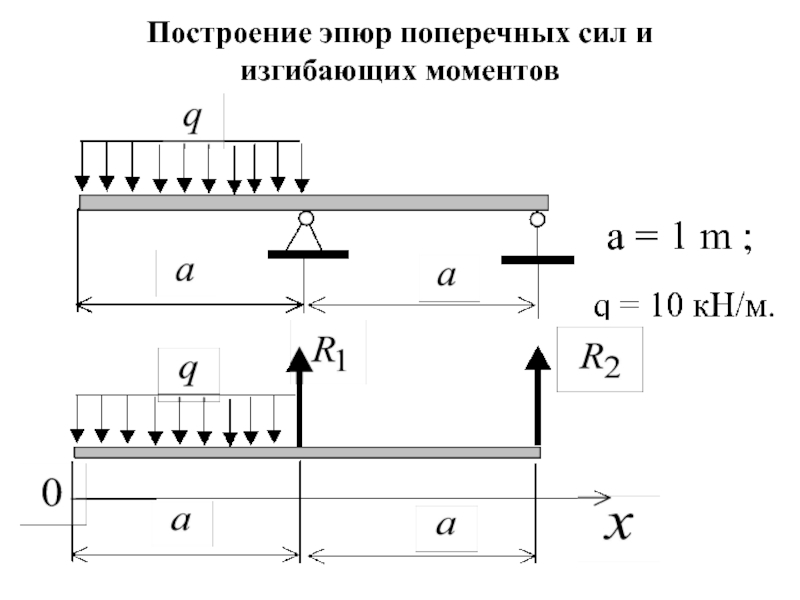 В результате чего определяют неизвестные усилия. После того, как лишние неизвестные найдены, эквивалентное состояние будет представлять собой статически определимую систему, находящуюся под действием заданной нагрузки и найденных сил Х

i. Рассчитав эту статически определимую раму, строят для нее эпюры усилий M, N, Q, известными способами, которыми пользовались при построении эпюр для статически определимых рам.

Существует и другой способ построения эпюры М. На основании принципа Даламбера, эпюру М можно построить на основании формулы:

М_ок = М₁·Х₁ + М₂·Х₂ + … + М_n·Х _n + М_Р = М_i·Х _i + М_Р

Т.е. для получения окончательной эпюры изгибающих моментов ординаты каждой их единичных эпюр умножаются на найденное значение соответствующего неизвестного, и все результаты суммируются (по отдельным точкам осей системы) с добавлением к ним ординат грузовой эпюры моментов.

1.4 Построение эпюр поперечных и продольных сил.

После того как решением системы канонических уравнений найдены неизвестные усилия Х_i , эти усилия и заданная внешняя нагрузка могут быть приложены к основной системе. Затем от их совместного действия обычным способом (как в статически определимых системах) могут быть определены поперечные и продольные силы, и построены эпюры N, Q.

Поперечные силы в статически неопределимой системе могут быть определены и другим путем – по окончательной эпюре изгибающих моментов и условия равновесия вырезанных стержней. Каждый стержень рамы рассматривается как простая статически определимая балка на двух опорах, с приложенными к ней изгибающими моментами, взятыми с окончательной эпюры изгибающих моментов и заданной внешней нагрузкой. Для каждой такой балки, в отдельности, строится эпюра поперечных сил. Потом все участки собираются на раму в целом. Поперечная сила считается положительной, если она дает момент от конца стержня на узел по часовой стрелке, и наоборот.

По эпюре поперечных сил и условия равновесия вырезанных узлов рамы строится эпюра продольных сил N. Для этого к вырезанным узлам прикладывают поперечные и продольные силы. При этом, продольные силы считаем положительными, т.е. направленными от узла. Поперечные силы прикладываются к узлу с учетом полученных значений и знаков. (см. по полученной эпюре поперечных сил). К узлу необходимо не забывать прикладывать и внешние силы, если они непосредственно действуют на этот узел. Проектируя приложенные к узлу силы на оси координат, получим два уравнения равновесия:

S Х = 0, S Y = 0

из которых, зная поперечные силы Q, найдем продольные силы N.

Начинать определение продольных сил надо с тех узлов, в которых сходятся не более двух стержней с неизвестными продольными силами.

---

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:  

---



Расчет и построение диаграмм сдвига и изгибающего момента в Mathcad | PTC

Примечание редактора. Эта статья блога изначально была написана как рабочий лист PTC Mathcad Prime. Чтобы получить наилучшие впечатления от чтения, загрузите рабочий лист Mathcad Prime 8 здесь. Если вам нужна программа для просмотра листов Mathcad Prime, загрузите Mathcad Prime бесплатно здесь.

Грузовой автомобиль, едущий по мосту, вызывает отклонение опорных балок, что приводит к различным напряжениям в балках. Точно так же, когда вы идете по полу в своем доме, балки или балки прогибаются под вашим весом. Прогиб является результатом нагрузки, которая связана с сдвигом, изгибающим моментом, наклоном балки и прогибом балки. В этом блоге и нескольких последующих я расскажу, как можно использовать Mathcad для расчета, построения графиков и получения этих взаимосвязей.

Построение эпюр поперечного и изгибающего моментов свободно опертых балок является одним из заданий базового курса инженерной статики. Mathcad можно использовать для расчета сдвигов и моментов, а также для построения диаграмм сдвигающих и изгибающих моментов.

В этом блоге я покажу, как это сделать для свободно опертых балок с различными условиями нагрузки.

Я сторонник создания функций, которые можно использовать несколько раз, а не просто решать одну проблему. Итак, во-первых, давайте создадим несколько функций, которые помогут решить и построить диаграммы сдвига и изгибающего момента для равномерно нагруженной свободно опертой балки.

Рисунки в этом блоге были созданы в Microsoft PowerPoint как встроенные объекты. Если вы загрузите связанный файл Mathcad и дважды щелкните рисунок, он откроется в PowerPoint.

Сначала рассчитаем левую реакцию R _A , суммируя момент относительно точки B, а затем рассчитаем правую реакцию R _B , суммировав вертикальные нагрузки.

После написания этих функций результаты будут протестированы. Момент по часовой стрелке будем считать положительным.
Переменная «Пролет» — это длина балки, а переменная «w» — равномерная нагрузка (сила/длина) по длине балки. Поскольку Mathcad поддерживает единицы измерения, пролет и нагрузка могут быть выражены в любых единицах длины и силы.

Стрелка вправо в приведенных ниже функциях — это Оператор вычисления символов из раздела Symbolics на вкладке Math . Он обеспечивает символическое решение, а не числовое решение.

Далее напишите функцию для сдвига на расстоянии x путем суммирования вертикальных нагрузок. Сдвиг на расстоянии x слева равен левой реакции за вычетом нагрузки, приложенной к балке между левой и расстоянием x (w*x).

Теперь напишите функцию для момента на расстоянии x, суммируя моменты относительно x.

Теперь, когда уравнения написаны, рассчитайте и постройте диаграммы сдвига и момента, используя функции графика XY. Вставьте график из меню Plots в действие Traces s . Выберите XY Plot с помощью кнопки Insert Plot .

Для создания графиков задайте значения для пролета и нагрузки, а затем создайте переменную диапазона для точек для построения. Переменная диапазона определяется начальным значением, второе значение которого устанавливает размер шага. Последнее число является конечным значением. Он создан так, как выглядит. Введите первое значение, затем введите запятую и введите второе значение, которое задает размер шага. Затем введите . . и введите конечное значение.

Уравнение для сдвига или момента будет отложено по оси Y.

Повторите проверку, используя метрические единицы. Задайте значения пролета и равномерной нагрузки, а также переменную диапазона z, которая установит точки для построения.

Теперь создадим диаграммы сдвига и момента для точечной нагрузки P, размещенной в любом месте вдоль балки на расстоянии «a» от левого конца. Создайте функции для описания нагрузки, сдвига и момента. Не обращайте внимания на вес бревна в этом упражнении. В этом примере я использую ключевое слово решить с помощью оператора символьного вычисления , чтобы продемонстрировать, как решать для R _A .

Теперь, когда уравнения для точечной нагрузки написаны, рассчитайте и постройте диаграммы сдвига и момента, используя функции графика XY.

Для создания графиков задайте значения для пролета, нагрузки и расстояния, а затем создайте переменную диапазона для точек для построения.

В этом последнем примере выводятся функции для треугольной нагрузки.

Как и в предыдущих примерах, создайте функции для реакций, а затем создайте функции для сдвига и момента.

В этом примере используется ключевое словоsolve с оператором символьного вычисления для получения функций для реакций.

Определите значения для диапазона, нагрузки и переменной диапазона z, которые будут устанавливать точки для построения. Отобразите значения переменной диапазона и рассчитанные сдвиги и моменты, которые будут включены в график.

Теперь, когда получены функции для равномерной нагрузки, точечной нагрузки и треугольной нагрузки, используйте эти функции для объединения нескольких условий нагружения.

Для этих примеров сочетания нагрузок будут использоваться численные результаты, и должны быть предоставлены значения условий нагрузки. Переменные диапазона будут использоваться для определения точек для построения и местоположений для расчета сдвигов и моментов. Важно оценить переменную диапазона (используя знак =), чтобы преобразовать переменную диапазона в вектор значений. 9.) Это стрелка, указывающая вправо над выражением. Он указывает Mathcad выполнять операцию поэлементно.

В следующих примерах показано сочетание точечных, равномерных и треугольных нагрузок. В этом блог, я использовал диаграммы сдвига и изгибающего момента, чтобы проиллюстрировать многие возможности Mathcad. Кроме того, я показал, как комбинировать функции для равномерной нагрузки, треугольной нагрузки и точечной нагрузки для расчета и построения графиков реакций, сдвигов и изгибающих моментов. Эти примеры иллюстрируют:

• Значительное использование функций
• Возможности использования оператора символьной оценки , включая использование ключевых слов
• Использование компонента Microsoft PowerPoint для создания графики
• Использование графиков XY
• Определение переменных диапазона для построения графика
• Оценка переменных диапазона для создания вектора значений
• Использование оператора векторизации для выполнения поэлементных операций

Мой следующий блог расширяет эти темы, показывая, как получить функции для максимального изгибающего момента балки для различных условий нагрузки.

Попробуйте Mathcad Prime

Загрузите бесплатную 30-дневную пробную версию Mathcad Prime, чтобы лично увидеть лучшие возможности Mathcad.

Получи это сейчас

---

Об авторе

Брент Максфилд из Солт-Лейк-Сити, штат Юта. Это идеальное место для него из-за его любви к активному отдыху. Он любит пешие прогулки и катание на лыжах в близлежащих горах, а также любит исследовать каньоны красных скал и пустыни в Южной Юте.

Брент Максфилд — зарегистрированный профессиональный инженер-строитель в штате Юта. Он окончил с отличием Университет Бригама Янга по специальности «строительство» и получил степень магистра инженерного менеджмента в УБЯ. Он был практикующим инженером-строителем в течение 36 лет.

В 2012 году Совет инженеров штата Юта наградил его званием «Инженер года штата Юта». Он активно участвует в профессиональных ассоциациях, входил в состав Совета директоров Ассоциации инженеров-строителей штата Юта и отделения EERI в штате Юта. Он также работал в Структурном консультативном комитете Комиссии по единым строительным нормам штата Юта.

Он активно использует PTC Mathcad в течение 20 лет. Он является автором книги «Essential PTC® Mathcad Prime® 3.0: руководство для новых и действующих пользователей», доступной на Amazon.com.

Как построить диаграмму изгибающего момента — ответы MATLAB

27 просмотров (последние 30 дней)

30 октября 2022 г.

Я написал фрагмент кода для решения любой проблемы с двумерными каркасными структурами. В качестве результата я сгенерировал следующее:

• Перемещение в каждом узле
• Shapefunction для изгибающего момента в каждом стержне M(x)
• Shapefunction для поперечной силы в каждом стержне V(x)
• Shapefunction для смещения каждого стержня У (х)

Теперь я хотел бы построить форму смещения, диаграмму поперечной силы и диаграмму изгибающего момента для всей конструкции. Для этого я планирую запускать каждую шейп-функцию в начальном узле элемента, затем отображать ее x=0:Length, а затем поворачивать под тем же углом, что и момент.

Как мне это сделать? Я понятия не имею, как повернуть и расположить сюжет соответственно.

Ссылки: Примерно так я хотел бы, чтобы мой график выглядел (для изгибающего момента и формы смещения): http://debug.pi.gr/BookImagesEn2/Book-B_3330_7a.jpg

Ответы (2)

Не могли бы вы прислать мне свой код?

Я работаю над подобным проектом, и он мне очень нужен

---

Не могли бы вы прислать мне свой код. У меня проблема с ним

Произошла ошибка

Не удалось выполнить действие из-за внесенных на страницу изменений. Перезагрузите страницу, чтобы увидеть ее обновленное состояние.

Переведено

Выберите веб-сайт

Выберите веб-сайт, чтобы получить переведенный контент, где он доступен, и увидеть местные события и предложения. В зависимости от вашего местоположения мы рекомендуем вам выбрать: .