Как определить объем колонны: Подсчёт объёмов работ по строительству каркасов

Подсчёт объёмов работ по строительству каркасов

Мы рекомендуем

Каркасом называют совокупность конструкционных элементов здания или постройки, которые формируют несущую часть сооружения. К этим элементам относятся: колонны, ригели, плиты и балки, элементы связи и жесткости. В основном, каркас применяется при строительстве промышленных и общественных зданий, но также используется и при строительстве жилых зданий.

Монолитные железобетонные каркасы

Подсчёт объёмов работ по устройству монолитных железобетонных конструкций заключается в определении объёма укладываемого бетона в м3. Объём бетона в конструкциях с жёсткой арматурой принимается с вычетом её объёма. Объём жёсткой арматуры исчисляют делением массы металла в тоннах на общую объёмную массу. Объём бетона, использованного для возведения конструкции, определяется по проектным данным или подсчитывается по размерам конструкций с указанием вида и марки бетона. Масса устанавливаемой арматуры указывается с разделением по видам арматуры и маркам стали, а масса сопутствующих деталей берётся отдельно по каждой разновидности.

Объём железобетонных колонн определятся по их сечению, умноженному на высоту колонн с подразделением в зависимости от высоты (до 4 м, до 6м, и более 6 м) и от периметра сечения (до 2 м, до З м, до 4 и более 4 м). Объём железобетонных балок и прогонов следует определять по их сечению, умноженному на длину, с подразделением по высоте балок (до 500, до 800 и более 800 мм). Длина прогонов и балок, опирающихся на колонны, принимается равной расстоянию между внутренними гранями колонн. Длина прогонов и балок, опирающихся на стены, определяется с учётом длины опорных частей, входящих в стены.

Сборные железобетонные каркасы

Объём работ по установке сборных железобетонных колонн и капителей определяют на 1 шт. Нормы на их установку составляют:

  • в производственных и жилых общественных зданиях — на 100 шт;
  • в зданиях специального назначения — на 100 м3 конструкций.

При подсчёте объёмов работ конструкции следует группировать в соответствии с их параметрами, принятыми в нормах и расценках.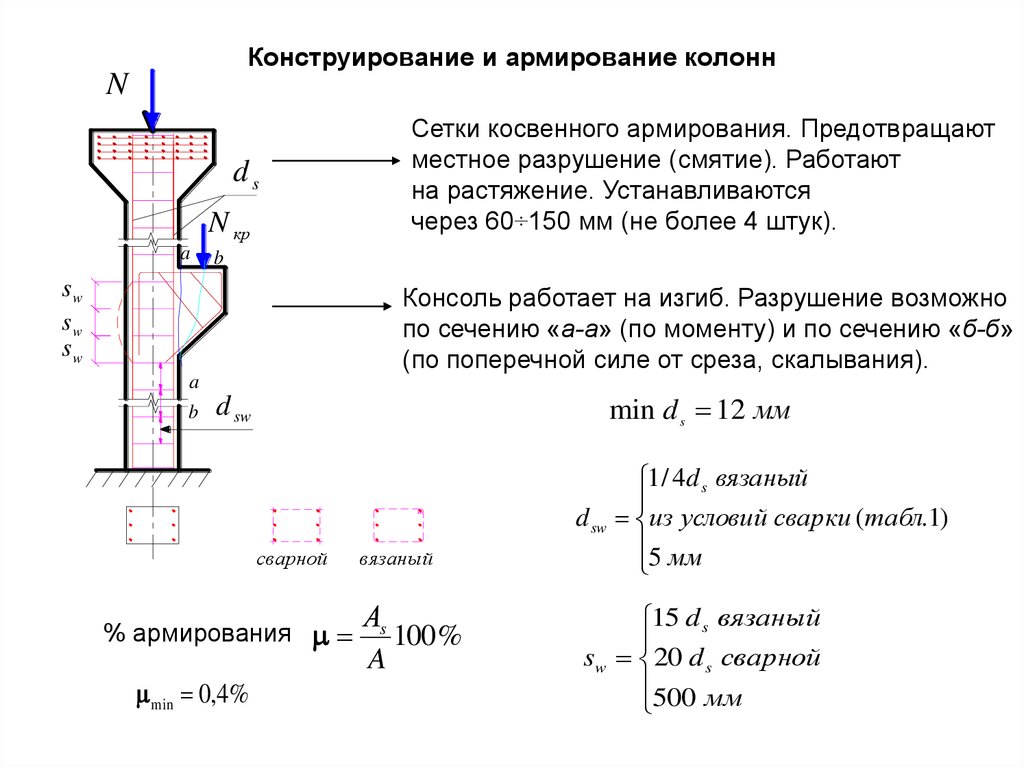 Количество элементов, их марки и масса приводятся в соответствии со спецификациями проекта. Массу стальных накладных изделий, устанавливаемых на стыках сборных железобетонных каркасов следует определять по спецификациям к проекту.

Стальные каркасы

Если для зданий высотой до 30 этажей чаще применяют монолитные или сборные железобетонные каркасы, то для зданий с большей этажностью целесообразно применять стальные каркасы. Расчёт объёма стальных каркасов измеряется в 1 т конструкций. Масса стальных конструкций принимается по спецификации с добавлением 1% на массу сварных швов (для конструкций, требующих сварки) и 3% к итогу на уточнение массы при разработке рабочих чертежей.

Деревянные каркасы

Объём работ по устройству деревянных каркасов зданий исчисляется в м3 древесины в деле, учитывая спецификации древесины, указанные проектом, без каких-либо добавок на отходы древесины, при этом объём брёвен надлежит исчислять по их диаметру в верхнем отрубе. Объём древесины для каркаса подсчитывается по отдельным элементам для стоек одинарных, составных, решетчатых (колонн), а также отдельно для элементов из брусьев и элементов из брёвен и пластин. В ведомости на устройство деревянного каракаса также должно быть учтено выполнение комплекса работ по защите деревянных конструкций от воздействия влаги, исчисляющиеся в м2.

Также необходимо упомянуть, что сметная стоимость каркасных элементов включается в разделы «Перекрытия» и «Покрытия», а отдельно стоящих колонн — в раздел «Стены».

Автор статьи:

Коллектив Дженерал Смета,
Есть вопросы? Свяжитесь с техподдержкой.

[email protected] | +7(495)369-97-69

формула через диаметр и высоту

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Нахождение объема цилиндра: формула и задачи

В данной публикации мы рассмотрим, как можно найти объем цилиндра и разберем примеры решения задач.

  • Формула вычисления объема цилиндра
    • Через площадь основания и высоту
    • Через радиус основания и высоту
    • Через диаметр основания и высоту
  • Примеры задач

Формула вычисления объема цилиндра

Через площадь основания и высоту

Объем (V) цилиндра равняется произведению его высоты и площади основания.

V = S ⋅ H

Через радиус основания и высоту

Как мы знаем, в качестве оснований цилиндра (равны между собой) выступает круг, площадь которого вычисляется так: S = π ⋅ R2. Следовательно, формулу для вычисления объема цилиндра можно представить в виде:

V = π ⋅ R2 ⋅ H

Примечание: в расчетах значение числа π округляется до 3,14.

Через диаметр основания и высоту

Как нам известно, диаметр круга равняется двум его радиусам: d = 2R. А значит, вычислить объем цилиндра можно следующим образом:

V = π ⋅ (d/2)2 ⋅ H

Примеры задач

Задание 1
Найдите объем цилиндра, если дана площадь его основания – 78,5 см2, а также, высота – 10 см.

Решение:
Применим первую формулу, подставив в нее известные значения:
V = 78,5 см2 ⋅ 10 см = 785 см3.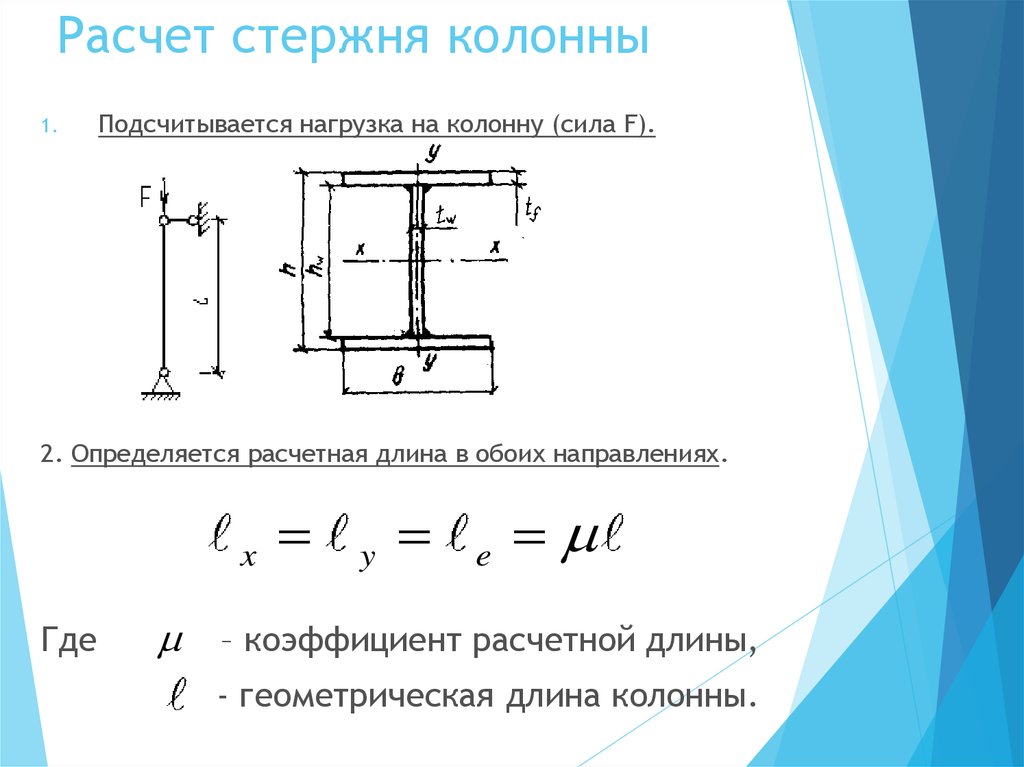

Задание 2


Высота цилиндра равна 6 см, а его диаметр – 8 см. Найдите объем фигуры.

Решение:
Воспользовавшись третьей формулой, в которой участвует диаметр, получаем:
V = 3,14 ⋅ (8/2 см)2 ⋅ 6 см = 301,44 см3.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Как рассчитать объем пустой колонки для колонки? — ВКБ48971

  1. Последнее обновление
  2. Сохранить как PDF

Артикул: 48971

ЦЕЛЬ или ЦЕЛЬ

Определить объем пустой колонки.

ОКРУЖАЮЩАЯ СРЕДА

  • Столбец
  • вычислить
  • пустой том
  • ВЭЖХ
  • УПЛК
  • АКЦИИ
  • Быстрорежущая сталь
  • Симметрия
  • БЭХ
  • ОСТ
  • БТР
  • XBridge

ПРОЦЕДУРА

  1. Использование Объем = пик х радиус 2 х Длина
  2. пи = 3,14
  3. r 2 и Длина должна быть переведена в сантиметры
  4. Диаметр колонны разделить на 2 = радиус
  5. радиус x радиус = r 2
  6. 3,14 x r 2   x L = объем в см 3
  7. см 3 = 1 мл

ДОПОЛНИТЕЛЬНАЯ ИНФОРМАЦИЯ

Объем пустой колонки 4,6 мм x 150 мм составляет 2,5 мл.

пи = 3,14

4,6 мм становятся 0,46 см, а 150 мм становятся 15 см.

0,46 см разделить на 2 = радиус 0,23 см

0,23 см x 0,23 см = 0,0529см 2

3,14 x 0,0529 см 2 x 15,0 см = 2,49 см 3

См.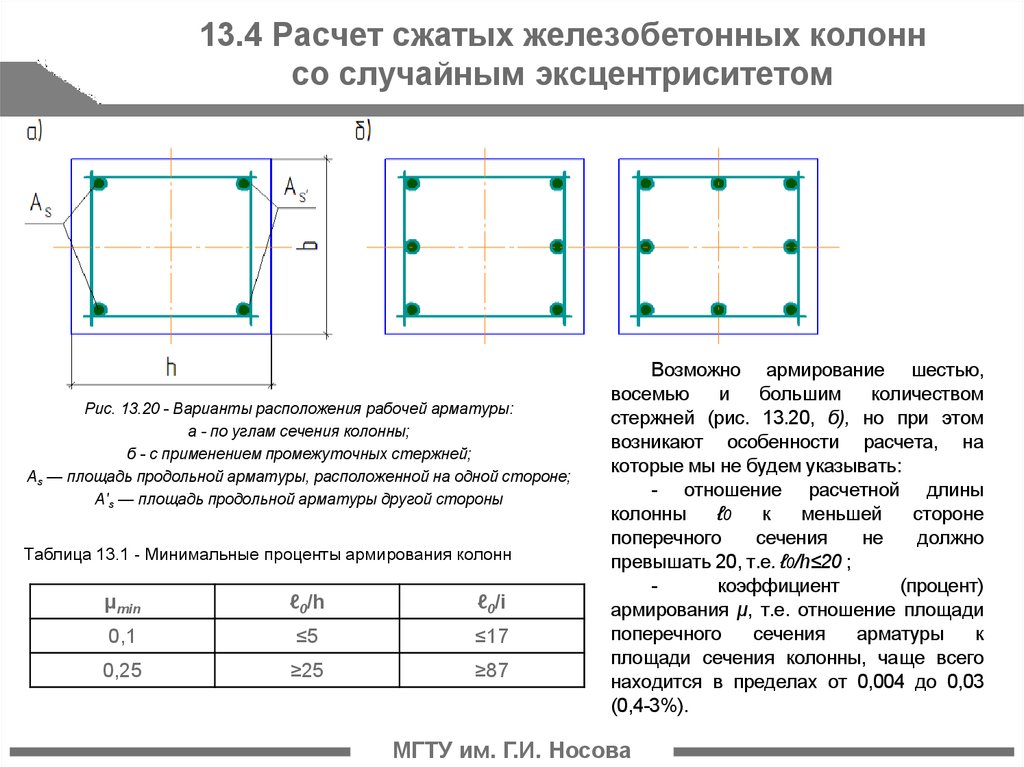 также —> Как определить объем пустот колонки?

id48971, ALLCOLCLR, ALLCOLHTR, ALLCOLHTRB, UPASMFTN, UPBINARY

Не можете найти решение? Нажмите здесь, чтобы запросить помощь.

  1. Наверх
    • Была ли эта статья полезной?
    1. Тип изделия
      Практическое руководство
      Аудитория
      Внешний
      Уровень достоверности
      Веб-издатель одобрен
      Семейство инструментов
      Альянс ВЭЖХ
      Семейство инструментов
      АКВИТИ серия
      Часто используемый
      Высокий
      Язык
      en-US
      Выпущено
      Да
      Перевод
      PE приостановлено
    2. Теги
      1. ACQUITY UPLC
      2. Альянс
      3. АПК
      4. Атлантида
      5. БЕХ
      6. БиоСьюит
      7. Колонка
      8. БД
      9. Решение
      10. СЕК
      11. Сферисорб
      12. Симметрия
      13. XBridge
      14. Xселект
      15. Экстерра

    Оценка объема колонки

    На наших мастер-классах время от времени возникает вопрос, как определить объем колонки ВЭЖХ.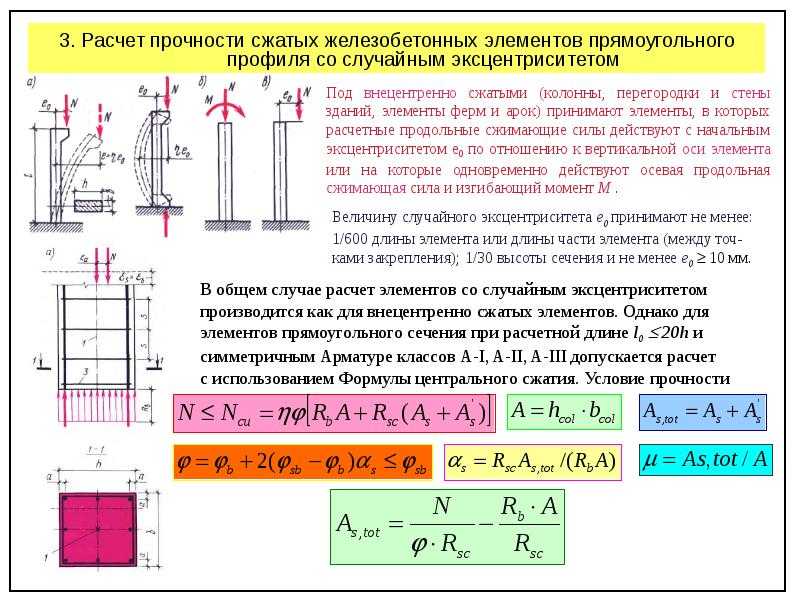 Я хотел бы поделиться парой эмпирических правил, которые я считаю очень полезными для оценки объема столбца, V M . Вычисление объема внутри столбца не представляет особой сложности, если столбец пуст. Вспомните еще на уроке геометрии в старшей школе, что объем (V) цилиндра равен

    V = Πr 2 h (1)

    Таким образом, для 150 x 4,6 мм в.д. колонна, h (высота) = L (длина) = 150 мм и r (радиус) = 0,5d c (диаметр колонны = 4,6 мм), что дает (Π)(150)(4,6/2) 2 = 2493 мм 2 = 2493 мкл ≈ 2,5 мл.

    4,6 мм в.д. Колонки

    Однако 2,5 мл — это не объем хроматографической колонки, поскольку она заполнена частицами. Сферические частицы имеют промежутки между ними, а также они пористые, поэтому внутри них есть промежутки. Эти пространства представляют объем подвижной фазы или объем колонки, которые нас действительно интересуют. Для большинства колонок для ВЭЖХ этот объем составляет около 60–70% объема пустой колонки. Давайте посмотрим, как мы можем сделать ярлык для этого. Если мы умножим любой фактор уравнения 1 на 60%, мы должны получить объем столбца. Для внутреннего диаметра 4,6 мм. столбец, если умножить Πr 2 на 60%, получаем 10 — мне всегда нравятся вычисления с участием 5 и 10, потому что я могу делать их в уме. Итак, для нашего внутреннего диаметра 4,6 мм. Теперь у нас есть столбец:

    V M ≈ 10 л (2)

       где L — длина в мм, а V M

    — в мкл. Обычно нас больше интересует V M  в мл, поэтому мы делим на 1000, иначе уравнение (3) можно переформулировать как


    V M ≈ 0,01 л (3)

       теперь 1% от 150 = 1,5 мл . Мы можем перепроверить, умножив пустой объем, 2,5 мл x 60% = 1,5 мл.

    Другие диаметры колонок

    Уравнение (3) очень удобно для оценки объема колонки с внутренним диаметром 4,6 мм. колонка а что делать если колонка другого диаметра? Нам нужно эмпирическое правило, которое включает в себя как L, так и d c . Обратите внимание, что 0,6 π (d c /2) 2 = (0,6 π/2) d c 2 = 0,47 d c 2 . Это близко к 0,5 d c 2

    V M ≈ 0,5 L d c 2 (4)

       где L и d c в мм, а V

    M в мкл. Мы можем использовать это, чтобы вычислить объем внутреннего диаметра 50 x 2,1 мм. колонка, которую можно использовать в приложении ЖХ-МС: V M = 0,5 x 50 x 2,12 = 110 мкл или ≈ 0,1 мл.

    2,1 мм в.д. – Специальный футляр
    Мы можем сделать еще одно сокращение для внутреннего диаметра 2,1 мм. колонка, которая является наиболее популярным диаметром колонки, кроме 4,6 мм. Мы могли бы использовать уравнение 2 или 3 и скорректировать изменение площади поперечного сечения и получить тот же результат. Поскольку площадь поперечного сечения пропорциональна отношению диаметров в квадрате, мы получаем (4,6/2,1) 2 = 4,8. Мы говорим здесь об оценках, так что мы можем округлить 4,8 до 5 для легкого вычисления в уме. Это означает, что объем 4,6 мм в.д. столбец примерно в пять раз больше, чем такой же столбец в 2,1 мм в.д. формат. Давайте быстро проверим это. Колонка 50 x 4,6 мм будет иметь объем V M ≈ 0,01 x 50 = 0,5 мл (уравнение 3). 2,1 мм в.д. версия этой колонки должна иметь 1/5 объема, поэтому 0,5 мл/5 = 0,1 мл = 100 мкл. Это достаточно близко к значению, которое мы рассчитали по уравнению 4 выше.

       Теперь у нас есть несколько простых способов оценить объем столбца. Один для внутреннего диаметра 4,6 мм. колонки (уравнение 2 или 3), одну для любой колонки (уравнение 4) и одну специально для колонки с внутренним диаметром 2,1 мм. столбец (уравнение 2 или 3 разделить на 5). Эти оценки должны быть в пределах примерно 10% от значения, которое вы измеряете хроматографически.

    Эта серия статей в блоге подготовлена ​​в сотрудничестве с Джоном Доланом, наиболее известным как один из ведущих мировых специалистов по устранению неполадок ВЭЖХ.