Способы того, как можно высчитать кубический метр объёма различных материалов

Часто приходится задаваться такими вопросами: «А как много нужно чего-нибудь, чтобы наполнить вот это?» Или наоборот: «А сколько этого поместится сюда?» Ведь постоянно приходится что-то куда-то переносить, перекладывать или перевозить, что-то строить, пристраивать или перестраивать. И тут приходится брать в руки обычную или лазерную рулетку и вспоминать единицу измерения объема — кубометр.

Содержание:

• Что такое кубометр
• Перевод в другие единицы
• Пример расчета
• Видео

Что такое кубометр

Кубический метр — это условная фигура (куб), имеющая длину, ширину и высоту, равную одному метру

Как рассчитать кубический метр, если эти параметры имеют другое значение? Если их произведение (результат перемножения) равно единице, то фигура, которую они составляют, имеет объем один кубометр. Например, объем размерами 1 м ширины, 0,5 м высоты и 2 м длины имеет в себе один кубометр.

В практической деятельности приходится высчитывать объемы различных помещений, и тут можно руководствоваться простой формулой: объем прямого параллелепипеда составляет произведение площади основания на высоту. Комната площадью 32,5 метра и высотой потолков 2,2 метра имеет 71,5 кубометра (куба). Часто помещение имеет наклонный потолок, и тут встает вопрос о высоте. В таком случае можно взять среднее значение этого параметра и получить приблизительный объем.

Если требуется точное значение, то надо помещение мысленно разделить на параллелепипед, имеющий высоту самой низкой стены и подсчитать его объем; затем высчитать объем параллелепипеда, имеющего такую же площадь и высоту, равную разности высот самой высокой и самой низкой стен, поделить пополам и прибавить к объему первого параллелепипеда.

Достаточно часто приходиться рассчитывать объемы различных полостей. Например, при заливке фундамента требуется знать необходимое количество бетонной смеси. Тут все достаточно просто. Точно так же умножаем площадь основания на высоту и получаем искомое значение. Важно вычисления и замер производить в тех единицах измерения, в каких требуется узнать искомое значение. В случае с бетонной смесью ее закупка производится обычно в кубах, поэтому и размеры опалубки под заливку фундамента измеряем в метрах.

Перевод в другие единицы

Для перевода в необходимое значение надо помнить довольно простые пропорции перевода метров в сантиметры и миллиметры.

Единицы длины:

• 1 м = 100 см = 1 000 мм

Единицы площади:

• 1 м² = 10 000 см² = 1 000 000 мм²

Единицы объема:

• 1 м³ = 1 000 000 см³ = 1 000 000 000 мм³

Количество жидкости очень часто измеряется в литрах, тут достаточно знать, что:

• 1 л = 1 000 см³
• 1 000 л = 1 м³

Довольно часто приходится рассчитывать объем, исходя из веса, и тут нужно знать плотность вещества. Проще всего с водой, плотность которой 1т/1м³. То есть тонна воды займет один м³ (куб), а тонна молока, например, займет примерно 1,030 куба.

Песок имеет плотность от 1,3 т/м³ до 1,8 т/м³. Это значит, что один м³ весит от 1,3 до 1,8 тонны.

Расчет кубатуры пиломатериалов имеет тонкости. Если доска обрезная и одинаковая, достаточно взять одну, измерить длину, толщину, ширину, перемножить эти параметры, а затем получившееся значение умножить на общее количество. Это и будет искомое значение.

Но при применении необрезной доски, как более доступной по цене, невозможно точно замерить размеры одной единицы, все образцы имеют различные пропорции. В таком случае материал укладывается в штабель с выравненными торцами без перехлеста досок внутри штабеля, и измеряются три параметра всей стопки, перемножаются с применением понижающего коэффициента от 0,5 до 0,7, что и является искомой величиной.

Бывает также, что приходится высчитывать вместимость цилиндрических объектов (бочек, цистерн и подобных). Основанием здесь служит круг, а площадь его равна произведению числа пи (π = 3.14) на квадрат радиуса (половины диаметра) или S=πR².

В практической жизни можно применить и такой достаточно простой способ определения объема жидкостей или сыпучих веществ — в кубометре содержится 1 тыс. литров или 100 десятилитровых ведер. Кому-то покажется хлопотным таскать и пересчитывать ведра с песком или водой, но этот способ точен и общедоступен.

Пример расчета

Допустим, нужно залить ленточный фундамент под сооружение размером 8 на 12 метров, разделенное на три помещения стенами длиной 8 и 6 метров. Примем ширину фундамента 40 см, высоту в метр. Длина составит 54 метра, а объем фундамента будет 0,4*1*54 = 21,6 м³. Это значение можно смело округлить до 22 м³.

Приготовление кубометра бетонной смеси для заливки фундамента требует примерно 350 кг цемента, 800 кг песка, 1200 кг щебня и 140 л воды. Значит, на весь фундамент нужно 154 мешка цемента по 50 кг (7,7 тонн), 17,6 тонн песка, 26,4 тонн щебня и примерно 3 кубометра воды.

Это совершенно приблизительный подсчет, навскидку, позволяющий просто прикинуть размер предстоящих материальных и трудовых затрат. Кстати, количество вынутого под фундамент грунта будет сопоставимо, а то и выше объема самого фундамента, хотя тот и не полностью находится в земле. Объясняется это тем, что траншея под фундамент роется шире для установки опалубки и сопутствующих работ.

Точно так же приходится рассчитывать потребный объем при, допустим, переезде или отправке каких-то товаров или грузов. Ведь переплачивать за лишний объем кузова заказанного автомобиля, транспортного контейнера или железнодорожного вагона никому не хочется.

Достаточно просто вспомнить (посмотреть в интернете) элементарные геометрические формулы из школьной программы и приложить здравый смысл. Ведь всегда можно приблизительно рассчитать объем мебели при переезде или коробок при отправке товара и оценить предстоящие усилия и затраты. А для более точных, окончательных расчетов всегда можно прибегнуть к помощи специалистов. Тем более что предварительный итог более или менее известен, и это может служить некоторой проверкой при согласовании условий.

Видео

Из этого видео вы узнаете, как самостоятельно рассчитать кубатуру.

Что такое кубометр дров, складометр: Разница

Во время закупки топлива на зиму у покупателей нередко возникает вопрос: куб дров – это сколько, как правильно определить их объем? В замешательство вводит и то, что поставщики могут продавать их по-разному, заявляя стоимость за кубометр дров, складометр или даже за машину. И если бывалые рабочие лесхоза могут буквально на глаз определить объем любой кучи поленьев, то обычные люди высчитывают кубометр дров или складометр дров расчетным методом. Причем он достаточно простой – ознакомьтесь с информацией ниже, и вы раз и навсегда решите для себя вопрос, как определить объем дров. 

Куб дров – это сколько?

Кубический метр – это единица объема, равняющаяся объему куба с ребрами длиной 1 метр. Вы наверняка знаете что стоимость топлива определяется в цене за куб дров.Но естественно, что 1 куб дров невозможно сложить настолько плотно, чтобы этот объем занимала чистая древесина. Потому для этого материала существует такое понятие, как 1 складометр дров или складочный кубический метр. Однако в складометрах зачастую измеряются поленья, которые находятся на складе и плотно уложены в штабеля. Реализуют чурки обычно навалом или насыпом (россыпью, без укладки). Как высчитать кубометр дров в таком случае? Как правило, 1 м3 насыпом равен приблизительно 0,7-0,75 складометра. А как измерить складометр дров более точно, рассмотрим чуть ниже.  

Кроме того, существует еще столярный куб. Но такое измерение кубатуры используют только для делового леса (кругляка) и для пиломатериалов.

Почему не стоит покупать на вес?

Возникает закономерный вопрос: если все так сложно, то почему не продавать поленья просто по весу? Некоторые продавцы так и поступают, а для расчета стоимости сначала взвешивают пустой автомобиль, затем груженный. Однако у кубометра дров вес не стабилен, он зависит не только от породы, но и от влажности древесины. Например, возьмем тот же дуб: при влажности 25% и 50% складометр дров весит 650 и 770 кг соответственно, а у некоторых других пород этот показатель колеблется в еще более внушительных пределах. Будь то дрова из ясеня или любого другого дерева — до и после выдержки при одинаковом объеме они будут иметь разный вес.Потому покупать чурки на вес невыгодно и неправильно.    

Как посчитать складометр дров?

Зачастую покупателей интересует вопрос, как посчитать кубометр дров, если они куплены насыпом. Для этого необходимо высчитать объем кузова или кучи поленьев. В первом случае умножаем длину, ширину и высоту, во втором считаем объем конуса через радиус и высоту (V=1/3πR2H). Полученное число нужно умножить на поправочный коэффициент, который будет зависеть от длины поленьев:

• 0,25 м – 0,8;
• 0,33 м – 0,78;
• 0,45 м – 0,75;
• 0,65 м – 0,73.

Это и будет объемом вашей покупки в складометрах.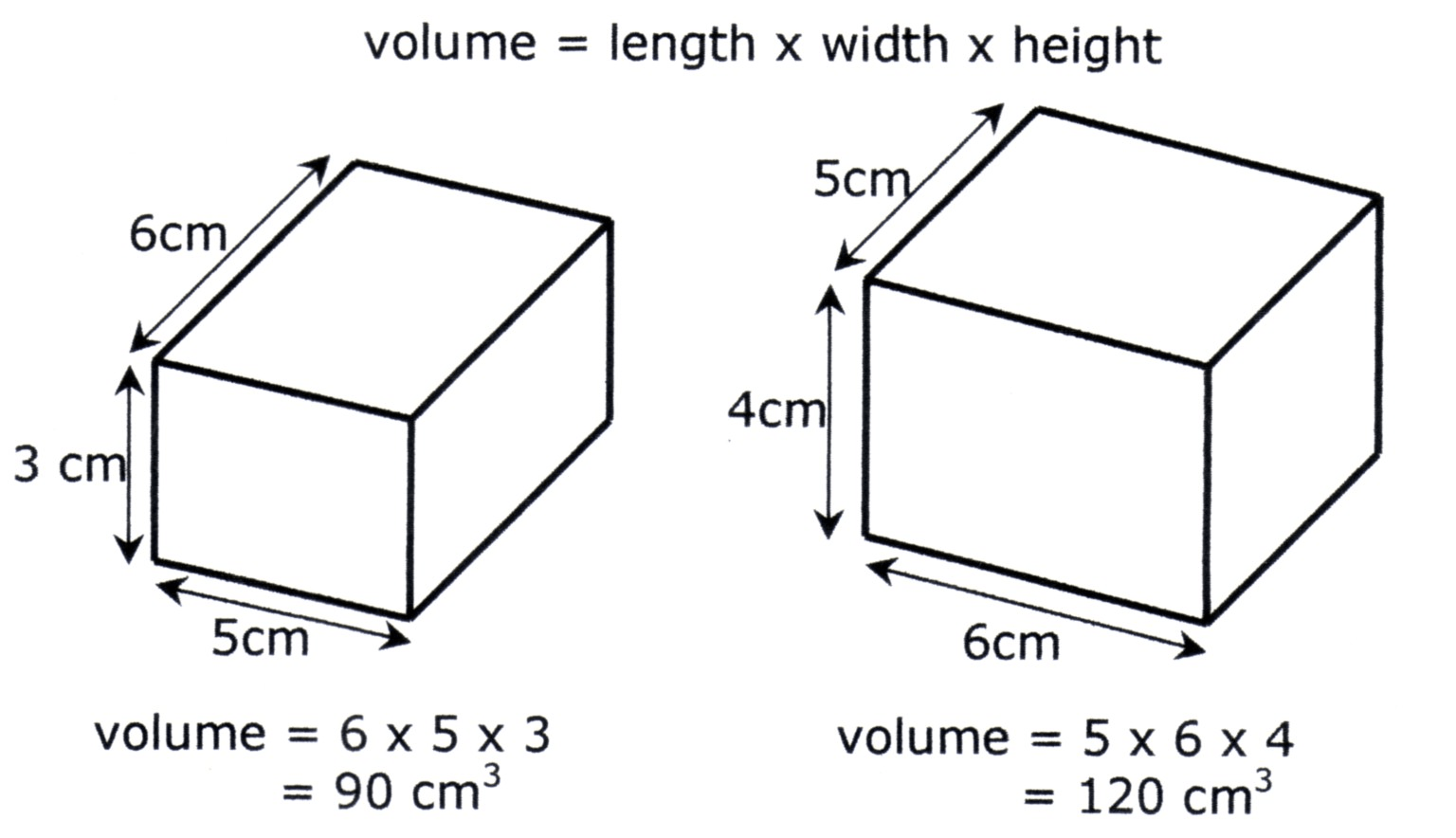 Так как поленья часто бывают неоднородными и не одинаковой длины, то в качестве поправочного коэффициента нередко используется усредненный – 0,75. Учитывайте это когда заказываете дрова из граба и прочих видов древесины. 

Рассмотрим, как посчитать складометр дров на примере. Вам привезли Камаз чурок насыпом. Длина кузова 4,1 м, ширина 2,5 м, высота 1,2 м. Длина поленьев в среднем 0,4 м. Если сомневаетесь в длине, лучше брать значение больше.

4,1*2,5*1,2 = 12,3м3 насыпом
12,3*0,75 = 9,22 складометра

Иногда покупателей также интересует вопрос: 1 складометр – это сколько кубов (цельной древесины)? 1 складометр равен 0.7 м3 древесины. На нашем примере нужно 9,22 умножить на 0,7, получится 6,454 м3 чистой древесины. Но в таких единицах дрова не измеряют – если поставщик говорит 1 кубометр дров, то он имеет ввиду насыпом или складометр. 

Теперь вы знаете, как определить кубометр дров, и что значат те или иные единицы измерения. Для покупки нужного количества останется только уточнить у продавца, какими именно кубометрами он считает поленья при продаже.

Объем куба — определение, формула, вывод и примеры

Объем куба — это общее количество кубических единиц, занимаемых им в трехмерном пространстве. Куб — это трехмерная фигура, имеющая шесть граней, двенадцать ребер и восемь вершин. Следовательно, объем куба — это пространство, ограниченное его шестью гранями. В отличие от 2d-фигур, он имеет дополнительные размеры помимо длины и ширины, которые называются высотой или толщиной. Следовательно, объем куба равен произведению его длины, ширины и высоты. Измеряется в кубических единицах. Чем больше величина его размеров, тем больше объем куба.

В этой статье мы обсудим определение и формулу объема куба вместе с примерами.

Каков объем куба?

Определение: Объем куба определяет количество кубических единиц, полностью занимаемых кубом. Единица объема куба выражается в кубических единицах, таких как сантиметры ³ , метры ³ , дюймы ³ , футы ³ и т. д.

Куб – это твердая трехмерная фигура, имеющая 6 квадратных граней или сторон. Объем куба будет равняться общему пространству, занимаемому им. Так как все грани куба имеют квадратную форму, значит, и длины ребер будут равны. Следовательно, длина, ширина и высота куба равны.

Если длина, ширина и высота куба равны «а», то;

Объем куба = a × a × a

Объем куба = a 3

Если мы знаем длину ребра, т.е. «а», то мы можем найти объем куба. Давайте научимся находить объем любой кубической структуры.

Объем куба Формула

Мы можем легко найти объем куба (V), зная длины его ребер. Предположим, что длина ребер куба равна «а». Тогда V будет произведением длины, высоты и ширины. Итак, формула объема куба:

Объем куба = длина × ширина × высота

Объем = а × а ×

Объем = а ³

Где «а» — длина стороны куба или ребер.

Вывод объема куба

Объем объекта определяется как количество пространства, которое занимает твердое тело. Мы знаем, что куб — ​​это трехмерный объект, у которого все стороны, то есть длина, ширина и высота, равны. Теперь для куба вывод объема будет следующим:

• Рассмотрим квадратный лист бумаги.
• Теперь площадь, которую займет квадратный лист, будет равна площади его поверхности, т. е. его длине, умноженной на его ширину.
• Поскольку квадрат будет иметь одинаковую длину и ширину, площадь поверхности будет равна « ² ».
• Теперь можно сделать куб, уложив несколько квадратных листов друг на друга так, чтобы высота равнялась единицам «а». Это дает высоту или толщину куба как «а».
• Теперь можно сделать вывод, что общая площадь, покрытая кубом, будет равна площади основания, умноженной на высоту.
• Итак, Объем куба = a ²  × a = a ³

Как найти объем куба?

Есть два метода, с помощью которых мы можем найти объем куба.

• Использование длины кромки
• Использование диагонали

Оба метода основаны на формулах и просты для понимания.

Объем куба с заданной длиной ребра

По формуле объема куба мы это знаем;

Объем = (Ребро куба) ³

Следовательно, зная длину ребра куба, мы легко можем найти его объем.

Пример: если длина ребра равна 3 см, объем куба;

Объем = 3 ³ = 3 х 3 х 3 = 27 куб.см.

Объем куба по диагонали

Объем куба, диагональ которого (d) задана, определяется как:

Объем куба = √3 × d 3 /9

Следовательно, измерив длину диагонали куба, мы можем оценить объем куба.

Пример: Если длина диагонали куба 3 дюйма, то объем будет:

Объем = √3 × d ³ /9 = √3 × 3 ³ /9 = 3√3 куб.дюйма

Проверка:  Диагональ куба Формула

Видео урок по объему куба

Для получения дополнительной информации об объемах кубов и прямоугольных параллелепипедов посмотрите видео ниже:

Площадь поверхности куба

Площадь поверхности куба – это общая площадь, занимаемая его внешней поверхностью.

Мы можем найти площадь поверхности куба, которая равна количеству квадратных единиц, полностью покрывающих поверхность куба. Общая формула площади поверхности куба со стороной «а» определяется формулой;

Площадь поверхности куба = 6a ²

Связанные статьи

• Куб
• Том
• Куб и параллелепипед
• Площадь поверхности куба
• Объем конуса
• Объем прямоугольного параллелепипеда
• Объем цилиндра
• Объем сферы
• Объем пирамиды
• Объем призмы

Решенные примеры для объема куба

Вопрос 1: Найдите объем куба, длина стороны которого 7 см.

Решение:

Дано, длина сторон куба равна 7см.

Мы знаем, Объем куба = (длина сторон куба) ³

Следовательно, Объем, V = (7 см)

3

В = 343 см ³

Вопрос 2: Найдите длину ребер куба, если его объем равен 125 см ³ .

Решение:

Дано, Объем куба = 125 см ³ .

Пусть длина ребер равна «a».

Мы знаем по формуле

Объем куба = (длина ребер куба) ³

Подставляя значение, получаем,

125 = ³

Или а = ³ √125

или а = 5 см

Следовательно, длина куба равна 5 см.

Вопрос.3 : Каков объем куба, длина диагонали которого 27см.

Решение : По формуле объема куба при заданной диагонали имеем;

Объем = √3 × d ³ /9

д = 27 см (дана)

Следовательно,

Объем куба = √3 × 27

3 /9

= √3 × (27 × 27 × 27)/9

= √3 × (27 × 27 × 3)

= 3788 (приблизительно)

Практические вопросы

1. Найдите объем куба с длиной ребра равной:
   • 4 см
   • 7 в
   • 11 м
   • 10 футов
2. Каков объем куба, если длина диагонали 15 см?

Узнайте о различных геометрических формах и размерах здесь, в BYJU’S, а также загрузите его приложение, чтобы получать персонализированные и интересные видео.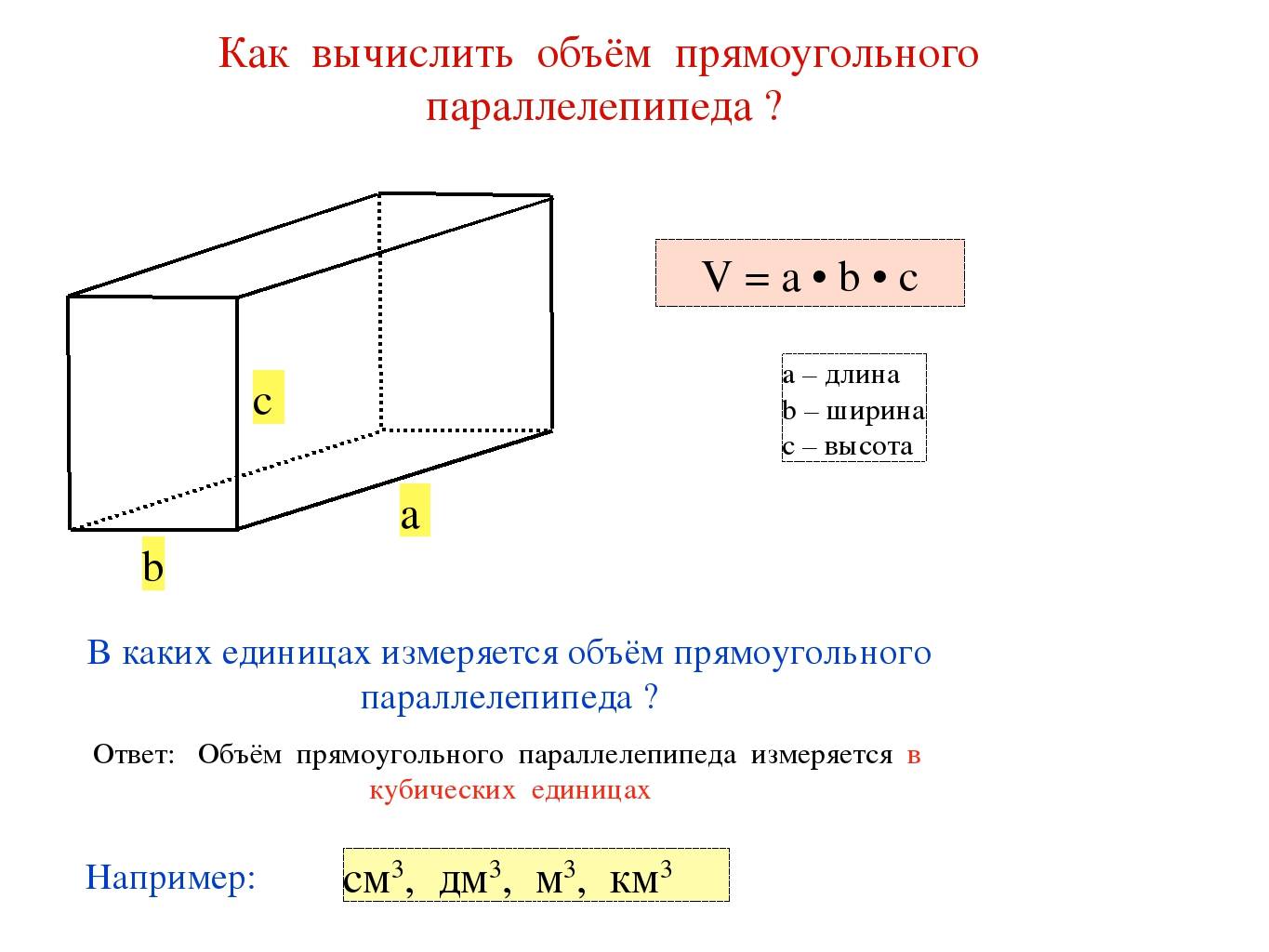

Часто задаваемые вопросы об объеме куба

Q1

Что понимается под объемом куба?

Объем куба – это полное трехмерное пространство, занимаемое кубом полностью.

Q2

Какова формула объема куба?

Формула объема куба:
Объем = a ³ , где a — длина его сторон или ребер.

Q3

Какова единица объема куба?

Единица объема куба выражается в кубических единицах или единицах измерения ³ , например см ³ , м ³ , ин ³ и т. д.

Q4

Какая связь между объемом куба к длине его ребра?

Объем куба равен ³ , что означает v ∝ a. Итак, объем куба прямо пропорционален его ребру.

Q5

Каков объем куба, если даны диагонали?

Объем куба, если даны диагонали, равен √3 × d ³ /9.

Кубические дюймы

Кубический дюйм (в ³ ) является мерой объема куба с длиной ребра 1 дюйм.

Что такое 1 кубический дюйм

1 кубический дюйм равен объему куба с ребрами размером 1 дюйм, как показано на рисунке ниже.

Это единица измерения объема в традиционной и имперской системах измерения США.

Как найти кубические дюймы

Объем куба рассчитывается как длина × ширина × высота. Поскольку длина ребра куба на рисунке выше равна 1 дюйму, его объем равен 1 из ³ . Эту же формулу можно использовать для трехмерных фигур, не являющихся кубами. Пока длины ребер указаны в дюймах, результатом умножения длины × ширины × высоты будет объем в дюймах 9.0013 3 .

Приведенный выше куб можно назвать единичным кубом, где единицей измерения в данном случае является дюйм. Один из способов визуализировать объем — использовать единичные кубы. Например, на рисунке ниже 16 единичных кубов. Поскольку размер каждого куба равен 1 в ³ , объем объекта равен 16 в ³ .

Таким образом, объем объекта можно оценить как количество единичных кубов, которые помещаются внутри объекта. В приведенном выше примере, поскольку прямоугольную призму можно разбить на целое число единичных кубов, ее объем можно рассчитать точно. В тех случаях, когда это невозможно, объем можно оценить, используя комбинацию целых и частичных единичных кубов. Также существует множество формул для объемов других фигур. Пока их размеры измеряются в дюймах, использование их формул даст объем в кубических дюймах.

Использование кубических дюймов

Кубический дюйм — это всего лишь одна из многих единиц измерения объема. Он в основном используется в Соединенных Штатах. Хотя он также в некоторой степени используется в Канаде и Великобритании, он не распространен, поскольку и Канада, и Великобритания приняли Международную систему единиц (СИ). Даже в США кубические дюймы широко не используются. Автомобильная промышленность является одной из немногих областей, в которых до сих пор используются кубические дюймы, в основном для измерения рабочего объема двигателя, или, точнее, рабочего объема в кубических дюймах. Однако литры также используются для этой же цели, особенно при упоминании новых автомобилей, а рабочий объем в кубических дюймах в основном используется в контексте коллекционирования классических автомобилей.

Большая часть остального мира использует единицы измерения объема СИ. Базовой единицей объема СИ является кубический метр, но также широко используется литр, производная единица объема СИ. Существует множество других единиц измерения объема в различных системах измерения, но в большинстве стран используется либо СИ, обычная или имперская система США, либо их комбинация.

Преобразование кубических дюймов

Ниже приведены отношения между кубическими дюймами и некоторыми широко используемыми единицами объема в различных системах измерения.

Кубические дюймы в кубические футы

Кубические дюймы ÷ 1,728 = кубические футы

Кубические дюймы в кубические метры

Кубические дюймы ÷ 61 023,744 = кубические метры

кубических дюймов в галлоны США

кубических дюймов ÷ 231 = галлоны США

кубических дюймов в литры

кубических дюймов ÷ 61,024 = литры

Кубические дюймы в миллилитры

Кубические дюймы × 16,387 = миллилитры

Поскольку используется очень много различных единиц объема, важно иметь возможность конвертировать между ними.