11 фактов, которые вы должны знать
Содержание: консольная балка- Определение консольной балки
- Диаграмма консольного тела без балки
- Граничные условия консольной балки
- Определите внутренний сдвиг и изгибающий момент в консольной балке как функцию от x
- Определение поперечной силы и изгибающего момента, действующих на расстоянии 2 м от свободного конца консольной балки с равномерно распределенной нагрузкой (UDL)
- Уравнение кривой прогиба консольной балки с равномерно распределенной нагрузкой
- Консольная балка Жесткость и вибрация
- Изгиб консольной балки из-за чистого изгибающего момента, вызывающего изгибающее напряжение
- Обнаружение изгибающего напряжения консоли, вызванного равномерно распределенной нагрузкой (UDL)
- Вопросы и ответы по консольной балке
«Консоль — это жесткий конструктивный элемент, который проходит горизонтально и поддерживается только одним концом.
https://en.wikipedia.org/wiki/CantileverОбычно он отходит от плоской вертикальной поверхности, например стены, к которой он должен быть прочно прикреплен. Как и другие элементы конструкции, консоль может быть выполнена в виде балки, плиты, фермы или плиты ».
Консольная балка — это балка, один конец которой закреплен, а другой конец — свободен. Неподвижная опора предотвращает смещение и вращательное движение балки на этом конце. Консольная балка позволяет выступать без какой-либо дополнительной поддержки. Когда нагрузка прилагается к свободному концу балки, консоль передает эту нагрузку на опору, где он прикладывает поперечную силу [V] и изгибающий момент [BM] к неподвижному концу.
Схема свободного тела консольной балкиРассмотрим консольную балку с точечной нагрузкой, действующей на свободный конец балки.
Схема свободного тела консольной балки представлена ниже:
Диаграмма свободного телаГраничные условия консольной балкиСилы реакции и момент в точке A можно рассчитать, применяя условия равновесия
\ сумма F_y = 0, \ сумма F_x = 0, \ сумма M_A = 0
Для горизонтального равновесия
\ сумма F_x = 0
R_ {HA} = 0Для вертикального равновесия
\ sum F_y = 0 \\ R_ {VA} -W = 0 \\ R_ {VA} = WПринимая момент относительно A, положительный момент по часовой стрелке и отрицательный момент против часовой стрелки.
WL-M_A = 0
M_A = WLОпределите внутренний сдвиг и изгибающий момент в консольной балке как функцию от x
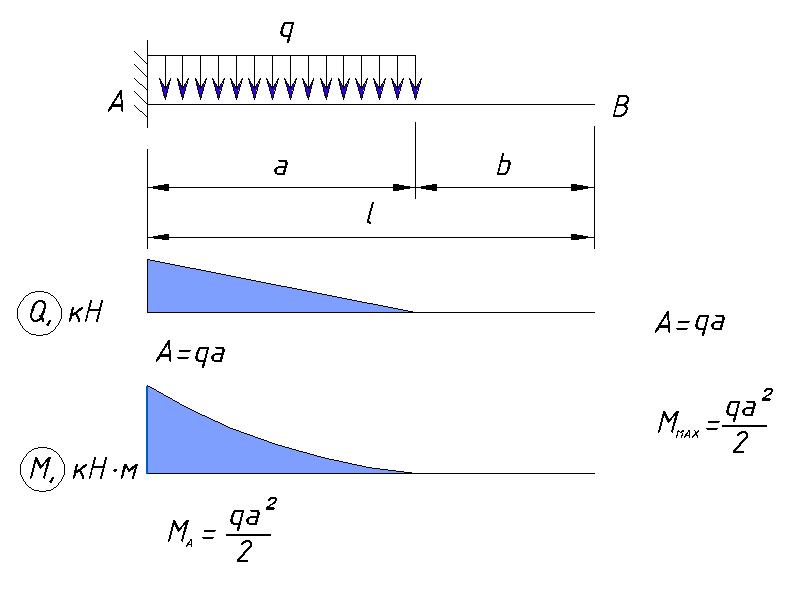
Рассмотрим консольную балку с равномерно распределенной нагрузкой, показанную на рисунке ниже.
Консольная балка с UDLРезультирующая нагрузка, действующая на балку из-за UDL, может быть определена как
W = Площадь прямоугольника
Ш = Д * ш
W = wL
Эквивалентная точечная нагрузка wL будет действовать в центре балки. т.е. при L / 2
Диаграмма свободного тела луча становится
Значение реакции в точке А можно рассчитать, применив условия равновесия.
\ сумма F_y = 0, \ сумма F_x = 0, \ сумма M_A = 0
Для горизонтального равновесия
\сумма F_x=0 \\R_{HA}=0Для вертикального равновесия
\ sum F_y = 0 \\ R_ {VA} -wL = 0 \\ R_ {VA} = wLПринимая момент относительно A, положительный момент по часовой стрелке и отрицательный момент против часовой стрелки.
wL * \ frac {L} {2} -M_A = 0 \\ M_A = \ frac {wL ^ 2} {2}Пусть XX — интересующий участок на расстоянии x от свободного конца.
В соответствии с обсуждавшимся ранее соглашением о знаках, если мы начнем вычислять поперечную силу с Левая сторона или левый конец балки, Сила, действующая вверх принимается как Положительный, и Сила, действующая вниз принимается как Negative.
Сила сдвига в точке A составляет
S.F_A = R_ {VA} = wLв районе ХХ
S.F_x = R_ {VA} -w [Lx] \\ S.F_x = wL-wL + wx = wxСила сдвига в точке B составляет
SF = R_ {VA} -wL \\ S.F_B = wL-wL = 0Значения силы сдвига в точках A и B показывают, что сила сдвига изменяется линейно от фиксированного конца к свободному концу.
Для BMD, если мы начнем вычислять изгибающий момент с Левая сторона или левый конец балки, Момент по часовой стрелке принимается как Положительный и Момент против часовой стрелки принимается как Negative.
BM в A
B.ЮФО и БМДОпределение поперечной силы и изгибающего момента, действующих на расстоянии 2 м от свободного конца консольной балки с равномерно распределенной нагрузкой (UDL)2}{2}=0
Рассмотрим консольную балку с равномерно распределенной нагрузкой, показанную на рисунке ниже. Только w = 20 Н / м. L = 10 м, x = 2 м
Результирующая нагрузка, действующая на балку из-за UDL, может быть определена как
W = Площадь прямоугольника
W = 20 * 10
W = 200 Н
Эквивалентная точечная нагрузка wL будет действовать в центре балки. т.е. при L / 2
Схема свободного тела луча становится,
Значение реакции в точке А можно рассчитать, применив условия равновесия.
\ сумма F_y = 0, \ сумма F_x = 0, \ сумма M_A = 0
Для горизонтального равновесия
\сумма F_x=0 \\R_{HA}=0Для вертикального равновесия
\ sum F_y = 0 \\ R_ {VA} -wL = 0 \\ R_ {VA} = 200 НПринимая момент относительно A, положительный момент по часовой стрелке и отрицательный момент против часовой стрелки.
200*\frac{10}{2}-M_A=0
\\M_A=1000 \;N-mПусть XX — интересующий участок на расстоянии x от свободного конца.
В соответствии с обсуждавшимся ранее соглашением о знаках, если мы начнем вычислять поперечную силу с Левая сторона или левый конец балки, Сила, действующая вверх принимается как Положительный, и Сила, действующая вниз принимается как Negative.
Сила сдвига в точке A составляет
S.F_A = R_ {VA} = wL \\ S.F_A = 200 Нв районе ХХ
S.F_x = R_ {VA} -w [Lx] \\ S.F_x = wL-wL + wx = wxдля x = 2 м
\\ S.F_x = wx = 20 * 2 = 40 \; N
Сила сдвига в точке B составляет
SF = R_ {VA} -wL \\ S.F_B = wL-wL = 0Значения силы сдвига в точках A и B показывают, что сила сдвига изменяется линейно от фиксированного конца к свободному концу.
Для BMD, если мы начнем вычислять изгибающий момент с Левая сторона или левый конец балки, Момент по часовой стрелке принимается как Положительный и Момент против часовой стрелки принимается как Negative. Где m = масса балки. Когда элемент подвергается равным и противоположным парам в плоскости элемента, это определяется как чистый изгиб. При чистом изгибе поперечная сила, действующая на балку, равна нулю. Допущения: материал однороден Закон Крюка применим Член призматический Пара наносится в плоскости члена После гибки не происходит коробления поперечного сечения балки. Профиль деформации должен быть линейным относительно нейтральной оси. Распределение напряжения линейно от нейтральной оси к верхним и нижним волокнам балки. Уравнение Эйлера-Бернулли для изгибающего момента дается формулой M = приложенный изгибающий момент по поперечному сечению балки. I = Второй момент инерции площади σ = изгибное напряжение, вызванное в стержне y = расстояние по вертикали между нейтральной осью луча и желаемым волокном или элементом в мм E = модуль Юнга в МПа R = радиус кривизны в мм Напряжение изгиба для консольной балки диаметром d, а приложенная нагрузка W может быть задана как, Напряжение изгиба будет действовать на неподвижную опору балки. Ответ: Жесткость можно определить как сопротивление прогибу при изгибе или как сопротивление деформации изгибающему моменту. Отношение максимальной нагрузки, приложенной к максимальному прогибу балки, можно назвать жесткостью балки. Ответ: Консольная балка — это балка, один конец которой закреплен, а другой конец — свободен. Неподвижная опора предотвращает смещение и вращательное движение балки на этом конце. Консольная балка позволяет выступать без какой-либо дополнительной поддержки. Когда нагрузка прилагается к свободному концу балки, консоль передает эту нагрузку на опору, где прикладывает поперечную силу [V] и изгибающий момент [BM] к неподвижному концу. Ответ: Для консольной балки, на которую действует равномерно распределенная нагрузка по длине балки, форма диаграммы поперечной силы будет представлять собой линейную кривую и Диаграмма изгибающего момента будет параболической кривой. Ответ: Для консольной балки, подверженной равномерно изменяющейся нагрузке по длине балки, форма диаграммы поперечных сил будет параболической кривой, а диаграмма изгибающего момента будет кубической кривой или кривой третьей степени. Ответ: Для консольной балки заданного пролета максимальное напряжение изгиба будет на фиксированном конце балки. Для направленной вниз нагрузки максимальное растягивающее изгибающее напряжение действует на верхнюю часть поперечного сечения, и макс. Ответ: Для консольной балки, подверженной моменту M по длине балки поперечная сила будет равна нулю, так как на балку не будет действовать внешняя изгибающая сила, а изгибающий момент останется постоянным по всей длине балки. Чтобы узнать о прочности материала (нажмите здесь.)и диаграмма изгибающего момента Открыть ✖Точечная нагрузка, действующая на балку, — это сила, приложенная в одной точке на заданном расстоянии от концов балки.ⓘ Точечная нагрузка [P] Атомная единица силыАттоньютонСантиньютонДеканьютонДециньютондинаэксаньютонFemtonewtonГиганьютонГрамм-силаГраве-силагектоньютонДжоуль / СантиметрДжоуль на метрКилограмм-силаКилоньютонКилопруд Килофунт-силаКип-силаМеганьютонМикроньютонMilligrave — силаМиллиньютонНаноньютонНьютонУнция-силаPetanewtonPiconewtonпрудФунт-фут в квадратную секундуПаундалФунт-силастенТераньютонТон-сила (Long)Тон-сила (метрическая система)Тон-сила (короткий)Йоттаньютон +10% -10% ✖Длина балки определяется как расстояние между опорами. створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр +10% -10%
✖Изгибающий момент — это реакция, возникающая в элементе конструкции, когда к элементу прилагается внешняя сила или момент, вызывающий изгиб элемента.
Грамм-сила-сантиметрКилограмм-сила-метрКилоньютон-метрметр микроньютонМиллиньютон-метрНьютон-метрНьютон Миллиметрстопы паундаль фунт-дюймфунт-сила футаТонна-сила (длинная) Метртонно-сила (метрическая) метртонна-силы (короткий) метр
⎘ копия
👎
Формула
сбросить
👍
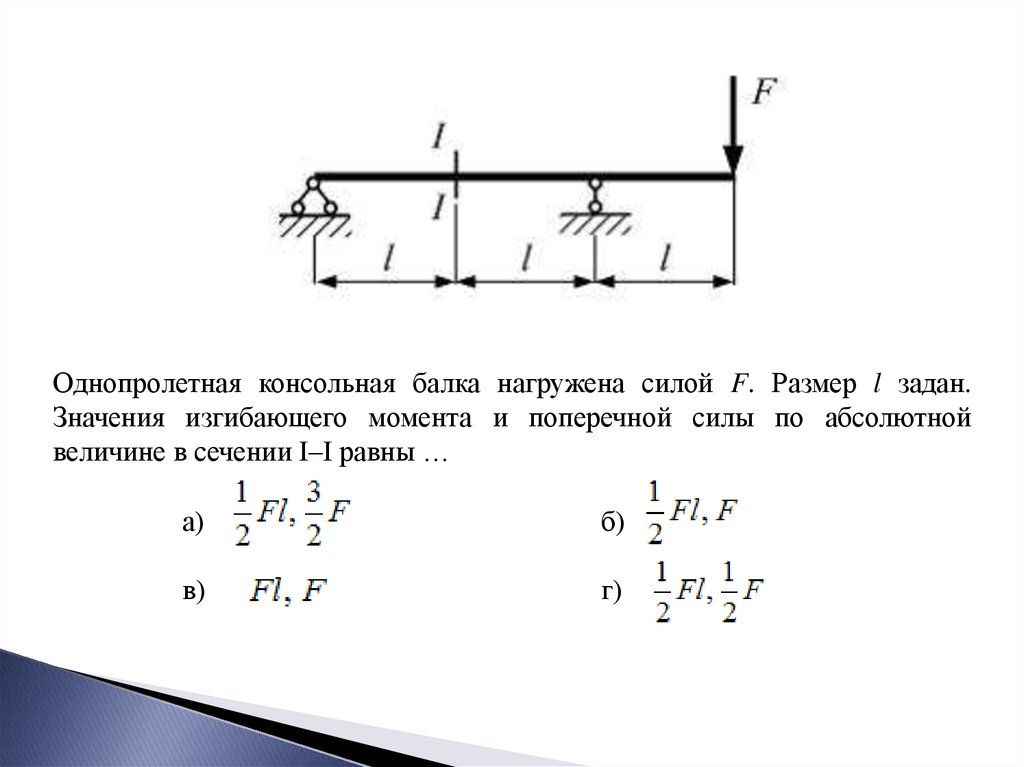
ШАГ 0: Сводка предварительного расчета ШАГ 1.
Изгибающий момент свободно опертых балок при равномерно изменяющейся нагрузке
Идти
Изгибающий момент = 0.1283*Равномерно изменяющаяся нагрузка*Длина балки
Фиксированный конечный момент неподвижной балки, несущей три равномерных точечных нагрузки
 3m}}
3m}} \ frac {M} {I} = \ frac {\ sigma_b} {y} = \ frac {E} {R} {-8}}
{-8}} σ = 3.238 \; МПа
Вопросы и ответы по консольной балкеQ.1 Как называется отношение максимальной нагрузки к максимальному прогибу балки?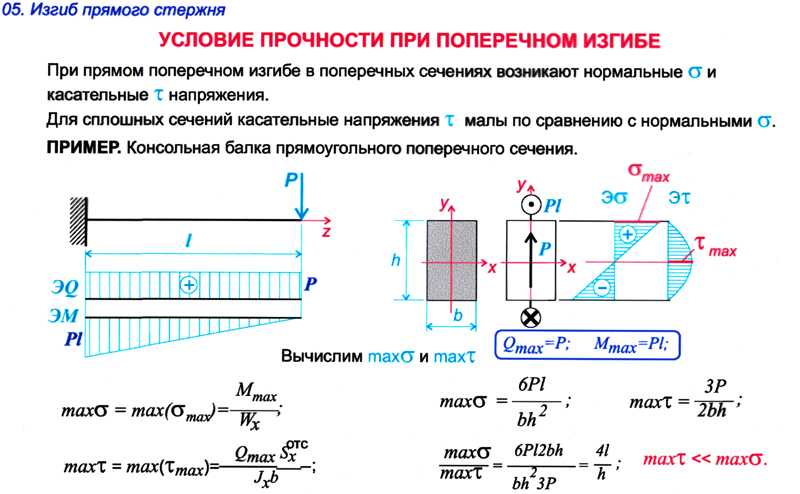 Какова будет форма диаграммы поперечной силы и изгибающего момента?
Какова будет форма диаграммы поперечной силы и изгибающего момента? сжимающее напряжение действует на нижнее волокно балки.
сжимающее напряжение действует на нижнее волокно балки.Максимальный изгибающий момент консольной балки, подверженной точечной нагрузке на свободном конце Калькулятор
 ⓘ Длина балки [l]
ⓘ Длина балки [l]

Максимальный изгибающий момент консольной балки, подверженной точечной нагрузке на свободном конце Решение
 2)/2)
2)/2)
Момент на неподвижном конце неподвижной балки, несущей две равномерно распределенные точечные нагрузки
Идти Фиксированный конечный момент = (2*Точечная нагрузка*Длина балки)/9
Изгибающий момент свободно опертой балки, подвергнутой точечной нагрузке в средней точке
Идти Изгибающий момент = ((Точечная нагрузка*Расстояние x от опоры)/2)
Момент на неподвижном конце неподвижной балки с точечной нагрузкой в центре
Идти Фиксированный конечный момент = (Точечная нагрузка*Длина балки)/8
Максимальный изгибающий момент консоли, подверженной UDL, по всему пролету
Идти Изгибающий момент = (-Нагрузка на единицу длины*Длина балки^2)/2
Максимальный изгибающий момент свободно опертой балки при равномерно распределенной нагрузке
Идти Изгибающий момент = (Нагрузка на единицу длины*Длина балки^2)/8
Максимальный изгибающий момент свободно опертых балок с точечной нагрузкой в центре
Идти Изгибающий момент = (Точечная нагрузка*Длина балки)/4
Максимальный изгибающий момент консольной балки, подверженной точечной нагрузке на свободном конце
Идти Изгибающий момент = (-Точечная нагрузка*Длина балки)
Максимальный изгибающий момент нависающей балки, подверженной сосредоточенной нагрузке на свободном конце
Идти Изгибающий момент = -Точечная нагрузка*Длина свеса
Максимальный изгибающий момент консольной балки, подверженной точечной нагрузке на свободном конце формула
Изгибающий момент = (-Точечная нагрузка*Длина балки)
M = (-P*l)
Что такое изгибающий момент консольной балки, подверженной точечной нагрузке на свободном конце
Изгибающий момент — это реакция, возникающая в консольной балке на неподвижной опоре, когда точечная нагрузка прикладывается к свободному концу консольной балки, заставляя балку болтаться.
Share
Copied!
Консольная балка – Моменты и силы (ручной расчет)
Последнее обновление: 31 декабря 2022 г. самых основ проектирования конструкций и выполнения ручных расчетов: Начнем с одной из наиболее часто используемых статических систем — консольной балки.
В этом посте мы шаг за шагом рассмотрим, как рассчитать силы и моменты консолей для различных ситуаций нагрузки.
Не будем долго говорить, давайте углубимся в это.
🙋♀️ Что такое консоль или консольная балка?
Консоль — это статическая система, действующая как балка при изгибе и сдвиге. Поэтому ее также называют консольной балкой. Он характеризуется наличием только одной опоры — фиксированной — на одном из двух концов.
В повседневной жизни мы окружены консолями. Вероятно, наиболее часто встречающимся примером консолей являются балконы.
Вот 10 примеров консолей
- Светофорные столбы и системы консольные над улицей
- Свесы крыш
- Строительство мостов методом уравновешенной консоли
- Балконы
- Крылья самолета
- Боковые зеркала на автомобиль
- Высотные здания (вертикальные консоли)
- Книжные полки, прикрепленные к стене
- Краны
- Лопасти ветряных турбин
Консоль в большинстве случаев представляет собой горизонтальную балку с фиксированной опорой на одном конце и без опоры на другом конце. Консоль может воспринимать как изгибающие моменты, так и поперечные усилия.
Давайте посмотрим на статическую систему.
Статическая система консольной балкиИз рисунка видно, что неподвижная опора (а) воспринимает
- реакцию момента М
- вертикальная сила реакции V и
- горизонтальная сила реакции H
Понимание статической системы конструкции, вероятно, является одной из самых сложных частей статики и проектирования конструкций в начале.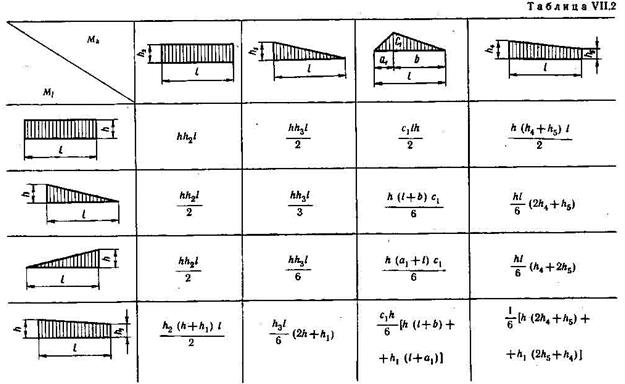
По моему опыту, этому тоже плохо учат в университете, да и информации о нем в сети очень мало, не так ли?
Итак, давайте рассмотрим несколько прикладных примеров.
- Высотные монолитные бетонные основания в качестве вертикальных консолей для придания жесткости зданию при воздействии горизонтальных нагрузок (ветер, землетрясения)
- Свес стропил скатных крыш также можно рассматривать как консольную балку. Однако чаще говорят, что стропила представляют собой неразрезную балку с консольным свесом.
- Столбы наружного освещения и светофора представляют собой вертикальные консольные балки.
- Балконы часто делают консольными. Когда мы говорим о балконах, мы говорим о консольных плитах, однако в большинстве случаев трехмерная конструкция преобразуется в двухмерную систему, как мы увидим далее.

⬇️ 2 примера ситуаций загрузки
Мы хотим, чтобы в этом блоге было немного радостно и реалистично, верно? Итак, давайте посмотрим на сценарии загрузки, к которым мы все можем относиться.
🧍 Я стою на балконе — Точечная нагрузка
Давайте рассмотрим пример, где человек — в данном случае я😊 — стоит на балконе и предположим, что я вешу 75 кг.
Я на балконе.Этот вес 75 кг можно напрямую перевести в 0,74 кН. Теперь, когда я стою двумя ногами в определенной точке, нагрузка сосредоточена, и, следовательно, 0,74 кН равняется точечной нагрузке на консольную плиту.
Как мы видели в предыдущем разделе, плита равна балке, и поэтому мы можем применить точечную нагрузку к консольной балке. 92 * 3м = 14,1 кН/м$
Линейная нагрузка на консольную балку🧮 Ручной расчет изгибающего момента и поперечных усилий – консоль
Теперь для расчета толщины и свойств материала балкона – или любого другого (консольного) конструкции необходимо рассчитать силы и моменты, действующие в балке.
Как правило, статически определимые конструкции, такие как консольные или свободно опертые балки, должны удовлетворять трем условиям равновесия:
- Горизонтальное равновесие $\sum H = 0$: Сумма всех горизонтальных нагрузок и реакций равна 0.
- Вертикальное равновесие $\sum V = 0$: Сумма всех вертикальных нагрузок и реакций равна 0.
- Момент равновесия $\sum M = 0$: Сумма всех моментов равна 0.
Давайте продолжим с двумя ситуациями нагружения, с которыми мы уже знакомы — точечной и линейной нагрузкой.
🔎 Изгибающий момент и поперечные силы от точечной нагрузки
1. Первое, что мы всегда рассчитываем в детерминированных конструкциях, это силы реакции/момент . В нашем случае это $V_a, H_a$ и $M_a$ на опоре A из-за условий равновесия.
Точечная нагрузка, приложенная к консольной балке.$\sum H = 0: H_a = 0$
$\sum V = 0: V_a – 0,74 кН = 0$ -> $V_a = 0,74 кН$
$\sum M = 0: M_a + 0,74 кН \ cdot 0,75m = 0$ -> $M_a = -0,56 кНм$
2. На основе сил реакции можно рассчитать сдвиг и распределение момента вдоль балки. Это также можно сделать без учета сил реакции для консольной балки. Параметр x вводится как длина между точкой a и любой точкой на балке.
На основе сил реакции можно рассчитать сдвиг и распределение момента вдоль балки. Это также можно сделать без учета сил реакции для консольной балки. Параметр x вводится как длина между точкой a и любой точкой на балке.
3. Перерезывающие силы и изгибающие моменты можно рассчитать в зависимости от x. Сделаем первый разрез в точке между опорой и точечной нагрузкой 0 Как и при расчете силы реакции, условия равновесия используются для расчета момента и поперечной силы в точке x $\sum H = 0: H_a = 0$ $ \sum V = 0: 0,74 кН – V_x = 0$ -> $V_x = 0,74 кН$ $\sum M = 0: M_x – (-0,56 кНм) – 0,74 кН \cdot x = 0$ -> $M_x = -0,56 кНм + 0,74 кН \cdot x$ Как мы видим, поперечная сила постоянна и не зависит от параметра x. Положим x = 0,5м и посмотрим, какие результаты мы получим для изгибающего момента: $M_{0,5м} = -0,56 кНм + 0,74 кН \cdot 0,5м = -0,19 кНм$ 4. Условия равновесия приводят к $\sum H = 0: H_a = 0$ $\sum V = 0: 0,74 кН – V_x – 0,74 кН = 0$ -> $V_x = 0 кН$ $\sum M = 0: M_x – (-0,56 кНм) – 0,74 кН \cdot x + 0,74 кН \cdot (x-0,75м) = 0$ $M_x = -0,56 кНм + 0,74 кН \cdot x – 0,74 кН \cdot x + 0,74 кН \cdot 0,75м = 0$ .. и на этом рисунке очень быстро видно, что изгибающий момент и поперечная сила равны 0. 5. Диаграммы изгибающего момента и силы сдвига Диаграммы могут быть построены с помощью инструмента, такого как Excel, с использованием приведенных выше формул или нарисованы вручную, если известна геометрическая форма распределения. Диаграмма поперечной силы – консоль Диаграмма изгибающего момента – консольная 1.Что касается точечной нагрузки, мы сначала вычисляем силы реакции $V_a, H_a$ и момент $M_a$ в детерминированной структуре – консольная балка – из-за условий равновесия. $\sum H = 0: H_a = 0$ $\sum V = 0: V_a – 14,1 кН/м \cdot 1,0m = 0$ -> $V_a = 14,1 кН$ $\sum M = 0 : M_a + 14,1 кН/м \cdot 1,0м \cdot 0,5м = 0$ -> $M_a = -7,05 кНм$ 2. Расчет распределения сдвига и момента вдоль балки от сил реакции. Это также можно сделать без учета сил реакции консольной балки. Параметр x вводится как длина между точкой a и любой точкой на балке. 3. Перерезывающие силы и изгибающие моменты можно рассчитать в зависимости от x. Сделаем разрез в точке между опорой и концом консоли 0 Как и при расчете силы реакции, условия равновесия используются для расчета момента и поперечной силы в точке x. $\sum H = 0: H_a = 0$ $\sum V = 0: V_x + 14,1 кН/м \cdot x – 14,1 кН = 0$ -> $V_x = 14,1кН – 14,1 кН/м \ cdot х$ 92}{2} = -1,76 кНм$ 4. Диаграммы изгибающего момента и силы сдвига Диаграммы могут быть построены с помощью инструмента, такого как Excel, с использованием приведенных выше формул или нарисованы вручную, если известны геометрические форма распределения. Диаграмма поперечной силы – консоль Диаграмма изгибающего момента – консоль После расчета сил и моментов необходимо выполнить расчет элемента. В нашем случае это проект балкона из бетона и арматуры, то есть мы выбираем тип бетона, рассчитываем необходимое количество арматуры и проверяем высоту поперечного сечения. Теперь я хотел бы услышать от вас: какой кантилевер вы знаете из «реального мира»? Я что-то забыл? Дайте нам знать в комментариях ниже📝 Колебания консольных балок: Отклонение, частота и исследовательское использование Кому: д-р Негабан ЭнгрМ 325H Скотт Уитни 23 апреля 1999 г. Введение Измерения свойств тонких пленок затруднены по сравнению с
сыпучие материалы. Один из способов нахождения модуля упругости тонкой
фильм из частотного анализа консольной балки. Прямая, горизонтальная
консольная балка под действием вертикальной нагрузки деформируется в кривую. Когда это
усилие снимается, балка возвращается к своей первоначальной форме; однако,
его инерция будет удерживать луч в движении. Таким образом, балка будет колебаться в
его характерные частоты. Если на пучок напылить тонкую пленку,
жесткость на изгиб изменится. Это изменение вызывает частоту
вибрации для переключения. Если измерить частотный сдвиг, пленки
можно рассчитать модуль упругости. Установка тонкой консольной балки Балки, изучаемые в этой статье, представляют собой длинные, тонкие, консольные балки. Фигура
1 ниже показан такой пучок. Один конец балки закреплен, а другой
конец свободен. Начало координатной оси находится на фиксированном конце, точка А . Рис. 1: Типовая изученная консольная балка Прогиб консольной балки Если свободный конец консольной балки подвергается точечной нагрузке, P ,
луч отклонится в кривую. См. рис. 2 ниже. Чем больше
нагрузка, тем больше прогиб, (x) . Рис. 2: Прогиб консольной балки под нагрузкой на закрепленном конце Если предположить, что балка претерпевает небольшие отклонения, она находится в линейно-упругом
область и имеет однородное поперечное сечение, следующие уравнения могут быть
используется (Гир, стр. Кривизна балки,
равна второй производной прогиба (2а) — Определение уравнений Когда сила P снимается со смещенной балки, балка
вернется к своей первоначальной форме. Однако инерция луча вызовет
луч вибрирует вокруг этого начального местоположения. Предполагая эластичность
модуль, инерция и площадь поперечного сечения ( A ) постоянны вдоль
длина балки, уравнение для этой вибрации (Вольтерра, стр. Уравнение (5) теперь можно записать в виде двух дифференциальных уравнений (Вольтерра,
п. Общее решение уравнения (6а) представляет собой линейную комбинацию тригонометрических
уравнения (Вольтерра, стр.312) Уравнения (8a) и (8b) можно объединить, чтобы получить (10) По Вольтерре, с. Подстановка уравнения (9) в (8a) или (8b) приведет к частоте
уравнение для консольной балки, Рис. 3: Константы колебаний консольной балки. Обратите внимание, поскольку
cosh( x ) большое, когда x большое, k n L потребности
найти с высокой точностью. Для каждой частоты существует характеристическая вибрация (Вольтерра,
п. 319) — Примеры режимов вибрации Типовые значения A n и частоты (для используемых лучей
в этом исследовании) показаны на рисунке 3 выше. Обратите внимание, что только первый
немногие моды вибрации имеют значительно большие значения константы А н . Таким образом, модами колебаний более высокого порядка можно пренебречь. Рисунок 4: Начальное смещение, вызванное каждой модой. С течением времени каждая мода будет вибрировать вокруг нулевого смещения.
линии с частотой, указанной на рисунке 3 выше. Рисунок 5 ниже показывает
эта вибрация для первых двух режимов, более высокие режимы действуют аналогично.
общее движение луча сложное; каждая характерная мода вибрирует с
различного размера, формы и частоты. Следующие файлы можно загрузить для просмотра анимации первого
несколько мод и полная вибрация консольной балки. Чтобы просмотреть их,
Необходимо загрузить Lotus Screencam Player: Scplayer. Общее движение: 325Htot.exe На рис. 6 ниже показаны показания пьезоэлектрического датчика, расположенного
вблизи закрепленного конца балки; этот датчик показывает взаимодействие каждого
режим вибрации. Также показана вибрация, предсказанная из уравнения (12)
в этом месте. Фактический и предсказанный сигналы почти идентичны;
основное различие между ними — демпфирование (как вязкое, так и Кельвина-Фойгта).
колебаний высших порядков в реальном сигнале. Рисунок 5: Вибрации первых двух характерных мод; другие режимы
вибрировать аналогично. Время t в микросекундах. Рисунок 6: Сигнал ZnO от вибрирующей консольной балки по сравнению с
теоретические колебания. Измерение модуля упругости
для тонких пленок -Причина использования частотного анализа Если консольную балку напылить тонкой пленкой, то изгиб
жесткость изменится. Рис. 7. Консольно-лучевое напыление, покрытое тонкой пленкой Теоретически жесткость можно определить по стационарной балке
под нагрузкой, P , см. формулы (2a,b). Предположим, что изгибная жесткость
был увеличен путем добавления тонкой пленки к пучку. Тогда, при условии применения
нагрузка была постоянной, прогиб на свободном конце уменьшится. Для
Для типичной балки, описанной выше, это изменение смещения чрезвычайно мало.
Например, алюминиевая балка с начальным перемещением (на свободном конце)
0,55 мм будет иметь начальное смещение 0,49мм при относительно
толстый (8м) ZnO
фильм. Однако тот же луч, покрытый ZnO, будет иметь свою основную частоту,
сдвиг с 329,7 Гц на 342,0 Гц. Для измерения можно использовать любой осциллограф.
вибрации балок, см. рис. 6 выше. Если взято достаточно точек данных,
преобразование Фурье сигнала может измерять частотные сдвиги, даже если
не более 0,2 Гц. Следовательно, частотный сдвиг может быть известен с помощью
высокая точность и возможность расчета модуля упругости пленки. — Определение уравнений Все уравнения, полученные в предыдущих разделах (1-13), по-прежнему можно
применяться к двухкомпонентной балке, если несколько констант изменены: EI заменен на E s I s +E f I f и исправлено
как показано ниже. Линейная массовая плотность балки с покрытием теперь (15) Заключение Из-за небольшого размера тонких пленок обычные методы измерения
их свойства часто не работают. Эти свойства тонкой пленки могут отличаться
от свойств объемного материала. Поэтому альтернативные методы измерения
должны быть разработаны. Одним из таких методов является вибрация консольных балок. Разрезать в точке между точечной нагрузкой и конечной точкой 0
Разрезать в точке между точечной нагрузкой и конечной точкой 0 Консольная балка.
Консольная балка. 👨🏫 Изгибающий момент и поперечные силы от линейной нагрузки

Вибраций консольных балок:
Вибраций консольных балок:
 Типичная балка, используемая в этом исследовании, имеет длину L = 30 мм, с = 5 мм в ширину и t = 0,5 мм в толщину. Материал балки нужно выбирать
так что его жесткость отличается от жесткости тонких пленок так, что
сдвиг частоты значителен. В этом исследовании использовались пленки оксида цинка (около
толщиной 5 м), поэтому
хорошая подложка — алюминий.
Типичная балка, используемая в этом исследовании, имеет длину L = 30 мм, с = 5 мм в ширину и t = 0,5 мм в толщину. Материал балки нужно выбирать
так что его жесткость отличается от жесткости тонких пленок так, что
сдвиг частоты значителен. В этом исследовании использовались пленки оксида цинка (около
толщиной 5 м), поэтому
хорошая подложка — алюминий. 602).
602). 310)
310)
Разделив уравнение (3) на X(x)f(t) : (5)
Поскольку левая часть уравнения (5) не меняется при изменении t ,
правая часть должна быть константой. Аналогично, поскольку правая половина уравнения
(5) не меняется как x варьируется, левая половина должна быть константой.
Поскольку каждая сторона постоянна, уравнение (4) справедливо, и метод
можно использовать разделение переменных. Обозначим эту константу.
Можно показать, что
является реальной величиной, и что
— собственные частоты луча. 311),
311), 312, константы C n ар
произвольный. Однако для того, чтобы динамическое решение для смещения
быть равным статическому решению (в момент времени t =0), C 2 должно быть равно ½. С этим значением для C 2 , X n (0)=0 и X n (L)=1 .
312, константы C n ар
произвольный. Однако для того, чтобы динамическое решение для смещения
быть равным статическому решению (в момент времени t =0), C 2 должно быть равно ½. С этим значением для C 2 , X n (0)=0 и X n (L)=1 .
 Чтобы получить полное перемещение консольной балки, просто добавьте все
смещения, найденные в уравнении (12) для каждой моды. Ниже на Рисунке 4 показано
смещение, вызванное каждой модой на т =0; также включено
полное начальное перемещение балки. От этих перемещений
видно, что даже третья характеристическая мода мало влияет на
полное смещение балки.
Чтобы получить полное перемещение консольной балки, просто добавьте все
смещения, найденные в уравнении (12) для каждой моды. Ниже на Рисунке 4 показано
смещение, вызванное каждой модой на т =0; также включено
полное начальное перемещение балки. От этих перемещений
видно, что даже третья характеристическая мода мало влияет на
полное смещение балки. exe
exe
1-й режим:
325h2st.exe
2-й режим:
325h3nd.exe
3-й режим:
325h4rd.exe
4-й режим:
325h5th.exe Изменение жесткости будет напрямую влиять на частоту
колебаний балок. Таким образом, модуль упругости пленки может быть
определяется по этому смещению частоты. См. рисунок 7 для схематического рисунка.
распыленного пучка; индекс s относится к подложке, а f
относится к фильму. Обратите внимание, высота фильма сильно преувеличена,
с .
Изменение жесткости будет напрямую влиять на частоту
колебаний балок. Таким образом, модуль упругости пленки может быть
определяется по этому смещению частоты. См. рисунок 7 для схематического рисунка.
распыленного пучка; индекс s относится к подложке, а f
относится к фильму. Обратите внимание, высота фильма сильно преувеличена,
с . Изменение в 0,06 мм слишком мало, чтобы его можно было измерить любым обычным
инструменты и более тонкая пленка ZnO (1 м)
даст неизмеримую разницу в водоизмещении. Таким образом, стационарный
измерения модуля упругости пленок затруднены, если не
невозможный.
Изменение в 0,06 мм слишком мало, чтобы его можно было измерить любым обычным
инструменты и более тонкая пленка ZnO (1 м)
даст неизмеримую разницу в водоизмещении. Таким образом, стационарный
измерения модуля упругости пленок затруднены, если не
невозможный.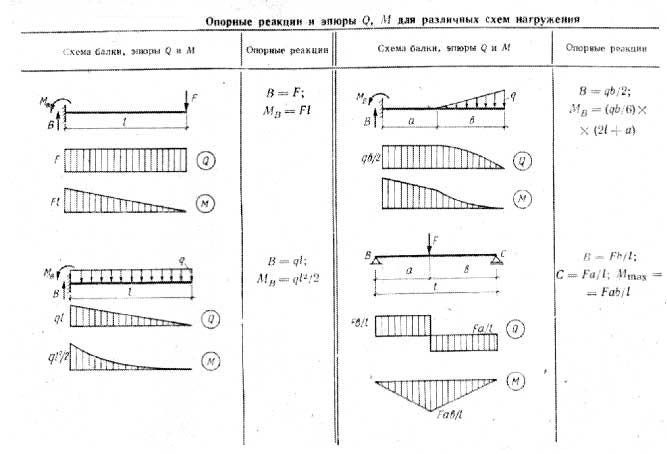 Предположения, изложенные ранее, все еще должны выполняться:
малые прогибы, линейно-упругие и однородное поперечное сечение. Последний
предположение означает, что толщина пленки не может меняться вдоль луча (сложная
делать при напылении длинных балок).
Предположения, изложенные ранее, все еще должны выполняться:
малые прогибы, линейно-упругие и однородное поперечное сечение. Последний
предположение означает, что толщина пленки не может меняться вдоль луча (сложная
делать при напылении длинных балок).