пошаговая инструкция — Строительный портал ПрофиДОМ

Под кубатурой помещения обычно подразумевается его объем, выраженный в кубических метрах. Если известны основные параметры помещения (длина, ширина и высота), то вычислить его кубатуру очень просто.

Однако, если строение имеет сложную форму, то посчитать его объем бывает довольно-таки затруднительно.

Как это сделать правильно. Для это нужно заглянуть на страницы он-лайн журнала ProfiDom.com.ua и прочитать нижеследующую пошаговую инструкцию

Для вычисления объемы помещения нам понадобится только калькулятор.

Шаг 1. Чтобы вычислить кубатуру помещения перемножьте его длину, ширину и высоту. То есть воспользуйтесь формулой:

К = Д х Ш х В, где:

К – кубатура помещения (объем, выраженный в кубических метрах),

Д, Ш и В – длина, ширина и высота помещения, выраженные в метрах, соответственно.

Например, если длина помещения составляет 11 метров, ширина – 5 метров, а высота – 2 метра, то его кубатура будет 11 х 5 х 2 = 110 кубометров.

Шаг 2. Если одна или несколько характеристик помещения неизвестны, то измерьте их, воспользовавшись строительной рулеткой или электронным дальномером. При использовании электронного дальномера следите, чтобы он был направлен строго перпендикулярно той стене, расстояние до которой измеряется. Чтобы повысить точность вычислений, высоту и ширину измерьте дважды – у противоположных стен, а затем найдите среднее арифметическое (сложите и разделите на 2).

Шаг 3. Пусть, например, измерения длины помещения показали 10,01 м и 10,03 м, измерения ширины – 5,25 м и 5,26 м, а измерение высоты – 2,50 м. В таком случае, кубатура помещения будет равняться:

(10,01+10,03)/2 х (5,25+5,26)/2 х 2,5 = 131,638

(в большинстве случаев, трех знаков после запятой вполне достаточно).

Шаг 4. Если известка площадь помещения, то для вычисления кубатуры просто умножьте эту площадь на высоту. Т.е., используйте формулу:

К = П х В, где 

П – площадь помещения, заданная в квадратных метрах (м²).

Так, например, если площадь помещения равняется 100 квадратных метров, а его высота – 3 метра, то его объем будет: 

100х3=300 (метров кубических).

Шаг 5. Если помещение имеет сложную форму, то для определения его площади воспользуйтесь соответствующими геометрическими формулами или разделите помещение на более простые участки. 

Так, например, арена цирка всегда имеет форму круга радиусом 13 метров. Следовательно, ее площадь будет равна πR²=3,14 х 169 = 531 (метр квадратный).

Если же, например, помещение состоит из трех комнат площадью 30, 20 и 50 м², то общая площадь помещения будет равняться 100 м².

Детальніше в цій категорії: « Как построить очистные сооружения для бытовых ливневых стоков При софинансировании жильцов коммунальщики работают лучше »

вгору

Калькулятор расчета объема резервуара и перевод литров в кубы в ООО ЗРК

Перевод литров в кубы

Выберете среду: ВодаБензинМолокоДиз.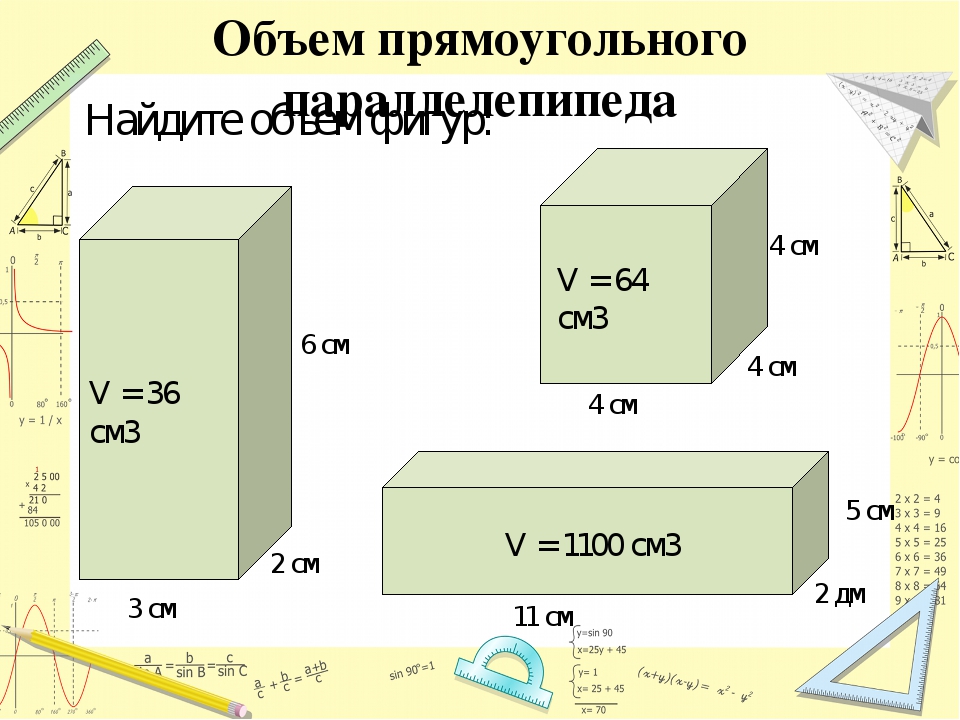 топливоМаслоНефтьСпирт

Введите объем в литрах:

Единица измерения объема – это кубический метр. Данный факт относится к числу общепринятых аксиом. Сторона этого куба равна одному метру. Этот показатель принято использовать, если необходимо определить объем бака, резервуара, либо цистерны. Определенные трудности вызывает расчет в связи с тем, что жидкости принято мерить в литрах. Пытаясь рассчитать величину актуального для хранения и сохранения жидкой субстанции резервуара либо цистерны, нужно учесть еще и вес вещества. Он не соответствует количеству литров.

Расчет объема резервуара

Выберите форму: ПрямоугольнаяЦилиндрическая

Длина в метрах:

Ширина в метрах:

Высота в метрах:

Всем, кто прилежно изучал школьный курс физики, известно, что минимальной площадью поверхности при максимальном объеме обладает сосуд в форме шара. Но шарообразные емкости сложны в изготовлении и непрактичны, поэтому производители изготавливают емкости в форме цилиндра или куба (прямоугольника).

ЦИЛИНДРИЧЕСКИЕ ЕМКОСТИ

Могут располагаться горизонтально или вертикально. Объем рассчитывается по формуле V=πr2h. То есть умножаем число π (3,14159) на радиус в квадрате и на высоту h цилиндра.

Пример: есть вертикальный цилиндрический резервуар диаметром 3 метра и высотой 5 метров. Рассчитываем объем: Радиус – 1,5 метра, в квадрате будет 2,25. Умножаем: 3,14159 ×2.25 ×5 (высота) = 35,34 м3. Итого, рабочий объем нашего резервуара будет равен 35 кубическим метрам, или 35 000 литрам (в 1 кубе – 1000 литров).

На практике конкретные размеры резервуара рассчитываются с учетом его функциональности. Например, горизонтальный резервуар диаметром 1 метр и длиной 10 метров будет просто неудобен в использовании. Его объем составит 7,8 куба. Если нам нужен резервуар такого объема, уместнее увеличить его диаметр и уменьшить длину – например, сделать диаметр 2 метра при длине 3 метра. Получим те же 7,8 куба при гораздо более функциональных размерах.

ПРЯМОУГОЛЬНЫЕ ЕМКОСТИ

Здесь все еще проще. Чтобы узнать полный объем, достаточно длину емкости умножить на ее ширину и высоту. Например, кубический резервуар со стороной 1 метр будет вмещать 1 куб жидкости. Емкость размером 3000 мм × 2000 мм × 2500 мм будет иметь объем 15 кубометров.

Почему большинство резервуаров имеют не квадратную или прямоугольную, а цилиндрическую форму? Потому что конструктивно такие емкости являются более прочными. Чтобы сварить куб, нужны 6 листов стали и 12 сварных швов. Цилиндрическая емкость имеет всего 3 поверхности: два круглых дна и цилиндрический корпус.

Корпус может быть сварен из одного листа металла, свернутого в цилиндр, для этого нужен всего 1 сварной шов. Плюс еще два круговых шва, чтобы приварить днища. Итого, в идеальном варианте всего 3 сварных шва – вместо 12 у куба.

Зачем тогда делают прямоугольные емкости? У них есть свои сферы использования. Например, их применяют в качестве пожарных емкостей – они обладают отличной эргономикой и хорошо вписываются в помещения, занимая минимум места.

В нашей компании вы можете заказать резервуар практически любого типа, формы и назначения. Мы предлагаем как типовые варианты, так и изготавливаем продукцию на заказ. Зная основные принципы расчета размеров и объема резервуаров, вы можете оценить, какой вариант для вас окажется наиболее подходящим.

Выбрать подходящую ёмкомсть в каталоге, производство металлических ёмкостей для разных задач.

Построение и применение доказуемых положительных и точных кубатурных формул | Журнал численного анализа IMA

Фильтр поиска панели навигации IMA Journal of Numerical AnalysisIMA JournalsЧисленный анализКнигиЖурналыOxford Academic Мобильный телефон Введите поисковый запрос

Закрыть

Фильтр поиска панели навигации IMA Journal of Numerical AnalysisIMA JournalsЧисленный анализКнигиЖурналыOxford Academic Введите поисковый запрос

Расширенный поиск

Журнальная статья

Получить доступ

Ян Глаубиц

Ян Глаубиц

Ищите другие работы этого автора на:

Оксфордский академический

Google Scholar

Журнал численного анализа IMA , drac017, https://doi. org/10.1093/imanum/drac017

Опубликовано:

20 мая 2022 г.

История статьи

9 0002 Фильтр поиска панели навигации IMA Journal of Numerical AnalysisIMA JournalsЧисленный анализКнигиЖурналыOxford Academic Мобильный телефон Введите поисковый запрос

Закрыть

Фильтр поиска панели навигации IMA Journal of Numerical AnalysisIMA JournalsЧисленный анализКнигиЖурналыOxford Academic Введите поисковый запрос

Advanced Search

Abstract

Многие приложения требуют многомерного численного интегрирования, часто в форме кубатурной формулы (CF). Желательно, чтобы эти КФ были положительными и точными для некоторых конечномерных функциональных пространств (и весовых функций). Хотя существует несколько эффективных процедур построения положительных и точных CF для многих стандартных случаев, в более общих условиях сделать это по-прежнему сложно. Здесь мы показываем, как можно использовать метод наименьших квадратов (LS) для получения доказуемых положительных и точных формул в общей многомерной обстановке. Таким образом, процедура использует только основные операции линейной алгебры, такие как решение задачи LS. В частности, доказано, что результирующие КФ ЛС гарантированно положительны и точны, если используется достаточно большое количество равнораспределенных точек данных. Мы также обсуждаем применение доказуемых положительных и точных КФ ЛП для построения вложенных устойчивых правил высокого порядка и положительных интерполяционных формул. Наконец, наши результаты проливают новый свет на некоторые существующие методы многомерного численного интегрирования и ограничения, при которых обеспечивается их успех.

© Автор(ы), 2022 г. Опубликовано Oxford University Press от имени Института математики и ее приложений. Все права защищены.

Раздел выпуска:

Статьи

В настоящее время у вас нет доступа к этой статье.

Скачать все слайды

Войти

Получить помощь с доступом

Получить помощь с доступом

Доступ для учреждений

Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:

Доступ на основе IP

Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.

Войдите через свое учреждение

Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.

1. Нажмите Войти через свое учреждение.
2. Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
3. Находясь на сайте учреждения, используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
4. После успешного входа вы вернетесь в Oxford Academic.

Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.

Войти с помощью читательского билета

Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.

Члены общества

Доступ члена общества к журналу достигается одним из следующих способов:

Войти через сайт сообщества

Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:

1. Щелкните Войти через сайт сообщества.
2. При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
3. После успешного входа вы вернетесь в Oxford Academic.

Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.

Вход через личный кабинет

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. См. ниже.

Личный кабинет

Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.

Просмотр учетных записей, вошедших в систему

Щелкните значок учетной записи в правом верхнем углу, чтобы:

• Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.
• Просмотр институциональных учетных записей, предоставляющих доступ.

Выполнен вход, но нет доступа к содержимому

Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.

Ведение счетов организаций

Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д.

Покупка

Стоимость подписки и заказ этого журнала

Варианты покупки книг и журналов в Oxford Academic

Краткосрочный доступ

Чтобы приобрести краткосрочный доступ, пожалуйста, войдите в свой личный аккаунт выше.

У вас еще нет личного кабинета? регистр

Построение и применение доказуемых положительных и точных кубатурных формул — доступ 24 часа

ЕВРО €36,00

32 фунта стерлингов

39 долларов США.

Реклама

Цитаты

Альтметрика

Дополнительная информация о метриках

Оповещения по электронной почте

Оповещение об активности статьи

Предварительные уведомления о статьях

Оповещение о новой проблеме

Получайте эксклюзивные предложения и обновления от Oxford Academic

Ссылки на статьи по телефону

• Последний

• Самые читаемые

• Самые цитируемые

C ⁰ — гибридные методы высокого порядка для бигармонических задач

Оценки погрешности линейной складной модели

Класс регуляризаций на основе нелинейной изотропной диффузии для обратных задач

Оценка максимальной нормы апостериорной ошибки для задач конвекции-диффузии

Неперекрывающиеся спектральные аддитивные методы Шварца для гибридных разрывных дискретизаций Галеркина

Реклама

Адаптивная кубатурная формула для эффективной оценки надежности нелинейных структурно-динамических систем

Адаптивная кубатурная формула для эффективной оценки надежности нелинейных структурно-динамических систем

• Сюй, июнь
;
• Конг, Вентилятор

Аннотация

Оценка распределения экстремальных значений (EVD) является важной темой анализа надежности нелинейных структурно-динамических систем. В данной работе предлагается новый метод получения БВВЭ. Метод максимальной энтропии (MEM) с дробными моментами в качестве ограничений используется для получения всего диапазона EVD. Затем предлагается адаптивная кубатурная формула для оценки дробных моментов, участвующих в МЭМ, которая тесно связана с эффективностью и точностью анализа надежности. Наборы из трех очков, которые включают в себя в общей сложности 2d ² + 1 точка интегрирования в размерности d генерируется в предложенной формуле. В связи с этим обеспечивается эффективность предлагаемой формулы. Кроме того, вводится «свободный» параметр, делающий предложенную формулу адаптивной по размерности. Параметр «свободный» определяется путем размещения одного набора точек, примыкающего к границе гиперсферы, содержащей основную часть полной вероятности. В связи с этим можно лучше воспроизвести хвостовое распределение и точнее оценить дробные моменты. Наконец, предложенный метод применяется к десятиэтажной каркасной конструкции сдвига при сейсмических воздействиях, которая проявляет сильную нелинейность.