Формула Мора. Правило Верещагина презентация, доклад
Формула Мора
Правило Верещагина
Доцент кафедры
самолетостроения
к.т.н. Мухин Д.В.
1. Интеграл Мора
Используется в тех случаях, когда требуется найти перемещение в направлении не совпадающем с направлением действия сил.
Сущность интеграла Мора в следующем идеальном построении:
1. Прикладываем в интересующем направлении внешнюю силу Ф.
2. Составляем для системы выражение для потенциальной энергии деформации U.
3. Дифференцируем выражение для U по Ф и получаем выражение для перемещения в направлении действия Ф (то есть в интересующем направлении)
4. В полученном выражении приравниваем Ф=0, получаем окончательное выражение.
Фиктивную силу Ф представляем в виде произведения скалярной величины Ф на единичный силовой фактор в соответствующем направлении.
Таким образом фиктивная сила в зависимости от интересующего нас направления будет выражена:
— в случае продольной силы. Определяем продольное перемещение. N1 – единичная продольная сила приложенная в интересующей нас точке.
— в случае горизонтальной перерезывающей силы. Определяем прогиб в горизонтальной плоскости. Qz1 – единичная горизонтальная перерезывающая сила приложенная в интересующей нас точке.
— в случае вертикальной перерезывающей силы. Определяем прогиб в вертикальной плоскости. Qy1 – единичная горизонтальная перерезывающая сила приложенная в интересующей нас точке.
— в случае крутящего момента. Определяем угол закручивания. MK1 – единичный крутящий момент приложенный в интересующей нас точке.
— в случае момента изгибающего в горизонтальной плоскости. Определяем угол поворота сечения в горизонтальной плоскости. My1 – единичный изгибающий момент в горизонтальной плоскости приложенный в интересующей нас точке.
— в случае момента изгибающего в вертикальной плоскости. Определяем угол поворота сечения в вертикальной плоскости. Mz1 – единичный изгибающий момент в вертикальной плоскости приложенный в интересующей нас точке.
После приложения фиктивной силы Ф значения силовых факторов в интересующем сечении будут равны сумме значений силовых факторов от исходной системы сил и от силы Ф.
— значения силовых факторов
до приложения силы Ф. (То есть в реально существующей системе)
Подставляем в формулу для внутренней энергии:
Дифференцируя по Ф, и принимая после этого Ф=0, находим перемещение.
(формулы громоздкие, поэтому на примере одного слагаемого)
Суммируя все интегралы находим перемещение
Формула носит название формула Мора, а входящие в формулу интегралы – интегралы Мора
Пример
Балка прямоугольного сечения с размерами b и 2b нагружена моментом М.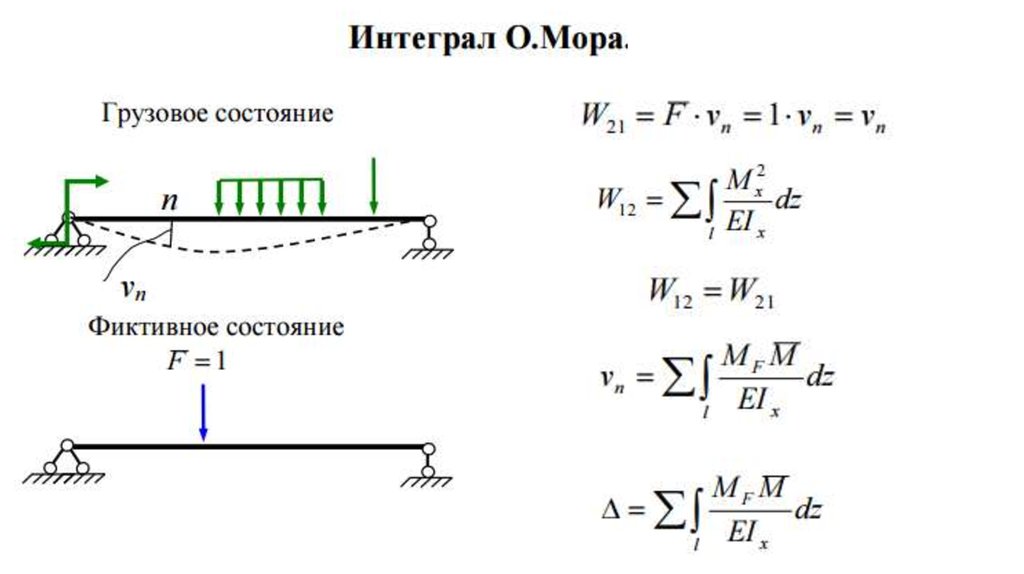 Модуль упругости материала Е, длина l заданы. Найти прогиб концевого сечения балки С
Модуль упругости материала Е, длина l заданы. Найти прогиб концевого сечения балки С
Решение
1. Строим эпюр изгибающего момента
Мx
x
М
l
2. Прикладываем единичную внешнюю силу в направлении интересующего перемещения
3. Строим эпюр изгибающего момента от единичной силы
Мx
x
М=-x
l
4. Составляем интеграл Мора
F=1
x
Mz
Mz=-xF=-x
5. Вычисляем интеграл
Интеграл Мора можно использовать для определения перемещений как прямолинейных, так и криволинейных стержневых систем.
Поскольку интеграл Мора вычисляется по длине, для криволинейных стержней вместо dx в подынтегральном выражении используется элемент длины дуги ds=ρdφ
где ρ — радиус кривизны стержня, который может быть постоянным, а может быть функцией от угловой координаты φ.
ρ
φ2
ds
dφ
φ1
φ
Пример:
Для кривого бруса в форме четверти круга найти горизонтальное перемещение точки А.
Нарисуем вспомогательную единичную систему и нагрузим ее горизонтальной единичной силой в точке А.
В полярной системе координат положение произвольного сечения характеризуется радиусом-вектором ρ (в нашей задаче ρ = Const — радиус круга) и углом φ от произвольно выбранной начальной точки дуги.
Изгибающий момент от внешних сил
Изгибающий момент от единичной силы
Горизонтальное перемещение точки А
Правило Верещагина
Правило Верещагина – графо-аналитический метод, позволяющий упростить вычисления интегралов, входящих в формулу Мора. Упрощение основано на том, что эпюры от единичных силовых факторов на прямолинейных участках оказываются линейными.
Предположим, что необходимо взять интеграл от произведения двух функций
Пусть вторая из этих функций — линейная
Тогда
Первый интеграл – площадь эпюры f1(z)
Второй интеграл – статический момент этой эпюры относительно оси ординат
По свойству статического момента
В сумме получаем
Выражение в скобках – значение функции f2 под центром тяжести первой фигуры
zЦТ – координата центра тяжести первого эпюра
h
ЦТ
h
ЦТ
h
ЦТ
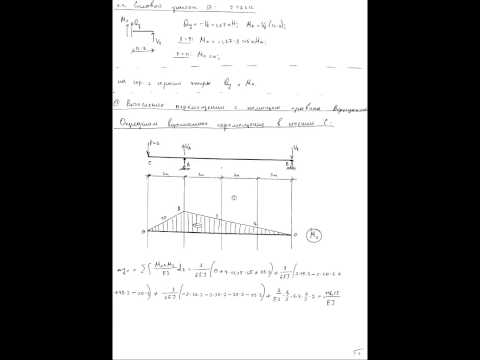
Пример
Однопролетная двухконсольная балка нагружена силой и моментом. Жесткость поперечного сечения на изгиб по длине постоянна. Линейный размер l задан. Найти прогиб сечения С от внешней нагрузки по абсолютной величине. (Влиянием поперечной силы на величину перемещения пренебречь).
1. Строим эпюр изгибающего момента от действительной нагрузки
2. Прикладываем единичную нагрузку в направлении интересующего перемещения
2. Прикладываем единичную нагрузку в направлении интересующего перемещения
3. Строим эпюр момента от приложенного единичного фактора
4. Находим интеграл Мора по правилу Верещагина
3. Формула Мора для определения температурных перемещений сечения по заданному направлению
В основу вывода формулы положен принцип возможных перемещений
Пусть дана система, находящаяся под действием температуры. Обозначим: n — число участков системы; i — номер ее произвольного участка.
Для определения перемещения сечения С по направлению v рассмотрим систему без температуры, нагруженную безразмерной обобщенной единичной силой, приложенной в сечении С по направлению v.
Схему системы под действием температуры обозначим Т, а схему нагружения системы обобщенной единичной силой обозначим 1. Приняв за возможное перемещение системы ее деформированное состояние в схеме Т, найдем работу внешних, реактивных и упругих сил схемы нагружения 1 на этом возможном перемещении. По принципу возможных перемещений сумма этих работ равна нулю, так как система в состоянии 1 находится в равновесии.
Работа внешних сил
Опоры В и D неподвижны, а реакция в опоре G направлена по нормали к любому ее возможному перемещению, поэтому работа реактивных сил
Для определения работы сил упругости Ау рассмотрим один и тот же элемент, вырезанный из схемы Т и схемы 1 двумя поперечными сечениями, расcтояние dS между которыми бесконечно мало.
Силы упругости в поперечном сечении элемента могут привестись к шести внутренним силовым факторам, которым присваиваем индекс 1.
Обозначим температуры крайних верхних и нижних, правых и левых волокон i-го участка соответственно Тв, Tн и Тп , Tл. Считаем, что температура в направлениях осей у и z сечения изменяется линейно, будучи соответственно функцией только у и только z.
Считаем, что температура в направлениях осей у и z сечения изменяется линейно, будучи соответственно функцией только у и только z.
Законы изменения температуры по поперечному сечению показаны на рис.
Очевидно, что
Температура на оси элемента
или
Пусть dδT — возможное перемещение центра тяжести поперечного сечения в схеме от изменения температуры элемента.
где α — коэффициент линейного расширения материала элемента.
Пусть dθTz — возможный относительный поворот концевых сечений элемента около оси z в схеме от изменения температуры
где — наибольший размер поперечного сечения в направлении оси у.
По аналогии, возможный относительный поворот концевых сечений элемента вокруг оси y
где — наибольший размер поперечного сечения в направлении оси z.
1. dAy — работа сил упругости в элементе dS по абсолютной величине равна работе внутренних силовых факторов состояния на возможных перемещениях состояния и противоположна ей по знаку, так как силы упругости всегда направлены в сторону, противоположную направлению изменения расстояния между точками тела.
2. Работа МК1, Qy1 и Qz1 равна нулю, так как концевые сечения элемента при нагреве относительно оси х не поворачиваются, a Qy1 и Qz1 перпендикулярны направлению dδT, поэтому
Подставляя сюда полученные ранее выражения и интегрируя полученное выражение по si —длине i-гo участка найдем работу сил упругости на i-м участке.
Суммируя эти интегралы по всем участкам системы, найдем Aу.
Складывая Ар с Ау и приравнивая сумму нулю, получим формулу Мора для определения температурных перемещений сечений стержневой системы по заданному направлению:
Метод Мора-Верещагина для определения угла излома в шарнире : Механика и Техника
Сообщения без ответов | Активные темы | Избранное
| eugrita |
| ||
15/04/10 |
| ||
| |||
| eugrita |
| |
15/04/10 | ||
| ||
| KAM |
| ||
19/09/07 |
| ||
| |||
| eugrita |
| ||
15/04/10 |
| ||
| |||
| KAM |
| ||
19/09/07 |
| ||
| |||
| eugrita |
| ||
15/04/10 |
| ||
| |||
| KAM |
| ||
19/09/07 |
| ||
| |||
| eugrita |
| ||
15/04/10 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 8 ] |
Модераторы: photon, profrotter, Парджеттер, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
Верещагин, Григорий [Идентификация WorldCat]
Обзор
Хронология публикации
.
Самые популярные произведения Григорий Верещагин
Релятивистская кинетическая теория: с приложениями в астрофизике и космологии
Григорий Верещагин(
)
11
выпуски опубликованы
между
2016
а также
2017
в
Английский
и проводится
817 член WorldCat
библиотеки
Мировой
«Релятивистская кинетическая теория нашла широкое применение в астрофизике и космологии. В последние годы интерес к ней возрос.
поскольку теперь экспериментаторы могут проводить надежные измерения физических систем, в которых релятивистские эффекты больше не проявляются. незначительный. Эта амбициозная монография разделена на три части. В ней представлены основные идеи и концепции этой теории,
уравнения и методы, включая вывод кинетических уравнений из релятивистской иерархии ББГКИ и обсуждение
соотношение между кинетическим и гидродинамическим уровнями описания. Вторая часть знакомит с элементами вычислительной физики
с особым упором на численное интегрирование уравнений Больцмана и родственные подходы, а также на многокомпонентную гидродинамику.
В третьей части представлен обзор приложений, начиная от ковариантной теории отклика плазмы, термализации релятивистских
плазма, комптонизация в статических и движущихся средах к кинетике самогравитирующих систем, космологическое структурообразование
и испускание нейтрино при гравитационном коллапсе» —
незначительный. Эта амбициозная монография разделена на три части. В ней представлены основные идеи и концепции этой теории,
уравнения и методы, включая вывод кинетических уравнений из релятивистской иерархии ББГКИ и обсуждение
соотношение между кинетическим и гидродинамическим уровнями описания. Вторая часть знакомит с элементами вычислительной физики
с особым упором на численное интегрирование уравнений Больцмана и родственные подходы, а также на многокомпонентную гидродинамику.
В третьей части представлен обзор приложений, начиная от ковариантной теории отклика плазмы, термализации релятивистских
плазма, комптонизация в статических и движущихся средах к кинетике самогравитирующих систем, космологическое структурообразование
и испускание нейтрино при гравитационном коллапсе» —
Солнце, звезды, Вселенная и общая теория относительности : международная конференция в честь Я. 95-летие Б. Зельдовича,
Минск, Беларусь, 20-23 апреля 2009 г.
Американский институт физики (англ.
)
95-летие Б. Зельдовича,
Минск, Беларусь, 20-23 апреля 2009 г.
Американский институт физики (англ.
)
6
выпуски опубликованы
между
2009 г.
а также
2010
в
Английский
и проводится
93 член WorldCat
библиотеки
Мировой
Электрон-позитронные пары в физике и астрофизике: от тяжелых ядер до черных дыр
Ремо Руффини (англ.
Книга
)
3
выпуски опубликованы
в
2010
в
Английский
и проводится
7 член WorldCat
библиотеки
Мировой
Благодаря взаимодействию физики и астрофизики мы наблюдаем в эти годы великолепный синтез теоретических, экспериментальных
и результаты наблюдений, происходящие из трех фундаментальных физических процессов. Первоначально они были предложены Дираком,
Брейта и Уилера и Заутера, Гейзенберга, Эйлера и Швингера. В течение почти семидесяти лет за всеми тремя следили
постоянными усилиями по экспериментальной проверке наземных экспериментов. Процесс Дирака, e+e-→2[gamma], был
пока самый успешный. Оно получило чрезвычайно точную экспериментальную проверку и привело также к огромному
количество новой физики в, возможно, одном из самых плодотворных экспериментальных направлений путем введения накопительных колец во Фраскати.
а за ними следуют крупнейшие ускорители мира: DESY, SLAC и т. д. Процесс Брейта-Уилера, 2[gamma]→e+e-, хотя концептуально
простой процесс, обратный процессу Дирака, был, безусловно, одним из самых трудных для экспериментальной проверки.
Только недавно, благодаря технологии, основанной на рентгеновском лазере на свободных электронах, и его многочисленным применениям в наземных экспериментах,
были достигнуты некоторые первые признаки его возможной проверки.
Первоначально они были предложены Дираком,
Брейта и Уилера и Заутера, Гейзенберга, Эйлера и Швингера. В течение почти семидесяти лет за всеми тремя следили
постоянными усилиями по экспериментальной проверке наземных экспериментов. Процесс Дирака, e+e-→2[gamma], был
пока самый успешный. Оно получило чрезвычайно точную экспериментальную проверку и привело также к огромному
количество новой физики в, возможно, одном из самых плодотворных экспериментальных направлений путем введения накопительных колец во Фраскати.
а за ними следуют крупнейшие ускорители мира: DESY, SLAC и т. д. Процесс Брейта-Уилера, 2[gamma]→e+e-, хотя концептуально
простой процесс, обратный процессу Дирака, был, безусловно, одним из самых трудных для экспериментальной проверки.
Только недавно, благодаря технологии, основанной на рентгеновском лазере на свободных электронах, и его многочисленным применениям в наземных экспериментах,
были достигнуты некоторые первые признаки его возможной проверки. Процесс поляризации вакуума в сильном электромагнитном
поле, введенное Заутером, Гейзенбергом, Эйлером и Швингером, ввело понятие критического электрического поля. Это было
безуспешно искали более сорока лет с помощью столкновений тяжелых ионов во многих ведущих ускорителях частиц по всему миру.
Новая ситуация сегодня состоит в том, что эти же самые процессы могут быть изучены в гораздо более грандиозном масштабе во время гравитационного поля.
коллапс, приводящий к образованию черной дыры, наблюдаемой в гамма-вспышках (GRB). Этот доклад посвящен
научная гонка. Теоретические и экспериментальные работы, разработанные в наземных лабораториях, сталкиваются с теоретическими
интерпретация космических наблюдений за явлениями, происходящими в космологических масштабах. Что стало ясно в последнее
десять лет заключается в том, что все три вышеупомянутых процесса, должным образом расширенные в рамках общей теории относительности, необходимы
для понимания физики гравитационного коллапса в черную дыру.
Процесс поляризации вакуума в сильном электромагнитном
поле, введенное Заутером, Гейзенбергом, Эйлером и Швингером, ввело понятие критического электрического поля. Это было
безуспешно искали более сорока лет с помощью столкновений тяжелых ионов во многих ведущих ускорителях частиц по всему миру.
Новая ситуация сегодня состоит в том, что эти же самые процессы могут быть изучены в гораздо более грандиозном масштабе во время гравитационного поля.
коллапс, приводящий к образованию черной дыры, наблюдаемой в гамма-вспышках (GRB). Этот доклад посвящен
научная гонка. Теоретические и экспериментальные работы, разработанные в наземных лабораториях, сталкиваются с теоретическими
интерпретация космических наблюдений за явлениями, происходящими в космологических масштабах. Что стало ясно в последнее
десять лет заключается в том, что все три вышеупомянутых процесса, должным образом расширенные в рамках общей теории относительности, необходимы
для понимания физики гравитационного коллапса в черную дыру. И наоборот, естественная арена, где эти
процессы, которые можно наблюдать во взаимодействии и в беспрецедентных масштабах, действительно является областью релятивистской астрофизики.
Мы систематически анализируем концептуальные разработки, последовавшие за основной работой Дирака и Брейта-Уилера. Мы также
вспомните, как основополагающая работа Борна и Инфельда вдохновила Заутера, Гейзенберга и Эйлера на эффективное лагранжево опережение.
к оценке скорости процесса образования электрон-позитронов в постоянном электрическом поле. В дополнение к рассмотрению
интуитивная полуклассическая трактовка квантово-механического туннелирования для описания процесса образования электрон-позитронов,
напомним расчеты в квантовой электродинамике скорости Швингера и эффективного лагранжиана для постоянного электромагнитного
поля.
И наоборот, естественная арена, где эти
процессы, которые можно наблюдать во взаимодействии и в беспрецедентных масштабах, действительно является областью релятивистской астрофизики.
Мы систематически анализируем концептуальные разработки, последовавшие за основной работой Дирака и Брейта-Уилера. Мы также
вспомните, как основополагающая работа Борна и Инфельда вдохновила Заутера, Гейзенберга и Эйлера на эффективное лагранжево опережение.
к оценке скорости процесса образования электрон-позитронов в постоянном электрическом поле. В дополнение к рассмотрению
интуитивная полуклассическая трактовка квантово-механического туннелирования для описания процесса образования электрон-позитронов,
напомним расчеты в квантовой электродинамике скорости Швингера и эффективного лагранжиана для постоянного электромагнитного
поля.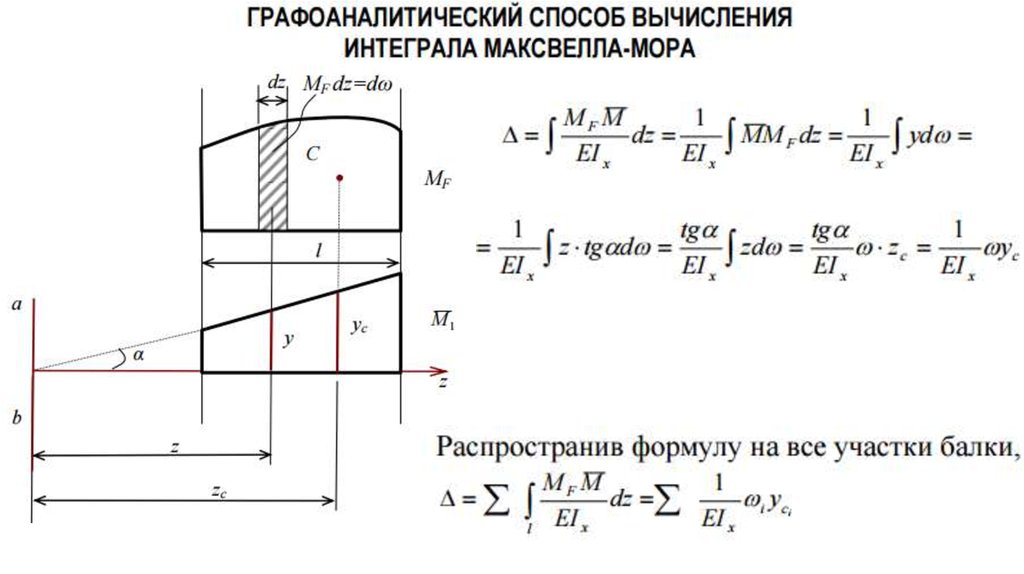 Мы также рассматриваем образование электронов-позитронов в обоих переменных во времени электромагнитных полях, изученное Брезиным,
Ицыксона, Попова, Никишова и Нарожного, а также соответствующие процессы, важные для рождения пар в фокусе когерентного
лазерные лучи, а также столкновение электронного луча и лазера. Наконец, мы сообщаем о некоторых текущих разработках, основанных на общей информации JWKB.
подход, который позволяет вычислить скорость Швингера в изменяющихся в пространстве и во времени электромагнитных полях. Мы также
вспомните пионерские работы Ландау и Лифшица и Рака о столкновении заряженных частиц, а также экспериментальные
успех AdA и ADONE в производстве электрон-позитронных пар. Затем мы переходим к возможной экспериментальной проверке
этих явлений. Мы рассматриваем: (A) экспериментальную проверку процесса e+e-→2[gamma], изученного Дираком.
Мы также рассматриваем образование электронов-позитронов в обоих переменных во времени электромагнитных полях, изученное Брезиным,
Ицыксона, Попова, Никишова и Нарожного, а также соответствующие процессы, важные для рождения пар в фокусе когерентного
лазерные лучи, а также столкновение электронного луча и лазера. Наконец, мы сообщаем о некоторых текущих разработках, основанных на общей информации JWKB.
подход, который позволяет вычислить скорость Швингера в изменяющихся в пространстве и во времени электромагнитных полях. Мы также
вспомните пионерские работы Ландау и Лифшица и Рака о столкновении заряженных частиц, а также экспериментальные
успех AdA и ADONE в производстве электрон-позитронных пар. Затем мы переходим к возможной экспериментальной проверке
этих явлений. Мы рассматриваем: (A) экспериментальную проверку процесса e+e-→2[gamma], изученного Дираком. Мы также кратко
вспомните очень успешные опыты е+е- аннигиляции в адронные каналы, в дополнение к дираковскому электромагнитному
канал; (B) текущие наземные эксперименты по обнаружению образования электрон-позитронов в сильных полях путем фокусировки когерентных
лазерные лучи и столкновения электронного луча с лазером; и (C) многолетние попытки обнаружить электрон-позитронное образование в
Кулоновские поля для большого атомного номера Z>137 в столкновениях тяжелых ионов. Эти попытки следуют классической теоретической работе
Попова и Зельдовича, Грейнера и их школ. Затем обратимся к астрофизике. Сначала мы рассмотрим основную работу по
энергетика и электродинамические свойства электромагнитной черной дыры и применение формулы Швингера вокруг
Черные дыры Керра-Ньюмана, открытые Дамуром и Руффини.
Мы также кратко
вспомните очень успешные опыты е+е- аннигиляции в адронные каналы, в дополнение к дираковскому электромагнитному
канал; (B) текущие наземные эксперименты по обнаружению образования электрон-позитронов в сильных полях путем фокусировки когерентных
лазерные лучи и столкновения электронного луча с лазером; и (C) многолетние попытки обнаружить электрон-позитронное образование в
Кулоновские поля для большого атомного номера Z>137 в столкновениях тяжелых ионов. Эти попытки следуют классической теоретической работе
Попова и Зельдовича, Грейнера и их школ. Затем обратимся к астрофизике. Сначала мы рассмотрим основную работу по
энергетика и электродинамические свойства электромагнитной черной дыры и применение формулы Швингера вокруг
Черные дыры Керра-Ньюмана, открытые Дамуром и Руффини. Мы фокусируемся только на массах черных дыр, превышающих критическую массу
нейтронных звезд, для удобства считающихся совпадающими с верхним пределом Роудса и Руффини, равным 3,2 M. В этом случае
Длина комптоновской волны электрона намного меньше кривизны пространства-времени, и все предыдущие результаты, выраженные инвариантно, могут
применяться в соответствии с хорошо установленными правилами принципа эквивалентности. Выводим соответствующую скорость электрон-позитронного
производство пар и ввести понятие диадосферы. Мы рассмотрим недавний прогресс в описании эволюции оптических
плотной электрон-позитронной плазмы в присутствии сверхкритического электрического поля, что актуально как в астрофизике, так и
а также в текущих экспериментах с лазерным лучом. В частности, мы рассматриваем недавний прогресс, основанный на теории Власова-Больцмана-Максвелла.
Мы фокусируемся только на массах черных дыр, превышающих критическую массу
нейтронных звезд, для удобства считающихся совпадающими с верхним пределом Роудса и Руффини, равным 3,2 M. В этом случае
Длина комптоновской волны электрона намного меньше кривизны пространства-времени, и все предыдущие результаты, выраженные инвариантно, могут
применяться в соответствии с хорошо установленными правилами принципа эквивалентности. Выводим соответствующую скорость электрон-позитронного
производство пар и ввести понятие диадосферы. Мы рассмотрим недавний прогресс в описании эволюции оптических
плотной электрон-позитронной плазмы в присутствии сверхкритического электрического поля, что актуально как в астрофизике, так и
а также в текущих экспериментах с лазерным лучом. В частности, мы рассматриваем недавний прогресс, основанный на теории Власова-Больцмана-Максвелла. уравнения для изучения обратной связи созданных электрон-позитронных пар на исходное постоянное электрическое поле. Мы доказательства
существование колебаний плазмы и ее взаимодействие с фотонами, приводящее к энергетическому и количественному равнораспределению фотонов,
электроны и позитроны. Наконец, мы рассмотрим недавний прогресс, достигнутый при использовании уравнений Больцмана для изучения эволюции
электрон-позитрон-фотонной плазмы к тепловому равновесию и определение ее характерных временных масштабов.
принципиальное отличие, вносимое правильной оценкой роли двух- и трехчастичных столкновений, прямых и обратных,
особенно свидетельствует. Затем мы приводим некоторые общие выводы. Результаты, рассмотренные в этом отчете, будут представлены
к решающим испытаниям в ближайшие годы как в физике, так и в астрофизике.
уравнения для изучения обратной связи созданных электрон-позитронных пар на исходное постоянное электрическое поле. Мы доказательства
существование колебаний плазмы и ее взаимодействие с фотонами, приводящее к энергетическому и количественному равнораспределению фотонов,
электроны и позитроны. Наконец, мы рассмотрим недавний прогресс, достигнутый при использовании уравнений Больцмана для изучения эволюции
электрон-позитрон-фотонной плазмы к тепловому равновесию и определение ее характерных временных масштабов.
принципиальное отличие, вносимое правильной оценкой роли двух- и трехчастичных столкновений, прямых и обратных,
особенно свидетельствует. Затем мы приводим некоторые общие выводы. Результаты, рассмотренные в этом отчете, будут представлены
к решающим испытаниям в ближайшие годы как в физике, так и в астрофизике. Упомянем лишь несколько основных шагов
при испытаниях по физике мы помним создание экспериментальных установок в Национальном центре зажигания в Университете Лоуренса.
Ливерморская национальная лаборатория, а также соответствующий французский проект Laser Mega Joule. В астрофизике эти результаты
будут проверены в галактических и внегалактических черных дырах, наблюдаемых в двойных рентгеновских источниках, активных ядрах галактик, микроквазарах
и в процессе гравитационного коллапса в нейтронную звезду, а также двух нейтронных звезд в черную дыру, порождающую
гамма-всплески. Астрофизическое описание звездных предшественников и начальных физических условий, приводящих к гравитационному
Процесс коллапса будет предметом следующего доклада. На сегодняшний день не найдено теоретического описания
объяснить либо испускание остатка сверхновой, либо образование заряженной черной дыры для гамма-всплесков.
Упомянем лишь несколько основных шагов
при испытаниях по физике мы помним создание экспериментальных установок в Национальном центре зажигания в Университете Лоуренса.
Ливерморская национальная лаборатория, а также соответствующий французский проект Laser Mega Joule. В астрофизике эти результаты
будут проверены в галактических и внегалактических черных дырах, наблюдаемых в двойных рентгеновских источниках, активных ядрах галактик, микроквазарах
и в процессе гравитационного коллапса в нейтронную звезду, а также двух нейтронных звезд в черную дыру, порождающую
гамма-всплески. Астрофизическое описание звездных предшественников и начальных физических условий, приводящих к гравитационному
Процесс коллапса будет предметом следующего доклада. На сегодняшний день не найдено теоретического описания
объяснить либо испускание остатка сверхновой, либо образование заряженной черной дыры для гамма-всплесков. Важный ток
прогресс в понимании таких явлений, а также электродинамической структуры нейтронных звезд, сверхновых
Взрыв и теории гамма-всплесков будут обсуждаться в вышеупомянутом следующем отчете. Что важно помнить
на данном этапе заключается только в том, что как сверхновые, так и процессы гамма-всплесков являются одними из самых энергичных и нестационарных явлений, когда-либо существовавших.
наблюдается во Вселенной: сверхновая может достичь энергии 1054 эрг в течение нескольких месяцев, а гамма-всплески могут испускать
до 1054 эрг за время всего в несколько секунд. Центральная роль нейтронных звезд в описании сверхновых.
а также черных дыр и электрон-позитронной плазмы, в описании гамма-всплесков, впервые введенном одним из нас (Р.Р.) в 1975,
широко признаны. В настоящем отчете
Важный ток
прогресс в понимании таких явлений, а также электродинамической структуры нейтронных звезд, сверхновых
Взрыв и теории гамма-всплесков будут обсуждаться в вышеупомянутом следующем отчете. Что важно помнить
на данном этапе заключается только в том, что как сверхновые, так и процессы гамма-всплесков являются одними из самых энергичных и нестационарных явлений, когда-либо существовавших.
наблюдается во Вселенной: сверхновая может достичь энергии 1054 эрг в течение нескольких месяцев, а гамма-всплески могут испускать
до 1054 эрг за время всего в несколько секунд. Центральная роль нейтронных звезд в описании сверхновых.
а также черных дыр и электрон-позитронной плазмы, в описании гамма-всплесков, впервые введенном одним из нас (Р.Р.) в 1975,
широко признаны. В настоящем отчете
Петлевая квантовая космология и вероятность инфляции обсуждаются только теоретические основы для решения этих тем. Григорий Верещагин(
)
Григорий Верещагин(
)
1
издание опубликовано
в
2018
в
Английский
и проводится
2 член WorldCat
библиотеки
Мировой
Второй ICRANet César Lattes Встреча сверхновых, нейтронных звезд и черных дыр: Рио-де-Жанейро — Нитерой — Жуан-Пессоа
— Ресифи — Форталеза, Бразилия, 13-22 апреля 2015 г.
Встреча Сезара Латте (
Книга
)
2
выпуски опубликованы
в
2015
в
Английский
и проводится
2 член WorldCat
библиотеки
Мировой
Вторая встреча César Lattes (2CL) проходила с 13 по 18 апреля 2015 года в городах Рио-де-Жанейро и Рио-де-Жанейро. через красивый Байя-да-Гуанабара, в Нитерой. Результаты этой очень насыщенной программы встречи представлены в
этот объем. Эта встреча является частью дополнительных встреч к 14-й конференции Марселя Гроссмана, организованной ICRANet.
В этой встрече 2CL приняли участие ученые, связанные с тремя крупными физическими институтами в Рио-де-Жанейро,
Centro Brasileiro de Pesquisas Físicas (CBPF), учреждение, в котором находится ICRANet, Федеральный университет Флуминенсе.
в Нитерой и Планетарий Рио. Участники приехали со всей Бразилии, проявив большой интерес к этой стране.
в релятивистской астрофизике, поскольку большая часть присутствующих довольно молода.0003
через красивый Байя-да-Гуанабара, в Нитерой. Результаты этой очень насыщенной программы встречи представлены в
этот объем. Эта встреча является частью дополнительных встреч к 14-й конференции Марселя Гроссмана, организованной ICRANet.
В этой встрече 2CL приняли участие ученые, связанные с тремя крупными физическими институтами в Рио-де-Жанейро,
Centro Brasileiro de Pesquisas Físicas (CBPF), учреждение, в котором находится ICRANet, Федеральный университет Флуминенсе.
в Нитерой и Планетарий Рио. Участники приехали со всей Бразилии, проявив большой интерес к этой стране.
в релятивистской астрофизике, поскольку большая часть присутствующих довольно молода.0003
Международная конференция в честь столетия со дня рождения Я.Б. Зельдович, «Субатомные частицы, нуклоны, атомы,
Вселенная: процессы и структура». С. Я. Килин(
)
С. Я. Килин(
)
1
издание опубликовано
в
2015
в
Английский
и проводится
2 член WorldCat
библиотеки
Мировой
Уровень аудитории
| 0 | 1 | |||
| Общий | Специальный | |||
Уровень аудитории: 0,00 (из
0,00
за Релятивист . .. к
0,00
за Релятивист
…)
.. к
0,00
за Релятивист
…)
АВТОМАТИЗАЦИЯ РАСЧЕТА АРОК. — Бесплатная онлайн-библиотека
УДК 539.3
Введение. Изогнутые стержни (арки) широко используются в ракетостроении. машиностроение, авиа- и судостроение, мосты, машиностроение и строительство. Это связано с преимуществами изогнутых стержней перед прямолинейных стержней за счет их большей несущей способности и жесткости.
Однако расчет напряженно-деформированного состояния арок
довольно сложно, поскольку необходимо учитывать
одновременно деформации изгиба, растяжения-сжатия и сдвига.
Особенно это касается определения движений в арках, т.к.
формула Верещагина здесь неприменима, так как фрахт и
единичные диаграммы нелинейны.
В этом случае мы должны использовать интеграл Морале, Кастильяно теорема и численные методы. Для упрощения расчета арок, предлагается использовать численно-аналитический вариант метода граничные элементы [1] и среда программирования MATLAB.
В литературе приводятся решения различных задач плоская деформация круглого стержня только с деформацией изгиба [2]. В 1938 г. профессор Н.К. Снитко получил решение проблемы плоская деформация круглого стержня с учетом изгиба и деформации растяжения-сжатия только для конкретного случая нагрузки: [q.sub.y]([alpha])=q=const, где q — интенсивность вертикального нагрузка.
Отсутствие достаточно точного аналитического решения задачи
Проблема плоской деформации круглого стержня способствовала
тот факт, что в ряде работ [3-5] рекомендуется заменить
криволинейных стержней набором прямолинейных стержней.
Данная модель дает погрешность не более 1,0 % при прямолинейном
стержень рисует дугу изогнутого стержня менее чем на 5[градусов] [6]. Это означает
что кольцо может быть представлено правильным многоугольником из 72 стержней,
арка в 180[градусов]-36 стержней и т. д. Далее расчет
криволинейный стержень можно выполнить методом граничных элементов
(БЭМ), силовой метод и другие методы.
Это означает
что кольцо может быть представлено правильным многоугольником из 72 стержней,
арка в 180[градусов]-36 стержней и т. д. Далее расчет
криволинейный стержень можно выполнить методом граничных элементов
(БЭМ), силовой метод и другие методы.
Если вы примените метод граничных элементов и MATLAB окружающей среды, вы можете значительно. уменьшить сложность расчета, упростить алгоритм и схемы расчета, повысить точность и достоверность результатов, и ввести это методологии в расчетную практику и учебный процесс высшие учебные заведения без особого труда.
В связи с этим целью статьи является практическое применение возможностей метода граничных элементов для решение достаточно трудоемких задач по напряженно-деформированному состоянию круговых арки и арочные конструкции.
Материалы и методы. Для достижения этой цели рассчитаем напряженно-деформированное состояние круглых арок в среде MATLAB.
Покажем на рис. 1 расчетную схему арки и запишем
основные уравнения, необходимые для расчета.
Система дифференциальных уравнений для плоского деформирования круговой стержень с учетом деформации изгиба и растяжения относительно радиального [??]([альфа]) и тангенциального смещения u([альфа]) имеет вид:
[математическое выражение невоспроизводимо], (1)
где EA-Жесткость сечения арки при растяжении-сжатии, кН;
EI-Жесткость сечения арки на изгиб, кН[м2]; R-радиус оси арки, м; [альфа]-Угловая координата, рад.; [q.sub.y] ([alpha])-Радиальная нагрузка арки (по нормали к ось), кН/м; [q.sub.x] ([альфа])-Касательная нагрузка арки, кН/м.
Решение задачи Коши о деформации плоской арки может представить в матричном виде следующим образом [1]:
1 2 3
EIv([альфа]) 1 [A.sub.11] [A.sub.12] -[A.sub.13]
EI [фи] ([альфа]) 2 [A.sub.22] -[A.sub.23]
M([альфа]) = 3 [A.sub.22]
Q([альфа]) 4
EAu([альфа]) 5 [A.sub.51] [A.sub.52] -[A.sub.53]
N([альфа]) 6
4 5 6
EIv ([альфа]) 1 - [A. sub.14] [A.sub.15] [A.sub.16]
EI [фи] ([альфа]) 2 - [A.sub.13] [A.sub.26]
M([альфа]) = 3 [A.sub.12] -[A.sub.36]
Q([альфа]) 4 [A.sub.11] -[A.sub.46]
EAu([альфа]) 5 -[A.sub.54] [A.sub.11] [A.sub.56]
N ([альфа]) 6 - [A.sub.64] [A.sub.11]
EIv([альфа]) 1 EIv(0) [B.sub.11]
EI [фи] ([альфа]) 2 EI [фи] (0) [B.sub.21]
М([альфа]) = 3 М(0) + -[B.sub.31]
Q([альфа]) 4 Q(0) -[B.sub.41]
EAu([альфа]) 5 EAu(0) -[B.sub.51]
N ([альфа]) 6 N (0) - [B.sub.61] (2)
sub.14] [A.sub.15] [A.sub.16]
EI [фи] ([альфа]) 2 - [A.sub.13] [A.sub.26]
M([альфа]) = 3 [A.sub.12] -[A.sub.36]
Q([альфа]) 4 [A.sub.11] -[A.sub.46]
EAu([альфа]) 5 -[A.sub.54] [A.sub.11] [A.sub.56]
N ([альфа]) 6 - [A.sub.64] [A.sub.11]
EIv([альфа]) 1 EIv(0) [B.sub.11]
EI [фи] ([альфа]) 2 EI [фи] (0) [B.sub.21]
М([альфа]) = 3 М(0) + -[B.sub.31]
Q([альфа]) 4 Q(0) -[B.sub.41]
EAu([альфа]) 5 EAu(0) -[B.sub.51]
N ([альфа]) 6 N (0) - [B.sub.61] (2)
где ЭИ 9([альфа])-Угол поворота сечения арки, кН [м2]; M([alpha])-изгибающий момент в сечении, кНм; Q([alpha])-поперечная сила в сечении, кН; N([альфа])-нормальная сила в сечения, кН.
Основные ортонормированные функции и члены радиальной нагрузки (рис. 1) после интегрирования принимают вид [1]:
[невоспроизводимое математическое выражение]. (3)
Следующим шагом является учет граничных условий для
поддерживающие арки. Для определения параметров
напряженно-деформированного состояния арки необходимо составить и
решить краевую задачу, учитывающую заданную опору
условия для граничных точек. На БЭМ это уравнение имеет вид
[1]
На БЭМ это уравнение имеет вид
[1]
[A.sub.*][X.sub.*] = -B, (4)
где [A.sub.*] -матрица граничных значений фундаментальных функции, учитывающие граничные условия арки;
[X.sub.*]-Матрица начальных и конечных параметров изгиба арки и растяжка;
B-Матрица нагрузки со значением граничной переменной [альфа].
Рассмотрим различные условия поддержки свода стопы.
С шарнирной опорой, схема которой представлена на рис. 2, представляли собой матрицы начального (X) и конечного (Y) параметров арка (5), где мы учли шарнирную опору из двух пограничные участки.
[невоспроизводимое математическое выражение] (5)
Из этих матриц следует, что в матрице [A.sub.*] столбцы 1, 3 и 5 необходимо обнулить и добавить элементы A(2.1) = -1; А(4.3) = -1; A (6.5) = -1 с учетом переноса параметры от Y до [X.sub.*]. Матричное уравнение границы значение задачи для арки на рис. 2 принимает вид:
1 2 3 4 5 6
1 [A.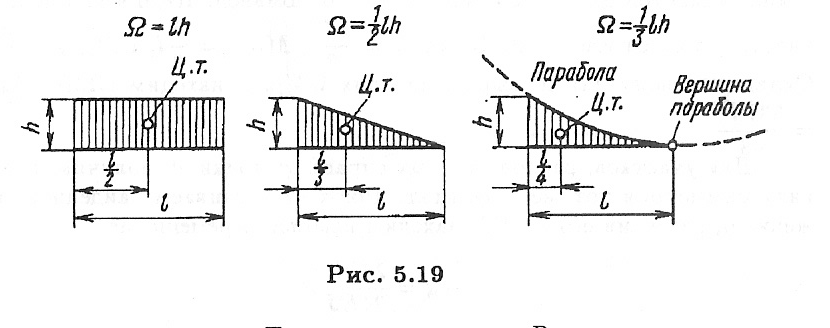 sub.12] - [A.sub.14] [A.sub.16]
2-1 [A.sub.22] -[A.sub.13] [A.sub.26]
3 -[A.sub.12] -[A.sub.36]
4 -1 -[A.sub.11] -[A.sub.46]
5 [A.sub.52] [A.sub.54] -[A.sub.56]
6 [A.sub.64] -1 - [A.sub.64]
1 EI [фи] ([пи]) - [B.sub.11] ([пи])
2 EI [фи] (0) - [B.sub.21] ([пи])
3 Q([pi]) [B.sub.31]([pi])
4 Q (0) = [B.sub.41] ([пи])
5 Н ([пи]) [B.sub.51] ([пи])
6 N (0) [B.sub.61] ([pi]) (6)
sub.12] - [A.sub.14] [A.sub.16]
2-1 [A.sub.22] -[A.sub.13] [A.sub.26]
3 -[A.sub.12] -[A.sub.36]
4 -1 -[A.sub.11] -[A.sub.46]
5 [A.sub.52] [A.sub.54] -[A.sub.56]
6 [A.sub.64] -1 - [A.sub.64]
1 EI [фи] ([пи]) - [B.sub.11] ([пи])
2 EI [фи] (0) - [B.sub.21] ([пи])
3 Q([pi]) [B.sub.31]([pi])
4 Q (0) = [B.sub.41] ([пи])
5 Н ([пи]) [B.sub.51] ([пи])
6 N (0) [B.sub.61] ([pi]) (6)
После решения уравнения (6) реакции арки будут: [H.sub.0] = [Q.sub.(0)]; [R.sub.0] = [N.sub.(0)]; [H.sub.K] = [Q.sub.([pi])] [R.sub.K] = [N.sub.([pi])], а напряженно-деформированное состояние во внутренних точках определяется уравнением (2).
Аналогично, составляя матрицы [X.sub.*], Y, получаем уравнение краевая задача для другого случая жесткого защемления и шарнирной опоры, показано на рис. 3.
1 2 3 4 5 6
1 -1 -[A.sub.13] -[A.sub.14] [A.sub.16]
2 -[A.sub.23] -[A.sub.13] [A.sub.26]
3 [A.sub.22] [A.sub.12] -[A.sub.36]
4 -1 [A.sub.11] -[A.sub.46]
5 - [A.sub. 53] - [A.sub.54] [A.sub.56]
6 - [A.sub.64] -1 [A.sub.11]
1 EI [фи] ([пи]) - [B.sub.11] ([пи])
2 Q([pi]) -[B.sub.21]([pi])
3 М (0) = [B.sub.31] ([пи])
4 Q (0) [B.sub.41] ([пи])
5 Н ([пи]) [B.sub.51] ([пи])
6 N (0) [B.sub.61] ([pi]) (7)
53] - [A.sub.54] [A.sub.56]
6 - [A.sub.64] -1 [A.sub.11]
1 EI [фи] ([пи]) - [B.sub.11] ([пи])
2 Q([pi]) -[B.sub.21]([pi])
3 М (0) = [B.sub.31] ([пи])
4 Q (0) [B.sub.41] ([пи])
5 Н ([пи]) [B.sub.51] ([пи])
6 N (0) [B.sub.61] ([pi]) (7)
После решения (7) реакции арки будут равны
[H.sub.0] = [Q.sub.(0)]; [R.sub.0] = [N.sub.(0)] ; [H.sub.K] = [Q.sub.([pi])]; [R.sub.K] = [N.sub.([pi])]; [M.sub.0] = [M.sub.(0)].
На рис. 4 показана схема следующего типа опоры для арки — жесткое защемление двух граничных точек.
Матричное уравнение краевой задачи для этого случая опора примет вид (8).
1 2 3 4 5 6
1 -[A.sub.13] -[A.sub.14] [A.sub.16]
2 -1 -[A.sub.23] -[A.sub.13] [A.sub.26]
3 [A.sub.22] [A.sub.12] -[A.sub.36]
4 -1 [A.sub.11] -[A.sub.46]
5 [A.sub.53] - [A.sub.54] [A.sub.56]
6 - [A.sub.64] -1 [A.sub.11]
1 М([пи]) -[B.sub.11]([пи])
2 Q([pi]) -[B.sub.21]([pi])
3 М (0) [B.sub.31] ([пи])
4 Q (0) = [B.sub.41] ([пи])
5 Н ([пи]) [B. sub.51] ([пи])
6 N (0) [B.sub.61] ([pi]) (8)
sub.51] ([пи])
6 N (0) [B.sub.61] ([pi]) (8)
Реакции арки будут равны
[H.sub.0] = [Q.sub.(0)]; [R.sub.0] = [N.sub.(0)]; [M.sub.0] = [M.sub.(0)]; [H.sub.K] = [Q.sub.([pi])]; [R.sub.K] = [N.sub.([pi])]; [M.sub.k] = [M.sub.([pi])].
Рассмотрим пример определения параметров напряженно-деформированное состояние арки при произвольной нагрузке и закреплении.
Результаты. Определить напряженно-деформированное состояние арки (рис. 5). результаты представлены численно (в виде таблицы) и визуально (в виде диаграмм).
Угловые координаты сосредоточенного момента и сосредоточенная сила [[альфа].sub.M] = [pi]/4; [[альфа].sub.F] = 3/4 [пи]. Угловые координаты равномерно распределенной нагрузки равны [[альфа].sub.H] = 0; [[альфа].sub.K] = [пи].
При заданных исходных данных вычисляем значения граничные параметры с использованием уравнения (7) и представить полученные результаты в виде Таблица 1.
Реакции арочных опор будут равны [H. sub.0]=20,00
кН, [R0]=200,88 кН, [M0]=147,14 кНм, [Hk]=6,96 кН,
[Rk] = 210,08 кН.
sub.0]=20,00
кН, [R0]=200,88 кН, [M0]=147,14 кНм, [Hk]=6,96 кН,
[Rk] = 210,08 кН.
Значения параметров напряженно-деформированного состояния обобщены в таблице 2.
Данные таблицы 2 свидетельствуют о том, что полученные результаты точный. Такой вывод обосновывается тем, что напряженно-деформированное состояние арки рассчитывали по уравнениям метод начальных параметров (2), где начальными параметрами были взято из таблицы 1.
Если решение точное, то опорные граничные условия должны удовлетворяться на правильном пьедестале, что подтверждается данными в Таблица 2.
Графики параметров напряженно-деформированного состояния дуги в декартовых координатах показаны на рис. 6-11.
Схемы на рисунках 6-11 можно легко изобразить на контуре арка.
Выводы. Уравнения краевых задач для определения
неизвестные начальные параметры дуг окружности при существующих
получены условия опоры граничных участков. На основе
основные понятия сопротивления материалов, динамики и прочности
структурирует методику расчета напряженно-деформированного состояния
круговых арок в среде MATLAB. Принимая во внимание
учет влияния распределенных и сосредоточенных нагрузок расчет
круговой арки.
Принимая во внимание
учет влияния распределенных и сосредоточенных нагрузок расчет
круговой арки.
Следует отметить, что формирование уравнений границы значение задач по расчету арок с разными опорами условиях значительно сокращает время других исследователей в решение задач расчета и анализа конструкций, содержащих круговые арки.
Представлена методика расчета напряженно-деформированного состояния Авторами имеет существенные преимущества перед известными методами. Это достаточно подробно описывает расчет действия внешний сосредоточенный момент и расчет всех кинематических параметры деформированного состояния дуги окружности.
В заключение отметим, что многочисленные задачи расчета колец и кольцевые системы [2, т. 1, с. 1, с. 321; 365] можно решить с помощью уравнения БЭМ 2) аналогично, но в более точной постановке с учетом изгиба и деформации растяжения-сжатия.
[Обратите внимание: некоторые нелатинские символы были исключены из этого
статья. ]
]
DOI10.15276/оп.2.52.2017.02
Поступила в редакцию 17.05.2017 г.
Принят 24 июля 2017 г.
Ссылки
[1.] [фраза опущена]
[2.] [фраза опущена]
[3.] [фраза опущена]
[4.] [фраза опущена]
[5.] [фраза опущена]
[6.] [фраза опущена]
Ссылки
[1.] Баженов В.А., Дащенко А.Ф., Коломиец Л.В., Оробей, В.Ф. (2001). Строительная механика. Специальный курс Применение мне тода граничнвх элементов [Структурная механика. Специальный курс. Применение метода граничных элементов. Одесса: Астропринт.
[2.] Биргера И.А., Пановко Я.Г. (Ред.). (1968) Прочность, устовчивость, колебанива. [Сила, стабильность, вибрации]. Москва: Машиностроение.
[3.] Александров А.В., Лащеников Б.Я., Шапошников А.В. Н.Н. (1983) Строительная механика. Тонкостенное Строительная механика. Тонкостенный пространственный Системы]. Москва: Стройиздат.
[4.] Оробей В., Коломиец Л. и Лымаренко А. (2015).
Метод граничных элементов в задаче об изгибе пластинчатых элементов
инженерия. Металлургическая и горнодобывающая промышленность. 4, 295-302.
и Лымаренко А. (2015).
Метод граничных элементов в задаче об изгибе пластинчатых элементов
инженерия. Металлургическая и горнодобывающая промышленность. 4, 295-302.
[5.] Коломиец Л., Оробей В., Лымаренко А. (2016) Методика граничный элемент в задачах об устойчивости плоских изгибаемых балок прямоугольное сечение. Структуры. Металлургическая и горнодобывающая промышленность Индустр. 3, 59-65.
[6.] Дарков А.В. и Шапошников Н.Н. (1985). Строительная механика [Строительная механика] Москва: Высшая школа.
В.Ф. Оробей, д.б.н., профессор,
О.Ф. Дащенко, д.б.н., проф.,
О.М. Лымаренко, к.б.н., доц. проф.
Одесский национальный политехнический университет, пр. Шевченко, 1, г. Одесса, Украина, 65044; электронная почта: [email protected]
Подпись: Рис. 1. Расчетная схема арки
Подпись: Рис. 2. Шарнирная арка
Подпись: Рис. 3. Жесткое защемление и шарнирная поддержка арок
Подпись: Рис. 4. Жесткое защемление арки
Подпись: Рис. 5. Нагрузка и фиксация в арке
5. Нагрузка и фиксация в арке
Подпись: Рис. 6. Схема арки EI[??], прогибы, кН[м.3]
Подпись: Рис. 7. Схема углов поворота арки El[phi], кН[м.суп.2]
Подпись: Рис. 8. Диаграмма изгибающих моментов М, кНм
Подпись: Рис. 9. Диаграмма поперечных усилий Q, кН
Подпись: Рис. 10. Диаграмма тангенциальных перемещений EAu, кНм
Подпись: Рис. 11. Схема нормальных сил N, кН
Таблица 1 Значение граничных параметров арки на рис. 5 Нет n/n Параметр Значение 1 Efy(rc), кН[м.2] -958,34 2 Q(n), кН -6,96 3 М(0), кН·м 147,14 4 Q(0), кН -20,00 5 Н(н), кН -210,08 6 Н(0), кН -200,88 Таблица 2 Результаты расчета арок в численном виде Угловые параметры напряженно-деформированного состояния координировать рад град Эа. Эа[фи]. М, кНм [10-3], [10-2], кН[м.суп.2] кН[м.суп.2] 0,0 0,0 0,0 0,0 147,14 0,095 0,133 1,86 119,79 0,17 10 0,497 3,35 93,72 0,26 15 1,038 4,48 6915 0,35 20 1,703 5,28 46,24 0,44 25 2,445 5,78 25,19 0,52 30 3,214 6,00 6,15 0,61 35 3,970 5,96 -10,74 0,70 40 4,673 5,71 -25,34 0,79 45 5,289 5,27 -67,55 0,87 50 5,760 4,25 -77,16 0,96 55 6,036 3,12 -83,98 1,05 60 6,100 1,92 -87,96 1,13 65 5,945 0,68 -89,07 1,22 70 5,570 -0,54 -87,30 1,31 75 4,980 -1,73 -82,67 1,40 80 4,189 -2,84 -75,20 1,48 85 3,219 -3,82 -64,9 1,57 90 2,095 -4,64 -52,03 1,66 95 0,853 -5,26 -36,50 1,75 100 -0,468 -5,65 -18,48 1,83 105 -1,824 -5,77 1,87 1,92 110 -3,165 -5,59 24,41 2,01 115 -4,435 -5,08 48,96 2,09 120 -5,578 -4,21 -75,35 2,18 125 -6,534 -2,96 103,36 2,27 130 -7,240 -1,32 132,79 2,36 135 -7,635 0,74 163,40 2,44 140 -7,673 2,85 139,20 2,53 145 -7,383 4,63 116,14 2,62 150 -6,813 6,10 94,39 2,71 155 -6,008 7,28 74,13 2,79160 -2,016 8,18 55,50 2,88 165 -3,879 8,83 38,66 2,97 170 -2,638 9,27 23,72 3,05 175 -1,334 9,51 10,80 3,14 180 0,0 9,58 0,0 Угловые параметры напряженно-деформированного состояния координатное состояние рад град Q, кН Eau.
 04.2013, 11:02
04.2013, 11:02 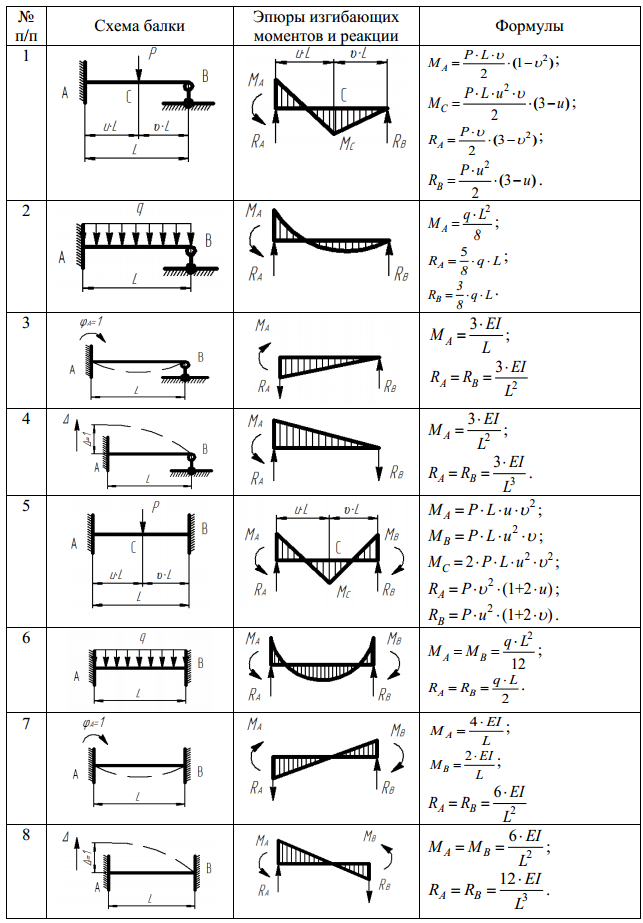 е фактически
е фактически Москва
Москва
 Москва
Москва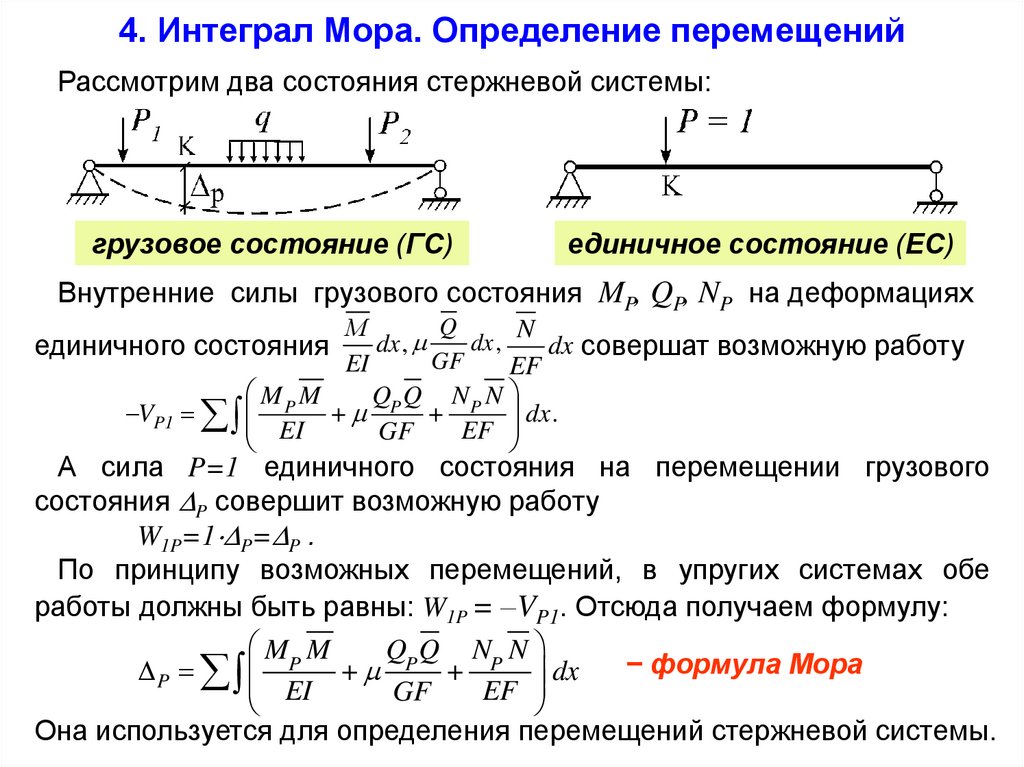 04.2013, 20:42
04.2013, 20:42  04.2013, 07:16
04.2013, 07:16 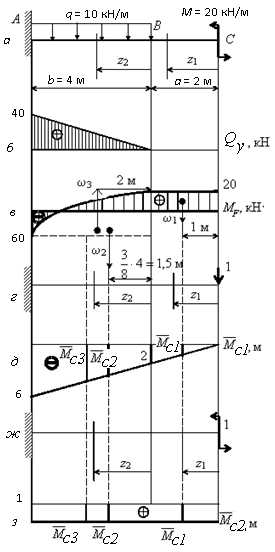 04.2013, 00:45
04.2013, 00:45  Москва
Москва