Формула верещагина: метод Верещагина

Содержание

метод Верещагина

Лекция 13 (продолжение). Примеры решения на вычисление перемещений методом Мора-Верещагина и задачи для самостоятельного решения

Определение перемещений в балках

Пример 1.

Определить перемещение точки К балки (см. рис.) при помощи интеграла Мора.

Решение.

1) Составляем уравнение изгибающего момента от внешней силы M_F.

2) Прикладываем в точке К единичную силу F = 1.

3) Записываем уравнение изгибающего момента от единичной силы .

4) Определяем перемещения

Пример 2.

Определить перемещение точки

К балки по способу Верещагина.

Решение.

1) Строим грузовую эпюру.

2) Прикладываем в точке К единичную силу.

3) Строим единичную эпюру.

4) Определяем прогиб

; ;

Пример 3.

Определить углы поворота на опорах А и В для заданной балки (см. рис.).

Решение.

Строим эпюры от заданной нагрузки и от единичных моментов, приложенных в сечениях А и В (см. рис.). Искомые перемещения определяем с помощью интегралов Мора

, которые вычисляем по правилу Верещагина.

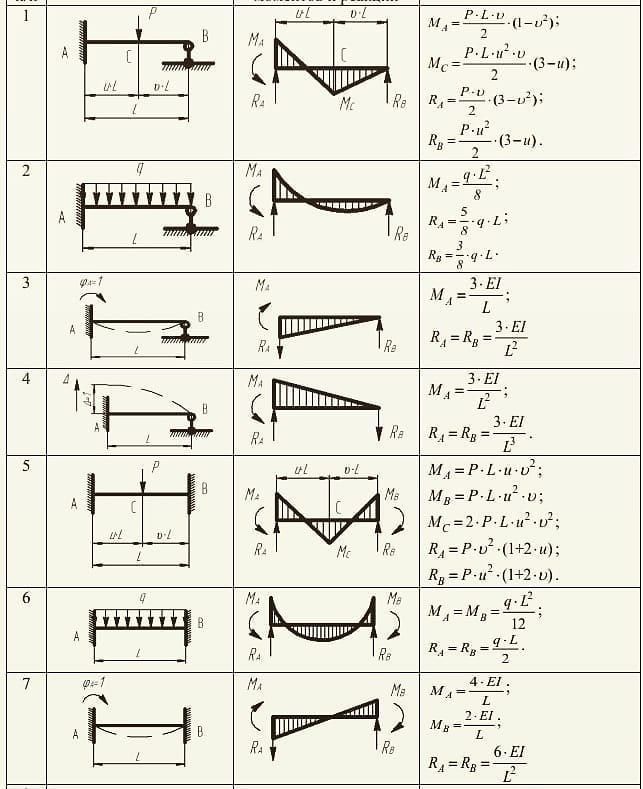
Находим параметры эпюр

C₁ = 2/3, C₂ = 1/3,

а затем и углы поворота на опорах А и В

Пример 4.

Определить угол поворота сечения С для заданной балки (см. рис.).

Решение.

Определяем опорные реакции R_A=R_B,

, , R_A = R_B = qa.

Строим эпюры изгибающего момента от заданной нагрузки и от единичного момента, приложенного в сечении С, где ищется угол поворота. Интеграл Мора вычисляем по правилу Верещагина. Находим параметры эпюр

C₂ = —C₁ = -1/4,

а по ним и искомое перемещение

Пример 5.

Определить прогиб в сечении С для заданной балки (см. рис.).

Решение.

1. Построение эпюр изгибающих моментов.

Эпюра M_F (рис. б)

Опорные реакции:

ВЕ: , ,

, R_B+ R_E = F, R_E = 0;

АВ: , R_А = R_В = F; , .

Вычисляем моменты в характерных точках , M_B = 0, M_C = Fa и строим эпюру изгибающего момента от заданной нагрузки.

Эпюра (рис. в).

В сечении С, где ищется прогиб, прикладываем единичную силу и строим от нее эпюру изгибающего момента, вычисляя сначала опорные реакции ВЕ — , , = 2/3; , , = 1/3, а затем моменты в характерных точках , , .

2. Определение искомого прогиба. Воспользуемся правилом Верещагина и вычислим предварительно параметры эпюр и :

Прогиб сечения С

Пример 6.

Определить прогиб в сечении С для заданной балки (см. рис.).

Решение.

Строим эпюры изгибающих моментов от заданной нагрузки и от единичной силы, приложенной в точке С. Пользуясь правилом Верещагина, вычисляем параметры эпюр ,

и находим искомый прогиб

Пример 7.

Определить прогиб в сечении С для заданной балки (см. рис.).

Решение.

1. Построение эпюр изгибающих моментов.

Опорные реакции:

, , R_A = 2qa,

, R_A+ R_D = 3qa, R_D = qa.

Строим эпюры изгибающих моментов от заданной нагрузки и от единичной силы, приложенной в точке С.

2. Определение перемещений. Для вычисления интеграла Мора воспользуемся формулой Симпсона, последовательно применяя ее к каждому из трех участков, на которые разбивается балка.

Участок АВ:

Участок ВС:

Участок СD:

Искомое перемещение

Пример 8.

Определить прогиб сечения А и угол поворота сечения Е для заданной балки (рис. а).

Решение.

1. Построение эпюр изгибающих моментов.

Эпюра М_F

(рис. в). Определив опорные реакции

, , R_B = 19qa/8,

, R_D = 13qa/8, строим эпюры поперечной силы Q и изгибающего момента М_F от заданной нагрузки.

Эпюра (рис. д). В сечении А, где ищется прогиб, прикладываем единичную силу и строим от нее эпюру изгибающего момента.

Эпюра (рис. е). Эта эпюра строится от единичного момента, приложенного в сечении Е, где ищется угол поворота.

2. Определение перемещений. Прогиб сечения А находим, пользуясь правилом Верещагина. Эпюру М_F на участках ВС и CD разбиваем на простые части (рис. г). Необходимые вычисления представляем в виде таблицы.

Номер части	1	2	3	4	5	6	7
	—qa³/6	2qa³/3	—qa³/2	qa³/4	qa³/4	—qa³	—qa³/2
C_i	-3a/4	-3a/4	-5a/6	-2a/3	—a/3	—a/6	0
	qa⁴/8	—qa⁴/2	5qa⁴/12	—qa⁴/6	—qa⁴/12	qa⁴/6	0	—qa⁴/24

Получаем .

Знак “минус” в результате означает, что точка А перемещается не вниз, как была направлена единичная сила, а вверх.

Угол поворота сечения Е находим двумя способами: по правилу Верещагина и по формуле Симпсона.

По правилу Верещагина, перемножая эпюры M_F и , по аналогии с предыдущим получим

Для нахождения угла поворота по формуле Симпсона вычислим предварительно изгибающие моменты посредине участков:

Искомое перемещение, увеличенное в EI_x раз,

Пример 9.

Определить, при каком значении коэффициента k прогиб сечения С будет равен нулю. При найденном значении k построить эпюру изгибающего момента и изобразить примерный вид упругой линии балки (см. рис.).

Решение.

Строим эпюры изгибающих моментов от заданной нагрузки и от единичной силы, приложенной в сечении С, где ищется прогиб.

По условию задачи V_C = 0. С другой стороны, . Интеграл на участке АВ вычисляем по формуле Симпсона, а на участке ВС – по правилу Верещагина.

Находим предварительно

Перемещение сечения С ,

Отсюда , .

При найденном значении k определяем значение опорной реакции в точке А: , , , исходя из которого находим положение точки экстремума на эпюре М согласно условию .

По значениям момента в характерных точках

, ,

строим эпюру изгибающего момента (рис. г).

Пример 10.

Определить вертикальное перемещение точки В консольной балки, изображенной на рисунке.

Решение.

Строим эпюру изгибающих моментов М от действия внешней сосредоточенной силы F: М_В = 0, М_А = –F2l (эпюра линейная).

По условию задачи требуется определить вертикальное перемещение у_В точки В консольной балки, поэтому строим единичную эпюру от действия вертикальной единичной силы F_i = 1, приложенной в точке В.

Учитывая, что консольная балка состоит из двух участков с разной жесткостью на изгиб, эпюры и М перемножаем с помощью правила Верещагина по участкам отдельно. Эпюры М ипервого участка перемножаем по формуле , а эпюры второго участка – как площадь эпюры М второго участка Fl²/2 на ординату 2l/3 эпюры второго участка под центром тяжести треугольной эпюры М этого же участка.

В этом случае формула дает:

Пример 11.

Определить вертикальное перемещение точки В однопролетной балки, изображенной на рисунке. Балка имеет постоянную по всей длине жесткость на изгиб EI.

Решение.

Строим эпюру изгибающих моментов М от действия внешней распределенной нагрузки: М_А = 0; M_D= 0;

Прикладываем в точке В единичную вертикальную силу F_i= 1 и строим эпюру (см. рис.):

откуда R_a= 2/3;

откуда R_d = 1/3, поэтому M_a = 0; M_d = 0; .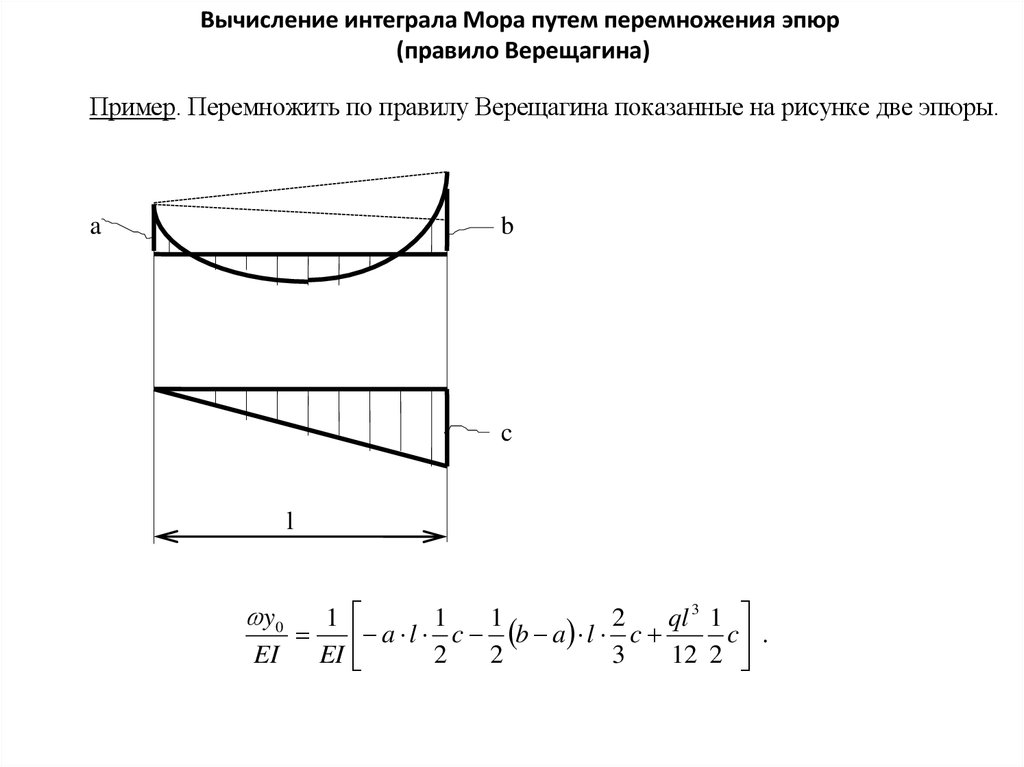

Разделим рассматриваемую балку на 3 участка. Перемножение эпюр 1-го и 3-го участков не вызывает трудностей, так как перемножаем треугольные эпюры. Для того чтобы применить правило Верещагина ко 2-му участку, разобьем эпюру М 2-го участка на две составляющие эпюры: прямоугольную и параболическую с площадью (см. таблицу).

Центр тяжести параболической части эпюры М лежит посередине 2-го участка.

Таким образом, формула при использовании правила Верещагина дает:

Пример 12.

Определить максимальный прогиб в двухопорной балке, нагруженной равномерно распределенной нагрузкой интенсивности q (см. рис.).

Решение.

Находим изгибающие моменты:

— от заданной нагрузки

— от единичной силы, приложенной в точке С, где ищется прогиб .

Вычисляем искомый наибольший прогиб, который возникает в среднем сечении балки

Пример 13.

Определить прогиб в точке В балки, показанной на рисунке.

Решение.

Строим эпюры изгибающих моментов от заданной нагрузки и единичной силы, приложенной в точке В. Чтобы перемножить эти эпюры, надо балку разбить на три участка, так как единичная эпюра ограничена тремя различными прямыми.

Операция перемножения эпюр на втором и третьем участках осуществляется просто. Затруднения возникают при вычислении площади и координат центра тяжести основной эпюры на первом участке.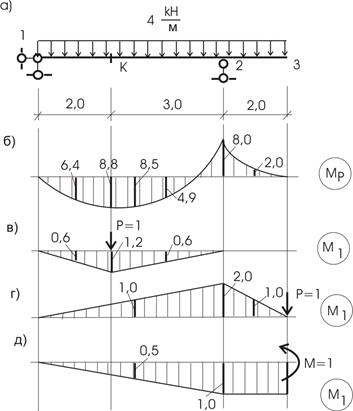 В таких случаях намного упрощает решение задачи построение расслоенных эпюр. При этом удобно одно из сечений принять условно за неподвижное и строить эпюры от каждой из нагрузок, приближаясь справа и слева к этому сечению. Целесообразно за неподвижное принимать сечение в месте перелома на эпюре единичных нагрузок.

Расслоенная эпюра, в которой за неподвижное принято сечение В, представлена на рисунке. Вычислив площади составных частей расслоенной эпюры и соответствующие им ординаты единичной эпюры, получаем

Пример 14.

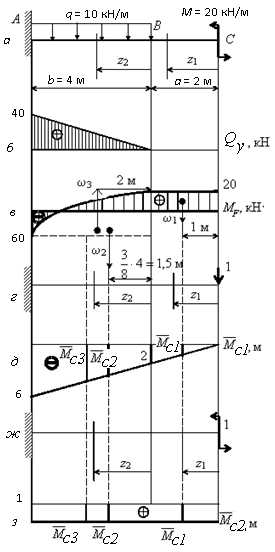
Определить перемещения в точках 1 и 2 балки (рис. а).

Решение.

Приведем эпюры М и Q для балки при а=2 м; q=10 кН/м; С=1,5а; М=0,5qa²; Р=0,8qa; М₀=М; =200 МПа (рис. б и в).

Далее определяем перемещения в точках 1 и 2 балки (рис. а). Состояние балки под действием заданной нагрузки обозначим q.

Определим вертикальное перемещение центра сечения, где приложен сосредоточенный момент. Для этого рассмотрим балку в состоянии под действием только сосредоточенной силы приложенной в точке 1 перпендикулярно оси балки (по направлению искомого перемещения ) (рис. г).

Вычислим опорные реакции, составив три уравнения равновесия

Проверка

Реакции найдены верно.

Для построения эпюры рассмотрим три участка (рис. г).

1 участок

2 участок

3 участок

По этим данным строим эпюру (рис. д) со стороны растянутых волокон.

Определим по формуле Мора с помощью правила Верещагина. При этом криволинейную эпюру , на участке между опорами, можно представить в виде сложения трех эпюр. Стрелка

Знак «минус» означает, что точка 1 перемещается вверх (в направлении противоположном ).

Определим вертикальное перемещение точки 2, где приложена сосредоточенная сила. Для этого рассмотрим балку в состоянии под действием только сосредоточенной силы приложенной в точке 2 перпендикулярно оси балки (по направлению искомого перемещения ) (рис. е).

Эпюра строится аналогично предыдущей.

Далее по формуле Мора

Точка 2 перемещается вверх.

Определим угол поворота сечения, где приложен сосредоточенный момент.

Формула Мора.

Правило Верещагина — презентация онлайн

Похожие презентации:

Курс лекций по сопротивлению материалов

Строительная механика. Теория определения перемещений деформируемых систем. (Часть 1. Лекция 2)

Курс лекций по сопротивлению материалов (1-10)

Определение перемещений сечений стержневых систем

Сопротивление материалов

Теория перемещений. Основные понятия и теоремы

Строительная механика. Теория определения перемещений деформируемых систем. (Часть 1. Лекция 1)

Курс лекций по сопротивлению материалов (модуль 1, лекции 1-8)

Курс лекций по сопротивлению материалов (11- 18)

Уравнения строительной механики. Вариационные принципы строительной механики

Формула Мора
Правило Верещагина
Доцент кафедры
самолетостроения
к.т.н. Мухин Д.В.

2. 1. Интеграл Мора

Используется в тех случаях, когда требуется найти перемещение в
направлении не совпадающем с направлением действия сил.

Сущность интеграла Мора в следующем идеальном построении:
1. Прикладываем в интересующем направлении внешнюю силу Ф.
2. Составляем для системы выражение для потенциальной энергии
деформации U.
3. Дифференцируем выражение для U по Ф и получаем выражение для
перемещения в направлении действия Ф (то есть в интересующем
направлении)
4. В полученном выражении приравниваем Ф=0, получаем окончательное
выражение.
Фиктивную силу Ф представляем в виде произведения
скалярной величины Ф на единичный силовой фактор в
соответствующем направлении.
Таким образом фиктивная сила в зависимости от
интересующего нас направления будет выражена:
N1Ф — в случае продольной силы. Определяем продольное
перемещение. N1 – единичная продольная сила
приложенная в интересующей нас точке.
Qz1Ф — в случае горизонтальной перерезывающей силы.
Определяем прогиб в горизонтальной плоскости. Qz1 –
единичная горизонтальная перерезывающая сила
приложенная в интересующей нас точке.

Q y1Ф — в случае вертикальной перерезывающей силы.
Определяем прогиб в вертикальной плоскости. Qy1 –
единичная горизонтальная перерезывающая сила
приложенная в интересующей нас точке.
M K1Ф — в случае крутящего момента. Определяем угол
закручивания. MK1 – единичный крутящий момент
приложенный в интересующей нас точке.
M y1Ф — в случае момента изгибающего в горизонтальной
плоскости. Определяем угол поворота сечения в
горизонтальной плоскости. My1 – единичный
изгибающий момент в горизонтальной плоскости
приложенный в интересующей нас точке.
M z1Ф — в случае момента изгибающего в вертикальной
плоскости. Определяем угол поворота сечения в
вертикальной плоскости. Mz1 – единичный изгибающий
момент в вертикальной плоскости приложенный в
интересующей нас точке.
После приложения фиктивной силы Ф значения силовых
факторов в интересующем сечении будут равны сумме
значений силовых факторов от исходной системы сил и от
силы Ф.

N N P N1Ф; Qу QуP Qу1Ф; Qz QzP Qz1Ф;
M K M KP M K1Ф; M y M yP M y1Ф; M y M zP M z1Ф.
N P , QyP , QzP , M KP , M yP , M zP — значения силовых факторов
до приложения силы Ф. (То есть в реально существующей
системе)
Подставляем в формулу для внутренней энергии:
l
U
0
l
0
N P N1Ф dx
2
2 EA
0
M KP M K1Ф dx
2
2GI K
k y QyP Qy1Ф dx
2
l
l
0
M
2GA
yP M y1Ф dx
2
2 EI y
l
0
l
0
k z QzP Qz1Ф dx
2
2GA
M zP M z1Ф 2 dx
2 EI z
Дифференцируя по Ф, и принимая после этого Ф=0, находим
перемещение.
(формулы громоздкие, поэтому на примере одного
слагаемого)
l
l
2
2
2
N P N1Ф dx
N P 2 N P N1Ф N1Ф dx
Ф 0
2 EA
2 EA
Ф 0 Ф 0
Ф 0
l
2
N P dx
Ф 0 2 EA
Ф 0
l
2 N P N1Фdx
Ф 0
2 EA
Ф 0
l
2
N1Ф dx
Ф 0 2 EA
l 2 N P N1Ф
l N1Ф 2
0
dx
dx
0 Ф 2 EA Ф 0 0 Ф 2 EA
Ф 0
l
l N P N1
l 2 N1Ф
N P N1
dx
dx
dx
0 EA
Ф 0 0 2 EA
Ф 0 0 EA
Ф 0
Суммируя все интегралы находим перемещение
U
N P N1
dx
Ф Ф 0 0 EA
0
l
l
l
l
M KP M K 1dx
GI K
0
0
k y QyP Q y1dx
M yP M y1dx
EI y
GA
l
k z QzPQz1dx
GA
0
l
M zP M z1dx
EI z
0
Формула носит название формула Мора, а входящие в
формулу интегралы – интегралы Мора
Пример
Балка прямоугольного сечения с размерами b и 2b нагружена
моментом М.

Модуль упругости материала Е, длина l заданы.
Найти прогиб концевого сечения балки С
Решение
1. Строим эпюр изгибающего момента
Мx
M
М
Mz
x
l
x
Mz=M
2. Прикладываем единичную внешнюю силу в
направлении интересующего перемещения
3. Строим эпюр изгибающего момента от единичной силы
Мx
М=-x
l
4. Составляем интеграл Мора
M x
С
dx
EI z
0
x
F=1
Mz
l
x
Mz=-xF=-x
5. Вычисляем интеграл
b 2b
Iz
12
3
12 M x
3 M
С
dx
4
4
E
8
b
2
Eb
0
l
l
3 Ml 2
0 x dx 4 Eb4
Интеграл Мора можно использовать для определения перемещений как
прямолинейных, так и криволинейных стержневых систем.
Поскольку интеграл Мора вычисляется по длине, для криволинейных стержней
вместо dx в подынтегральном выражении используется элемент длины дуги ds=ρdφ
где ρ — радиус кривизны стержня, который может быть постоянным, а может быть
функцией от угловой координаты φ.

ρ
2
M zP M z1
EI z d
1
dφ
φ1
φ
φ2
ds
Пример:
Для кривого бруса в форме четверти круга найти горизонтальное перемещение
точки А.
Нарисуем вспомогательную единичную систему и нагрузим ее горизонтальной
единичной силой в точке А.
В полярной системе координат
положение произвольного
сечения характеризуется
радиусом-вектором ρ (в нашей
задаче ρ = Const — радиус
круга) и углом φ от произвольно
выбранной начальной точки
дуги.
Изгибающий момент от внешних сил
M F F sin
Изгибающий момент от единичной силы
M1 1 1 cos 1 cos
Горизонтальное перемещение точки А
Aгор
2
M M
F 1 d
EI z
1
2
0
F sin 1 cos
F 3
d
EI z
2 EI z
2
sin ( ) ( 1 cos ( ) )
d 0.5
1
0
Правило Верещагина
Правило Верещагина – графо-аналитический метод,
позволяющий упростить вычисления интегралов, входящих в
формулу Мора. Упрощение основано на том, что эпюры от
единичных силовых факторов на прямолинейных участках
оказываются линейными.

Предположим, что необходимо взять интеграл от
произведения двух функций
l
J f1 ( z ) f 2 ( z )dz
0
Пусть вторая из этих функций — линейная f 2 ( z) b kz
Тогда
l
l
J b f1 ( z )dz k zf1 ( z )dz
0
0
Первый интеграл – площадь эпюры f1(z)
l
f ( z)dz
1
0
Второй интеграл – статический момент этой эпюры
относительно оси ординат
1
По свойству статического момента
l
zЦТ – координата
0 zf1 ( z)dz 1zЦТ центра тяжести
первого эпюра
В сумме получаем
J 1b k 1 z ЦТ 1 (b kzЦТ )
Выражение в скобках – значение функции f2 под центром
тяжести первой фигуры
J 1 f 2 ( z ЦТ )
ЦТ
h
ЦТ
h
ЦТ
h
l
l
l
l/2
lh / 3
lh / 2
lh
l /3
l/4
Пример
Однопролетная двухконсольная балка нагружена силой и
моментом. Жесткость поперечного сечения на изгиб по
длине постоянна. Линейный размер l задан. Найти прогиб
сечения С от внешней нагрузки по абсолютной величине.

(Влиянием поперечной силы на величину перемещения
пренебречь).
1. Строим эпюр изгибающего момента от действительной
нагрузки
2. Прикладываем единичную нагрузку в направлении
интересующего перемещения
3. Строим эпюр момента от приложенного единичного
фактора
4. Находим интеграл Мора по правилу Верещагина
1
с
EJ
1 Fl 3
1 2 2 1 2 1
2 Fl 3 l 2 Fl 3 l 6 EJ
x

19. 3. Формула Мора для определения температурных перемещений сечения по заданному направлению

В основу вывода формулы положен принцип возможных перемещений
Пусть дана система, находящаяся под действием
температуры. Обозначим: n — число участков
системы; i — номер ее произвольного участка.
C
Для определения перемещения сечения С по
направлению v рассмотрим систему без температуры,
нагруженную безразмерной обобщенной единичной
B
силой, приложенной в сечении С по направлению v.
Схему системы под действием температуры
обозначим Т, а схему нагружения системы
обобщенной единичной силой обозначим 1.

Приняв за
возможное перемещение системы ее
деформированное состояние в схеме Т, найдем
работу внешних, реактивных и упругих сил схемы
нагружения 1 на этом возможном перемещении. По
принципу возможных перемещений сумма этих работ
равна нулю, так как система в состоянии 1 находится B
в равновесии.
dS
G
v
D
T
dS
1
C
v
1
D
G
Работа внешних сил
AP 1 v
dS
G
C
Опоры В и D неподвижны, а реакция в опоре G
направлена по нормали к любому ее возможному
перемещению, поэтому работа реактивных сил
v
B
AR 0
Для определения работы сил упругости Ау
рассмотрим один и тот же элемент, вырезанный из
схемы Т и схемы 1 двумя поперечными
сечениями, расcтояние dS между которыми
бесконечно мало.
Силы упругости в поперечном сечении элемента
могут привестись к шести внутренним силовым
факторам, которым присваиваем индекс 1.
D
T
dS
1
G
C
v
B
1
D
Обозначим температуры крайних верхних и нижних, правых и левых волокон i-го
участка соответственно Тв, Tн и Тп , Tл.

Считаем, что температура в направлениях
осей у и z сечения изменяется линейно, будучи соответственно функцией только у
и только z.
Законы изменения температуры по поперечному сечению показаны на рис.
TB
y z
Очевидно, что
TC
a
C N1
y
C
C’
x
x
z
b
M21
B B’
TC T y y 0 T z z 0
TH
dS
dδT
dS
B
TП
или
A
T(y)
A’
TЛ
Температура на оси
элемента
A
hy
T T
T b TH a
T y B Н y B
a b
a b
T TЛ
T с TЛ d
T z П
z П
с d
c d
TB b TH a TП с TЛ d
a b
c d
c
d
h3
T(z)
Пусть dδT — возможное перемещение центра тяжести поперечного сечения в
схеме от изменения температуры элемента.
d T TC dS
где α — коэффициент линейного расширения материала элемента.
Пусть dθTz — возможный относительный поворот концевых сечений элемента около
оси z в схеме от изменения температуры
T y
d zT
dS
hy
где T y TВ TН , h y — наибольший размер поперечного сечения в направлении оси
у.

По аналогии, возможный относительный поворот концевых сечений элемента
вокруг оси y
Tz
d yT
dS
hz
где Tz TП TЛ , hz — наибольший размер поперечного сечения в направлении оси z.
1. dAy — работа сил упругости в элементе dS по абсолютной величине равна
работе внутренних силовых факторов состояния на возможных перемещениях
состояния и противоположна ей по знаку, так как силы упругости всегда
направлены в сторону, противоположную направлению изменения расстояния
между точками тела.
2. Работа МК1, Qy1 и Qz1 равна нулю, так как концевые сечения элемента при
нагреве относительно оси х не поворачиваются, a Qy1 и Qz1 перпендикулярны
направлению dδT, поэтому
dAy M z1d zT M y1d yT Nd T
Подставляя сюда полученные ранее выражения и интегрируя полученное
выражение по si —длине i-гo участка найдем работу сил упругости на i-м участке.
Ty
Tz
Ayi M z1
M y1
N1 Tc ds
hy
hz
si
Суммируя эти интегралы по всем участкам системы, найдем Aу.

Ty
Tz
Ay M z1
M y1
N1 Tc ds
hy
hz
i 1 si
n
Складывая Ар с Ау и приравнивая сумму нулю, получим формулу Мора для
определения температурных перемещений сечений стержневой системы по
заданному направлению:
Ap Ay 0;
Ty
Tz
1 v M z1
M y1
N1 Tc ds 0;
hy
hz
i 1 si
n
Ty
Tz
v M z1
M y1
N1 Tc ds;
hy
hz
i 1 si
n

English Русский Правила

Метод площади момента — StructuralWiki

Материал из StructuralWiki

Перейти к: навигация, поиск

Метод нахождения прогибов в каркасной конструкции с использованием кривой площади момента.

Содержимое

1 Первая теорема
2 Вторая теорема
3 Каталожные номера
4 Внешние ссылки

Первая теорема

Рисунок, иллюстрирующий первую теорему

Теорема 1: Изменение наклона между любыми двумя точками на кривой упругости равно площади диаграммы M/EI между этими двумя точками.

где

М момент
EI Жесткость при изгибе
… изменение наклона между точками A и B
A, B … точки на кривой упругости

Вторая теорема

Рисунок, иллюстрирующий вторую теорему

Теорема 2: Отклонение касательной в точке B на упругой кривой относительно касательной в точке A равно «моменту» диаграммы между точками A и B вычисляется относительно точки A (точка на кривой упругости), где должно быть определено отклонение.

где

М момент
EI Жесткость при изгибе
… отклонение касательной в точке B относительно касательной в точке A
… центроид диаграммы M/EI, измеренный по горизонтали от точки A
A, B … точки на кривой упругости

Ссылки

Рассел С. Хиббелер: структурный анализ, 3-е издание, Prentice Hall, 1995, глава 8, с. 354-569, ISBN 0-02-354041-9

Внешние ссылки

Прогиб консольной балки по методу момента площади
Прогиб свободно опертой балки по методу момента площади
Колин Капрани: Структурный анализ III Метод площади момента — теоремы Мора (конспект лекций), 2007 г.

Главная > Темы > Традиционные методы анализа e
Основы	Традиционные методы анализа · Свойства сечения · Круг Мора · Диаграмма взаимодействия
Теория	Уравнения упругости
Силы и напряжения	Кручение · Изгиб · Сдвиг · Главное напряжение
Базовая статистика	Уравнения балок · Метод моментов-площадей · Правило Верещагина · Матрица жесткости · Фиксированные концевые моменты · Определенная статика · Неопределенная статика · Теорема Максвелла о взаимных перемещениях · Закон Бетти 9005
	Линии влияния · Принцип Мюллера-Бреслау
Базовая динамика	Демпфирование · Матрица масс · Матрица демпфирования
Энергетические методы	Внешняя работа и энергия деформации · Принцип работы и энергия · Метод виртуальной работы · Метод единичной нагрузки · Теорема Кастильяно
Приблизительные методы	Метод распределения моментов
Графический	Кремона Диаграмма

См. также	Методы вычислительного анализа
Родственные категории	Традиционные методы анализа

[PDF] Космологические модели с gurzadyan-xue Dark Energy

doi: 10.1088/0264-9381/23/15/020
Corpus ID: 119391615

9023 @Artushclicle @artclecle @artcleclicle @artcleclicle @artcleclicle. title={Космологические модели с темной энергией Гурзадяна-Сюэ}, автор={Г. В. Верещагин и Г. Егорян}, journal={Классическая и квантовая гравитация}, год = {2006}, объем = {23}, страницы={5049- 5061} }

Г. Верещагин, Г. Егорян
Опубликовано 4 января 2006 г.
Физика
Классическая и квантовая гравитация

параметр) значение плотности темной энергии в замечательном согласии с текущими наборами космологических данных, в отличие от многочисленных феноменологических сценариев, где постулируется соответствующее значение. Эта формула предполагает возможность изменения физических констант, таких как скорость света и гравитационная постоянная. Учитывая несколько космологических моделей, основанных на этом…

Просмотр на IOP Publishing

arxiv.org

Интегральное уравнение темной энергии Джорджовского-Гурзадяна и диаграмма Хаббла

Мы рассматриваем наблюдательные аспекты значения плотности темной энергии из квантовых флуктуаций вакуума, первоначально основанных на модели Гурзадяна-Сюэ. Приводим интеграл Джорджовского–Гурзадяна…

Феноменологическая модель темной энергии с гибридной динамической космологической постоянной

Исследуем темную энергию (ТЭ), связывая ее с энергией вакуума или космологической постоянной Λ, которая считается динамической по своей природе. Наш подход феноменологический и относится к области…

Dark Energy Из вакуумных колебаний

S. Djorgovski, V. Gurzadyan
Physics
2006

Dark Energy Model

Физика

2005

Две феноменологические модели Λ, а именно. и , изучаются в предположении, что G — переменный во времени параметр. Обе модели показывают, что G обратно пропорциональна времени, как было предложено ранее…

Модель темной энергии в космологии Калуцы-Клейна

У. Мухопадхьяй, И. Чакраборти, С. Рэй, А.А. Усмани
Физика
2014

в космологии Калуцы-Клейна. Физические особенности и ограничения настоящей модели были изучены и обсуждены…

ОБОБЩЕННАЯ МОДЕЛЬ ДЛЯ ТЕМНОЙ ЭНЕРГИИ Λ

У. Мухопадхьяй, П. Рэй, С. Рэй, С. Чоудхури
Физика
2009

Уравнения поля Эйнштейна в сферически-симметричном пространстве-времени рассматриваются здесь в связи с исследованием темной энергии. Получен набор решений для кинематической Λ-модели, а именно…

Переменное уравнение состояния для обобщенной модели темной энергии

С. Рэй, Ф. Рахаман, У. Мухопадхьяй, Р. Саркар
Физика
2011

Мы представляем модель современной ускоряющейся Вселенной и фокусируемся на различных важных физических переменных, участвующих в модели, в соответствии с феноменологическим предположением Λ∝h3 с предписанием…

Диаграмма Хаббла гамма-всплесков, откалиброванная с космологией Гурзадяна-Сюэ

Х. М. Куэста, Р. Туркати, К. Фурланетто, Х. Хачатрян, С. Мирзоян, Г. Егорян
Физика
20017
Контекст. Поскольку гамма-всплески (GRB) являются самыми яркими среди известных космических объектов, они обладают существенным потенциалом для космологических исследований, если их правильно использовать в качестве стандартных свечей. Цели. Мы…
НЕПАРАМЕТРИЧЕСКОЕ ОПРЕДЕЛЕНИЕ КРАСНОГО СМЕЩЕНИЯ ИНДЕКСА ЭВОЛЮЦИИ ТЕМНОЙ ЭНЕРГИИ
- H. Ziaeepour
- Физика
- 2007
Мы предлагаем непараметрический метод определения знака γ — показателя эволюции красного смещения темной энергии. Это важно для различения моделей с положительной энергией, космологической…
Феноменология модели Λ-CDM: возможность ускорения Вселенной с положительным давлением Физика 9{3}$ выбран здесь для исследования космологии Λ-CDM. Модель может следовать по динамике, в основе…
, показывая 1-10 из 17 ссылок
Сорт Byrelevancemost, затронутая Papersercession
Скрытая инвариантность в космологических моделях Gurzadyan-x.
2006

Физические константы и формула Гурзадяна-Сюэ для темной энергии

Г. Верещагин
Физика
2006

Мы рассматриваем космологические следствия формулы для плотности темной энергии, полученной Гурзадяном и Сюэ1,2, которая предсказывает значение, соответствующее наблюдаемому. Космологические модели с различными…

Прогон G и Λ при низких энергиях из физики на MX: возможные космологические и астрофизические последствия

И. Шапиро, Дж. Сола, Х. Штефанчич
Физика 7

Подход ренормализационной группы (РГ) к космологии является эффективным методом изучения возможной эволюции космологических параметров с точки зрения квантовой теории поля (КТП) в…

A Изменение скорости света во времени как решение задачи космологические загадки

А. Альбрехт, Дж. Магейхо
Физика
1999

Мы рассматриваем космологические последствия более быстрого перемещения света в ранней Вселенной. Мы предлагаем рецепт вывода поправок к уравнениям космологической эволюции при скорости…