Формула Мора и правило Верещагина
Правило Верещагина — графо-аналитический прием вычисления интегралов, входящих в формулы Мора. Правило применимо, если ось участка прямолинейна, и удобно применимо, если жесткость поперечных сечений по длине участка постоянна. [c.223]Применение метода единичной нагрузки (Максвелла—Мора) с использованием правила Верещагина или формулы Симпсона. [c.309]
При проектировании валов (осей) следует рассчитать прогибы и углы поворота (перекосы) характерных сечений, например, в опорах вала, местах установки зубчатых колес и сравнить их с, допускаемыми. Прогибы и углы поворота вычисляют, используя интеграл Мора или правило Верещагина в табл. 16.3 приведены формулы для определения углов поворота сечений и прогибов двухопорного вала постоянного сечения от сил в зубчатом зацеплении (F,, и ) и от консольной нагрузки (F ). [c.419]
В 1924 г.

Используя формулы Jz = bh /Зб F = bh/2 для геометрических характеристик поперечного сечения (см. табл. П.З), с помощью интеграла Мора (7.18) и правила Верещагина (7.19) вычисляем коэффициенты уравнения (свободный член — сумма произведений ЭМ на ЭМ и на ЭУУ )
[c.309]
П.З), с помощью интеграла Мора (7.18) и правила Верещагина (7.19) вычисляем коэффициенты уравнения (свободный член — сумма произведений ЭМ на ЭМ и на ЭУУ )
[c.309]
Решение. Перемещение определяем методом Мора при этом в общей формуле учитываем два слагаемых, отражающих влияние изгибающих моментов и продольных сил (напоминаем, что в этом случае правило Верещагина для вычисления интеграла Мора неприменимо) [c.324]
ФОРМУЛА МОРА И ПРАВИЛО ВЕРЕЩАГИНА [c.158]
Способ перемножения эпюр — правило Верещагина. Если жесткость поперечного сечения стержня на участке постоянна, то каждый интеграл формулы Максвелла —Мора (9.3) можно подсчитывать через произведение площади со эпюры снлы от заданных сил на координату Ё эпюры такого же усилия от единичной фиктивной обобщенной силы (обязательно прямолинейной), приходящейся против центра тяжести первой эпюры (рис. 9.5).
Вычислим интеграл Мора с помощью правила А. К. Верещагина. При перемножении трапеций используем формулу ( 0.15). В результате вычислений получим
[c.214]
К. Верещагина. При перемножении трапеций используем формулу ( 0.15). В результате вычислений получим
[c.214]
Коэффициент бц, называемый также главным перемещением, и член Д р вычисляются по правилам вычисления перемещений в статически определимых системах, т. е. по формуле Мора с применением правила Верещагина для рам с прямотинейпым контуром. Для основной системы строим эпюру моментов от единичной силы (единичную эпюру), приложенной взамен искомой силы (рис. 3.105, в). Затем строим эпюру моментов от заданной нагрузки (грузовую эпюру, рис. 3.105, г). [c.326]
Относительная стрела прогиба балок может быть определена по методу Мора с использованием правила Верещагина (см. 4-1). В частности, для балки, свободнолежа-щей на двух опорах с равномерно распределенной нагрузкой общим весом Р (рис. 4-5), имеем (см. формулу 4-9) [c.137]
Способ перемножения эяюр — правило Верещагина. Если жесткость поперечного сечения стержня на участке постоянна, то каждый интеграл формулы Максвелла — Мора (185) можно подсчитывать через произведение площади ю эпюры усилия от заданных сил (рис. 167) на координату эпюры такого же усилия от единичной фиктизной обобщенной силы (обязательно прямолинейной), приходящейся против центра тяжести первой эпюры. Практически это тавило Верещагина применяют для определения линейных и угловых перемещелий в балочно-рамных системах от действия изгибающих
Если жесткость поперечного сечения стержня на участке постоянна, то каждый интеграл формулы Максвелла — Мора (185) можно подсчитывать через произведение площади ю эпюры усилия от заданных сил (рис. 167) на координату эпюры такого же усилия от единичной фиктизной обобщенной силы (обязательно прямолинейной), приходящейся против центра тяжести первой эпюры. Практически это тавило Верещагина применяют для определения линейных и угловых перемещелий в балочно-рамных системах от действия изгибающих
Вычисление интеграла Мора по формуле (7-3) может быть ныпо нено по правилу Верещагина (указания об области применимости этого правила, данные выше, остаются в силе). Соответствующая формула может быть записана в виде [c.140]
Формулы (211) и (212) назыЁаются интегралами Мора. Графоаналитический способ вычисления этих интегралов приводит к правилу Верещагина. Рассмотрим это правило. [c.267]
Есть случаи, когда вычисление интеграла Мора не может быть выполнено по правилу Верещагина. tg a2: — вертикальная координата линейного участка изгибающего момента M l S, расположенного ниже центроида участка кривой M?,
tg a2: — вертикальная координата линейного участка изгибающего момента M l S, расположенного ниже центроида участка кривой M?,
- Таким образом, Интеграл Максвелла-Мора линейной части системы с постоянной жесткостью представляет собой кривизну изгибающего момента за счет ординаты MK o линейного участка, которая расположена ниже центроида кривой. Произведение эпюры MRMC считается положительным,если оно расположено на одной стороне оси стержня, и отрицательным, если оно находится на другой стороне. Положительный результат умножения графика
подразумевает, что направление фактического движения совпадает с направлением единичного удара. В частном случае, если оба графика MF и MK линейны, то одна из областей может быть умножена на соответствующую ординату. Согласно правилу Верещагина, если и участок, и МК имеют криволинейные формы, или жесткость стержней в рассматриваемых областях переменная, то в сложном контуре участка М ф или М р невозможно определить смещение, они делятся на простые участки,а площадь и расположение центроида известны. Для риса. 33.12 приведено
Для риса. 33.12 приведено
значение площади центроида и координаты простой фигуры. Например. В консольной балке Людмила Фирмаль
определенного поперечного сечения, нагружая сосредоточенной нагрузкой F, определить прогиб поперечного сечения(фиг. 33.13, а). Решение. Исходя из заданной нагрузки на балку, постройте график изгибающего момента MF(фактическое состояние), как показано на рисунке. 33.13, 6). Для определения прогиба поперечного сечения применяют вертикальную концентрацию Ffl=l_ (мнимое состояние) (без силы) и строят график изгибающего момента MV(рис. 33.13, б). Графики MF и MV являются линейными, поэтому вы можете вычислить любую область. Площадь участка Mr равна (Bf=F/2 / 2. Вертикальная ось участка, расположенного под центром тяжести треугольного участка МР, равна МВС-21/3. Поперечный прогиб _ д _ ° >
fm bc_E1g21_FF B F~EJ~2EJ3 ~ 3EJ’ Результат положительный, поэтому смещение сечения b совпадает с направлением силы FB=1 и направлено вниз.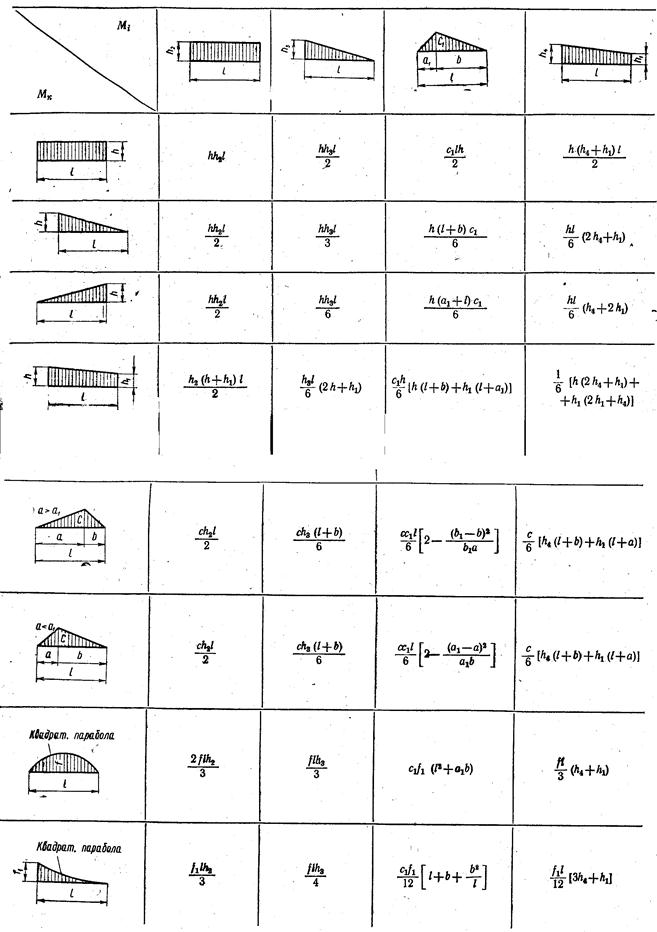
Смотрите также:
Примеры решения задач технической механике
Если вам потребуется помощь по технической механике вы всегда можете написать мне в whatsapp.
2.8 Основные варианты перемножения эпюр
2.8 Основные варианты перемножения эпюр
Очевидно, что разнообразие приложенных нагрузок и геометрических схем конструкций приводит к различным, с точки зрения геометрии, перемножаемым эпюрам. Для реализации правила Верещагина нужно знать площади геометрических фигур и координаты их центров тяжести. На рис.29 представлены некоторые основные варианты, возникающие в практических расчетах.
Для перемножения эпюр сложной формы их необходимо разбивать на простейшие. Например, для перемножения двух эпюр, имеющих вид трапеции, нужно одну из них разбить на треугольник и прямоугольник, умножить площадь каждого из них на ординату второй эпюры, расположенную под соответствующим центром тяжести, и результаты сложить.
Если указанные выше действия проделать в общем виде, то получим для таких сложных случаев формулы, удобные для использования в практических расчетах (рис.30). Так, результат перемножения двух трапеций (рис.30,а):
(2.21)
Рис. 29
По формуле (2.21) можно перемножить и эпюры, имеющих вид «перекрученных» трапеций (рис.30,б), но при этом произведение ординат, расположенных по разные стороны от осей эпюр, учитывается со знаком минус.
Если одна из перемножаемых эпюр очерчена по квадратной параболе (что соответствует нагружению равномерно распределенной нагрузкой), то для перемножения со второй (обязательно линейной) эпюрой ее рассматривают как сумму (рис.30,в) или разность (рис.30,г) трапециидальной и параболической эпюр. Результат перемножения в обоих случаях определяется формулой:
Рекомендуемые файлы
(2. 22)
22)
но значение f при этом определяется по-разному (рис. 30, в, г).
Рис. 30
Возможны случаи, когда ни одна из перемножаемых эпюр не является прямолинейной, но хотя бы одна из них ограничена ломаными прямыми линиями. Для перемножения таких эпюр их предварительно разбивают на участки, в пределах каждого из которых по крайней мере одна эпюра являетя прямолинейной.
Рассмотрим использование правила Верещагина на конкретных примерах.
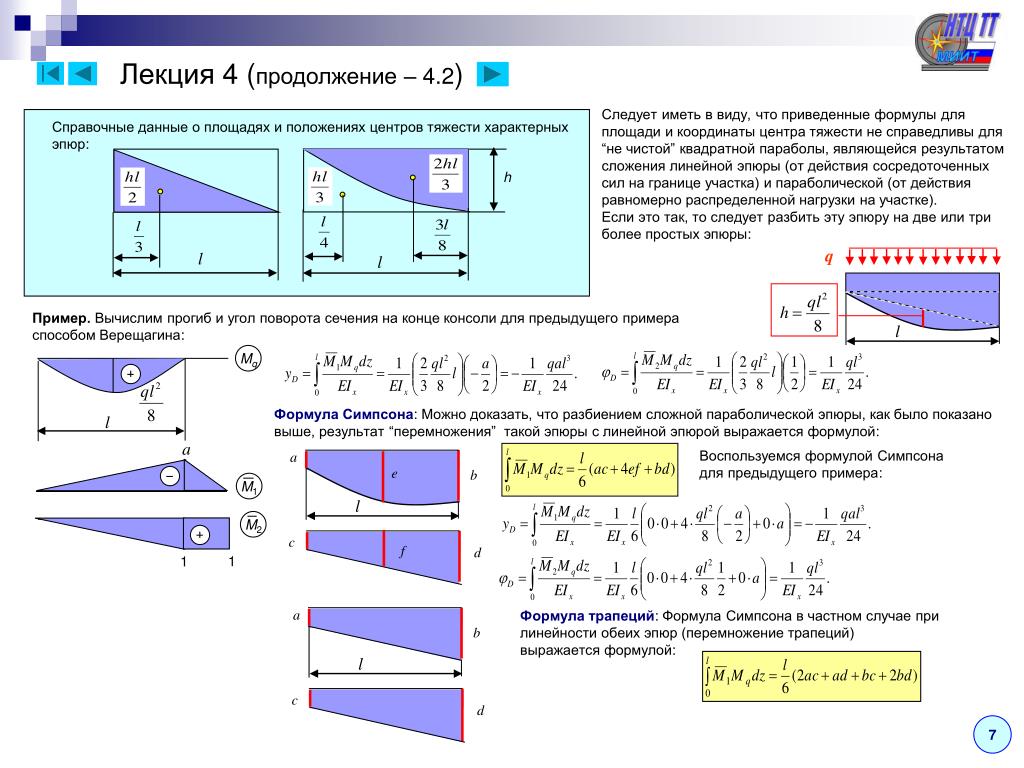
Пример 15. Определить прогиб в середине пролета и угол поворота левого опорного сечения балки, нагруженной равномерно распределенной нагрузкой (рис.31,а), способом Верещагина.
Последовательность расчета способом Верещагина – такая же, как и в методе Мора, поэтому рассмотрим три состояния балки: грузовое – при действии распределенной нагрузки q; ему соответствует эпюра Mq (рис.31,б), и два единичных состояния — при действии силы приложенной в точке С (эпюра , рис.31,в), и момента , приложенного в точке В (эпюра , рис. 31,г).
31,г).
Прогиб балки в середине пролета:
.
Аналогичный результат был получен ранее методом Мора (см. пример 13). Следует обратить внимание на тот факт, что перемножение эпюр выполнялось для половины балки, а затем, в силу симметрии, результат удваивался. Если же площадь всей эпюры Mq умножить на расположенную под ее центром тяжести ординату эпюры (на рис.31,в), то величина перемещения будет совершенно иной и неправильной так как эпюра ограничена ломаной линией. На недопустимость такого подхода уже указывалось выше.
А при вычислении угла поворота сечения в точке В можно площадь эпюры Mq умножить на расположенную под ее центром тяжести ординату эпюры (, рис.31,г), так как эпюра ограничена прямой линией:
Этот результат также совпадает с результатом, полученным ранее методом Мора (см. пример 13).
Рис. 31
Пример 16. Определить горизонтальное и вертикальное перемещения точки А в раме (рис. 32,а).
32,а).
Как и в предыдущем примере, для решения задачи необходимо рассмотреть три состояния рамы: грузовое и два единичных. Эпюра моментов MF, соответствующая первому состоянию, представлена на рис.32,б. Для вычисления горизонтального перемещения прикладываем в точке А по направлению искомого перемещения (т.е. горизонтально) силу , а для вычисления вертикального перемещения силу прикладываем вертикально (рис.32,в,д). Соответствующие эпюры и показаны на рис.32,г,е.
Горизонтальное перемещение точки А:
При вычислении на участке АВ трапеция (эпюра MF) разбита на треугольник и прямоугольник, после чего треугольник с эпюры «умножен» на каждую из этих фигур. На участке ВС криволинейная трапеция разделена на криволинейный треугольник и прямоугольник, а для перемножения эпюр на участке СД использована формула (2.21).
Знак » — «, полученный при вычислении , означает, что точка А перемещается по горизонтали не влево (в этом направлении приложена сила ), а вправо.
Вертикальное перемещение точки А:
Здесь знак » — » означает, что точка А перемещается вниз, а не вверх.
Отметим, что единичные эпюры моментов, построенные от силы , имеют размерность длины, а единичные эпюры моментов построенные от момента , являются безразмерными.
Рис.32
Пример 17. Определить вертикальное перемещение точки А плоско-пространственной системы (рис.33,а).
Люди также интересуются этой лекцией: 6.2. Способы обмена данными.
Рис.23
Как известно (см. гл.1), в поперечных сечениях стержней плоско-пространственной системы возникают три внутренних силовых фактора: поперечная сила Qy, изгибающий момент Mx и крутящий момент Mкр. Так как влияние поперечной силы на величину перемещения незначительно (см. пример 14, рис.27), то при вычислении перемещения методом Мора и Верещагина из шести слагаемых остаются только два.
Для решения задачи построим эпюры изгибающих моментов Mx,q и крутящих моментов Мкр,q от внешней нагрузки (рис. 33,б), а затем в точке А приложим силу по направлению искомого перемещения, т.е. вертикального (рис.33,в), и построим единичные эпюры изгибающих моментов и крутящих моментов (рис.33,г). Стрелками на эпюрах крутящих моментов показаны направления закручивания соответствующих участков плоско-пространственной системы.
33,б), а затем в точке А приложим силу по направлению искомого перемещения, т.е. вертикального (рис.33,в), и построим единичные эпюры изгибающих моментов и крутящих моментов (рис.33,г). Стрелками на эпюрах крутящих моментов показаны направления закручивания соответствующих участков плоско-пространственной системы.
Вертикальное перемещение точки А:
При перемножении эпюр крутящих моментов произведение берется со знаком «+», если стрелки, указывающие направление кручения, сонаправленны, и со знаком » — » – в противном случае.
Определение перемещения методом Мора. Правило Верещагина (Реферат)
УО «БГУИР»
кафедра инженерной графики
РЕФЕРАТ
на тему:
«ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ МЕТОДОМ МОРА. ПРАВИЛО ВЕРЕЩАГИНА»
МИНСК, 2008
Рассмотрим теперь общий метод
определения перемещений, пригодный для
любой, линейно деформируемой системы
при любой нагрузке.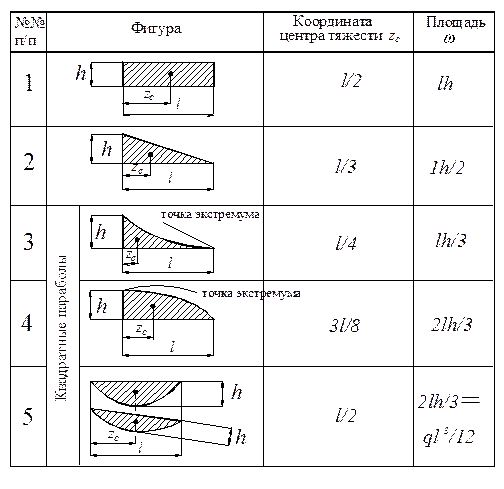 Этот метод предложен
выдающимся немецким ученым О. Мором.
Этот метод предложен
выдающимся немецким ученым О. Мором.
Пусть, например, требуется определить вертикальное перемещение точки А балки, представленной на рис. 7.13, а. Заданное (грузовое) состояние обозначим буквой к. Выберем вспомогательное состояние той же балки с единичной
силой, действующей в точке A и в направлении искомого перемещения. Вспомогательное состояние обозначим буквой i (рис. 7.13,6).
Вычислим работу внешних и внутренних сил вспомогательного состояния на перемещениях, вызванных действием сил грузового состояния.
Работа внешних сил будет равна произведению единичной силы на искомое перемещение ya
а работа внутренних сил по абсолютной величине равна интегралу
Имеем
или
(1)
Формула (7.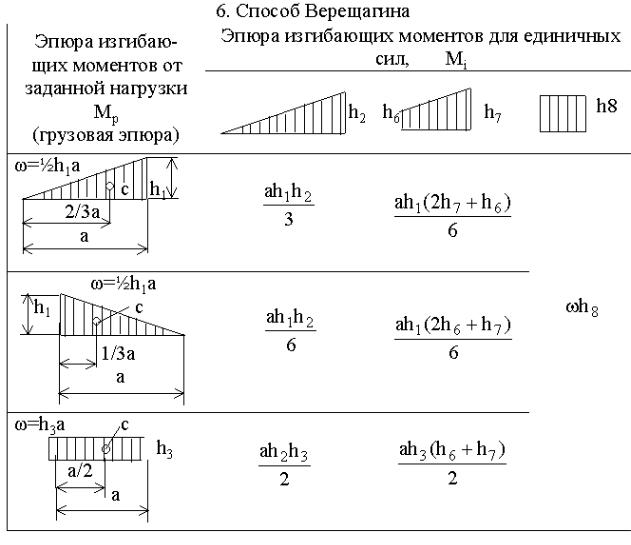 33) и есть формула Мора
(интеграл Мора), которая дает возможность
определить перемещение в любой точке
линейно-деформируемой системы.
33) и есть формула Мора
(интеграл Мора), которая дает возможность
определить перемещение в любой точке
линейно-деформируемой системы.
В этой формуле подынтегральное произведение MiMk положительно, если оба изгибающих момента имеют одинаковый знак, и отрицательно, если Mi и Мк имеют разные знаки.
Если бы мы определяли угловое перемещение в точке А, то в состоянии i следовало бы приложить в точке А момент, равный единице (без размерности).
Обозначая буквой Δ любое перемещение (линейное или угловое), формулу (интеграл) Мора напишем в виде
(2)
В общем случае аналитическое выражение Mi и Мк может быть различным на разных участках балки или вообще упругой системы. Поэтому вместо формулы (2) следует пользоваться более общей формулой
(3)
Если стержни системы работают не на изгиб, а на растяжение (сжатие), как, например, в фермах, то формула Мора имеет вид
(4)
В этой формуле произведение NiNK
положительно, если оба усилия
растягивающие или оба сжимающие.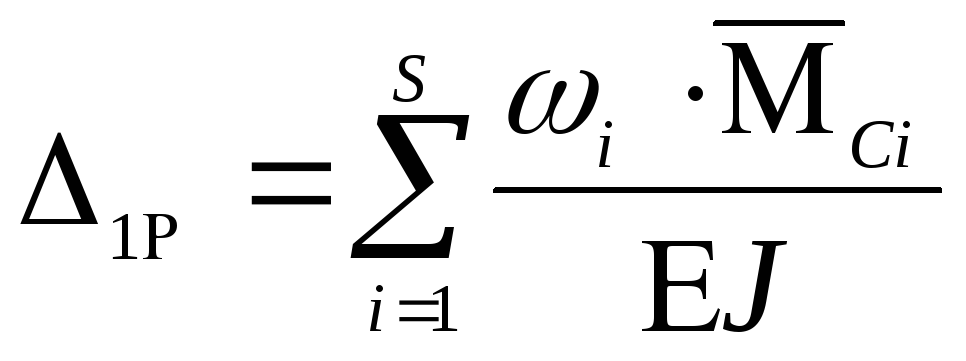 Если
стержни одновременно работают и на
изгиб и на растяжение (сжатие), то в
обычных случаях, как показывают
сравнительные расчеты, перемещения
можно определять, учитывая лишь изгибающие
моменты, так как влияние продольных сил
весьма мало.
Если
стержни одновременно работают и на
изгиб и на растяжение (сжатие), то в
обычных случаях, как показывают
сравнительные расчеты, перемещения
можно определять, учитывая лишь изгибающие
моменты, так как влияние продольных сил
весьма мало.
По тем же соображениям, как отмечалось ранее, в обычных случаях можно не учитывать влияния поперечных сил.
Вместо непосредственного вычисления интеграла Мора можно пользоваться графо-аналитическим приемом «способом перемножения эпюр», или правилом Верещагина.
Рассмотрим две эпюры изгибающих моментов, из которых одна Мк имеет произвольное очертание, а другая Мi прямолинейна (Рис 7.14, а и б).
Сечение стержня на участке AВ будем считать постоянным. В этом случае
(5)
Величина MKdz представляет собой элементарную площадь dωk эпюры Мк (заштрихована на рисунке). Таким образом,
(6)
Но
(7)
следовательно,
(8)
Но представляет собой статический момент
площади эпюры Мк относительно
некоторой оси у, проходящей
через точку О, равный ωkzc,
где ωk
— площадь эпюры моментов; zс
— расстояние от оси у
до центра тяжести эпюры Мк. Из чертежа видно, что
Из чертежа видно, что
(9)
где Мсi — ордината эпюры Mi, расположенная под центром тяжести эпюры Мк (под точкой С). Следовательно,
(10)
т. е. искомый интеграл равен произведению площади эпюры Мк (любой по очертанию) на расположенную под ее центром тяжести ординату прямолинейной эпюры Мсi. Значение величины ωкМсi считается положительным, если обе эпюры располагаются по одну сторону стержня, и отрицательным, если они располагаются по разные стороны. Положительный результат перемножения эпюр означает, что направление перемещения совпадает с направлением единичной силы (или момента).
Необходимо помнить, что ордината Мсi берется обязательно в прямолинейной эпюре. В том частном случае, когда обе эпюры прямолинейные, можно умножить площадь любой из них на соответствующую ординату другой.
Для стержней переменного сечения
правило Верещагина перемножения эпюр
неприменимо, так как в этом случае уже
нельзя выносить величину EJ
из-под знака интеграла.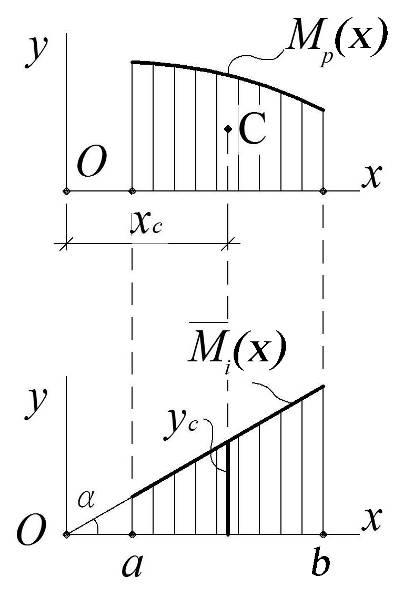 В
этом случае следует выразить EJ
как функцию абсциссы сечения
и затем уже вычислять интеграл Мора
(1).
В
этом случае следует выразить EJ
как функцию абсциссы сечения
и затем уже вычислять интеграл Мора
(1).
При ступенчатом изменении жесткости стержня интегрирование (или перемножение эпюр) производят для каждого участка отдельно (со своим значением EJ) и затем суммируют результаты.
В табл. 1 приведены значения площадей некоторых простейших эпюр и координат их центра тяжести.
Таблица 1
Вид эпюры | Площадь эпюры | Расстояние до центра тяжести |
Возрождая традиции: в НГАСУ (Сибстрин) открылась выставка творческих работ преподавателей кафедры Дизайна и искусства 10 февраля 2022 года в НГАСУ (Сибстрин) стартовала выставка творческих работ преподавателей кафедры Дизайна и искусства «Дела традиций».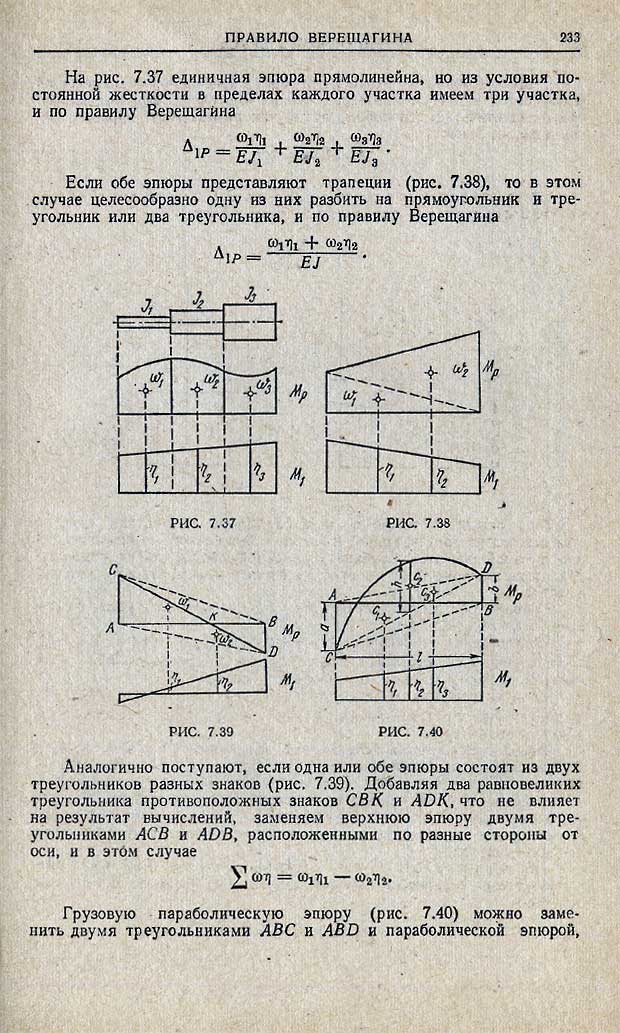 Экспозиция включает выполненные на высоком профессиональном уровне живописные и графические портреты и пейзажи. Картины не однородны по сюжету и композиции: одни насыщенные и напряженные, другие светлые и лиричные, но объединяет их общая тема – свято следовать традициям художественного искусства. Кроме натурных работ, на выставке представлены дизайнерские проекты – графические иллюстрации, фотографии уникальных авторских ювелирных украшений и скульптуры из самозатвердевающей японской глины.
«Наша цель – познакомить нынешних студентов и будущих абитуриентов, гостей вуза, а также преподавателей и сотрудников университета с творческим потенциалом преподавателей новой кафедры Дизайна и искусств НГАСУ (Сибстрин), – отметила, открывая мероприятие, заведующая кафедрой ДИ Ирина Карнаева.
Экспозиция включает выполненные на высоком профессиональном уровне живописные и графические портреты и пейзажи. Картины не однородны по сюжету и композиции: одни насыщенные и напряженные, другие светлые и лиричные, но объединяет их общая тема – свято следовать традициям художественного искусства. Кроме натурных работ, на выставке представлены дизайнерские проекты – графические иллюстрации, фотографии уникальных авторских ювелирных украшений и скульптуры из самозатвердевающей японской глины.
«Наша цель – познакомить нынешних студентов и будущих абитуриентов, гостей вуза, а также преподавателей и сотрудников университета с творческим потенциалом преподавателей новой кафедры Дизайна и искусств НГАСУ (Сибстрин), – отметила, открывая мероприятие, заведующая кафедрой ДИ Ирина Карнаева. |
Студентка Сибстрина стала первой на межвузовской конференции по применению информационных технологий 2 февраля 2022 года в Новосибирске в дистанционном формате прошла межвузовская научно-практическая конференция с международным участием «Информационные технологии и информационная безопасность в профессиональной деятельности».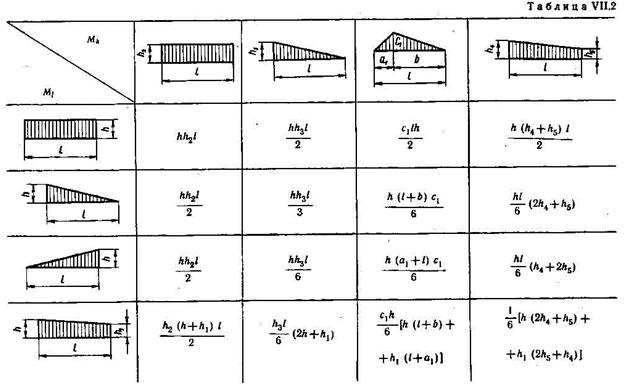 В ее работе приняли участие научно-педагогические работники и обучающиеся образовательных организаций: Новосибирского государственного архитектурно-строительного университета (Сибстрин), Сибирского государственного университета геосистем и технологий, Сибирского государственного университета путей сообщения, Новосибирского высшего военного командного училища Министерства обороны Российской Федерации, Сибирского государственного университета телекоммуникаций и информатики, Национального университета обороны имени Первого Президента… В ее работе приняли участие научно-педагогические работники и обучающиеся образовательных организаций: Новосибирского государственного архитектурно-строительного университета (Сибстрин), Сибирского государственного университета геосистем и технологий, Сибирского государственного университета путей сообщения, Новосибирского высшего военного командного училища Министерства обороны Российской Федерации, Сибирского государственного университета телекоммуникаций и информатики, Национального университета обороны имени Первого Президента… |
С Международным днем женщин и девочек в науке! Сегодня, 11 февраля, отмечается Международный день женщин и девочек в науке. Инициатором праздника в 2015 году выступила Генеральная Ассамблея ООН с целью достижения полного и равного доступа к науке, а также обеспечения гендерного равенства и расширения прав и возможностей женщин. Новосибирский государственный архитектурно-строительный университет (Сибстрин) занимает ведущие позиции в области образования и науки в сферах строительства, архитектуры и жилищно-коммунального хозяйства. Такого высокого результата не удалось бы добиться без инициативных, трудолюбивых, умных и талантливых женщин – преподавателей, ученых, аспиранток и студенток, занимающихся научными исследованиями и принимающих активное участие в научной и общественной жизни вуза. Среди известных ученых НГАСУ (Сибстрин), руководителей структурных подразделений, институтов и факультетов, научных руководителей магистрантов и аспирантов немало представительниц … Такого высокого результата не удалось бы добиться без инициативных, трудолюбивых, умных и талантливых женщин – преподавателей, ученых, аспиранток и студенток, занимающихся научными исследованиями и принимающих активное участие в научной и общественной жизни вуза. Среди известных ученых НГАСУ (Сибстрин), руководителей структурных подразделений, институтов и факультетов, научных руководителей магистрантов и аспирантов немало представительниц … |
Преподаватели НГАСУ (Сибстрин) помогают в решении глобальных задач одной из крупнейших металлургических и горнодобывающих компаний мира С 2 по 4 февраля 2022 года Институтом дополнительного образования в рамках сотрудничества с крупнейшим за Уралом сталелитейным предприятием ЕВРАЗ ЗСМК была организована поездка в г. Новокузнецк профессора НГАСУ (Сибстрин) Галины Амбросовой. На данный момент в Институте дополнительного образования НГАСУ (Сибстрин) обучается 22 специалиста комбината на направлениях профпереподготовки «Проектирование, строительство и эксплуатация гидротехнических сооружений» и «Водоснабжение и водоотведение».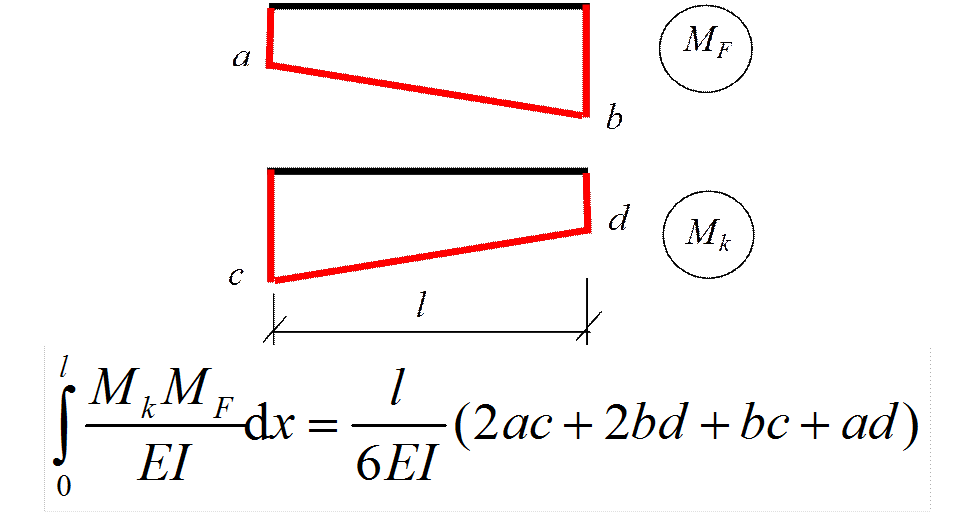 2 февраля Галина Тарасовна провела итоговый контроль по дисциплине «Очистка сточных вод» у группы слушателей направления «Водоснабжение и водоотведение», лекции для которых проводятся в дистанционном формате. В ходе встречи были рассмотрены конкретные производственные моменты
2 февраля Галина Тарасовна провела итоговый контроль по дисциплине «Очистка сточных вод» у группы слушателей направления «Водоснабжение и водоотведение», лекции для которых проводятся в дистанционном формате. В ходе встречи были рассмотрены конкретные производственные моменты |
Формула Мора Правило Верещагина Доцент кафедры самолетостроения к
Формула Мора Правило Верещагина Доцент кафедры самолетостроения к. т. н. Мухин Д. В.
1. Интеграл Мора Используется в тех случаях, когда требуется найти перемещение в направлении не совпадающем с направлением действия сил. Сущность интеграла Мора в следующем идеальном построении: 1. Прикладываем в интересующем направлении внешнюю силу Ф. 2. Составляем для системы выражение для потенциальной энергии деформации U. 3. Дифференцируем выражение для U по Ф и получаем выражение для перемещения в направлении действия Ф (то есть в интересующем направлении) 4. В полученном выражении приравниваем Ф=0, получаем окончательное выражение.
В полученном выражении приравниваем Ф=0, получаем окончательное выражение.
Фиктивную силу Ф представляем в виде произведения скалярной величины Ф на единичный силовой фактор в соответствующем направлении. Таким образом фиктивная сила в зависимости от интересующего нас направления будет выражена: — в случае продольной силы. Определяем продольное перемещение. N 1 – единичная продольная сила приложенная в интересующей нас точке. — в случае горизонтальной перерезывающей силы. Определяем прогиб в горизонтальной плоскости. Qz 1 – единичная горизонтальная перерезывающая сила приложенная в интересующей нас точке. — в случае вертикальной перерезывающей силы. Определяем прогиб в вертикальной плоскости. Qy 1 – единичная горизонтальная перерезывающая сила приложенная в интересующей нас точке.
— в случае крутящего момента. Определяем угол закручивания. MK 1 – единичный крутящий момент приложенный в интересующей нас точке. — в случае момента изгибающего в горизонтальной плоскости. Определяем угол поворота сечения в горизонтальной плоскости. My 1 – единичный изгибающий момент в горизонтальной плоскости приложенный в интересующей нас точке. — в случае момента изгибающего в вертикальной плоскости. Определяем угол поворота сечения в вертикальной плоскости. Mz 1 – единичный изгибающий момент в вертикальной плоскости приложенный в интересующей нас точке.
Определяем угол поворота сечения в горизонтальной плоскости. My 1 – единичный изгибающий момент в горизонтальной плоскости приложенный в интересующей нас точке. — в случае момента изгибающего в вертикальной плоскости. Определяем угол поворота сечения в вертикальной плоскости. Mz 1 – единичный изгибающий момент в вертикальной плоскости приложенный в интересующей нас точке.
После приложения фиктивной силы Ф значения силовых факторов в интересующем сечении будут равны сумме значений силовых факторов от исходной системы сил и от силы Ф. — значения силовых факторов до приложения силы Ф. (То есть в реально существующей системе) Подставляем в формулу для внутренней энергии:
Дифференцируя по Ф, и принимая после этого Ф=0, находим перемещение. (формулы громоздкие, поэтому на примере одного слагаемого)
Суммируя все интегралы находим перемещение Формула носит название формула Мора, а входящие в формулу интегралы – интегралы Мора
Пример Балка прямоугольного сечения с размерами b и 2 b нагружена моментом М. Модуль упругости материала Е, длина l заданы. Найти прогиб концевого сечения балки С Решение 1. Строим эпюр изгибающего момента Мx M М Mz x l x Mz=M
Модуль упругости материала Е, длина l заданы. Найти прогиб концевого сечения балки С Решение 1. Строим эпюр изгибающего момента Мx M М Mz x l x Mz=M
2. Прикладываем единичную внешнюю силу в направлении интересующего перемещения 3. Строим эпюр изгибающего момента от единичной силы Мx М=-x l 4. Составляем интеграл Мора x F=1 Mz x Mz=-x. F=-x
5. Вычисляем интеграл
Интеграл Мора можно использовать для определения перемещений как прямолинейных, так и криволинейных стержневых систем. Поскольку интеграл Мора вычисляется по длине, для криволинейных стержней вместо dx в подынтегральном выражении используется элемент длины дуги ds=ρdφ где ρ — радиус кривизны стержня, который может быть постоянным, а может быть функцией от угловой координаты φ. ρ dφ φ1 φ φ2 ds
Пример: Для кривого бруса в форме четверти круга найти горизонтальное перемещение точки А. Нарисуем вспомогательную единичную систему и нагрузим ее горизонтальной единичной силой в точке А. В полярной системе координат положение произвольного сечения характеризуется радиусом-вектором ρ (в нашей задаче ρ = Const — радиус круга) и углом φ от произвольно выбранной начальной точки дуги.
В полярной системе координат положение произвольного сечения характеризуется радиусом-вектором ρ (в нашей задаче ρ = Const — радиус круга) и углом φ от произвольно выбранной начальной точки дуги.
Изгибающий момент от внешних сил Изгибающий момент от единичной силы Горизонтальное перемещение точки А
Правило Верещагина – графо-аналитический метод, позволяющий упростить вычисления интегралов, входящих в формулу Мора. Упрощение основано на том, что эпюры от единичных силовых факторов на прямолинейных участках оказываются линейными. Предположим, что необходимо взять интеграл от произведения двух функций Пусть вторая из этих функций — линейная Тогда Первый интеграл – площадь эпюры f 1(z) Второй интеграл – статический момент этой эпюры относительно оси ординат
По свойству статического момента z. ЦТ – координата центра тяжести первого эпюра В сумме получаем Выражение в скобках – значение функции f 2 под центром тяжести первой фигуры h ЦТ
Пример Однопролетная двухконсольная балка нагружена силой и моментом. Жесткость поперечного сечения на изгиб по длине постоянна. Линейный размер l задан. Найти прогиб сечения С от внешней нагрузки по абсолютной величине. (Влиянием поперечной силы на величину перемещения пренебречь). 1. Строим эпюр изгибающего момента от действительной нагрузки
Жесткость поперечного сечения на изгиб по длине постоянна. Линейный размер l задан. Найти прогиб сечения С от внешней нагрузки по абсолютной величине. (Влиянием поперечной силы на величину перемещения пренебречь). 1. Строим эпюр изгибающего момента от действительной нагрузки
2. Прикладываем единичную нагрузку в направлении интересующего перемещения 3. Строим эпюр момента от приложенного единичного фактора
4. Находим интеграл Мора по правилу Верещагина
3. Формула Мора для определения температурных перемещений сечения по заданному направлению В основу вывода формулы положен принцип возможных перемещений Пусть дана система, находящаяся под действием температуры. Обозначим: n — число участков системы; i — номер ее произвольного участка. C Для определения перемещения сечения С по направлению v рассмотрим систему без температуры, нагруженную безразмерной обобщенной единичной B силой, приложенной в сечении С по направлению v. Схему системы под действием температуры обозначим Т, а схему нагружения системы обобщенной единичной силой обозначим 1. Приняв за возможное перемещение системы ее деформированное состояние в схеме Т, найдем работу внешних, реактивных и упругих сил схемы нагружения 1 на этом возможном перемещении. По принципу возможных перемещений сумма этих работ равна нулю, так как система в состоянии 1 находится B в равновесии. d. S G v D T d. S 1 C v 1 D G
Схему системы под действием температуры обозначим Т, а схему нагружения системы обобщенной единичной силой обозначим 1. Приняв за возможное перемещение системы ее деформированное состояние в схеме Т, найдем работу внешних, реактивных и упругих сил схемы нагружения 1 на этом возможном перемещении. По принципу возможных перемещений сумма этих работ равна нулю, так как система в состоянии 1 находится B в равновесии. d. S G v D T d. S 1 C v 1 D G
Работа внешних сил d. S G C Опоры В и D неподвижны, а реакция в опоре G направлена по нормали к любому ее возможному перемещению, поэтому работа реактивных сил Для определения работы сил упругости Ау рассмотрим один и тот же элемент, вырезанный из схемы Т и схемы 1 двумя поперечными сечениями, расcтояние d. S между которыми бесконечно мало. Силы упругости в поперечном сечении элемента могут привестись к шести внутренним силовым факторам, которым присваиваем индекс 1. v B D T d. S 1 G C v B 1 D Обозначим температуры крайних верхних и нижних, правых и левых волокон i-го участка соответственно Тв, Tн и Тп , Tл. Считаем, что температура в направлениях осей у и z сечения изменяется линейно, будучи соответственно функцией только у и только z.
Считаем, что температура в направлениях осей у и z сечения изменяется линейно, будучи соответственно функцией только у и только z.
Законы изменения температуры по поперечному сечению показаны на рис. TB y z Очевидно, что A A T(y) a A’ x b M 21 TH d. S B c d h 2 TП dδT x z B B’ d. S C N 1 y C’ TЛ или hy Температура на оси элемента C T(z) Пусть dδT — возможное перемещение центра тяжести поперечного сечения в схеме от изменения температуры элемента. где α — коэффициент линейного расширения материала элемента. Пусть dθTz — возможный относительный поворот концевых сечений элемента около оси z в схеме от изменения температуры где — наибольший размер поперечного сечения в направлении оси у.
По аналогии, возможный относительный поворот концевых сечений элемента вокруг оси y где — наибольший размер поперечного сечения в направлении оси z. 1. d. Ay — работа сил упругости в элементе d. S по абсолютной величине равна работе внутренних силовых факторов состояния на возможных перемещениях состояния и противоположна ей по знаку, так как силы упругости всегда направлены в сторону, противоположную направлению изменения расстояния между точками тела. 2. Работа МК 1, Qy 1 и Qz 1 равна нулю, так концевые сечения элемента при нагреве относительно оси х не поворачиваются, a Qy 1 и Qz 1 перпендикулярны направлению dδT, поэтому Подставляя сюда полученные ранее выражения и интегрируя полученное выражение по si —длине i-гo участка найдем работу сил упругости на i-м участке.
2. Работа МК 1, Qy 1 и Qz 1 равна нулю, так концевые сечения элемента при нагреве относительно оси х не поворачиваются, a Qy 1 и Qz 1 перпендикулярны направлению dδT, поэтому Подставляя сюда полученные ранее выражения и интегрируя полученное выражение по si —длине i-гo участка найдем работу сил упругости на i-м участке.
Суммируя эти интегралы по всем участкам системы, найдем Aу. Складывая Ар с Ау и приравнивая сумму нулю, получим формулу Мора для определения температурных перемещений сечений стержневой системы по заданному направлению:
| |
Эта статья цитируется в 4 научных статьях (всего в 4 статьях) Эффективные теории и уравнения начальной загрузки А.V. vereshachagin A , V. V. vereshachagin B , К. М. Семенов-Тянь-Шанский B
A Университет Бергена Резюме: В этой статье мы рассматриваем общие свойства эффективных теорий поля. Заметим, что свобода фиксации условий перенормировки в эффективной теории поля не так велика, как кажется.Учет минимального набора требований корректности пертурбативной схемы, основанной на формуле Дайсона для $S$-матрицы, приводит к жестким ограничениям на существенные параметры теории и, следовательно, на возможный набор условий перенормировки. Полный текст: PDF-файл (304 КБ) Версия на английском языке: Библиографические базы данных: УДК: 517.9 Поступила: 18.11.2002 Ссылка: А.В. Верещагин, В. В. Верещагин, К. М. Семенов-Тян-Шанский, “Эффективные теории и уравнения бутстрапа”, Вопросы квантовой теории поля и статистической физики. Часть 17, Зап. научн. Сем. ПОМИ, 291, ПОМИ, СПб, 2002, 78–108; Дж. Матем. науч. (Нью-Йорк), 125:2 (2005), 144–158 Цитирование в формате AMSBIB Варианты подключения: Ссылки на статьи в Google Scholar: русские цитаты,
английские цитаты Эта публикация цитируется в следующих статьях: |
АВТОМАТИЗАЦИЯ РАСЧЕТА АРОК. - Бесплатная онлайн-библиотека - Бесплатная онлайн-библиотекаСтраница/ссылка: URL-адрес страницы: HTML-ссылка:В литературе приводятся решения различных задач плоская деформация круглого стержня только с деформацией изгиба [2]. В 1938 г. профессор Н.К. Снитко получил решение проблемы плоская деформация круглого стержня с учетом изгиба и деформации растяжения-сжатия только для конкретного случая нагрузки: [кв.sub.y]([alpha])=q=const, где q — интенсивность вертикального нагрузка. Отсутствие достаточно точного аналитического решения
Проблема плоской деформации круглого стержня способствовала
тот факт, что в ряде работ [3-5] рекомендуется заменить
криволинейных стержней набором прямолинейных стержней. Данная модель дает погрешность не более 1,0 % при прямолинейном стержень рисует дугу изогнутого стержня менее чем на 5[градусов] [6].Это означает что кольцо может быть представлено правильным многоугольником из 72 стержней, арка в 180[градусов]-36 стержней и т. д. Далее расчет криволинейный стержень можно выполнить методом граничных элементов (БЭМ), силовой метод и другие методы.  Если вы примените метод граничных элементов и MATLAB окружающей среды, вы можете значительно. уменьшить сложность расчета, упростить алгоритм и схемы расчета, повысить точность и достоверность результатов, и ввести это методологии в расчетную практику и учебный процесс высшие учебные заведения без особого труда. В связи с этим целью статьи является практическое применение возможностей метода граничных элементов для решение достаточно трудоемких задач по напряженно-деформированному состоянию круговых арки и арочные конструкции. Материалы и методы. Для достижения этой цели рассчитаем напряженно-деформированное состояние круглых арок в среде MATLAB. Покажем на рис. 1 расчетную схему арки и запишем основные уравнения, необходимые для расчета. Система дифференциальных уравнений для плоского деформирования круговой стержень с учетом деформации изгиба и растяжения относительно радиального [??]([альфа]) и тангенциального смещения u([альфа]) имеет вид: [невоспроизводимое математическое выражение], (1) где EA-Жесткость сечения арки при растяжении-сжатии, кН; EI-Жесткость сечения арки на изгиб, кН[м. Решение задачи Коши о деформации плоской арки может представить в матричном виде следующим образом [1]:
1 2 3
EIv([альфа]) 1 [A.sub.11] [A.sub.12] -[A.sub.13]
EI [фи] ([альфа]) 2 [A.sub.22] -[A.подраздел 23]
M([альфа]) = 3 [A.sub.22]
Q([альфа]) 4
EAu([альфа]) 5 [A.sub.51] [A.sub.52] -[A.sub.53]
N([альфа]) 6
4 5 6
EIv ([альфа]) 1 - [A.sub.14] [A.sub.15] [A.sub.16]
EI [фи] ([альфа]) 2 - [A.sub.13] [A.sub.26]
M([альфа]) = 3 [A.sub.12] -[A.sub.36]
Q([альфа]) 4 [A.sub.11] -[A.подраздел 46]
EAu([альфа]) 5 -[A.sub.54] [A.sub.11] [A.sub.56]
N ([альфа]) 6 - [A.sub.64] [A.sub.11]
EIv([альфа]) 1 EIv(0) [B.sub.11]
EI [фи] ([альфа]) 2 EI [фи] (0) [B.sub.21]
М([альфа]) = 3 М(0) + -[B.sub.31]
Q([альфа]) 4 Q(0) -[B.где ЭИ 9([альфа])-Угол поворота сечения арки, кН[м.суп.2]; M([alpha])-изгибающий момент в сечении, кНм; Q([alpha])-поперечная сила в сечении, кН; N([альфа])-нормальная сила в сечения, кН. Основные ортонормированные функции и условия радиальной нагрузки (рис. 1) после интегрирования принимают вид [1]: [математическое выражение не воспроизводимо]. (3) Следующим шагом является учет граничных условий для поддерживающие арки. Для определения параметров напряженно-деформированного состояния арки необходимо составить и решить краевую задачу, учитывающую заданную опору условия для граничных точек.На БЭМ это уравнение имеет вид [1] [A.sub.*][X.sub.*] = -B, (4) где [A.sub.*] -Матрица граничных значений фундаментальных функции, учитывающие граничные условия арки; [X.sub.*]-Матрица начальных и конечных параметров изгиба арки и растяжка; Матрица B-нагрузки со значением граничной переменной [альфа]. Рассмотрим различные условия супинатора. С шарнирной опорой, схема которой показана на рис.2, представляли собой матрицы начального (X) и конечного (Y) параметров арка (5), где мы учли шарнирную опору из двух пограничные участки. [невоспроизводимое математическое выражение] (5) Из этих матриц следует, что в матрице [A.sub.*] столбцы 1, 3 и 5 необходимо обнулить и добавить элементы A(2.1) = -1; А(4.3) = -1; A (6.5) = -1 с учетом переноса параметры от Y до [X.sub.*]. Матричное уравнение границы значение задачи для арки на рис. 2 принимает вид:
1 2 3 4 5 6
1 [A.sub.12] - [A.sub.14] [A.sub.16]
2-1 [A.sub.22] -[A.sub.13] [A.sub.26]
3 -[A.sub.12] -[A.sub.36]
4 -1 -[A.sub.11] -[A.sub.46]
5 [A.sub.52] [A.sub.54] -[A.sub.56]
6 [А.sub.64] -1 -[A.sub.64]
1 EI [фи] ([пи]) - [B.sub.11] ([пи])
2 EI [фи] (0) - [B.sub.21] ([пи])
3 Q([pi]) [B.sub.31]([pi])
4 Q (0) = [B.sub.41] ([пи])
5 Н ([пи]) [B.sub.51] ([пи])
6 N (0) [B.После решения уравнения (6) реакции арки будут: [H.sub.0] = [Q.sub.(0)]; [R.sub.0] = [N.sub.(0)]; [H.sub.K] = [Q.sub.([pi])] [R.sub.K] = [N.sub.([pi])], а напряженно-деформированное состояние во внутренних точках определяется уравнением (2). Аналогично, составляя матрицы [X.sub.*], Y, получаем уравнение краевая задача для другого случая жесткого защемления и шарнирной опоры, показано на рис. 3.
1 2 3 4 5 6
1 -1 -[A.sub.13] -[A.sub.14] [A.sub.16]
2 -[A.sub.23] -[A.sub.13] [A.sub.26]
3 [А.Sub.22] [A.sub.12] -[A.sub.36]
4 -1 [A.sub.11] -[A.sub.46]
5 - [A.sub.53] - [A.sub.54] [A.sub.56]
6 - [A.sub.64] -1 [A.sub.11]
1 EI [фи] ([пи]) - [B.sub.11] ([пи])
2 Q([pi]) -[B.sub.21]([pi])
3 М (0) = [B.sub.31] ([пи])
4 Q (0) [B.sub.41] ([пи])
5 Н ([пи]) [B.sub.51] ([пи])
6 N (0) [B.sub.61] ([pi]) (7)
После решения (7) реакции арки будут равны [Х.суб.0] = [Q.sub.(0)]; [R.sub.0] = [N.sub.(0)] ; [H.sub. На рис. 4 показана схема следующего типа опоры для арки - жесткое защемление двух граничных точек. Матричное уравнение краевой задачи для этого случая опора примет вид (8).
1 2 3 4 5 6
1 -[A.sub.13] -[А.sub.14] [A.sub.16]
2 -1 -[A.sub.23] -[A.sub.13] [A.sub.26]
3 [A.sub.22] [A.sub.12] -[A.sub.36]
4 -1 [A.sub.11] -[A.sub.46]
5 [A.sub.53] - [A.sub.54] [A.sub.56]
6 - [A.sub.64] -1 [A.sub.11]
1 М([пи]) -[B.sub.11]([пи])
2 Q([pi]) -[B.sub.21]([pi])
3 М (0) [B.sub.31] ([пи])
4 Q (0) = [B.sub.41] ([пи])
5 Н([пи]) [Б.суб.51]([пи])
6 N (0) [B.sub.61] ([pi]) (8)
Реакции арки будут равны [H.sub.0] = [Q.sub.(0)]; [R.sub.0] = [N.sub.(0)]; [M.sub.0] = [M.sub.(0)]; [H.sub.K] = [Q.sub.([pi])]; [R.sub.K] = [N.sub.([pi])]; [M.sub.k] = [M.sub.([pi])]. Рассмотрим пример определения параметров
напряженно-деформированное состояние арки при произвольной нагрузке и закреплении. Результаты.Определить напряженно-деформированное состояние арки (рис. 5). То результаты представлены численно (в виде таблицы) и визуально (в виде диаграмм). Угловые координаты сосредоточенного момента и сосредоточенная сила [[альфа].sub.M] = [pi]/4; [[альфа].sub.F] = 3/4 [пи]. Угловые координаты равномерно распределенной нагрузки равны [[альфа].sub.H] = 0; [[альфа].sub.K] = [пи]. При заданных исходных данных вычисляем значения граничные параметры с использованием уравнения(7) и представить полученные результаты в виде Таблица 1. Реакции арочных опор будут равны [H.sub.0]=20,00 кН, [R0]=200,88 кН, [M0]=147,14 кНм, [Hk]=6,96 кН, [Rk] = 210,08 кН. Значения параметров напряженно-деформированного состояния обобщены в таблице 2. Данные таблицы 2 свидетельствуют о том, что полученные результаты
точный. Такой вывод обосновывается тем, что
напряженно-деформированное состояние арки рассчитывали по уравнениям
метод начальных параметров (2), где начальными параметрами были
взято из таблицы 1. Если решение точное, то опорные граничные условия должны удовлетворяться на правильном пьедестале, что подтверждается данными в Таблица 2. Диаграммы параметров напряженно-деформированного состояния дуги в декартовых координатах показаны на рис. 6-11. Схемы на рисунках 6-11 можно легко изобразить на контуре арка. Выводы. Уравнения краевых задач для определения неизвестные начальные параметры дуг окружности при существующих получены условия опоры граничных участков.На основе основные понятия сопротивления материалов, динамики и прочности структурирует методику расчета напряженно-деформированного состояния круговых арок в среде MATLAB. Принимая во внимание учет влияния распределенных и сосредоточенных нагрузок расчет круговой арки. Следует отметить, что формирование уравнений границы
значение задач по расчету арок с разными опорами
условиях значительно сокращает время других исследователей в
решение задач расчета и анализа конструкций, содержащих
круговые арки. Представлена методика расчета напряженно-деформированного состояния Авторами имеет существенные преимущества перед известными методами. Это достаточно подробно описывает расчет действия внешний сосредоточенный момент и расчет всех кинематических параметры деформированного состояния дуги окружности. В заключение отметим, что многочисленные задачи расчета колец и кольцевые системы [2, т. 1, с. 1, с. 321; 365] можно решить с помощью уравнения БЭМ 2) аналогично, но в более точной постановке с учетом изгиба и деформации растяжения-сжатия. [Обратите внимание: некоторые нелатинские символы были исключены из этого статья.] DOI10.15276/оп.2.52.2017.02 Поступила в редакцию 17.05.2017 г. Принято 24 июля 2017 г. Ссылки [1.] [фраза опущена] [2.] [фраза опущена] [3.] [фраза опущена] [4.] [фраза опущена] [5.] [фраза опущена] [6.] [фраза опущена] Ссылки [1. [2.] Биргера И.А., Пановко Я.Г. (Ред.). (1968) Прочность, устовчивость, колебанива. [Сила, стабильность, вибрации]. Москва: Машиностроение. [3.] Александров А.В., Лащеников Б.Я., Шапошников А.В. Н.Н. (1983) Строительная механика. Тонкостенное Строительная механика. Тонкостенный пространственный Системы]. Москва: Стройиздат. [4.] Оробей В., Коломиец Л. и Лымаренко А. (2015). Метод граничных элементов в задаче об изгибе пластинчатых элементов инженерия. Металлургическая и горнодобывающая промышленность. 4, 295-302. [5.] Коломиец Л., Оробей В., Лымаренко А.(2016) Метод
граничный элемент в задачах об устойчивости плоских изгибаемых балок
прямоугольное сечение. Структуры. Металлургическая и горнодобывающая промышленность
Индустр. [6.] Дарков А.В. и Шапошников Н.Н. (1985). Строительная механика [Строительная механика] Москва: Высшая школа. В.Ф. Оробей, д.б.н., профессор, О.Ф. Дащенко, д.б.н., проф., О.М. Лымаренко, к.б.н., доц. проф. Одесский национальный политехнический университет, пр. Шевченко, 1, Одесса, Украина, 65044; электронная почта: [email protected] Подпись: Рис. 1. Расчетная схема арки Подпись: Рис. 2. Шарнирная арка Подпись: Рис. 3. Жесткое защемление и шарнирная поддержка арок Подпись: Рис. 4. Жесткое защемление арки Подпись: Рис. 5. Нагрузка и фиксация в арке Подпись: Рис. 6. Схема арки EI[??], прогибы, кН[м.3] Подпись: Рис. 7. Схема углов поворота арки Эл[фи], кН[м.суп.2] Подпись: Рис. 8. Диаграмма изгибающих моментов М, кНм Подпись: Рис. 9. Диаграмма поперечных усилий Q, кН Подпись: Рис. 10. Диаграмма тангенциальных перемещений EAu, кНм Подпись: Рис.
Таблица 1 Значение граничных параметров
арки на рис. 5
Нет n/n Параметр Значение
1 Efy(rc), кН[м.2] -958,34
2 Q(n), кН -6.96
3 М(0), кН·м 147,14
4 Q(0), кН -20,00
5 Н(н), кН -210,08
6 Н(0), кН -200,88
Таблица 2 Результаты расчета арок в численном виде
Угловые параметры напряженно-деформированного состояния
координировать
рад град Эа. Эа[фи]. М, кНм
[10-3], [10-2],
кН[м.суп.2] кН[м.суп.2]
0,0 0.0 0,0 0,0 147,14
0,09 5 0,133 1,86 119,79
0,17 10 0,497 3,35 93,72
0,26 15 1,038 4,48 6915
0,35 20 1,703 5,28 46,24
0,44 25 2,445 5,78 25,19
0,52 30 3,214 6,00 6,15
0,61 35 3,970 5,96 -10,74
0,70 40 4,673 5,71 -25,34
0,79 45 5.289 5,27 -67,55
0,87 50 5,760 4,25 -77,16
0,96 55 6,036 3,12 -83,98
1,05 60 6,100 1,92 -87,96
1,13 65 5,945 0,68 -89,07
1,22 70 5,570 -0,54 -87,30
1,31 75 4,980 -1,73 -82,67
1,40 80 4,189 -2,84 -75,20
1,48 85 3,219 -3,82 -64,9
1,57 90 2.095 -4,64 -52,03
1,66 95 0,853 -5,26 -36,50
1,75 100 -0,468 -5,65 -18,48
1,83 105 -1,824 -5,77 1,87
1,92 110 -3,165 -5,59 24,41
2,01 115 -4,435 -5,08 48,96
2,09 120 -5,578 -4,21 -75,35
2,18 125 -6,534 -2,96 103,36
2,27 130 -7,240 -1,32 132,79
2,36 135 -7. АВТОРСКОЕ ПРАВО 2017 Одесский национальный политехнический университет Copyright 2017 Gale, Cengage Learning. Все права защищены. Верещагин, Григорий [Идентификация WorldCat]Самые популярные произведения Григорий Верещагин Релятивистская кинетическая теория: с приложениями в астрофизике и космологии Григорий Верещагин( )11 выпуски опубликованы между 2016 и 2017 в английский и проводится 199 член WorldCat библиотеки Мировой "Релятивистская кинетическая теория имеет широкое применение в астрофизике и космологии.  Интерес вырос в последние годы
поскольку теперь экспериментаторы могут проводить надежные измерения физических систем, в которых релятивистские эффекты больше не проявляются.
незначительный. Эта амбициозная монография разделена на три части. В ней представлены основные идеи и концепции этой теории,
уравнения и методы, включая вывод кинетических уравнений из релятивистской иерархии ББГКИ и обсуждение
соотношение между кинетическим и гидродинамическим уровнями описания.Вторая часть знакомит с элементами вычислительной физики
с особым упором на численное интегрирование уравнений Больцмана и родственные подходы, а также на многокомпонентную гидродинамику.
В третьей части представлен обзор приложений, начиная от ковариантной теории отклика плазмы, термализации релятивистских
плазма, комптонизация в статических и движущихся средах к кинетике самогравитирующих систем, космологическое структурообразование
и испускание нейтрино при гравитационном коллапсе" --
Солнце, звезды, Вселенная и общая теория относительности: международная конференция в честь Я. Интерес вырос в последние годы
поскольку теперь экспериментаторы могут проводить надежные измерения физических систем, в которых релятивистские эффекты больше не проявляются.
незначительный. Эта амбициозная монография разделена на три части. В ней представлены основные идеи и концепции этой теории,
уравнения и методы, включая вывод кинетических уравнений из релятивистской иерархии ББГКИ и обсуждение
соотношение между кинетическим и гидродинамическим уровнями описания.Вторая часть знакомит с элементами вычислительной физики
с особым упором на численное интегрирование уравнений Больцмана и родственные подходы, а также на многокомпонентную гидродинамику.
В третьей части представлен обзор приложений, начиная от ковариантной теории отклика плазмы, термализации релятивистских
плазма, комптонизация в статических и движущихся средах к кинетике самогравитирующих систем, космологическое структурообразование
и испускание нейтрино при гравитационном коллапсе" --
Солнце, звезды, Вселенная и общая теория относительности: международная конференция в честь Я. 95-летие Б. Зельдовича,
Минск, Беларусь, 20-23 апреля 2009 г.
Американский институт физики (англ.
) 95-летие Б. Зельдовича,
Минск, Беларусь, 20-23 апреля 2009 г.
Американский институт физики (англ.
) 6 выпуски опубликованы между 2009 г. и 2010 в английский и проводится 95 член WorldCat библиотеки Мировой Электрон-позитронные пары в физике и астрофизике: от тяжелых ядер до черных дыр Ремо Руффини (англ. Книга ) 3 выпуски опубликованы в 2010 в английский и проводится 7 член WorldCat библиотеки Мировой Благодаря взаимодействию физики и астрофизики мы наблюдаем в эти годы великолепный синтез теоретических, экспериментальных и результаты наблюдений, происходящие из трех фундаментальных физических процессов. 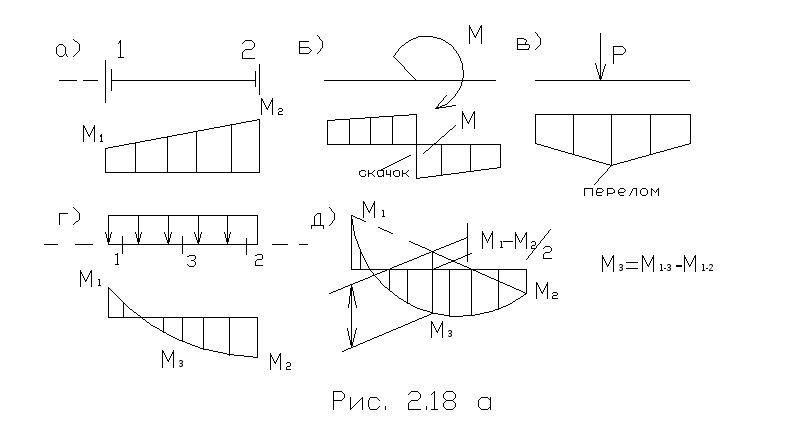 Первоначально они были предложены Дираком,
Брейта и Уилера и Заутера, Гейзенберга, Эйлера и Швингера. В течение почти семидесяти лет за всеми тремя следили
постоянными усилиями по экспериментальной проверке наземных экспериментов. Процесс Дирака, e+e-→2[gamma], был
пока самый успешный. Оно получило чрезвычайно точную экспериментальную проверку и привело также к огромному
количество новой физики в, возможно, одном из самых плодотворных экспериментальных направлений путем введения накопительных колец во Фраскати.
Далее следуют крупнейшие акселераторы мира: DESY, SLAC и др.Процесс Брейта-Уилера, 2[gamma]→e+e-, хотя концептуально
простой процесс, обратный процессу Дирака, был, безусловно, одним из самых трудных для экспериментальной проверки.
Только недавно, благодаря технологии, основанной на рентгеновском лазере на свободных электронах, и его многочисленным применениям в наземных экспериментах,
были достигнуты некоторые первые признаки его возможной проверки. Первоначально они были предложены Дираком,
Брейта и Уилера и Заутера, Гейзенберга, Эйлера и Швингера. В течение почти семидесяти лет за всеми тремя следили
постоянными усилиями по экспериментальной проверке наземных экспериментов. Процесс Дирака, e+e-→2[gamma], был
пока самый успешный. Оно получило чрезвычайно точную экспериментальную проверку и привело также к огромному
количество новой физики в, возможно, одном из самых плодотворных экспериментальных направлений путем введения накопительных колец во Фраскати.
Далее следуют крупнейшие акселераторы мира: DESY, SLAC и др.Процесс Брейта-Уилера, 2[gamma]→e+e-, хотя концептуально
простой процесс, обратный процессу Дирака, был, безусловно, одним из самых трудных для экспериментальной проверки.
Только недавно, благодаря технологии, основанной на рентгеновском лазере на свободных электронах, и его многочисленным применениям в наземных экспериментах,
были достигнуты некоторые первые признаки его возможной проверки. Процесс поляризации вакуума в сильном электромагнитном
поле, введенное Заутером, Гейзенбергом, Эйлером и Швингером, ввело понятие критического электрического поля.Это было
безуспешно искали более сорока лет с помощью столкновений тяжелых ионов во многих ведущих ускорителях частиц по всему миру.
Новая ситуация сегодня состоит в том, что эти же самые процессы могут быть изучены в гораздо более грандиозном масштабе во время гравитационного поля.
коллапс, приводящий к образованию черной дыры, наблюдаемой в гамма-вспышках (GRB). Этот доклад посвящен
научная гонка.Теоретические и экспериментальные работы, разработанные в наземных лабораториях, сталкиваются с теоретическими
интерпретация космических наблюдений за явлениями, происходящими в космологических масштабах. Что стало ясно в последнее
десять лет заключается в том, что все три вышеупомянутых процесса, должным образом расширенные в рамках общей теории относительности, необходимы
для понимания физики гравитационного коллапса в черную дыру. Процесс поляризации вакуума в сильном электромагнитном
поле, введенное Заутером, Гейзенбергом, Эйлером и Швингером, ввело понятие критического электрического поля.Это было
безуспешно искали более сорока лет с помощью столкновений тяжелых ионов во многих ведущих ускорителях частиц по всему миру.
Новая ситуация сегодня состоит в том, что эти же самые процессы могут быть изучены в гораздо более грандиозном масштабе во время гравитационного поля.
коллапс, приводящий к образованию черной дыры, наблюдаемой в гамма-вспышках (GRB). Этот доклад посвящен
научная гонка.Теоретические и экспериментальные работы, разработанные в наземных лабораториях, сталкиваются с теоретическими
интерпретация космических наблюдений за явлениями, происходящими в космологических масштабах. Что стало ясно в последнее
десять лет заключается в том, что все три вышеупомянутых процесса, должным образом расширенные в рамках общей теории относительности, необходимы
для понимания физики гравитационного коллапса в черную дыру. И наоборот, естественная арена, где эти
процессы, которые можно наблюдать во взаимодействии и в беспрецедентных масштабах, действительно является областью релятивистской астрофизики.
Мы систематически анализируем концептуальные разработки, последовавшие за основной работой Дирака и Брейта-Уилера. Мы тоже
вспомните, как основополагающая работа Борна и Инфельда вдохновила Заутера, Гейзенберга и Эйлера на эффективное лагранжево опережение.
к оценке скорости процесса образования электрон-позитронов в постоянном электрическом поле.В дополнение к рассмотрению
интуитивная полуклассическая трактовка квантово-механического туннелирования для описания процесса образования электрон-позитронов,
напомним расчеты в квантовой электродинамике скорости Швингера и эффективного лагранжиана для постоянного электромагнитного
поля. И наоборот, естественная арена, где эти
процессы, которые можно наблюдать во взаимодействии и в беспрецедентных масштабах, действительно является областью релятивистской астрофизики.
Мы систематически анализируем концептуальные разработки, последовавшие за основной работой Дирака и Брейта-Уилера. Мы тоже
вспомните, как основополагающая работа Борна и Инфельда вдохновила Заутера, Гейзенберга и Эйлера на эффективное лагранжево опережение.
к оценке скорости процесса образования электрон-позитронов в постоянном электрическом поле.В дополнение к рассмотрению
интуитивная полуклассическая трактовка квантово-механического туннелирования для описания процесса образования электрон-позитронов,
напомним расчеты в квантовой электродинамике скорости Швингера и эффективного лагранжиана для постоянного электромагнитного
поля.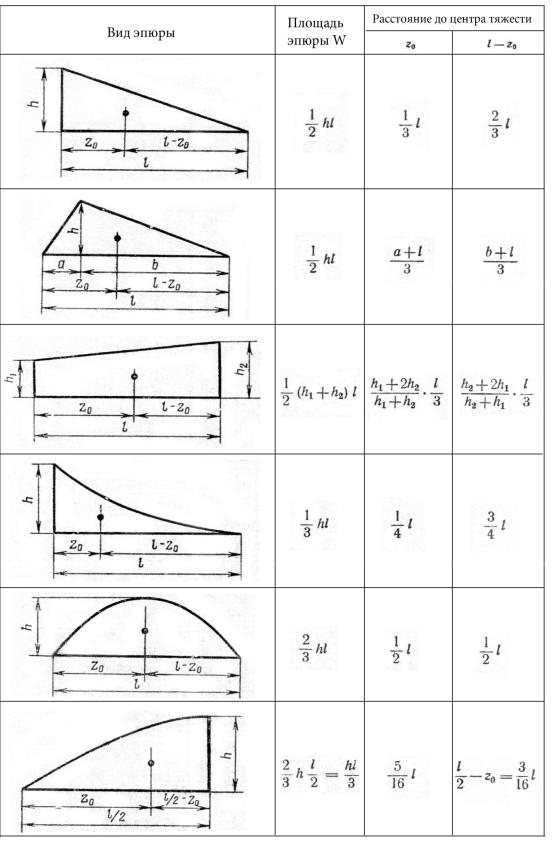 Мы также рассматриваем образование электронов-позитронов в обоих переменных во времени электромагнитных полях, изученное Брезиным,
Ицыксона, Попова, Никишова и Нарожного, а также соответствующие процессы, важные для рождения пар в фокусе когерентного
лазерные лучи, а также столкновение электронного луча и лазера.Наконец, мы сообщаем о некоторых текущих разработках, основанных на общей информации JWKB.
подход, который позволяет вычислить скорость Швингера в изменяющихся в пространстве и во времени электромагнитных полях. Мы тоже
вспомните пионерские работы Ландау и Лифшица и Рака о столкновении заряженных частиц, а также экспериментальные
успех AdA и ADONE в производстве электрон-позитронных пар. Затем мы переходим к возможной экспериментальной проверке
этих явлений.Мы рассматриваем: (A) экспериментальную проверку процесса e+e-→2[gamma], изученного Дираком. Мы также рассматриваем образование электронов-позитронов в обоих переменных во времени электромагнитных полях, изученное Брезиным,
Ицыксона, Попова, Никишова и Нарожного, а также соответствующие процессы, важные для рождения пар в фокусе когерентного
лазерные лучи, а также столкновение электронного луча и лазера.Наконец, мы сообщаем о некоторых текущих разработках, основанных на общей информации JWKB.
подход, который позволяет вычислить скорость Швингера в изменяющихся в пространстве и во времени электромагнитных полях. Мы тоже
вспомните пионерские работы Ландау и Лифшица и Рака о столкновении заряженных частиц, а также экспериментальные
успех AdA и ADONE в производстве электрон-позитронных пар. Затем мы переходим к возможной экспериментальной проверке
этих явлений.Мы рассматриваем: (A) экспериментальную проверку процесса e+e-→2[gamma], изученного Дираком. Мы также кратко
вспомните очень успешные опыты е+е- аннигиляции в адронные каналы, в дополнение к дираковскому электромагнитному
канал; (B) текущие наземные эксперименты по обнаружению образования электрон-позитронов в сильных полях путем фокусировки когерентных
лазерные лучи и столкновения электронного луча с лазером; и (C) многолетние попытки обнаружить электрон-позитронное образование в
Кулоновские поля для большого атомного номера Z>137 в столкновениях тяжелых ионов.Эти попытки следуют классической теоретической работе
Попова и Зельдовича, Грейнера и их школ. Затем обратимся к астрофизике. Сначала мы рассмотрим основную работу по
энергетика и электродинамические свойства электромагнитной черной дыры и применение формулы Швингера вокруг
Черные дыры Керра-Ньюмана, открытые Дамуром и Руффини. Мы также кратко
вспомните очень успешные опыты е+е- аннигиляции в адронные каналы, в дополнение к дираковскому электромагнитному
канал; (B) текущие наземные эксперименты по обнаружению образования электрон-позитронов в сильных полях путем фокусировки когерентных
лазерные лучи и столкновения электронного луча с лазером; и (C) многолетние попытки обнаружить электрон-позитронное образование в
Кулоновские поля для большого атомного номера Z>137 в столкновениях тяжелых ионов.Эти попытки следуют классической теоретической работе
Попова и Зельдовича, Грейнера и их школ. Затем обратимся к астрофизике. Сначала мы рассмотрим основную работу по
энергетика и электродинамические свойства электромагнитной черной дыры и применение формулы Швингера вокруг
Черные дыры Керра-Ньюмана, открытые Дамуром и Руффини. Мы фокусируемся только на массах черных дыр, превышающих критическую массу
нейтронных звезд, для удобства принято, что оно совпадает с верхним пределом Роудса и Руффини, равным 3.2 М. В этом случае
Длина комптоновской волны электрона намного меньше кривизны пространства-времени, и все предыдущие результаты, выраженные инвариантно, могут
применяться в соответствии с хорошо установленными правилами принципа эквивалентности. Выводим соответствующую скорость электрон-позитронного
производство пар и ввести понятие диадосферы. Мы рассмотрим недавний прогресс в описании эволюции оптических
плотной электрон-позитронной плазмы в присутствии сверхкритического электрического поля, что актуально как в астрофизике, так и
а также в текущих экспериментах с лазерным лучом.В частности, мы рассматриваем недавний прогресс, основанный на теории Власова-Больцмана-Максвелла. Мы фокусируемся только на массах черных дыр, превышающих критическую массу
нейтронных звезд, для удобства принято, что оно совпадает с верхним пределом Роудса и Руффини, равным 3.2 М. В этом случае
Длина комптоновской волны электрона намного меньше кривизны пространства-времени, и все предыдущие результаты, выраженные инвариантно, могут
применяться в соответствии с хорошо установленными правилами принципа эквивалентности. Выводим соответствующую скорость электрон-позитронного
производство пар и ввести понятие диадосферы. Мы рассмотрим недавний прогресс в описании эволюции оптических
плотной электрон-позитронной плазмы в присутствии сверхкритического электрического поля, что актуально как в астрофизике, так и
а также в текущих экспериментах с лазерным лучом.В частности, мы рассматриваем недавний прогресс, основанный на теории Власова-Больцмана-Максвелла. уравнения для изучения обратной связи созданных электрон-позитронных пар на исходное постоянное электрическое поле. Мы доказательства
существование колебаний плазмы и ее взаимодействие с фотонами, приводящее к энергетическому и количественному равнораспределению фотонов,
электроны и позитроны. Наконец, мы рассмотрим недавний прогресс, достигнутый при использовании уравнений Больцмана для изучения эволюции
электрон-позитрон-фотонной плазмы к тепловому равновесию и определение ее характерных временных масштабов.То
принципиальное отличие, вносимое правильной оценкой роли двух- и трехчастичных столкновений, прямых и обратных,
особенно свидетельствует. Затем мы приводим некоторые общие выводы. Результаты, рассмотренные в этом отчете, будут представлены
к решающим испытаниям в ближайшие годы как в физике, так и в астрофизике. уравнения для изучения обратной связи созданных электрон-позитронных пар на исходное постоянное электрическое поле. Мы доказательства
существование колебаний плазмы и ее взаимодействие с фотонами, приводящее к энергетическому и количественному равнораспределению фотонов,
электроны и позитроны. Наконец, мы рассмотрим недавний прогресс, достигнутый при использовании уравнений Больцмана для изучения эволюции
электрон-позитрон-фотонной плазмы к тепловому равновесию и определение ее характерных временных масштабов.То
принципиальное отличие, вносимое правильной оценкой роли двух- и трехчастичных столкновений, прямых и обратных,
особенно свидетельствует. Затем мы приводим некоторые общие выводы. Результаты, рассмотренные в этом отчете, будут представлены
к решающим испытаниям в ближайшие годы как в физике, так и в астрофизике. Упомянем лишь несколько основных шагов
при испытаниях по физике мы помним создание экспериментальных установок в Национальном центре зажигания в Университете Лоуренса.
Ливерморская национальная лаборатория, а также соответствующий французский проект Laser Mega Joule.В астрофизике эти результаты
будут проверены в галактических и внегалактических черных дырах, наблюдаемых в двойных рентгеновских источниках, активных ядрах галактик, микроквазарах
и в процессе гравитационного коллапса в нейтронную звезду, а также двух нейтронных звезд в черную дыру, порождающую
гамма-всплески. Астрофизическое описание звездных предшественников и начальных физических условий, приводящих к гравитационному
Процесс коллапса будет предметом следующего доклада.На сегодняшний день не найдено теоретического описания
объяснить либо испускание остатка сверхновой, либо образование заряженной черной дыры для гамма-всплесков. Упомянем лишь несколько основных шагов
при испытаниях по физике мы помним создание экспериментальных установок в Национальном центре зажигания в Университете Лоуренса.
Ливерморская национальная лаборатория, а также соответствующий французский проект Laser Mega Joule.В астрофизике эти результаты
будут проверены в галактических и внегалактических черных дырах, наблюдаемых в двойных рентгеновских источниках, активных ядрах галактик, микроквазарах
и в процессе гравитационного коллапса в нейтронную звезду, а также двух нейтронных звезд в черную дыру, порождающую
гамма-всплески. Астрофизическое описание звездных предшественников и начальных физических условий, приводящих к гравитационному
Процесс коллапса будет предметом следующего доклада.На сегодняшний день не найдено теоретического описания
объяснить либо испускание остатка сверхновой, либо образование заряженной черной дыры для гамма-всплесков. Важный ток
прогресс в понимании таких явлений, а также электродинамической структуры нейтронных звезд, сверхновых
Взрыв и теории гамма-всплесков будут обсуждаться в вышеупомянутом следующем отчете.Что важно помнить
на данном этапе заключается только в том, что как сверхновые, так и процессы гамма-всплесков являются одними из самых энергичных и нестационарных явлений, когда-либо существовавших.
наблюдается во Вселенной: сверхновая может достичь энергии 1054 эрг в течение нескольких месяцев, а гамма-всплески могут испускать
до 1054 эрг за время всего в несколько секунд. Центральная роль нейтронных звезд в описании сверхновых.
а также черных дыр и электрон-позитронной плазмы, в описании гамма-всплесков, начатом одним из нас (Р.Р.) в 1975 г.,
широко признаны.В настоящем отчете обсуждаются только теоретические основы для рассмотрения этих тем. Важный ток
прогресс в понимании таких явлений, а также электродинамической структуры нейтронных звезд, сверхновых
Взрыв и теории гамма-всплесков будут обсуждаться в вышеупомянутом следующем отчете.Что важно помнить
на данном этапе заключается только в том, что как сверхновые, так и процессы гамма-всплесков являются одними из самых энергичных и нестационарных явлений, когда-либо существовавших.
наблюдается во Вселенной: сверхновая может достичь энергии 1054 эрг в течение нескольких месяцев, а гамма-всплески могут испускать
до 1054 эрг за время всего в несколько секунд. Центральная роль нейтронных звезд в описании сверхновых.
а также черных дыр и электрон-позитронной плазмы, в описании гамма-всплесков, начатом одним из нас (Р.Р.) в 1975 г.,
широко признаны.В настоящем отчете обсуждаются только теоретические основы для рассмотрения этих тем. Вторая ICRANet César Lattes Встреча сверхновых, нейтронных звезд и черных дыр: Рио-де-Жанейро - Нитерой - Жуан-Пессоа
- Ресифи - Форталеза, Бразилия, 13-22 апреля 2015 г.
Встреча Сезара Латте (
Книга
) Вторая ICRANet César Lattes Встреча сверхновых, нейтронных звезд и черных дыр: Рио-де-Жанейро - Нитерой - Жуан-Пессоа
- Ресифи - Форталеза, Бразилия, 13-22 апреля 2015 г.
Встреча Сезара Латте (
Книга
) 2 выпуски опубликованы в 2015 в английский и проводится 2 член WorldCat библиотеки Мировой Вторая встреча César Lattes (2CL) проходила с 13 по 18 апреля 2015 года в городах Рио-де-Жанейро и Рио-де-Жанейро. через красивый Байя-да-Гуанабара, в Нитерой.  Результаты этой очень насыщенной программы встречи представлены в
этот объем. Эта встреча является частью дополнительных встреч к 14-й конференции Марселя Гроссмана, организованной ICRANet.
В этой встрече 2CL приняли участие ученые, связанные с тремя крупными физическими институтами в Рио-де-Жанейро,
Centro Brasileiro de Pesquisas Físicas (CBPF), учреждение, в котором находится ICRANet, Федеральный университет Флуминенсе.
в Нитерой и Планетарий Рио.Участники приехали со всей Бразилии, проявив большой интерес к этой стране.
в релятивистской астрофизике, поскольку большая часть присутствующих довольно молода.
Международная конференция в честь столетия со дня рождения Я.Б. Зельдович, "Субатомные частицы, нуклоны, атомы,
Вселенная: процессы и структура».
С. Результаты этой очень насыщенной программы встречи представлены в
этот объем. Эта встреча является частью дополнительных встреч к 14-й конференции Марселя Гроссмана, организованной ICRANet.
В этой встрече 2CL приняли участие ученые, связанные с тремя крупными физическими институтами в Рио-де-Жанейро,
Centro Brasileiro de Pesquisas Físicas (CBPF), учреждение, в котором находится ICRANet, Федеральный университет Флуминенсе.
в Нитерой и Планетарий Рио.Участники приехали со всей Бразилии, проявив большой интерес к этой стране.
в релятивистской астрофизике, поскольку большая часть присутствующих довольно молода.
Международная конференция в честь столетия со дня рождения Я.Б. Зельдович, "Субатомные частицы, нуклоны, атомы,
Вселенная: процессы и структура».
С. Я Килин(
) Я Килин(
) 1 издание опубликовано в 2015 в английский и проводится 2 член WorldCat библиотеки Мировой 12-й итало-корейский симпозиум по релятивистской астрофизике: ICRANet, Пескара, 4–8 июля 2011 г. ( ) 1 издание опубликовано в 2013 в английский и проводится 2 член WorldCat библиотеки Мировой Петлевая квантовая космология и вероятность инфляции Григорий Верещагин( ) 1 издание опубликовано в 2018 в английский и проводится 2 член WorldCat библиотеки Мировой
Уровень аудитории
Связанные личности Крышки Альтернативные имена Григорий Верещагин onderzoeker Верещагин Г. Верещагин Григорий. Верещагин Григорий Васильевич Верещагин Григорий Васильевич 1978- Языки
%PDF-1.5
%
1 0 объект
>
эндообъект
3 0 объект /CreationDate (D:20201217112917+02'00')
/ModDate (D:20201217112917+02'00')
/Режиссер
>>
эндообъект
2 0 объект
>
эндообъект
4 0 объект
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
/XОбъект >
>>
/MediaBox [0 0 595,32 841,92]
/Содержание [33 0 R 34 0 R 35 0 R]
/Группа >
/Вкладки /S
/Анноты [36 0 R]
>>
эндообъект
5 0 объект
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. Исследование содержания режимов газовых возмущений на основе измерений параметров атмосферы на высотах мезосферы и нижней термосферы [v1]Рабочий документ Статья Версия 1 Эта версия не рецензируется Версия 1
: Получено: 23 июля 2021 г. / Утверждено: 26 июля 2021 г. / В сети: 26 июля 2021 г. (18:04:42 CEST) Также существует рецензируемая статья этого препринта. Лебле, С.; Верещагин, С.; Бахметьева, Н.В.; Григорьев, Г.И. Исследование состава мод газовых возмущений на основе измерения параметров атмосферы на высотах мезосферы и нижней термосферы. Атмосфера 2021 , 12 , 1123. Ссылка на журнал: Атмосфера 2021, 12, 1123 Цитировать как:Лебле, С.; Верещагин, С.; Бахметьева, Н.В.; Григорьев, Г.И. Исследование состава мод газовых возмущений на основе измерения параметров атмосферы на высотах мезосферы и нижней термосферы. Атмосфера 2021 , 12 , 1123. Лебле, С.; Верещагин, С.; Бахметьева, Н.В.; Григорьев, Г.I. Исследование состава мод газовых возмущений на основе измерения параметров атмосферы на высотах мезосферы и нижней термосферы. Атмосфера 2021, 12, 1123. Копировать ОТМЕНИТЬ КОПИРОВАТЬ ДЕТАЛИ ЦИТАТА Абстрактный Основным результатом работы является оценка энтропийной моды, сопровождающей волновое возмущение, наблюдаемое в диапазоне высот атмосферы 90-120 км. Ключевые словаэкспоненциальная атмосфера; акустическая волна; диагностика; проекционные операторы; искусственные периодические неровности; нейтральная температура; плотность ПредметФИЗИЧЕСКИЕ НАУКИ, Акустика Это статья с открытым доступом, распространяемая в соответствии с лицензией Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы. Комментарии (0)Мы приветствуем комментарии и отзывы широкого круга читателей. См. критерии для комментариев и наше заявление о разнообразии. что это?Добавьте запись об этом обзоре в Publons, чтобы отслеживать и демонстрировать свой опыт рецензирования в журналах со всего мира. ×Прозрачность мгновенно созданной электрон-позитрон-фотонной плазмы | Ежемесячные уведомления Королевского астрономического обществаАннотацияЗадача о разлете релятивистской плазмы, возникающей при выделении большого количества энергии в малом объеме, рассматривалась многими авторами.Мы используем аналитическое решение Бисноватого-Когана и Мурзиной для сферически-симметричного релятивистского разложения. Получены кривые блеска и спектры прозрачности электрон-позитрон-фотонной плазмы. Сравним наши результаты с работой Гудмана. 1 ВВЕДЕНИЕ Задача о выделении большого количества энергии в малом объеме впервые была рассмотрена Ферми (1950), предложившим статистическую теорию для расчета высокоэнергетических столкновений протонов с множественным рождением частиц. Аналогичная задача рассматривалась применительно к гамма-всплескам (GRB) в сферической геометрии.Гудман (1986) рассмотрел судьбу большого количества энергии в фотонах и электрон-позитронных парах, первоначально ограниченных сферой, находящейся в равновесии при температуре выше МэВ, а затем позволившей ей свободно расширяться. Он численно решал уравнения релятивистской гидродинамики. Он обнаружил, что плазма расширяется и остывает до нерелятивистских температур. Из-за релятивистского сжатия в лабораторной системе отсчета он образует оболочку. Приближенное аналитическое решение задачи о релятивистском сферическом разлете в вакуум мгновенно созданной ультрарелятивистской плазмы было дано Бисноватым-Коганом и Мурзиной (1995). В данной работе мы использовали это решение для нахождения наблюдаемых спектров прозрачности электрон-протон-фотонной плазмы.Проблема по своей природе динамична, поскольку фотосфера быстро меняется со временем. Единственный метод, доступный для расчета эмиссии фотосферы в таком динамическом случае, — это метод Руффини, Сиутсоу и Верещагина (2013). Этот метод решает уравнение переноса излучения, предполагая, что функция источника является изотропной и тепловой. Результаты, представленные в нашей статье, имеют двоякое применение. B и интерпретировали тепловой первый эпизод как почти чистую электрон-позитрон-фотонную плазму, достигающую прозрачности. Следует иметь в виду, что наблюдаемая в некоторых всплесках фотосферная составляющая большой длительности (порядка секунд) не может быть объяснена в рамках этой модели.Обычно это интерпретируется в рамках релятивистской модели ветра Пачинского (1990). В разделе 2 мы вводим решение Бисноватого-Когана и Мурзиной (1995), в разделе 3 дается метод расчета кривых блеска и спектров. В разделе 4 представлены численные результаты. Обсуждение и заключение следуют. 2 ПРИБЛИЖЕННОЕ РЕШЕНИЕ РЕЛЯТИВИСТСКИХ ГИДРОДИНАМИЧЕСКИХ УРАВНЕНИЙ Для получения реалистичного профиля оболочки мы использовали решение Бисноватого-Когана и Мурзиной (1995), подробнее см. Рис. 1. Уравнение состояния оптически толстой электрон-позитрон-фотонной плазмы в зависимости от сопутствующей температуры T . Рис. 1. Уравнение состояния оптически толстой электрон-позитрон-фотонной плазмы в зависимости от сопутствующей температуры T . при высоких температурах K B T » M M E C 2 , где K B - это постоянная Больцмана, м E c скорость света, уравнение состояния ультрарелятивистское. \begin{ уравнение} \ epsilon (t, r) = \ frac {2 \ epsilon _ {10} g_0 f (t, r) \ tilde {f} (t, r)} {\ xi r ^ 3} {\ rm ,} \end{eqnarray} (1)\begin{eqnarray} \ Gamma (t, r) = \ sqrt {\ frac {rf (t, r)} {2 \ xi \ tilde {f} (t, r)}} {\ rm ,} \end{eqnarray} (2)где f и |$\tilde{f}$| приведены в Приложении А, ξ = ct − r измеряет глубину внутри оболочки, где г 0 и ϵ 10 являются параметрами раствора. 1 Для больших t решение описывает тонкую оболочку с постоянной лабораторной шириной (см. Пиран, Шеми и Нараян, 1993; Руффини и др., 1999, 2000), распространяющуюся радиально с Γ ≫ 1, см. рис. 2. 1 Для больших t решение описывает тонкую оболочку с постоянной лабораторной шириной (см. Пиран, Шеми и Нараян, 1993; Руффини и др., 1999, 2000), распространяющуюся радиально с Γ ≫ 1, см. рис. 2.Рисунок 2. Лабораторные радиальные профили плотности энергии (вверху), фактора Лоренца (в центре) и оптической толщины (внизу) при t = 250 R 0 / c . Две вертикальные линии представляют собой радиусы, на которых τ( t , r , ϕ = 0) = 1.Основная часть энергии уже излучалась, что видно на верхней панели. Рис. 2. Лабораторные радиальные профили плотности энергии (вверху), фактора Лоренца (в центре) и оптической толщины (внизу) при t = 250 R 0 / c . Две вертикальные линии представляют собой радиусы, на которых τ( t , r , ϕ = 0) = 1. Основная часть энергии уже излучена, как видно из верхней панели. Из плотности сопутствующей энергии сопутствующая температура может быть найдена как 1/4 , где σ SB — постоянная Стефана–Больцмана. {\pm} \Gamma (1-\beta\cos\phi) \frac{{\rm d}R}{\cos (\phi)} {\rm,}
\end{eqnarray} (4)где ϕ - лабораторный угол между радиальным направлением и четырехимпульсом фотона, ϕ 0 - тот угол на начальном радиусе, от которого производится интегрирование, β - скорость в единиц скорости света, r — радиус испускания фотона, а R out — радиус, на котором фотон покидает оболочку. Интегрирование должно производиться по мировой линии фотона.Руффини и соавт. (2013) предложили два разных приближения для расчета кривых блеска и спектров: нечеткое и четкое фотосферное. В приближении острой фотосферы предполагается, что энергия, содержащаяся в малом объеме, высвобождается мгновенно во время, радиус и угол, определяемые условием τ( t , r , ϕ) = 1. E , испускаемое в лабораторном телесном угле dΩ, равно d E = 3ϵd В dΩ/(8Λ 4 ), где Λ = Γ(1 − β cos ϕ) — доплеровский фактор, d В — лабораторный объем, связанный с выбросом. {\pm} \Gamma (1-\beta\cos\phi) \frac{{\rm d}R}{\cos (\phi)} {\rm,}
\end{eqnarray} (4)где ϕ - лабораторный угол между радиальным направлением и четырехимпульсом фотона, ϕ 0 - тот угол на начальном радиусе, от которого производится интегрирование, β - скорость в единиц скорости света, r — радиус испускания фотона, а R out — радиус, на котором фотон покидает оболочку. Интегрирование должно производиться по мировой линии фотона.Руффини и соавт. (2013) предложили два разных приближения для расчета кривых блеска и спектров: нечеткое и четкое фотосферное. В приближении острой фотосферы предполагается, что энергия, содержащаяся в малом объеме, высвобождается мгновенно во время, радиус и угол, определяемые условием τ( t , r , ϕ) = 1. E , испускаемое в лабораторном телесном угле dΩ, равно d E = 3ϵd В dΩ/(8Λ 4 ), где Λ = Γ(1 − β cos ϕ) — доплеровский фактор, d В — лабораторный объем, связанный с выбросом. Чтобы вычислить светлые кривые, D E интегрирован на фотосферу для данного времени прибытия T A = T E - COS (φ) ( R E / C 9067/ C ), где R E 9067 и T и T E - это радиальное положение и лабораторное время излучения, T A = 0 для фотона, испущенного в начале координат.3 \mathrm{d}\nu _l \mathrm{d}\Omega _l \mathrm{d}A}{\exp \left(\frac{h\nu _l}{k T_l}\right)-1}{\ м,}
\end{eqnarray} (5)где величины с индексом l измерены в лабораторной системе отсчета, dΩ l измеряет угловой размер детектора. Интегрирование по поверхности d A выполнено для учета излучающей площади на фотосфере. Из-за экспоненциальной зависимости оптической толщины от радиальной координаты (см. уравнения 3 и 4) переход от оптически толстого к оптически тонкому состоянию действительно резкий. Чтобы вычислить светлые кривые, D E интегрирован на фотосферу для данного времени прибытия T A = T E - COS (φ) ( R E / C 9067/ C ), где R E 9067 и T и T E - это радиальное положение и лабораторное время излучения, T A = 0 для фотона, испущенного в начале координат.3 \mathrm{d}\nu _l \mathrm{d}\Omega _l \mathrm{d}A}{\exp \left(\frac{h\nu _l}{k T_l}\right)-1}{\ м,}
\end{eqnarray} (5)где величины с индексом l измерены в лабораторной системе отсчета, dΩ l измеряет угловой размер детектора. Интегрирование по поверхности d A выполнено для учета излучающей площади на фотосфере. Из-за экспоненциальной зависимости оптической толщины от радиальной координаты (см. уравнения 3 и 4) переход от оптически толстого к оптически тонкому состоянию действительно резкий.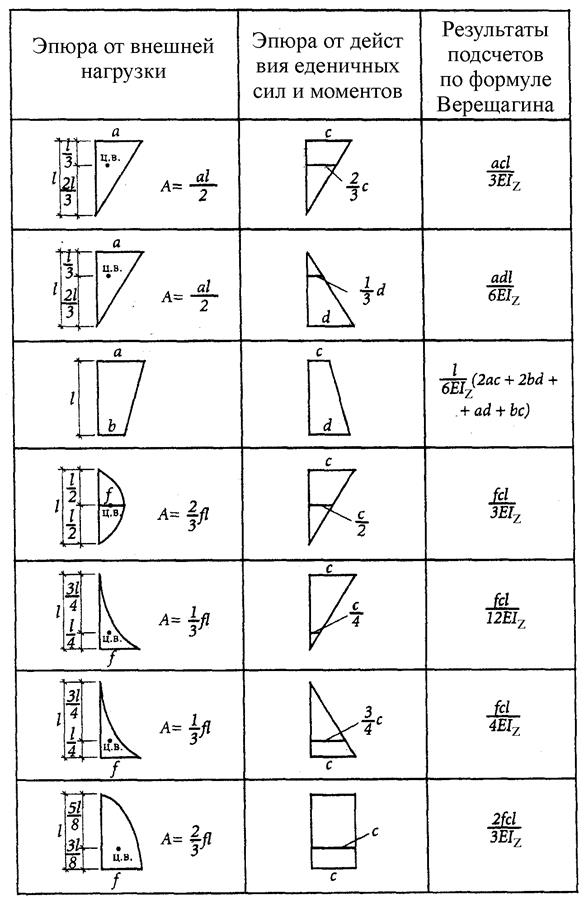 {\основной },
\end{equation} (6)где S ν - функция источника. Хорошо известно, что при большой оптической глубине функция источника для рассеяния соответствует тепловому изотропному распределению фотона с температурой T ( r , t ). Кроме того, для энергопреобладающих потоков Белобородов (2010) показал, что когерентное рассеяние сохраняет изотропию поля излучения вместе с чернотельной формой спектра, как если бы излучение распространялось в вакууме.В самом деле, свободно распространяющийся фотон в ускоряющейся оболочке с Γ ∝ r не меняет своего угла в сопутствующей системе отсчета. Последнее условие фактически используется Бисноватым-Коганом и Мурзиной (1995) для получения приближенного аналитического решения. Поскольку для ускоряющихся оболочек диффузией излучения можно пренебречь (Руффини и др., 2013), мы можем использовать функцию источника как тепловую планковскую функцию r )) и уравнение (6) можно проинтегрировать численно. {\основной },
\end{equation} (6)где S ν - функция источника. Хорошо известно, что при большой оптической глубине функция источника для рассеяния соответствует тепловому изотропному распределению фотона с температурой T ( r , t ). Кроме того, для энергопреобладающих потоков Белобородов (2010) показал, что когерентное рассеяние сохраняет изотропию поля излучения вместе с чернотельной формой спектра, как если бы излучение распространялось в вакууме.В самом деле, свободно распространяющийся фотон в ускоряющейся оболочке с Γ ∝ r не меняет своего угла в сопутствующей системе отсчета. Последнее условие фактически используется Бисноватым-Коганом и Мурзиной (1995) для получения приближенного аналитического решения. Поскольку для ускоряющихся оболочек диффузией излучения можно пренебречь (Руффини и др., 2013), мы можем использовать функцию источника как тепловую планковскую функцию r )) и уравнение (6) можно проинтегрировать численно. Тогда поток в заданное время прихода получается интегрированием по частотам, взвешенным по поверхности излучения, а полный поток получается дополнительным интегрированием по времени прихода. Тогда поток в заданное время прихода получается интегрированием по частотам, взвешенным по поверхности излучения, а полный поток получается дополнительным интегрированием по времени прихода.4 ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫПрименим теперь приближенное аналитическое решение уравнений релятивистской гидродинамики, полученное Бисноватым-Коганом и Мурзиной (1995), к оптически толстой электрон-позитронной плазме. Параметры, входящие в уравнения (1) и (2), могут быть связаны с полной энергией E 0 , ограниченной сферой радиусом R 0 следующим образом:\begin{eqnarray} R_0 = h _ {\ rm shell} = 3 \ sqrt {\ frac {\ delta _ {\ rm fit}} {g_0}} {\ rm ,} \end{eqnarray} (7)\begin{eqnarray} E_0 = 4 \pi g_0 \epsilon _{10} \times 1.{-2} {\гм .} \ end {eqnarray} (9) Мы выполняем вычисление для E 0 = 10 54 ERG и R 0 = 10 8 см, соответствующие начальной температуре K B T 0 = 6,5 МэВ. Радиальные профили лабораторной плотности энергии ϵ l , фактора Лоренца и оптической толщины показаны на рис. Поскольку решение Бисноватого-Когана и Мурзиной (1995) не воспроизводит разделение передней части оболочки и световой поверхности, относительное положение фотона внутри оболочки не меняется со временем существенно, если он распространяется радиально. Оболочка имеет фотонную толщину (Руффини и др.2013): фотоны разделяются, потому что локально плотность пар уменьшается слишком быстро, чтобы поддерживать столкновения. Зависимость оптической толщи от ξ в заданное лабораторное время t точно повторяет изменение плотности сопутствующей энергии: от внешней границы к центру она сначала увеличивается, а затем уменьшается. На рис. 3 показаны интегрированные по времени спектры из точных и нечетких приближений, а также спектр, полученный Гудманом (1986), который был сдвинут в область более низких энергий в 2,3 раза. Рисунок 3. Интегрированные по времени спектры: аппроксимация сплошной линией-нечеткостью, аппроксимация пунктирной линией-четкой линией, спектр штрихпунктирной линией из Гудмана (1986) и спектр планковской линией с двумя пунктирными линиями. Рис. 3. Интегрированные по времени спектры: аппроксимация сплошной линией-нечеткостью, аппроксимация пунктирной линией-резкой линией, спектр штрихпунктирной линией из Гудмана (1986) и планковский спектр с двумя пунктирными линиями. Для сравнения эти два последних были сдвинуты в сторону меньшей энергии в 2,3 раза. Рис. 4. Иллюстрация различия в методах расчета Гудмана и нашего.Серая область соответствует оболочке в лабораторное время, для которого оптическая толщина фотона, распространяющегося радиально, равна единице. Это область, в которой спектр вычисляется Гудманом (1986). Оболочка также представлена в более крупное лабораторное время с кривой, соединяющей d V с d V 1 , которая представляет собой схематическое изображение поверхности τ = 1 на заданной глубине ξ. Рис. 4. Иллюстрация различия методов расчета Гудмана и нашего. Это объясняет два отличия нашего результата от результата Гудмана.Во-первых, интегральный по времени спектр шире при низкой энергии, потому что наблюдаемая температура жидкого элемента за пределами прямой видимости в наших расчетах уменьшается. Во-вторых, пиковая энергия смещается в сторону более низкой энергии из-за совместного эффекта увеличения объема излучения и снижения наблюдаемой температуры за пределами прямой видимости. Наклоны низких энергий близки во всех случаях, и в них преобладает излучение высоких широт. Напротив, в высокоэнергетической части спектра преобладают фотоны, излучаемые вдоль луча зрения, для которых важную роль играет профиль температур. Кривые блеска для резкого и нечеткого приближений представлены на рис. 5. Оба приближения дают близкие результаты, даже если восходящая часть не разрешена для приближения резкой фотосферы. Из-за узкого профиля лабораторной плотности энергии излучение достигает своего максимума и вскоре уменьшается: нет плато излучения, продолжающегося в течение времени прохождения света, как сообщает Ruffini et al. (2013) для конечного ветра. Это потому, что они рассматривали другой радиальный профиль для оболочки.Тем не менее время, необходимое для излучения 90% энергии, составляет порядка R 0 / c . Рис. 5. Кривые блеска для нечеткой (сплошная кривая) и резкой (штриховая кривая) фотосферы. Они почти неразличимы. Для сравнения штрихпунктирной линией показана кривая блеска, которая была бы получена от оптически тонкого шара радиусом R 0 , равномерно заполненного изотропным излучением. Рис. 5. Кривые блеска для нечеткой (сплошная кривая) и резкой (штриховая кривая) фотосферы. 5 ОБСУЖДЕНИЕВ наших расчетах мы использовали упрощающее предположение, что пары эффективно рекомбинируют, поэтому их числовая плотность везде определяется уравнением (3).Тем не менее Гримсруд и Вассерман (1999) изучали их рекомбинацию, рассматривая уравнение Больцмана в случае статического и бесконечного ветра. Они показали, что процесс рекомбинации пар замирает на радиусе R ± , меньшем, чем R ph . Выше R ± плотность сопутствующих пар уменьшается пропорционально r −3 . Тот же эффект учитывается в модели пожарной оболочки, см. Ruffini et al.(1999, 2000). Соотношение между оптической толщиной для комптоновского рассеяния и процесса рекомбинации пар составляет:\begin{eqnarray} \ frac {\ tau _ {\ pm}} {\ tau} = \ frac {\ sigma _ \ pm } {\ sigma _T} \ приблизительно 0,8 {\ rm ,} \end{eqnarray} (10)где σ ± — сечение процесса рекомбинации пар.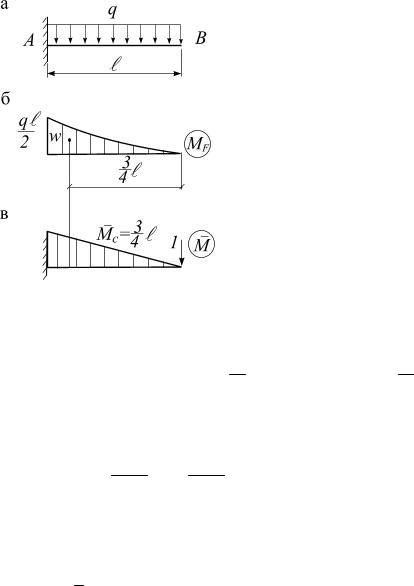 Сопутствующая температура R ± может быть найдена путем решения уравнения (54) Гримсруд и Вассерман (1999). Мы нашли k B T ± ∼ 0.042 M M E C C 2 , быть рядом с фотосрелкой, где температура K B T ~ 0.040 M E C 2 (см. Например, Ruffini и др. 2013). Это означает, что оптическая толщина увеличивается при рассмотрении процесса рекомбинации замораживания пар, что приводит к небольшому увеличению значения R ph . Во-вторых, оптическая толщина для пар R ph определяется как Сопутствующая температура R ± может быть найдена путем решения уравнения (54) Гримсруд и Вассерман (1999). Мы нашли k B T ± ∼ 0.042 M M E C C 2 , быть рядом с фотосрелкой, где температура K B T ~ 0.040 M E C 2 (см. Например, Ruffini и др. 2013). Это означает, что оптическая толщина увеличивается при рассмотрении процесса рекомбинации замораживания пар, что приводит к небольшому увеличению значения R ph . Во-вторых, оптическая толщина для пар R ph определяется как\begin{eqnarray} \tau _{\pm \gamma} (R_{{\rm ph}}) = \tau (R_{{\rm ph}}) \times \frac{n_\gamma}{n_{\pm}} \gg 1 {\ гм,} \end{eqnarray} (11)где неравенство верно, поскольку τ( R ph ) = 1 по определению и n γ ≫ n ± . Отсюда следует, что даже при свободном течении излучения пары все еще сильно связаны с ним и продолжают ускоряться радиационным давлением: их лоренц-фактор Г - возрастает пропорционально r . Для такого истечения Белобородов (2011) показал, что изотропия поля излучения сохраняется в ускоряющей сопутствующей системе пар и ее температура падает как r −1 . Это означает, что наблюдаемая температура постоянна и никакого влияния на спектр не ожидается. Отсюда следует, что даже при свободном течении излучения пары все еще сильно связаны с ним и продолжают ускоряться радиационным давлением: их лоренц-фактор Г - возрастает пропорционально r . Для такого истечения Белобородов (2011) показал, что изотропия поля излучения сохраняется в ускоряющей сопутствующей системе пар и ее температура падает как r −1 . Это означает, что наблюдаемая температура постоянна и никакого влияния на спектр не ожидается. Последний вопрос, который необходимо обсудить, — это влияние профиля температур внутри оболочки. Аксенов, Руффини и Верещагин (2013) рассмотрели отделение фотонов от ультрарелятивистских каботажных ветров с различными профилями температуры электронов. Они показали, что спектральный индекс при низкой энергии сильно зависит от выбранного профиля. Такая температурная зависимость естественно возникает при рассмотрении реалистичного профиля расширяющейся плазмы. Тем не менее положение фотона в оболочке существенно не меняется при расширении ниже R ph для ускоренных истечений, поэтому влияния температурного профиля на комптонизацию фотона вблизи фотосферы в спектре не ожидается. 6 ЗАКЛЮЧЕНИЕМы рассмотрели аналитическое решение Bisnovatyi-Kogan & Murzina (1995) для сферического расширения большого количества энергии в малом объеме и применили его к электронно-позитронной плазме, первоначально ограниченной макроскопическим объемом.Учитывая динамическую эволюцию оболочки, мы рассчитали поток и энергетическое распределение фотосферного излучения так, как его видит удаленный покоящийся наблюдатель в лабораторной системе отсчета. Мы обнаружили, что спектр шире, чем у Планка и у Гудмана (1986), и смещен в сторону более низких энергий из-за интегрирования по прицельным параметрам (или углам между лучом зрения и радиальным направлением) в динамическая фотосфера. Численные результаты, полученные в приближении резкой и нечеткой фотосферы, совпадают. Мы дополнительно представили кривую блеска от такого события, показывающую, что максимум излучения достигается за короткий промежуток времени по сравнению со временем прохождения светом оболочки R 0 / c . Затем поток резко падает. Благодарим Бисноватого-Когана Г.С., а также Сивцова И.А. за полезные обсуждения и комментарии. DB поддерживается совместной докторской программой Erasmus Mundus грантом № 2011-1640 от EACEA Европейской комиссии. ССЫЛКИ, , . ,МНИРАН ,2013 , том.436 стр.L54 . ,МНИРАН ,2010 , том.407 стр.1033 . ,ApJ ,2011 , vol.737 стр.68 , . ,Физ. Ред. D ,1995 , том.52 стр.4380 . ,Прог. Теор. физ. ,1950 , том.5 стр.570 . ,ApJ ,1986 , vol.308 стр. L47 , . ,МНРАН ,1999 , том.300 стр.1158 . ,Сов. физ. JETP ,1954 , том.27 стр.29 . , Анн. сов. акад. науч. физ. ,1953 , том.17 стр.51 , , , , . , ApJ ,2013 , vol.763 стр.125 . ,ApJ ,1990 , vol.363 стр.218 , , . ,МНИРАН ,1993 , том.263 стр.861 , , , . ,A&A ,1999 , том.350 стр.334 , , , . , A&A ,2000 , том.359 стр.855 , , . , ApJ ,2013 , vol.772 стр.11 , и др. , . ,AIP Conf. сер. Том. 910, Космология и гравитация: XII Бразильская школа космологии и гравитации ,2007 Нью-Йорк Am. Инст. физ. стр.55 , . ,Радиационные процессы в астрофизике ,1979 Нью-Йорк Уайли . 2 \ epsilon} {r} = 0 {\ rm ,}
\end{eqnarray} (A2), где v таково, что Γ = (1 − v 2 ) 1/2 .Bisnovatyi-Kogan & Murzina (1995) делает следующие изменения переменных ξ = R - R , г = γ 2 / R 2 , ε 1 = ε R 4 , ε 1 = ε 10 exp (-4τ), г = г = г 0 exp (2φ), y 1 = y / (2 г ) = r /(2Γ 2 ), |$x_1=\tau -(\phi /\sqrt{3})$| и |$x_2=\tau +(\phi /\sqrt{3})$|.{-x_1}{\гм,}
\ end {eqnarray} (A10) Где ξ A , ξ , ξ , ξ , ξ B и ξ B 1 - 2 \ epsilon} {r} = 0 {\ rm ,}
\end{eqnarray} (A2), где v таково, что Γ = (1 − v 2 ) 1/2 .Bisnovatyi-Kogan & Murzina (1995) делает следующие изменения переменных ξ = R - R , г = γ 2 / R 2 , ε 1 = ε R 4 , ε 1 = ε 10 exp (-4τ), г = г = г 0 exp (2φ), y 1 = y / (2 г ) = r /(2Γ 2 ), |$x_1=\tau -(\phi /\sqrt{3})$| и |$x_2=\tau +(\phi /\sqrt{3})$|.{-x_1}{\гм,}
\ end {eqnarray} (A10) Где ξ A , ξ , ξ , ξ , ξ B и ξ B 1 -\ Начало {eqnarray} \xi _a = (2-\sqrt{3}) \frac{\xi _b}{\xi _a} {\rm,} \end{eqnarray} (A11)\begin{eqnarray} \xi _{a1}-\xi _b =\xi _b-\xi _a = \xi _0 \end{eqnarray} (A12)\begin{eqnarray} \ hphantom {\ xi _ {a1} - \ xi _b} = \ sqrt {\ frac {\ delta _ {\ rm fit}} {2g_0}} \ sqrt {\ frac {1} {2- \ sqrt {3} }} \left(1+\frac{2-\sqrt{3}}{2+\sqrt{3}}\frac{k-\sqrt{3}}{k} \right) {\rm ,} \end{eqnarray} (A13), где, наконец, мы наложили ξ a 1 = 0 и ξ 0 = |ξ b 1 |.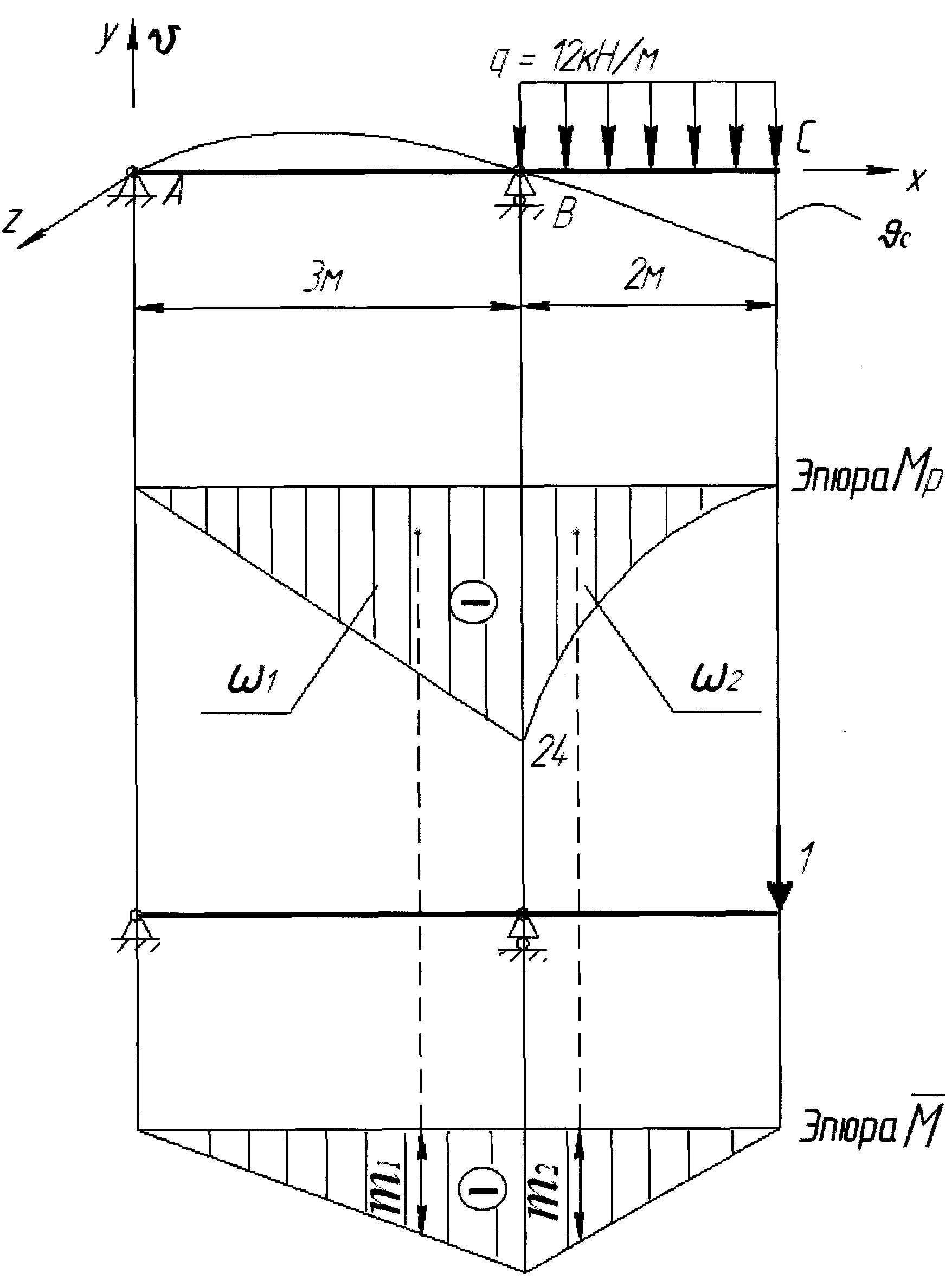 | |||||||||||
 научн. Сем. ПОМИ, 2002, том 291, страницы 78–108 (Ми знсл1623)
научн. Сем. ПОМИ, 2002, том 291, страницы 78–108 (Ми знсл1623)
 ~В.~Верещагин, В.~В.~Верещагин, К.~М.~Семенов-Тян-Шанский
~В.~Верещагин, В.~В.~Верещагин, К.~М.~Семенов-Тян-Шанский  , Верещагин А., Верещагин В., “Локализуемые эффективные теории, бутстрап и параметры адронных резонансов”, Спектроскопия адронов, Материалы конференции AIP, 717, 2004, 260–264
, Верещагин А., Верещагин В., “Локализуемые эффективные теории, бутстрап и параметры адронных резонансов”, Спектроскопия адронов, Материалы конференции AIP, 717, 2004, 260–264  2];
R-радиус оси арки, м; [альфа]-Угловая координата, рад.;
[q.sub.y] ([alpha])-Радиальная нагрузка арки (по нормали к
ось), кН/м; [q.sub.x] ([альфа])-Касательная нагрузка арки, кН/м.
2];
R-радиус оси арки, м; [альфа]-Угловая координата, рад.;
[q.sub.y] ([alpha])-Радиальная нагрузка арки (по нормали к
ось), кН/м; [q.sub.x] ([альфа])-Касательная нагрузка арки, кН/м. sub.41]
EAu([альфа]) 5 EAu(0) -[B.sub.51]
N ([альфа]) 6 N (0) - [B.sub.61] (2)
sub.41]
EAu([альфа]) 5 EAu(0) -[B.sub.51]
N ([альфа]) 6 N (0) - [B.sub.61] (2)

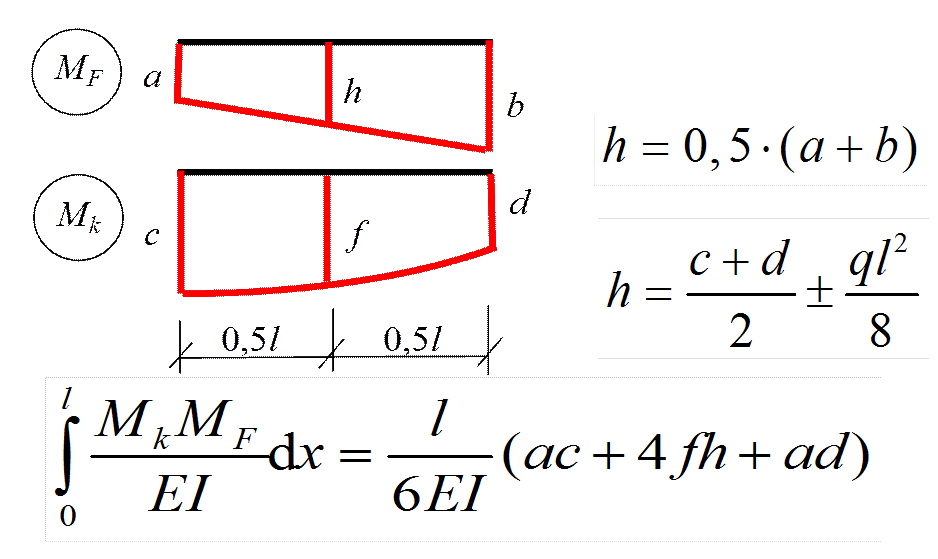 sub.61] ([пи]) (6)
sub.61] ([пи]) (6)
 K] =
[Q.sub.([pi])]; [R.sub.K] = [N.sub.([pi])]; [M.sub.0] = [M.sub.(0)].
K] =
[Q.sub.([pi])]; [R.sub.K] = [N.sub.([pi])]; [M.sub.0] = [M.sub.(0)].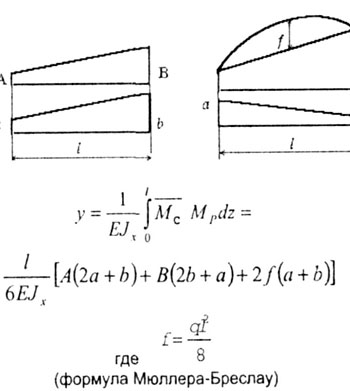


 ] Баженов В.А., Дащенко А.Ф., Коломиец Л.В.,
Оробей, В.Ф. (2001). Строительная механика. Специальный
курс Применение мне тода граничнвх элементов [Структурная механика.
Специальный курс. Применение метода граничных элементов. Одесса:
Астропринт.
] Баженов В.А., Дащенко А.Ф., Коломиец Л.В.,
Оробей, В.Ф. (2001). Строительная механика. Специальный
курс Применение мне тода граничнвх элементов [Структурная механика.
Специальный курс. Применение метода граничных элементов. Одесса:
Астропринт.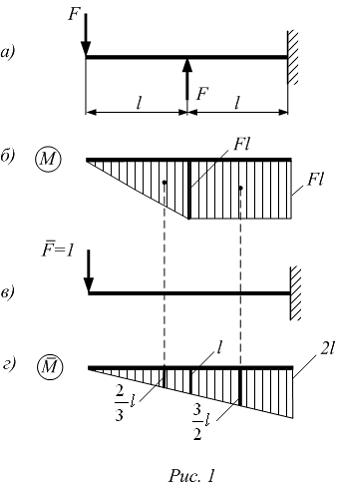 3, 59-65.
3, 59-65. 11. Схема нормальных сил N, кН
11. Схема нормальных сил N, кН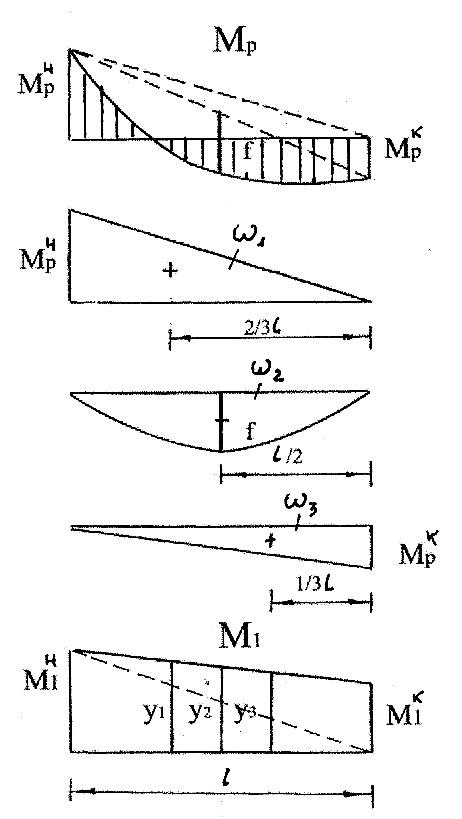 635 0,74 163,40
2,44 140 -7,673 2,85 139,20
2,53 145 -7,383 4,63 116,14
2,62 150 -6,813 6,10 94,39
2,71 155 -6,008 7,28 74,13
2,79 160 -2,016 8,18 55,50
2,88 165 -3,879 8,83 38,66
2,97 170 -2,638 9,27 23,72
3,05 175 -1,334 9,51 10,80
3,14 180 0,0 9.58 0,0
Угловые параметры напряженно-деформированного состояния
координатное состояние
рад град Q, кН Eau. Н, кН
[10-4],
кНм
0,0 0,0 -20,0 0,0 -200,88
0,09 5 -19,15 -0,033 -202,59
0,17 10 -18,16 -0,092 -204,22
0,26 15 -17,02 -0,200 -205,76
0,35 20 -15,76 -0,371 -207,19
0.44 25 -14,38 -0,617 -208,50
0,52 30 -12,88 -0,943 -209,69
0,61 35 -11,29 -1,348 -210,75
0,70 40 -9,61 -1,831 -211,66
0,79 45 -7,86 -2,383 -214,30
0,87 50 -5,89 -2,993 -214,90
0,96 55 -3,87 -3,643 -215,33
1,05 60 -1,83 -4,310 -215,57
1,13 65 0,24 -4,973 -215,64
1,22 70 2,30 -5,608 -215,53
1.31 75 04,34 -6,192 -214,24
1,40 80 6,35 -6,704 -214,78
1,48 85 8,31 -7,124 -214,14
1,57 90 10,21 -7,433 -213,33
1,66 95 12,03 -7,618 -212,36
1,75 100 13,76 -7,668 -211,23
1,83 105 15,38 -7,578 -209,96
1,92 110 16,89 -7,345 -208,55
2,01 115 18,26 -6,975 -207,02
2,09 120 19,50 -6,478 -205,37
2.
635 0,74 163,40
2,44 140 -7,673 2,85 139,20
2,53 145 -7,383 4,63 116,14
2,62 150 -6,813 6,10 94,39
2,71 155 -6,008 7,28 74,13
2,79 160 -2,016 8,18 55,50
2,88 165 -3,879 8,83 38,66
2,97 170 -2,638 9,27 23,72
3,05 175 -1,334 9,51 10,80
3,14 180 0,0 9.58 0,0
Угловые параметры напряженно-деформированного состояния
координатное состояние
рад град Q, кН Eau. Н, кН
[10-4],
кНм
0,0 0,0 -20,0 0,0 -200,88
0,09 5 -19,15 -0,033 -202,59
0,17 10 -18,16 -0,092 -204,22
0,26 15 -17,02 -0,200 -205,76
0,35 20 -15,76 -0,371 -207,19
0.44 25 -14,38 -0,617 -208,50
0,52 30 -12,88 -0,943 -209,69
0,61 35 -11,29 -1,348 -210,75
0,70 40 -9,61 -1,831 -211,66
0,79 45 -7,86 -2,383 -214,30
0,87 50 -5,89 -2,993 -214,90
0,96 55 -3,87 -3,643 -215,33
1,05 60 -1,83 -4,310 -215,57
1,13 65 0,24 -4,973 -215,64
1,22 70 2,30 -5,608 -215,53
1.31 75 04,34 -6,192 -214,24
1,40 80 6,35 -6,704 -214,78
1,48 85 8,31 -7,124 -214,14
1,57 90 10,21 -7,433 -213,33
1,66 95 12,03 -7,618 -212,36
1,75 100 13,76 -7,668 -211,23
1,83 105 15,38 -7,578 -209,96
1,92 110 16,89 -7,345 -208,55
2,01 115 18,26 -6,975 -207,02
2,09 120 19,50 -6,478 -205,37
2.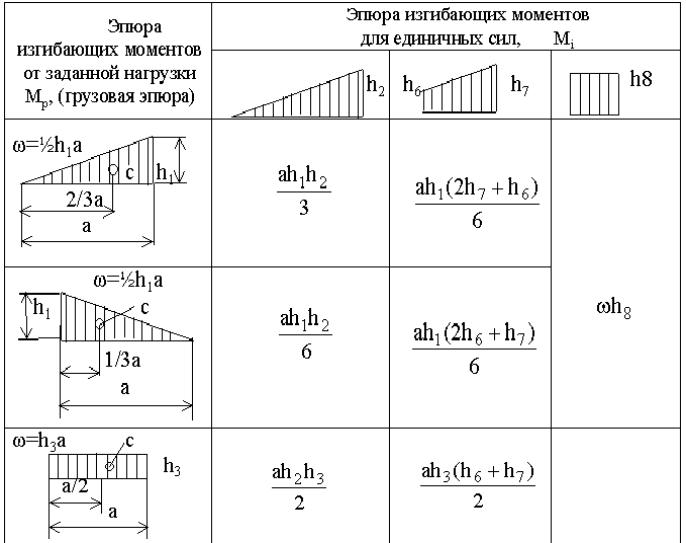 18 125 20,59 -5,871 -203,62
2,27 130 21,53 -5,175 -201,78
2,36 135 22,30 -4,421 -199,86
2,44 140 -16,95 -3,645 -201,38
2,53 145 -16,07 -2,882 -202,82
2,62 150 -15,06 -2,165 -204,18
2,71 155 -1394 -1,520 -205,44
2,79 160 -12,72 -0,970 -206,61
2,88 165 -11,40 -0,532 -207,66
2,97 170 -9,99 -0,219 -208,59
3.05 175 -8,50 -0,040 -209,40
3,14 180 -6,96 0,0 -210,08
18 125 20,59 -5,871 -203,62
2,27 130 21,53 -5,175 -201,78
2,36 135 22,30 -4,421 -199,86
2,44 140 -16,95 -3,645 -201,38
2,53 145 -16,07 -2,882 -202,82
2,62 150 -15,06 -2,165 -204,18
2,71 155 -1394 -1,520 -205,44
2,79 160 -12,72 -0,970 -206,61
2,88 165 -11,40 -0,532 -207,66
2,97 170 -9,99 -0,219 -208,59
3.05 175 -8,50 -0,040 -209,40
3,14 180 -6,96 0,0 -210,08

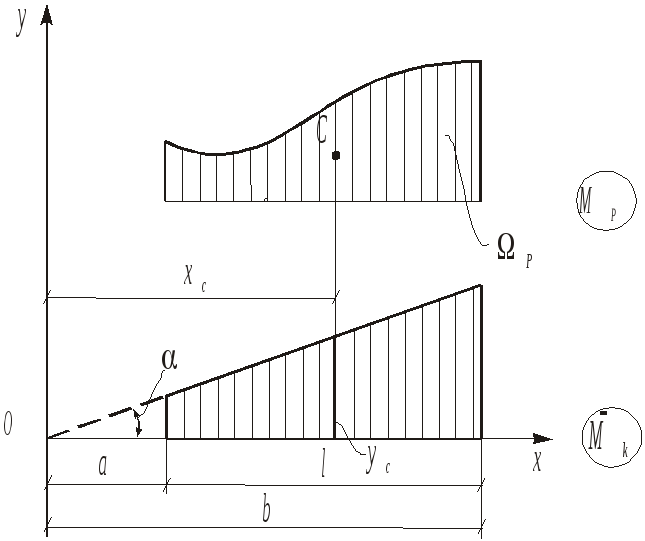

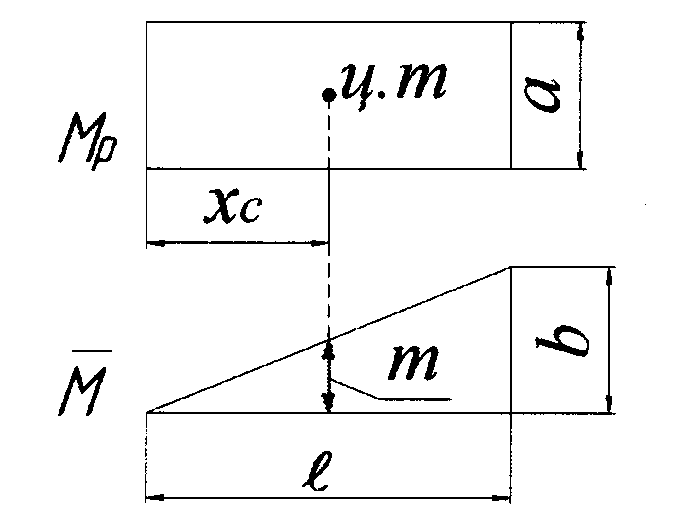
 -
Минеральная галерея
-
Минеральная галерея 32 841,92]
/Содержание 37 0 Р
/Группа >
/Вкладки /S
>>
эндообъект
6 0 объект
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595,32 841,92]
/Содержание 39 0 Р
/Группа >
/Вкладки /S
>>
эндообъект
7 0 объект
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595,32 841,92]
/Содержание 40 0 Р
/Группа >
/Вкладки /S
>>
эндообъект
8 0 объект
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841,92]
/Содержание 43 0 Р
/Группа >
/Вкладки /S
>>
эндообъект
9 0 объект
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595,32 841,92]
/Содержание 45 0 Р
/Группа >
/Вкладки /S
>>
эндообъект
10 0 объект
>
/ExtGState >
/XОбъект >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595,32 841,92]
/Содержание 58 0 Р
/Группа >
/Вкладки /S
>>
эндообъект
11 0 объект
>
/ExtGState >
/XОбъект >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841,92]
/Содержание 65 0 Р
/Группа >
/Вкладки /S
>>
эндообъект
12 0 объект
>
/ExtGState >
/XОбъект >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595,32 841,92]
/Содержание 69 0 Р
/Группа >
/Вкладки /S
>>
эндообъект
13 0 объект
>
/ExtGState >
/XОбъект >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595,32 841,92]
/Содержание 74 0 Р
/Группа >
/Вкладки /S
>>
эндообъект
14 0 объект
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
32 841,92]
/Содержание 37 0 Р
/Группа >
/Вкладки /S
>>
эндообъект
6 0 объект
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595,32 841,92]
/Содержание 39 0 Р
/Группа >
/Вкладки /S
>>
эндообъект
7 0 объект
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595,32 841,92]
/Содержание 40 0 Р
/Группа >
/Вкладки /S
>>
эндообъект
8 0 объект
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841,92]
/Содержание 43 0 Р
/Группа >
/Вкладки /S
>>
эндообъект
9 0 объект
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595,32 841,92]
/Содержание 45 0 Р
/Группа >
/Вкладки /S
>>
эндообъект
10 0 объект
>
/ExtGState >
/XОбъект >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595,32 841,92]
/Содержание 58 0 Р
/Группа >
/Вкладки /S
>>
эндообъект
11 0 объект
>
/ExtGState >
/XОбъект >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841,92]
/Содержание 65 0 Р
/Группа >
/Вкладки /S
>>
эндообъект
12 0 объект
>
/ExtGState >
/XОбъект >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595,32 841,92]
/Содержание 69 0 Р
/Группа >
/Вкладки /S
>>
эндообъект
13 0 объект
>
/ExtGState >
/XОбъект >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595,32 841,92]
/Содержание 74 0 Р
/Группа >
/Вкладки /S
>>
эндообъект
14 0 объект
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 32 841,92]
/Содержание 75 0 Р
/Группа >
/Вкладки /S
>>
эндообъект
15 0 объект
>
/ExtGState >
/XОбъект >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595,32 841,92]
/Содержание 77 0 Р
/Группа >
/Вкладки /S
>>
эндообъект
16 0 объект
>
/ExtGState >
/XОбъект >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595,32 841,92]
/Содержание 81 0 Р
/Группа >
/Вкладки /S
>>
эндообъект
17 0 объект
>
/ExtGState >
/XОбъект >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841,92]
/Содержание 88 0 Р
/Группа >
/Вкладки /S
>>
эндообъект
18 0 объект
>
/ExtGState >
/XОбъект >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595,32 841,92]
/Содержание 95 0 Р
/Группа >
/Вкладки /S
>>
эндообъект
19 0 объект
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595,32 841,92]
/Содержание 96 0 Р
/Группа >
/Вкладки /S
>>
эндообъект
20 0 объект
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
32 841,92]
/Содержание 75 0 Р
/Группа >
/Вкладки /S
>>
эндообъект
15 0 объект
>
/ExtGState >
/XОбъект >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595,32 841,92]
/Содержание 77 0 Р
/Группа >
/Вкладки /S
>>
эндообъект
16 0 объект
>
/ExtGState >
/XОбъект >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595,32 841,92]
/Содержание 81 0 Р
/Группа >
/Вкладки /S
>>
эндообъект
17 0 объект
>
/ExtGState >
/XОбъект >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841,92]
/Содержание 88 0 Р
/Группа >
/Вкладки /S
>>
эндообъект
18 0 объект
>
/ExtGState >
/XОбъект >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595,32 841,92]
/Содержание 95 0 Р
/Группа >
/Вкладки /S
>>
эндообъект
19 0 объект
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595,32 841,92]
/Содержание 96 0 Р
/Группа >
/Вкладки /S
>>
эндообъект
20 0 объект
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 32 841,92]
/Содержание 98 0 Р
/Группа >
/Вкладки /S
>>
эндообъект
21 0 объект
>
эндообъект
22 0 объект
>
эндообъект
23 0 объект
>
эндообъект
24 0 объект
>
эндообъект
25 0 объект
>
эндообъект
26 0 объект
>
эндообъект
27 0 объект
>
эндообъект
28 0 объект
>
эндообъект
29 0 объект
>
эндообъект
30 0 объект
>
эндообъект
31 0 объект
>
эндообъект
32 0 объект
>
ручей
х
32 841,92]
/Содержание 98 0 Р
/Группа >
/Вкладки /S
>>
эндообъект
21 0 объект
>
эндообъект
22 0 объект
>
эндообъект
23 0 объект
>
эндообъект
24 0 объект
>
эндообъект
25 0 объект
>
эндообъект
26 0 объект
>
эндообъект
27 0 объект
>
эндообъект
28 0 объект
>
эндообъект
29 0 объект
>
эндообъект
30 0 объект
>
эндообъект
31 0 объект
>
эндообъект
32 0 объект
>
ручей
х Лебле, С.; Верещагин, С.; Бахметьева, Н.В.; Григорьев, Г.И. Исследование состава мод газовых возмущений на основе измерения параметров атмосферы на высотах мезосферы и нижней термосферы.Атмосфера 2021, 12, 1123.
Копировать
Лебле, С.; Верещагин, С.; Бахметьева, Н.В.; Григорьев, Г.И. Исследование состава мод газовых возмущений на основе измерения параметров атмосферы на высотах мезосферы и нижней термосферы.Атмосфера 2021, 12, 1123.
Копировать Исследование является прямым продолжением и развитием последних результатов по диагностике акустической волны с разделением по направлению распространения.Оценка вклада энтропийной моды основана на измерениях трех динамических переменных (возмущений температуры, плотности и вертикальной скорости) нейтральной атмосферы методом резонансного рассеяния радиоволн на искусственных периодических неоднородностях ионосферной плазмы. . Измерение динамических параметров атмосферы выполнено на нагревательной установке СУРА. Математическая основа алгоритма разделения мод основана на технике оператора динамического проектирования.Операторы строятся через собственные векторы оператора эволюции координат преобразованной системы балансовых уравнений гидротермодинамики.
Исследование является прямым продолжением и развитием последних результатов по диагностике акустической волны с разделением по направлению распространения.Оценка вклада энтропийной моды основана на измерениях трех динамических переменных (возмущений температуры, плотности и вертикальной скорости) нейтральной атмосферы методом резонансного рассеяния радиоволн на искусственных периодических неоднородностях ионосферной плазмы. . Измерение динамических параметров атмосферы выполнено на нагревательной установке СУРА. Математическая основа алгоритма разделения мод основана на технике оператора динамического проектирования.Операторы строятся через собственные векторы оператора эволюции координат преобразованной системы балансовых уравнений гидротермодинамики.
 Ландау (1953) заметил, что начальное расширение системы можно рассматривать в рамках релятивистской гидродинамики. Из-за высокой релятивистской скорости сталкивающихся частиц область столкновения оказывается сильно сжатой в одном направлении. Следовательно, задача может быть сведена к одномерной релятивистской гидродинамике в плоской геометрии. Ландау нашел приближенное решение этой задачи. Позднее точное решение было дано Халатниковым (1954).
Ландау (1953) заметил, что начальное расширение системы можно рассматривать в рамках релятивистской гидродинамики. Из-за высокой релятивистской скорости сталкивающихся частиц область столкновения оказывается сильно сжатой в одном направлении. Следовательно, задача может быть сведена к одномерной релятивистской гидродинамике в плоской геометрии. Ландау нашел приближенное решение этой задачи. Позднее точное решение было дано Халатниковым (1954). Затем из-за экспоненциальной зависимости плотности пар от температуры и, следовательно, от радиуса система внезапно становится прозрачной.Он вычислил энергетическое распределение потока фотонов, принимаемого удаленным наблюдателем, путем интегрирования по объему системы в момент прозрачности. Оказалось, что спектр близок к тепловому.
Затем из-за экспоненциальной зависимости плотности пар от температуры и, следовательно, от радиуса система внезапно становится прозрачной.Он вычислил энергетическое распределение потока фотонов, принимаемого удаленным наблюдателем, путем интегрирования по объему системы в момент прозрачности. Оказалось, что спектр близок к тепловому. Во-первых, в случае очень низкого загрязнения барионами это естественное продолжение работы Руффини и др.(2013), которые рассмотрели конечные профили ветра. Он также находит прямое применение при интерпретации спектров некоторых гамма-всплесков в контексте модели огненной оболочки, см., например, Руффини и соавт. (2007) и ссылки в нем. Действительно, Муччино и соавт. (2013) проанализировали короткий GRB0
Во-первых, в случае очень низкого загрязнения барионами это естественное продолжение работы Руффини и др.(2013), которые рассмотрели конечные профили ветра. Он также находит прямое применение при интерпретации спектров некоторых гамма-всплесков в контексте модели огненной оболочки, см., например, Руффини и соавт. (2007) и ссылки в нем. Действительно, Муччино и соавт. (2013) проанализировали короткий GRB0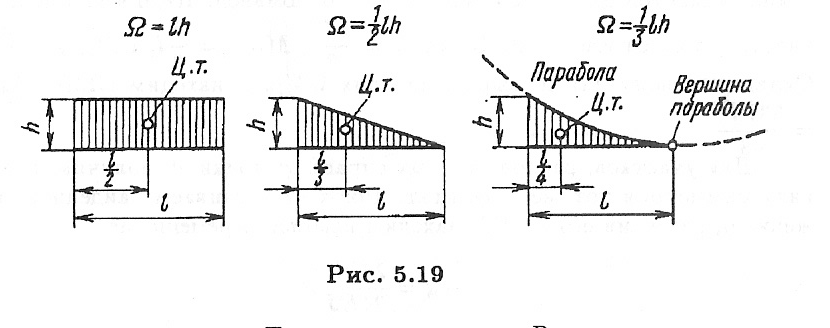 в Приложении, справедливое для ультрарелятивистского уравнения состояния ϵ = 3 P , где ϵ — плотность энергии и P — давление, а ультрарелятивистская скорость расширения v ≈ c .Для оптически толстой системы электрон-позитронных пар и фотонов все частицы дают вклад в уравнение состояния. Предполагая тепловое равновесие, можно найти уравнение состояния в этой системе. Она представлена на рис. 1 для разных значений размерной сопутствующей температуры T .
в Приложении, справедливое для ультрарелятивистского уравнения состояния ϵ = 3 P , где ϵ — плотность энергии и P — давление, а ультрарелятивистская скорость расширения v ≈ c .Для оптически толстой системы электрон-позитронных пар и фотонов все частицы дают вклад в уравнение состояния. Предполагая тепловое равновесие, можно найти уравнение состояния в этой системе. Она представлена на рис. 1 для разных значений размерной сопутствующей температуры T . При нерелятивистских температурах ( k B T ≪ m e c 2 ) уравнение состояния также является ультрарелятивистским, поскольку вклад нерелятивистской пары электрон-позитронный (см. также Goodman 1986). Как видно из рис. 1, максимальное отклонение от значения 1/3 достигается при температуре 12 процентов.Этот факт оправдывает ультрарелятивистское уравнение состояния в оптически толстой электрон-позитрон-фотонной плазме. Известно также, что такая плазма, будучи оптически толстой, расширяется с ускорением и достигает ультрарелятивистской скорости расширения, прежде чем стать прозрачной (см. Гудман, 1986). Следовательно, к этой системе можно применить решение Бисноватого-Когана и Мурзиной (1995).
При нерелятивистских температурах ( k B T ≪ m e c 2 ) уравнение состояния также является ультрарелятивистским, поскольку вклад нерелятивистской пары электрон-позитронный (см. также Goodman 1986). Как видно из рис. 1, максимальное отклонение от значения 1/3 достигается при температуре 12 процентов.Этот факт оправдывает ультрарелятивистское уравнение состояния в оптически толстой электрон-позитрон-фотонной плазме. Известно также, что такая плазма, будучи оптически толстой, расширяется с ускорением и достигает ультрарелятивистской скорости расширения, прежде чем стать прозрачной (см. Гудман, 1986). Следовательно, к этой системе можно применить решение Бисноватого-Когана и Мурзиной (1995). Такие параметры типичны для модели гамма-всплесков огненной оболочки (см., например, Руффини и др., 2007). Мы установили для параметра k значение |$1+\sqrt{3}/2$|, как предписано Бисноватым-Коганом и Мурзиной (1995).
Такие параметры типичны для модели гамма-всплесков огненной оболочки (см., например, Руффини и др., 2007). Мы установили для параметра k значение |$1+\sqrt{3}/2$|, как предписано Бисноватым-Коганом и Мурзиной (1995). Это поведение необходимо противопоставить тому, которое было обнаружено Ruffini et al. (2013) для простого оболочечного профиля релятивистского ветра с конечной продолжительностью: оптическая толщина как функция ξ увеличивается до значения насыщения, от которого она остается постоянной вплоть до внутренней границы истечения.Отсюда следует, что время выброса t e на луче зрения увеличивается с глубиной ξ внутри оболочки. В нашем более сложном профиле внешняя и внутренняя части оболочки становятся прозрачными раньше центральной части: для данного лабораторного времени имеется две фотосферы t e . Однако в заданное время прихода t a фотосфера только одна: излучение внутренней части оболочки приходит к наблюдателю позже.
Это поведение необходимо противопоставить тому, которое было обнаружено Ruffini et al. (2013) для простого оболочечного профиля релятивистского ветра с конечной продолжительностью: оптическая толщина как функция ξ увеличивается до значения насыщения, от которого она остается постоянной вплоть до внутренней границы истечения.Отсюда следует, что время выброса t e на луче зрения увеличивается с глубиной ξ внутри оболочки. В нашем более сложном профиле внешняя и внутренняя части оболочки становятся прозрачными раньше центральной части: для данного лабораторного времени имеется две фотосферы t e . Однако в заданное время прихода t a фотосфера только одна: излучение внутренней части оболочки приходит к наблюдателю позже. Он получил наблюдаемый спектр путем интегрирования как по углам излучения, так и по радиальной координате в фиксированное лабораторное время, соответствующее моменту прозрачности на луче зрения, см. нижнюю панель рис. 2. Эта область интегрирования показана на серый на рис. 4. В нашем расчете динамика фотосферы учитывается в явном виде: для каждого момента прихода спектр от поверхности, определяемый τ( r , t , ϕ 0 ) = 1 равен вычислено.Уравнение (4) показывает, что оптическая толщина увеличивается с ϕ 0 , поэтому точки, удовлетворяющие τ = 1 для данного ξ, смещаются на большее время и радиус, чем точка на луче зрения. Эта поверхность схематично показана на рис. 4. Наконец, выполняется интегрирование по временам прихода.
Он получил наблюдаемый спектр путем интегрирования как по углам излучения, так и по радиальной координате в фиксированное лабораторное время, соответствующее моменту прозрачности на луче зрения, см. нижнюю панель рис. 2. Эта область интегрирования показана на серый на рис. 4. В нашем расчете динамика фотосферы учитывается в явном виде: для каждого момента прихода спектр от поверхности, определяемый τ( r , t , ϕ 0 ) = 1 равен вычислено.Уравнение (4) показывает, что оптическая толщина увеличивается с ϕ 0 , поэтому точки, удовлетворяющие τ = 1 для данного ξ, смещаются на большее время и радиус, чем точка на луче зрения. Эта поверхность схематично показана на рис. 4. Наконец, выполняется интегрирование по временам прихода. Для сравнения эти два последних были сдвинуты в сторону меньшей энергии в 2,3 раза.
Для сравнения эти два последних были сдвинуты в сторону меньшей энергии в 2,3 раза. Серая область соответствует оболочке в лабораторное время, для которого оптическая толщина фотона, распространяющегося радиально, равна единице. Это область, в которой спектр вычисляется Гудманом (1986). Оболочка также представлена в более крупное лабораторное время с кривой, соединяющей d V с d V 1 , которая представляет собой схематическое изображение поверхности τ = 1 на заданной глубине ξ.
Серая область соответствует оболочке в лабораторное время, для которого оптическая толщина фотона, распространяющегося радиально, равна единице. Это область, в которой спектр вычисляется Гудманом (1986). Оболочка также представлена в более крупное лабораторное время с кривой, соединяющей d V с d V 1 , которая представляет собой схематическое изображение поверхности τ = 1 на заданной глубине ξ.
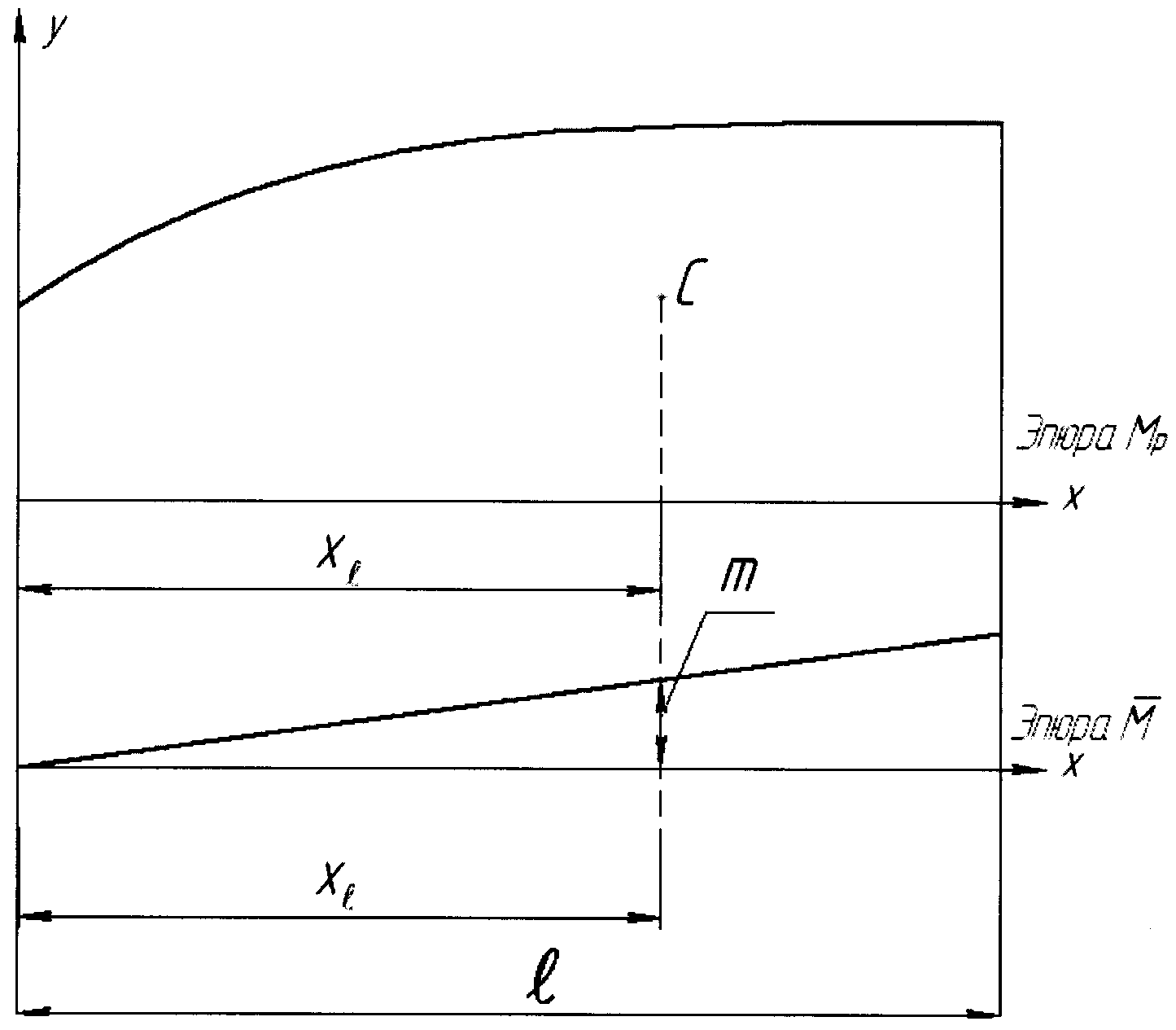 Они почти неразличимы. Для сравнения штрихпунктирной линией показана кривая блеска, которая была бы получена от оптически тонкого шара радиусом R 0 , равномерно заполненного изотропным излучением.
Они почти неразличимы. Для сравнения штрихпунктирной линией показана кривая блеска, которая была бы получена от оптически тонкого шара радиусом R 0 , равномерно заполненного изотропным излучением. При больших радиусах, когда излучение свободно течет и пересекает оболочку, параметр Комптона y много меньше единицы, так как температура нерелятивистская и τ < 1, поэтому искажение спектра мало.
При больших радиусах, когда излучение свободно течет и пересекает оболочку, параметр Комптона y много меньше единицы, так как температура нерелятивистская и τ < 1, поэтому искажение спектра мало.