Сила реакции опоры: определение и формула
Статика — один из разделов современной физики, который изучает условия нахождения тел и систем в механическом равновесии. Для решения задач на равновесие важно знать, что такое сила реакции опоры. Данная статья посвящена подробному рассмотрению этого вопроса.
Второй и третий законы Ньютона
Прежде чем рассматривать определение силы реакции опоры, следует вспомнить о том, что вызывает движение тел.
Причиной нарушения механического равновесия является действие на тела внешних или внутренних сил. В результате этого действия тело приобретает определенное ускорение, которое вычисляется с помощью следующего равенства:
F = m*a
Эта запись известна как второй закон Ньютона. Здесь сила F является результирующей всех действующих на тело сил.
Если одно тело воздействует с некоторой силой F1¯ на второе тело, то второе оказывает действие на первое с точно такой же по абсолютной величине силой F2¯, но она направлена в противоположном направлении, чем F1¯. То есть справедливо равенство:
F1¯ = -F2¯
Эта запись является математическим выражением для третьего ньютоновского закона.
При решении задач с использованием этого закона школьники часто допускают ошибку, сравнивая эти силы. Например, лошадь везет телегу, при этом лошадь на телегу и телега на лошадь оказывают одинаковые по модулю силы. Почему же тогда вся система движется? Ответ на этот вопрос можно правильно дать, если вспомнить, что обе названные силы приложены к разным телам, поэтому они друг друга не уравновешивают.
Сила реакции опоры
Сначала дадим физическое определение этой силы, а затем поясним на примере, как она действует. Итак, силой нормальной реакции опоры называется сила, которая действует на тело со стороны поверхности. Например, мы поставили стакан с водой на стол. Чтобы стакан не двигался с ускорением свободного падения вниз, стол воздействует на него с силой, которая уравновешивает силу тяжести. Это и есть реакция опоры. Ее обычно обозначают буквой N.
Сила N — это контактная величина. Если имеется контакт между телами, то она появляется всегда. В примере выше значение величины N равно по модулю весу тела. Тем не менее это равенство является лишь частным случаем. Реакция опоры и вес тела — это совершенно разные силы, имеющие различную природу. Равенство между ними нарушается всегда, когда изменяется угол наклона плоскости, появляются дополнительные действующие силы, или когда система движется ускоренно.
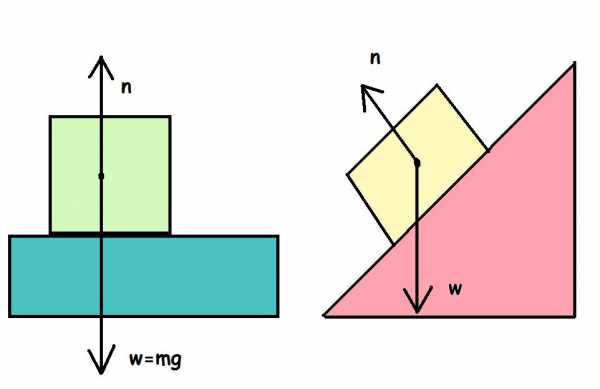
Сила N называется нормальной потому, что она всегда направлена перпендикулярно плоскости поверхности.
Если говорить о третьем законе Ньютона, то в примере выше со стаканом воды на столе вес тела и нормальная сила N не являются действием и противодействием, поскольку обе они приложены к одному телу (стакану с водой).
Физическая причина появления силы N
Как было выяснено выше, сила реакции опоры препятствует проникновению одних твердых тел в другие. Почему появляется эта сила? Причина заключается в деформации. Любые твердые тела под воздействием нагрузки деформируются сначала упруго. Сила упругости стремится восстановить прежнюю форму тела, поэтому она оказывает выталкивающее воздействие, что проявляется в виде реакции опоры.
Если рассматривать вопрос на атомном уровне, то появление величины N — это результат действия принципа Паули. При небольшом сближении атомов их электронные оболочки начинают перекрываться, что приводит к появлению силы отталкивания.
Многим может показаться странным, что стакан с водой способен деформировать стол, но это так. Деформация настолько мала, что невооруженным глазом ее невозможно наблюдать.
Как вычислять силу N?

Сразу следует сказать, что какой-то определенной формулы силы реакции опоры не существует. Тем не менее имеется методика, применяя которую, можно определить N для совершенно любой системы взаимодействующих тел.
Методика определения величины N заключается в следующем:
- сначала записывают второй закон Ньютона для данной системы, учитывая все действующие в ней силы;
- находят результирующую проекцию всех сил на направление действия реакции опоры;
- решение полученного уравнения Ньютона на отмеченное направление приведет к искомому значению N.
При составлении динамического уравнения следует внимательно и правильно расставлять знаки действующих сил.
Найти реакцию опоры можно также, если пользоваться не понятием сил, а понятием их моментов. Привлечение моментов сил справедливо и является удобным для систем, которые имеют точки или оси вращения.
Далее приведем два примера решения задач, в которых покажем, как пользоваться вторым ньютоновским законом и понятием момента силы для нахождения величины N.
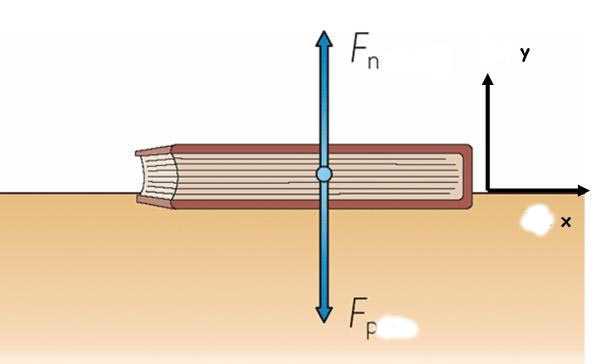
Задача со стаканом на столе
Выше уже был приведен этот пример. Предположим, что пластиковый стакан объемом 250 мл наполнен водой. Его поставили на стол, а сверху на стакан положили книгу массой 300 грамм. Чему равна сила реакции опоры стола?
Запишем динамическое уравнение. Имеем:
m*a = P1 + P2 — N
Здесь P1 и P2 — вес стакана с водой и книги соответственно. Поскольку система находится в равновесии, то a=0. Учитывая, что вес тела равен силе тяжести, а также пренебрегая массой пластикового стакана, получаем:
m1*g + m2*g — N = 0 =>
N = (m1 + m2)*g
Учитывая, что плотность воды равна 1 г/см3, и 1 мл равен 1 см3, получаем согласно выведенной формуле, что сила N равна 5,4 ньютона.
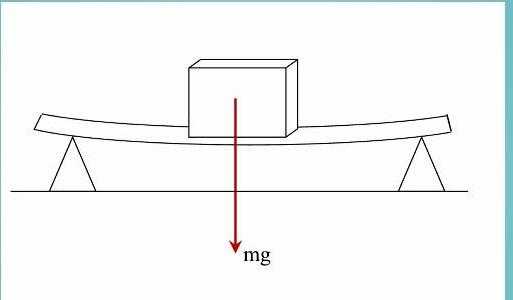
Задача с доской, двумя опорами и грузом

Доска, массой которой можно пренебречь, лежит на двух твердых опорах. Длина доски равна 2 метра. Чему будет равна сила реакции каждой опоры, если на эту доску посередине положить груз массой 3 кг?
Прежде чем переходить к решению задачи, следует ввести понятие момента силы. В физике этой величине соответствует произведение силы на длину рычага (расстояние от точки приложения силы до оси вращения). Система, имеющая ось вращения, будет находиться в равновесии, если суммарный момент сил равен нулю.

Возвращаясь к нашей задаче, вычислим суммарный момент сил относительно одной из опор (правой). Обозначим длину доски буквой L. Тогда момент силы тяжести груза будет равен:
M1 = -m*g*L/2
Здесь L/2 — рычаг действия силы тяжести. Знак минус появился потому, что момент M1 осуществляет вращение против часовой стрелки.
Момент силы реакции опоры будет равен:
M2 = N*L
Поскольку система находится в равновесии, то сумма моментов должна быть равной нулю. Получаем:
M1 + M2 = 0 =>
N*L + (-m*g*L/2) = 0 =>
N = m*g/2 = 3*9,81/2 = 14,7 Н
Заметим, что от длины доски сила N не зависит.
Учитывая симметричность расположения груза на доске относительно опор, сила реакции левой опоры также будет равна 14,7 Н.
fb.ru
Сила нормальной реакции — Howling Pixel
Си́ла норма́льной реа́кции (иногда нормальная реакция опоры) — сила, действующая на тело со стороны опоры и направленная перпендикулярно («по нормали», «нормально») к поверхности соприкосновения. Распределена по площади зоны соприкосновения. Подлежит учёту при анализе динамики движения тела. Фигурирует в законе Амонтона — Кулона.
Одним из часто обсуждаемых примеров для иллюстрации силы нормальной реакции является случай нахождения небольшого тела на наклонной плоскости. При этом для простоты считается, что сила реакции приложена в одной точке соприкосновения.
Для расчёта в этом случае используется формула
- |N→|=mgcosθ{\displaystyle |{\vec {N}}|=mg\cos \theta },
где |N→|{\displaystyle |{\vec {N}}|} — модуль вектора силы нормальной реакции, m{\displaystyle m} — масса тела, g{\displaystyle g} — ускорение свободного падения, θ{\displaystyle \theta } — угол между плоскостью опоры и горизонтальной плоскостью.
Выписанной формулой отражается тот факт, что вдоль направления, перпендикулярного наклонной плоскости, движения нет. Это значит, что величина силы нормальной реакции равна проекции силы тяжести mg{\displaystyle mg} на указанное направление.
Из закона Амонтона — Кулона следует, что для модуля вектора силы нормальной реакции справедливо соотношение:
- |N→|=|F→|μ,{\displaystyle |{\vec {N}}|={\frac {|{\vec {F}}|}{\mu }},}
где F→{\displaystyle {\vec {F}}} — сила трения скольжения, а μ{\displaystyle \mu } — коэффициент трения.
Поскольку сила трения покоя вычисляется по формуле
- |f→|=mgsinθ,{\displaystyle |{\vec {f}}|=mg\sin \theta ,}
можно экспериментальным путём найти такое значение угла θ{\displaystyle \theta }, при котором сила трения покоя будет равна силе трения скольжения:
- mgsinθ=μmgcosθ.{\displaystyle mg\sin \theta =\mu mg\cos \theta .}
Отсюда выражается коэффициент трения:
- μ=tg θ.{\displaystyle \mu =\mathrm {tg} \ \theta .}
Зако́н Амонто́на — Куло́на — эмпирический закон, устанавливающий линейную связь между поверхностной силой трения, возникающей при относительном скольжении тел, и силой нормальной реакции, действующей на тело со стороны поверхности.
Наклонная плоскостьНаклонная плоскость — это плоская поверхность, установленная под углом к горизонтали. Наклонная плоскость является одним из простых механизмов. Она позволяет поднимать груз вверх, прикладывая к нему усилие, заметно меньшее, чем сила тяжести, действующая на этот груз.
Примерами наклонных плоскостей служат пандусы и трапы. Принцип наклонной плоскости можно видеть также в таких колющих и режущих инструментах, как стамеска, топор, плуг, клин, винт.
СилаСи́ла — физическая векторная величина, являющаяся мерой воздействия на данное тело со стороны других тел или полей. Приложение силы обусловливает изменение скорости тела или появление деформаций и механических напряжений.
Деформация может возникать как в самом теле, так и в фиксирующих его объектах — например, пружинах.
Воздействие всегда осуществляется посредством полей, создаваемых телами и воспринимаемых рассматриваемым телом. Различные взаимодействия сводятся к четырём фундаментальным; согласно Стандартной модели физики элементарных частиц, эти фундаментальные взаимодействия (слабое, электромагнитное, сильное и, возможно, гравитационное) реализуются путём обмена калибровочными бозонами.
Для обозначения силы обычно используется символ F — от лат. fortis (сильный).
Важнейший физический закон, в который входит сила, — второй закон Ньютона. Он гласит, что в инерциальных системах отсчёта ускорение материальной точки по направлению совпадает с приложенной силой, а по модулю пропорционально модулю силы и обратно пропорционально массе материальной точки.
Слово «сила» в русском языке является многозначным и нередко используется (само или в сочетаниях, в науке и обиходных ситуациях) в смыслах, отличных от физического определения термина.
Сила трения скольженияСила трения скольжения — сила, возникающая между соприкасающимися телами при их относительном движении.
Опытным путём установлено, что сила трения зависит от силы давления тел друг на друга (силы реакции опоры), от материалов трущихся поверхностей, от скорости относительного движения, но не зависит от площади соприкосновения.
Величина, характеризующая трущиеся поверхности, называется коэффициентом трения, и обозначается латинской буквой k{\displaystyle k} или греческой буквой μ{\displaystyle \mu }. Она зависит от природы и качества обработки трущихся поверхностей. Кроме того, коэффициент трения зависит от скорости. Впрочем, чаще всего эта зависимость выражена слабо, и если большая точность измерений не требуется, то μ{\displaystyle \mu } можно считать постоянным. В первом приближении величина силы трения скольжения может быть рассчитана по формуле:
F=μN{\displaystyle F=\mu N}
μ{\displaystyle \mu } — коэффициент трения скольжения,
N{\displaystyle N} — сила нормальной реакции опоры.
Силами трения называются тангенциальные взаимодействия между соприкасающимися телами, возникающие при их относительном перемещении.
Опыты с движением различных соприкасающихся тел (твёрдых по твёрдым, твёрдых в жидкости или газе, жидких в газе и т. п.) с различным состоянием поверхностей соприкосновения показывают, что силы трения проявляются при относительном перемещении соприкасающихся тел и направлены против вектора относительной скорости тангенциально к поверхности соприкосновения. При этом всегда в большей или меньшей степени происходит преобразование механического движения в другие формы движения материи — чаще всего в тепловую форму движения, и происходит нагревание взаимодействующих тел.
Список обозначений в физикеСписок обозначений в физике включает обозначения понятий в физике из школьного и университетского курсов. Также включены и общие математические понятия и операции для того, чтобы сделать возможным полное прочтение физических формул.
Для обозначения физических величин и понятий в физике используются буквы латинского и греческого алфавитов, а также несколько специальных символов и диакритических знаков. Поскольку количество физических величин больше количества букв в латинском и греческом алфавитах, одни и те же буквы используются для обозначения различных величин. Для некоторых физических величин принято несколько обозначений (например для энергии, скорости, длины и других), чтобы предотвратить путаницу с другими величинами в данном разделе физики.
ТрениеТре́ние — процесс механического взаимодействия соприкасающихся тел при их относительном смещении в плоскости касания (внешнее трение) либо при относительном смещении параллельных слоёв жидкости, газа или деформируемого твёрдого тела (внутреннее трение, или вязкость). Далее в этой статье под трением понимается лишь внешнее трение. Изучением процессов трения занимается раздел физики, который называется механикой фрикционного взаимодействия, или трибологией.
Трение главным образом имеет электронную природу при условии, что вещество находится в нормальном состоянии. В сверхпроводящем состоянии вдалеке от критической температуры основным «источником» трения являются фононы, а коэффициент трения может уменьшиться в несколько раз.
Трение покояТре́ние поко́я, трение сцепления — сила, возникающая между двумя неподвижными контактирующими телами и препятствующая возникновению относительного движения. Эту силу необходимо преодолеть для того, чтобы привести два контактирующих тела в движение друг относительно друга. Возникает при микроперемещениях (например, при деформации) контактирующих тел. Трение покоя наблюдается до перехода к движению на макроуровне, когда начинает действовать сила трения качения или скольжения. Действует в направлении, противоположном направлению возможного относительного движения. Максимальная сила трения покоя обычно несколько выше, чем сила трения скольжения.
В 1779 году французский физик Кулон установил, от чего зависит максимальная сила трения покоя. Оказалось, что сила трения покоя зависит от того, с какой силой прижимаются друг к другу соприкасающиеся предметы. Также было установлено, что трение покоя зависит от материала соприкасающихся поверхностей.
Примером силы трения покоя может служить эскалатор со стоящим на нем человеком. Также эта сила проявляется в забитом в доску гвозде, завязанном банте или шнурке и т.д.
Максимальная сила трения покоя в простейшем приближении: F≈k0N{\displaystyle F\approx k_{0}N}, где k0{\displaystyle k_{0}} — коэффициент трения покоя
На других языках
This page is based on a Wikipedia article written by authors
(here).
Text is available under the CC BY-SA 3.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.
howlingpixel.com
Сила реакции опоры: определение и формула
Статика — один из разделов современной физики, который изучает условия нахождения тел и систем в механическом равновесии. Для решения задач на равновесие важно знать, что такое сила реакции опоры. Данная статья посвящена подробному рассмотрению этого вопроса.
Второй и третий законы Ньютона
Прежде чем рассматривать определение силы реакции опоры, следует вспомнить о том, что вызывает движение тел.
Причиной нарушения механического равновесия является действие на тела внешних или внутренних сил. В результате этого действия тело приобретает определенное ускорение, которое вычисляется с помощью следующего равенства:
F = m*a
Эта запись известна как второй закон Ньютона. Здесь сила F является результирующей всех действующих на тело сил.
Если одно тело воздействует с некоторой силой F1¯ на второе тело, то второе оказывает действие на первое с точно такой же по абсолютной величине силой F2¯, но она направлена в противоположном направлении, чем F1¯. То есть справедливо равенство:
F1¯ = -F2¯
Эта запись является математическим выражением для третьего ньютоновского закона.
При решении задач с использованием этого закона школьники часто допускают ошибку, сравнивая эти силы. Например, лошадь везет телегу, при этом лошадь на телегу и телега на лошадь оказывают одинаковые по модулю силы. Почему же тогда вся система движется? Ответ на этот вопрос можно правильно дать, если вспомнить, что обе названные силы приложены к разным телам, поэтому они друг друга не уравновешивают.
Сила реакции опоры
Сначала дадим физическое определение этой силы, а затем поясним на примере, как она действует. Итак, силой нормальной реакции опоры называется сила, которая действует на тело со стороны поверхности. Например, мы поставили стакан с водой на стол. Чтобы стакан не двигался с ускорением свободного падения вниз, стол воздействует на него с силой, которая уравновешивает силу тяжести. Это и есть реакция опоры. Ее обычно обозначают буквой N.
Сила N — это контактная величина. Если имеется контакт между телами, то она появляется всегда. В примере выше значение величины N равно по модулю весу тела. Тем не менее это равенство является лишь частным случаем. Реакция опоры и вес тела — это совершенно разные силы, имеющие различную природу. Равенство между ними нарушается всегда, когда изменяется угол наклона плоскости, появляются дополнительные действующие силы, или когда система движется ускоренно.

Сила N называется нормальной потому, что она всегда направлена перпендикулярно плоскости поверхности.
Если говорить о третьем законе Ньютона, то в примере выше со стаканом воды на столе вес тела и нормальная сила N не являются действием и противодействием, поскольку обе они приложены к одному телу (стакану с водой).
Физическая причина появления силы N

Как было выяснено выше, сила реакции опоры препятствует проникновению одних твердых тел в другие. Почему появляется эта сила? Причина заключается в деформации. Любые твердые тела под воздействием нагрузки деформируются сначала упруго. Сила упругости стремится восстановить прежнюю форму тела, поэтому она оказывает выталкивающее воздействие, что проявляется в виде реакции опоры.
Если рассматривать вопрос на атомном уровне, то появление величины N — это результат действия принципа Паули. При небольшом сближении атомов их электронные оболочки начинают перекрываться, что приводит к появлению силы отталкивания.
Многим может показаться странным, что стакан с водой способен деформировать стол, но это так. Деформация настолько мала, что невооруженным глазом ее невозможно наблюдать.
Как вычислять силу N?
Сразу следует сказать, что какой-то определенной формулы силы реакции опоры не существует. Тем не менее имеется методика, применяя которую, можно определить N для совершенно любой системы взаимодействующих тел.
Методика определения величины N заключается в следующем:
- сначала записывают второй закон Ньютона для данной системы, учитывая все действующие в ней силы;
- находят результирующую проекцию всех сил на направление действия реакции опоры;
- решение полученного уравнения Ньютона на отмеченное направление приведет к искомому значению N.
При составлении динамического уравнения следует внимательно и правильно расставлять знаки действующих сил.
Найти реакцию опоры можно также, если пользоваться не понятием сил, а понятием их моментов. Привлечение моментов сил справедливо и является удобным для систем, которые имеют точки или оси вращения.
Далее приведем два примера решения задач, в которых покажем, как пользоваться вторым ньютоновским законом и понятием момента силы для нахождения величины N.
Задача со стаканом на столе
Выше уже был приведен этот пример. Предположим, что пластиковый стакан объемом 250 мл наполнен водой. Его поставили на стол, а сверху на стакан положили книгу массой 300 грамм. Чему равна сила реакции опоры стола?
Запишем динамическое уравнение. Имеем:
m*a = P1 + P2 — N
Здесь P1 и P2 — вес стакана с водой и книги соответственно. Поскольку система находится в равновесии, то a=0. Учитывая, что вес тела равен силе тяжести, а также пренебрегая массой пластикового стакана, получаем:
m1*g + m2*g — N = 0 =>
N = (m1 + m2)*g
Учитывая, что плотность воды равна 1 г/см3, и 1 мл равен 1 см3, получаем согласно выведенной формуле, что сила N равна 5,4 ньютона.
Задача с доской, двумя опорами и грузом

Доска, массой которой можно пренебречь, лежит на двух твердых опорах. Длина доски равна 2 метра. Чему будет равна сила реакции каждой опоры, если на эту доску посередине положить груз массой 3 кг?
Прежде чем переходить к решению задачи, следует ввести понятие момента силы. В физике этой величине соответствует произведение силы на длину рычага (расстояние от точки приложения силы до оси вращения). Система, имеющая ось вращения, будет находиться в равновесии, если суммарный момент сил равен нулю.
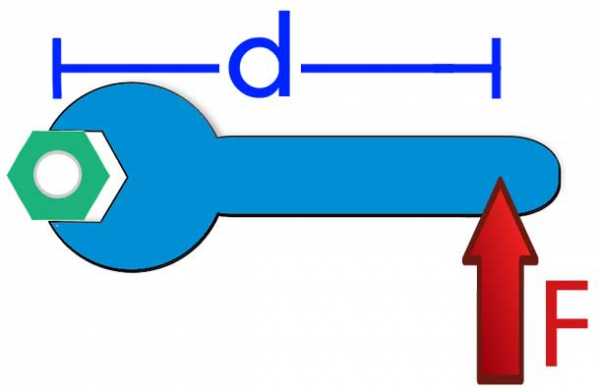
Возвращаясь к нашей задаче, вычислим суммарный момент сил относительно одной из опор (правой). Обозначим длину доски буквой L. Тогда момент силы тяжести груза будет равен:
M1 = -m*g*L/2
Здесь L/2 — рычаг действия силы тяжести. Знак минус появился потому, что момент M1 осуществляет вращение против часовой стрелки.
Момент силы реакции опоры будет равен:
M2 = N*L
Поскольку система находится в равновесии, то сумма моментов должна быть равной нулю. Получаем:
M1 + M2 = 0 =>
N*L + (-m*g*L/2) = 0 =>
N = m*g/2 = 3*9,81/2 = 14,7 Н
Заметим, что от длины доски сила N не зависит.
Учитывая симметричность расположения груза на доске относительно опор, сила реакции левой опоры также будет равна 14,7 Н.
autogear.ru
Как найти силу трения скольжения 🚩 f трения формула 🚩 Естественные науки
Инструкция
Случай 1. Формула для силы трения скольжения: Fтр = мN, где м – коэффициент трения скольжения, N – сила реакции опоры, Н. Для тела, скользящего по горизонтальной плоскости, N = G = mg, где G — вес тела, Н; m – масса тела, кг; g – ускорение свободного падения, м/с2. Значения безразмерного коэффициента м для данной пары материалов даны в справочной литературе. Зная массу тела и пару материалов. скользящих друг относительно друга, найдите силу трения.Случай 2. Рассмотрите тело, скользящее по горизонтальной поверхности и двигающееся равноускоренно. На него действуют четыре силы: сила, приводящее тело в движение, сила тяжести, сила реакции опоры, сила трения скольжения. Так как поверхность горизонтальная, сила реакции опоры и сила тяжести направлены вдоль одной прямой и уравновешивают друг друга. Перемещение описывает уравнение: Fдв — Fтр = ma; где Fдв – модуль силы, приводящей тело в движение, Н; Fтр – модуль силы трения, Н; m – масса тела, кг; a – ускорение, м/с2. Зная значения массы, ускорения тела и силы, воздействующей на него, найдите силу трения. Если эти значения не заданы прямо, посмотрите, есть ли в условии данные, из которых можно найти эти величины.
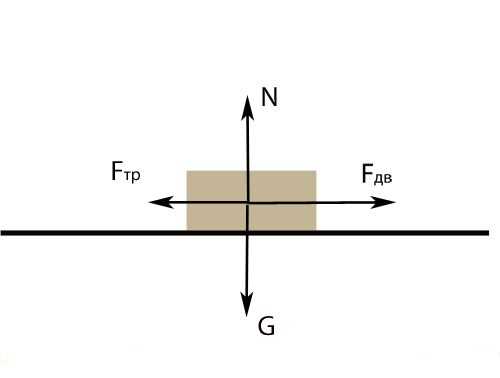 Пример задачи 1: на брусок массой 5 кг, лежащий на поверхности, воздействуют силой 10 Н. В результате брусок двигается равноускоренно и проходит 10 метров за 10 секунд. Найдите силу трения скольжения.
Пример задачи 1: на брусок массой 5 кг, лежащий на поверхности, воздействуют силой 10 Н. В результате брусок двигается равноускоренно и проходит 10 метров за 10 секунд. Найдите силу трения скольжения.Уравнение для движения бруска:Fдв — Fтр = ma. Путь тела для равноускоренного движения задается равенством: S = 1/2at^2. Отсюда вы можете определить ускорение: a = 2S/t^2. Подставьте данные условия: а = 2*10/10^2 = 0,2 м/с2. Теперь найдите равнодействующую двух сил: ma = 5*0,2 = 1 Н. Вычислите силу трения: Fтр = 10-1 = 9 Н.
Случай 3. Если тело на горизонтальной поверхности находится в состоянии покоя, либо двигается равномерно, по второму закону Ньютона силы находятся в равновесии : Fтр = Fдв.
Пример задачи 2: бруску массой 1 кг, находящемуся на ровной поверхности, сообщили импульс, в результате которого он проехал 10 метров за 5 секунд и остановилось. Определите силу трения скольжения.Как и в первом примере, на скольжение бруска влияют сила движения и сила трения. В результате этого воздействия тело останавливается, т.е. приходит равновесие. Уравнение движения бруска: Fтр = Fдв. Или: N*м = ma. Брусок скользит равноускоренно. Рассчитайте его ускорение подобно задаче 1: a = 2S/t^2. Подставьте значения величин из условия: а = 2*10/5^2 = 0,8 м/с2. Теперь найдите силу трения: Fтр = ma = 0,8*1 = 0,8 Н.
Случай 4. На тело, самопроизвольно скользящее по наклонной плоскости, действуют три силы: сила тяжести (G), сила реакции опоры (N) и сила трения (Fтр). Сила тяжести может быть записана в таком виде: G = mg, Н, где m – масса тела, кг; g – ускорение свободного падения, м/с2. Поскольку эти силы направлены не вдоль одной прямой, запишите уравнение движения в векторном виде.
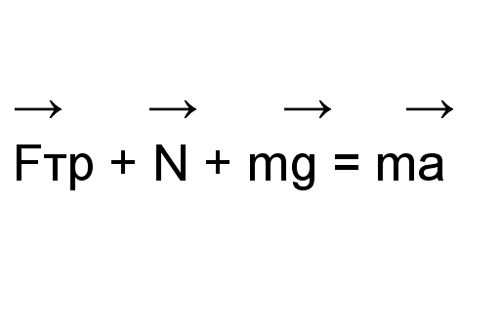
Сложив по правилу параллелограмма силы N и mg, вы получите результирующую силу F’. Из рисунка можно сделать выводы: N = mg*cosα; F’ = mg*sinα. Где α – угол наклона плоскости. Силу трения можно записать формулой: Fтр = м*N = м*mg*cosα. Уравнение для движения принимает вид: F’-Fтр = ma. Или: Fтр = mg*sinα-ma.
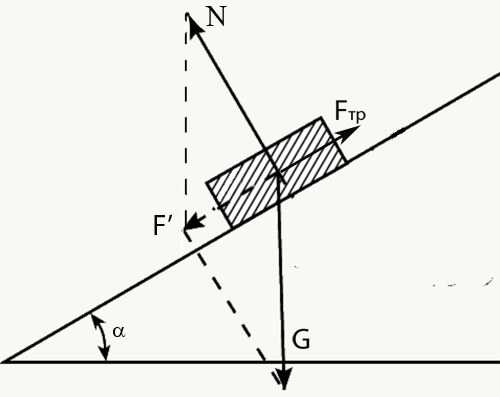
Случай 5. Если же к телу приложена дополнительная сила F, направленная вдоль наклонной плоскости, то сила трения будет выражаться: Fтр = mg*sinα+F-ma, если направление движения и силы F совпадают. Или: Fтр = mg*sinα-F-ma, если сила F противодействует движению.
Пример задачи 3: брусок массой 1 кг соскользнул с вершины наклонной плоскости за 5 секунд, пройдя путь 10 метров. Определите силу трения, если угол наклона плоскости 45о. Рассмотрите также случай, когда на брусок воздействовала дополнительная сила 2 Н, приложенная вдоль угла наклона по направлению движения.Найдите ускорение тела аналогично примерам 1 и 2: а = 2*10/5^2 = 0,8 м/с2. Вычислите силу трения в первом случае: Fтр = 1*9,8*sin(45о)-1*0,8 = 7,53 Н. Определите силу трения во втором случае: Fтр = 1*9,8*sin(45о)+2-1*0,8= 9,53 Н.
Случай 6. Тело двигается по наклонной поверхности равномерно. Значит, по второму закону Ньютона система находится в равновесии. Если скольжение самопроизвольное, движение тела подчиняется уравнению: mg*sinα = Fтр.Если же к телу приложена дополнительная сила (F), препятствующая равноускоренному перемещению, выражение для движения имеет вид: mg*sinα–Fтр-F = 0. Отсюда найдите силу трения: Fтр = mg*sinα-F.
Коэффициент трения – это совокупность характеристик двух тел, которые соприкасаются друг с другом. Существует несколько видов трения: трение покоя, трение скольжения и трение качения. Трение покоя представляет собой трение тело, которое находилось в покое, и было приведено в движение. Трение скольжения происходит при движении тела, данное трение меньше трения покоя. А трение качения происходит, когда тело катиться по поверхности. Обозначается трение в зависимости от вида, следующим образом: μск — трение скольжения, μо- трение покоя, μкач – трение качения.

Инструкция
Сила трения катящего тела определяется радиусом предмета. В большинстве случаев при вычислении трения качения транспортного средства, когда величина радиуса колеса постоянна, ее определяют в коэффициент трения. При определении коэффициента трения в ходе эксперимента, тело размещается на плоскости под наклоном и вычисляется угол наклона. При этом необходимо учитывать, что при определении коэффициента трения покоя заданное тело начинает двигаться, а при определении коэффициента трения скольжения движется со скоростью, которая постоянна.Коэффициент трения можно также вычислить в ходе эксперимента. Необходимо поместить объект на наклонную плоскость и вычислить угол наклона. Таким образом, коэффициент трения определяется по формуле: μ=tg(α), где μ — сила трения, α – угол наклона плоскости.
Видео по теме
При относительном движении двух тел между ними возникает трение. Оно также может возникнуть при движении в газообразной или жидкой среде. Трение может как мешать, так и способствовать нормальному движению. В результате этого явления на взаимодействующие тела действует сила трения.

Инструкция
Наиболее общий случай рассматривает силу трения скольжения, когда одно из тел закреплено и покоится, а другое скользит по его поверхности. Со стороны тела, по которому скользит движущееся тело, на последнее действует сила реакции опоры, направленная перпендикулярно плоскости скольжения. Эта сила обозначается буквой N.Тело может также и покоится относительно закрепленного тела. Тогда сила трения, действующая на него FтрВ случае движения тела относительно поверхности закрепленного тела сила трения скольжения становится равна произведения коэффициента трения на силу реакции опоры: Fтр = ?N.
Если поверхность расположена горизонтально, то сила реакции опоры по модуля равна силе тяжести, действующей на тело, то есть N = mg, где m — масса скользящего тела, g — ускорение свободного падения, равное примерно 9,8 м/(с^2) на Земле. Отсюда, Fтр = ?mg.Пусть теперь на тело действует постоянная сила F>Fтр = ?N, параллельная поверхности соприкасающихся тел. При скольжении тела, результирующая составляющая силы в горизонтальном направлении будет равна F-Fтр. Тогда по второму закону Ньютона, ускорение тела будет связано с результирующей силой по формуле: a = (F-Fтр)/m. Отсюда, Fтр = F-ma. Ускорение тела можно найти из кинематических соображений.
Часто рассматриваемый частный случай силы трения проявляется при соскальзывании тела с закрепленной наклонной плоскости. Пусть ? — угол наклона плоскости и пусть тело соскальзывает равномерно, то есть без ускорения. Тогда уравнения движения тела будут выглядеть так: N = mg*cos?, mg*sin? = Fтр = ?N. Тогда из первого уравнения движения силу трения можно выразить как Fтр = ?mg*cos?.Если тело движется по наклонной плоскости с ускорением a, то второе уравнение движение будет иметь вид: mg*sin?-Fтр = ma. Тогда Fтр = mg*sin?-ma.
Видео по теме
Если сила, направленная параллельно поверхности, на которой стоит тело, превышает силу трения покоя, то начнется движение. Оно будет продолжаться до тех пор, пока движущая сила будет превышать силу трения скольжения, зависящую от коэффициента трения. Рассчитать этот коэффициент можно самостоятельно.

Вам понадобится
- Динамометр, весы, транспортир или угломер
Инструкция
Найдите массу тела в килограммах и установите его на ровную поверхность. Присоедините к нему динамометр, и начинайте двигать тело. Делайте это таким образом, чтобы показатели динамометра стабилизировались, поддерживая постоянную скорость движения. В этом случае сила тяги, измеренная динамометром, будет равна с одной стороны силе тяги, которую показывает динамометр, а с другой стороны силе тяжести, умноженной на коэффициент трения скольжения. Сделанные измерения позволят найти данный коэффициент из уравнения. Для этого поделите силу тяги на массу тела и число 9,81 (ускорение свободного падения) μ=F/(m•g). Полученный коэффициент трения скольжения будет один и тот же для всех поверхностей такого же типа, как и те на которых производилось измерение. Например, если тело из дерева двигалось по деревянной доске, то этот результат будет справедлив для всех деревянных тел, двигающихся скольжением по дереву, с учетом качества его обработки (если поверхности шершавые, значение коэффициента трения скольжения измениться).Можно измерить коэффициент трения скольжения и другим способом. Для этого установите тело на плоскости, которая может менять свой угол относительно горизонта. Это может быть обыкновенная дощечка. Затем начинайте аккуратно поднимать ее за один край. В тот момент, когда тело придет в движение, скатываясь в плоскости как сани с горки, найдите угол ее уклона относительно горизонта. Важно, чтобы тело при этом не двигалось с ускорением. В этом случае, измеренный угол будет предельно малым, при котором тело начнет двигаться под действием силы тяжести. Коэффициент трения скольжения будет равен тангенсу этого угла μ=tg(α).
В общем случае, для нахождения коэффициента трения скольжения, силу трения поделите на силу реакции опоры, с которой тело давит на поверхность, на которой располагается
Видео по теме
Трение – процесс взаимодействия двух тел, вызывающий замедление движения при смещении друг относительно друга. Найти силу трения – значит определить величину воздействия, направленную в сторону, противоположную движению, по причине которой тело теряет энергию и, в конце концов, останавливается.

Инструкция
Сила трения – векторная величина, которая зависит от многих факторов: давление тел друг на друга, материалы, из которых они были изготовлены, скорость движения. Площадь поверхности при этом значения не имеет, поскольку чем она больше, тем больше взаимное давление (сила реакции опоры N), которая уже участвует в нахождении силы трения. Эти величины пропорциональны друг другу и связаны коэффициентом трения μ, который можно считать постоянной величиной, если большая точность расчетов не требуется. Итак, чтобы найти силу трения, нужно вычислить произведение:Fтр = μ•N.Приведенная физическая формула относится к трению, вызванному скольжением. Оно может быть сухим и влажным, если между телами присутствует жидкая прослойка. Силу трения всегда следует принимать во внимание при определении совокупности сил, действующих на тело, при решении задач.
Трение качения возникает при вращении одного тела по поверхности другого. Оно присутствует на границе соприкосновения тел, которая постоянно меняется. Тем не менее, сила трения постоянно противодействует движению. Исходя из этого, она равна соотношению произведения коэффициента трения качения и прижимающей силы к радиуса вращающегося тела:Fтркач = f•N/r.
Следует различать коэффициента трения скольжения и качения. В первом случае это величина, не имеющая размерности, во втором она представляет собой расстояние между прямыми линиями, характеризующими направление прижимающей силы и силы реакции опоры. Следовательно, она измеряется в мм.
Коэффициент трения качения – это, как правило, известная величина для распространенных материалов. Например, для железа по железу он равен 0,51 мм, для железа по дереву – 5,6, дерева по дереву – 0,8-1,5 и т.д. Найти его можно по формуле соотношения момента трения к прижимающей силе.
Сила трения покоя появляется при минимальных перемещениях тел или деформации. Эта сила всегда присутствует при сухом скольжении. Максимальное ее значение равно μ•N. Существует также внутреннее трение, внутри одного тела между его слоями или частями.
Обратите внимание
Равномерное движение тела характеризуется равновесием между внешней силой и силой трения.
www.kakprosto.ru
Репетитор-онлайн — подготовка к ЦТ
Пример 21. По дну водоема, наклоненному под углом 60° к горизонту, начинает скользить тело массой 10 кг, полностью находящееся в воде. Найти модуль равнодействующей всех сил, приложенных к телу, если между телом и дном водоема воды нет, а коэффициент трения составляет 0,15.
Решение. Так как между телом и дном водяная прослойка отсутствует, то сила Архимеда на тело не действует.
Искомой величиной является модуль векторной суммы всех сил, приложенных к телу:
F→=F→тр+mg→+N→,
где N→ — сила нормальной реакции опоры; mg→ — сила тяжести; F→тр — сила трения. Указанные силы и система координат изображены на рисунке.
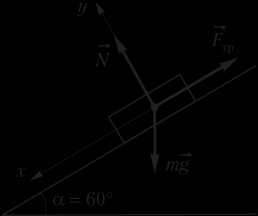
Вычисление модуля результирующей силы F проведем в соответствии с алгоритмом.
1. Определим проекции сил, приложенных к телу, на координатные оси:
проекция силы трения
Fтрx=−Fтр=−μN;
проекция силы тяжести
(mg)x=mgsin60°=0,53mg;
проекция силы реакции опоры
N x = 0;
проекция силы трения
Fтр y=0;
проекция силы тяжести
(mg)y=−mgcos60°=−0,5mg;
проекция силы реакции опоры
N y = N,
где m — масса тела; g — модуль ускорения свободного падения; µ — коэффициент трения.
2. Вычислим проекции равнодействующей на координатные оси, суммируя соответствующие проекции указанных сил:
Fx=Fтр x+(mg)x=−μN+0,53mg;
Fy=(mg)y+Ny=−0,5mg+N.
Движение по оси Oy отсутствует, т.е. F y = 0, или, в явном виде:
−0,5mg+N=0.
Отсюда следует, что
N=0,5mg,
что позволяет получить формулу для расчета силы трения:
Fтр=μN=0,5μmg.
3. Искомое значение равнодействующей:
F=Fx2+Fy2=|Fx|=−0,5μmg+0,53mg=0,5mg(3−μ).
Произведем вычисление:
F=0,5⋅10⋅10(3−0,15)=79 Н.
vedy.by
Примеры расчета опорных реакций. Основы сопромата, расчетные формулы
На тело человека, идущего или бегущего по поверхности Земли, действуют извне аэродинамические силы сопротивления атмосферы, силы реакции опоры.
Аэродинамические силы распределены по поверхности тела и возрастают приблизительно пропорционально площади фронтальной проекции поверхности тела и квадрату скорости движения.
Одной из наиболее существенных сил является сила реакции опорной поверхности, воздействующая на стопы человека. В соответствии с кинетостатическим принципом Д»Аламбера, эти силы равны и противоположны силам аэродинамического сопротивления, весу частей тела и силам инерции, появляющимся в теле вследствие изменения скоростей движения его частей. Поэтому величина опорных реакций может служить своеобразным индикатором, показывающим одновременное действие всех сил на организм при локомоции.
В течение опорного времени тело человека получает необходимый импульс, являющийся результатом активного действия мускулатуры.
Опорные реакции неравномерно распределены на некоторой сравнительно небольшой площади контакта между стопой и поверхностью опоры. Распределение изменяется в течение времени опоры: вначале давление создается на пятку, затем при постановке всей стопы на опору оно возникает в области плюсневых костей (см. рис. 15.19) и здесь в момент отталкивания от опоры давление достигает максимальной величины. Местоположение максимума давления на стопу изменяется при изменении темпа локомоции, вида локомоции (бег, прыжки, ходьба и пр.). Наиболее часто этот максимум располагается посредине стопы в районе головок плюсневых костей (см. рис. 15.19).
По правилам механики силовое взаимодействие между стопой и опорой может быть представлено одним равнодействующим вектором силы и одним равнодействующим вектором момента сил (см. рис. 15.19). При измерениях с помощью динамометрических платформ, установленных на одном уровне с опорной поверхностью, регистрируются шесть эквивалентных компонент этих двух векторов. Из них три компоненты являются проекциями вектора равнодействующей силы: вертикальная сила — это проекция на нормаль к поверхности платформы (совпадающая с гравитационной вертикалью),
продольная и боковая силы — проекции, расположенные в горизонтальной плоскости, соответственно, по направлению движения и перпендикулярно направлению движения тела (рис. 15.20). Остальные три компоненты — это проекции равнодействующего вектора момента сил на те же направления. Так как продольная и боковая компоненты момента сил зависят только от величины вертикальной силы и от значения координат предполагаемой точки приложения этой силы на плоскости динамометрической платформы, то, приравнивая указанные компоненты момента нулю, находят уравнение для вычисления двух координат точки приложения вертикальной силы.
При ходьбе графики компонент опорной реакции имеют два максимума (рис. 15.21). Первый максимум удерживает тело от падения вперед и возникает на опоре приблизительно в конце отталкивания с носка противоположной ноги. Сила реакции опоры приложена к пятке тормозящей ноги и направлена вверх-назад и слегка внутрь стопы. Момент сил во время опоры на пятку сравнительно
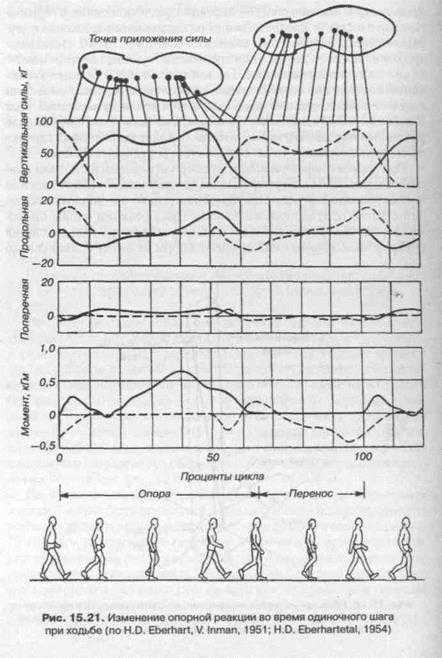 |
невелик, а направление его действия выражено нечетко. Второй максимум на графиках компонент опорных реакций, названный задним толчком, возникает в конце опорной фазы ноги приблизительно перед началом перенесения опоры на противоположную ногу. При заднем толчке реакция опоры приложена в области плюсне-фаланговых суставов и направлена вверх-вперед и слегка внутрь стопы. Преодолевая инерцию тела и вес, эта сила разгоняет тело в направлении движения, а также способствует боковому движению в сторону противоположной ноги, пятка которой ставится на опору.
Между главными максимумами находится пауза в изменениях величины опорной реакции. В это время стопа полностью стоит на опоре и в некоторый момент времени, названный моментом вертикали, тело находится над стоящей стопой, а переносная нога проходит рядом с опорой. Сила реакции опоры приложена вблизи середины стопы и направлена вертикально вверх. Момент сил реакции опоры препятствует развороту стопы носком наружу.
Отмечены небольшие величины боковой силы и момента сил. Это связано с тем, что локомоции осуществляются преимущественно в сагиттальной плоскости, а небольшие боковые силы возникают из-за стремления тела компенсировать небольшие отклонения от сагиттального направления.
Вертикальная и продольная силы опорной реакции, а также некоторые кинематические характеристики, зарегистрированные современными способами тензометрирования и осциллографиро-вания, показаны на рис. 15.21 и рис. 15.22.
Движения общего центра тяжести (ОЦТ) тела и перемещение тела в целом. Компоненты силы опорной реакции связаны с движением ОЦТ при локомоциях. Если пренебречь незначительным аэродинамическим сопротивлением, то из принципа Д»Аламбера следует, что компоненты F . и F. векторов равнодействующих сил опорной реакции на стопах правой и левой ног зависят от ускорения Wi центра тяжести тела следующим образом: т W. = F n . + F M — G r (i = 1, 2, 3), где т — масса и G — вес тела.
Из этой зависимости могут быть выведены, в частности, некоторые общие свойства вертикальной силы при локомоциях. После однократного интегрирования по времени одиночного шага получим уравнение для проекции импульсов сил на гравитационную вертикаль:
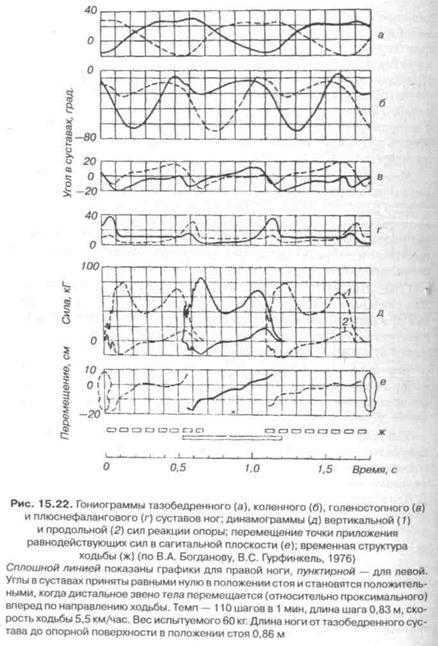 |

Отмечено, что за одиночный шаг среднее по времени значение вертикальных сил равно весу тела и это физически очевидно, так как иначе тело опускалось бы или поднималось. Точно так же выявлено, что средние значения продольных и боковых сил, а также момента сил реакции опоры приблизительно равны нулю.
Если учесть одновершинный, близкий к треугольнику, характер изменения вертикальной силы при беге и наличие фазы полета, то на основании данных формул можно получить следующее ориентировочное правило для оценки величины вертикальной силы при локомоциях человека: при ходьбе F 3 2G, при беге F > 2G. Двойное интегрирование исходной зависимости для действующих сил по времени дает точные значения величин перемещения общего центра тяжести тела в пространстве. Эти исследования были выполнены при ходьбе (G. Demeny, 1887; Н. Elftman, 1938; G А Са-vagna, R. Margaria, 1966; V. Ihman, 1966) и беге (W.O Fenn 1930″ Н. Elftman, 1940 и др.).
Пт ССЛеД0ВаНИЯ многих авторов показывают, что центр тяжести ЩТ) перемещается подобно шарику в желобе с полуэллиптическим сечением, занимая наивысшее положение на правой или левой стенке желоба в момент вертикали и наинизшее на дне желоба — во время двойной опоры. Кривая перемещения ЦТ напоминает синусоиду, причем ее амплитуда составляет от 4 до 6 см.
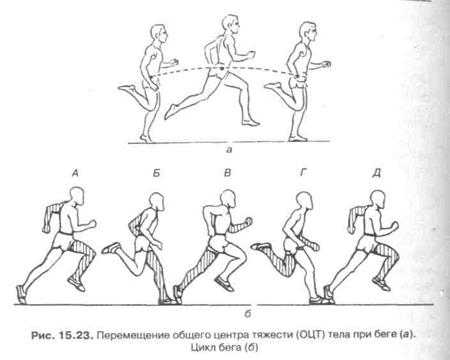
При беге ЦТ перемещается как бы по стенке перевернутого желоба и занимает свое самое низкое положение во время опоры и самое высокое положение в середине свободного полета тела фис. 15.23). На проекции сбоку кривая перемещений ЦТ, так же
|
как и при ходьбе, напоминает синусоиду. Однако ее амплитуда, как следует из ориентировочного правила для величин опорных реакций при локомоциях, больше, чем при ходьбе, и составляет приблизительно 10-12 см (Д.А. Семенов, 1939; Н.А. Бернштёйн и др., 1940; J. Saunders et al. 1953).
Следует отметить, что исследования движений ОЦТ тела иногда выявляют небольшую асимметрию ходьбы у здоровых людей, эта асимметрия резко возрастает у больных (J. Gersten et al, 1969), и ее регистрация вместе с наблюдением других кинематических нарушений может служить диагностическим целям (М. Murray, 1967; М.П. Полян, А.С. Витензон, 1969; и др.).
Периодичность траектории движения ОЦТ тела характеризуется не только временем цикла, но и расстоянием, на которое ЦТ сместится в пространстве за время локомоторного цикла, и, в частности, за время двойного шага.
Ихнографическим методом исследования установлено, что следы стоп при ходьбе располагаются на следовой дорожке иначе, чем
при беге (Д.А. Семенов, 1939; D.P. Roche, 1972 и др.). Во время нормальной ходьбы стопа ставится на опору с пятки, но пр
starer.ru
Как найти силу реакции опоры
Автор КакПросто!
Сила реакции опоры относится к силам упругости, и всегда направлена перпендикулярно поверхности. Она противостоит любой силе, которая заставляет тело двигаться перпендикулярно опоре. Для того чтобы рассчитать ее нужно выявить и узнать числовое значение всех сил, которые действуют на тело, стоящее на опоре.

Статьи по теме:
Вам понадобится
- — весы;
- — спидометр или радар;
- — угломер.
Инструкция
Определите массу тела с помощью весов или любым другим способом. Если тело находится на горизонтальной поверхности (причем неважно, движется оно или пребывает в состоянии покоя), то сила реакции опоры равна силе тяжести действующей на тело. Для того чтобы рассчитать ее умножьте массу тела на ускорение свободного падения, которое равно 9,81 м/с² N=m•g.Когда тело движется по наклонной плоскости, направленной под углом к горизонту, сила реакции опоры находится под углом в силе тяжести. При этом она компенсирует только ту составляющую силы тяжести, которая действует перпендикулярно наклонной плоскости. Для расчета силы реакции опоры, с помощью угломера измерьте угол, под которым плоскость располагается к горизонту. Рассчитайте силу реакции опоры, перемножив массу тела на ускорение свободного падения и косинус угла, под которым плоскость находится к горизонту N=m•g•Cos(α).
В том случае, если тело движется по поверхности, которая представляет собой часть окружности с радиусом R, например, мост, пригорок то сила реакции опоры учитывает силу, действующую по направлению из центра окружности, с ускорением, равным центростремительному, действующую на тело. Чтобы рассчитать силу реакции опоры в верхней точке, от ускорения свободного падения отнимите отношение квадрата скорости к радиусу кривизны траектории.Получившееся число умножьте на массу движущегося тела N=m•(g-v²/R). Скорость должна быть измерена в метрах в секунду, а радиус в метрах. При определенной скорости значение ускорения, направленного от центра окружности, может сравняться, и даже превысить ускорение свободного падения, в этот момент сцепление тела с поверхностью пропадет, поэтому, например, автомобилистам, нужно четко контролировать скорость на таких участках дороги.
Если же кривизна направлена вниз, и траектория тела вогнутая, то рассчитайте силу реакции опоры, прибавив к ускорению свободного падения отношение квадрата скорости и радиуса кривизны траектории, а получившийся результат умножьте на массу тела N=m•(g+v²/R).
Если известна сила трения и коэффициент трения, силу реакции опоры рассчитайте, поделив силу трения на этот коэффициент N=Fтр/μ.
Совет полезен?
Распечатать
Как найти силу реакции опоры
Статьи по теме:
Не получили ответ на свой вопрос?
Спросите нашего эксперта:
www.kakprosto.ru