Как отследить динамику роста в Microsoft Excel – База знаний Timeweb Community

Сравнение показателей в таблице за определенный период – одна из популярных задач, которая стоит перед пользователями Microsoft Excel. Чаще всего это осуществляется путем вывода вспомогательного столбца, где значения указаны в процентах, и сразу становится понятно, насколько сильной была позитивная или негативная динамика.

В этой статье я на простом примере предлагаю разобраться с соответствующим оформлением таблицы.

Предварительные действия

Сначала понадобится подготовить таблицу, чтобы кроме ввода функций далее от вас ничего не требовалось. Выберите два общих значения, которые будете сравнивать. Если это должна быть, например, месячная выручка, сначала сделайте сводную таблицу по дням и ссылайтесь на нее при создании общей суммы. Выведите два значения, динамику между которыми нужно сравнивать, чтобы перейти далее. На изображении ниже показан самый простой пример подходящей таблицы.

Создайте вспомогательный столбец для вывода процентов. Введите для него совершенно любое удобное для вас название и задайте визуальное оформление в соответствии со стилем основной таблицы.

Сейчас стоит учитывать, что тип ячейки, в которой будут отображаться проценты, является общим. При расчетах в таком случае появится очень большое значение в виде обычного числа. Поэтому понадобится изменить формат ячеек, чтобы проценты выводились корректно.

1. Для этого выделите необходимые ячейки и щелкните по любой из них правой кнопкой мыши. Из контекстного меню выберите пункт

   «Формат ячеек».

2. Отобразится отдельное окно, в котором будет выбрана вкладка «Число». На ней выберите «Процентный» и определите количество знаков после запятой или оставьте его по умолчанию. После этого сохраните новый формат ячейки.

На этом подготовительные действия завершены, поэтому можно приступить к заполнению формул и вычислении положительной или негативной динамики.

Комьюнити теперь в Телеграм

Подпишитесь и будьте в курсе последних IT-новостей

Подписаться

Создание формулы отслеживания динамики роста

В следующей инструкции я постараюсь наглядно описать каждое действие при написании функции, чтобы вы понимали, какие значения берутся, как они сравниваются и что получается в итоге. Если вы сделали таблицу такого же формата, как и в примере, достаточно будет выполнить точно такие же действия, чтобы отследить динамику роста в процентах.

1. Выделите ячейку, где должны выводиться проценты и напишите первую часть формулы =(C2 — B2). Это поможет определить разницу между суммами за два разных месяца. Соответственно, если номера ячеек в вашей таблице другие, замените их, отняв сумму второго значения от первого.

2. После скобок добавьте /B2, чтобы разделить это все на сумму первого значения, то есть на 100%, если говорить о стандартных математических операциях с процентами.

3. Нажмите Enter и посмотрите на результат. В моем случае сумма за первый месяц была 102 000, за второй — 124 000, а разница – 22 000. Получается, динамика роста является положительной и равняется 21,62%. У вас значение будет другим, в соответствии с суммами в таблице.

4. Если далее в таблице должно происходить такое же сравнение значений и вывод процентов, просто зажмите левой кнопкой мыши правый угол текущей ячейки и растяните ее вниз.

5. В итоге таблица сама заполнится, и на экране появится список всех процентов, характеризующих положительную или отрицательную динамику роста.

Далее ничего вас не ограничивает, вы можете сравнивать показатели бесконечное количество раз. Отнимать и добавлять проценты, чтобы понять общую сумму изменений и заниматься дальнейшим взаимодействием с электронной таблицей для своих целей.

Формула отслеживания динамики роста по норме

Иногда расчеты подразумевают наличие нормы, то есть средневзвешенной суммы, которая является оптимальной. Вы можете использовать только это значение, чтобы сравнить его с другими показателями и вычислить проценты. Давайте наглядно разберемся с изменениями, которые вносятся в этом типе расчетов.

1. Найдите ту ячейку, где будет указана норма. Если ее еще нет, создайте и введите необходимое число. Формула будет немного отличаться от предыдущей. Вам нужно в качестве первого значения как раз и задать эту ячейку, полностью закрепив ее при помощи знаков $.

2. Больше никаких изменений вводить не нужно, достаточно нажать Enter, чтобы ознакомиться с результатом.

3. При растягивании формула тоже будет считаться корректно, поскольку ранее вы полностью закрепили одну ячейку.

В этом случае формула обретает вид =(C2-$B$9)/$B$9, где $B$9 – номер той самой закрепленной ячейки, а C2 – сумма второго месяца, от которой и отнимается норма для вычисления процентов.

На основе созданной таблицы вы можете добавлять наглядный график, визуально демонстрирующий динамику роста. Детальнее о его создании рассказано в другой моей статье по ссылке ниже.

Подробнее: Как создать диаграмму темпов роста в Microsoft Excel

Средние показатели динамики: уровень ряда, абсолютный прирост, темп роста

Средний уровень ряда определяет обобщенную величину абсолютных уровней. Он определяется по средней, исчисленной из значений, меняющихся во времени. Методы расчета среднего уровня интервального и моментного рядов динамики разные.

Средний уровень из абсолютных уровней для интервальных рядов динамики рассчитывается по формуле средней арифметической:

1. При равных интервалах используют среднюю арифметическую простую:

где у — абсолютные уровни ряда;

n — число уровней ряда.

2. При неравных интервалах используют среднюю арифметическую взвешенную:

где у1,…,уn — уровни ряда динамики;

t1,… tn — веса, длительность интервалов времени.

Средний уровень моментного ряда динамики рассчитывается по формуле:

1. С равностоящими уровнями рассчитывается по формуле средней хронологической моментного ряда:

где у1,…,уn — уровни периода, за который делается расчет;
n — число уровней;
n-1 — длительность периода времени.

2. С неравностоящими уровнями рассчитывается по формуле средней хронологической взвешенной:

где у1,…,уn — уровни рядов динамики;
t — интервал времени между смежными уровнями

Средний абсолютный прирост в задачах статистики

Средний абсолютный прирост определяется как среднее из абсолютных приростов за равные промежутки времени одного периода. Он рассчитывается по формулам:

1. По цепным данным об абсолютных приростах за ряд лет рассчитывают средний абсолютный прирост как среднюю арифметическую простую:

где n — число степенных абсолютных приростов в исследуемом периоде.

2. Средний абсолютный прирост рассчитывают через базисный абсолютный прирост в случае равных интервалов

где m — число уровней ряда динамики в исследуемом периоде, включая базисный.

Средний темп роста

Средний темп роста есть свободная обобщающая характеристика интенсивности изменения уровней ряда динамики и показывает, во сколько раз в среднем за единицу времени изменяется уровень ряда динамики.

В качестве основы и критерия правильности вычисления среднего темпа роста (снижения) применяется обобщающий показатель, который рассчитывается как произведение цепных темпов роста, равное темпу роста за весь рассматриваемый период. Если значение признака образуется как произведение отдельных вариантов, то используют среднюю геометрическую.

Так как средний темп роста представляет собой средний коэффициент роста, выражен в процентах, то для равностоящих рядов динамики расчеты по средней геометрической сводятся к вычислению средних коэффициентов роста из цепных по «цепному способу»:

где n — число цепных коэффициентов роста;
Кц — цепные коэффициенты роста;
Кб — базисный коэффициент роста за весь период.

Определение среднего коэффициента роста может быть упрощено, если будут ясны уровни динамического ряда. Так как произведение цепных коэффициентов роста равно базисному, то в подкоренное выражение подставляют базисный коэффициент роста.

Формула для определения среднего коэффициента роста для равностоящих рядов динамики по «базисному способу» будет такая:

Средний темп прироста

Средние темпы прироста рассчитываются на основе средних темпов роста (Тр) вычитанием из последних 100%:

Для того чтобы определить средний коэффициент прироста (Кпр), нужно из значений коэффициентов роста (Кр) вычесть единицу.

Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.

14.7: Гидродинамика — Физика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

4059

• OpenStax
• OpenStax

Цели обучения

• Описать характеристики потока
• Рассчитать расход
• Опишите взаимосвязь между расходом и скоростью
• Объясните следствия уравнения неразрывности для сохранения массы

Первая часть этой главы посвящена статике жидкости, изучению покоящихся жидкостей. Остальная часть этой главы посвящена гидродинамике, изучению движения жидкостей. Даже самые простые формы движения жидкости могут быть довольно сложными. По этой причине мы ограничим наше исследование идеальные жидкости во многих примерах. Идеальная жидкость — это жидкость с пренебрежимо малой вязкостью . Вязкость — это мера внутреннего трения в жидкости; мы рассмотрим его более подробно в разделе «Вязкость и турбулентность». В нескольких примерах мы исследуем несжимаемую жидкость, для изменения объема которой требуется чрезвычайно большая сила, поскольку плотность в несжимаемой жидкости постоянна на всем протяжении.

Характеристики потока

Векторы скорости часто используются для иллюстрации движения жидкости в таких приложениях, как метеорология. Например, ветер — текучее движение воздуха в атмосфере — может быть представлен векторами, указывающими скорость и направление ветра в любой заданной точке на карте. На рисунке \(\PageIndex{1}\) показаны векторы скорости, описывающие ветры во время урагана Артур в 2014 г.

Рисунок \(\PageIndex{1}\): Векторы скорости показывают направление ветра во время урагана Артур. Обратите внимание на циркуляцию ветра вокруг глаза урагана. Скорость ветра максимальна вблизи глаз. Цвета представляют относительную завихренность, меру вращения или вращения воздуха.

Другим методом представления движения жидкости является линия тока . Линия тока представляет собой путь небольшого объема жидкости при ее течении. Скорость всегда тангенциальна к линии тока. На диаграммах на рисунке \(\PageIndex{2}\) линии тока используются для иллюстрации двух примеров движения жидкостей по трубе. Первая жидкость имеет ламинарный поток (иногда описываемый как установившийся поток), представленный гладкими параллельными линиями тока. Обратите внимание, что в примере, показанном в части (а), скорость жидкости максимальна в центре и уменьшается у стенок трубы из-за вязкости жидкости и трения между стенками трубы и жидкостью. Это особый случай ламинарного потока, когда трение между трубой и жидкостью велико, что известно как граничные условия отсутствия проскальзывания.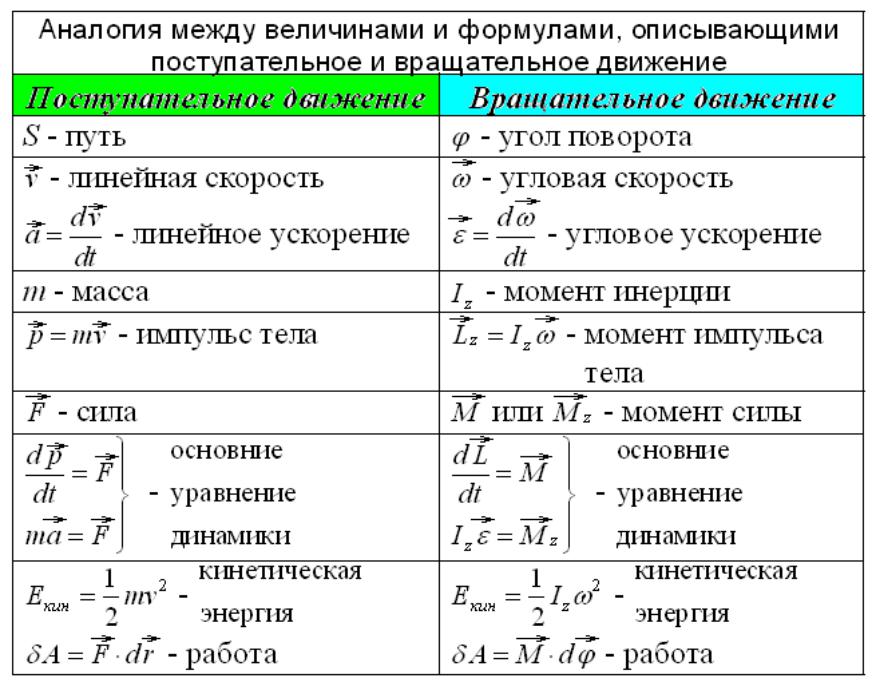 Вторая диаграмма представляет турбулентный поток , в котором линии тока нерегулярны и меняются со временем. В турбулентном потоке пути потока жидкости нерегулярны, поскольку различные части жидкости смешиваются друг с другом или образуют небольшие круглые области, напоминающие водовороты. Это может произойти, когда скорость жидкости достигает определенной критической скорости.

Рисунок \(\PageIndex{2}\): (a) Ламинарный поток можно представить себе как слои жидкости, движущиеся по параллельным правильным траекториям. (b) В турбулентном потоке области жидкости движутся нерегулярными, встречными путями, что приводит к перемешиванию и завихрению.

Скорость потока и его связь со скоростью

Объем жидкости, проходящей через заданное место через площадь в течение определенного периода времени, называется скоростью потока \(Q\), или, точнее, объемной скоростью потока. Символами это записывается как

\[Q = \frac{dV}{dt} \label{14.13}\]

, где \(V\) — объем, а \(t\) — прошедшее время. На рисунке \(\PageIndex{3}\) объем цилиндра равен \(Ax\), поэтому расход равен

\[Q = \frac{dV}{dt} = \frac{d}{ dt} (Ax) = A \frac{dx}{dt} = Av \ldotp\]

Единицей расхода в системе СИ является м ³ /с, но широко используются и другие единицы измерения \(Q\), например, литры в минуту (л/мин). Обратите внимание, что литр (л) равен 1/1000 кубического метра или 1000 кубических сантиметров (10 ⁻³ м ³ или 10 ³ см ³ ).

Рисунок \(\PageIndex{3}\): Расход — это объем жидкости, протекающей мимо точки через площадь \(A\) в единицу времени. Здесь заштрихованный цилиндр жидкости течет мимо точки \(P\) по однородной трубе за время \(t\).

Расход и скорость являются связанными, но совершенно разными физическими величинами. Чтобы прояснить различие, рассмотрим скорость течения реки. Чем больше скорость воды, тем больше расход реки. Но скорость течения также зависит от размера и формы реки. Быстрый горный поток несет гораздо меньше воды, чем, например, река Амазонка в Бразилии.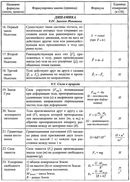 На рисунке \(\PageIndex{3}\) показан объемный расход. Объемный расход равен \(Q = \frac{dV}{dt} = Av\), где A — площадь поперечного сечения трубы, а v — величина скорости.

Точное соотношение между расходом \(Q\) и средней скоростью \(v\) равно

\[Q = Av,\]

где \(A\) — площадь поперечного сечения и \(v \) — средняя скорость. Соотношение говорит нам, что скорость потока прямо пропорциональна как средней скорости жидкости, так и площади поперечного сечения реки, трубы или другого трубопровода. Чем больше трубопровод, тем больше его площадь поперечного сечения. На рисунке \(\PageIndex{3}\) показано, как получается это отношение. Заштрихованный цилиндр имеет объем \(V = Ad\), который проходит через точку \(P\) за время \(t\). Разделив обе части этого соотношения на \(t\), мы получим

\[\frac{V}{t} = \frac{Ad}{t} \ldotp \label{eq14.14A} \]

Заметим, что \(Q = \frac{V}{t}\ ), а средняя скорость равна \(v = \frac{d}{t}\). Таким образом, уравнение \ref{eq14.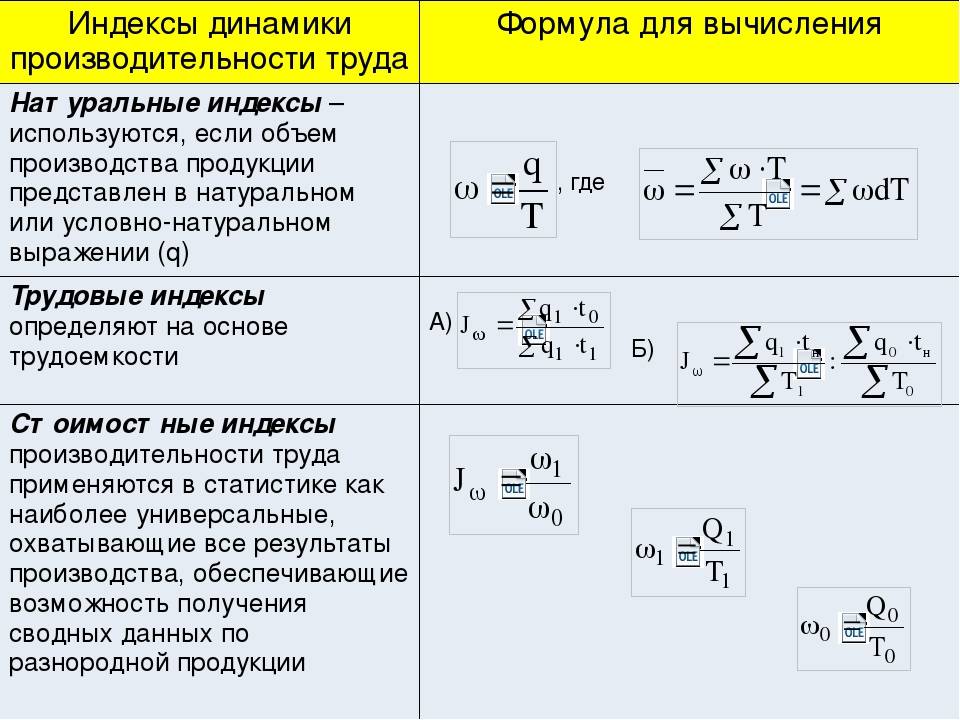 14A} принимает вид

\[Q = Av.\]

На рисунке \(\PageIndex{4}\) показана несжимаемая жидкость, текущая по трубе с уменьшающимся радиусом. Поскольку жидкость несжимаема, через любую точку трубки за заданное время должно пройти одинаковое количество жидкости, чтобы обеспечить непрерывность потока. Поток является непрерывным, потому что они не являются источниками или поглотителями, которые добавляют или удаляют массу, поэтому масса, втекающая в трубу, должна быть равна массе, вытекающей из трубы. В этом случае, поскольку площадь поперечного сечения трубы уменьшается, скорость обязательно должна увеличиваться. Эту логику можно расширить, чтобы сказать, что скорость потока должна быть одинаковой во всех точках трубы. В частности, для произвольных точек 1 и 2

\[\begin{split} Q_{1} & = Q_{2}, \\ A_{1} v_{1} & = A_{2} v_{2} \ldotp \end{split} \label{ 14.14}\]

Это называется уравнением неразрывности и справедливо для любой несжимаемой жидкости (с постоянной плотностью). Следствия уравнения неразрывности можно наблюдать, когда вода течет из шланга в узкую форсунку: она вытекает с большой скоростью — в этом назначение форсунки. И наоборот, когда река впадает в один конец водохранилища, вода значительно замедляется и, возможно, снова набирает скорость, когда выходит из другого конца водохранилища. Другими словами, скорость увеличивается, когда площадь поперечного сечения уменьшается, и скорость уменьшается, когда площадь поперечного сечения увеличивается.

Рисунок \(\PageIndex{4}\): Когда трубка сужается, тот же объем занимает большую длину. Чтобы один и тот же объем прошел точки 1 и 2 за заданное время, скорость должна быть больше в точке 2. Процесс точно обратим. Если жидкость течет в противоположном направлении, ее скорость уменьшается, когда трубка расширяется. (Обратите внимание, что относительные объемы двух цилиндров и соответствующие стрелки вектора скорости нарисованы не в масштабе.)

Поскольку жидкости практически несжимаемы, уравнение неразрывности справедливо для всех жидкостей. Однако газы сжимаемы, поэтому уравнение следует применять с осторожностью к газам, если они подвергаются сжатию или расширению.

Пример 14.5: Расчет скорости жидкости через насадку

Насадка диаметром 0,500 см присоединена к садовому шлангу радиусом 0,900 см. Скорость потока через шланг и сопло составляет 0,500 л/с. Рассчитайте скорость воды:

1. в шланге и
2. в форсунке.

Стратегия

Мы можем использовать соотношение между расходом и скоростью, чтобы найти обе скорости. Мы используем нижний индекс 1 для шланга и 2 для насадки. 9{2}} (1,96\; м/с) = 25,5\; м/с \ldotp$$

Значение

Скорость 1,96 м/с соответствует воде, вытекающей из шланга без насадки. Форсунка создает значительно более быстрый поток, просто сужая поток в более узкую трубку.

Решение последней части примера показывает, что скорость обратно пропорциональна квадрату радиуса трубы, что приводит к большим эффектам при изменении радиуса. Мы можем задуть свечу на довольно большом расстоянии, например, сжав губы, тогда как задувание свечи с широко открытым ртом совершенно неэффективно.

Сохранение массы

Скорость потока жидкости также может быть описана массовым расходом или массовым расходом. Это скорость, с которой масса жидкости движется мимо точки. Снова обратитесь к рисунку \(\PageIndex{3}\), но на этот раз рассмотрите массу в заштрихованном объеме. Массу можно определить из плотности и объема:

\[m = \rho V = \rho Ax \ldotp\]

Тогда массовый расход равен

\[\frac{dm}{dt} = \frac{d}{dt} (\rho Ax) = \rho A \frac{dx}{dt} = \rho Av,\]

где \(\rho\) — плотность, A — площадь поперечного сечения, а v — величина скорости. Массовый расход является важной величиной в гидродинамике и может использоваться для решения многих задач. Рассмотрим рисунок \(\PageIndex{5}\). Труба на рисунке начинается на входе с площадью поперечного сечения A ₁ и сужается до выхода с меньшей площадью поперечного сечения A ₂ . Масса жидкости, поступающей в трубу, должна быть равна массе жидкости, выходящей из трубы. По этой причине скорость на выходе (v ₂ ) больше, чем скорость на входе (v ₁ ). Используя тот факт, что масса жидкости, поступающей в трубу, должна быть равна массе жидкости, выходящей из трубы, можно найти связь между скоростью и площадью поперечного сечения, взяв скорость изменения массы в и массу выход:

\[\begin{split} \left(\dfrac{dm}{dt}\right)_{1} & = \left(\dfrac{dm}{dt}\right)_{2} \ \ \rho_{1} A_{1} v_{1} & = \rho_{2} A_{2} v_{2} \ldotp \end{split} \label{14.15}\]

Уравнение \ref{14.15} также известно как уравнение неразрывности в общем виде. Если плотность жидкости остается постоянной из-за сужения, т. е. жидкость несжимаема, то плотность сокращается из уравнения неразрывности,

\[A_{1} v_{1} = A_{2} v_{2} \ldotp\]

Уравнение сокращается, чтобы показать, что объемный расход в трубе равен объемному расходу на выходе из трубы.

Рисунок \(\PageIndex{5}\): Геометрия для вывода уравнения неразрывности. Количество жидкости, поступающей в площадь поперечного сечения (заштриховано), должно равняться количеству жидкости, выходящей из площади поперечного сечения, если жидкость несжимаема.

---

Эта страница под названием 14.7: Fluid Dynamics распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   ОпенСтакс

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Программа OER или Publisher

   ОпенСтакс

   Показать оглавление

   нет

2. Теги

   1. расход
   2. идеальная жидкость
   3. ламинарный поток
   4. источник@https://openstax. org/details/books/university-physics-volume-1
   5. турбулентный поток
   вязкость

Формулы и версии формул — Управление цепочками поставок | Динамика 365

• Статья
• 06.01.2023

Формула определяет материалы, ингредиенты и результаты конкретного процесса непрерывного производства. Вместе с соответствующим маршрутом формула определяет весь процесс непрерывного производства. Формулы используются для планирования и производства продуктов в непрерывном производстве.

Формула состоит из ингредиентов и количеств, необходимых для производства определенного количества продукта формулы. В зависимости от задачи, которую вы выполняете, вы можете получить доступ к функциям формулы из управления запасами и складом или управления информацией о продуктах.

Формулы и строки формул

Формула состоит из одной или нескольких строк формул, определяющих ингредиенты или элементы, из которых состоит формула. Строка формулы может содержать позиции спецификации (BOM), позиции формулы, позиции промежуточного веса, приобретенные позиции, сопутствующие продукты или побочные продукты. Поскольку многие элементы используются в нескольких продуктах, элемент может использоваться более чем в одной формуле.

Примером формулы является рецепт шоколадного печенья. Ингредиенты для этой формулы используют несколько линий, таких как мука, сахар, яйца, масло и шоколадная стружка. Формула шоколадного печенья содержит ингредиенты, которые, вероятно, используются в других формулах. Пока вы готовите печенье с шоколадной крошкой, могут остаться остатки, такие как крошки, или некоторые печенья могут быть перепеченными или недоваренными. Эти элементы могут быть настроены как сопутствующие продукты или побочные продукты, в зависимости от производственных операций.

При создании строки формулы вы используете тип строки, чтобы указать, как система должна обрабатывать строку при выполнении сводного планирования и создании партийных заказов. Каждый тип линии дает другой результат. В следующей таблице описаны типы линий, которые вы можете выбрать.

Тип линии	Описание
Товар	Выберите Товар , если товар является сырьем или полуфабрикатом, который выбирается из запасов, или когда товар является услугой.
Фантом	Выберите Phantom , если вы хотите расчленить любые элементы формул более низкого уровня, содержащиеся в строках формул. Когда вы оцениваете пакетный заказ и элементы формулы разнесены, компоненты компонентов отображаются в виде строк формулы в пакетном заказе. Кроме того, соответствующие маршруты добавляются к производственному маршруту. Элементы формулы расчленяются с использованием текущей конфигурации. Когда вы используете тип линии Phantom , вы можете обрабатывать конфигурации производства и измерения, которые возникают на разных уровнях рецептуры. Если вы выберете Phantom для продукта на экспресс-вкладке Engineer на странице Сведения о выпущенном продукте , а затем использовать этот продукт в формуле, тип строки формулы изменяется на Phantom . Вы не можете выбрать Фантом для товара промежуточного веса или для товаров с типом производства Сопутствующий продукт , Побочный продукт или Элемент планирования .
Поставка с привязкой	Select Ограниченная поставка , чтобы создать пакетный заказ, производственный заказ, канбан, заказ на перемещение или заказ на покупку для ингредиента, содержащегося в строке формулы. Связанный заказ определяется на основе настроек заказа по умолчанию и типа производства ингредиента и создается при оценке партии заказа.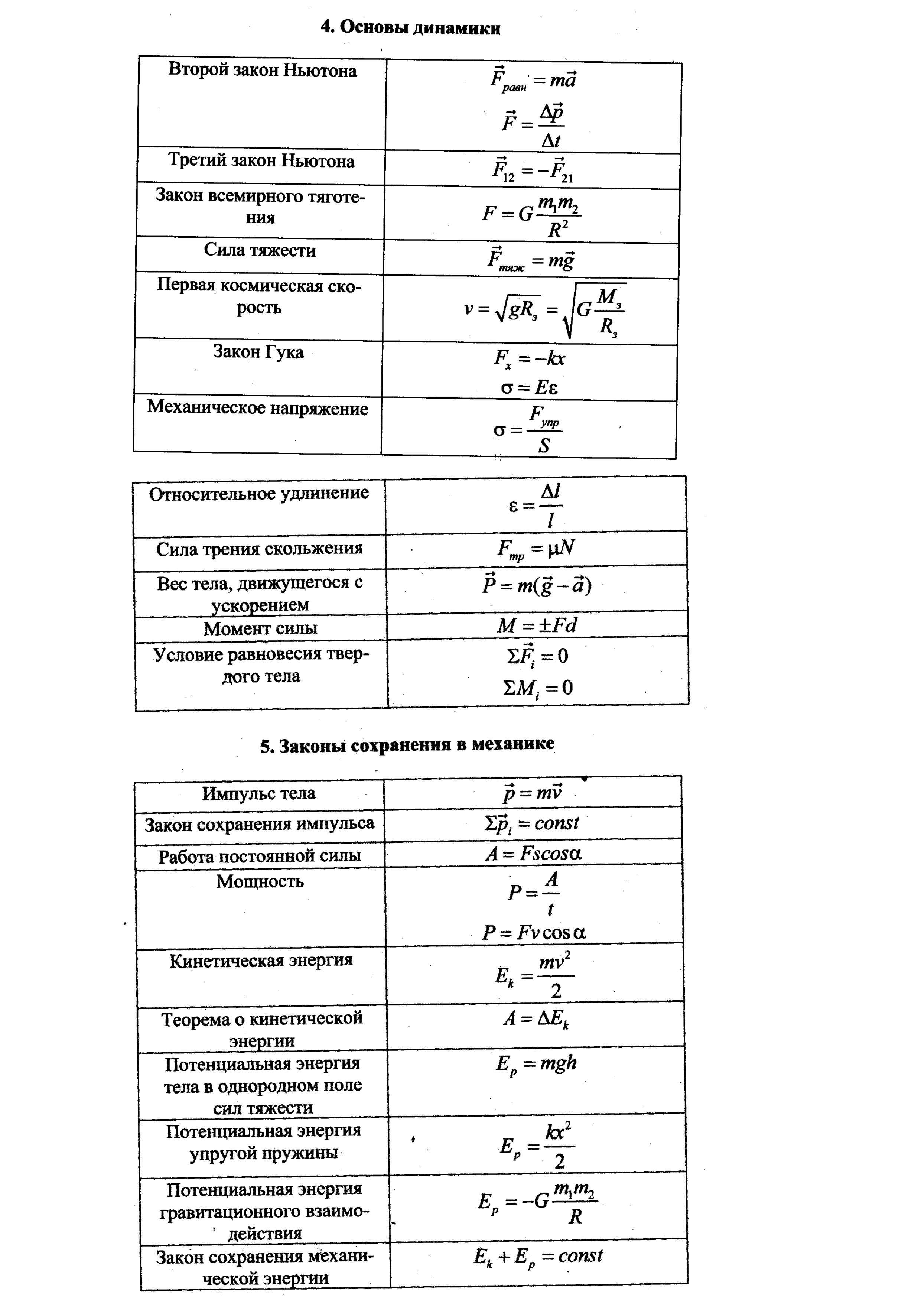 Требуемое количество ингредиентов зарезервировано для заказа партии.
Поставщик	Выберите Поставщик , если в производственном процессе используется субподрядчик, и вы хотите создать вспомогательное производство или заказ на покупку для субподрядчика. Услуга или работа, которую выполняет субподрядчик, должна быть создана с использованием позиции формулы или позиции услуги. Вы можете прикрепить элемент к родительскому элементу в виде строки формулы. Маршрут должен содержать операцию, назначенную операционному ресурсу субподрядчика. Эта операция прикрепляется к строке формулы с помощью Опер. Поле № .

Версии формулы

При создании новой формулы необходимо сначала создать версию формулы, прежде чем добавлять элементы строки формулы и их конкретные характеристики. Каждая формула должна иметь хотя бы одну версию. Кнопка Approved в версии формулы становится доступной только после успешного сохранения записи версии. Каждая запись версии формулы связана с одним или несколькими сопутствующими и побочными продуктами, которые могут производиться при производстве готового продукта. Многие продукты могут быть изготовлены из одних и тех же ингредиентов в партиях разного размера, в нескольких количествах или с разным выходом. Вы можете создать столько версий формулы, сколько вам нужно.

Для управления несколькими активными версиями формулы используйте диапазоны дат действия или поля количества «от». Несколько активных версий формулы могут существовать только в том случае, если диапазон дат и количество «от» не перекрываются.

В отличие от спецификаций, где одна спецификация часто связана со многими версиями спецификации, для каждой формулы обычно существует только одна версия формулы. Помните, что для размеров покрытия и количества для данного продукта можно активировать только одну версию формулы. Однако многие версии формул могут существовать по другим причинам, и их можно выбрать вручную при создании пакетного заказа.

Утверждение и активация формул и версий формул

Формулы и версии формул должны быть утверждены, прежде чем их можно будет использовать для планирования и производства. Формулы обычно активируются перед использованием. Однако во время производства вы можете выбрать версию формулы, которая утверждена, но не активирована.

Чтобы защитить формулу или версию формулы, можно установить параметры Редактирование блока и Удаление блока утверждения в Параметры управления производством стр.

Если вы выберете Редактирование блока и формула будет утверждена, никакие поля в строках формулы не могут быть удалены или отредактированы. Однако, если вы удалите утверждение формулы, вы можете удалить и изменить строки формулы. Вы также можете создавать новые формулы и новые версии формул.

Если выбрать Блокировать удаление утверждения , вы не сможете удалить утверждение утвержденной формулы или версии формулы. Однако вы можете создавать новые формулы и новые версии формул, а также удалять активацию версии формулы.

Вы можете добавить дополнительные уровни контроля, используя функцию электронной подписи. Если пользователь настроен так, что во время утверждения формулы требуется электронная подпись, при активации формулы появляется страница Подпись . Пользователь должен быть авторизован для электронной подписи, а сертификат должен быть успешно проверен, прежде чем изменение может быть зафиксировано. Если подпись не может быть аутентифицирована, утверждение или удаление утверждения отклоняется, а изменение, которое инициировало утверждение или удаление утверждения, возвращается в исходное состояние.

Использовать функцию «Масштабируемость»

Функция «Масштабируемость» доступна только в том случае, если для всех компонентов позиции в формуле установлено значение Переменное потребление . Эта функция недоступна, если для компонентов элемента задано значение Фиксированное потребление или Пошаговое потребление . При использовании функции «Масштабируемость» при изменении ингредиента в формуле корректируется количество других выбранных вами ингредиентов. Размер формулы также корректируется. Аналогичным образом, если вы измените размер формулы, изменится количество всех масштабируемых ингредиентов. Эта функция предназначена специально для создания и обслуживания формул. Он не указывает, будет ли количество ингредиента увеличиваться или уменьшаться в пакетном заказе.

Использование Поэтапное потребление

Поэтапное потребление устраняет необходимость ввода количества ингредиента на вкладке Строка формулы . Вместо этого шаг потребления настраивается таким образом, что он имеет значение Из серии и значение Количество . Выбирается информация из записи Шаговое потребление на серию, которая соответствует количеству в пакетном заказе. Пошаговое потребление полезно, когда уровень потребления не является линейным по отношению к размеру пакетного заказа и увеличивает потребность только при достижении определенного порога количества.