Глава 3. Динамика
Задачи на динамику часто входят в задания единого государственного экзамене по физике. Для решения этих задач необходимо понимать смысл законов Ньютона, уметь применять их в простейших ситуациях и знать свойства ряда сил: тяжести, трения, упругости и нескольких других.
Первый закон Ньютона определяет такие системы отсчета, в которых тело, не испытывающее воздействий со стороны других тел (сил), движется прямолинейно и равномерно. Такие системы отсчета называются инерциальными, а движение в отсутствии сил — движением по инерции.
Согласно второму закону Ньютона ускорение тела относительно инерциальных систем отсчета определяется из уравнения
(3.1) |
где — масса тела, — векторная сумма сил, действующих на тело (эту сумму часто называют равнодействующей или результирующей силой).
Третий закон Ньютона утверждает, что всегда существует взаимное действие тел друг на друга, причем силы, с которыми действуют друг на друга взаимодействующие тела, равны по величине и противоположны по направлению.
Чтобы использовать уравнение (3.1) для нахождения ускорений тел необходимо задать законы для действующих на них сил. Рассмотрим ряд сил, с которыми приходится сталкиваться в школьном курсе физики.
На любое тело, находящееся вблизи поверхности Земли действует сила притяжения со стороны Земли, которая называется силой тяжести. Эта сила пропорциональна массе тела и может быть записана в виде
(3.2) |
где — вектор ускорения свободного падения, величина которого равна м/с2 (в расчетах часто используют значение м/с2 ).
При соприкосновении тел возникают контактные взаимодействия. Сила, перпендикулярная поверхности и возникающая при контакте тела с этой поверхностью, называется силой нормальной реакции поверхности. При скольжении тела по поверхности или при попытке его сдвинуть возникает сила, параллельная поверхности, и препятствующая движению тела.
Если тело растягивает или сжимает пружину, на тело со стороны пружины действует сила, которая называется силой упругости. Свойства силы упругости определяются законом Гука, в котором утверждается, что сила упругости пропорциональна удлинению пружины
(3.3) |
Здесь — длина деформированной пружины, — длина этой пружины в недеформированном состоянии, — коэффициент пропорциональности, который называется коэффициентом жесткости (или просто жесткостью) пружины.
При движении тела в воздухе, воде или в другой среде на тело со стороны этой среды действует сила сопротивления, величина которой при небольших скоростях тела пропорциональна его скорости
(3.4) |
Здесь — скорость тела, — коэффициент пропорциональности, зависящий от свойств среды и геометрии тела. Для больших скоростей сила сопротивления определяется формулой . Направлена сила сопротивления противоположно скорости тела и тормозит его движение.
Для больших скоростей сила сопротивления определяется формулой . Направлена сила сопротивления противоположно скорости тела и тормозит его движение.
Рассмотрим теперь задачи.
В задаче 3.1.1 из второго закона Ньютона (3.1) заключаем, что данное тело движется равноускоренно 0,5 м/с2 (ответ 4).
Единицей силы является «Ньютон», который определяется посредством второго закона Ньютона (3.1): 1 Ньютон (1 Н) — это сила, которая телу массой 1 кг сообщает ускорение 1 м/с 2 (ответ 3).
В задаче 3.1.3 только один из четырех предложенных ответов говорит о связи силы с ускорением (ответ 3). Остальные варианты ответов говорят о связи силы и скорости, поэтому они не верны. Аналогичный вопрос (но поставленный графически) предлагается в задаче 3.1.4 Согласно второму закону Ньютона вектор результирующей силы направлен так же, как и вектор ускорения тела (ответ 3), а не как вектор скорости и тем более не как вектор суммы или разности скорости и ускорения (эти векторы вообще нельзя складывать, т.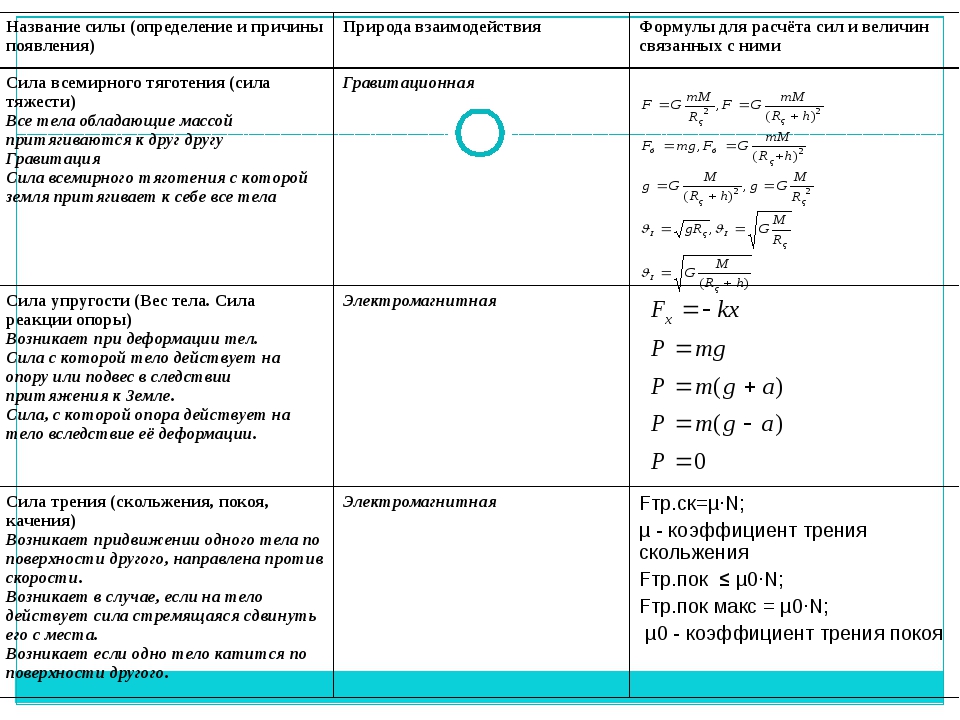 к. они имеют разные размерности).
к. они имеют разные размерности).
Несколько следующих задач посвящены простейшим вычислениям на основе второго закона Ньютона. В задаче 3.1.5 второй закон Ньютона в проекциях на вертикальную ось для тела, движущегося вместе с лифтом (т.е. с таким же ускорением) дает
где – сила реакции, действующая на тело со стороны пола (см. рисунок). Отсюда находимо силу реакции
(ответ 2).
Основная идея решения задачи 3.1.6 заключается в том, чтобы из данных кинематических характеристик движения (пути и времени) найти ускорение тела, а затем из второго закона Ньютона — силу. Из закона равноускоренного движения находим, что ускорение тела равно м/с2. Поэтому Н (правильный ответ — 3).
В задаче 3.1.7 нужно найти силу, которая сообщает телу массой ускорение, направленное вертикально вверх и вдвое превосходящее по величине ускорение свободного падения. Поскольку на рассматриваемое тело действуют только искомая сила и сила тяжести (см. рисунок), второй закон Ньютона для этого тела в проекциях на вертикальную ось дает
Поскольку на рассматриваемое тело действуют только искомая сила и сила тяжести (см. рисунок), второй закон Ньютона для этого тела в проекциях на вертикальную ось дает
Поскольку , из этой формулы находим, что (ответ 3).
В задаче 3.1.8 второй закон Ньютона в проекциях на горизонтальную ось дает
(см. рисунок). Отсюда находим, что м/с2 (ответ 1).
В задаче 3.1.9 проверяется понимание школьником векторного характера второго закона Ньютона. Из закона (3.1) следует, что величина ускорения тела определяется величиной (модулем) равнодействующей силы:
Находя величину равнодействующей силы
получим м/с2 (ответ 4).
Равнодействующей двух сил называется их векторная сумма. Из закона векторного сложения заключаем, что величина суммы векторов не может превосходить суммы величин векторов-слагаемых, и обязательно больше их разности. Поэтому величина равнодействующей сил 30 и 10 Н в задаче 3.1.10 не может равняться 19 Н (ответ 3).
По третьему закону Ньютона силы, с которыми мальчики в задаче 3.2.1 действуют друг на друга, равны. Поэтому массы и ускорения мальчиков связаны соотношением . Отсюда находим ускорение второго мальчика м/с2 (ответ 2).
Поскольку силы, действующие на канат из задачи 3.2.2 со стороны обеих команд, уравновешивают друг друга, ускорение каната равно нулю. Очевидно, что и любая часть каната, и в частности, его часть от первой команды до какой-то средней точки также будет в равновесии. А поскольку на эту часть каната действуют только сила со стороны одной из команд и сила со стороны другой части каната (сила натяжения), то условие равновесия этой части каната дает , откуда заключаем, что = 5000 Н (ответ 1).
Силы, о которых говорится в третьем законе Ньютона (силы действия и противодействия) приложены к разным телам. В задаче 3.2.3 одна из них действует со стороны Земли на тело (сила тяжести), и, следовательно, вторая должна действовать со стороны тела на Землю — это сила притяжения Земли к телу (ответ 3).
Если бы лифт в задаче 3.2.4 покоился, то вместе с ним покоилось бы и тело, и, следовательно, сила реакции пола равнялась бы силе тяжести. По третьему закону Ньютона с такой же силой и тело действовало бы на пол. Т.е. в этом случае выполнялось бы равенство =20 Н. Здесь же =10 Н, что означает, что сила тяжести больше силы реакции, и, следовательно, тело вместе с лифтом движется вниз. Применяя второй закон Ньютона к телу, найдем его ускорение, которое равно ускорению лифта: м/с
Весы измеряют силу, с которой лежащее на весах тело действует на них (или они на тело). Поэтому показания весов в задаче 3. 2.5 будут наибольшими, если наибольшей является сила реакции. А эта сила увеличивается по сравнению с силой тяжести, если лифт имеет ускорение, направленное вверх. Поэтому правильный ответ в этой задаче — 2.
Умение использовать условия равновесия тел (и понимание ситуаций, когда это можно делать) часто проверяется в заданиях единого государственного экзамена по физике. Например, в задаче 3.2.6 тело находится в равновесии на пружине. Ясно, что в этом положении сила тяжести уравновешивается силой упругости. Используя закон Гука (3.3) для силы упругости и приравнивая силу упругости силе тяжести, получим , где — жесткость пружины, — ее удлинение (ответ 1).
При падении тела на вертикально стоящую пружину (задача 3.2.7) оно движется следующим образом. До контакта с пружиной тело движется с ускорением . После контакта на тело кроме силы тяжести действует сила упругости, направленная вертикально вверх. При этом пока укорочение пружины не достигло величины , сила упругости меньше силы тяжести, и по второму закону Ньютона ускорение тела направлено вертикально вниз. Поэтому скорость тела при таких значениях укорочения пружины продолжает увеличиваться. Начиная с того момента, когда укорочение пружины станет больше значения , суммарная сила, действующая на тело, будет направлена вверх, и, следовательно, скорость тела будет уменьшаться. Поэтому максимальной скорость тела будет на высоте от поверхности (ответ
Поэтому скорость тела при таких значениях укорочения пружины продолжает увеличиваться. Начиная с того момента, когда укорочение пружины станет больше значения , суммарная сила, действующая на тело, будет направлена вверх, и, следовательно, скорость тела будет уменьшаться. Поэтому максимальной скорость тела будет на высоте от поверхности (ответ
Поскольку нити в задаче 3.2.8 нерастяжимы, все тела имеют одинаковые ускорения. Сила натяжения первой нити сообщает его четырем одинаковым телам, сила натяжения четвертой нити — одному такому телу. Поэтому из второго закона Ньютона заключаем, что последняя в четыре раза меньше первой (правильный ответ — 4).
Из формулы (3.4) для силы сопротивления следует, что свободно падающее тело движется в среде следующим образом (задача 3.2.9). При малых скоростях сила сопротивления мала по сравнению с силой тяжести, поэтому тело имеет ускорение, близкое к ускорению свободного падения, и его скорость возрастает временем. При этом возрастает и сила сопротивления среды, которая при некоторой скорости тела сравнивается с силой тяжести. А поскольку эти силы противоположны, ускорение тела становится равным нулю, и тело движется с постоянной скоростью (ответ 1).
При этом возрастает и сила сопротивления среды, которая при некоторой скорости тела сравнивается с силой тяжести. А поскольку эти силы противоположны, ускорение тела становится равным нулю, и тело движется с постоянной скоростью (ответ 1).
Поскольку тело в задаче 3.2.10 падает с большой высоты, оно успевает разогнаться до такой скорости, что сила сопротивления воздуха равна по величине силе тяжести, и тело движется с постоянной скоростью (см. предыдущую задачу). После отражения от поверхности скорость тела меняет свое направление на противоположное, а ее величина остается такой же (сразу после удара). А поскольку сила сопротивления определяется скоростью, то величина силы сопротивления также не меняется, а ее направление меняется на противоположное. Поэтому после удара сумма сил сопротивления и тяжести равна , и, следовательно, ускорение тела равно (ответ 3).
Механическая работа — определение, формула, виды, свойства
Для нас привычно понятие «работа» в бытовом смысле. Работая, мы совершаем какое-либо действие, чаще всего полезное. В физике (если точнее, то в механике) термин «работа» показывает, какую силу в результате действия приложили, и на какое расстояние тело в результате действия этой силы переместилось.
Работая, мы совершаем какое-либо действие, чаще всего полезное. В физике (если точнее, то в механике) термин «работа» показывает, какую силу в результате действия приложили, и на какое расстояние тело в результате действия этой силы переместилось.
Например, нам нужно поднять велосипед по лестнице в квартиру. Тогда работа будет определяться тем, сколько весит велосипед и на каком этаже (на какой высоте) находится квартира.
Механическая работа — это физическая величина, прямо пропорциональная приложенной к телу силе и пройденному телом пути.
Чтобы рассчитать работу, нам необходимо умножить численное значение приложенной к телу силы F на путь, пройденный телом в направлении действия силы S. Работа обозначается латинской буквой А.
Механическая работа А = FS A — механическая работа [Дж] F — приложенная сила [Н] S — путь [м] |
Если под действием силы в 1 ньютон тело переместилось на 1 метр, то данной силой совершена работа в 1 джоуль.
Поскольку сила и путь — векторные величины, в случае наличия между ними угла формула принимает вид.
Механическая работа А = FScosα A — механическая работа [Дж] F — приложенная сила [Н] S — путь [м] α — угол между векторами силы и перемещения [] |
Числовое значение работы может становиться отрицательным, если вектор силы противоположен вектору скорости. Иными словами, сила может не только придавать телу скорость для совершения движения, но и препятствовать уже совершаемому перемещению. В таком случае сила называется противодействующей.
Для совершения работы необходимы два условия:
- чтобы на тело действовала сила,
- чтобы происходило перемещение тела.

Сила, действующая на тело, может и не совершать работу. Например, если кто-то безуспешно пытается сдвинуть с места тяжелый шкаф. Сила, с которой человек действует на шкаф, не совершает работу, поскольку перемещение шкафа равно нулю.
Запомнить!
Работа равна нулю, если при приложенной силе перемещение отсутствует.
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Полезная и затраченная работа
Был такой мифологический персонаж у древних греков — Сизиф. За то, что он обманул богов, те приговорили его после смерти вечно таскать огромный булыжник вверх по горе, откуда этот булыжник скатывался — и так без конца. В общем, Сизиф делал совершенно бесполезное дело с нулевым КПД. Поэтому бесполезную работу и называют «сизифов труд».
Чтобы разобраться в понятиях полезной и затраченной работы, давайте пофантазируем и представим, что Сизифа помиловали и камень больше не скатывается с горы, а КПД перестал быть нулевым.
Полезная работа в этом случае равна потенциальной энергии, приобретенной булыжником. Потенциальная энергия, в свою очередь, прямо пропорциональна высоте: чем выше расположено тело, тем больше его потенциальная энергия. Выходит, чем выше Сизиф прикатил камень, тем больше полезная работа.
Потенциальная энергия Еп = mgh m — масса тела [кг] g — ускорение свободного падения [м/с2] h — высота [м] На планете Земля g ≈ 9,8 м/с2 |
Затраченная работа в нашем примере — это механическая работа Сизифа. Механическая работа зависит от приложенной силы и пути, на протяжении которого эта сила была приложена.
Механическая работа А = FS A — механическая работа [Дж] F — приложенная сила [Н] S — путь [м] |
И как же достоверно определить, какая работа полезная, а какая затраченная?
Все очень просто! Задаем два вопроса:
- За счет чего происходит процесс?
- Ради какого результата?
В примере выше процесс происходит ради того, чтобы тело поднялось на какую-то высоту, а значит — приобрело потенциальную энергию (для физики это синонимы).
Происходит процесс за счет энергии, затраченной Сизифом — вот и затраченная работа.
Мощность
На заводах по всему миру большинство задач выполняют машины. Например, если нам нужно закрыть крышечками тысячу банок колы, аппарат сделает это в считанные минуты. У человека эта задача заняла бы намного больше времени. Получается, что машина и человек выполняют одинаковую работу за разные промежутки времени. Для того, чтобы описать скорость выполнения работы, нам потребуется понятие мощности.
Например, если нам нужно закрыть крышечками тысячу банок колы, аппарат сделает это в считанные минуты. У человека эта задача заняла бы намного больше времени. Получается, что машина и человек выполняют одинаковую работу за разные промежутки времени. Для того, чтобы описать скорость выполнения работы, нам потребуется понятие мощности.
Мощностью называется физическая величина, равная отношению работы ко времени ее выполнения.
Мощность N = A/t N — мощность [Вт] A — механическая работа [Дж] t — время [с] |
Один ватт — это мощность, при которой работа в один джоуль совершается за одну секунду.
Также для мощности справедлива другая формула:
Мощность N = Fv N — мощность [Вт] F — приложенная сила [Н] v — скорость [м/с] |
Как и для работы, для мощности справедливо правило знаков: если векторы направлены противоположно, значение мощности будет отрицательным.
Поскольку сила и скорость — векторные величины, в случае наличия между ними угла формула принимает следующий вид:
Мощность N = Fvcosα N — мощность [Вт] F — приложенная сила [Н] v — скорость [м/с] α — угол между векторами силы и скорости [] |
Примеры решения задач
Задача 1
Ложка медленно тонет в большой банке меда. На нее действуют сила тяжести, сила вязкого трения и выталкивающая сила. Какая из этих сил при движении тела совершает положительную работу? Выберите правильный ответ:
- Выталкивающая сила.
- Сила вязкого трения.

- Сила тяжести.
- Ни одна из перечисленных сил.
Решение
Поскольку ложка падает вниз, перемещение направлено вниз. В ту же сторону, что и перемещение, направлена только сила тяжести. Это значит, что она совершает положительную работу.
Ответ: 3.
Задача 2
Ящик тянут по земле за веревку по горизонтальной окружности длиной L = 40 м с постоянной по модулю скоростью. Модуль силы трения, действующей на ящик со стороны земли, равен 80 H. Чему равна работа силы тяги за один оборот?
Решение
Поскольку ящик тянут с постоянной по модулю скоростью, его кинетическая энергия не меняется. Вся энергия, которая расходуется на работу силы трения, должна поступать в систему за счет работы силы тяги. Отсюда находим работу силы тяги за один оборот:
Ответ: 3200 Дж.
Задача 3
Тело массой 2 кг под действием силы F перемещается вверх по наклонной плоскости на расстояние l = 5 м. Расстояние тела от поверхности Земли при этом увеличивается на 3 метра. Вектор силы F направлен параллельно наклонной плоскости, модуль силы F равен 30 Н. Какую работу при этом перемещении в системе отсчета, связанной с наклонной плоскостью, совершила сила F?
Решение
В данном случае нас просят найти работу силы F, совершенную при перемещении тела по наклонной плоскости. Это значит, что нас интересуют сила F и пройденный путь. Если бы нас спрашивали про работу силы тяжести, мы бы считали через силу тяжести и высоту.
Работа силы определяется как скалярное произведение вектора силы и вектора перемещения тела. Следовательно:
A = Fl = 30 * 5 = 150 Дж
Ответ: 150 Дж.
Задача 4
Тело движется вдоль оси ОХ под действием силы F = 2 Н, направленной вдоль этой оси. На рисунке приведен график зависимости проекции скорости vx тела на эту ось от времени t. Какую мощность развивает эта сила в момент времени t = 3 с?
Решение
На графике видно, что проекция скорости тела в момент времени 3 секунды равна 5 м/с.
Мощность можно найти по формуле N = Fv.
N = FV = 2×5 = 10 Вт
Ответ: 10 Вт.
Попробуйте онлайн-курс подготовки к ЕГЭ по физике с опытным преподавателем в Skysmart!
Обобщающий урок по физике в 10 классе на тему «Динамика материальной точки»
Повторение и обобщение темы «Динамика материальной точки»
Цели урока:
Образовательная: повторить и систематизировать материал по теме «Основы динамики»- основные законы, определения, формулы; научить определять логическую связь между понятиями и явлениями;
Воспитательная: повторить формирование навыков коллективной работы, повышение познавательной деятельности и активности учащихся;
Развивающая: развитие интереса к физике, развитие речи учащихся, развитие умения видеть в окружающих процессах физические явления и уметь их обобщать.

Тип урока: Урок обобщения и систематизации знаний.
Оборудование: опорные обобщающие конспекты, карточки-задания, раздаточный материал (тесты), обобщающие таблицы, бланки для ответов, мультипроектор, презентация к уроку
ХОД УРОКА
Ум заключается не только в знаниях, но и в умении применять знания на деле
Аристотель (384-322гг. до н.э.). древнегреческий философ
I. Организация начала урока . Вступительное слово учителя.
Мы изучили весь курс физики средней школы и сегодня продолжаем повторять изученный материал. Тема нашего урока «Динамика материальной точки» Эпиграфом сегодняшнего урока я выбрала слова древнегреческого философа Аристотеля. Какова будет цель нашего урока?
Учитель уточняет цели и задачи урока, знакомит учащихся с этапами урока
Учитель: Целью нашего урока будет систематизация знаний по теме «Динамика материальной точки». Результатом работы будет схема со структурой этой темы .
Результатом работы будет схема со структурой этой темы .
Что называется материальной точкой?
Что изучает динамика? (Динамика изучает причину изменения скорости, причину ускорения).
Прежде всего, нужно напомнить, что динамика — логическое продолжение кинематики. Динамика изучает причины, которыми обусловлено движение
Человек не только стремится к знаниям, не только их получает, но и их систематизирует. Ньютон создавал механику, как попытку создать систему, объясняющую мир, и это ему удалось.
Ожидаемый результат: после повторения и систематизации пройденного материала, успешно выполнить, предлагаемый тест
II. Актуализация знаний учащихся.
1. Повторение понятия — Силы.Учитель:
Что называется силой? (Сила – величина, характеризующая взаимодействие тел.
 )
)Чем характеризуется сила?
Какие две силы считаются равными?
Как измерить силу?
Как складываются силы, действующие на тело?
Назовите единицу измерения силы
Как измерить силу? а) эталонная пружина (динамометр) б) через ускорение (расчет )
На каком принципе основано применение динамометра?
Учитель: Давайте вспомним, какие силы мы знаем?
Учащиеся:
сила тяжести,
сила упругости,
сила трения,
архимедова сила,
сила всемирного тяготения,
вес тела.
Работа в группах
Систематизация знаний по теме «Виды сил». Раздаются группам обобщающие таблицы «Виды сил» Каждая группа выполняет определённую часть таблицы
Взаимопроверка и оценка работы одноклассников.
Сила тяжести
Как направлена сила тяжести?
От чего зависит сила тяжести?
На чем основано измерение массы тел?
От чего зависит ускорение свободного падения?
Что называется весом тела?
Как направлен вес тела?
От чего зависит вес тела?
Что называется невесомостью?
Как изменится вес тела при перемещении с полюса на экватор? А масса тела?
Почему тела падают с одинаковыми ускорениями?
Всегда ли вес тела равен силе тяжести?
Сила всемирного тяготения
Где проявляются силы тяготения
Как направлены силы тяготения?
Что общего в движении падающего яблока и Луны?
Почему не приближаются друг к другу предметы, находящиеся в комнате, хотя они взаимно притягиваются?
Сила трения
Когда возникает сила трения? Как она направлена ?
Назовите виды силы трения
Когда возникает сила трения скольжения?
От чего зависит сила трения скольжения?
От чего зависит коэффициент трения?
Как уменьшить силу трения скольжения?
Чему равна сила трения, если тело движется равномерно?
Почему ящик труднее сдвинуть с места, чем сохранять движение?
Какие санки скатятся с горы быстрее: с одним или двумя седоками?
Может ли автомобиль двигаться равномерно по горизонтальному участку с выключенным двигателем?
Сила упругости
Что называется деформацией?
В чем причина силы упругости?
Как направлена сила упругости?
Почему возникает сила реакции опоры?
Как движется тело под действием силы упругости?
На каком принципе работает динамометр?
Зачем у динамометров делают ограничитель растяжения пружины?
 Повторение законов динамики.
Повторение законов динамики.Учитель: На какие законы опирается динамика?
Учащиеся: Основные законы по теме «Динамика»
I закон Ньютона.
II закон Ньютона.
III закон Ньютона.
Закон Гука.
Закон всемирного тяготения.
Учитель: Сформулируйте первый закон Ньютона
Учащиеся: ( варианты )
Существуют такие СО, относительно которых свободные тела движутся равномерно и прямолинейно
Тело будет находиться в покое или двигаться равномерно и
прямолинейно, пока действие со стороны других тел не выведет его из этого состояния
В инерциальной СО тело, не подверженное внешним воздействиям, находится в покое или движется равномерно и прямолинейно
2.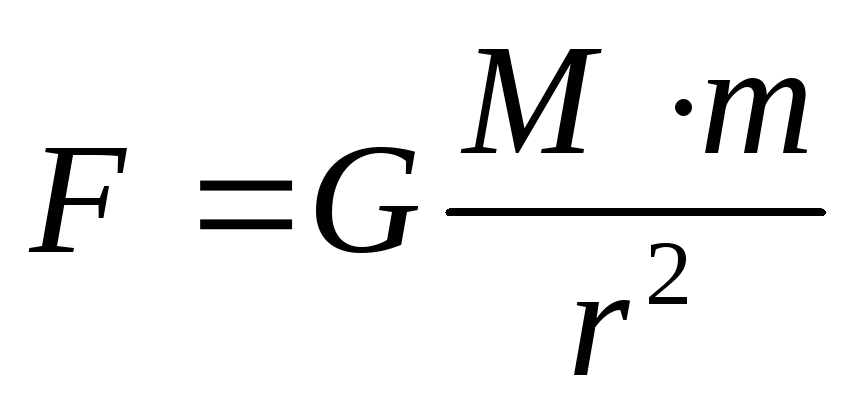 Что называется инерцией? Примеры
Что называется инерцией? Примеры
Какая СО называется инерциальной?
В каком случае тело движется равномерно?
Почему споткнувшийся человек падает вперед, а поскользнувшийся – назад?
Почему парашютист по истечении некоторого времени падения с раскрытым парашютом, падает равномерно, а не ускоренно? 7.Заяц, спасаясь от преследуемой его собаки, делает резкие прыжки в сторону. Почему собаке трудно поймать зайца, хотя она бегает быстрее?
Как движется тело, если F = 0?
Объясните опыт. Пустой стакан сверху накрыт открыткой, на которой лежит монета. При резком ударе по открытке монета падает в стакан. (Рисунок)
Учитель: Первый закон Ньютона выполняется для изолированных тел. Но в реальном мире, который нас окружает, практически не встречается изолированных тел. Обычно тела взаимодействуют с другими, и не всегда при этом действие сил скомпенсировано. Такие тела выходят из состояния покоя и начинают двигаться с ускорением.
Обычно тела взаимодействуют с другими, и не всегда при этом действие сил скомпенсировано. Такие тела выходят из состояния покоя и начинают двигаться с ускорением.
Сформулируйте второй закон Ньютона
Ускорение, с которым двигается тело пропорционально равнодействующей сил, действующей на тело, и обратно пропорционально массе этого тела
Особенности второго закона Ньютона:
Для любых сил
F – причина а, определяет а
Вектор а сонаправлен F
Если действуют несколько сил, то берется результирующая сила
ma = F1 + F2 + F3 + . . .
5. Если F = 0 , то а = 0 ( первый закон Ньютона )
Как этот закон записать?
Как ускорение связано с силой?
Как направлено ускорение тела?
Учитель: Первые два закона Ньютона объясняют поведение тел во многих ситуациях, но как выглядит взаимодействие двух тел между собой?
Сформулируйте третий закон Ньютона
силы, с которыми взаимодействуют два тела, равны по модулю и противоположны по направлению. Здесь нужно отметить особенности сил:
Здесь нужно отметить особенности сил:
Действуют только парами.
Всегда при взаимодействии.
Силы одной природы.
не уравновешиваются
для сил любой природы
Учитель: Следует заметить, что силы, с которыми взаимодействуют два тела, никогда себя не уравновешивают, так как они приложены к разным телам
Как этот закон записать?
В чем заключены особенности этого закона?
Почему в III законе силы не уравновешивают друг друга?
Почему нельзя поднять себя за волосы?
Если топор застрял в бревне, как лучше его извлечь ударяя о
твердую опору: вниз поленом или вниз обухом топора?
Почему при прыжке в момент приземления нужно сгибать колени?
Тело брошено под углом к горизонту.
 Куда направлено ускорениетела, если сопротивление воздуха не учитывать?
Куда направлено ускорениетела, если сопротивление воздуха не учитывать?Почему сорняки не рекомендуется вырывать рывком?
Учитель:
Сформулируйте закон всемирного тяготения
Между всеми телами действуют силы взаимного притяжения – гравитационные силы.
Учащиеся: Закон всемирного тяготения гласит:
Все тела притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.
G — коэффициент пропорциональности, который назвали гравитационной постоянной. Численно она равна:
Как называется коэффициент пропорциональности в формуле ЗВТ?
Как опытным путем было установлено значение G?
Как был использован ЗВТ для открытия новых планет?
Почему закон получил название «всемирного»?
Учитель:
Сформулируйте закон Гука
Учащиеся: Закон всемирного тяготения гласит:
сила упругости, возникающая при деформации тела, пропорциональна удлинению тела и направлена в сторону, противоположную направлению перемещений частиц тела при деформации:
(Fупр)х = -кх
4. При каких условиях выполняется закон Гука?
При каких условиях выполняется закон Гука?
5. Что называется коэффициентом жесткости? Единицы измерения.
6. От чего зависит коэффициент жесткости?
III. Проверь себя (тест) IV. Подведение итогов урока.Учитель: Наш урок подошёл к концу. Все о чем мы с вами сегодня говорили можно обобщить в виде схемы.( СМ приложение)
V. Рефлексия.Учитель: Наш урок я хотела бы закончить словами Исаака Ньютона, которые он написал перед смертью:
«Не знаю, чем я могу казаться миру, но самому себе я кажусь мальчиком, играющим у моря, которому удалось найти более красивый камушек, чем другим: но океан неизвестного лежит передо мной».
Возьмите листочки, не подписывая их, напишите три существительных, которые пришли вам в голову после этого урока.
VI. Домашнее задание: повторение темы «Законы сохранения», п.п. 28-36, выписать и повторить формулы
| 1. |
Основные понятия
Сложность: лёгкое |
1 |
2.
|
Действие магнитного поля на проводник с током
Сложность: лёгкое |
1 |
| 3. |
Электродвигатель
Сложность: лёгкое |
1 |
4.
|
Динамик
Сложность: среднее |
2 |
| 5. |
Микрофон
Сложность: среднее |
2 |
6.
|
Условные обозначения
Сложность: среднее |
2 |
| 7. |
Четыре установки (вариант 1)
Сложность: сложное |
3 |
8.
|
Четыре установки (вариант 2)
Сложность: сложное |
3 |
| 9. |
Вовочкины эксперименты
Сложность: сложное |
3 |
08.
 Вопросы к зачету по теме «Динамика. Законы сохранения в механике.»
Вопросы к зачету по теме «Динамика. Законы сохранения в механике.»Вопросы для подготовки к зачету по теме «Динамика. Законы сохранения в механике.»
5. Взаимодействие тел. Понятие силы. Принцип суперпозиции. Сила упругости, силы трения.
6. Законы Ньютона.
7. Сила тяжести. Закон всемирного тяготения. Вес тела. Невесомость.
8. Импульс тела. Импульс силы. Закон сохранения импульса.
9. Механическая работа и мощность. Единицы измерения работы и мощности.
10. Кинетическая энергия. Потенциальная энергия тела поднятого над поверхностью Земли. Потенциальная энергия упруго деформированного тела. Закон сохранения полной механической энергии.
Ответы.
Часть 1. Основные физические величины, единицы их измерения, формулы для нахождения.
|
Наименование |
Обозначения |
Единицы измерения в СИ |
Формулы |
|
Сила |
F |
Н (Ньютон) |
— |
|
Масса |
m |
кг (килограмм) |
— |
|
Сила упругости (Закон Гука) |
Fупр |
Н (Ньютон) |
Fупр=-kx |
|
Сила тяжести |
Fтяж |
Н (Ньютон) |
Fтяж=mg |
|
Сила трения |
Fтр | Н (Ньютон) | Fтр = μ·N |
|
Второй закон Ньютона |
— |
— | |
|
Закон всемирного тяготения |
— |
— |
|
|
Вес тела |
P | Н (Ньютон) | P = N |
|
Импульс тела
|
P | кг·м/с (килограмм-метр в секунду ) | P = m·v |
|
Импульс силы |
F·t | Н·с (ньютон на мекунду) | F·t=m·v-m·v0=Δp |
|
Закон сохранения импульса |
— | — |
m1·v1 + m2·v2 = m1·v1’ + m2·v2’ — упругое соударение m1·v1 + m2·v2 = (m1 + m2)·v’ — неупругое соударение |
|
Механическая работа |
A | Дж (джоуль) | A=F·S·cosα |
|
Механическая мощность |
N | Вт (ватт) | N=A/t |
|
Кинетическая энергия |
Eк | Дж (джоуль) | |
|
Потенциальная энергия тела, поднятого над поверхностью Земли |
Eп , Ep | Дж (джоуль) |
Ep=m·g·h |
|
Потенциальная энергия упруго деформированного тела |
Eп, Ep | Дж (джоуль) | Ep=k·x2/2 |
|
Закон сохранения полной механической энергии |
— | — | Ek1 + Ep1 = Ek2 + Ep2 |
Часть 2. Основные понятия.
Основные понятия.
- Подробности
- Просмотров: 2095
Механика на ЕГЭ по физике
Механика — раздел физики, изучающий виды, законы движения. На ЕГЭ встречается в номерах 1-7, 27-29. Примерно половина экзамена! Неудивительно, ведь механика в физике включает понятия скорости, ускорения, силы, массы, энергии, колебаний, волн. Хотите полностью освоить тему? Подумайте о курсах подготовки к ЕГЭ. Там дают много полезного материала, он пригодится на итоговой аттестации, для учебы в университете. В статье изучим основы механики в физике, рассмотрим главные формулы для ЕГЭ.
Теория
Изучение механики начнем с теории. Важнейшим понятием является материальная точка — объект с пренебрежимо малыми размерами. Сохраняется только масса. Тело обозначают материальной точкой, когда оно движется поступательно, а расстояния, изучаемые в задаче, много больше размеров. В механике рассматриваются также абсолютно твердые тела. Расстояние между двумя любыми точками таких объектов остается постоянным.
В механике рассматриваются также абсолютно твердые тела. Расстояние между двумя любыми точками таких объектов остается постоянным.
Следующее определение для задач ЕГЭ — перемещение, т.е. вектор, проведенный из точки начала движения в точку его окончания. Не путайте перемещение и путь. Путь — участок траектории, пройденный материальной точкой за определенный промежуток времени. Отношение перемещения ко времени называется скоростью: v = s / t. Задачи по механике в физике иногда рассматривают две скорости, связанные с разными системами координат. Применяется закон сложения скоростей v2 = v1 + v. Здесь v2, v1 — скорости точки в двух системах отсчета, v — скорость системы 1, движущейся относительно системы 2.
В заданиях по механике из ЕГЭ по физике встречается понятие ускорения — величина, отражающая быстроту изменения скорости. Она представляет собой отношение скорости к пройденному времени: a = v / t. Как и скорость, является векторной величиной. Если траектория вогнутая, ускорение делится на две составляющие. Тангенциальная направлена по касательной к траектории, нормальная перпендикулярно к ней. Далее рассмотрим виды движения:
Тангенциальная направлена по касательной к траектории, нормальная перпендикулярно к ней. Далее рассмотрим виды движения:
|
Название |
Определение |
Уравнение |
|
Равномерное прямолинейное |
Тело перемещается с постоянной скоростью, за равные промежутки времени проходит равные отрезки пути |
s = s0 + vt или x = x0 + vxt |
|
Равноускоренное прямолинейное |
Тело движется с постоянным ускорением |
x = x0 + v0t + at2 / 2 или vx = v0x + axt |
|
Движение под углом к горизонту |
Тело брошено под углом к горизонту с начальной скоростью, движется по криволинейной траектории |
x = v0cosαt и h = v0sinαt − gt2 / 2 |
|
Равномерное движение по окружности |
Материальная точка имеет круговую траекторию, скорость в каждой точке траектории направлена по касательной к окружности. |
Период: T = 2πr / v Частота: υ = 1 / T Угловая скорость: ω = φ / t = 2πυ, где φ — угол поворота Ускорение: a=4π2Rv2 |
Следующий раздел для подготовки к ЕГЭ — динамика. Описывает законы движения тел, рассматривает инерциальные системы отсчета. Они определяются следующим образом: если на тело не воздействуют никакие силы (или они уравновешены), то тело находится в состоянии покоя или движется равномерно, прямолинейно. Количество систем в природе не ограничено, законы механики в них одинаковы. Неинерциальные системы — движущиеся относительно инерциальных с ускорением. Условие существования инерциальных систем обнаружил Ньютон, оно называется первым законом Ньютона.
Важные формулы касаются массы. Под термином понимают величину, определяющую гравитационные, инертные свойства. Чем тяжелее тело, тем оно инертнее, тем большее ускорение придает при взаимодействии. Второй закон Ньютона выражает соотношение F = ma. В формуле появляется понятие силы — меры взаимодействия (влияния друг на друга) тел. В механике различают силы трения, упругости, гравитационные силы. В задачах иногда встречается принцип суперпозиции: если на тело действует сразу несколько сил, их складывают, представив в виде одной, называемой равнодействующей. С силой связан третий закон Ньютона: для каждого действия есть противодействие, равное по модулю, противоположное по направлению. Запишем в виде F1 = -F2 или m1a1 = -m2a2. Еще несколько важных сил:
Второй закон Ньютона выражает соотношение F = ma. В формуле появляется понятие силы — меры взаимодействия (влияния друг на друга) тел. В механике различают силы трения, упругости, гравитационные силы. В задачах иногда встречается принцип суперпозиции: если на тело действует сразу несколько сил, их складывают, представив в виде одной, называемой равнодействующей. С силой связан третий закон Ньютона: для каждого действия есть противодействие, равное по модулю, противоположное по направлению. Запишем в виде F1 = -F2 или m1a1 = -m2a2. Еще несколько важных сил:
- упругости. Возникает в результате деформации, направлена на возвращение тела в изначальную форму. Определяется законом Гука Fупр = -kx, k — жесткость тела, x — модуль удлинения;
- трение покоя. Два тела соприкасаются, не двигаясь относительно друг друга. Fпок = μпN, N — сила реакции опоры, а μ — коэффициент трения;
- трение скольжения. Соприкасающиеся тела движутся. Сила направлена противоположно движению.
 Fтр = μN;
Fтр = μN; - трение качения. Возникает, когда тело катится подобно колесу. Трение качения намного меньше скольжения. Fкач = μN.
Задания из ЕГЭ
Теорию разобрали, теперь попробуем решить задачи из ЕГЭ.
Задание 1. На брусок массой 5 кг, движущийся по горизонтальной поверхности, действует сила трения скольжения 20 Н. Чему равна сила трения скольжения, если коэффициент трения уменьшится в 4 раза при неизменной массе?
Решение. Формула для трения скольжения: Fтр = μN. Движение горизонтальное, по второму закону Ньютона N = mg. Масса не меняется, следовательно, при уменьшении коэффициента сила уменьшается в 4 раза. 20 Н / 4 = 5 Н.
Ответ: 5
Задание 2. В каком случае Земля считается материальной точкой?
1) рассчитывается длина экватора;
2) изучается земная атмосфера;
3) измеряется расстояние от Земли до Луны;
4) рассчитывается скорость движения Земли относительно Солнца.
Решение. В номерах 1, 2 изучаются свойства Земли, важны форма и размер. В номерах 3, 4 изучаемые расстояния намного больше радиуса Земли, ее можно считать материальной точкой.
В номерах 3, 4 изучаемые расстояния намного больше радиуса Земли, ее можно считать материальной точкой.
Ответ: 34
Задание 3. Тело равномерно движется по окружности радиусом 2 м. По графику определите модуль линейной скорости тела в интервале 0 < t < π.
Решение. Найдем связь угловой и линейной скорости: v = Rω = Rφ / t. В указанном интервале t изменяется в промежутке от -π / 4 до π / 4, следовательно, φ = π / 4 — (-π / 4) = π / 2. v = 2 • π / 2 : π = 1.
Ответ: 1.
Задание 4. Математический маятник колеблется с угловой амплитудой 1 градус. Уменьшили длину нити маятника и массу привязанной дробинки, оставив угловую амплитуду прежней. Определите изменение величин.
А) период колебаний
Б) запас полной механической энергии
1) увеличится
2) уменьшится
3) не изменится
Решение. Период колебаний определяется выражением T=2lg. При уменьшении длины нити уменьшается период колебаний. Кроме того, уменьшится потенциальная энергия, общая механическая также станет меньше.
Кроме того, уменьшится потенциальная энергия, общая механическая также станет меньше.
Ответ: 22
Задание 5. Используя рисунок, определите, чему равна проекция ускорения на ось Х через 2 секунды.
Решение. Ускорение — отношение изменения скорости к изменению t. Скорость в первую секунду была равна нулю, в точке v1 стала 1 м/с. Δv = 1 — 0 = 1. Вычисляем ускорение: 1 / 2 = 0,5 м/с2.
Ответ: 0,5.
Мы изучили теорию по механике, разобрались, как решать задания из ЕГЭ по физике. Материал будет полезен при подготовке к экзамену, поэтому сохраните его, повторяйте. Не забывайте практиковаться, решать тематические задачи. Желаем вам удачи на итоговой аттестации!
количество, которое имеет размер и направление, как сила | ||
количество, которое имеет размер только | ||
это то, что может вызвать изменение скорости материального тела 90 030 F=ма | ||
количество энергии, переданной силой, действующей на расстоянии | ||
скорость, с которой выполняется работа или преобразуется энергия | ||
стандартная метрическая единица измерения кинетической энергии | ||
единица мощности | ||
запасенная энергия позиции, которой обладает объект | ||
трение двух предметов друг о друга, когда один или оба движутся | ||
раздел классической механики или машиностроения, описывающий движение тел (объектов) и систем (групп объектов) без учета сил, вызывающих движение | ||
первый закон Ньютона | тело остается в покое или, если уже находится в движении, остается в однородном морионе с постоянной скоростью по прямой линии, если только на него не действует неуравновешенная внешняя сила | |
второй закон Ньютона | ускорение, создаваемое конкретной силой, действующей на тело, прямо пропорционально величине силы и обратно пропорционально массе тела | |
описывает сумму потенциальной энергии и кинетической энергии, присутствующих в компонентах механической системы. | ||
название стремления движущегося объекта оставаться в движении или покоящегося объекта оставаться в покое, если на него не действует сила | ||
скорость, с которой что-то увеличивает скорость | ||
пройденное расстояние в единицу времени (м/с) | ||
вектор или величина вектора от начального положения до последующего положения, принимаемого телом | ||
это графическое изображение, часто используемое для анализа сил, действующих на свободное тело | ||
ньютон — единица силы (Н) | ||
упрощенное изложение, обычно с использованием цифр и других символов, выражающее составные части химического соединения, метод получения вещества или процедуру достижения желаемого значения или результата | ||
сила, возникающая в результате ускорения под действием силы тяжести на массу объекта | ||
масса – это количество инерции, которой обладает объект, или пропорция между силой и ускорением | ||
когда вы соединяете голову одного вектора с хвостом другого |
| Формула | ||
|---|---|---|
| Определение и объяснения | ||
S_ {av} = \ dfrac {d} {\ delta t} | S AV — это средняя скорость ( скаляр) d — расстояние Δ t — прошедшее время | |
v_{av} = \dfrac{x_f — x_i}{t_f — t_i} =\dfrac{\Delta x}{\ Delta t} | V AV AV — это средняя скорость (вектор) Δ x — это смещение (вектор) Δ T — это время, прошедшее время | |
A_ {AV} = \ dfrac{v_f — v_i}{t_f — t_i} =\dfrac{\Delta v}{\Delta t} | a av — среднее ускорение (вектор) Δ v — изменение скорости (вектор) Δ t — прошедшее время | |
v_{av} = \dfrac{v_i + v_f}{2} | V AV AV — это средняя скорость (вектор) V I — начальная скорость (вектор) V F является конечной скоростью (вектор) | V_ { f} = v_{i} + a \Delta t | v f — конечная скорость (вектор) v i — начальная скорость (вектор) a вектор) |
\Delta x = v_i \Delta t + \dfrac{1}{2} a (\Delta t)^2 | Δ x — смещение (вектор) i v — начальная скорость (вектор) a — ускорение (вектор) | |
\Delta x = v_f \Delta t — \dfrac{1}{2} a (\Delta t)^2 | Δ x — смещение (вектор) v f — конечная скорость (вектор) a — ускорение (вектор) | |
\Delta x = \dfrac{v_f+v_i}{2} \Delta t | Δ x — смещение (вектор) 92 91 f v v Окончательная скорость (вектор) V I — начальная скорость (вектор) | |
V ^ 2_f = v ^ 2_i + 2 A \ Cdot \ Delta x | V F — конечная скорость (вектор) v i — начальная скорость (вектор) Δ x — смещение (вектор) a — ускорение (вектор) |
Физика — Динамика Линейная — Ньютоны Законы
На этой странице мы будем рассматривать только линейное движение, затем на других страницах
перейдем к рассмотрению более общего случая, включающего вращение.
Чтобы не было вращательного движения, мы могли бы либо предположить, что объект рассматриваемое является частицей (его масса сосредоточена в одной точке). или мы могли бы предположить, что любые силы, действующие на объект, действуют на его центр масс.
Законы Ньютона
Законы Ньютона обычно излагаются в той или иной форме, подобной следующей.
- Первый закон. Объект, находящийся в состоянии покоя, остается в состоянии покоя, если на него не действует внешнее сила. Движущийся объект продолжает двигаться с постоянной скоростью, если только действует внешняя сила.
- Второй закон. Ускорение объекта направлено в сторону сети. на него действует внешняя сила. Он пропорционален чистой внешней силе, и обратно пропорциональна массе объекта.
- Третий закон — Силы всегда возникают в равных и противоположных парах. Если объект А
действует на объект B с такой же, но противоположной силой
Б на объекте А.

Эти законы определены для линейного движения, а не для вращательного движения.Эйлер определили аналогичные законы для вращающихся объектов, но прежде чем мы перейдем к разработке общих законы для объекта как с линейным, так и с угловым движением, я думаю, это важно чтобы быть очень ясно о наших предположениях.
Итак, на этой странице мы будем рассматривать только линейное движение. Чтобы было вращательного движения, мы могли бы либо предположить, что рассматриваемый объект является частицей (его масса сосредоточена в одной точке). или мы могли бы предположить что любые силы, действующие на объект, действуют на его центр масс.
Соотношение между силой и ускорением количественно выражается в секундах Ньютона. закон, который говорит, что ускорение равно:
- Пропорционально чистой внешней силе.
- Обратно пропорциональна его массе.
- В направлении силы.
Итак, если правильно подобрать единицы измерения, то:
F=ма
| где: | |||
символ | описание | тип | шт. |
| Ф | чистая сила | вектор | кг м/с 2 |
| м | масса | скаляр | кг |
| и | ускорение | вектор | м/с 2 |
Альтернативная форма этого уравнения состоит в том, что Сила представляет собой скорость изменения импульса, или интегрирование обеих частей дает: импульс — это линейный интеграл от сила.
Я думаю, что важно очень четко понимать предположения и условия с этим уравнением. Это может показаться педантичным, но когда мы переходим к случаю, когда объект вращается, тогда все становится сложнее и менее инициативно. Таким образом, остальная часть этой страницы предназначена для того, чтобы наше понимание было максимально ясным.
Инерция и внешние силы
F в приведенном выше уравнении представляет собой результирующую внешнюю силу, другими словами, вектор
сумма всех внешних сил. Этой внешней силе соответствует равная и
противоположной «внутренней» или «инерционной» силе (как и следует из третьего закона). Этот
силу инерции можно рассматривать как сопротивление массы случайному изменению скорости.
Эту силу инерции, естественно, не следует включать в уравнение F=ma (иначе
результирующая сила всегда будет равна нулю), но это, например, «реальная» сила,
это окажет влияние на другие объекты и может быть задействовано, когда мы рассматриваем
вращения.Например, попробуйте ускорить большую массу (не против силы тяжести) и
вы можете почувствовать силу инерции, противодействующую ускорению.
Этой внешней силе соответствует равная и
противоположной «внутренней» или «инерционной» силе (как и следует из третьего закона). Этот
силу инерции можно рассматривать как сопротивление массы случайному изменению скорости.
Эту силу инерции, естественно, не следует включать в уравнение F=ma (иначе
результирующая сила всегда будет равна нулю), но это, например, «реальная» сила,
это окажет влияние на другие объекты и может быть задействовано, когда мы рассматриваем
вращения.Например, попробуйте ускорить большую массу (не против силы тяжести) и
вы можете почувствовать силу инерции, противодействующую ускорению.
Векторная форма уравнения
До сих пор мы измеряли силу и ускорение в направлении, они действуют. Когда мы делаем это, мы можем работать в одном измерении и использовать скаляры для всех величин.
Когда мы моделируем физику в нашей программе, мы можем работать в некоторых координатах
система, которая может быть не выровнена по направлению силы и ускорения. Чтобы избежать постоянной смены систем координат, вместо этого мы можем представить ньютоны
второй закон в терминах векторов.
Чтобы избежать постоянной смены систем координат, вместо этого мы можем представить ньютоны
второй закон в терминах векторов.
Итак, уравнение принимает вид:
=м
Где: m скаляр и , являются векторами (векторами, указанными стрелкой выше).
Альтернативное обозначение
При умножении вектора на скаляр просто умножайте каждый член вектора скаляром следующим образом:
Итак, мы говорим, что масса действует пропорционально одинаково в каждом измерении. одинаково.
Нам не нужно использовать для этого матричное представление, но если мы хотим использовать матричное обозначения по другим причинам, мы можем легко сделать это следующим образом:
Хотя реальный мир имеет 3 измерения (по крайней мере, в ньютоновских терминах), мы можем
ограничивать движение двумя измерениями, например бильярдным столом (ну, это
не совсем так, но вы понимаете, о чем я, можете ли вы придумать пример получше?).
Поэтому, если мы работаем в двух измерениях, нам нужно использовать только двумерные векторы.
Относительные и абсолютные величины
Некоторые величины всегда относительны, то есть для того, чтобы их измерить должны выбрать произвольную нулевую точку. Другие величины, такие как ускорение абсолютны, потому что мы не можем выбрать нулевое значение, если наша система отсчета Если точка отсчета ускоряется, то законы Ньютона не действуют внутри этой системы отсчета. ссылки.
| Ньютоновская физика | Эйнштейновская физика | |
| время | родственник | родственник |
| расстояние | родственник | родственник |
| скорость | родственник | абсолютный |
| ускорение | абсолютный | абсолютный |
Система отсчета.

Система отсчета похожа на ориентацию нашей системы координат. Мы можем выбрать для наблюдения и измерения величины в любой декартовой системе координат при условии, что оси взаимно перпендикулярны. Одна система отсчета может двигаться относительно другого.
Например, мы можем измерить движение человека, идущего в поезде, в системе отсчета поезда или в системе отсчета земли, или в системе отсчета какого-то совершенно другого объекта, движущегося по поверхность земли.
Получается, что законы Ньютона соблюдаются вне зависимости от системы отсчета из которого мы наблюдаем, при условии, что:
- Мы последовательны, мы не можем смешивать, скажем, измерения скорости в одной системе отсчета с ускорением, измеренным в другой системе отсчета, не принимая эту в учетную запись.
- Законы Ньютона не обязательно применяются при наблюдении из вращающейся системы отсчета,
например, неподвижный объект, на который не действуют никакие силы, может показаться
вращаться вокруг вращающейся системы отсчета.
- Две системы отсчета не ускоряются относительно друг друга.
Итак, когда мы продолжим обсуждение ротации, мы должны быть очень осторожны.
В приведенной ниже структуре программирования сохраняется смена системы отсчета. в структуре «преобразования».
У нас может быть иерархия вложенных систем отсчета, как в приведенном выше примере, земля движется относительно солнца, солнце движется относительно… и так на.
В этих вложенных системах отсчета может помочь упростить проблемы, если мы сможем разработать правила, позволяющие переводить количества вверх и вниз по иерархии следующим образом:
Масса — изменение системы отсчета
Масса не должна изменяться при просмотре в разных системах отсчета
Force — изменение системы отсчета
Сила не должна изменяться при условии, что две системы отсчета не
движутся относительно друг друга, или если они движутся, то они движутся вместе с
постоянная относительная линейная скорость. Если система отсчета ускоряется,
то силу необходимо пересчитать из суммы местных ускорений объектов
и ускорение локальной системы отсчета. Затем умножьте это вместе
ускорение массой.
Если система отсчета ускоряется,
то силу необходимо пересчитать из суммы местных ускорений объектов
и ускорение локальной системы отсчета. Затем умножьте это вместе
ускорение массой.
F абс. =Fl + F’ = m * al + m * ar
| где: | |||
символ | описание | тип | шт. |
| Фл | Сила в местных координатах. | вектор | кг м/с 2 |
| Ф’ | дополнительная составляющая силы из-за ускорения системы отсчета. | вектор | кг м/с 2 |
| м | масса | скаляр | кг |
| все | ускорения в местных координатах. | вектор | м/с 2 |
| ар | ускорение системы отсчета. | вектор | м/с 2 |
Ускорение — изменение системы отсчета
Ускорение, измеренное в системе отсчета над местной, равно сумма местного ускорения объектов и местного ускорения систему отсчета относительно системы отсчета над ней.
аа = ал + ар
Скорость — изменение системы отсчета
Скорость, измеренная в системе отсчета выше местной, равна сумма локальной скорости объектов и скорости локальной системы отсчета относительно системы отсчета над ним.
ва = вл + вр
Позиция — изменение системы отсчета
Позиция, измеренная в системе отсчета над местной, является сумма локального положения объектов и положения локальной системы отсчета относительно системы отсчета над ним.
па = пл + пр
Структура программирования
Структура преобразования содержит относительное положение объекта, это означает
что любые структуры внутри этого могут быть определены в локальных координатах и
инерционный каркас объекта.
Каждый объект содержит свои собственные динамические данные, такие как информация о массе и кинематике.
Где хранить скорость и ускорение? Это кажется естественным для он должен храниться в данных кинематики для объекта, поскольку он специфичен для этого объект. Однако эти величины измеряются в приведенной выше системе отсчета. объекта (они были бы равны нулю относительно самого себя). Поэтому я думаю, что лучше всего удерживать его в структуре данных кинематики, но помнить, что это относительно к системе отсчета над ним.
Из третьего закона мы знаем, что силы всегда действуют парами, поэтому нам нужно
удерживать силы в отдельной структуре, связанной с двумя объектами. Этот
гарантирует, что величина силы должна быть сохранена только один раз. Строго
гравитация также должна быть связана с двумя объектами, точно так же, как контакт
силы, однако в случае гравитации другим объектом обычно является земля,
поэтому, вероятно, более эффективно рассматривать это как частный случай. Я не уверен
необходимо сохранить силу инерции, так как ее можно вычислить из m
* a, однако, вероятно, полезно иметь его, когда мы делаем вычисления
чтобы в поступательной динамике сначала отработать все силы, потом работать
из ускорений от этого.
Я не уверен
необходимо сохранить силу инерции, так как ее можно вычислить из m
* a, однако, вероятно, полезно иметь его, когда мы делаем вычисления
чтобы в поступательной динамике сначала отработать все силы, потом работать
из ускорений от этого.
Для такой симуляции нескольких объектов, как эта, мы могли бы начать с поиска для объекта, внешние силы которого можно определить, в приведенном выше примере ни один из объектов не является независимым.Таким образом, нам, возможно, придется настроить набор уравнений определить силу инерции, действующую на каждый объект, через силы, действующие на другие объекты.
Что такое Сила?
На этой странице не объясняется, что такое сила, я не уверен, что кто-нибудь знает? Все
мы пытаемся построить математическую модель для определения его эффектов. Мы
мы не можем видеть силу, хотя, если мы становимся частью системы, мы можем чувствовать ее по
прижимаясь к объекту. Таким образом, мы можем получить некоторое интуитивное представление о силе, но
когда мы смотрим на систему извне, мы можем видеть не только силы, но и их эффекты. Так
здесь нас интересует моделирование только измеримых эффектов.
Так
здесь нас интересует моделирование только измеримых эффектов.
Физические формулы | Список всех формул физики
Понимание понятий в физике — базовый блок, без которого никуда.
Часто, когда кто-то понимает, что теории досконально, мы видим, что они могут легко обнаружить отношение между величинами, по которым они могут построить формулы, которые обычно выводят его, и обучение для них будет простым.
Вопросы по физике — это то, что бросает вызов вашим навыкам и знаниям в области физики. Они основаны на трех вещах:
Для изучения того, что предоставляется и что запрашивается в числовом виде.
Далее нужно использовать правильную формулу.
Ввод значений и правильный расчет.
Чтобы решить все эти виды проблем, которые находятся в форме вопросов, необходимо иметь правильное понимание предмета физических формул, а также его концепции.
Здесь предоставлены все физические формулы в простом формате, чтобы создать хранилище, в котором ученый может получить любые необходимые формулы.
Важная физика Formuls
Planck Contrance H = 6,63 × 10 -34 JS = 4.136 × 10 -15 EV.S
Гравитационная постоянная G = 6,67 × 10 -11 м 3 кг −1 с −2
Постоянная Больцмана k = 1.38 × 10 -23 J / K
Молярная газовая постоянная r = 8.314 J / (Mol k)
Номер Avogadro NA = 6.023 × 10 23 MOL -1
Заряд Электрона e = 1.
 602 × 10 -19 × 10 -19 C
602 × 10 -19 × 10 -19 Cдиэлектрическая проницаемость вакуума 0 = 8,85 × 10 -12 F / M
Coulob Constance 1 / 4πε 0 = 8.9875517923 (14) × 10 9 Н·м 2 /C 2
Постоянная Фарадея F = 96485 Кл/моль
Масса электрона m e = = 96485 Кл/моль1 × 10 -31 кг
кгМасса протона M P = 1.6726 × 10 -27 кг
Масса нейтронов M N = 1.
 6749 × 10 -27 кг
6749 × 10 -27 кгStefan-Boltzmann Constance Σ = 5.67 × 10 -8 W / (M 2 K 4 )
Rydberg Constance R ∞ = 1.097 × 10 -1 M -1
Магнетон Бора µ B = 9.27 × 10 -24 J / T
RARCEIUS BOHR A 0 = 0.529 × 10 -10 M
стандартная атмосфера ATM = 1.01325 × 10 5 PA
Wien постоянная b знак равно 2,9 × 10 −3 м K .
Волна = ∆x ∆t волна = средняя скорость ∆x = смещение ∆t = прошедшее время.

V AVG = (VI + VF *) 2
V AVG = Средняя скорость
VI = начальная скорость
VF = конечная скорость, которая является еще одним определением средней скорости который работает, где буква a постоянна.
A = ускорение
∆v = изменение скорости
∆t = истекшее время.
∆x = перемещение
vi = начальная скорость
∆t = прошедшее время
a = ускорение
Используйте эту формулу, если у вас нет vf.
∆x = перемещение
vf = конечная скорость
∆t = прошедшее время
a = ускорение
Используйте эту формулу, если у вас нет vi.
F = сила
m = масса
Тогда a = ускорение Второй закон Ньютона.
F — результирующая сила, действующая на массу m.
Вт = вес
м = масса
г = ускорение, вызванное силой тяжести.
Тогда мы видим, что вес объекта массой m. Говорят, что на самом деле это всего лишь второй закон Ньютона.
µ = коэффициент трения
Н = нормальная сила
Здесь µ может быть либо кинетическим коэффициентом трения µk, либо статическим коэффициентом трения.
W = работа t
F = сила
d = расстояние
θ = угол между F и направлением движения
KE = кинетическая энергия
m = масса
v = скорость 9000
м = масса
г = ускорение свободного падения
h = высота
Вт = выполненная работа
KE = кинетическая энергия.
«Работа-энергия», которую мы узнали, — это теорема о том, что работа, совершаемая чистой силой над объектом, равна изменению кинетической энергии объекта.
Мы можем записать это как E = KE + PE
E = полная энергия
KE = кинетическая энергия
PE = потенциальная энергия
Вт = работа
∆t = затраченное время
Мощность – это количество работы что делается в единицу времени, то есть мощность — это скорость, с которой выполняется работа.
Лист формул физики.инд
%PDF-1.6 % 348 0 объект > эндообъект 345 0 объект > эндообъект 347 0 объект >поток application/pdf
Границы | Закрытая двумерная поверхность Dynamics
1.
 Введение
Введение Биологические системы имеют разнообразную морфологию и испытывают большие деформации формы во время движения. Такая «хореография» подвижности формы характерна не только для всех живых организмов и клеток [1], но и для белков, нуклеиновых кислот и вообще для всех биомакромолекул. Подвижность формы, представляющая собой движение двумерных поверхностей, может быть результатом активных (с затратой энергии) или пассивных (без затрат энергии) процессов. Временной масштаб динамики формы может варьироваться от медленного (нанометр в наносекунду) до очень быстрого (нанометр в фемтосекунду) [2, 3].Медленно движущиеся поверхности рассматриваются как системы с избыточным демпфированием. Примером является подвижность клеток. В этом случае для описания движения можно использовать хорошо развитый формализм Хельфриха, где разложение свободной энергии по степеням тензора кривизны дает крупнозернистое моделирование мембран [4]. Однако, в то время как формализм [4] применим к медленно движущимся поверхностям, он неприменим к быстро движущимся поверхностям, где могут быть приспособлены биомолекулы. Динамика поверхности для белков или ДНК [2, 3] может достигать нм / фс диапазона.Так что поверхности могут быть представлены как виртуальные трехмерные псевдоримановы многообразия. Мы вывели полностью общие уравнения движения для трех многообразий [5], но намеренно опустили пространное обсуждение движения двумерных поверхностей, которое является темой данной статьи.
Динамика поверхности для белков или ДНК [2, 3] может достигать нм / фс диапазона.Так что поверхности могут быть представлены как виртуальные трехмерные псевдоримановы многообразия. Мы вывели полностью общие уравнения движения для трех многообразий [5], но намеренно опустили пространное обсуждение движения двумерных поверхностей, которое является темой данной статьи.
В настоящее время уже достигнут значительный прогресс в гидродинамических моделях мембранной динамики. Роль геометрических ограничений в самосборке была выяснена путем объединения термодинамики, свободных энергий взаимодействия и геометрии [6, 7].Формализм Хельфриха обеспечивает основу для чисто дифференциально-геометрического подхода, согласно которому поверхностная плотность потенциальной энергии мембраны рассматривается как функционал статической кривизны [4], см. также обзорные статьи [8–10]. Модель была усовершенствована путем добавления уравнений баланса сил и моментов [11, 12]. Также сообщалось о конкретных динамических уравнениях, учитывающих изгиб, а также электродинамические эффекты [13–15]. Кроме того, теории активных мембран, включая внешние силы, расширили понимание пассивных мембран [16–19].
Кроме того, теории активных мембран, включая внешние силы, расширили понимание пассивных мембран [16–19].
Среди замечательных аспектов жидких липидных мембран, выведенных из большого количества теоретических работ [8–10], является то, что физическое поведение мембраны в масштабе длины ее собственной толщины в первом приближении может быть выражено чисто геометрический гамильтониан [4, 20, 21]. Связанные уравнения Эйлера-Лагранжа [22, 23], так называемые «уравнения формы», представляют собой уравнения в частных производных четвертого порядка, и найти общее аналитическое решение, как правило, сложно, даже если оно было решено аналитически [24] и численно для некоторых частные [25–32] и общие случаи [33, 34].
В гидродинамике материальные частицы можно рассматривать как вершину геометрической фигуры, а виртуальные слои — как поверхности, и можно искать уравнения движения для таких поверхностей. Мы называем этот формализм дифференциально-вариационными поверхностями (ДВП) (или ДВП-формализмом) [5].
В этой статье мы предлагаем другой подход к проблеме «хореографии формы». Мы используем формализм DVS, тензорное исчисление движущихся поверхностей и первый закон термодинамики, чтобы вывести окончательное уравнение для динамики замкнутой двумерной поверхности (позже называемой поверхностью) и решить его аналитически для случая равновесия.Другими словами, мы выводим общие уравнения движения для замкнутых двумерных поверхностей и без каких-либо априорных предположений о симметрии показываем, что формы с постоянной средней кривизной являются равновесными решениями. В отличие от закона Юнга-Лапласа эти решения являются универсально правильными описаниями капиллярных поверхностей, а также молекулярных поверхностей. Кроме того, наши уравнения движения (20–25) являются общими и точными. Это продвигает наше понимание гидродинамики, потому что обобщает идеальные магнито-гидродинамические уравнения и уравнения Навье-Стокса [5] и, в отличие от Навье-Стокса, как мы показываем в этой статье, тривиально разрешимы для равновесных форм. Чтобы продемонстрировать справедливость этих уравнений и их аналитических решений, мы применим их к мицеллам. В рамках нашего формализма становится простой задачей показать мицеллы пластинчатой, цилиндрической, сферической формы и установить их оптимальный сферический радиус.
Чтобы продемонстрировать справедливость этих уравнений и их аналитических решений, мы применим их к мицеллам. В рамках нашего формализма становится простой задачей показать мицеллы пластинчатой, цилиндрической, сферической формы и установить их оптимальный сферический радиус.
Для наглядности дадим краткое описание мицелл и их строения. Мицелла состоит из монослоя липидных молекул, содержащих гидрофильную головку и гидрофобный хвост. Эти амфифильные молекулы в водной среде спонтанно агрегируют в мономолекулярный слой, удерживаемый вместе за счет гидрофобного эффекта [35, 36] (см. также 5, 37–40) слабыми нековалентными силами [41].Они образуют гибкие разнообразные поверхности с различной топологией, но в условиях термодинамического равновесия они имеют сферическую, пластинчатую (плоскую) или цилиндрическую форму.
2. Методы
В этом разделе мы представляем основы тензорного исчисления для движущихся поверхностей и суммируем теоремы, которые мы прямо или косвенно использовали для вывода уравнений динамики двумерных поверхностей. Предварительные сведения по дифференциальной геометрии, которые мы здесь использовали, доступны в учебнике по тензорному исчислению [42] и в нашей работе [5].
Предварительные сведения по дифференциальной геометрии, которые мы здесь использовали, доступны в учебнике по тензорному исчислению [42] и в нашей работе [5].
2.1. Основы дифференциальной геометрии
Пусть S i ( i = 1, 2) — координаты подвижной поверхности S и X α — координаты в объемлющем евклидовом пространстве Поверхность достаточно гладкая для достаточной дифференцируемости в пространстве-времени и выражается как X α = X α ( t, S i ) в окружающих координатах.Уравнение поверхности для вектора положения R→:
R→=R→(Xα)=R→(t,Si) (1) Рисунок 1 . Графическое изображение произвольной поверхности и ее локальной касательной плоскости. S→1,S→2,N→ — базовые векторы локальной касательной плоскости и локальная нормаль к поверхности соответственно. X→1,X→2,X→3 — произвольные базисные векторы объемлющего евклидова пространства, а R→=R→(X)=R→(t,S) — радиус-вектор точки. V→ — произвольная поверхностная скорость, а C, V 1 , V 2 отображают проекции скорости на направления N→,S→1,S→2 соответственно.
V→ — произвольная поверхностная скорость, а C, V 1 , V 2 отображают проекции скорости на направления N→,S→1,S→2 соответственно.
Скалярное произведение ковариантных базисов X→α=∂αR→ является метрическим тензором:
Xαβ=X→αX→β (2), где ∂α=∂/∂Xα. Матрица, обратная ковариантной метрике, образует контравариантную: XαβXβγ=δγα (дельта Кронекера δγα). В объемлющем евклидовом пространстве в силу взаимной линейной независимости базисных векторов символы Кристоффеля Γβγα=X→α·∂βX→γ равны нулю и, следовательно, ковариантные/контравариантные производные становятся частными ∇ α = ∂ α .
Базисные векторы поверхностей Si→=∂iR→ и метрические тензоры Sij,Sij определяются аналогичным образом
Sij=S→i·S→j (3), где ∂i=∂/∂Si и SabSbc=δac.Поверхностные символы Кристоффеля, заданные формулой Γjki=S→i·∂jS→k, не являются нулями, а ковариантные/контравариантные производные отличаются от частных ∇ i ≠ ∂ i .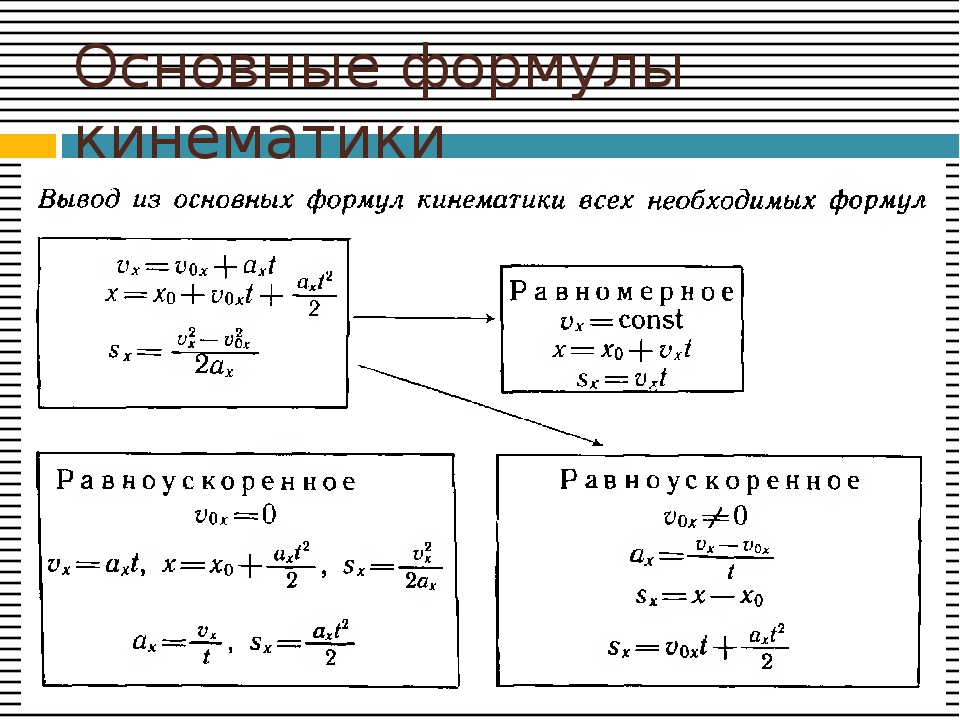 Символы пространства/поверхности Кристоффеля образуют основную концепцию для определения криволинейных производных на смешанных тензорах пространства/поверхности:
Символы пространства/поверхности Кристоффеля образуют основную концепцию для определения криволинейных производных на смешанных тензорах пространства/поверхности:
, где Xiγ — тензор сдвига, так что
S→i=XiαX→α и Sij=S→i·S→j=XiαX→αXjβX→β=XiαXjβXαβ.Заметим, что в (4) символы Кристоффеля с греческими индексами равны нулю.
Используя (2, 4), можно непосредственно доказать метрилинность поверхностного метрического тензора ∇ i S mn = 0, откуда следует S→m·∇iS→n=0, это означает, что S→m⊥∇iS→n являются ортогональными векторами, поэтому:
∇iS→j=N→Bij (5), где N→ — единичная нормаль к поверхности, а B ij — симметричный тензор кривизны. След тензора смешанной кривизны — это средняя кривизна Bii, а определитель — гауссова кривизна.Частный случай:
, где λ — некоторая ненулевая константа, является сферой, если поверхность замкнута. Согласно (5, 6), нахождение тензора кривизны косвенно влечет за собой отождествление поверхности.
Согласно (5, 6), нахождение тензора кривизны косвенно влечет за собой отождествление поверхности.
2.2. Основы тензорного исчисления для движущихся поверхностей
Все уравнения, написанные выше, в целом верны для движущихся поверхностей. Перейдем теперь к краткому обзору определений координатной скорости V α , граничной скорости C (что совпадает с нормальной скоростью), касательной скорости V i (рис. 1), времени производные поверхностных тензоров и пространственно-поверхностных интегралов.Оригинальные определения можно найти в учебниках [42, 43].
Предположим, что В α — координатная скорость, определяемая как:
Vα=∂Xα∂t (7)Тогда, учитывая, что вектор положения R→ (1) отслеживает координату частицы S i , поверхностная скорость может быть записана как:
V→=∂R→(t,Si)∂t=∂R→∂Xα∂Xα(t,Si)∂t=VαX→α (8) Таким образом, V α является составляющей поверхностной скорости V→. С учетом (8) нормальную скорость поверхности C можно представить в виде:
С учетом (8) нормальную скорость поверхности C можно представить в виде:
C называется скоростью границы раздела, инвариантна и ее знак зависит от выбора нормали к поверхности. Проекция поверхностной скорости на касательную плоскость (рис. 1) равна V i тангенциальная скорость:
С учетом (9, 10) поверхностную скорость можно записать как V→=CN→+ViS→i.
Рисунок 2 .Геометрическая интерпретация скорости поверхности раздела C и криволинейной производной по времени ∇˙ применительно к инвариантному полю F. Точка выбрана произвольно, так что она лежит на F ( S t ) ∈ Кривая S t , а B является соответствующей точкой на поверхности S t +Δ t . P — точка, в которой S t нормаль к поверхности, примененная к точке A , пересекает поверхность S t +Δ 5По геометрической конструкции для достаточно малых Δ t → 0, ∠ APB → π/2, AB→≈V→Δt и AP≈V→N→Δt. С другой стороны, по тому же геометрическому построению поле F в точке B можно оценить как F ( B ) ≈ F ( A ) + t∂F 1 t , а с точки зрения поверхности S t +Δ t значение F ( B ) можно оценить как F(P)+ΔtVi ∇i I F показывает скорость изменения в F ∈ S T + δ T + δ T и вдоль BP ≈ δ TV I .
С другой стороны, по тому же геометрическому построению поле F в точке B можно оценить как F ( B ) ≈ F ( A ) + t∂F 1 t , а с точки зрения поверхности S t +Δ t значение F ( B ) можно оценить как F(P)+ΔtVi ∇i I F показывает скорость изменения в F ∈ S T + δ T + δ T и вдоль BP ≈ δ TV I .
Поверхностная скорость вообще и межфазная скорость в частности имеет четкую геометрическую интерпретацию. Предположим, что поверхности в два близких момента времени t, t +Δ t равны S t , S t
1 +Δ 910. Тогда для произвольно выбранных A ∈ S t и соответствующей точки B ∈ S t 902 вектор скорости приблизительно равен 9, умноженному на t 902 времени: AB→≈V→Δt (рис. 2).Если P является точкой, в которой нормаль к поверхности N→∈St пересекает поверхность S t +Δ t , то для бесконечно малого Δ t , ∠ →
2).Если P является точкой, в которой нормаль к поверхности N→∈St пересекает поверхность S t +Δ t , то для бесконечно малого Δ t , ∠ →APB и AP→V→·N→Δt, поэтому:
C=limΔt→0APΔt (11)Скорость интерфейса C — мгновенная скорость интерфейса в нормальном направлении.
2.3. Инвариантное дифференцирование времени
Среди ключевых определений в исчислении движущихся поверхностей, пожалуй, одним из самых важных является инвариантная производная по времени ∇˙.Как мы уже говорили, инвариантная производная по времени уже хорошо определена в литературе [42, 43]. В этом абзаце мы просто даем геометрически интуитивное определение.
Пусть гладкий функционал F определен на поверхности F ∈ S t . Инвариантная производная по времени должна быть определена так, чтобы: (1) она была свободна от выбора системы отсчета (инвариантность) и (2) правильно учитывала деформации вдоль нормали.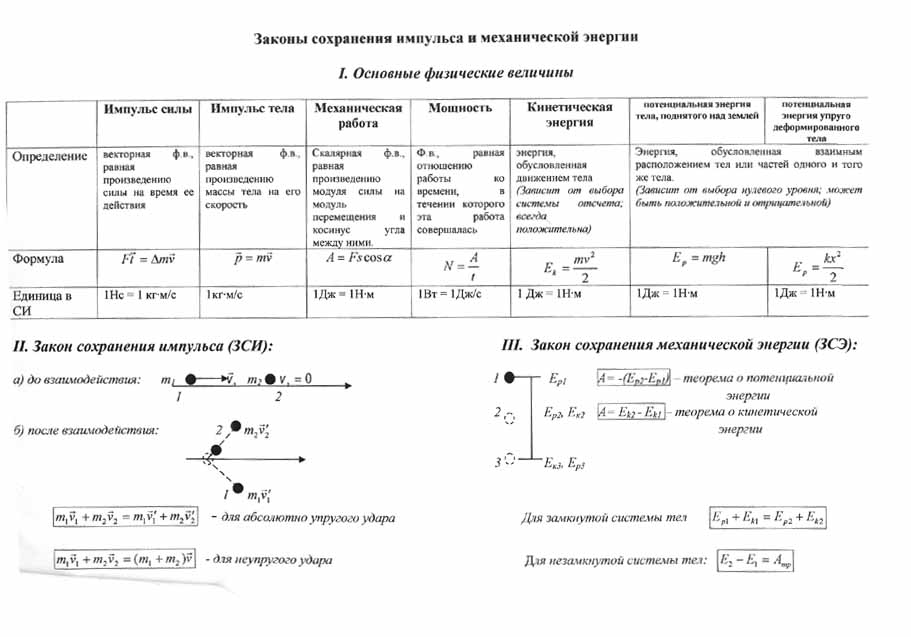 Мы объясняем важность нормальных деформаций в подразделе интегрирования. Этого можно добиться с помощью следующего геометрического построения: для произвольно выбранной точки A из S t поверхности A ∈ S t 915 S 909 B найдем точки T + Δ T + δ T и P Так что B является пересечением скорости поверхности до S T + δ T и P — пересечение поверхности нормали к S t +Δ t (рис. 2).Тогда инвариантная производная по времени ∇˙ может быть определена как:
Мы объясняем важность нормальных деформаций в подразделе интегрирования. Этого можно добиться с помощью следующего геометрического построения: для произвольно выбранной точки A из S t поверхности A ∈ S t 915 S 909 B найдем точки T + Δ T + δ T и P Так что B является пересечением скорости поверхности до S T + δ T и P — пересечение поверхности нормали к S t +Δ t (рис. 2).Тогда инвариантная производная по времени ∇˙ может быть определена как:
(12) геометрическое, поэтому должно быть инвариантом. Из геометрического построения (12) можно оценить значение F в точке B , так что
F(B)≈F(A)+Δt∂F∂t (13)B, P ∈ S t +Δ t являются близкими точками, поэтому согласно определению ковариантной производной F ( B ) можно оценить как 9: F(B)≈F(P)+ΔtVi∇iF (14)
с ∇ I I F показывает скорость изменения в F ∈ S 9095 T + Δ T
и δ T · V I Указывает BP . Определение значений F ( A ), F ( P ) из (13, 14) и подстановка их в (12) дает ∇˙F=∂F∂t-Vi∇iF (15)
Определение значений F ( A ), F ( P ) из (13, 14) и подстановка их в (12) дает ∇˙F=∂F∂t-Vi∇iF (15)Определение (15) распространяется на смешанные тензоры пространства/поверхности по следующей формуле:
∇˙tβjαi = ∂tβjαi∂t-vk∇ktβjαi + vγγγμαtβjμi-vγγγμtμjαi + γ˙kitβjαk-γ˙jktβkαi (16), где аналог символа Кристоффеля Γ˙ji для движущихся поверхностей определяется формулой Γ˙ji=∇jVi-CBji.Производная (16) удовлетворяет: коммутативности со сжатием, произведением и цепными правилами, метрилинными свойствами по отношению к объемлющей метрике и не коммутирует с поверхностной производной [42]. Согласно (12) инвариантная производная по времени обращается в нуль при применении к не зависящим от времени скалярам.
2.4. Временное дифференцирование интегралов
Исчисление движущихся поверхностей эффективно благодаря двум фундаментальным теоремам о производных по времени от пространственных и поверхностных интегралов [42].В оценке принципа наименьшего действия лагранжиана центральную роль играет дифференцирование по времени поверхностных и пространственных интегралов, откуда строго выясняется зависимость от геометрии.
Пусть скалярное поле F = F ( t, S ) определено на евклидовой области Ω, которая имеет границу поверхности S и поверхность эволюционирует со скоростью интерфейса C , в то время как объем движется (расширяется или сжимается). Аналогично предположим, что замкнутая поверхность эволюционирует и F = F ( t, S ) снова является некоторым скалярным функционалом, определенным на эволюционирующей поверхности S .Затем существуют теоремы для получения производной пространственного и поверхностного интегралов от F подынтегральной функции:
ddt∫ΩFdΩ=∫Ω∂F∂tdΩ+∫SCFdS (17) ddt∫SFdS=∫S∇˙FdS-∫SCFBiidS (18) В правой части (17, 18) первые члены показывают, как изменяется скалярное поле, а вторые члены показывают, как развивается геометрия. В учебниках по тензорному исчислению есть строгие математические доказательства этих формул; мы не воспроизводим их здесь. Вместо этого мы интуитивно показываем, почему необходимо учитывать только скорость поверхности раздела. Строгое математическое доказательство следует из основной теоремы исчисления
Строгое математическое доказательство следует из основной теоремы исчисления
В случае интеграла по объему или интеграла по поверхности можно показать, что b ′( t ) заменяется граничной скоростью C .
Интуитивное объяснение довольно простое. Предположим, что скорости поверхности раздела нет, тогда скорость на замкнутой поверхности имеет только касательную составляющую. Для каждого заданного времени касательная скорость (если нет граничной скорости) переводит каждую точку в соседнюю точку и, следовательно, не добавляет новую площадь к замкнутой поверхности (или новый объем к замкнутому пространству, или новую длину к замкнутой кривой) .Таким образом, тангенциальная скорость просто вызывает вращательное движение (или равномерное поступательное движение) объекта и может быть исключена из аддитивных членов при интегрировании. Возможно, это утверждение легче понять для одномерного движения.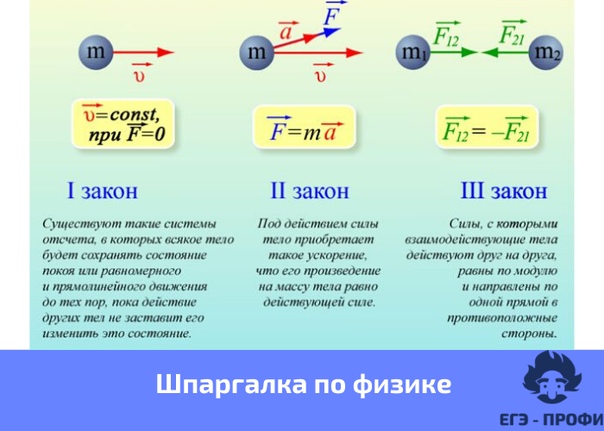 Предположим, что материальная точка движется по некоторой траектории (некоторой замкнутой кривой или петле), тогда в каждой точке скорость материальной точки является касательной к кривой. Теперь можно перевести это движение в движение замкнутой кривой, где петля имеет только тангенциальную скорость.В этом аспекте встроенная петля только вращается (равномерно перемещается в плоскости) без локального изменения длины, поэтому тангенциальная скорость кривой не добавляет новой длины кривой (то же самое верно для открытой кривой с фиксированными концами).
Предположим, что материальная точка движется по некоторой траектории (некоторой замкнутой кривой или петле), тогда в каждой точке скорость материальной точки является касательной к кривой. Теперь можно перевести это движение в движение замкнутой кривой, где петля имеет только тангенциальную скорость.В этом аспекте встроенная петля только вращается (равномерно перемещается в плоскости) без локального изменения длины, поэтому тангенциальная скорость кривой не добавляет новой длины кривой (то же самое верно для открытой кривой с фиксированными концами).
3. Общие уравнения поверхностных движений
Полностью неограниченные и точные уравнения для движущихся трехмерных поверхностей в электромагнитном поле, когда взаимодействие с окружающей средой игнорируется, читается как
∇˙ρ+∇i(ρVi)=ρCBii (20) ∂α(ρVα(∇˙C+2Vi∇iC+ViVjBij) −Vα(14µ0FµνFµν+AµJµ))=fa (21) ∫SρVi(∇˙Vi+Vj∇jVi-C∇iC-CVjBji)dS=∫ΩfiaidΩ (22) где ρ — поверхностная плотность массы, V α , V i — координатная и тангенциальная составляющие поверхностной скорости, C — граничная скорость, α = 0, 1, 2, 3 для четырехмерного пространственно-временного объемлющего пространства Минковского, i = 0, 1, 2 для псевдориманова многообразия (поверхности), B ij — тензор кривизны поверхности, тензор электромагнитного поля, Fα=Jα-∂βFβα, J α – α-компонента четырехтока J→=(Jα), f, f i – нормальная и тангенциальная компоненты F→=(Fα ), a , a i — нормальная и тангенциальная составляющие ∂A→/∂t (здесь A→=(Aα) — четырехвектор), S , Ω — поверхностный и пространственный интегралы соответственно. Точный вывод (20–22) дан в нашей работе [5], мы не воспроизводим вывод этой системы в этой статье, а лишь упомянем, что первое является следствием сохранения массы, второе и третье уравнения взяты из минимума принцип действия лагранжиана и подразумевают движение по нормали (21) и по касательной (22). Для двумерной поверхностной динамики пространство Минковского становится евклидовым, так что α = 1, 2, 3, а поверхность представляет собой двумерное риманово многообразие i = 1, 2.Так что после моделирования потенциальной энергии как отрицательного объемного интеграла внутреннего давления и взаимодействия включений с окружающей средой (20–22) еще больше упрощается как
Точный вывод (20–22) дан в нашей работе [5], мы не воспроизводим вывод этой системы в этой статье, а лишь упомянем, что первое является следствием сохранения массы, второе и третье уравнения взяты из минимума принцип действия лагранжиана и подразумевают движение по нормали (21) и по касательной (22). Для двумерной поверхностной динамики пространство Минковского становится евклидовым, так что α = 1, 2, 3, а поверхность представляет собой двумерное риманово многообразие i = 1, 2.Так что после моделирования потенциальной энергии как отрицательного объемного интеграла внутреннего давления и взаимодействия включений с окружающей средой (20–22) еще больше упрощается как
где P + , Π – внутреннее гидродинамическое и осмотическое давление соответственно. Вывод (20–22) можно найти у Свинтрадзе [5]. Мы выводим (23-25) в разделе Приложения.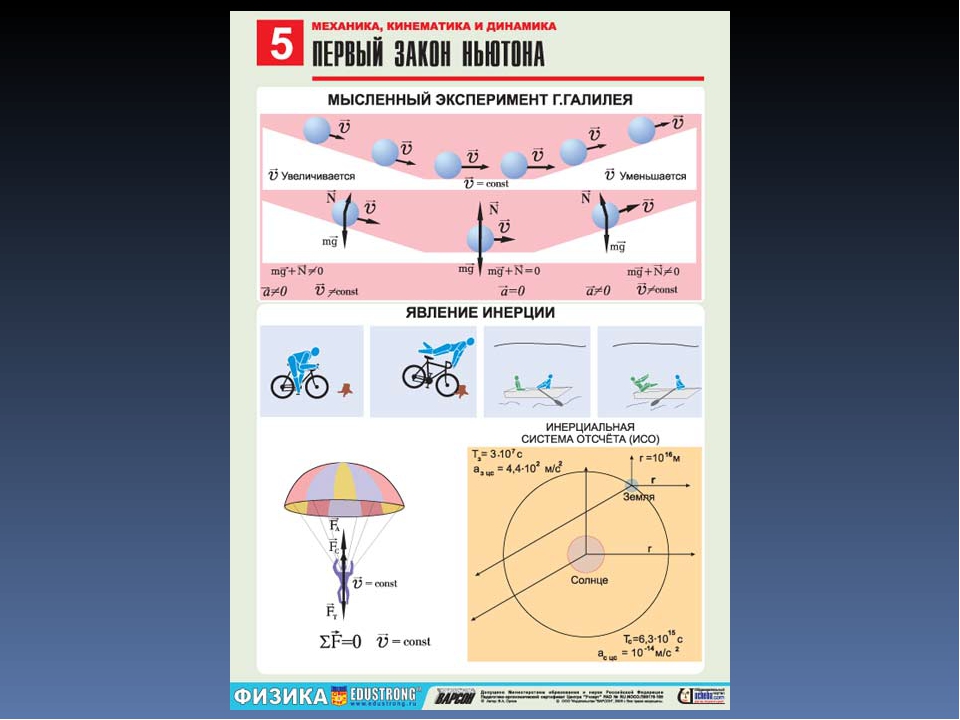 Примечательно, что из последней системы уравнений только второе уравнение (24) отличается от уравнений динамической пленки жидкости [42, 44]
Примечательно, что из последней системы уравнений только второе уравнение (24) отличается от уравнений динамической пленки жидкости [42, 44]
, где σ — поверхностное натяжение. Уравнение (26) справедливо только тогда, когда поверхность может быть описана с постоянным во времени поверхностным натяжением [42, 44], что означает, что поверхность однородна и поверхностное натяжение постоянно, а (24) не имеет этого ограничения. Используя (26) в (24) и учитывая, что в равновесных процессах внутреннее давление такое же, как и внешнее, получается точно такое же уравнение движения в нормальном направлении (39), как и при использовании первого закона термодинамики ( увидеть ниже).
∂α(σVαBii+(P++Π)Vα)=-(∂αP++∂αΠ)Vα (27)Следует отметить, что (23–25) также следует из (20–22), если применить тот же формализм, что и в (30–32). Действительно, пространство является трехмерным евклидовым, так что α = 1, 2, 3, а поверхность двумерной римановой ( i = 1, 2) для относительно медленно движущихся поверхностей, а потенциальная энергия может быть записана как:
U=∫Ω(14µ0FµνFµν+AµJµ) =∫Ω(-ϵ02E2+1µ0B2-qφ+A→J→)dΩ (28), где E→,B→ — электрическое и магнитное поля, а q,φ,A→,J→ — плотность заряда, электрический потенциал, магнитный векторный потенциал и вектор плотности тока соответственно. С учетом формализма (30–32) находим
С учетом формализма (30–32) находим
Принимая во внимание (29) и то, что давление создается нормальной силой, приложенной к поверхности, находим fa=-Vα∂α(P++Π) и в касательном направлении fiai=0, тогда (20–22) принимает вид (23–25). Электромагнитная потенциальная энергия может быть обобщена, если принять во внимание окружающую среду, которая входит в энергетические термины в виде связанных и свободных зарядов, а электрические/магнитные поля заменены векторами поляризации и намагниченности [5].
4. Результаты и обсуждение
4.1. Общие предположения
В этом разделе мы применяем основы термодинамики и фундаментальные теоремы исчисления движущихся поверхностей для демонстрации кратчайшего вывода уравнения, описывающего движение однородной, замкнутой двумерной поверхности с неизменным во времени поверхностным натяжением в нормальном направлении (27). Рассмотрим систему, состоящую из водной среды с образовавшейся в ней замкнутой поверхностью (рис. 3). Система изолирована с постоянной температурой, и на поверхности нет ни поглощенного, ни рассеянного тепла; другими словами, процесс является адиабатическим.Согласно первому закону термодинамики, поскольку теплота не рассеивается и не поглощается, изменение внутренней энергии поверхности должно составлять
3). Система изолирована с постоянной температурой, и на поверхности нет ни поглощенного, ни рассеянного тепла; другими словами, процесс является адиабатическим.Согласно первому закону термодинамики, поскольку теплота не рассеивается и не поглощается, изменение внутренней энергии поверхности должно составлять
, где δ Вт — бесконечно малая работа, совершенная над подсистемой, а dE — бесконечно малое изменение внутренней энергии. Поскольку температура системы постоянна, дифференциал внутренней энергии подсистем можно представить как
, где U — полная потенциальная энергия поверхности.По определению элементарная работа, совершаемая над подсистемой, равна
. δW=(P-+Π)dΩ (32) где, P − , Π – внешнее гидродинамическое и осмотическое давление, приложенное к поверхности окружающей средой соответственно, а Ω – объем, который поверхность заключает в себе границу S площади поверхности. Предположим, что поверхность однородна (т. е. частицы материала равномерно распределены по поверхности), так что полная потенциальная энергия есть интегрирование потенциальной энергии на единицу площади по поверхности, тогда
е. частицы материала равномерно распределены по поверхности), так что полная потенциальная энергия есть интегрирование потенциальной энергии на единицу площади по поверхности, тогда
, где σ — потенциальная энергия на единицу площади и называется поверхностным натяжением бумаги.Поскольку мы обсуждаем простейший случай системы, состоящей из водной среды и единственной замкнутой поверхности, можно предположить, что поверхностное натяжение не является переменным во времени. Используя (30–33) после нескольких строк алгебры, мы оштрафовали на
∫SσdS=∫Ω(P-+Π)dΩ (34)Рисунок 3 . Графическое изображение изолированной системы, содержащей водный раствор. Молекулы воды представлены красными и белыми палочками. Граница системы показана белыми гранями с черными краями. Подсистема-мицелла представляет собой замкнутую поверхность, синее пятно в центре системы.
Если предположить, что поверхность движется так, что (34) остается в силе при любых вариациях времени, то дифференцирование по времени левой части должно быть равно дифференцированию по времени правого интеграла. Поскольку в правой части стоит интеграл по пространству, дифференцирование по времени можно включить в интеграл, используя общие теоремы дифференцирования пространственного и поверхностного интегралов (17–18), так что теорема интегрирования пространственного интеграла, учитывающая С учетом объемного движения выполняется, следовательно:
Поскольку в правой части стоит интеграл по пространству, дифференцирование по времени можно включить в интеграл, используя общие теоремы дифференцирования пространственного и поверхностного интегралов (17–18), так что теорема интегрирования пространственного интеграла, учитывающая С учетом объемного движения выполняется, следовательно:
Для вычисления производной поверхностного интеграла по времени необходимо учесть теорему о дифференцировании поверхностного интеграла по времени (18), из которой следует, что при неизменном во времени поверхностном натяжении
ddt∫SσdS=∫S-σCBiidS (36) Где C=VαNα — скорость поверхности раздела, N α — компонент α нормали к поверхности и V = ∂ X α /∂ t — координатная скорость, X — координатная скорость, X общая координата, а Bii — это след тензора смешанной кривизны, обычно известного как средняя кривизна. После нескольких строк алгебры, складывающих (34–36), мы находим
После нескольких строк алгебры, складывающих (34–36), мы находим
Обобщенная теорема Гаусса преобразует поверхностный интеграл в левой части (37) в пространственный интеграл, так что
(38)Комбинация (37) и (38) немедленно дает уравнение движения поверхности в нормальном направлении
∂α(σVαBii+(P-+Π)Vα)=-(∂αP-+∂αΠ)Vα (39)Для равновесных процессов внутреннее и внешнее давления идентичны P − = P + , так что (39) становится идентичным уравнению движения в нормальном направлении, наблюдаемому из основных уравнений (23–27).Также следует отметить, что (39) справедливо только для движения однородных поверхностей с неизменным во времени поверхностным натяжением в нормальном направлении, поэтому оно не демонстрирует деформации в тангенциальных направлениях. Уравнение (39) еще более упрощается, когда поверхность приходит в равновесие с растворителем, где расходимость поверхностной скорости ∂αVα (стационарная граница раздела) вместе с ∂ P /∂ t (где P = P − +Π) обращается в нуль, то решение (39) с учетом условия (35) принимает вид
Результат (40) показывает, что решение представляет собой постоянную среднюю кривизну (СМС) поверхностей. Такие CMC редки, и их может быть много, если ослабить условие, которое мы ограничили системой. Мы рассматриваем изолированную систему, где поверхность является замкнутой подсистемой, эти два предварительных условия математически означают, что обсуждаемая нами поверхность является компактной вложенной поверхностью в ℝ 3 . Согласно теореме единственности А. Д. Александрова, если компактная поверхность, вложенная в ℝ 3 , имеет постоянную ненулевую среднюю кривизну, то она является сферой [45]. Соответственно решение (40) есть сфера (поскольку мы имеем компактное двумерное многообразие в евклидовом пространстве).Когда
Такие CMC редки, и их может быть много, если ослабить условие, которое мы ограничили системой. Мы рассматриваем изолированную систему, где поверхность является замкнутой подсистемой, эти два предварительных условия математически означают, что обсуждаемая нами поверхность является компактной вложенной поверхностью в ℝ 3 . Согласно теореме единственности А. Д. Александрова, если компактная поверхность, вложенная в ℝ 3 , имеет постоянную ненулевую среднюю кривизну, то она является сферой [45]. Соответственно решение (40) есть сфера (поскольку мы имеем компактное двумерное многообразие в евклидовом пространстве).Когда
поверхность является сфероидом (или цилиндром, если ослабить ограничение на компактность, делающее цилиндр бесконечно длинным) и становится плоской (опять же, когда аргумент компактности ослабляется) или другой формой с нулевой средней кривизной, когда аргумент компактности не ослабляется, но контур поверхности остается фиксированным . Этот удивительно простой и элегантный вывод объясняет все формы, которые поверхности могут принимать в водном растворе в равновесных условиях.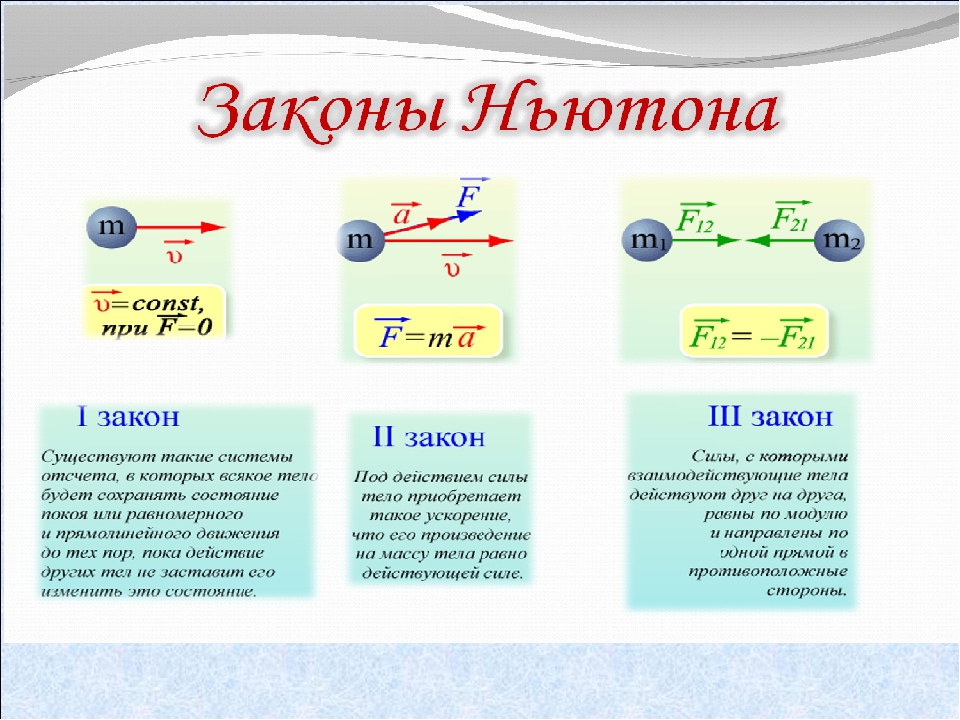 Если условие компактности ослаблено, то (40) предсказывает, что в дополнение к цилиндру и плоскости все другие поверхности CMC также являются равновесными формами для движущихся поверхностей.Принимая во внимание, что поверхностное натяжение вообще может быть функцией многих переменных, таких как гауссова кривизна, жесткость на изгиб, спонтанная кривизна, концентрация молекул, геометрия молекул ПАВ и т. д., то (39) может предсказать возможные деформации различной формы поверхности и их широкий диапазон статических форм. В самом деле, если учесть, что поверхностное натяжение, определяемое как потенциальная энергия на единицу площади, может быть функцией средней кривизны σ=σ(Bii), то в разложении Тейлора σ(Bii) естественным образом возникают все дополнительные члены.Эти обобщения и флуктуации температуры могут быть включены в уравнения, но это не входит в задачу данной статьи и должно рассматриваться отдельно. Можно даже предложить σ как не зависящий от времени гамильтониан Хельфриха, и тогда (39, 40) станет уравнением статических форм для однородных поверхностей с неизменным во времени поверхностным натяжением.
Если условие компактности ослаблено, то (40) предсказывает, что в дополнение к цилиндру и плоскости все другие поверхности CMC также являются равновесными формами для движущихся поверхностей.Принимая во внимание, что поверхностное натяжение вообще может быть функцией многих переменных, таких как гауссова кривизна, жесткость на изгиб, спонтанная кривизна, концентрация молекул, геометрия молекул ПАВ и т. д., то (39) может предсказать возможные деформации различной формы поверхности и их широкий диапазон статических форм. В самом деле, если учесть, что поверхностное натяжение, определяемое как потенциальная энергия на единицу площади, может быть функцией средней кривизны σ=σ(Bii), то в разложении Тейлора σ(Bii) естественным образом возникают все дополнительные члены.Эти обобщения и флуктуации температуры могут быть включены в уравнения, но это не входит в задачу данной статьи и должно рассматриваться отдельно. Можно даже предложить σ как не зависящий от времени гамильтониан Хельфриха, и тогда (39, 40) станет уравнением статических форм для однородных поверхностей с неизменным во времени поверхностным натяжением.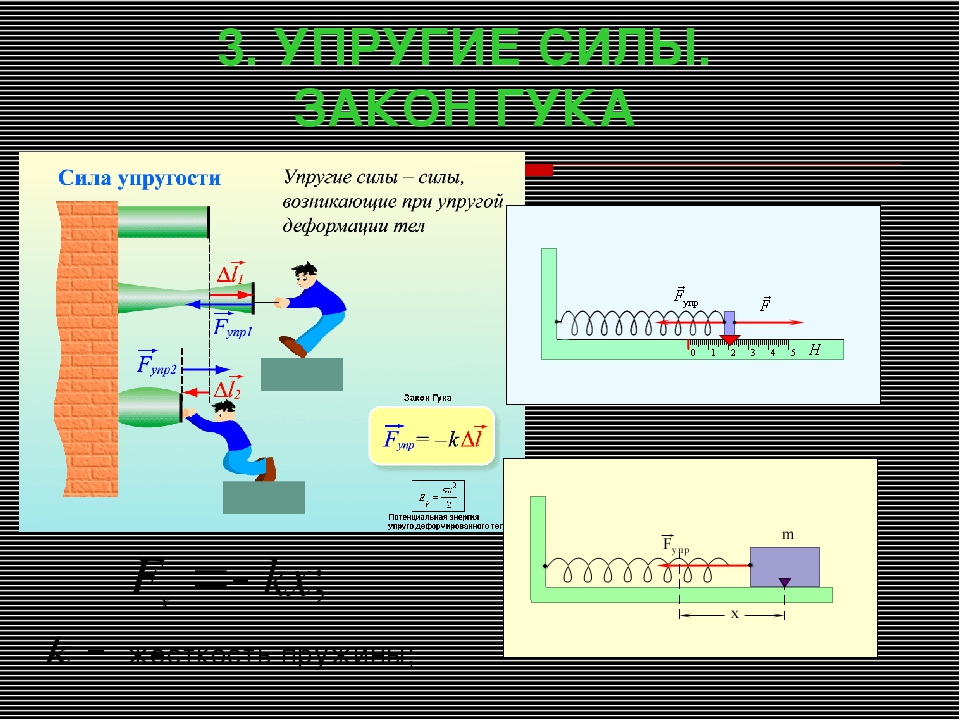 На самом деле мы поясним это утверждение в следующем подразделе.
На самом деле мы поясним это утверждение в следующем подразделе.
4.2. Актуальность уравнения формы
Здесь мы даем краткое сравнение наших уравнений движения с формализмом Хельфриха и показываем, что уравнение формы является стационарным приближенным решением уравнения нормального движения (39).
Предположим, что система передемпфирована, поэтому изменения кинетической энергии намного меньше, чем изменения потенциальной энергии. Во всех наших уравнениях мы моделируем потенциальную энергию как
Предположим, что гамильтониан системы H=∫SρV2/2dS+∫ΩP-dΩ моделируется как свободная энергия на поверхности ∫S(σ0+k/2(Bii-K0)2+kKG)dS, где σ 0 — классически определенное постоянное поверхностное натяжение, k — постоянная жесткости при изгибе, K 0 — спонтанная кривизна и K G — гауссова кривизна.Такая интерпретация свободной энергии называется моделью спонтанной кривизны [8, 31]. Поскольку система передемпфирована, изменение кинетической энергии бесконечно мало, поэтому в первом приближении δ∫SρV2/2dS≈0 и имеем
H=∫SρV22dS+∫ΩP-dΩ =∫S(σ0+k/2(Bii-K0)2+kKG)dSδ∫ΩP-dΩ=δ∫S(σ0+k/2(Bii-K0)2+kKG) дС (42) Для оценки вариации гамильтониана заметим, что согласно дифференцированию по времени пространственных интегралов (17) δ∫ΩP-dΩ=∫Ω∂P-/∂tdΩ+∫SCP-dS. С другой стороны, вариация свободной энергии Хелфриха, которую можно ограничить нормальными вариациями [8], составляет
С другой стороны, вариация свободной энергии Хелфриха, которую можно ограничить нормальными вариациями [8], составляет
, где N — нормальная координата, и, таким образом, скорость поверхности раздела равна C = ∂ N /∂ t .Для стационарных или близких к стационарным форм ∂ P − /∂ t ≈ 0 с учетом (42, 43) и вариации ∫ΩP-dΩ находим
∫S(σ0Bii−k(∇a∇aBii−12(Bii−K0)[(Bii−K0)Bii−2(Bii)2+4KG]))CdS=∫SCP−dS (44)Последнее уравнение (44) должно выполняться для любой скорости поверхности раздела C , поэтому
σ0Bii−k(∇a∇aBii−12(Bii−K0)[(Bii−K0)Bii−2(Bii)2+4KG])=P− (45) (45) в точности соответствует уравнению формы [4, 8, 22, 23, 31]. Обратите внимание, что уравнение формы (45) может быть получено из уравнения движения в нормальном направлении (39) для случая, близкого к стационарному. Действительно, согласно (39) с учетом того, что поверхностное давление можно моделировать из (44, 45), находим
Действительно, согласно (39) с учетом того, что поверхностное давление можно моделировать из (44, 45), находим
Учитывая, что для стационарных форм ∂P-/∂t=0,∂αVα=0, последнее уравнение имеет тривиальное решение
σ0,Bii−k(∇a∇aBii−12(Bii−K0)[(Bii−K0)Bii−2(Bii)2+4KG])=P0 (47) где σ0,,P0 — некоторые постоянные поверхностное натяжение и давление соответственно. Эти расчеты формально устанавливают, что уравнение формы является приближенным решением наших уравнений движений, ограниченных условиями: неизменное во времени поверхностное натяжение и стационарные границы раздела; и действителен только для систем с избыточным демпфированием.Заметим, что аналитическое решение (40) является точным и справедливым только для поверхностей, находящихся в равновесии с окружающей средой, тогда как уравнение формы является приближенным решением для стационарных поверхностей. Неудивительно, что стационарные формы геометрически богаче, чем равновесные. Равновесные формы могут принимать только постоянную среднюю кривизну.
4.3. Физическое применение, мицелла
Мы можем подвергнуть уравнение (39) и его решение (40) испытанию на гомогенную мицеллярную поверхность, уравновешенную водным раствором.На основании (40) можно рассчитать минимальное значение радиуса мицеллы. Значение следа тензора смешанной кривизны для сферы равно
где R радиус.
Рассчитаем значение поверхностного давления, когда мицелла еще может существовать. Липиды в мицелле удерживаются на поверхности за счет гидрофобных взаимодействий со средней энергией в области водородных связей. Поскольку значения энергии водородной связи в литературе несколько неопределенны, в первом приближении мы берем среднюю энергию для интервала энергий водородной связи и приписываем ее молекуле липида.Нижняя граница интервала (минимальная энергия) для водородной связи XH ··· Y составляет около 1 кДж на моль ( CH ··· C ед.), а верхняя граница – около 161 кДж на моль ( ед. FH ··· F блок), нижнее и верхнее значения взяты по ссылкам [46, 47].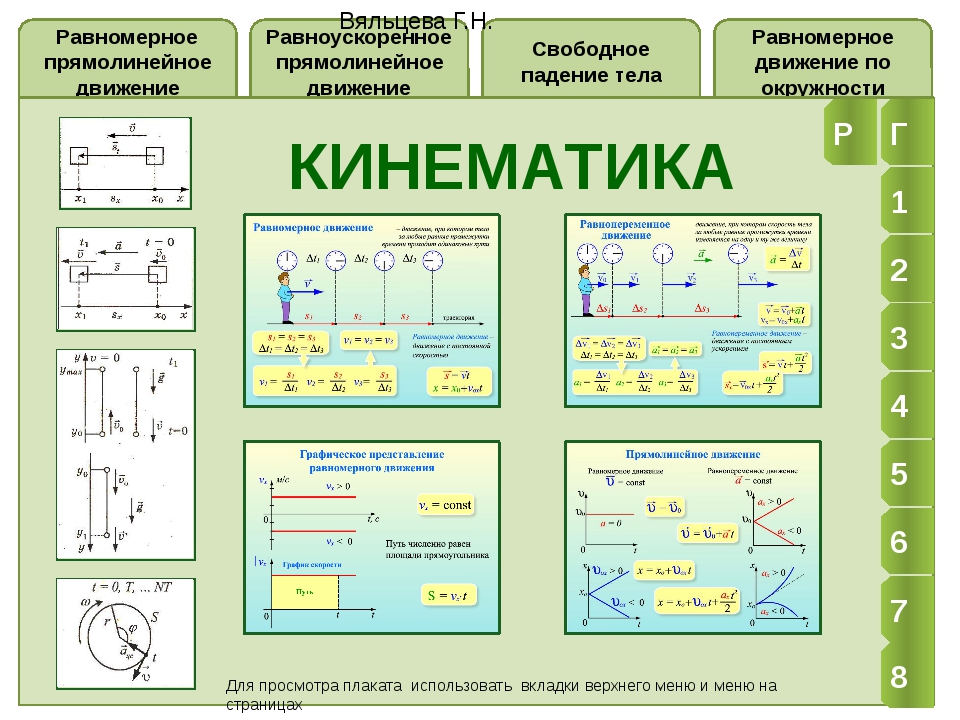 Следовательно, средняя энергия составляет примерно (1+161)/2 = 81 кДж / моль ≈ 13·10 −20 Дж . Оценить энергию водородной связи, приходящуюся на молекулу неопределенной формы (молекулу липида), в первом приближении следует приписать ей среднюю энергию и рассмотреть сферическую форму с радиусом инерции.Конечно, это низкоуровневое приближение, но даже такие грубые расчеты дают разумные результаты. После всех этих грубых оценок давление, необходимое для перемещения одного липида с поверхности, чтобы вызвать критические деформации поверхности, составляет около средней энергии на средний объем молекулы липида
Следовательно, средняя энергия составляет примерно (1+161)/2 = 81 кДж / моль ≈ 13·10 −20 Дж . Оценить энергию водородной связи, приходящуюся на молекулу неопределенной формы (молекулу липида), в первом приближении следует приписать ей среднюю энергию и рассмотреть сферическую форму с радиусом инерции.Конечно, это низкоуровневое приближение, но даже такие грубые расчеты дают разумные результаты. После всех этих грубых оценок давление, необходимое для перемещения одного липида с поверхности, чтобы вызвать критические деформации поверхности, составляет около средней энергии на средний объем молекулы липида
где 4πrG3/3 – расчетный объем молекулы липида, рассматриваемой как сфера с радиусом вращения r G ≈ 1 нм .С другой стороны, поверхностное натяжение жидкого монослоя при оптимальной упаковке липидов составляет около σ ≈ 3·10 −2 Н / м [7, 48, 49], используя эти и (48, 49) в (40) расчетный радиус мицеллы равен
R≈2·3·10-23,1·107=19,3±0,1Å (50) Эти расчеты дают минимальный радиус в нанометровом масштабе и очень хорошо согласуются с экспериментальными и расчетными схемами [50, 51]. Чтобы дополнительно подтвердить результат (50), мы запустили моделирование Micelle Builder на основе CHARMM [52, 53] для 100 молекул фосфолипидов (липидов DHPC).В результате моделирования (рис. 4) образовалась сферическая мицелла диаметром 38,5 ± 0,1 Å. Эти расчеты действительно показывают, что даже такие грубые оценки дают разумную точность.
Чтобы дополнительно подтвердить результат (50), мы запустили моделирование Micelle Builder на основе CHARMM [52, 53] для 100 молекул фосфолипидов (липидов DHPC).В результате моделирования (рис. 4) образовалась сферическая мицелла диаметром 38,5 ± 0,1 Å. Эти расчеты действительно показывают, что даже такие грубые оценки дают разумную точность.
Рисунок 4 . Смоделированные трехмерные координаты мицеллы в водном растворе отображают сферу диаметром 38,5 Å. (слева) дигексаноилфосфатидилхолин (фосфолипиды ДГФХ) смоделированы в виде оранжевых шариков. (справа) Картирование Гаусса при разрешении контура 8Å мицеллы показывает сферическую структуру.
Для получения более убедительных оценок необходимо учитывать, что ни липиды не являются сферическими, ни гидрофобные взаимодействия на липид не являются средней энергией одинарной водородной связи. Во втором приближении липиды больше не являются неопределенными сферами, а имеют четко определенную геометрию поверхностно-активного вещества. Гидрофобная энергия больше не является средней энергией одинарной водородной связи, а составляет 1 кДж на моль на единицу — CH 2 -. Во всех моделях атомов мы использовали липидную молекулу дигексаноилфосфатидилхолина (DHPC), имеющую 12- CH 2 — единиц (рис. 5) на гидрофобный хвост, поэтому гидрофобная энергия составляет около 12 кДж / моль ≈ 1.99·10 −20 Дж . Точный расчет объема молекул липидов с использованием калькулятора объема полостей, каналов и расщелин [54] дает оценку объема около 894Å 3 . Используя это значение, можно получить
Гидрофобная энергия больше не является средней энергией одинарной водородной связи, а составляет 1 кДж на моль на единицу — CH 2 -. Во всех моделях атомов мы использовали липидную молекулу дигексаноилфосфатидилхолина (DHPC), имеющую 12- CH 2 — единиц (рис. 5) на гидрофобный хвост, поэтому гидрофобная энергия составляет около 12 кДж / моль ≈ 1.99·10 −20 Дж . Точный расчет объема молекул липидов с использованием калькулятора объема полостей, каналов и расщелин [54] дает оценку объема около 894Å 3 . Используя это значение, можно получить
С другой стороны, используя такое же поверхностное натяжение монослоя жидкости при оптимальной упаковке липидов, получаем R = 27 ± 0,1 Å. Моделирование всех атомов также генерирует сферическую структуру диаметром 54 ± 0.1Å (рис. 5). В этой оценке все же есть некоторая неопределенность, так как мы приписали 1 кДж/моль энергии на единицу − CH 2 − и опирались на данные литературы [46, 47], тогда как в другой литературе упоминается, что гидрофобные взаимодействия около 4 кДж/моль на единицу − CH 2 − [55].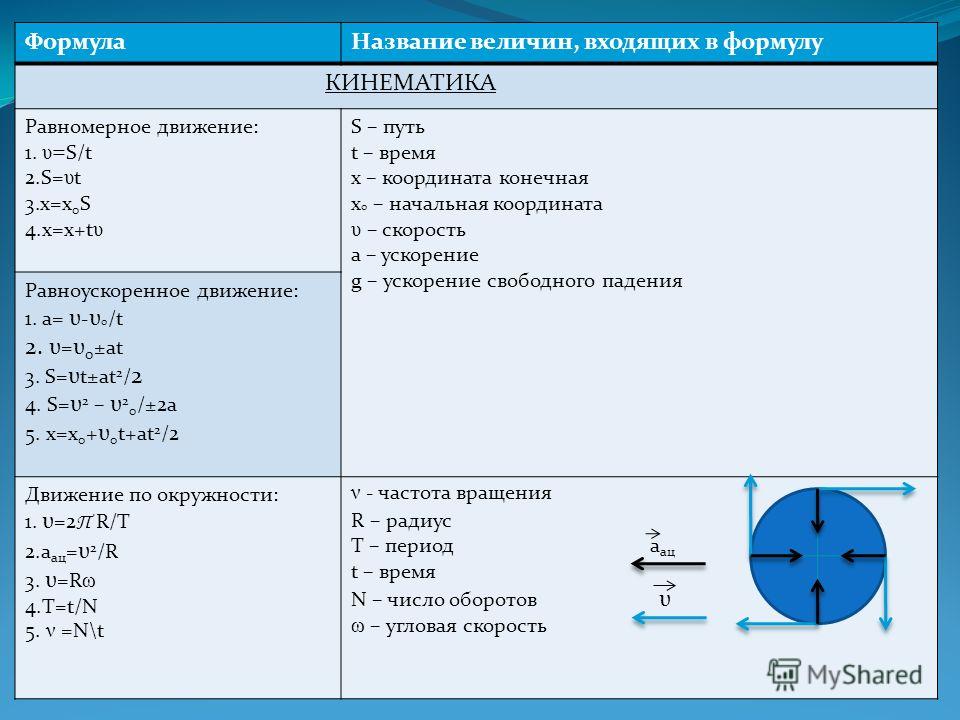 На наш взгляд, это несоответствие может быть разрешено, если рассчитать гидрофобную энергию, исходя из потенциальной энергии
На наш взгляд, это несоответствие может быть разрешено, если рассчитать гидрофобную энергию, исходя из потенциальной энергии
, где E→Ch3 — электрическое поле на − CH 2 −, ϵ 0 — диэлектрическая проницаемость в вакууме, а Ω обозначает объем молекул липидов.Уравнение (52) непосредственно вытекает из члена FμνFμν, записанного в уравнениях движения (20–22 и 28–29). Для электростатики
U=∫Ω14μ0FμνFμνdΩ=-∫Ωϵ02ECh32dΩ (53), поэтому следует перейти к тщательному расчету электрического поля для каждой − CH 2 − единиц, затем взять сумму электрического поля и возвести ее в квадрат (мы не собираемся делать это в этой статье). Также может возникнуть вопрос, почему в этих расчетах не учитывается энергия гидрофильного взаимодействия. Гидрофильная головка липидной молекулы находится в контакте с молекулами воды, поэтому не требуется никакой работы, чтобы вытащить ее в водном растворе из липидного слоя.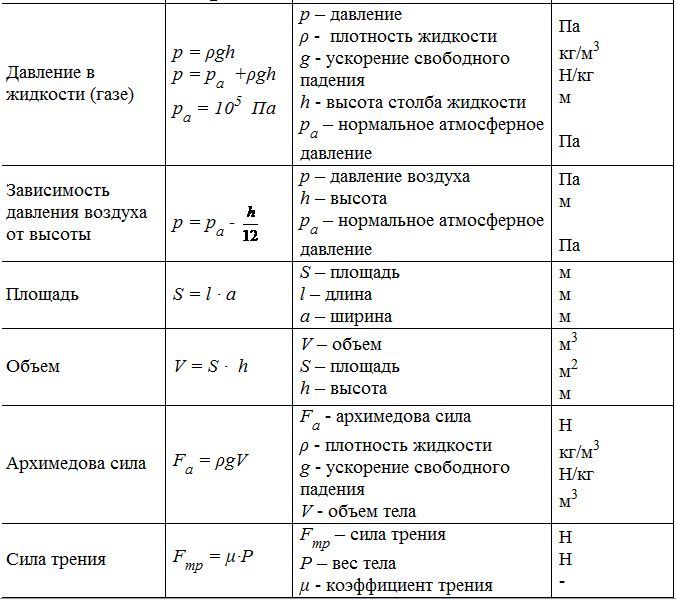 Поэтому энергией гидрофильного взаимодействия можно пренебречь. Основная работа ведется по преодолению гидрофобных взаимодействий между липидными хвостами.
Поэтому энергией гидрофильного взаимодействия можно пренебречь. Основная работа ведется по преодолению гидрофобных взаимодействий между липидными хвостами.
Рисунок 5 . Моделирование всего атома мицеллы DHPC. (A) На рисунке показана геометрия молекулы поверхностно-активного вещества DHPC, используемая в моделировании, и дано параметрическое описание объема, площади поверхности, сферичности и эффективного радиуса. (B) Указывает результат атомистического моделирования, очерченный по карте Гаусса, и диаметр мицеллы, измеренный с помощью PyMol.Диаметр смоделированной мицеллы составляет 54,0 Å с погрешностью измерения 0,1 Å.
5. Заключение
Мы представили основу для анализа динамики двумерной поверхности (обозначенной в тексте как мицелла) с использованием первого закона термодинамики и исчисления движущихся поверхностей. В окончательных уравнениях нормального движения (39,27) мы предполагаем, что поверхность однородна и имеет неизменное во времени поверхностное натяжение. Однако общие уравнения (23–25) не имеют этих ограничений и указывают произвольное движение по нормальной деформации, а также в касательных направлениях, но являются аналитически более сложными.Решения нормальных уравнений движения в условиях равновесия удивительно просты и отображают все возможные равновесные формы. Мы применили формализм для оценки оптимального радиуса мицеллы и сравнили оценки со всеми моделями атомов. Даже для низкоуровневых приближений мы обнаружили замечательное соответствие между теоретически рассчитанным радиусом и радиусом, полученным из атомистического моделирования и из экспериментов. Теорию легко применить к любым замкнутым поверхностям; такими являются везикулы, мембраны, капли воды или мыльные пленки.
Однако общие уравнения (23–25) не имеют этих ограничений и указывают произвольное движение по нормальной деформации, а также в касательных направлениях, но являются аналитически более сложными.Решения нормальных уравнений движения в условиях равновесия удивительно просты и отображают все возможные равновесные формы. Мы применили формализм для оценки оптимального радиуса мицеллы и сравнили оценки со всеми моделями атомов. Даже для низкоуровневых приближений мы обнаружили замечательное соответствие между теоретически рассчитанным радиусом и радиусом, полученным из атомистического моделирования и из экспериментов. Теорию легко применить к любым замкнутым поверхностям; такими являются везикулы, мембраны, капли воды или мыльные пленки.
В заключение, хотя аналитическое решение (40) выглядит как обобщенный закон Юнга-Лапласа, разница очевидна. Bii — это след тензора смешанной кривизны, известный как средняя кривизна, и когда средняя кривизна постоянна, он определяет весь класс поверхностей с постоянной средней кривизной (CMC). Обобщенный закон Юнга-Лапласа априори сформулирован для сферических морфологий и поэтому в некоторых частных случаях может быть получен из (40) постоянной средней кривизны форм.Условием соблюдения частного случая является компактность. Однако аргумент компактности можно ослабить в нашем выводе, если рассматриваемая система будет намного больше, чем подсистема. Следовательно, решение (40) эффективно предсказывает образование всех поверхностей ККМ, в то время как закон Юнга-Лапласа верен только для сферических структур. Также при выводе соотношения Юнга-Лапласа одной из краеугольных идей является предположение о сферических симметриях, в то время как наш вывод свободен от симметрий и объясняет, почему поверхности ККМ имеют такие многочисленные формы в природе, наблюдаемые даже на молекулярном уровне.Действительно, согласно полученным результатам, любая однородная замкнутая поверхность с неизменным во времени поверхностным натяжением принимает форму ККМ, когда приходит в равновесие с окружающей средой.
Обобщенный закон Юнга-Лапласа априори сформулирован для сферических морфологий и поэтому в некоторых частных случаях может быть получен из (40) постоянной средней кривизны форм.Условием соблюдения частного случая является компактность. Однако аргумент компактности можно ослабить в нашем выводе, если рассматриваемая система будет намного больше, чем подсистема. Следовательно, решение (40) эффективно предсказывает образование всех поверхностей ККМ, в то время как закон Юнга-Лапласа верен только для сферических структур. Также при выводе соотношения Юнга-Лапласа одной из краеугольных идей является предположение о сферических симметриях, в то время как наш вывод свободен от симметрий и объясняет, почему поверхности ККМ имеют такие многочисленные формы в природе, наблюдаемые даже на молекулярном уровне.Действительно, согласно полученным результатам, любая однородная замкнутая поверхность с неизменным во времени поверхностным натяжением принимает форму ККМ, когда приходит в равновесие с окружающей средой.
Вклад авторов
Автор подтверждает, что является единственным автором этой работы и одобрил ее публикацию.
Заявление о конфликте интересов
Автор заявляет, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.
Благодарности
Мы благодарим д-ра Франка Джулихера (MPIPKS) и д-ра Эрвина Фрея (LMU) за стимулирующие дискуссии. Статья в ее нынешнем виде была инициирована в Центре физики Аспена, который поддерживается грантом Национального научного фонда PHY-1607611 и частично поддерживается грантом Фонда Саймонса.
Дополнительный материал
Дополнительный материал к этой статье можно найти в Интернете по адресу: https://www.frontiersin.org/articles/10.3389/fphy.2018.00136/full#дополнительный материал
Сноски
Каталожные номера
1. Cahalan MD, Parker I. Хореография клеточной подвижности и динамика взаимодействия, визуализированная с помощью двухфотонной микроскопии в лимфоидных органах. Annu Rev Immunol . (2008) 26 : 585–626. doi: 10.1146/annurev.иммунол.24.021605.0
Annu Rev Immunol . (2008) 26 : 585–626. doi: 10.1146/annurev.иммунол.24.021605.0
Реферат PubMed | Полный текст перекрестной ссылки | Академия Google
2. Пал С.К., Пеон Дж., Багчи Б., Зеваил А.Х. Биологическая вода: фемтосекундная динамика гидратации макромолекул. J Phys Chem B (2002) 106 :12376–95. дои: 10.1021/jp0213506
Полнотекстовая перекрестная ссылка | Академия Google
3. Ван С., Фибиг Т., Шиманн О., Бартон Дж. К., Зевайл А. Х. Фемтосекундное прямое наблюдение переноса заряда между основаниями в ДНК. Proc Natl Acad Sci USA. (2000) 97 :14052–5. doi: 10.1073/pnas.250483297
Реферат PubMed | Полный текст перекрестной ссылки | Академия Google
4. Хелфрич В. Упругие свойства липидных бислоев: теория и возможные эксперименты. Z Naturforsch C (1973) 28 :693–703.
Реферат PubMed | Академия Google
6. Исраэлахвили Дж. Н., Митчелл Д.Дж., Нинхэм Б.В. Теория самосборки углеводородных амфифилов в мицеллы и бислои. J Chem Soc Faraday Trans 2 (1976) 72 :1525–68.
Н., Митчелл Д.Дж., Нинхэм Б.В. Теория самосборки углеводородных амфифилов в мицеллы и бислои. J Chem Soc Faraday Trans 2 (1976) 72 :1525–68.
Академия Google
7. Исраэлахвили Дж.Н., Митчелл Д.Дж., Нинхэм Б.В. Теория самосборки липидных бислоев и везикул. Биохим Биофиз Acta (1977) 470 :185–201.
Реферат PubMed | Академия Google
9. Липовски Р., Сакманн Э. Структура и динамика мембран. Амстердам: Эльзевир (1995).
Академия Google
10. Seifert U. Конфигурации жидкостных мембран и пузырьков. Расширенная физика . (1997) 46 : 13–137.
Академия Google
13. Скривен Л.Е. Динамика уравнения движения межфазной поверхности для ньютоновских поверхностных жидкостей. Химическая инженерия .(1960) 12 : 98–108.
Академия Google
15. Gao LT, Feng XQ, Yin YJ, Gao H. Электромеханическая жидкокристаллическая модель пузырьков. J Mech Phys Solids (2008) 56 : 2844–62. doi: 10.1016/j.jmps.2008.04.006
J Mech Phys Solids (2008) 56 : 2844–62. doi: 10.1016/j.jmps.2008.04.006
Полнотекстовая перекрестная ссылка | Академия Google
17. Рамасвами С., Тонер Дж., Прост Дж. Неравновесные флуктуации, бегущие волны и нестабильности в активных мембранах. Phys Rev Letter. (2000) 84 :3494–7.doi: 10.1103/PhysRevLett.84.3494
Реферат PubMed | Полный текст перекрестной ссылки | Академия Google
20. Кэнэм П.Б. Минимальная энергия изгиба как возможное объяснение двояковогнутой формы эритроцита человека. Дж Теор Биол . (1970) 26 : 61–81.
Реферат PubMed | Академия Google
23. Чжун-Кан О.Ю., Хелфрих В. Энергия изгиба мембран везикул: общие выражения для первого, второго и третьего вариантов энергии формы и приложения к сферам и цилиндрам. Phys Rev A (1989) 39 :5280–8.
Реферат PubMed | Академия Google
24. Младенов И.А.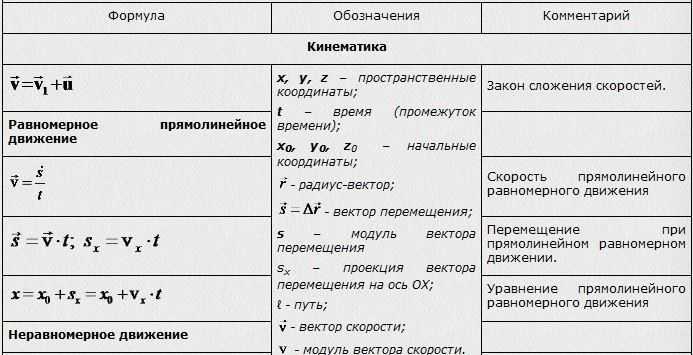 М., Джонджоров П.А., Хаджилазова М.Т., Василев В.М. Равновесные конфигурации липидных бислойных мембран и углеродных наноструктур. Коммьюнити Теор Физ . (2013) 59 : 213–28. дои: 10.1088/0253-6102/59/2/14
М., Джонджоров П.А., Хаджилазова М.Т., Василев В.М. Равновесные конфигурации липидных бислойных мембран и углеродных наноструктур. Коммьюнити Теор Физ . (2013) 59 : 213–28. дои: 10.1088/0253-6102/59/2/14
Полнотекстовая перекрестная ссылка | Академия Google
25. Светина С., Жекш Б. Энергия изгиба мембраны и определение формы фосфолипидных везикул и эритроцитов. Eur Biophys J. (1989) 17 : 101–11.
Реферат PubMed | Академия Google
28. Seifert U, Berndl K, Lipowsky R. Преобразования формы везикул: фазовая диаграмма для моделей спонтанного искривления и двухслойного взаимодействия. Phys Rev A (1991) 44 : 1182–202.
Реферат PubMed | Академия Google
30. Jülicher F, Lipowsky R. Преобразования формы везикул с внутримембранными доменами. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics (1996) 53 :2670–83.
Реферат PubMed | Академия Google
31.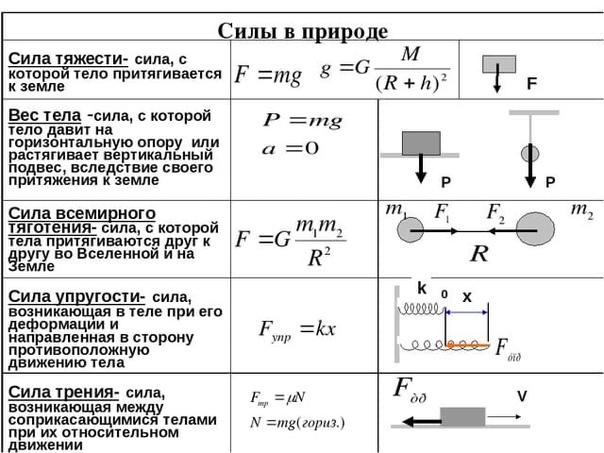 Jülicher F, Seifert U. Уравнения формы для осесимметричных пузырьков: разъяснение. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics (1994) 49 :4728–31.
Jülicher F, Seifert U. Уравнения формы для осесимметричных пузырьков: разъяснение. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics (1994) 49 :4728–31.
Реферат PubMed | Академия Google
32. Мяо Л., Зайферт У., Вортис М., Доберейнер Х.Г. Почкование переходов пузырьков жидкость-бислой: эффект эластичности разности площадей. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics (1994) 49 :5389-407.
Реферат PubMed | Академия Google
33. Генрих В., Светина С., Жекш Б. Неосесимметричные формы пузырьков в обобщенной модели двухслойной пары и переход между сплюснутой и вытянутой осесимметричными формами. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics (1993) 48 :3112–23.
Реферат PubMed | Академия Google
34. Краль-Иглич В., Светина С., Жекш Б. Существование неосесимметричных форм двухслойных пузырьков, предсказанное моделью двухслойной пары. Евро Биофиз J . (1993) 22 : 97–103.
Евро Биофиз J . (1993) 22 : 97–103.
Реферат PubMed | Академия Google
38. Свинтрадзе Д.В. Движущиеся макромолекулярные поверхности в условиях гидрофобного/гидрофильного стресса. Biophys J. (2015) 108 :512a. doi: 10.1016/j.bpj.2014.11.2807
Полнотекстовая перекрестная ссылка | Академия Google
39. Свинтрадзе Д.В. Подвижность клеток и факторы роста по дифференциально-вариационным поверхностям. Biophys J. (2016) 110 :623a.doi: 10.1016/j.bpj.2015.11.3342
Полнотекстовая перекрестная ссылка | Академия Google
40. Свинтрадзе Д.В. Геометрическое разнообразие живых организмов и вирусов. Biophys J. (2017) 112 :309a. doi: 10.1016/j.bpj.2016.11.1676
Полнотекстовая перекрестная ссылка | Академия Google
41. Tanford C. Формирование гидрофобного эффекта мицелл и биологических мембран. Нью-Йорк, штат Нью-Йорк: Wiley-Interscience (1973).
Академия Google
42.Гринфельд П. Введение в тензорный анализ и исчисление движущихся поверхностей. Нью-Йорк, штат Нью-Йорк: Springer (2010).
Академия Google
43. Adamard J. Mmoire sur le problme danalyse relatif lquilibre des Plass elastiques encastres. Творчество, Герман, Том 2; 1968.
44. Гринфельд П. Точные нелинейные уравнения для пленок жидкости и соответствующие адаптации теорем сохранения из классической гидродинамики. J Geom Symm Phys. (2009) 16 : 1–21.
Академия Google
45. Александров А.Д. Теорема единственности для поверхностей в целом. Ленинградский ун-т, 13, 19 (1958), 58. Am Math Soc Trans (Серия 2). (1958) 21 : 412–6.
46. Ларсон Дж., МакМахон Т. Газофазные бигалогенидные и псевдобигалогенидные ионы. Ионно-циклотронный резонанс определение энергий водородных связей в XHY-формах (X, Y= F, Cl, Br, CN). Неорг. хим. (1984) 23 :2029–33.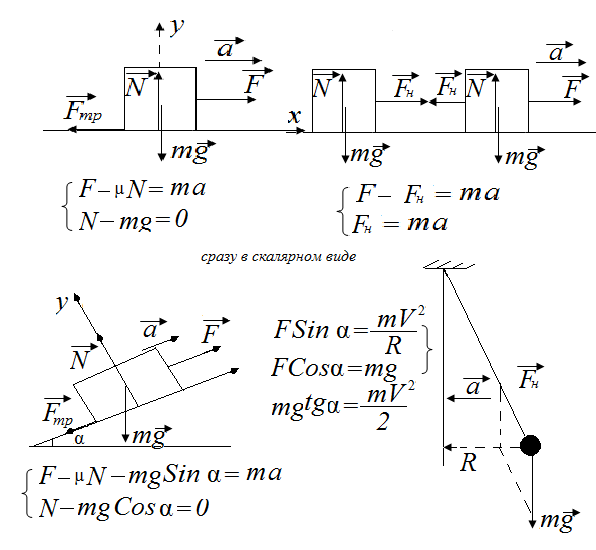
Академия Google
47.Эмсли Дж. Очень сильная водородная связь. Chem Soc Rev. (1980) 9 : 91–124.
Академия Google
49. Исраэлачвили Ю.Н. Межмолекулярные и поверхностные силы: исправленное третье издание. Амстердам: Academic Press (2011).
50. Феллер С.Э., Чжан Ю., пастор Р.В. Компьютерное моделирование границ раздела жидкость/жидкость. II. Зависимость поверхностного натяжения бислоя и монослоя от площади. J Chem Phys . (1995) 103 :10267–76.
Академия Google
51.Эгбертс Э., Марринк С.Дж., Берендсен Х.Дж. Моделирование молекулярной динамики фосфолипидной мембраны. Евро Биофиз J . (1994) 22 : 423–36.
Реферат PubMed | Академия Google
53. Cheng X, Jo S, Lee HS, Klauda JB, Im W. Конструктор мицелл CHARMM-GUI для чистых/смешанных мицеллярных и комплексных систем белок/мицелла. Модель J Chem Inf. (2013) 53 :2171–80.
 Ускорение — быстрота изменения направления
Ускорение — быстрота изменения направления Механическая энергия — это энергия, связанная с движением или положением объекта
Механическая энергия — это энергия, связанная с движением или положением объекта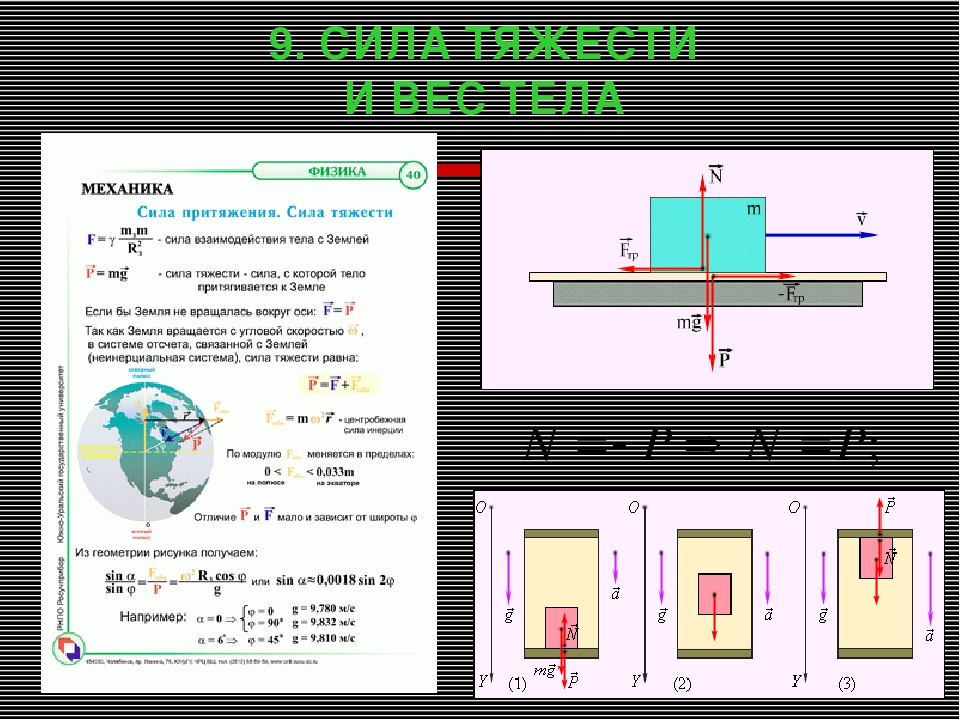 объектов из-за g= 9,81 м/с²
объектов из-за g= 9,81 м/с²