Эпюры поперечных сил и изгибающих моментов
Эпюрами внутренних поперечных сил и изгибающих моментов называют графическое представление распределения функций Q и M по длине балки при изгибе.
Посмотреть подробные примеры построения эпюр >>
Эпюры строятся для визуального представления распределения внутренних силовых факторов и определения опасных (т.е. наиболее нагруженных) с точки зрения прочности участков бруса.
Рассмотрим некоторые примеры на построение эпюр в балках:
Эпюры при чистом изгибе
Для консольной балки:
Рис. 1
имеем два силовых участка (AB и BC) и на каждом из них, применяя метод сечений, будем рассматривать, например правую от сечения часть, используя формулы и правило знаков для расчета внутренних силовых факторов.
Отсчет координаты z можно вести от единого начала координат или для каждого силового участка в отдельности.
I силовой участок (BC): 0 ≥ z1 ≥ 2a (рис.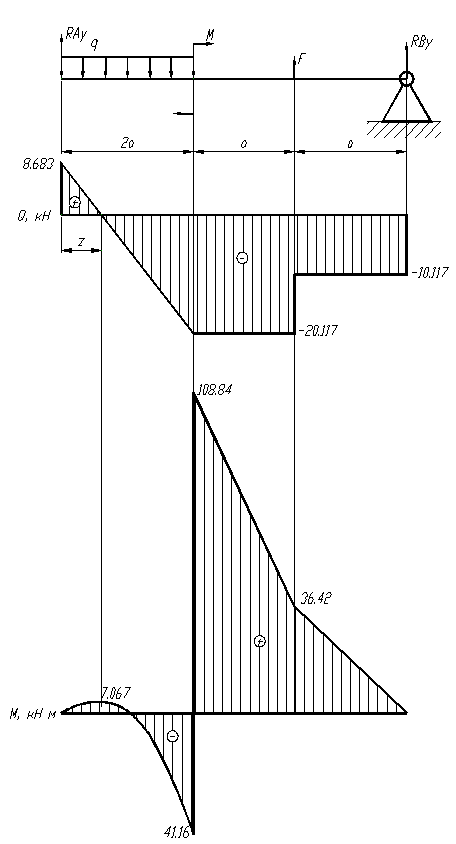
Рис. 2
т.е. Q(z1)=0 на всем участке, а M(z1)=m=const.
Ординаты эпюр Q и M со знаком плюс (+) будем откладывать вверх от нулевой (базовой) линии, при этом эпюру M будем строить на сжатых волокнах.
II силовой участок (AB): 2a ≥ z2 ≥ 5a (рис. 2 а,д)
Откладывая на границах участков в сечениях C, B и A значения полученных ординат Q и M, строим эпюры (рис. 2 б, в).
Более нагруженным оказался участок AB, он и является опасным: Mmax=|2m|.
Так как поперечные силы Q по всей длине балки равны нулю, балка испытывает чистый изгиб.
Эпюры при поперечном изгибе
Построение эпюр Q и M для балки, изображенной на рис. 3
Рис. 3
проводим аналогично, но рассматривать будем левые от сечений части, т.к. в правые войдут реакции в заделке, что несколько усложняет вычисления.
I силовой участок (AB): 0 ≥ z1 ≥ l1 (рис. 4, а, г)
Q(z1)= F=const, на всем участке постоянная величина,
M(z1)=F×z1, уравнение прямой, график строим по двум граничным точкам:
M(z1=0)=F×0=0 – в сечении A;
M(z1=l1)=F× l1 — в сечении B.
Рис. 4
II силовой участок (BC): l1 ≥ z2 ≥ (l1+ l2) (рис. 4, а, д)
Q(z2)= F-F=0;
M(z2)=F×z2— F×(z2— l1)=F ×l1=const.
Построив эпюры Q и M по всей длине балки (рис. 4 а, б, в), видим, что на первом участке — деформация прямого поперечного изгиба, т.к. Q≠0, M≠0; а на втором – прямого чистого изгиба.
Опасным является сечение B, в котором действуют Qmax=F, Mmax=Fl1.
Геометрическая проверка эпюр
Геометрическая проверка правильности построения эпюр Q и M по дифференциальным зависимостям заключается в следующем:
где α, β – углы наклона касательных к эпюрам Q и M относительно оси абсцисс (базовой линии).
На участке “AB” α1=0 (линия эпюры Q горизонтальна), следовательно,
распределенная нагрузка отсутствует;
функция M (z1) – возрастающая.
На участке “BC”:
Так как все дифференциальные проверки выполняются, эпюры построены верно.
Эпюры для двухопорных балок
Рассматривая расчетные схемы такого типа, как двухопорная балка (рис. 5),
Рис. 5
необходимо вначале найти опорные реакции и только потом строить эпюры.
Определим реакции в обеих опорах, для этого используем два независимых уравнения статики, т.к. у нас плоская система параллельных сил.
Обычно, рекомендуется использовать суммы моментов вокруг опорных точек, например: ∑MA=0 и ∑MB=0.
Записываем уравнения и находим значения реакций:
Чтобы убедиться в правильности полученных значений необходимо провести «арифметическую проверку» тождества по оставшемуся из зависимых уравнений: ∑FY=0 или ∑MС=0.
Проверим через сумму сил, приложенных к балке (включая найденные опорные реакции). Она должна равняться нулю (при округлении значений, может появиться погрешность).
Для построения эпюр рассмотрим два силовых участка:
Рис. 6
I участок (AC): 0 ≥ z1 ≥2a (рис. 6, а, г)
Q(z1)=RA-qz1 — прямая, которую строим по двум граничным точкам:
M(z1)=RAz1-qz1(z1/2)= RAz1-qz12/2 – парабола.
Строим эту кривую по трем точкам: по двум граничным (0 и 2a) и z*, которая соответствует Mmax(z*), и дифференциальной зависимости:
Определяем экстремум эпюры M на участке:
II участок (BC): 0 ≥ z2
Q(z2)= -RB= -2/3qa;
M(z2)=RBz2,
M(z2=0)=0,
M(z2=a)=2/3qa2.
Выполним проверку дифференциальных зависимостей.
I силовой участок: 0 ≥ z1 ≥ 2a
— направлена вниз, функция Q(z1) – убывающая.
— проверка визуально: чем больше угол наклона β1, тем больше значение Q(z1).
II силовой участок: 0 ≥ z2 ≥ a.
следовательно, q=0.
функция M(z) – убывающая.
Все проверки выполнены, следовательно, эпюры построены верно.
По эпюрам видно, что опасных сечений два (рис. 6):
По моменту при z1*=4/3a
По силе в сечении «A»
После построения и проверки эпюр можно приступать к расчетам балки на прочность и жесткость.
Подробные примеры построения эпюр >
Лекции по сопромату >
Примеры решения задач >
Эпюра поперечных сил — как построить?
Привет! Сегодня будем учиться строить эпюры поперечных сил. В этой статье я расскажу, что такое поперечная сила, чем интересна и полезна при проведении расчетов на прочность и жесткость. По уже сложившейся традиции, как и с другими эпюрами, будем рассматривать три способа построения эпюры поперечных сил: подробный, упрощенный и быстрый. Для того чтобы рассчитать поперечную силу в сечении нужно уметь пользоваться уравнениями равновесия конструкции. Поэтому перед изучением данной статьи, если вы не знаете этого материала, рекомендую изучить его, перейдя по указанной ссылке выше. Ну что же перейдем непосредственно к обучению!
Эпюра поперечных сил — это график показывающий распределение поперечных сил в сечениях, загруженного элемента, работающего на поперечный изгиб.
Подробный способ построения эпюры поперечных сил
В качестве примера, возьмем балку, частично загрузим ее распределенной нагрузкой q, а часть оставим без нагрузки, чтобы рассмотреть всевозможные случаи:
Первым делом нужно определить все внешние силы, действующие на конструкцию, то есть помимо распределенной нагрузки на балку будет действовать реакции, возникающие в опорах. Если вы до сих пор не умеете их определять, то обязательно изучите этот материал. В этой статье, я подробно на этом останавливаться не буду. Вот какие значения реакций получаться для рассматриваемого примера:
Разбиваем балку на участки
После подготовительного этапа можно приступать к расчету поперечных сил. На отдельных участках балки поперечная сила будет меняться по определенному закону. Как раз, наша задача научиться определять эти законы. Зная закон изменения поперечной силы на участке, можно определить ее значения в любом сечении в пределах этого участка. Так как, поперечная сила меняется по линейному закону, для построения эпюры достаточно определить ординаты на границах участков. Границами участков служат места приложения сосредоточенных сил, а также начало и конец распределенной нагрузки, то есть для нашего случая нужно рассмотреть два участка.
Важно! Для эпюры изгибающих моментов, границей участков также служит место приложения сосредоточенного момента. На эпюру же поперечных сил моменты не оказывают никакого влияния. Однако, так как эпюры поперечных сил и изгибающих моментов строятся, обычно, вместе, то эту границу так же нужно намечать.
Метод сечений
Приступим непосредственно к расчету. Для установления закона изменения поперечной силы, будем использовать метод сечений. Мысленно рассекаем балку на две части, в пределах 1-го участка, на расстоянии x1 от правого торца балки.
Каждую часть балки уравновешиваем путем приложения сосредоточенной силы Qy1 и момента Mx1. Эти силовые факторы, заменяют действие частей балки друг на друга. Для определения этих величин, достаточно рассмотреть равновесие одной из рассеченных частей.
Правила знаков для поперечной силы
Очень важно на данном этапе выбрать правильное направление поперечной силы. Она должна иметь такое направление, при котором часть балки, при неподвижном (закрепленном) противоположном от рассечения месте, стремилась повернутся ПО часовой стрелке.
Также многие авторы рекомендуют просто запомнить такое правило:
- Для правой отсеченной части, направлять поперечную силу вверх;
- Для левой отсеченной части, направлять поперечную силу вниз.
Вводим систему координат для первого участка
Для удобства выберем правую часть, так как здесь меньше нагрузки, которую нужно учитывать в расчете. Также, мы можем не учитывать момент Mx1, так как в этом уроке, нас интересует только поперечная сила. В рассматриваемом сечении вводим локальную систему координат:
- Ось z будет иметь горизонтальное направление;
- Ось y будет направлена вертикально;
- Ось x будет направлена перпендикулярно плоскости чертежа (на нас).
Записываем уравнение равновесия для первого участка и строим эпюру
Для нахождения поперечной силы на первом участке достаточно записать одно уравнение равновесия – сумму проекций все сил на вертикальную ось y. Эта сумма должна быть равна нулю:
Из полученного уравнения, следует:
Таким образом, поперечная сила в пределах первого участка равна 1 кН. Откладываем это значение на графике:
Положительное значение поперечной силы откладывается выше нулевой линии, отрицательное ниже (как в нашем случае). Эпюры штрихуются перпендикулярно нулевой линии, на каждом участке проставляются знаки, на границах участков указываются численные значения.
Расчет второго участка
Проделываем те же действия, что выполняли для первого участка. Рассекаем балку в пределах рассматриваемого участка на расстоянии z2 от левого торца балки:
Зарисовываем отдельно расчетный элемент, отбросив правую часть и заменив ее действие Qy2 и Mx2. Вводим локальную систему координат:
Для того чтобы рассчитать такой участок, с распределенной нагрузкой, воспользуемся хитростью, которой часто пользуются при решении задач по теоретической механике. Свернем эту нагрузку до сосредоточенной силы. Для этого умножим интенсивность q на длину действия нагрузки – z
Записываем уравнение равновесия для второго участка:
Выражаем поперечную силу:
Это закон, по которому меняется поперечная сила на втором участке. Чтобы получить значения для построения эпюры, нужно в это уравнение вместо z2 подставить координаты характерных сечений. Как и говорилось ранее, поперечная сила меняется по линейному закону (исключениями могут быть только схемы с трапециевидной нагрузкой), поэтому для построения эпюры достаточно вычислить значения на границах участка. В сечении A (при z2=0) поперечная сила будет равна:
В середине пролета, при z2=2м получим:
По полученным значениям, строим эпюру поперечных сил на втором участке:
Вот собственно и все! Эпюра поперечных сил построена. Согласитесь, длинное руководство получилось?! Так вот, далее я расскажу, как построить эту эпюру намного быстрее, а в конце покажу как это делается за несколько секунд.Сделайте небольшой перерыв на чай, и возвращайтесь к чтению!
Упрощенный способ построения эпюры
Итак, продолжим изучать технологии построения эпюры поперечных сил. В этом методе будем учиться рассчитывать эту эпюру без вынесения отдельных участков балки и без записи уравнений равновесия. Будем выводить сразу следствия из этих уравнений. Также как, в первом случае, балку нужно разбить на 2 участка.
Первый участок
Запишем закон изменения поперечной силы на первом участке. Для этого отметим сечение С, отстающее от правого торца балки на величину z1. Поперечная сила в этом сечении будет равна сумме проекций всех сил на вертикальную ось, находящихся справа (или слева) от сечения. Мы ведем расчет этого участка справа-налево, так как в данном случае справа нагрузки меньше.
Для того чтобы правильно записать уравнение поперечных сил для любого участка, нужно придерживаться следующих правил:
- Если нагрузка относительно рассматриваемого сечения стремится повернуть ПО часовой стрелки, то в уравнении она учитывается со знаком «+»;
- Если нагрузка относительно рассматриваемого сечения стремится повернуть ПРОТИВ часовой стрелки, то в уравнении она учитывается со знаком «-».
Продемонстрирую вышеописанные правила на нашем примере. Относительно сечения С, сила RB, находящаяся справа от сечения, стремится повернуть против часовой стрелки, поэтому в уравнение она пойдет со знаком «-»:
Как видно из уравнения, поперечная сила, на первом участке, не зависит от координаты z1, поэтому во всех сечениях она одинаковая.
Кстати, помните я писал, что нагрузку можно учитывать, как справа, так и слева? Так вот, давайте запишем уравнение, просуммировав нагрузку, находящуюся слева от сечения С и посмотрим результат.
Реакция RA, относительно сечения С, стремится повернуть ПО часовой стрелке, в уравнение пойдет с плюсом:
Нагрузку q, сворачиваем до сосредоточенной силы, как в подробном способе. Она стремится повернуться ПРОТИВ часовой стрелке, в уравнение пойдет со знаком «минус»:
Подставляя численные значения нагрузки, получим следующий результат:
Теперь перейдем ко второму участку.
Второй участок
Здесь ситуация похожая, подробно комментировать уже не буду, приведу схему и расчет:
По выполненным расчетам двух участков, можно построить уже знакомую эпюру:
Как видите, эпюра поперечных рассчитывается достаточно просто. В последнем разделе я расскажу, как можно построить ее и вовсе устно.
Быстрый способ построения эпюры
Как вы уже, наверное, заметили, эпюра поперечных сил имеет скачки в тех местах, где прикладываются сосредоточенные усилия, а в местах где приложена распределенная нагрузка, эпюра постоянно меняется по линейному закону. Эти свойства эпюры можно использовать при построении. Давайте рассмотрим такую балку:
Определим для нее опорные реакции:
Расчет быстрым способом рекомендую производить слева-направо. В этом случае для скачков эпюры будут следующие правила знаков:
- Если приложенная сила направлена вверх, то и скачек на эпюре будет вверх, на величину силы;
- Если приложенная сила направлена вниз, то и скачек на эпюре будет вниз, на величину силы.
С учетом данных правил, получим вот такую эпюру поперечных сил:
Прокомментирую: в точке А, сила направлена вверх, эпюра поднимается на 4 кН, в точке С, опускается до нуля, т.к. приложенная сила направлена вниз и так далее. С сосредоточенным усилиями думаю все просто и понятно.
Там, где есть, распределенная нагрузка, эпюра меняется не скачкообразно, а постепенно. И чтобы узнать насколько эпюра измениться от действия распределенной нагрузки от ее начала и до конца, нужно умножить интенсивность q на длину ее действия:
Вот собственно и все, что хотелось рассказать об эпюрах поперечных сил! Вы можете задавать любые вопросы по материалам статьи в комментариях ниже. Также рекомендую подписаться на наши соц. сети, чтобы не пропустить новые и интересные материалы.
После освоения данного урока, можете смело приступать к изучению техник построения эпюр изгибающих моментов. Данная статья является продолжением серии статей о том, как строятся эпюры для балок, работающих на поперечный изгиб.
Спасибо за внимание!)
Построение эпюр изгибающих моментов и поперечных сил для балок
Очень важно уметь строить эпюры для балок, работающих на изгиб! Так как построение эпюр, является неотъемлемой частью любого прочностного расчёта и большинство элементов, из которых состоят современные инженерные сооружения, работают на изгиб. Поэтому в сопромате, очень много внимания уделяется как раз данным эпюрам: поперечных сил и изгибающих моментов. Для краткости, их ещё называют эпюрой моментов и эпюрой сил. В этой статье, рассмотрим, как рассчитать эпюры традиционным методом, а также быстрым, с помощью которого эпюры рисуются за считаные минуты. В статье, построение показано на примере консольной и опирающейся на две опоры балки. Показано, как учитывать сосредоточенные силы и моменты, а также распределённые нагрузки.
Построение эпюр для консольной балки
В качестве первого примера, возьмём балку, защемлённую с левого торца жёсткой заделкой и загруженной силой равной 5 кН и моментом равным 10 кНм. Длины участков даны на расчётной схеме. Нам предстоит рассмотреть два участка. Границами участков будут являться места приложения сил, моментов, начало и конец приложения распределённых нагрузок.
Первым делом, вводим систему координат, ось x пускаем вдоль оси балки, ось y перпендикулярно ей, а ось z будет перпендикулярна плоскости, в которой размещены две первые оси и будет направлена «к нам».
В поперечных сечениях балки под действием приложенной нагрузки будут возникать два внутренних силовых фактора: поперечная сила и изгибающий момент. Наша задача выяснить, какой величины эти факторы во всех сечениях балки. Для наглядности, результат решения фиксируют в виде так называемых эпюр.
Эпюра строится по всей длине балки, ордината эпюры, под исследуемым сечением, показывает величину внутреннего усилия в этом сечении.
Эпюра поперечных сил
Начнём знакомство с поперечными силами с правила знаков для эпюр. После чего последовательно рассчитаем и построим эпюры для первого и второго участка балки.
Правило знаков для поперечной силы
При построении эпюр поперечных сил нужно придерживаться следующих правил знаков:
- Если внешняя сила стремится повернуть балку по часовой стрелке, то поперечную силу считаем положительной. Эпюру откладываем выше нулевой линии со знаком плюс.
- Если сила поворачивает балку против часовой стрелки, то поперечная сила будет отрицательной, и на эпюре будет откладывать ниже нулевой линии.
Возможно, сейчас будет немного непонятны данные правила, но прочитав следующие 2 блока статьи, вы поймёте, как применять эти правила в действии.
Поперечные силы на первом участке
Рассмотрим первым участок равный двум метрам. Сделаем мысленно сечение на расстоянии x1 от свободного торца и запишем законы изменения эпюр на этом участке. Законы эти выражаются из уравнений равновесия статики. Статика говорит нам, что тело находится в равновесии, если выполняются следующие условия:
Если суммы проекций всех сил на обе оси равны нулю и сумма моментов относительно точки равна нулю.
Для поперечной силы возьмём сумму проекций на ось y:
Из этого уравнения выражаем поперечную силу Q = F. Так как внешняя сила стремиться повернуть балку по часовой стрелке, то поперечную силу считаем положительной. Причем видно, из полученного закона поперечной силы, что Q постоянна по всей длине участка. Откладываем на эпюре Q = F = 5 кН. Эпюру подписываем как Qy, где y значит, что направление поперечные силы совпадет с направлением этой оси.
Поперечные силы на втором участке
На втором участке, поперечная сила будет равна: Qy2 = Qy1;
Так как на этом участке, действует все та же сила F. Момент в уравнениях поперечных сил не учитывается, что является следствием уравнений статики.
Эпюра изгибающих моментов
В этом блоке статьи будем учиться строить эпюру моментов, здесь нюансов несколько больше, чем для эпюры поперечных сил. Начнём, пожалуй, с правил знаков, которые приняты для этой эпюры.
Правила знаков для изгибающих моментов
- Если внешняя сила или момент растягивают «верхние волокна» то эпюра откладывается сверху.
- Если сила или момент силы растягивают «нижние волокна», то эпюра откладывается ниже нулевой линии.
То есть, обычно, при построении эпюр изгибающий моментов знаки не указываются. Эти эпюры откладываются со стороны «растянутых волокон». Так, и удобнее читать эпюры и откладывать их.
Не всегда их откладывают так! Студентов некоторых специальностей, чаще всего машиностроительных, учат откладывать эпюры со стороны «сжатых волокон». Строители откладывают со стороны «растянутых волокон», в своих статьях я буду придерживаться этого правила, так как привык к нему.
Изгибающий момент на первом участке
Для изгибающих моментов на первом участке, запишем сумму моментов, относительно точки С, в которой ранее сделали сечение:
Отсюда получаем:
Это закон изменения изгибающих моментов по длине участка. В отличие от поперечных сил, изгибающие моменты будут меняться в пределах этого участка.
- Если подставить вместо x1 — ноль, который соответствует началу участка, то получим, что М = 0.
- Если подставим вместо x1 — 2 (конец участка), то получим:
С учётом вышеописанных правил знаков, мысленно представляем себе, что сила стремится растянуть верхние волокна, поэтому откладываем рассчитанные значения на эпюре сверху, получив эпюру в виде прямоугольного треугольника. Обязательно, подписываем эпюру как Mz, где z означает, что все изгибающие моменты поворачивают относительно этой оси.
Будет продолжение…
1.12. Эпюры внутренних сил и моментов.
При расчете на прочность стержневых элементов конструкций необходимо знать законы изменения внутренних усилий (сил и моментов) в поперечных сечениях балки по ее длине. Эти законы можно изобразить с помощью специальных графиков, называемых эпюрами соответствующих внутренних силовых факторов.
Например, эпюрой изгибающих моментов (эпюрой M) называется график, изображающий закон изменения величин этих моментов по длине балки. Аналогично эпюрой поперечных сил (эпюройQ) или эпюрой продольных сил (эпюройN) называется график, изображающий изменение поперечных или продольных сил по длине балки.
Каждая ордината эпюры M (илиQ, илиN) представляет собой величину изгибающего момента (или поперечной силы, или продольной силы) в соответствующем поперечном сечении балки.
1.13. Правила построения эпюр внутренних силовых факторов
Рассмотрим на конкретном примере построение эпюр для балки, находящейся под действием системы сил, расположенных в одной плоскости (параллельной плоскости чертежа).
Построим эпюры Q иMдля свободно-опертой балки, изображенной на рис. 1.8,a, при следующих исходных данных:
; ; ; .
Вначале определим опорные реакции. Для этого отбросим опоры и заменим их влияние на балку опорными реакциями и(рис. 1.8,б). Реакцииипредставляют собой вертикальную и горизонтальную составляющие полной реакции шарнирно-неподвижной опорыA; сила жеявляется полной реакцией опорыB. Направление опорных реакций выбирается произвольно; если в результате расчета значение какой-либо реакции получается отрицательным, то, значит, в действительности ее направление противоположно предварительно принятому.
Сначала определим опорную реакцию , составив для этого сумму проекций всех сил на горизонтальную осьx:
;=0.
Очевидно, что не только в рассматриваемом случае, а всегда при действии на горизонтальную балку только вертикальной нагрузки горизонтальная опорная реакция равна нулю.
Для определения опорной реакции составим уравнение моментов всех сил относительно точкиB. Опорные реакцииипроходят через эту точку, а потому их моменты относительно нее равны нулю:
;,
где и- равнодействующие погонной равномерно распределенной нагрузки интенсивностьюqна длинеисоответственно.
,
.
Рис. 1.8
Аналогично составим сумму моментов всех сил относительно точки A:
;,
,
.
Для проверки правильности найденных значений опорных реакций составим сумму проекций всех сил на ось y:
;,
,
.
Составленное уравнение удовлетворяется тождественно, что указывает на правильность определения опорных реакций.
Для определения аналитических зависимостей дляN,QиMпо длине балки выделим на ней участки. Назовем участком балки каждую ее часть, в пределах которой законы изменения поперечной силы и изгибающего момента остаются неизменными. Границами участков являются поперечные сечения балки, в которых к ней приложены сосредоточенные нагрузки (в том числе и опорные реакции) или в которых начинается либо заканчивается распределенная нагрузка, или в которых интенсивность этой нагрузки начинает изменяться по новому закону. Текущая координатаxна каждом участке может отсчитываться как от левого, так и от правого конца балки. В первом случае при записи уравнений равновесия участка необходимо учесть все нагрузки, расположенные левее рассматриваемого сечения, а во втором — правее рассматриваемого сечения. Влияние отброшенной части балки на рассматриваемую заменяется внутренними силамиN,Qи моментомM, направленными в соответствии с принятым правилом знаков.Рассматриваемая балка (рис. 1.8) имеет три участка.
Рассмотрим Участок I(рис. 1.9):
,
.
Рис. 1.9
(1.1)
..
Зависимость для Qна этом участке — линейная, а потому для построения эпюрыQна этом участке достаточно определить величины поперечной силы при двух значениях:
при =0 (на левом конце балки — в начале участка I)
== 6,5;
при=(в конце участка I — при отсчете от левого конца балки)
.
,
(1.2)
.При =0 (на левом конце балки — в начале участка I)
=0;
при =(в конце участка I- при отсчете от левого конца балки)
.
В формулах (1.1), (1.2) — равнодействующая равномерно распределенной нагрузки в пределах отрезка длинойучастка I. Она приложена в середине этого отрезка, а потому ее момент относительно рассматриваемого сечения равен (-). Знак изгибающего момента отрицателен потому, что моментдействует против часовой стрелки.
На первом участке поперечная сила меняет знак с плюса на минус, следовательно в каком-то сечении этого участка она равна нулю. Определим координату этого сечения, приравняв нулю выражение для Qв формуле (1.1):
.
Теперь, воспользовавшись формулой (1.2) найдем значение изгибающего момента в этом сечении балки:
.
Трех точек будет вполне достаточно для построения эпюры M, которая на первом участке изменяется по квадратичному закону.
Ординаты эпюр, соответствующие положительным значениям внутренних усилий, откладываем вверх от осей этих эпюр, а отрицательные — вниз (оси эпюр параллельны оси балки).
Рассмотрим УчастокII(рис. 1.10):
.
.
(1.3)
..
(1.4)
Рис. 1.10
.При =(в начале участка II — при отсчете от левого конца балки)
;
при =(в конце участка II — при отсчете от левого конца балки)
.Рассмотрим УчастокIII(рис. 1.11):
.
(1.5)
.Рис. 1.11
При=0 (на правом конце балки — в начале участка III);
при =(в конце участка III — при отсчете от правого конца балки)
.
.
.
(1.6)
При=0 (на правом конце балки — в начале участка III);
при =(в конце участка III — при отсчете от правого конца балки)
.
На третьем участке поперечная сила меняет знак с плюса на минус, следовательно в каком-то сечении этого участка она равна нулю. Определим координату этого сечения, приравняв нулю выражение для Qв формуле (1.5):
.
.
Теперь, воспользовавшись формулой (1.6), найдем значение изгибающего момента в этом сечении балки:
.
Анализируя эпюры поперечных сил Q(рис. 1.8,в) и изгибающих моментовM(рис. 1.8,г), можно отметить следующие наблюдения.
1. В сечении, в котором к балке приложена сосредоточенная внешняя сила, перпендикулярная к оси балки (в том числе и опорная реакция в виде сосредоточенной силы), значение поперечной силы Qизменяется скачкообразно на величину приложенной силы. Когда сосредоточенная внешняя сила направлена вверх, на эпюреQ(при перемещении слева направо) имеется скачок вверх, а когда сила направлена вниз — скачок вниз.
2. В сечении, в котором к балке приложен сосредоточенный внешний момент (в том числе и опорная реакция в виде сосредоточенного момента), значение изгибающего момента Mизменяется скачкообразно на величину приложенного момента; когда сосредоточенный внешний момент действует по часовой стрелке, на эпюреM(при перемещении слева направо) имеется скачок вверх, а когда момент действует против часовой стрелки — скачок вниз, т. е. в обоих случаях в сторону сжатых волокон.
3. В сечении, в котором поперечная сила Qобращается в нуль, на эпюре моментов имеется максимум (если при перемещении слева направо поперечная сила меняет знак с плюса на минус) или минимум (если при перемещении слева направо поперечная сила меняет знак с минуса на плюс).
Аналитическое обоснование последнего и ряда других наблюдений будет приведено в последующих разделах.
Эпюры поперечных сил и изгибающих моментов для балок и плоских рам
из «Механика химических производств Изд3»
Прежде чем приступить к построению эпюр, примем следующие правила знаков поперечной силы и изгибающего момента. Знак (Зу (или Qx) зависит от того, с какой стороны от сечения производится суммирование внешних сил (рнс. 2.3) при суммировании от левого конца балки положительный знак дает равнодействующая внешних сил, направленных вверх при движении к сечению справа — положительной будет считаться равнодействующая сил, направленных вниз. Наоборот — знак минус . [c.35]Другими словами, если поперечная сила Qy вращает рассматриваемую часть балки по часовой стрелке-—знак плюс , против часовой стрелки — знак минус . [c.35]
Прн определении знака изгибающего момента М (или Му) учитывают характер дефор.мации балки под внешней нагрузкой изгиб балки выпуклостью вниз соответствует знаку плюс , выпуклостью вверх — минус (рис. 2.4). Иными словами, эпюры изгибающих моментов строят на сжатом волокне балки. [c.35]
Рассмотрим характер эпюр, получающихся от различных нагрузок на примерах балок, закрепленных консольно или расположенных на двух опорах. [c.35]
При нагружении консольной балки распределенной нагрузкой интенсивностью д (рис. 2.6, а) поперечная сила в сечении г составит 0 у — —дг и, соответственно, Qyл = О, а Qyв = —д1. Изгибающий момент в сечении 2 составит Мх — —дг г/2) = = —дг 12 тогда Ма А = 0 и Мхв = д1 /2. Следовательно, по длине балки поперечная сила изменяется по линейному закону, а изгибающий момент М — по закону квадратичной параболы, выпуклостью навстречу направлению распределенной нагрузке д. Эпюры Qy и Мх показаны на рис. 2.6,6. [c.36]
Балка имеет два участка нагружения (рис. 2.7, а). На участке / на расстоянии 2 из условия равновесия левой отсеченной части получаем Qy — Уа — Р 1 —а)/I M — Р 1 —a)z/l. [c.37]
Эпюры Qy и M.v приведены на рнс. 2.7,6. [c.37]
Выделим элементарный участок балки длиной dz (рис, 2,8), на котором действует лищь распределенная нагрузка интенсивностью q. Пусть в левом сечении вырезанного участка действуют внутренние силовые факторы Qy и Мх, а в правом сечении — Qy + dQy и Мх -f dMx. [c.37]
Таким образом, производная от поперечной силы по длине балкн равна интенсивности нагрузки, а производная от изгибающего момента равна поперечной силе. [c.38]
переход Mx- Qy — q может быть осуществлен дифференцированием, обратный — интегрированием. [c.38]
Полученные дифференциальные зависимости справедливы для сечений, в которых не приложены сосредоточенные силы и моменты. [c.38]
Для облегчения построения эпюр или контроля правильности их укажем следующие правила, некоторые нз них являются следствиями дифференциальных зависимостей между д, Q f, М , другие вытекают из метода сеченнй. [c.38]
Полезно иметь в виду, что на концевой шарнирной опоре поперечная сила Qy равна реакции опоры, а изгибающий момент Мх == О, если в опорном сечении не приложен сосредоточенный момент. [c.38]
Примечай н е. Легко заметить, что для крайнего правого участка СО более рационально составлять уравнение моментов, отсчитывая г от правого конца балки. В этом случае запись имела бы следующий вид. [c.40]
Полученные уравнения позволяют построить эпюры Qy и Мх (рис. 2.9,6). [c.40]
Эпюры Мг (знак минус означает сжимающую силу, см. разд. 2.2), Ру и Мх приведены на рис. 2.10,6. [c.41]
Случай пространственного нагружения плоских рам будет рассмотрен в разделе 10.1. [c.41]
Вернуться к основной статье
Пример 3. Построение эпюр усилий в шарнирной балке 032
Рис. 1
Дано расчетную схему шарнирной балки (рис. 1) и приложенною к ней внешнюю нагрузку.
Нужно:
1) Определить опорные реакции.
2) Построить эпюры внутренних усилий: эпюру продольных сил (рис. 2, Еп.Nx), поперечных сил (рис. 2, Еп.Qz) и изгибающих моментов (рис. 2, Еп.My).
Решение:
1) Определение опорных реакций.
Спроектируем силу на ось и (рис. 2).
Ее проекции равны:
кН;
кН.
Поскольку в сквозном шарнире изгибающий момент равен нулю, то балку, изображенную на рис.1, можно рассчитывать как две отдельные балки (рис. 2, I, II). Расчет начинаем с балки, в которой количество опорных реакций соответствует количеству уравнений статического равновесия статики (для плоских задач — три уравнения). Опорная реакция (где находится шарнир) первой балки, передается на другие балки с противоположным знаком.
I — балка
Сумма моментов всех сил относительно точки :
;
;
кН.
Сумма моментов всех сил относительно точки :
;
;
кН.
II — балка
Сумма проекций всех сил на ось :
;
;
кН.
Сумма моментов всех сил относительно точки :
Поскольку треугольник — прямоугольный равнобедренный треугольник, то м.
;
;
кН.
Сумма моментов всех сил относительно точки :
Поскольку треугольник — прямоугольный равнобедренный треугольник, то м.
;
;
кН.
Проверка (сумма проекций всех сил на ось ):
.
2) Построение эпюр внутренних усилий.
Обозначаем характерные точки и определяем в них значение усилий, используя соответствующее правило знаков для построения эпюр внутренних усилий.
Построение эпюры продольных сил (Еп.Nx, кН):
Л;
Пр.
Строим эпюру продольных сил (рис.2).
Построение эпюры поперечных сил (Еп.Qz, кН):
Л;
Пр;
Л;
Пр;
Л;
Пр;
Л;
Пр;
Л;
Пр.
Строим эпюру поперечных сил (рис.2).
Построение эпюры изгибающих моментов (Еп.My, кН·м):
;
Пр;
Л;
;
;
;
;
.
Строим эпюру изгибающих моментов (рис.2).
Рис. 2
Понравилась статья! Поддержи проект! Ставь ЛАЙК!
Эпюры изгибающих моментов и поперечных сил
Содержание:
Эпюры изгибающих моментов и поперечных сил
Рисунок изгибающего момента и силы сдвига Из приведенного выше обсуждения видно, что сила, действующая на поперечное сечение TP балки, такова, что она уравновешивает изгибающий момент M и боковую силу<2 при одном и том же поперечном сечении. Итак, значения M и<2 в любом поперечном сечении определяют величину силы, действующей на это cross-section.
- To упрощается исследование распределения напряжений балки, полезно графически представить изгибающий момент и изменение боковых сил по длине балки. beam. In на таком изображении абсцисса представляет положение поперечного сечения, ось ординат представляет значение изгибающего момента или боковой силы, действующей на это поперечное сечение, а положительное значение откладывается над горизонтальной осью.
Отрицательный-ниже оси. Например, рассмотрим самонесущую балку с сосредоточенной нагрузкой P (рис.66)*).Реакция в данном случае такова i, — = t и I.= t- Вы можете взять раздел TP слева от P9 и сделать вывод, что в этом разделе. Приятель.- (2 = — г и Yi = — х.(А)
Такие графические изображения называются фигурами изгибающих моментов и боковых сил соответственно. Людмила Фирмаль
Направление поперечной силы и изгибающего момента такое же, как и на рисунке 1.(1-x). (с)
Заметим, что ранее полученное выражение (b)является a-I-b, можно свести его к этой простой форме. << Это интересно отметить. Что фигура боковой силы состоит из 2 прямоугольников с равными площадями. Рассматривая противоположные признаки этих областей, можно сделать вывод, что общая площадь фигуры сдвиговой силы равна нулю.
Этот результат не является случайным. Интегральное уравнение(50)、 。 Существует G -. си.• ;«.Я… YAG=(<1) «■В А Где пределы A и B указывают, что интеграл выполняется по всей длине балки от конца A до конца B. Это нормально. Часть уравнения (b)представляет собой общую площадь участка, где P-поперечная мощность реки 1.Левая сторона такая же.
После интегрирования уравнение дает точный момент разница МВт-МА на концах B и A. В случае свободно движущегося луча, момент в конце исчезает. Поэтому ЭПУ-рис. 67.Рожь поперечная сила равна ’■Нуль. • Если на балку действует более одной силы (рис. 67), то балка делится на несколько секций, и для каждой секции (?)И М. Р%(х-Эр). (Да Для 3-го участка балки, а именно al <x < aa, удобнее рассматривать правую сторону балки, чем левую side. In в этом случае, вы получите: , 0» — (/?,- П. С.)М = /?, (/- х)-Р9 (/- -6.) Наконец, в последнем разделе»луч»、 (г) М= -•/?, М = # н: й -.(Ч.) Из Формулы (e)-g — (h) видно, что боковые силы остаются постоянными в каждом сечении балки.
Изгибающий момент каждой секции балки является линейной функцией x Людмила Фирмаль
Таким образом, фигура боковой силы получается как, как показано на рисунке. 67, 6.. So, в соответствующем сюжете сюжета он представлен косой прямой line. To проведя эти линии, из формул (e) и(h) мы увидим, что на краях пучка x = 0 и X = /момент равен нулю.
Момент под нагрузкой получается путем подстановки формулы (эмо и*(h), x = al9 x * = at и x-a, respectively. So, для вышеуказанных моментов получаем следующие значения: М = Rxav м = P9ag-РДА — а), м = RJb9. Используя эти значения, можно легко построить график изгибающего момента, как показано на рисунке. 67, стр. В практических приложениях важно найти максимальное или максимальное сечение изгибающего момента. Низкое значение.
Для сосредоточенной нагрузки, описанной на Рис. 1. 67, максимальный изгибающий момент происходит под нагрузкой Рг. Эта нагрузка соответствует изгибающему моменту » точка dt%», где тангенс угла наклона диаграммы меняет знак на diagram. In кроме того, из Формулы (50) видно, что касательная угла наклона фигуры изгибающего момента в любой точке равна боковой силе.
Поэтому изгибающий момент будет максимальным или минимальным значением в той части, где изменяется боковая сила 8нак. Если поперечная сила по длине балки изменяется от положительного до отрицательного значения, например, при нагрузке Pt на фиг. 5, 67, то тангенс угла наклона диаграммы изгибающего момента также изменяется от положительного до отрицательного.
Поэтому в этом сечении существует максимальный изгибающий момент. Изменение Q от отрицательного значения до положительного указывает на минимальный изгиб moment.(rtgptitp〜PT) представляет собой параболу tt’pigptpttp, в центре которой находится вертикальная ось Пролет балки (рис. 68, с).
Моменты на обоих концах, то есть x = 0 и x=/, равны нулю, момент имеет максимальное значение в центре пролета, а боковая сила меняет знак. Это максимальное значение получается подставляя x-y в формулу (i)、 М= * — • / Vimax 8 * Если равномерная нагрузка q охватывает только часть пролета (рис. 69), то 3 участка длины a должны рассматриваться отдельно. b и c. Rt и определить реакцию? замените рав таким же образом, аспредёред, пелелелел.
Результаты QB нагрузки. «Из уравнения статики моментов для B и-A、 Боковая сила разгруженной левой части балки и изгибающий момент(0 < x <o)、 Г = /? И М-Р ИКС. (Дж) В случае поперечного сечения mn, взятого в нагрузочном сечении балки, сила поперечного сечения получается вычитанием нагрузки q (x-a)\из реакции? Он расположен в левой части этого раздела.
Изгибающий момент того же участка получается путем вычитания момента нагрузки на левой стороне этого участка из реакции moment. -. (к)Правый участок балки без нагрузки, с учетом правой силы любого участка、 И-(1) Используя уравнения 0, (k) и (I), можно легко построить график сдвиговых сил и изгибающих моментов.
Диаграмма поперечной силы (рис.69, б) состоит из горизонтального сегмента оси, который соответствует ненагруженной части балки, и наклонной линии, < cx & x>, которая соответствует равномерно нагруженной части. — я. ..• Т-ПГ. МП IM 11.11 III V f г.* Лу. б. th. * (Рисунок 69, с) 2 заштрихованные линии arsr и brk» 1 Кривая с вертикальной осью, соответствующей нагрузочной части балки. Максимальный изгибающий момент в точке ех.
Это соответствует точке ех>, где боковая сила меняет знак. В точках С1 и параболы, наклонных линий Ayacr и c1r2r связались, соответственно, это получается из-за того, что на рисунках боковых сил в точках с и<2 нет резкого изменения величины боковой силы. Так… Рисунок 69.
Исходя из Формулы (50), нет резкого изменения наклона изгибающего момента предвестников в соответствующей точке. д / 2.4 м — ► ’ Ш [12М г * −7.виртуальная память 1. 1 шт 5о0кгно. / 24М… г. /.Ом. например: ’КК / м Один. 1ШР. 1М. / — 7,6 М-Д. — с. / г -/, 2М — <б-ин■э-. 56. Здесь. Г / / 77 / Л 500кг. 500кг. Iyyokg K500kg 12m | — 7, ВМ-72М Что?/ Рисунок 72.
2.Создайте конкретную масштабную диаграмму поперечных сил и изгибающих моментов и найдите значения максимальных положительных и отрицательных полей «речных сил и изгибающих моментов» консоли, показанной на рисунке. 73. 50кг. — «А + 12м4» ТС-я- <И 500кг. Хромой. 500кг. ] $ Ыб ’/ * — 7лм. 5. / shshlp [±7] — да. я-и -/. 7,5 м. 500кг. 500м рисунок 73. «У» ч> 3.На консоли, герметизированной с правого конца, имеется полная нагрузка Р, интенсивность которой равномерно возрастает от нуля.
График левого края 74, L боковая сила и изгибающий момент показаны штрихами динамика на рисунке. — 4. Решение. Расстояние консоли x og * le *боковые силы сечения m, разнесенные по концам, будут численно равны затененной части нагрузки. Полная нагрузка P заштрихована, потому что она представлена областью треугольника AC B икс * / 5-я часть равна R. используя условности ранее принятых знаков (рис. 64)、 Мы получаем Xa * — РИТЭГ-
Итак, диаграмма силы сдвига показана на рисунке. 74, точка B с параболой ab с перпендикулярной осью к с, изгибающий момент сечения mn При принятии момента штриховки части груза относительно центра тяжести секции mp. So … ВА Х м = п£т Диаграмма 74. Этот момент представлен на рисунке кривой axbx. 74, С. 4.Балка длиной l отвечает за 2 равные нагрузки P (рис.75) на ее концах, а равновесие удерживается равномерно распределенным противодействием.
Построить график боковых сил и изгибающих моментов. Ответ. Сюжет получается из рисунка ’ 68, b и 68, вместо замены Path-2?/. а. балка длиной l = 12 м имеет сосредоточенную нагрузку P = 1000 кг в середине длины (рис. 76) и имеет равномерную реакцию по всей длине. Найти численно максимальный изгибающий момент. Построить график боковых сил и изгибающих моментов.
Ответ. Пользователь (ы), которые смотрели Mt9X — 1500 человек. График, необходимый для каждой половины балки, аналогичен графику, показанному на рисунке. 71, б и 71, стр. 6.As показанный на фиг. 1 отдельно стоящий пучок длиной I передает Р1, и интенсивность его распределения 3 равномерно возрастает. 77, a. для £ = 12 м и/ = 12 м создайте конкретный масштабный график боковых сил и изгибающих моментов.
Решение. Реакция поддержки в данном случае такова / ?, = — o * P = 4 t и = 8 t. боковая сила Сечения ТП получается путем вычитания заштрихованная часть нагрузки от реакции так У ЭУРа от поперечных сил показана на рис. 77 параболических по АСВ. Изгибающий момент профиля tp М.
Этот момент представлен 77-й кривой axxxx. Максимальный момент возникает в точке СХ, где боковая сила меняет знак М. То есть, Х — > р=. 7000кг-ом 600. GTTTTT Диаграмма 75、 компания GTT. компания GTT. Рисунок 76. 7.Автономная Балка A B несет распределенную нагрузку, представленную линией ASV. = р -.Затем о поперечной силе и изгибающем моменте поперечного сечения ТП、 Г = ГХ-и M = rxx в-п-л-Дж.
Таким образом, можно получить боковые силы и изгибающие моменты для любого сечения в сечении ДБ балки. 8.Найдите UI™в предыдущей задаче. Часов%= 1 = 12 м, б-5 м, п-12т СП 1+ » ответ. Mtz1 = 22,4 ТМ T% ✓1> / 77 ′ ПВЛ п, п (■И>% 1 1 x f Ю\ 6.)\ СиДжей. \ Рисунок 78.、
9.Составьте конкретную масштабную диаграмму поперечной силы и изгибающего момента и найдите значения максимальной положительной и отрицательной поперечной силы и изгибающего момента балки с консолью (рис.79). д-400кг / м. gptlgt gtttttttttttggt А. * АО О. В. •7000кг | . я — » 7730×8 500кг. Ноги. 1. — 400 фунтов. 5. / д = 300lg / м СиДжея г * — с Диаграмма 79 Ф ЗЕТ. Да.) Решение. Если показано на рис. 79, а, то реакция составляет 670 кг и 3300 кг, а боковая сила левого участка балки равна (2 = 670-400 х).
Она показана на рисунке диагональной линией ab. Боковое усилие правой части балки определяется, как показано на наклонной линии B * s консоли. Изгиб Мистер Си. Момент левого сечения балки равен M = 670 x-400.Он нарисован раболой 0 / Х6 6|.Максимальный момент возникает в точке Е и соответствует точке е. f где боковая сила изменяет знак.
Фигура изгибающего момента в правом сечении такая же, как и в консоли, и нарисована параболическим bxcx, который касается горизонтальной оси в точке C. • 10. 2 равные коэффициенты*(рис. 80) — длина/балок равномерно распределенной нагрузки. Найти расстояние d между опорами таким образом, чтобы изгибающий момент в центре балки был численно равен изгибающему моменту балки. support. In в этом случае постройте график силы сдвига и изгибающего момента. Ответ. <1 = 0,686 /. 、
Смотрите также:
Эпюры изгибающих моментов и поперечных сил
Чертеж диаграмм свободного тела
Диаграммы свободного тела — это диаграммы, используемые для отображения относительной величины и направления всех сил, действующих на объект в данной ситуации. Диаграмма свободного тела — это особый пример векторных диаграмм, которые обсуждались в предыдущем разделе. Эти диаграммы будут использоваться на протяжении всего нашего изучения физики. Размер стрелки на диаграмме свободного тела отражает величину силы. Направление стрелки показывает направление действия силы.Каждая стрелка силы на диаграмме помечена, чтобы указать точный тип силы. Обычно на диаграмме свободного тела объект изображают в виде прямоугольника и проводят стрелку силы из центра прямоугольника наружу в направлении, в котором действует сила. Пример диаграммы свободного тела показан справа
На приведенной выше диаграмме свободного тела показаны четыре силы, действующие на объект. Объекты , а не , обязательно всегда имеют четыре силы, действующие на них.Бывают случаи, когда количество сил, изображенных на диаграмме свободного тела, будет равно одному, двум или трем. Не существует жесткого правила относительно количества сил, которые должны быть изображены на диаграмме свободного тела. Единственное правило для рисования диаграмм свободного тела состоит в том, чтобы изобразить все силы, которые существуют для этого объекта в данной ситуации. Таким образом, для построения диаграмм свободного тела чрезвычайно важно знать различные типы сил. Если вам дано описание физической ситуации, начните с использования вашего понимания типов сил, чтобы определить, какие силы присутствуют.Затем определите направление, в котором действует каждая сила. Наконец, нарисуйте прямоугольник и добавьте стрелки для каждой существующей силы в соответствующем направлении; Обозначьте каждую стрелку силы в соответствии с ее типом. При необходимости обратитесь к списку сил и их описанию, чтобы понять различные типы сил и их соответствующие символы.
Примените метод, описанный в параграфе выше, для построения диаграмм свободного тела для различных ситуаций, описанных ниже.Ответы показаны и объяснены внизу этой страницы.
- Книга покоится на столе. Изобразите силы, действующие на книгу. Смотрите ответ.
- Гимнастка держится за перекладину, неподвижно подвешена в воздухе. Штанга поддерживается двумя веревками, прикрепленными к потолку. Изобразите силы, действующие на комбинацию гимнастки и перекладины. Смотрите ответ.
- Яйцо свободно падает из гнезда на дереве.Пренебрегайте сопротивлением воздуха. Изобразите силы, действующие на яйцо при его падении. Смотрите ответ.
- Белка-летяга скользит (нет крыло закрылков ) от дерева до земли с постоянной скоростью. Учитывайте сопротивление воздуха. Изобразите силы, действующие на белку. Смотрите ответ.
- К книге прилагается сила, направленная вправо, чтобы перемещать ее по столу с ускорением вправо. Учитывайте силы трения. Пренебрегайте сопротивлением воздуха.Изобразите силы, действующие на книгу. Смотрите ответ.
- К книге прилагается сила, направленная вправо, чтобы перемещать ее по столу с постоянной скоростью. Учитывайте силы трения. Пренебрегайте сопротивлением воздуха. Изобразите силы, действующие на книгу. Смотрите ответ.
- Студент колледжа кладет рюкзак на плечо. Рюкзак неподвижно подвешивается на одной лямке с одного плеча. Изобразите вертикальные силы, действующие на рюкзак. Смотрите ответ.
- Парашютист спускается с постоянной скоростью. Учитывайте сопротивление воздуха. Изобразите силы, действующие на парашютиста. Смотрите ответ.
- Сила, приложенная справа, чтобы тащить сани по рыхлому снегу с ускорением вправо. Пренебрегайте сопротивлением воздуха. Изобразите силы, действующие на салазки. Смотрите ответ.
- Футбольный мяч движется вверх к своему пику после того, как игрок загрузил .Пренебрегайте сопротивлением воздуха. Изобразите силы, действующие на футбольный мяч, когда он поднимается вверх к своей вершине. Смотрите ответ.
- Автомобиль движется вправо и снижает скорость. Пренебрегайте сопротивлением воздуха. Изобразите силы, действующие на автомобиль. Смотрите ответ.
Ответы
Здесь показаны ответы на вышеупомянутое упражнение. Если вы испытываете трудности с рисованием диаграмм свободного тела, вам следует об этом позаботиться.Продолжайте просматривать список сил и их описание, а также эту страницу, чтобы получить удобство при построении диаграмм свободного тела.
1. Книга покоится на столе. Диаграмма свободного тела для этой ситуации выглядит так:
Вернуться к вопросам
Вернуться к информации о диаграммах свободного тела
Возврат к онлайн-списку описаний сил
2.Гимнастка, держась за перекладину, неподвижно висит в воздухе. Штанга поддерживается двумя веревками, прикрепленными к потолку. Изобразите силы, действующие на комбинацию гимнастки и перекладины. Диаграмма свободного тела для этой ситуации выглядит так:
Вернуться к вопросам
Вернуться к информации о диаграммах свободного тела
Возврат к онлайн-списку описаний сил
3. Яйцо свободно падает из гнезда на дереве.Пренебрегайте сопротивлением воздуха. Диаграмма свободного тела для этой ситуации выглядит так:
Вернуться к вопросам
Вернуться к информации о диаграммах свободного тела
Возврат к онлайн-списку описаний сил
4. Белка-летяга скользит (№ крыло закрылки ) от дерева до земли с постоянной скоростью. Учитывайте сопротивление воздуха. Диаграмма свободного тела для этой ситуации выглядит так:
Вернуться к вопросам
Вернуться к информации о диаграммах свободного тела
Возврат к онлайн-списку описаний сил
5.К книге прилагается сила, направленная вправо, чтобы перемещать ее по столу с ускорением вправо. Учитывайте силы трения. Пренебрегайте сопротивлением воздуха. Диаграмма свободного тела для этой ситуации выглядит так:
Вернуться к вопросам
Вернуться к информации о диаграммах свободного тела
Возврат к онлайн-списку описаний сил
6. К книге прилагается сила, направленная вправо, чтобы перемещать ее по столу с постоянной скоростью.Учитывайте силы трения. Пренебрегайте сопротивлением воздуха. Диаграмма свободного тела для этой ситуации выглядит так:
Вернуться к вопросам
Вернуться к информации о диаграммах свободного тела
Возврат к онлайн-списку описаний сил
7. Студент колледжа кладет рюкзак на плечо. Рюкзак неподвижно подвешивается на одной лямке с одного плеча. Диаграмма свободного тела для этой ситуации выглядит так:
Вернуться к вопросам
Вернуться к информации о диаграммах свободного тела
Возврат к онлайн-списку описаний сил
8.Парашютист спускается с постоянной скоростью. Учитывайте сопротивление воздуха. Диаграмма свободного тела для этой ситуации выглядит так:
Вернуться к вопросам
Вернуться к информации о диаграммах свободного тела
Возврат к онлайн-списку описаний сил
9. Сила, приложенная вправо, тянет сани по рыхлому снегу с ускорением вправо. Пренебрегайте сопротивлением воздуха.Диаграмма свободного тела для этой ситуации выглядит так:
Вернуться к вопросам
Вернуться к информации о диаграммах свободного тела
Возврат к онлайн-списку описаний сил
10. Футбольный мяч движется вверх к своей вершине после того, как игрок загрузил . Пренебрегайте сопротивлением воздуха. Диаграмма свободного тела для этой ситуации выглядит так:
Вернуться к вопросам
Вернуться к информации о диаграммах свободного тела
Возврат к онлайн-списку описаний сил
11.Автомобиль движется вправо и сбавляет скорость. Пренебрегайте сопротивлением воздуха. Диаграмма свободного тела для этой ситуации выглядит так:
Вернуться к вопросам
Вернуться к информации о диаграммах свободного тела
Возврат к онлайн-списку описаний сил
диаграмм сил свободного тела — видео по физике от Brightstorm
Диаграмма силы свободного тела используется, чтобы показать все силы, действующие на объект, чтобы предсказать результирующую силу и, в конечном итоге, путь объекта.Каждая сила изображена в виде векторной стрелки.
Давайте посмотрим на некоторые диаграммы силы тела силы. В основном это диаграммы, которые показывают силу или силы, действующие на объект, и помогают нам проиллюстрировать, как эти силы взаимодействуют, перемещая этот объект или не перемещая этот объект. Давайте рассмотрим пару примеров, давайте возьмем книгу, и если у меня есть книга, и я ее уроню, очевидно, что сила, действующая правильно, это сила гравитации.Но если у меня есть книга, и я держу ее на столе, хорошо, что сила тяжести по-прежнему действует на эту книгу. Но книга движется неправильно, в книге нет никаких изменений. На книгу действует еще одна сила, которую мы называем нормальной силой. Итак, если я нарисовал диаграмму своей книги, у меня есть сила, которую я собираюсь назвать fg силой тяжести, но у меня есть другая сила, действующая на эту книгу, и это нормальная сила, это таблица, применяющая равную силу к эту книгу, чтобы она не упала на землю, ладно.
Давайте посмотрим на падающий воздушный шар. Причина, по которой мы используем воздушный шар, заключается в том, что я хочу, чтобы что-то падало с постоянной скоростью, хорошо. Потому что, если он просто падает, как эта книга, у нас в значительной степени просто сила тяжести, хорошо. Но этот падающий шар с постоянной скоростью снова имеет силу тяжести fg, заставляющую его опускаться, но постоянная скорость означает, что он не ускоряется, он движется с постоянной скоростью. Здесь на него действует другая сила, и это сила трения или сопротивления воздуха, которая толкает его вверх, хорошо.Итак, две силы на падающем воздушном шаре — это нормально.
Давайте возьмем книгу на столе и переместим ее по столу. Итак, у меня явно есть сила ускорения, которую я прилагаю к книге, чтобы заставить ее двигаться. Хорошо, но когда я перемещаю его по столу, на него действует другая сила, и эта сила — трение стола, хорошо. Так что он снова применяет силу к этой книге. У меня также есть сила, прикладывающая к ней нисходящее давление, это сила тяжести, а затем у меня есть сила, равная силе, идущей вверх, которая является нормальной силой, сила стола прилагается обратно к книге.Итак, посмотрите, как мы можем использовать диаграмму, чтобы проиллюстрировать все различные силы, которые взаимодействуют с движущимися и неподвижными объектами.
Механическая карта — диаграммы осевых сил и крутящие моменты
В качестве альтернативы разделению тела пополам и выполнению анализа равновесия для нахождения внутренних сил и моментов мы также можем использовать графические подходы для построения этих внутренних сил и моментов по длине тела.Если анализ равновесия является наиболее прямым подходом к нахождению внутренних сил и моментов в одном поперечном сечении, то графические подходы являются наиболее простыми подходами для нахождения внутренних сил или внутренних моментов по всей длине балки, вала или другого тела. . Это может быть полезно в сложных сценариях нагружения, где может быть неочевидно, где существуют максимальные внутренние силы или внутренние моменты. Однако в качестве компромисса нам нужно будет построить каждый тип внутренней нагрузки отдельно (один график для внутренних осевых сил, один для внутренних поперечных сил, один для внутренних крутящих моментов и один для внутренних изгибающих моментов).
В сложных ситуациях нагружения, таких как нагрузки на эту горизонтальную потолочную балку, может быть трудно определить, где внутренние силы и внутренние моменты будут наибольшими. Построив график внутренних сил и моментов, мы сможем более легко определить эти максимальные внутренние нагрузки, и мы сможем спроектировать балку соответствующим образом, чтобы выдерживать эти нагрузки. Внутренняя осевая сила (N) и внутренний крутящий момент (T) действуют вдоль длина балки или вала.В этом разделе мы сосредоточимся на методах, используемых для построения графиков для внутренних осевых сил , и внутренних моментов , .Это будут сила и момент, действующие по длине балки или вала. График осевой силы используется в основном для вертикальных колонн или кабелей, поддерживающих множественные нагрузки по своей длине. Диаграмма крутящего момента используется в основном для валов, поддерживающих несколько входов и выходов. Каждый из этих графиков будет иметь различное практическое применение, но мы сгруппировали их здесь, потому что процесс, используемый для создания каждого из двух графиков, очень похож.
Создание диаграммы осевой силы
Диаграмма осевых сил будет отображать внутренние осевые (нормальные) силы в балке, колонне или кабеле, которые поддерживают множественные силы по длине самой балки.Это можно представить как внутреннее растяжение или сжатие сил. Наиболее подходящими практическими сценариями, соответствующими этому описанию, будут основные опорные колонны в многоэтажном здании или подвесные кабели, которые используются для поддержки нескольких нагрузок.
Основные вертикальные опорные колонны в этом здании будут выдерживать множественные нагрузки, действующие по длине колонны. Изображение Jun Seita CC-BY-NC 2.0.Чтобы создать график осевой силы для тела, мы будем использовать следующий процесс.
- Решите для всех внешних сил , действующих на тело.
- Нарисуйте диаграмму свободного тела тела по горизонтали . В случае вертикальных конструкций поверните корпус так, чтобы он находился горизонтально и все силы действовали горизонтально
- Под диаграммой свободного тела нарисуйте набор осей. Ось x будет представлять местоположение (выровненное с диаграммой свободного тела выше), а ось y будет представлять внутренние осевые силы, с положительными числами, указывающими на растяжение, и отрицательными числами, показывающими сжатие.
- Начиная с нуля в правой части графика, вы переместитесь вправо, обратите внимание на силы на диаграмме свободного тела выше. Двигаясь вправо по своему участку, сохраняйте устойчивость, кроме …
- Прыгните на вверх на на величину силы для любых сил на нашей диаграмме свободного тела к слева .
- Прыжок вниз на величину силы для любых сил вправо .
- Любые моменты или вертикальные силы, приложенные к телу, можно игнорировать.
Чтобы прочитать график, вам просто нужно найти интересующее место на диаграмме свободного тела выше и прочитать соответствующее значение по оси Y вашего графика.Опять же, положительные числа представляют внутреннее натяжение в этом месте, а отрицательные числа представляют внутреннее сжатие в этом месте.
Создание диаграммы крутящего момента
Диаграмма крутящего момента будет отображать внутренний крутящий момент внутри вала, который поддерживает несколько входов и / или выходов по своей длине. Наиболее актуальными практическими сценариями, соответствующими этому описанию, являются валы в сложных системах с шестеренчатым или шкивным приводом.
Этот линейный вал имеет один вход, который передает крутящий момент на несколько выходов через шкивы.Изображение Wtshymanski CC-BY-SA 4.0Чтобы создать диаграмму крутящего момента для вала, мы будем использовать следующий процесс.
- Решите для всех внешних моментов , действующих на вал.
- Нарисуйте схему свободного тела вала горизонтально, , вращая вал, если необходимо, так, чтобы все крутящие моменты действовали вокруг горизонтальной оси.
- Под диаграммой свободного тела нарисуйте набор осей. Ось x будет представлять местоположение (выровнено с диаграммой свободного тела выше), а ось y будет представлять внутренний крутящий момент, с положительными числами, указывающими вектор внутреннего крутящего момента вправо, и отрицательными числами, указывающими на внутренний крутящий момент. момент налево.
- Начиная с нуля в правой части графика, вы переместитесь вправо, обратите внимание на моменты на диаграмме свободного тела выше. Двигаясь вправо по своему участку, сохраняйте устойчивость, кроме …
- Перейти на вверх на на величину момента для любых моментов на нашей диаграмме свободного тела, где вектор момента будет указывать на влево на .
- Перейти на вниз на на величину момента для любых моментов на нашей диаграмме свободного тела, где вектор момента будет указывать на вправо на .
- Вы можете игнорировать любые силы на диаграмме свободного тела или моменты, не относящиеся к оси x.
Чтобы прочитать график, вам просто нужно найти интересующее местоположение на диаграмме свободного тела выше и прочитать соответствующее значение по оси Y на вашем графике.
15A: Законы Ньютона № 2: Виды сил, создание диаграмм свободного тела
На объект не действует «сила движения». Как только у вас есть сила или силы, приложенные к объекту всем (включая любое поле силы на массу в месте расположения объекта), которое касается объекта, у вас есть все силы.Не добавляйте фиктивную «силу движения» к диаграмме свободного тела. Особенно соблазнительно добавить фиктивную силу, когда нет реальных сил в направлении, в котором движется объект. Однако имейте в виду, что объекту не нужна сила, чтобы продолжать движение в том направлении, в котором он движется; движение с постоянной скоростью — это то, что делает объект, когда на него нет действующей силы.
Теперь, когда вы немного попрактиковались в использовании диаграмм свободного тела, пришло время обсудить, как их создавать.Когда вы рисуете свободную диаграмму тела, вам нужно помнить о нескольких вещах:
- Включите только те силы, которые действуют НА объект, диаграмму свободного тела которого вы рисуете. Любая сила, приложенная этим объектом к какому-либо другому объекту, относится к диаграмме свободного тела другого объекта.
- Все силы — это силы контакта, и у каждой силы есть агент. Агент — это «то, что проявляет силу». Другими словами, агент — это форма жизни или вещь, которая толкает или тянет объект.Ни один агент не может воздействовать на объект силой, не контактируя с ним. (Мы используем точку зрения поля, а не точку зрения действия на расстоянии для фундаментальных сил природы. Так, например, это гравитационное поле Земли в месте расположения объекта, а не материальное сама земля, которая оказывает на объект гравитационную силу.)
Мы собираемся представить различные виды сил на примерах. Вот первый пример:
Пример 15-1
Человек подбрасывает камень в воздух.Нарисуйте диаграмму свободного тела камня, пока он находится в воздухе. (Ваша диаграмма свободного тела применима в любое время после того, как камень покинет руку метателя, до последнего момента перед тем, как камень вступит в контакт с тем, что ему суждено ударить.) Пренебрегайте любыми силами, которые могут быть приложены к камню со стороны воздуха.
Решение
Если вы видите камень, летящий по воздуху, вам может показаться, что ничего не касается камня. Но гравитационное поле Земли находится повсюду в непосредственной близости от Земли.Его нельзя заблокировать. Его нельзя экранировать. Он в воздухе, в воде, даже в грязи. Он находится в прямом контакте со всем, что находится поблизости от земли. Он воздействует на каждый объект у поверхности земли. Мы называем эту силу гравитационной силой. Вы уже изучили гравитационную силу. Мы даем краткий обзор этого здесь.
Гравитационная сила, действующая на объекты, расположенные у поверхности Земли.
Поскольку у Земли есть масса, у нее есть гравитационное поле.Гравитационное поле — это поле силы на массу. Это незаметно. Это не важно. Это бесконечный набор векторов силы на массу, по одному в каждой точке пространства вблизи поверхности Земли. Каждый вектор силы на массу направлен вниз, к центру Земли, и вблизи поверхности Земли имеет величину \ (9.80 \ dfrac {N} {kg} \). Для обозначения вектора гравитационного поля Земли в любой точке, где он существует, используется символ \ (\ vec {g} \). Таким образом, \ (\ vec {g} = 9.80 \ dfrac {N} {kg} \) вниз.Действие гравитационного поля Земли заключается в приложении силы к любому объекту, находящемуся в гравитационном поле Земли. Сила называется гравитационной силой и равна произведению массы объекта и вектора гравитационного поля Земли: \ (F_g = m \ vec {g} \). Величина силы тяжести определяется как
.\ [F_g = mg \ label {15-1} \]
, где \ (g = 9.80 \ dfrac {N} {kg} \) — величина вектора гравитационного поля Земли. Направление гравитационной силы у поверхности Земли — вниз, к центру Земли.
Вот диаграмма свободного тела и соответствующая таблица сил для примера \ (\ ref {15-1} \):
| Таблица сил | |||
| Символ =? | Имя | Агент | Жертва |
| \ [F_g = mg \ notag \] | Гравитационная сила | Гравитационное поле Земли | Скала |
Примечание:
1) Единственное, что касается объекта, когда он находится в воздухе (не считая самого воздуха), — это гравитационное поле Земли.Итак, на объект действует только одна сила, а именно сила тяжести. Стрелка, представляющая вектор силы, нарисована так, что конец стрелки касается объекта, а стрелка проходит от объекта в направлении силы.
2) Если иное не оговорено и не обозначено на схеме, вверх идет к верху страницы, а вниз — к низу страницы.
3) Стрелка, показывающая ускорение, должна быть рядом, но не касаться объекта.(Если он касается объекта, можно принять это за силу.)
4) На диаграмме свободного тела нет информации о скорости.
5) Нет силы руки, действующей на объект, потому что в данный момент рука больше не касается объекта. Когда вы рисуете диаграмму свободного тела, учитываются только силы, действующие на объект в момент, изображенный на диаграмме. Ускорение объекта зависит только от сил, действующих в данный момент на объект.Сила руки представляет только исторический интерес.
6) Касательно таблицы сил:
a) Убедитесь, что для любой нарисованной вами схемы свободного тела вы можете составить полную таблицу сил. От вас не требуется прилагать таблицу сил к каждой нарисованной вами диаграмме свободного тела, но вы должны ожидать, что вам придется создавать таблицу сил более одного раза.
б) В таблице сил агент — это форма жизни или вещь, которая оказывает силу, а жертва — это объект, на который действует сила.Убедитесь, что в каждом случае жертва является объектом, для которого строится диаграмма свободного тела.
c) В данном случае есть только одна сила, поэтому в таблице сил есть только одна запись.
г) Для любого объекта, находящегося у поверхности Земли, агентом силы тяжести является гравитационное поле Земли. Это нормально сокращать это до «Земля», потому что гравитационное поле Земли можно рассматривать как невидимую часть Земли, но НЕЛЬЗЯ называть это «гравитацией».«Гравитация — это предметный заголовок, соответствующий типу силы гравитационной силы, гравитация — не агент.
Пример 15-2
Шар массы m неподвижно висит на веревке. Нарисуйте схему свободного тела мяча и составьте соответствующую таблицу сил.
Решение
Для решения этой задачи вам потребуется следующая информация о строках:
Сила, оказываемая натянутой струной на предмет, к которому она прикреплена
(Это также относится к веревкам, тросам, цепям и т. П.)
Сила, прилагаемая веревкой к объекту, к которому она прикреплена, всегда направлена от объекта по длине веревки.
Обратите внимание, что указанная сила создается веревкой, а не, например, каким-либо человеком, тянущим за другой конец веревки.
Сила, оказываемая струной на объект, называется «силой натяжения», и ее величина обычно обозначается символом \ (F_T \).
Примечание. Не существует формулы для определения силы натяжения.Если он не указан, единственный способ получить его — использовать закон Ньютона 2 nd .
Вот диаграмма свободного тела мяча и соответствующая таблица сил для примера 15-2:
| Символ =? | Имя | Агент | Жертва |
|---|---|---|---|
| \ [F_T \ notag \] | Сила натяжения | Строка | Мяч |
| \ [F_g = mg \ notag \] | Гравитационная сила | Гравитационное поле Земли | Мяч |
Пример 15-3
Сани массой \ (м \) тянутся вперед по горизонтальной поверхности без трения с помощью горизонтального троса, прикрепленного к передней части салазок.Нарисуйте схему свободного тела салазок и предоставьте соответствующую таблицу сил.
Решение
Помимо веревки и гравитационного поля земли, сани соприкасаются с твердой поверхностью. Поверхность проявляет силу, о которой нам нужно знать, чтобы создать диаграмму свободного тела для этого примера.
Нормальная сила
Когда объект находится в контакте с поверхностью, эта поверхность оказывает на объект силу. Поверхность давит на объект.Сила, действующая на объект, направлена от поверхности перпендикулярно поверхности. Сила называется нормальной силой, потому что «нормальная» означает перпендикулярная, и, как уже упоминалось, сила перпендикулярна поверхности. Мы используем символ \ (F_N \) для обозначения величины нормальной силы.
Примечание: не существует формулы, которая бы сообщила вам, какова нормальная сила. Если он не указан, единственный способ получить его — использовать закон Ньютона 2 nd .
Вот схема свободного тела салазок и соответствующая таблица сил.
| Имя | Агент | Жертва | |
|---|---|---|---|
| \ [F_N \ notag \] | Нормальная сила | Горизонтальная поверхность | Сани |
| \ [F_T \ notag \] | Сила натяжения | Веревка | Сани |
| \ [F_g = mg \ notag \] | Гравитационная сила | Гравитационное поле Земли | Сани |
Примечание. Слово «Свободный» в «Диаграмме свободного тела» относится к тому факту, что объект нарисован вне окружения.Не включайте в диаграмму свободного тела окружающую обстановку (например, горизонтальную поверхность, по которой скользят сани в имеющемся футляре).
Пример 15-4
Блок массой \ (m \) опирается на горизонтальную поверхность без трения. Блок находится к западу от стены, выходящей на запад. Блок прикреплен к стене идеальной безмассовой несжатой / нерастянутой пружиной, силовая постоянная которой равна \ (k \). Пружина расположена перпендикулярно стене. Человек отодвигает блок на расстояние x прямо от стены и отпускает его из состояния покоя.Нарисуйте схему свободного тела блока, подходящую для первого момента после выпуска. Приведите соответствующую таблицу сил.
Решение
Теперь у нас впервые есть пружина, оказывающая силу на объект, для которого мы рисуем диаграмму свободного тела. Итак, нам нужно знать о силе, оказываемой пружиной.
Сила, создаваемая пружиной
Сила, прилагаемая идеальной безмассовой пружиной к объекту, контактирующему с одним концом пружины, направлена по длине пружины, а
\ (\ bullet \) от объекта, если пружина растянута,
\ (\ bullet \) к объекту, если пружина сжата.
Чтобы пружина оказывала давление на объект в корпусе растянутой пружины, объект должен быть прикреплен к концу пружины. Не так в случае с сжатой пружиной. Пружина может давить на объект независимо от того, прикреплена ли пружина к объекту.
Сила зависит от величины \ (| x | \), на которую пружина растягивается или сжимается, и от меры жесткости пружины, известной как силовая постоянная пружины, также известная как жесткость пружины и представленная символом \ (к \).Величина силы пружины обычно обозначается символом \ (F_s \). Сила пружины прямо пропорциональна величине растяжения \ (| x | \). Жесткость пружины \ (k \) — это постоянная пропорциональности. Таким образом,
\ [F_s = k | x | \ label {15-2} \]
Вот диаграмма свободного тела блока и соответствующая таблица сил для примера 15-4:
| Имя | Агент | Жертва | |
|---|---|---|---|
| \ [F_N \ notag \] | Нормальная сила | Горизонтальная поверхность | Блок |
| \ [F_s = k | x | \ notag \] | Сила пружины | Весна | Блок |
| \ [F_g = mg \ notag \] | Гравитационная сила | Гравитационное поле Земли | Блок |
Пример 15-5
С вашей точки зрения ящик массы \ (m \) скользит вправо по плоскому бетонному полу.Ничто твердое не соприкасается с обрешеткой, кроме пола. Нарисуйте схему свободного тела ящика. Приведите соответствующую таблицу сил.
Решение
Из нашего опыта с предметами, скользящими по бетонному полу, мы знаем, что в данный момент ящик замедляется. Он замедляется из-за кинетического трения.
Кинетическое трение
Поверхность, по которой скользит объект, оказывает (в дополнение к нормальной силе) тормозящую силу на этот объект.Тормозящая сила действует в направлении, противоположном скорости движения объекта. В случае скольжения объекта по сухой поверхности твердого тела (например, пола) мы называем тормозящую силу кинетической силой трения. Кинетический означает движение, и мы включаем прилагательное кинетический, чтобы прояснить, что мы имеем дело с объектом, который находится в движении.
Приведенная ниже кинетическая формула трения является эмпирическим результатом. Это означает, что он получен непосредственно из экспериментальных результатов.Работает только в случае скольжения предметов по сухим поверхностям. Это не относится, например, к случаю скольжения объекта по смазанной поверхности.
Мы используем символ \ (F_ {kf} \) для кинетической силы трения. Формула кинетического трения показывает
.\ [F_ {kf} = \ mu_K F_N \ label {15-3} \]
\ (F_N \) — величина нормальной силы. Его наличие в формуле говорит о том, что чем сильнее поверхность давит на объект, тем больше сила трения.
\ (\ mu_K \) (mu-sub-K) называется коэффициентом кинетического трения. Его значение зависит от материалов, из которых изготовлены объект и поверхность, а также от гладкости двух контактных поверхностей. У него нет юнитов. Это всего лишь цифра. Величина кинетической силы трения составляет некоторую долю величины нормальной силы; \ (\ mu_K \) и есть эта дробь. Значения \ (\ mu_K \) для различных пар материалов можно найти в справочниках. Они имеют тенденцию находиться между \ (0 \) и \ (1 \).Фактическое значение для данной пары материалов зависит от гладкости поверхности и обычно указывается только с одной значащей цифрой.
ВАЖНО: \ (\ mu_K \) — это коэффициент (без единиц измерения), используемый при расчете силы трения. Это не сила.
Вот диаграмма свободного тела и таблица сил для рассматриваемого случая. Ящик движется вправо и замедляется — у него есть ускорение влево.
| Символ =? | Имя | Агент | Жертва |
|---|---|---|---|
| \ [F_N \ notag \] | Нормальная сила | Бетонный пол | Ящик |
| \ [F_ {kf} = \ mu_ {K} F_ {N} \ notag \] | Кинетическая сила трения | Бетонный пол | Ящик |
| \ [F_g = mg \ notag \] | Гравитационная сила | Гравитационное поле Земли | Ящик |
Пример 15-6
Человек толкнул кирпич по плиточному полу к стене, обращенной на восток, захватив пружину нерастянутой длины \ (L_0 \) и постоянной силы \ (k \) между стеной и концом кирпича, обращенным к стене. .Этот конец кирпича находится на расстоянии d от стены. Человек выпустил кирпич, но пружина не может сдвинуть его с места — кирпич остается там, где он был, когда человек выпустил его. Нарисуйте схему свободного тела для кирпича и предоставьте соответствующую таблицу сил.
Решение
Сила трения действует на покоящийся объект. Обычно неподвижный объект сильнее цепляется за поверхность, с которой он контактирует, чем тот же объект, когда он скользит по той же поверхности.Здесь мы имеем дело со статическим трением.
Сила статического трения
Поверхность, не обладающая трением, может оказывать силу статического трения на предмет, который находится в контакте с этой поверхностью. Сила статического трения параллельна поверхности. Он находится в направлении, противоположном направлению приближающегося движения неподвижного объекта. Направление приближающегося движения — это направление, в котором объект ускорялся бы, если бы не было статического трения.
Как правило, формулы для расчета статического трения не существует — чтобы найти силу статического трения, вы используете 2-й закон Ньютона.Сила статического трения является любой, чтобы сделать результирующую силу, параллельную поверхности, равной нулю.
Мы используем символ \ (F_ {sf} \) для обозначения величины силы статического трения.
ОСОБЫЙ СЛУЧАЙ: Представьте, что вы пытаетесь толкнуть холодильник по полу. Представьте, что вы толкаете горизонтально и постепенно увеличиваете силу, с которой толкаете. Первоначально, чем сильнее вы толкаете, тем больше сила статического трения. Но он не может расти вечно. Для любого такого случая существует максимально возможная величина силы статического трения.{\ mbox {max possible}} = \ mu_s F_N) \) применимо только тогда, когда вопрос касается максимально возможной силы статического трения. Вы можете использовать эту формулу, если говорится, что объект вот-вот поскользнется, или если вопрос заключается в том, насколько сильно нужно толкнуть объект, чтобы сдвинуть его с места. Это также пригодится, когда вы хотите знать, останется ли объект на месте. В таком случае вы должны использовать 2 nd Ньютона, чтобы узнать величину силы статического трения, необходимой для предотвращения ускорения объекта.Затем вы сравните эту величину с максимально возможной величиной силы статического трения.
Вот диаграмма свободного тела кирпича и таблица сил для примера 15-6:
| Символ =? | Имя | Агент | Жертва |
|---|---|---|---|
| \ [F_N \ notag \] | Нормальная сила | Кафельный пол | Кирпич |
| \ [F_ {sf} \ notag \] | Сила статического трения | Кафельный пол | Кирпич |
| \ [F_g = mg \ notag \] | Гравитационная сила | Гравитационное поле Земли | Кирпич |
| \ [F_s = k | x | \ notag \] | Сила пружины | Весна | Кирпич |
Авторы и указание авторства
Диаграммы усилийдля болтов SWedge
Диаграмма усилия болта, как определено в SWedge, представляет доступную силу растяжения, которую болт может приложить к клину в любой точке по длине болта.То есть, если плоскость клина пересекает болт в определенном месте по его длине, какова максимальная сила растяжения, которую болт может приложить к клину. Это предполагает, что болт приводится в движение при чистом натяжении.
Для болтов с механической анкеровкой диаграмма сил представляет собой просто горизонтальную линию, поскольку будет применяться постоянная опорная сила, независимо от того, где плоскость клина пересекает болт.
Для дюбелей, тросов, разъемных болтов или болтов Swellex диаграмма сил определяется с учетом каждого возможного режима разрушения при растяжении по длине опоры (растяжение, отрыв и снятие изоляции, если применимо).Режим отказа, который создает МИНИМАЛЬНУЮ силу, определяет опорную силу, которая может быть создана в каждой точке опоры.
Для опоры, определяемой пользователем, диаграмма сил явно определяется пользователем, свойства растяжения (например, прочность на растяжение, прочность плиты, прочность сцепления) не вводятся.
Например, возможная диаграмма усилия болта для залитого дюбеля с длиной соединения менее 100% и нагрузкой на пластину, которая меньше прочности на разрыв, проиллюстрирована ниже.
Диаграмма усилия болтадля залитого дюбеля
Дополнительные примеры типичных диаграмм усилия болта см. В следующих разделах:
Болт с механической фиксацией
Дюбель с затиркой
Болт троса
Набор сплит / Swellex
Определяется пользователем
В дополнение к диаграмме усилия болта, существуют два других фактора, которые в конечном итоге определяют опорную силу, которую может передать болт в SWedge — эффективность ориентации болта и прочность на сдвиг.См. Эти темы для получения дополнительной информации.
Обзор реализации опоры болта в SWedge см. В разделе «Опорная сила болта». Здесь обсуждаются все параметры, которые влияют на несущую способность болта, и резюмируются все возможные случаи.
Интерпретация диаграмм усилия болта
Пользователь должен понимать, что диаграмма усилия болта, реализованная в SWedge, не обязательно отражает истинное состояние напряжения или нагрузки, создаваемой данным болтом.Диаграмма силы просто представляет собой максимально доступную растягивающую силу, которую данный болт теоретически может приложить к клину в любой точке по его длине. Это основано на предположениях, описанных для каждого типа болта в SWedge.
Помните, что анализ SWedge — это анализ предельного равновесия. Смещения и деформации в таком анализе не учитываются. Для реалистичного моделирования взаимодействия опоры и выемки грунта, а также для расчета фактических деформаций и нагрузки, возникающей в опоре, требуются более сложные методы численного анализа, такие как методы конечных элементов или конечных разностей.
Моделирование опоры в SWedge — простой, но полезный метод учета влияния опорной системы на клин при анализе предельного равновесия. Он не предназначен для моделирования воздействия клина на опорную систему, и диаграммы усилия болта не следует интерпретировать таким образом.
Обзор диаграмм силы и свободного тела — видео и стенограмма урока
Ключевые силы и правила
Правило № 1: Линии стрелок должны быть прямыми, а сила должна быть направлена в определенном направлении.
Кривая не имеет смысла. Если вы толкнете в два направления одновременно, это будет диагональ, но все же прямая линия. Может быть, кривая означает, что сила со временем меняется. Но если со временем что-то изменится, вам нужно будет нарисовать более одной диаграммы сил. Все диаграммы должны иметь прямые линии.
Правило № 2: Изобразите силы, действующие на точку, стрелками, указывающими от объекта.
Людям нравится рисовать стрелки, удаляющиеся от края объекта, но в физике мы знаем, что силы действуют в определенном месте.Если объект представляет собой частицу, рисование точки имеет смысл. Но даже с более крупным объектом забавной формы, этот объект все еще имеет точку посередине, называемую центром масс . Это место, в котором, кажется, действуют силы. Если бы силы не действовали в центре масс, объект начал бы вращаться. Поэтому, если это не вращающийся объект, каждая стрелка должна указывать от точки. И они всегда уходят, а не навстречу. В основном это касается аккуратности: если вы наведете стрелки на точку или смешаете их вместе, это может сбить с толку и неясно.
Правило № 3: Если объект давит на твердую неподвижную поверхность, приложите к этой поверхности нормальную силу под углом 90 градусов.
Если бы не было нормальной силы, объект прошел бы через поверхность, на которой он сидит. В большинстве случаев это будет просто объект, лежащий на земле или на столе, при этом нормальная сила направлена прямо вверх. Но если объект находится на склоне, он по-прежнему находится под углом 90 градусов к поверхности. Или, если вы сами прижимаете объект к углу стены, у вас могут быть две нормальные силы.
Правило № 4: Сила тяжести (Fg) действует прямо вниз.
На все на Земле всегда действует сила тяжести, падаете вы или полностью неподвижны. Когда вы неподвижны, это просто потому, что нормальная сила земли уравновешивает силу тяжести.
Правило № 5: Натяжение струны действует в обоих направлениях, в направлении струны.
Если у вас есть веревка, соединяющая два объекта, оба объекта чувствуют натяжение веревки.
Правило номер 6: Трение действует противоположно направлению движения или направлению, в котором объект мог бы двигаться, если бы мог.
Допустим, у вас есть блок на рампе, но из-за трения он остается на рампе и не двигается. Трение будет действовать вверх по склону, параллельно ему, потому что оно всегда действует против направления движения. Если бы не трение, блок двигался бы вниз по склону, поэтому трение должно действовать вверх по склону. С другой стороны, если вы толкаете блок вверх по склону руками, то вниз по склону будет действовать трение — всегда противоположное направлению движения.
Резюме урока
Диаграмма свободного тела — это изображение или эскиз, используемый физиками и инженерами для отображения сил, действующих на объект, со стрелками, представляющими силы. Чем длиннее стрелка, тем сильнее сила. Усилие на самом деле довольно просто: это просто толчок или тяга. Полезно иметь способ представить силы, действующие на объект, потому что люди могут регистрировать информацию с помощью изображений намного быстрее, чем слова или числа.
Вот некоторые из наиболее важных правил рисования диаграмм свободного тела:
- Правило № 1: Линии стрелок должны быть прямыми.
- Правило № 2: Нарисуйте силы, действующие на точку, стрелками, указывающими от объекта. Обычно это происходит из-за того, что для невращающегося объекта центр масс этого объекта является местом, в котором, кажется, действуют силы.
- Правило № 3: Если объект давит на твердую поверхность, приложите к этой поверхности нормальную силу под углом 90 градусов.
- Правило № 4: Сила тяжести действует прямо вниз.
- Правило номер 5: Натяжение струны действует в обоих направлениях, в направлении струны.
- Правило номер 6: Трение действует противоположно направлению движения или направлению, в котором объект мог бы двигаться, если бы мог.
Часть 4
Часть 4Часть 4: Диаграммы свободного тела
Сила, действующая на тело (т. Е. На объект), математически представляется в виде вектор. Диаграмма сил , , которая также известна как Диаграмма свободного тела , — эскиз, в котором все векторы силы, действующие на объекте начальными точками в месте расположения объект.
Сила F , действующая на тело (т.е. объект), равна математически представлен вектором в том смысле, что он имеет величину || F || который применяется в заданном направлении. Величина || F || измеряется в Ньютонах, , где 1 Ньютон — сила, необходимая для ускорения массы 1 кг при со скоростью 1 метр в секунду в секунду (т.е. 1 N = 1 кг · м / сек 2 ).
Диаграмма сил , , которая также известна как диаграмма свободного тела , — это эскиз, в котором нарисованы все векторы сил, действующие на объект. с их начальными точками в месте расположения объекта.Сеть Сила , действующая на тело, представляет собой сумму всех сил на силовой диаграмме.
ПРИМЕР 8 10-килограммовый блок, лежащий на столе, прикреплен «безмассовой» веревкой к 5-килограммовому блоку. блок, свисающий с конца (с веревкой, проходящей через «без трения» шкив).Нарисуйте диаграмму свободного тела и определите чистую силу, если блок 10 кг испытывающий силу трения величиной 30 ньютонов.
Решение: Начнем с силы тяжести F силы тяжести тянет 10-килограммовый блок к Земле, что согласно третьему закону Ньютона которому противодействует сила, нормальная (т. е. перпендикулярная) к столу, которая сопротивляется падают 10 кг блоков. Если блок не движется вертикально, то F нормальная и F сила тяжести должна иметь одинаковую величину. так что они компенсируют друг друга (т.е, нет чистой силы вверх или вниз).
Используя закон Ньютона F = ma , мы можем показать, что блок 5 кг подвержен действию гравитационная сила Поскольку || F 5 кг || = 49 N , блок 5 кг применяет сила
к блоку 10кг.Наконец, сила трения F трение сопротивляется горизонтальному движению блока, поэтому применяется в направление — i , или
F применено = 49 i Ньютонов Таким образом, чистая сила равна
F трение = -30 i Ньютонов
F нетто = F сила тяжести + F нормальный + F прикладной + F трение = 0 + 49 i -30 i = 19 и
В примере 8 чистая сила F чистая = 19 i означает что 10-килограммовый блок ускоряется вправо со скоростью 1.9 метров на секунда в секунду. Напротив, если бы трение имело величину 49 Ньютонов, он вообще не двигался бы, т. Е. Покоился бы с Блок 5 кг также находится в состоянии покоя, так как он висит в воздухе.
Если результирующая сила, действующая на тело, равна 0, то говорят, что тело находится в состоянии равновесия . Когда это происходит, равновесие часто может использоваться для определения неизвестные величины на диаграмме свободного тела.
ПРИМЕР 9 Блок весом 50 кг подвешен на 2 идентичных тросах одинаковой длины, образующей 45 угла с горизонтом.Если блок остается неподвижным с течением времени, то какова величина растягивающее усилие каждого троса на блоке? Решение: В этом случае диаграмма свободного тела с массой 50 кг выглядит так: приведено на рисунке ниже.
Сила тяжести
Если мы позволим F обозначать (неизвестную) величину силы, оказываемой кабель, затем Следовательно, чистая сила равна
F Плотность = 50 кг · в 0, -9.8 м / сек 2 ñ = á 0, -490 N ñ Поскольку F net = 0 (равновесие), имеем
2 Ф 2
= 490, F = 4902 2
= 346.