4.4. Построение эпюр, проверка решения, определение перемещений от температурного воздействия

Построение эпюр

Построение окончательной эпюры (М)^t представлено на рис. 4.4.1–4.4.3.

Правила построения эпюр (Q) и (N) подробно рассмотрены в разделе 4.3. Пользуясь этими правилами строим эпюры (Q)^t и (N)^t – рис. 4.4.4, 4.4.5.

Кинематическая проверка

Найдем угол поворота сечения на левой опоре (рис. 4.3.13), который по условию должен быть равен нулю. Дополнительная эпюра , необходимая для нахождения угла поворота, представлена на рис. 4.4.6.

Проверка подтверждает правильность решения.

Проверка равновесия рамы в целом (рис. 4.4.7)

Условия равновесия выполняются.

Определение перемещений сечения k

Линейное перемещение _kt

Единичные эпюры (M₁)_и (N₁)_для определения линейного перемещения сечения k представлены на рис. 4.3.14 и 4.4.8 соответственно.

Перемещения определяются по формуле

Полное линейное перемещение

Угол поворота _kt

Единичная эпюра (M₁)_для определения угла поворота сечения k представлена на рис. 4.3.15.

Построение деформированной схемы рамы

Деформированная схема рамы представлена на рис.

4.4.9.

4.5. Построение эпюр, проверка решения, определение перемещений от кинематического воздействия

Построение эпюр

Построение окончательной эпюры (М)^ представлено на рис. 4.5.1–4.5.3.

Эпюры (Q)^ и (N)^ представлены на рис. 4.5.4, 4.5.5.

Кинематическая проверка

Найдем угол поворота сечения на левой опоре (рис. 4.3.13), который по условию должен быть равен нулю.

Проверка подтверждает правильность решения.

Проверка равновесия рамы в целом (рис. 4.5.6)

Очевидно, что

Условия равновесия выполняются.

Определение перемещений сечения k

Линейное перемещение _k

Единичная эпюра (M₁)_для определения линейного перемещения сечения k представлена на рис. 4.3.14.

Перемещения определяются по формуле

– по условию.

м.

Угол поворота _k

Единичная эпюра (M₁)_для определения угла поворота сечения k представлена на рис. 4.3.15.

рад.

Построение деформированной схемы рамы

Деформированная схема рамы представлена на рис. 4.5.7

3

5. Контрольные вопросы по методу сил

1. Какая система называется статически неопределимой? Как найти степень статической неопределимости?

2. Что принимается за неизвестные метода сил? Что такое основная и эквивалентная системы метода сил?

3. Как вы понимаете идею метода сил?

4. Как с помощью суммарной единичной эпюры проверить правильность коэффициентов канонических уравнений?

5. Как определяются свободные члены канонических уравнений при расчете на температурные воздействия, на заданные смещения?

6. Каков физический смысл и особенности канонических уравнений метода сил?

7. Каков физический смысл коэффициентов при неизвестных и свободных членов в канонических уравнениях?

Метод перемещений

6.

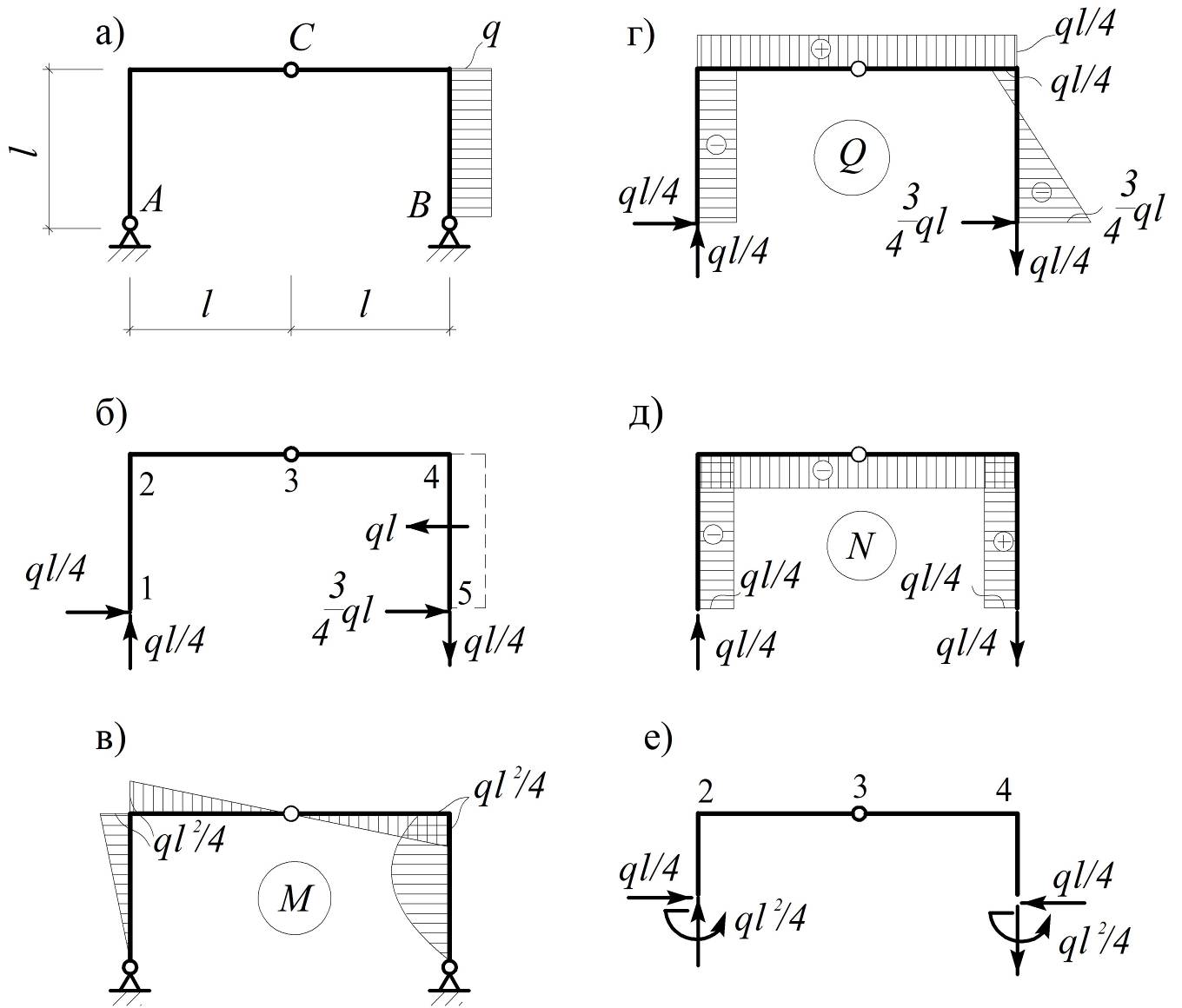Расчет балки методом перемещений, Исходные данные, схемы балок

Для одной из заданных схем балок, изображенных на рис. 6.1–6.24 требуется:

1. изобразить расчетную схему, основную систему и эквивалентную системы;

2. изобразить основную систему, деформированную единичным и заданными воздействиями. Показать на этих рисунках величины, входящие в канонические уравнения;

3. построить эпюры внутренних силовых факторов, возникающих от нагрузки, изменения температуры и заданного смещения опор;

4. найти линейное и угловое перемещения сечения k при всех трех воздействиях;

5. изобразить балку, деформированную каждым из трех воздействий отдельно.

Принять: жесткость балки EI, высоту поперечного сечения h = 0,1 L, коэффициент теплового расширения

α – постоянными по длине балки; жесткость податливых связей равной k = EI/L³ (податливость –  = L³/EI), φ = ∆/L. Другие данные принять по табл. 6.1.

Таблица 6.1

Номер варианта	1	2	3	4	5	6	7
F, кН	4	4	6	8	4	6	4
q, кН/м	2	1	2	3	1	2	3
М, кНм	2	3	2	1	4	2	6
L,м	2	4	6	4	2	2	4
, м	0,01	0,02	0,03	0,04	0,01	0,02	0,03
t, С	10	5	15	10	5	10	15

Реферат на тему Расчет статически неопределимой рамы методом сил

Задача №5.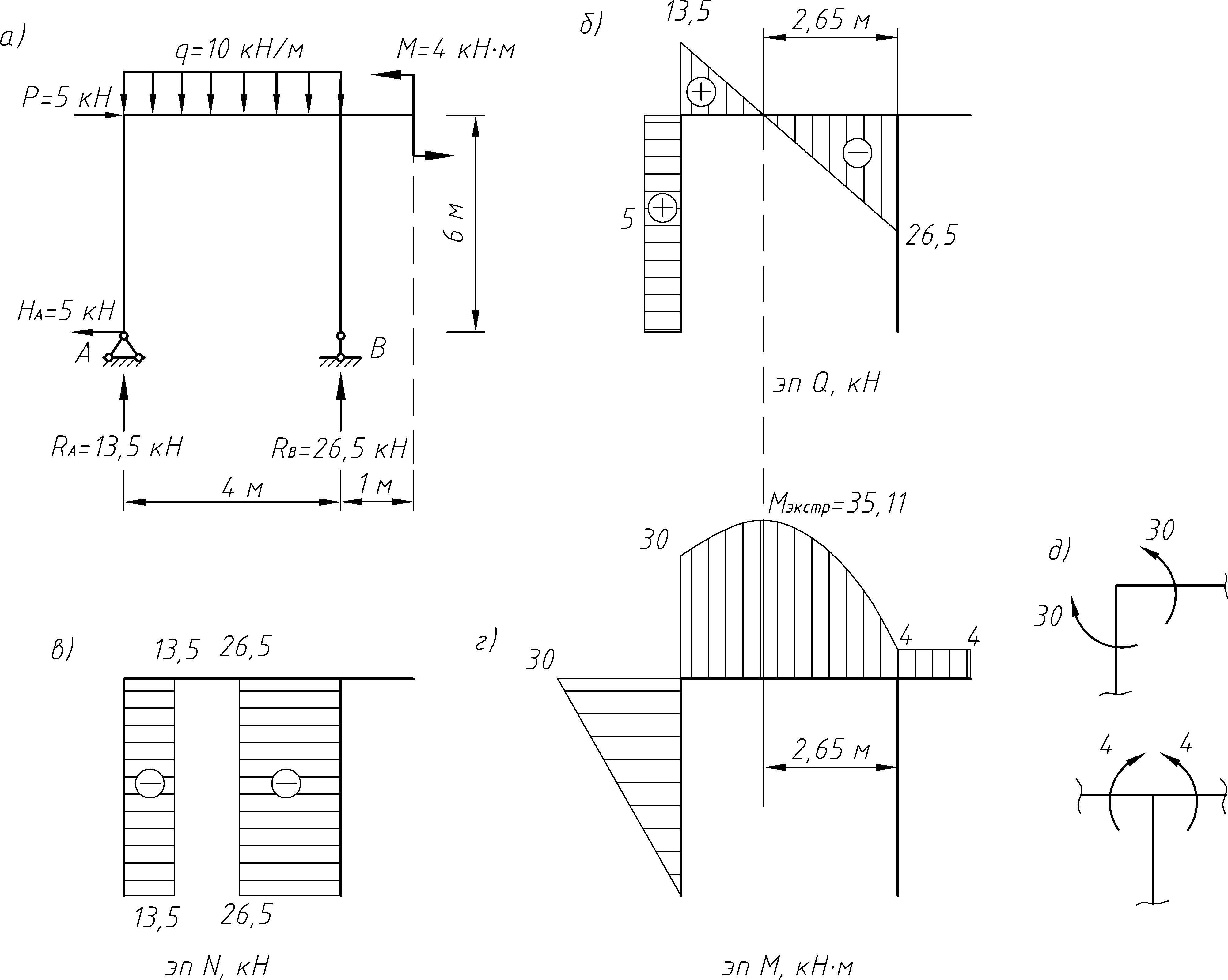

Расчет статически неопределимой рамы методом сил

Для статически неопределимой Е-образной рамы с одной скользящей и двумя неподвижными опорами используя метод сил, формулу Мора и правило Верещагина необходимо определить реакции опор и построить эпюры моментов, поперечных и продольных сил

Построить эпюры M, Q и N.

Решение

Данная система дважды статически неопределима, так как рама прикреплена пятью связями, а уравнений статики для их определения – три. Выбираем основную систему путем отбрасывания лишних связей и заменой их неизвестными усилиями Х₁ и Х₂. Фактически Х₁ будет являться реакцией опоры С, а Х₂– вертикальной составляющей реакции опоры В.

Составляем систему канонических уравнений метода сил:

d₁₁×Х₁ + d₁₂×Х₂ + D_1Р = 0;

d₂₁×Х₁ + d₂₂×Х₂ + D_2Р = 0.

Для определения коэффициентов при неизвестных и свободных членах необходимо построить эпюры изгибающих моментов поочередно для каждой силы.

Эпюра единичных изгибающих моментов от единичной силы Х₁

Эпюра единичных изгибающих моментов от единичной силы Х₂

Грузовая эпюра от заданной нагрузки – силы Р.

Подсчитываем коэффициенты по формуле Мора используя правило Верещагина:

где – величина изгибающего момента единичной эпюры Х_j в точке, где расположен центр тяжести фигуры, образованной единичной эпюрой Х_i;

– площадь фигуры, образованной единичной эпюрой Х_i.

Например, для трапециевидного участка длиной L и размерами сторон м и М единичной эпюры Х₁ находим координату центра тяжести для трапеции:

;

Далее находим значение М^ц.т. в этой точке для всех эпюр.

– для эпюры Х₁ это будет:

,

– для эпюры Х₂ в любой точке данного участка М равно а, следовательно:

– для эпюры Р это будет:

Соответственно площади эпюр на данном участке будут равны:

Аналогичным образом находим составляющие уравнения Мора для других, более простых участков и вычисляем требуемые коэффициенты:

Подставив найденные коэффициенты в систему канонических уравнений и сократив на и а³ получим систему двух уравнений с двумя неизвестными:

×Х₁ + ×Х₂ + Р = 0; 56×Х₁ + 11×Х₂ + 6Р = 0;

×Х₁ + ×Х₂ + ×Р = 0.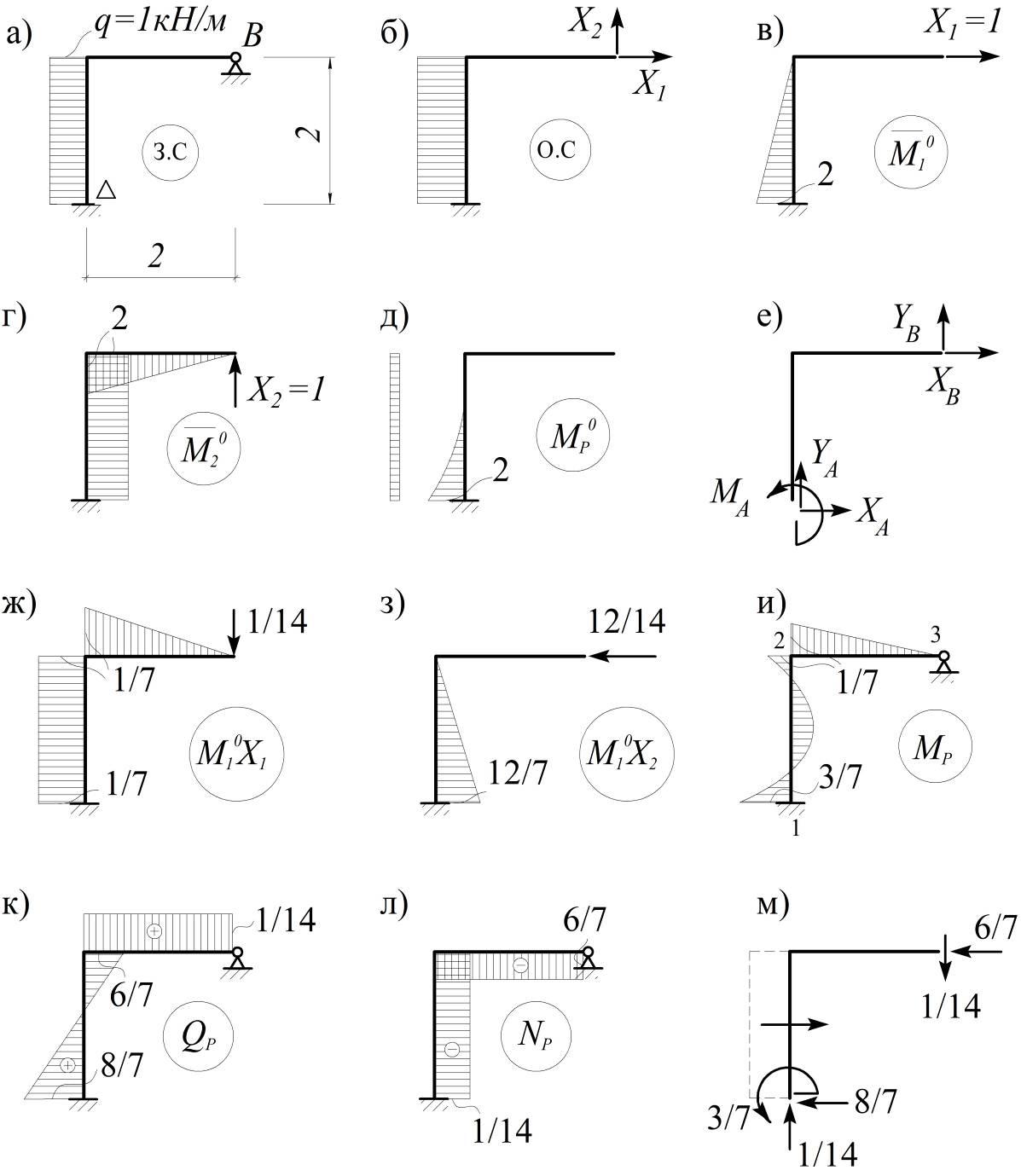 11×Х₁ + 10×Х₂ + 7Р = 0;

Вычитая из первого уравнения второе, получим более простое выражение, из которого выразим Х₂ и подставим затем во второе уравнение;

45Х₁ + Х₂ – Р = 0;®Х₂ = Р – 45Х₁;

11 Х₁ + 10Р – 450 Х₁ + 5Р = 0;

Х₁ = Р = 0,034Р;

Х₂ = Р – Р = –Р = –0,538Р;

Найдя значения неизвестных усилий Х₁ и Х₂, обратимся к основной системе и найдем Х_А, У_А и Х_В.

SУ = 0;

У_А – Х₁ – Х₂ – Р = 0;

У_А = Х₁ + Х₂ + Р = 0,034Р – 0,538Р + Р = 0,496Р;

SМ_А = 0;

Х₁×а + Х_В×а – Р×а = 0;

Х_В = Р – Х₁ = 0,966Р;

SХ = 0;

Х_А – Х_В = 0;

Х_А = Х_В = 0,966Р;

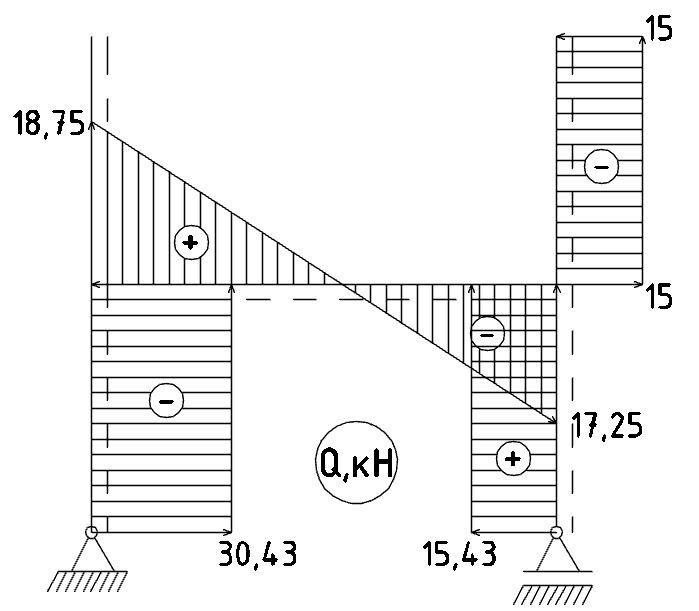
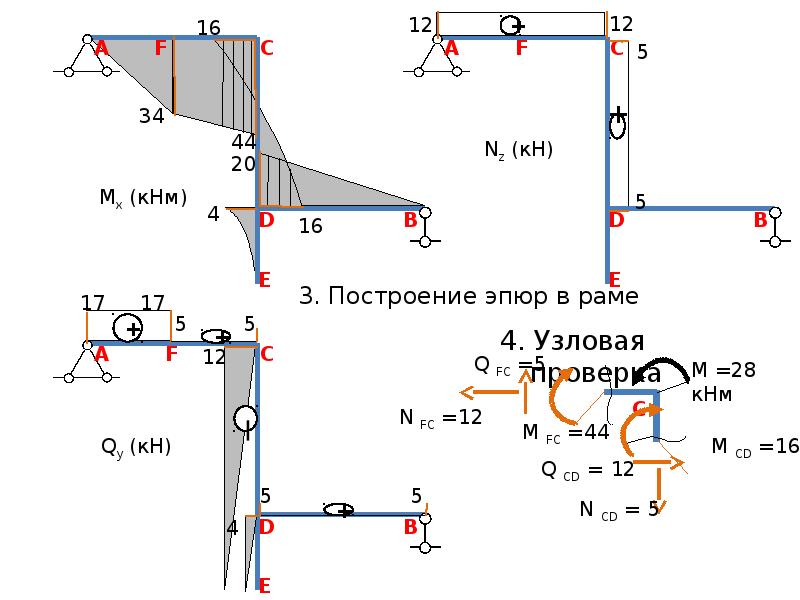
Зная значения всех усилий, действующих на раму, строим эпюры М, Q и N:

Линия Best Fit

• Оценка: С 6 по 8, средняя школа
  

  Это упражнение позволяет пользователю ввести набор данных, нанести данные на координатную сетку и определить уравнение для линии наилучшего соответствия.

  Этот интерактив оптимизирован для настольных компьютеров и планшетов.

  • Нанесите точки, щелкнув в любом месте сетки, или нанесите набор точек, введя пару координат в текстовое поле и нажав Добавить точку .
  • Установите флажок Удалить точки и щелкните любую точку, чтобы удалить ее. Вы также можете щелкнуть и перетащить любую точку, чтобы изменить ее местоположение.
  • При установке флажка Show Guess , на сетке появится фиолетовая линия. Перетащите фиолетовые точки на аппроксимируйте линию наилучшего соответствия визуально. Уравнение этой прямой будет появляются справа. Также можно ввести наклон и точку пересечения по оси Y, чтобы изменить линию наилучшего соответствия.
  • При установке флажка Показать линию наилучшего соответствия , будет отображаться линия регрессии методом наименьших квадратов площади. Появится уравнение этой линии и коэффициент корреляции ( r ).
  • Сетка может увеличиваться и уменьшаться по мере добавления новых точек. Используйте увеличительное стекло + и – для увеличения.
  • Чтобы увидеть другую часть сетки, выделите поле Переместить график и с помощью мыши перетащите график.
  • Вы можете сбросить исходные параметры графика или использовать Поле Zoom to Fit , чтобы график автоматически выбирал параметры, которые оптимально отображают все ваши точки.
  Приведенные ниже данные показывают количество набранных очков и минут, сыгранных шестью игроками «Лос-Анджелес Лейкерс» в сезоне 2004–05. (Для этого исследования «начинающим» является любой игрок, который в среднем проводил более 20 минут за игру.)

  Очки, набранные по горизонтальной оси, и минуты по вертикальной оси.

   

  ИГРОК Очки Минуты Коби Брайант 1819 90 066 2689 Кэрон Батлер 1195 2746 Чаки Аткинс 1115 2903 Ламар Одом 975 2320 Крис Михм 735 1870 Джумейн Джонс 577 1830

  90 060 Введите 1819,2689 1195,2746 1115,2903 975,2320 90 066 735,1870 577,1830

   

  Установите флажок Show Line of Best Fit , чтобы увидеть линейную аппроксимацию этих данных. Коэффициент корреляции ( r ) показывает, насколько хорошо линия аппроксимирует данные. Если | р | = 1, линия идеально соответствует данным; если | р | = 0, строка вообще не соответствует данным. В общем, чем ближе | р | равно 1, тем лучше подходит.

  • Каков коэффициент корреляции ( r ) для этого набора данных?
  • Удалить данные Коби Брайанта. Как это меняет уравнение регрессии и значение r  ?
  • Заменить данные Коби Брайанта и удалить данные другого игрока. Повторите этот процесс для каждого игрока в списке. Для какого игрока удаление данных оказывает наибольшее влияние на уравнение регрессии и r значение? О чем свидетельствует изменение?
  • Можете ли вы объяснить изменения, произошедшие при удалении данных?

  Вы можете провести аналогичные расследования для других видов спорта, просмотрев статистику Высшей лиги бейсбола (MLB), Национальной футбольной лиги (NFL), Национальной женской баскетбольной ассоциации (WNBA), Высшей футбольной лиги (MLS) или других видов спорта, которые заинтересовать вас.

  Стандарты и ожидания NCTM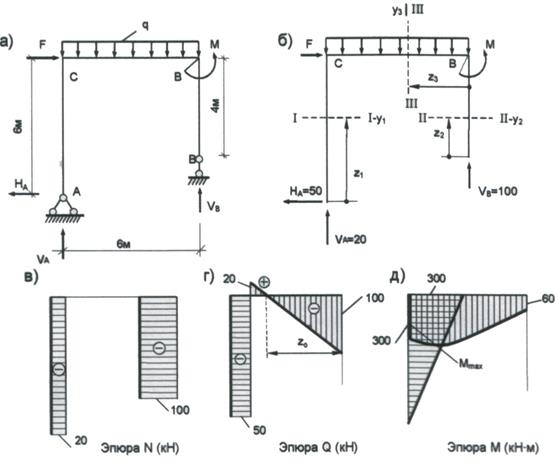
  • Вероятность / Анализ данных и статистика
  • 6-8
  • Средняя школа (9-12)
  • Анализ данных и вероятность

• Проблемы с запуском апплета?

plotly grouped stacked bar chart python

AlleBilderVideosBücherMapsNewsShopping

suchoptionen

python plotly — stacked + grouped bar chart

stackoverflow.com › вопросы › python-plot лы-стак…

Похоже, что в Plotly нет способа создавать как гистограммы с накоплением, так и сгруппированные гистограммы, но есть обходной путь, который может решить вашу проблему.

python — Plotly: сгруппированная и сгруппированная столбчатая диаграмма, разные цвета для …

Plotly Express: сгруппированная и сгруппированная столбцов данных

сложенная и сгруппированная столбчатая диаграмма — python

столбцы …

Добавить сообщение из stackoverflow.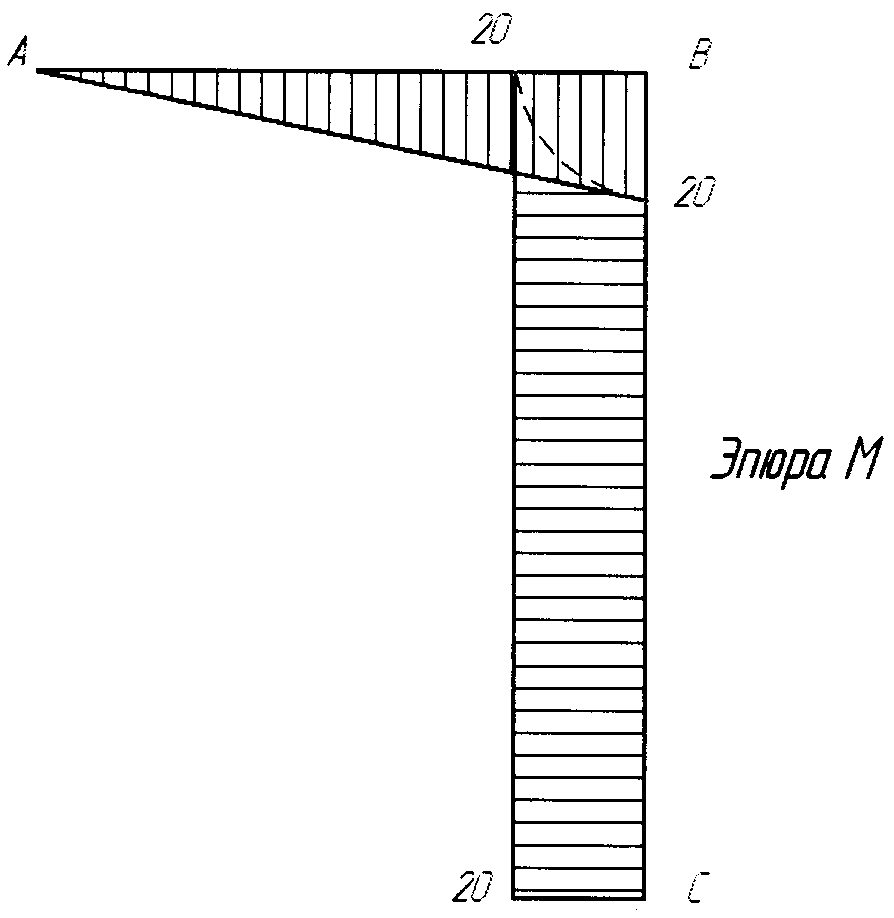 com

Сгруппированная + столбчатая гистограмма — Форум сообщества Plotly

community.plotly.com › сгруппированная гистограмма дискретные значения индекса, такие как «Калифорния», «Техас» и т. д.? Я пробовал это, но …

Гистограммы в Python — Plotly

plotly.com › python › гистограммы

Более 32 примеров гистограмм, включая изменение цвета, размера, логарифмических осей и т. д. Поведение линейчатой ​​диаграммы с накоплением по умолчанию можно изменить на сгруппированное (также …

Гистограмма с Plotly Express · Гистограммы в Dash · Столбчатые и сгруппированные гистограммы

Как построить сгруппированную гистограмму с накоплением в plotly | by Moritz Körber

medium.com › How-to-plot-a-grouped-stacked-bar-…

22.08.2020 · plotly упрощает создание интерактивной гистограммы с накоплением или группировкой в ​​Python, назначая нужный тип атрибута макета …

Столбчатые и сгруппированные гистограммы с использованием Plotly (Python)

fronkan. hashnode.dev › столбцы с накоплением и сгруппированием…

08.01.2020 · В этом посте я расскажу, как с помощью plotly создать гистограмму со сгруппированными и сгруппированными столбцами. Это довольно просто создать …

Изображение

Все значения

Все значения

Как построить гистограмму с группировкой в ​​​​графике Plotly — Moritz Körber

www.moritzkoerber .com › посты › сюжетно- grouped-st…

11.09.2020 · plotly упрощает создание интерактивной линейчатой ​​диаграммы с накоплением или группировкой в ​​Python путем присвоения нужного типа атрибуту макета …

Как создать сгруппированную гистограмму с помощью Plotly Express в Python .graph_objects. В этой статье вы узнаете, как… В относительном режиме бары складываются.

Нарисуйте сюжет Barplot в Python (пример) | Интерактивная гистограмма

Statisticsglobe.com › plotly-barplot-python

Популярной альтернативой сгруппированным гистограммам являются так называемые гистограммы с накоплением.