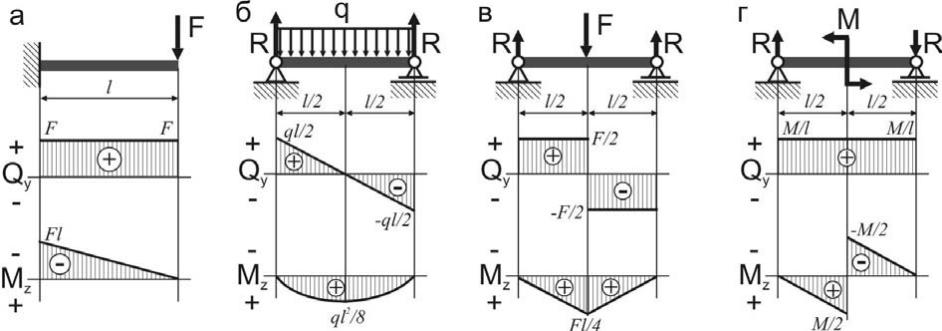
Сопротивление материалов. Эпюры крутящих моментов.
Сопротивление материалов
Построение эпюр крутящих моментов
Для наглядного изображения распределения крутящих моментов вдоль оси бруса строят эпюры крутящих моментов — графическое отображение величины крутящих моментов на каждом участке бруса.
Крутящий момент в сечениях бруса определяется с помощью метода сечения. Так как равномерно вращающийся или неподвижный вал находится в равновесии, очевидно, что внутренние силы, возникающие в поперечном сечении, должны уравновешивать внешние моменты, действующие на рассматриваемую часть бруса. Отсюда следует, что крутящий момент в любом поперечном сечении численно равен алгебраической сумме внешних моментов, приложенных к брусу справа или слева от сечения.
Эпюры крутящих моментов дают возможность определить опасное сечение. В частности, если брус имеет постоянное поперечное сечение по всей длине, то опасными будут сечения на участке, где возникает наибольший крутящий момент.
Следует очень внимательно отнестись к определению знаков крутящего момента. Крутящий момент считается положительным, если при взгляде со стороны сечения результирующий момент внешних пар сил, приложенных к рассматриваемой части бруса, будет направлен против часовой стрелки, и наоборот (это положение условно и принимается для облегчения проверки расчетов, выполненных несколькими исполнителями).
Рассматривая величины крутящих моментов, действующих в каждом конкретном сечении бруса, полагаем, что в сечении, где приложен вращающий (скручивающий) момент, значения крутящего момента изменяются скачкообразно (принцип смягченных граничных условий).
***
Пример построения эпюры крутящих моментов
Силовая передача (трансмиссия), изображенная на рис. 2 состоит из вала, на котором размещены три шестерни — одна ведущая (А) и две ведомые (В и С).
К шестерням приложены вращающие моменты: РА= 300 Нм, РВ = 120 Нм, РС= 180 Нм.
Построим эпюру крутящих моментов для этой силовой передачи.
Решение
Очевидно, что свободные концы вала, (вращающиеся в подшипниках) не подвержены действию вращающих моментов, т. е. крутящие моменты на участках 1 и 4 равны нулю.
К шестерне А приложен вращающий момент 300 Н м, следовательно в сечении, расположенном под этой шестерней скачкообразно возникает крутящий момент, равный 300 Нм, и величина этого момента сохраняется неизменной по всем сечениям участка 2 (до шестерни В).
К шестерне В приложен вращающий момент 120 Нм, который направлен в противоположную сторону от ведущего скручивающего момента, приложенного к шестерне А. Следовательно крутящий момент на участке 3 будет равен разности крутящих моментов, приложенных к шестерням А и В. На эпюре это отобразится в виде ступени величиной
На всем протяжении участка 3 величина этого крутящего момента будет сохраняться неизменной, до сечения, расположенного под шестерней С.
К шестерне С приложен вращающий момент 180 Нм, направление которого противоположно моменту, приложенному к ведущей шестерне А, поэтому, начиная с сечения под шестерней С, крутящий момент будет равен разнице между скручивающим моментом шестерни А и моментами, приложенными к шестерням В и С, т. е.
МКРс = ТА — ТВ — ТС= 300 — 120 — 180 = 0 Нм, и величина этого момента будет распространяться на весь участок 4, расположенный за шестерней С.
Построив эпюру крутящих моментов, действующих в сечениях вала данной силовой передачи как показано на рис. 2, отмечаем, что максимальной величины — 300 Нм крутящий момент достигает на участке 2, т. е. этот участок и является критическим (наименее надежным).
Теперь попробуем изменить расположение шестерен на валу, разместив ведущую шестерню А между ведомыми шестернями В и С, как показано на рис. 3. Приложенные к шестерням вращающие моменты оставим без изменения и построим эпюру крутящих моментов для измененной конструкции (рис. 3).
3).
Из полученной эпюры видно, что на участке 2 (между шестернями В и А) крутящий момент равен —120 Нм, на участке 3 — +180 Нм, а на участках 1 и 4 крутящие моменты равны нулю, как и в предыдущей конструкции. И если в рассмотренной ранее конструкции максимальный крутящий момент достигал 300 Нм, то теперь его величина снизилась до 180 Нм.
Рациональным размещением шестерен на валу силовой передачи мы смогли значительно уменьшить максимальный крутящий момент, возникающий в сечениях этого вала, повысив надежность передачи. При этом передаточные отношения и функционал самой передачи не изменились.
***
Материалы раздела «Деформация кручения»:
- Понятие о кручении цилиндрического бруса (вала)
- Построение эпюр крутящих моментов
- Деформации и напряжения, возникающие при кручении
- Расчеты на прочность и жесткость при кручении
- Расчет цилиндрических винтовых пружин
Основные гипотезы и допущения Сопромата
Главная страница
- Страничка абитуриента
Дистанционное образование
- Группа ТО-81
- Группа М-81
- Группа ТО-71
Специальности
- Ветеринария
- Механизация сельского хозяйства
- Коммерция
- Техническое обслуживание и ремонт автотранспорта
Учебные дисциплины
- Инженерная графика
- МДК.
 01.01. «Устройство автомобилей»
01.01. «Устройство автомобилей» - Карта раздела
- Общее устройство автомобиля
- Автомобильный двигатель
- Трансмиссия автомобиля
- Рулевое управление
- Тормозная система
- Подвеска
- Колеса
- Кузов
- Электрооборудование автомобиля
- Основы теории автомобиля
- Основы технической диагностики
- Основы гидравлики и теплотехники
- Метрология и стандартизация
- Сельскохозяйственные машины
- Перевозка опасных грузов
- Материаловедение
- Менеджмент
- Техническая механика
- Советы дипломнику
Олимпиады и тесты
- «Инженерная графика»
- «Техническая механика»
- «Двигатель и его системы»
- «Шасси автомобиля»
- «Электрооборудование автомобиля»
Лабораторная работа — Построение эпюр поперечных сил и изгибающих моментов
Министерство науки и образования Республики Казахстан
Алматинский колледж строительства и менеджмента
Кафедра технических дисциплин
Контрольная РАБОТА НА ТЕМУ:
«Построение эпюр поперечных сил и изгибающих моментов»
Руководитель:
преподаватель Косс М. С.
С.
Выполнил:
Джиланкозов Ташбулат
Алматы 2009 год
Задача № 1
Построить эпюры внутренних усилий Q и М для балки изображенной на следующем чертеже (рис. 1): F=5кН F=5кН
A B
C D
X1
RA RB
X 2
X 3
а =2м а =2м а =2м
Эпюра «Q»
4
-4
Эпюра «М»
Рис. 1
Решение:
I . Составляем уравнение равновесия и определяем опорные реакции R A и R B.
Σ MA = F1 • a + F2 • 2a – RB • 3a = 0;
отсюда RB = F1 • a + F2 • 2a = 5• 2 + 5 • 2 • 2 = 5 кН ;
3a 3 • 2
Σ M В = R А • 3a – F1 • 2a – F2 • a = 0;
отсюда R А = F1 • 2a – F2 • a = 5 • 2 • 2 + 5• 2 = 5 кН .
3 a 3 • 2
Проверка:
ΣУ = R А – F 1 – F 2 + RB = 0;
ΣУ = 5 – 5 – 5 + 5 = 0.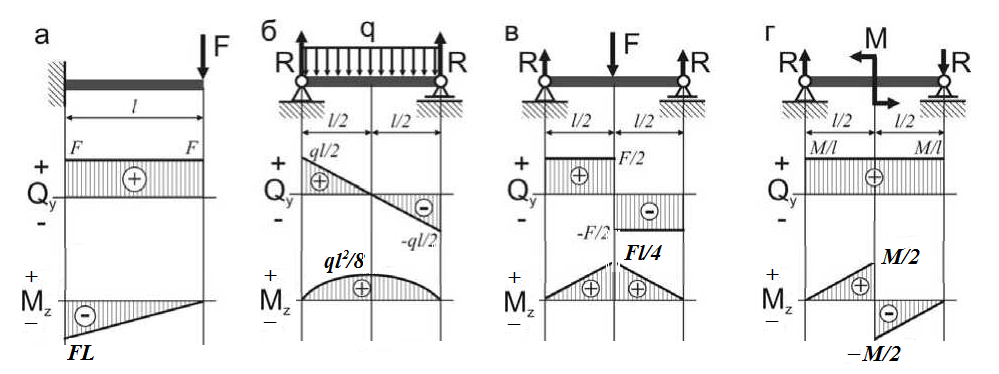
II . Проводим сечения х1, х2, х3 и определяем внутренние усилие для построения эпюры “Q ”:
0 ≤ х1 ≤ 2м (участок АС)
х1 = 0; Q х1 = RA = 5кН;
х1 = 2м; Q х1 = RA = 5кН;
2м ≤ х2 ≤ 4м (участок CD)
х2 = 2м; Q х2 = R А – F 1 = 5 – 5 = 0;
х2 = 4м; Q х2 = R А – F 1 = 5 – 5 = 0;
4м ≤ х3 ≤ 6м (участок DB)
х3 = 4м; Q х3 = R А – F 1 – F 2 = 5 – 5 – 5 = — 5;
х3 = 6м; Q х3 = R А – F 1 – F 2 = 5 – 5 – 5 = — 5.
III . В проведённых сечениях определяем внутренние усилие для построения эпюры “М”:
0 ≤ х1 ≤ 2м (участок АС)
х1 = 0; M х1 = R А • х1 = 5 • 0 = 0;
х1 = 2м; M х1 = R А • х1 = 5 • 2 = 10кН • м;
2м ≤ х2 ≤ 4м (участок CD)
х2 = 2м; M х2 = R А • х2 – F 1(х2 – а) = 5 • 2 – 5(2 – 2) = 10кН • м;
х2 = 4м; M х2 = R А • х2 – F 1(х2 – а) = 5 • 4 – 5(4 – 2) = 10кН • м;
4м ≤ х3 ≤ 6м (участок DB)
х3 = 4м; M х3 = R А • х3 – F 1(х3 – а) – F 2(х3 –2а) = 5 • 4 – 5(4 – 2) – 5(4 – 2 • 2)= =10кН • м;
х3 = 6м; M х3 = R А • х3 – F 1(х3 – а) – F 2(х3 –2а) = 5 • 6– 5(6 – 2) – 5(6 – 2 • 2)=0
Задача № 2
Построить эпюры внутренних усилий Q и М для балки изображенной на следующем чертеже (рис. 2): А F = 10кН В
2): А F = 10кН В
С
Х1
RA Х2 RB
L1 = 5м L2 = 5м
L = 10м
Эпюра «Q»
5
— 5
Эпюра «М»
Рис. 2
Решение:
I . Составляем уравнение равновесия и определяем опорные реакции R A и R B.
Σ MA = F • L1 + RB • L = 0;
RB = F • L1 = 10 • 5 = 5 кН ;
L 10
Σ M В = R А • L – F • L2 = 0;
R А = F • L2 = 10 • 5 = 5 кН .
L 10
Проверка:
ΣУ = R А – F + RB = 0;
ΣУ = 5 – 10 + 5 = 0.
II . Проводим сечения х1, х2 и определяем внутренние усилие для построения эпюры “Q ”:
0 ≤ х1 ≤ 5м (участок АС)
х1 = 0; Q х1 = RA = 5кН;
х1 = 5м; Q х1 = RA = 5кН;
5м ≤ х2 ≤ 10м (участок CВ)
х2 = 5м; Q х2 = R А – F = 5 – 10 = — 5кН;
х2 = 10м; Q х2 = R А – F = 5 – 10 = — 5кН.
III . В проведённых сечениях определяем внутренние усилие для построения эпюры “М”:
0 ≤ х1 ≤ 5м (участок АС)
х1 = 0; M х1 = R А • х1 = 5 • 0 = 0;
х1 = 5м; M х1 = R А • х1 = 5 • 5 = 25кН • м;
5м ≤ х2 ≤ 10м (участок CВ)
х2 = 5м; M х2 = R А • х2 – F х2 – 10) = 5 • 5 – 10 (5 – 10) = 25кН • м;
2 2
х2 = 10м; M х2 = R А • х2 – F х2 – 10) = 5 • 10 – 10(10 – 10) = 0.
2 2
Задача № 3
Построить эпюры поперечных сил Q и изгибающих моментов М для балки изображённой на следуещем чертеже (рис. 3): g = 4кН/м
A B
gL
Х
R A R B
L = 6м
Эпюра «Q»
12
— 12
Эпюра «М»
Рис .3
Решение:
I . Составляем уравнение равновесия и определяем опорные реакции R A и R B.
Составляем уравнение равновесия и определяем опорные реакции R A и R B.
Σ MA = g • L • L – RB • L = 0;
2
RB = g • L • L = 4 • 6 = 12 кН ;
2 2
L
Σ M В = R А • L – g • L • L = 0;
2
R А = g • L • L = 4 • 6 = 12кН.
2 2
L
Проверка:
ΣУ = R А – g • L + RB = 0;
ΣУ = 12 – 4 • 6 + 12 = 0.
II . Проводим сечения и определяем внутренние усилие для построения эпюр Q и М:
“Q ”
0 ≤ х1 ≤ 6м
х1 = 0; Q х1 = RA – g • х = 12 – 4 • 0 = 12 кН;
х1 = L = 3м; Q х1 = RA – g • х = 12 – 4 • 3 = 0;
2
х1 = L = 6м; Q х1 = RA – g • х = 12 – 4 • 6 = — 12кН ;
“М”
х1 = 0; M х1 = R А • х – g • х • х = 12 • 0 – 4 • 0 • 0 = 0;
2 2
х1 = L = 3м; M х1 = R А • х – g • х • х = 12 • 3 – 4 • 3 • 3 = 12кН • м;
2 2 2
х1 = L = 6м; M х1 = R А • х – g • х • х = 12 • 6 – 4 • 6 • 6 = 0;
2 2
Задача № 4
Построить эпюры поперечных сил Q и изгибающих моментов М для балки изображённой на следующем чертеже (рис. 4): F1 =2кН F2 =10кН
4): F1 =2кН F2 =10кН
A B
C D
X1
RA RB
X2
X3
м 2 м 3 м
Эпюра «Q»
5,7
3,7
-6,3
Эпюра «М»
Рис. 4
Решение:
I . Составляем уравнение равновесия и определяем опорные реакции R A и R B.
Σ MA = F1 • СА + F2 • DA – RB • BA = 0;
RB = F1 • CA + F2 • DA = 2• 2 + 10 • 4 = 6,28 кН ;
BA 7
Σ M В = R А • AB – F1 • CB – F2 • DB = 0;
R А = F1 • CB + F2 • DB = 2 • 5 + 10 • 3 = 5,7 кН .
AB 7
Проверка:
ΣУ = R А + RB – F 1 – F 2 = 0;
ΣУ = 5,7 + 6,28 – 2 – 10 = — 0,02 .
II . Проводим сечения х1, х2, х3 и определяем внутренние усилие для построения эпюры “Q ”:
0 ≤ х1 ≤ 2м (участок АС)
х1 = 0; Q х1 = RA = 5,7кН;
х1 = 2м; Q х1 = RA = 5,7кН;
2м ≤ х2 ≤ 4м (участок CD)
х2 = 2м; Q х2 = R А – F 1 = 5,7 – 2 = 3,7кН;
х2 = 4м; Q х2 = R А – F 1 = 5,7 – 2 = 3,7кН;
4м ≤ х3 ≤ 7м (участок DB)
х3 = 4м; Q х3 = R А – F 1 – F 2 = 5,7 – 2 – 10 = — 6,3кН;
х3 = 7м; Q х3 = R А – F 1 – F 2 = 5,7 – 2 – 10 = — 6,3кН.
III . В проведённых сечениях определяем внутренние усилие для построения эпюры “М”:
0 ≤ х1 ≤ 2м (участок АС)
х1 = 0; M х1 = R А • х1 = 5,7 • 0 = 0;
х1 = 2м; M х1 = R А • х1 = 5,7 • 2 = 11,4кН • м;
2м ≤ х2 ≤ 4м (участок CD)
х2 = 2м; M х2 = R А • х2 – F 1(х2 – 2) = 5,7 • 2 – 2(2 – 2) = 11,4кН • м;
х2 = 4м; M х2 = R А • х2 – F 1(х2 – 2) = 5 • 4 – 2(4 – 2) = 18,8кН • м;
4м ≤ х3 ≤ 7м (участок DB)
х3 = 4м; M х3 = R А • х3 – F 1(х3 –2) – F 2(х3 – 4) = 5,7 • 4 – 2(4 – 2) – 10(4 – 4)= =18,8кН • м;
х3 = 7м; M х3 = R А • х3 – F 1(х3 – 2) – F 2(х3 – 4) = 5,7 • 7– 2(7 – 2) – 10(7 – 4)= = — 0,1кН • м.
Задача № 5
Построить эпюры поперечных сил Q и изгибфющих моментов М для балки изображенной на следующем чертеже (рис. 5):
Рис. 5
Решение
I . Составляем расчетную схему балки и определяем опорные реакции Ra и Rb :
Σ MA =0
Σ MA =q• 1/2a+q•2a+F•2a+M-Rb •4a
отсюда Rb = -q•1/2a+q•2a+F•2a+M = -4•2•0.5•2 + 4•2•2 +5•2•2 +10 = 6,75 кН
4a 4•2
Rb =6,75 кН
Σ Mb =0
Σ Mb =-q•3a•3.5a+Ra •4a-F•2a+M
отсюда Ra = q•3a•3.5a+ F•2a-M=4•3•2•3.5•2+5•2•2-10=22,25 кН
4 a 4•2
Ra =22,25 kH
Для проверки определения опорных реакций, составляем сумму проекций всех сил приложенных к балке на вертикальную ось y:
Σ Fy =0
Σ Fy =- q•3a+Ra -F=Rb =-4•3•2+22,75-5+6,75=-24+22,25-5+6,75=0
II . Выделяем характерные точки, вечисляем значения поперечных сил и моментов в сечениях, проходящих через эти точки.
Выделяем характерные точки, вечисляем значения поперечных сил и моментов в сечениях, проходящих через эти точки.
Характерными являются крайняя точка О, опорные сечения А и В и точки приложения нагузок D и E.
Вычисляем значения поперечных сил в сечениях, проходящих через указанные точки.
В сечение О:
Q =0
В сечение А слева:
Q А лев = — q • a =-4•2=-8 kH
В сечение А справа:
Q А прав = — q • a + Ra =-4•2+22,25 kH
(в сечение А справа имеет место скачек равный величине опорной реакции Ra )
В сечение D слева:
QD лев = — q •3 a + Ra =-4•3•2+22,25=-1,75 kH
В сечение D справо:
QD прав = — q •3 a + Ra — F =-4•3-2+22,25-5=—6,75 kH
(в сечение D справо имеет место скачок равный величине приложенной силы F=5 kH)
На участке AD, как и на консоле ОА, эпюра поперечных сил ограничивается наклонной прямой, т. к. на обоих участках действует равномерно распределенная нагрузка. Наклон прямых на участках ОА и AD одинаков, в связи с равной интенсивностью распределенной нагрузки. В точке С сила Q имеет нулевое значение; расстояние до него определяем из подобия треугольных элнментов эпюры на участке АD. В сечение В поперечная сила отрицательна и численно равна Rb =6,75kH
к. на обоих участках действует равномерно распределенная нагрузка. Наклон прямых на участках ОА и AD одинаков, в связи с равной интенсивностью распределенной нагрузки. В точке С сила Q имеет нулевое значение; расстояние до него определяем из подобия треугольных элнментов эпюры на участке АD. В сечение В поперечная сила отрицательна и численно равна Rb =6,75kH
Вычисляем значение моментов по характерным точкам:
В сечение О:
Мо =0
В сечение А:
МА =- q • a •а/2=-4•2•2/2=-8кН•м
(в сечение А на консоли эпюра М имеет вид параболы, т.к. консоль загружена равномерно распределенной нагрузкой)
В сечение С:
Мс = — q •2,5 a •2,5а/2+ Ra •1,5 a =-4•2,5•2•2,5•2+22,25•1,5•2=16,75 kH •м
В сечение D: 2
MD =-q •3a•1,5a+Ra •2a=-4•3•2•1,5•2+12,25•2•2=-23
На участке АD ето значение момента является МАХ. На эпюре моментов в этом сечении (в точке С) имеет место перегиб. Эпюра моментов имеет вид параболы.
На эпюре моментов в этом сечении (в точке С) имеет место перегиб. Эпюра моментов имеет вид параболы.
В сечение Е слева:
МЕлев =- q •3 a •2,5 a + Ra •3 a — F • a =-4•3•2•2,5•2+22,25•3•2=13,5 kH • м
В сечение Е справа:
МЕправ = МЕлев +М=13,5+10=23,5кН•м
На участке DE и ЕВ свободных от распределенной нагрузки, эпюра моментов ограничена прямыми наклонными линиями; в сечении Е имеет место скачек на величину приложенной пары сил М=5кНм.
Список использованной литературы
1. Ляпунов А.М. «Сборник задач по технической механике».
2. Жарковский Б.И. «Курс лекций по технической механике».
3. Мухин В.С., Саков И.А. «Техническая механика».
4. Д.В.Бычков, М.О.Миров: «Теоретическая механика».
5. Н.С.Улитин: «Сопротивление материалов».
Осевые диаграммы, диаграммы сдвига и моментов – StructNotes
Опубликовано Автор: Ho-Shing Chau структурный элемент . Они помогают определить материал, размер и тип элемента с учетом набора нагрузок, которые он может выдержать без разрушения конструкции.
Чрезвычайно важно соблюдать единообразие знаков! Мы собираемся определить положительное соглашение о знаках : Чтобы соответствовать нашему соглашению, BMD рисуются на стороне сжатия элемента. Как показано на рисунке ниже, это означает, что сторона сжатия элемента представляет собой положительный изгибающий момент. Лучший способ изучить AFD, SFD и BMD — попрактиковаться в их рисовании на нескольких примерах. Но прежде чем мы это сделаем, мы должны понять следующие основы:
- ΣForces = 0; ΣМоменты = 0
- Момент = Сила x Расстояние
- Сдвиг = скорость изменения момента (также известная как производная или наклон момента)
- Если сдвиг равен нулю, изгибающий момент постоянен (также может быть равен нулю).

- БМД сплошная. AFD и SFD могут быть не непрерывными.
- Неподвижные концы имеют момент реакции . Концы штифтов/роликов НЕ имеют момента
- Фермы НЕ имеют диаграмм поперечной силы и изгибающего момента. (Элементы фермы имеют только осевые усилия: сжатие или растяжение.)
- Изгибающий момент в шарнире равен нулю.
Все AFD, SFD и BMD следуют этим основным правилам. Мы будем обращаться к ним по мере выполнения следующих основных шагов в каждом примере:
- Найдите силы/моменты реакции опоры.
- Определение осевых/поперечных сил.
- Начертите диаграммы осевой/поперечной силы.
- Определить изгибающий момент.
- Нарисуйте диаграмму изгибающего момента.
Пример 1
Это балка с распределенными и точечными нагрузками. Прежде чем мы начнем, мы должны подумать о следующем:
- Каковы изгибающие моменты на опорах?
- Каковы формы AFD, SFD и BMD?
Посмотреть решение
Пример 2
Это та же балка, что и в примере 1, но теперь в середине пролета есть шарнир.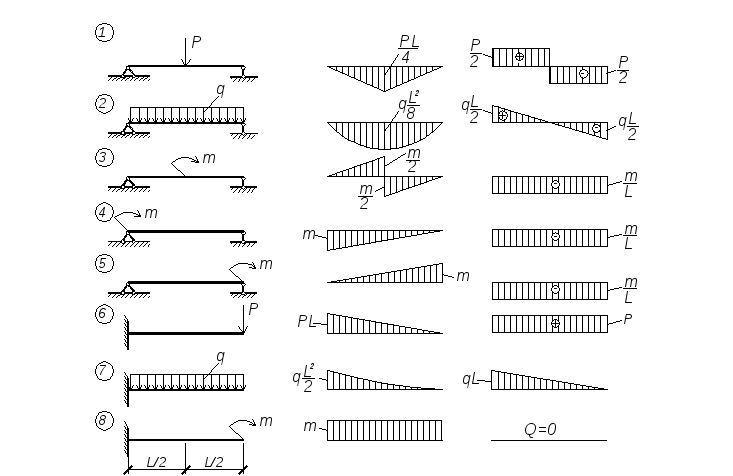 Итак, как шарнир влияет на диаграммы силы и момента?
Итак, как шарнир влияет на диаграммы силы и момента?
Посмотреть решение
Пример 3
Это та же балка, что и в примере 1, но теперь у нее консольный конец без дополнительных усилий. Итак, как это влияет на диаграммы силы и момента? 9Пример 4 Итак, как эта добавленная точечная нагрузка влияет на диаграммы силы и момента?
Посмотреть решение
Пример 5
Это рама с одной опорой и точечной нагрузкой. Прежде чем мы начнем, мы должны подумать о следующем:- Каковы силы сдвига в вертикальных элементах?
- Где находятся осевые силы?
Посмотреть решение
Пример 6
Это рама с распределенной нагрузкой. Прежде чем мы начнем, мы должны подумать о следующем:
- Каковы изгибающие моменты в колоннах?
- Где находятся осевые силы? Пример 7 Без выполнения каких-либо расчетов, как это одно изменение повлияет на формы AFD, SFD и BMD?
- Сила сдвига — это сила, действующая параллельно площади поперечного сечения конструкции, перпендикулярно оси балки или элемента.
- Сила сдвига — это сила, которая заставляет верхнюю и нижнюю части конструкции скользить относительно друг друга.
- Силы сдвига могут быть вызваны внешними нагрузками, такими как вес конструкции или силы ветра или сейсмической активности.
- Изгибающий момент — это момент, который создается при приложении к конструкции внешней силы, заставляющей ее изгибаться или изгибаться.
- Изгибающий момент рассчитывается путем умножения силы на расстояние между точкой приложения и точкой опоры.
- Сила сдвига и изгибающий момент играют решающую роль в определении прочности и устойчивости конструкции. Инженеры используют эти концепции для проектирования конструкций, способных выдерживать нагрузки и силы, с которыми они могут столкнуться в течение своей жизни.
- Простые опоры
- Роликовая опора
- Шарнирная опора (или) опора со штифтом
- Фиксированные опоры 901 55
- Зажимные опоры (или) встроенные опоры
- Сосредоточенная или точечная нагрузка,
- Равномерно распределенная нагрузка и
- Равномерно изменяющаяся нагрузка.

- Сила F, действующая вертикально вверх на сечения 1-1
- Сила F + dF действует вертикально вниз на сечения 2-2.
- Нагрузка w × dx, действующая вниз
- Моменты M и (M + dM) действуют на сечения 1-1 и 2-2 соответственно.
Посмотреть решение
Пример 8
Это рама с фиксированными и шарнирными опорами, в дополнение к шарниру в одной из колонн.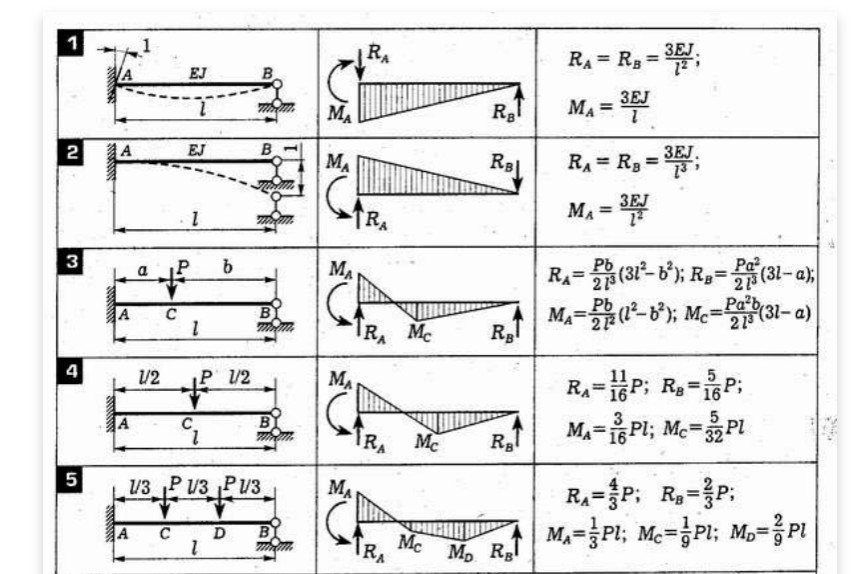 Без выполнения каких-либо расчетов, каковы формы AFD, SFD и BMD?
Без выполнения каких-либо расчетов, каковы формы AFD, SFD и BMD?
View Solution
Фотография на обложке Источник: CSI
Теги: осевой, изгиб, схема, сила, момент, сдвигКатегории: ОсновыСила сдвига и изгибающий момент: SFD и BMD
Что такое сила сдвига и изгибающий момент?
Сила сдвига и изгибающий момент — два фундаментальных понятия в проектировании конструкций, которые описывают внутренние силы и моменты внутри конструкции. Ее можно описать следующим образом:
Диаграмма поперечной силы и изгибающего момента
Диаграммы изгибающего момента и поперечной силы представляют собой диаграммы, отображающие изменение изгибающего момента и поперечной силы соответственно по длине элемента конструкции. Это будет зависеть от типа конструктивного элемента, нагрузки, опорных реакций и т. д. Таким образом, представление о различных конструктивных элементах, таких как балки, и различных условиях поддержки необходимо для понимания SFD и BMD.
Типы жестких опор
Опоры — это структурный компонент, обеспечивающий жесткость в нескольких направлениях и гибкость в нескольких направлениях. Ниже приведены некоторые характеристики нескольких опор:
Ниже приведены некоторые характеристики нескольких опор:
(a) Роликовая опора – выдерживает только вертикальные силы и не обеспечивает жесткости для горизонтальных сил и моментов.
(b) Шарнирная опора или штифтовое соединение – выдерживает только горизонтальные и вертикальные нагрузки. Он не обеспечивает жесткости против вращения.
(c) Неподвижная опора или встроенный конец. Он будет противостоять горизонтальной силе, вертикальной силе и изгибающему моменту, действующему на него.
Примечание. Расстояние между двумя опорами называется «пролетом».
Типы балок
Балка определяется как конструктивный элемент, подвергающийся поперечным сдвиговым нагрузкам во время своей работы. Из-за этих поперечных сдвигающих нагрузок на балки действует переменная сила сдвига и переменный изгибающий момент.
Классификация балок зависит от нескольких факторов, таких как определение луча, использование лучей и т. Д. Здесь типы балок, основанные на их определении, приведены:
Статически определяющий луча
a Beam. является статически определимым, если все компоненты его реакции можно рассчитать, применяя три условия статического равновесия.
(1) Просто опертая балка: Балка с двумя простыми опорами
(2) Нависающая балка
(3) Консольная балка: Балка, закрепленная на одном конце и свободная на другом
Статически неопределимая балка статические условия равновесия, балка называется статически неопределимой.
(1) Неподвижные балки
(2) Подпертые консольные балки
(3) Неразрезная балка: Балка считается неразрезной, если она имеет более двух опор
Типы нагрузки
Ниже приведены важные типы нагрузки, действующей на балку:
(i) Сосредоточенная или точечная нагрузка: если внешняя нагрузка действует в точке
(ii) Равномерно распределенная нагрузка: нагрузка распределена по балке, скорость нагрузки w одинакова по длине
(iii ) Равномерно изменяющаяся нагрузка: нагрузка распределяется по балке, скорость нагрузки меняется от точки к точке вдоль балки
Поперечная сила в поперечном сечении балки представляет собой сумму всех вертикальных сил либо с левой, либо с правой стороны этого поперечного сечения. А изгибающий момент в поперечном сечении балки — это сумма всех моментов либо с левой, либо с правой стороны этого поперечного сечения.
Для рисования SFD и BMD следует использовать правильное соглашение о знаках. и это можно объяснить следующим образом:
Правила знаков для силы сдвига
Если двигаться слева направо, примите все силы, направленные вверх, как положительные, а силы, направленные вниз, как отрицательные.
Или, если поперечная сила пытается повернуть элемент по часовой стрелке, она считается положительной, а если поперечная сила пытается повернуть элемент против часовой стрелки, считается отрицательной.
Правила знаков для изгибающего момента
При движении слева направо момент по часовой стрелке считается положительным, а против часовой стрелки — отрицательным.
Или, если силы создают провисающий момент, он принимается как положительный, а если силы создают захватывающий момент, он принимается как отрицательный.
Важные моменты для построения диаграмм поперечной силы и изгибающего момента
Чертеж SFD и BMD важен для правильного анализа элемента конструкции. Он будет осуществляться исходя из действующей на него внешней нагрузки и типа опоры для конкретной балки. Вот несколько моментов, которые следует учитывать при построении изгибающего момента и диаграммы сдвига.
(i) Рассмотрите левую или правую часть секции.
(ii) Положительные значения поперечной силы и изгибающих моментов нанесены выше, а отрицательные значения ниже базовой линии.
(iii) Диаграмма поперечной силы резко увеличивается или уменьшается, т. е. по вертикальной прямой линии в сечении с вертикальной точечной нагрузкой.
(iv) Сила сдвига между двумя вертикальными нагрузками будет постоянной; следовательно, диаграмма поперечной силы между двумя вертикальными нагрузками будет горизонтальной.
(v) Изгибающий момент на двух опорах свободно опертой балки и на свободном конце консоли будет равен нулю.
Взаимосвязь между нагрузкой, поперечной силой и изгибающим моментом
Поперечная сила, изгибающий момент и внешняя нагрузка, действующая на балку, могут быть взаимосвязаны. Отношение может быть получено на основе чистой силы, действующей на сечение. Это можно объяснить ниже:
Балка несет равномерно распределенную нагрузку w на единицу длины. Рассмотрим равновесие части балки между сечениями 1-1 и 2-2.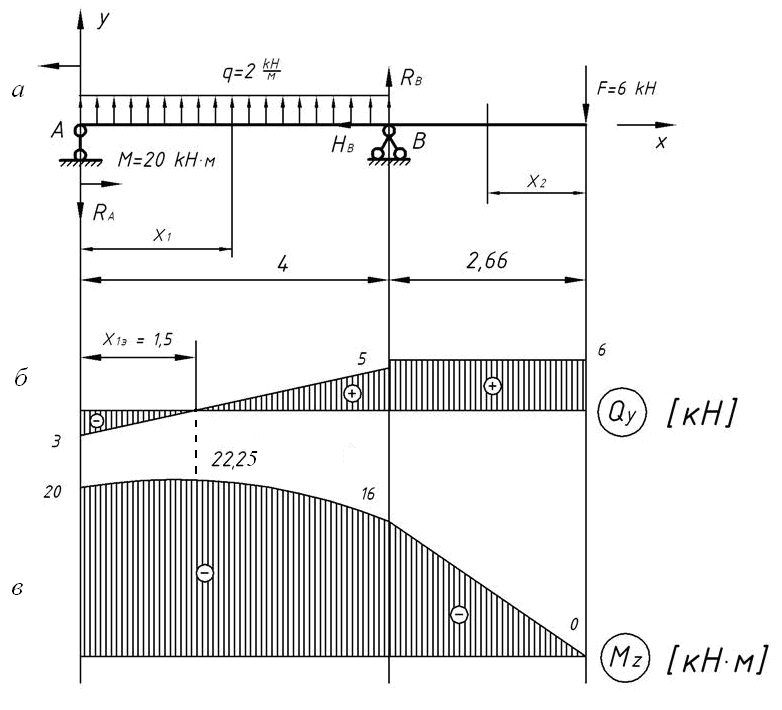
F = поперечная сила в сечении 1-1
F + dF = поперечная сила в сечении 2-2,
M = изгибающий момент в сечении 1-1,
M + dM = изгибающий момент в сечении 2 -2.
Силы и моменты, действующие на длину «dx» балки:
Часть балки длиной dx находится в равновесии. Следовательно, разделив силы, действующие на эту деталь по вертикали, мы получим
–dF = w.dx
dF/dx = -w
Приведенное выше уравнение показывает, что скорость изменения поперечной силы равна скорости нагружения.
Взяв моменты сил и пар относительно сечений 2-2, получим
Пренебрегая высшими степенями малых величин, получим
F.