Эпюры для балок | Строительные конструкции

  

 

Эпюры с точки зрения математики — это просто графики соответствующих функций, поэтому и правила построения эпюр ни чем не отличаются от общих правил построения графиков функций. Для этого достаточно иметь соответствующее функциональное или дифференциальное уравнение.

В частности именно для этого нас, начиная со средних классов школы, подгружали такими достаточно абстрактными математическими понятиями как переменные, функция, аргумент функции, график функции, производная и дифференциал функции.

При этом школьнику, особенно мечтающему стать писателем или водителем, труднее всего объяснить, зачем эти самые функции, графики и прочие абстракции ему нужны, если после экзаменов он больше никогда в жизни о них не вспомнит? Во всяком случае до тех пор, пока у него самого не появятся дети, которым снова нужно будет выучить эти понятия и термины.

Между тем с инженерами, физиками и представителями прочих точных наук дело обстоит иначе. Так например студенты строительных специальностей на втором году обучения с удивлением узнают, что у абстрактных функций и их графиков, а также производных и дифференциалов есть вполне конкретный смысл. А в чем этот смысл заключается, мы ниже и рассмотрим на примере балок.

Примечание: перед продолжением чтения данной статьи настоятельно рекомендую ознакомиться с основами теории сопротивления материалов.

Эпюры распределенной нагрузки

Это может показаться странным, но когда мы изображаем равномерно распределенную нагрузку, действующую по всей длине балки, например такую:

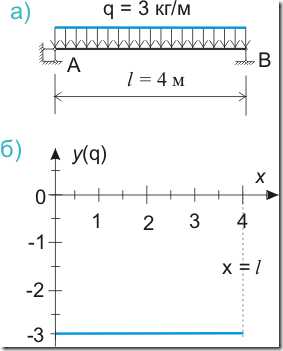
Рисунок 545.1. Равномерно распределенная нагрузка, а) общепринятое изображение, б) график функции — равномерно распределенной нагрузки

То это с одной стороны вроде бы просто нагрузка q = 3 кг/м, равномерно распределенная по всей длине балки (рис.545.1.а)), а с другой стороны — это график функции у, показывающий изменение значения функции в зависимости от изменения значения аргумента х (рис.545.1.б)). Соответственно функциональное уравнение в данном случае будет иметь вид:

у = — 3 = const (545.1)

или 

q = — 3 = const (545.1.2)

А смысл этих достаточно простых уравнений в том, что значение нагрузки является постоянной величиной и не зависит от значения аргумента функции, в данном случае от положения рассматриваемого поперечного сечения.

Примечание: В данном случае знак «-» используется потому, что нагрузка направлена вниз.

Вроде бы ничего сложного, но это и есть основные принципы построения эпюр для распределенной нагрузки.

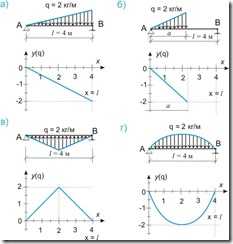
Конечно же распределенная нагрузка может быть не только равномерно распределенной, действующей по всей длине балки, но и линейно или нелинейно изменяющейся, или действующей не по всей длине балки, а также может быть направлена не вниз, а вверх. Некоторые возможные варианты распределенных нагрузок показаны на рисунке 545.2:

 

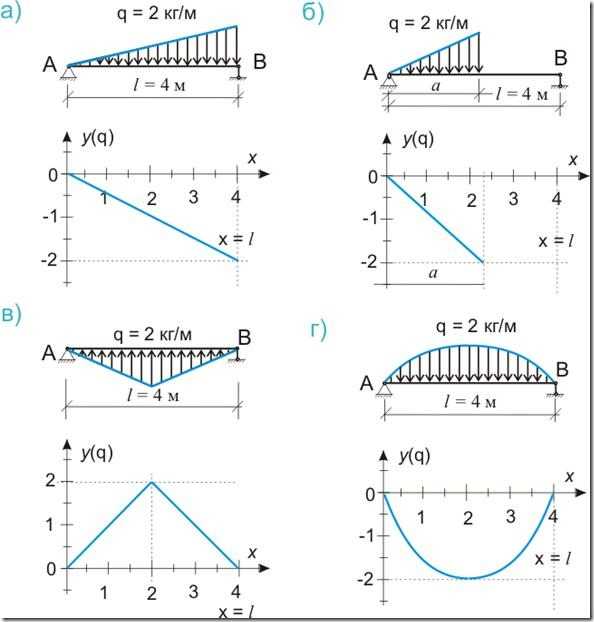
Рисунок 545.2. Распределенные нагрузки: а) линейно изменяющаяся, б) линейно изменяющаяся, действующая не по всей длине балки, в) линейно изменяющаяся, описываемая двумя уравнениями, г) нелинейно изменяющаяся.

Но общего принципа построения эпюр нагрузок и составления соответствующего уравнения или уравнений это ни как не меняет.

Так функциональное уравнение для нагрузки, показанной на рисунке 545.2.а):

y = — x/2 (545.2)

По той простой причине, что максимальное значение нагрузки q = 2 кг/м будет в конце балки длиной l = 4 м. Другими словами значение функции у = 2 при аргументе функции х = 4.

Для нагрузки, показанной на рисунке 545.2.в) на участке от начала балки до середины:

y = x (545.3.1)

на участке от середины до конца балки:

у = 2 — х (545.3.2)

Одним словом почти для любой распределенной нагрузки можно составить уравнение, описывающее характер изменения этой нагрузки. А если нагрузка уж слишком мудреная или на балку действуют несколько распределенных нагрузок, то можно воспользоваться принципом суперпозиции, но об этом чуть позже.

Все это хорошо, скажете вы, но зачем нам строить эпюры нагрузки, ведь они у нас и так как бы есть? Действительно от студентов строительных вузов не требуют строить эпюры нагрузок. Считается, что это и так понятно. Не спорю, для тех, кому и так понятно, могут эту часть статьи пропустить (хотя уже поздно), а всем остальным это новое знание должно пригодиться, так как дальше мы будем работать именно с уравнениями функций.

Построение эпюр поперечных сил

Расчет строительных конструкций, в частности балок, основан на общих принципах статического равновесия системы. Исходя из этих принципов, мы можем заменить любые опоры балки сосредоточенными силами — опорными реакциями, при этом балка все равно останется в состоянии статического равновесия.

Но и это еще не все, теоретически мы можем отсечь любую часть балки, а вместо отсеченной части приложить в месте полученного сечения еще некоторые силы или даже моменты сил так, чтобы балка опять оставалась в состоянии статического равновесия. На этой теоретической предпосылке основан метод сечений, упоминавшийся выше.

Конечно же поперечные силы (действие продольных сил мы пока не рассматриваем) и изгибающие моменты, которые необходимо приложить в различных сечениях балки для сохранения статического равновесия системы, могут иметь разные значения. При этом эпюры поперечных сил и изгибающих моментов как раз и показывают нам, как изменяются значения поперечных сил и изгибающих моментов в поперечных сечениях по длине балки.

Собственно именно для этого эпюры и нужны, так как позволяют даже визуально определить сечение в котором действуют максимальные нормальные и(или) касательные напряжения. Весь остальной расчет на прочность — дело техники. Но вернемся к эпюрам, в частности рассмотрим равномерно распределенную нагрузку показанную на рисунке 545.1, как наиболее простую.

Когда мы рассекаем балку, и рассматриваем оставшуюся часть, то часть нагрузки, действующей на балку, также отсекается:

Рисунок 545.3. Отсечние части балки вместе с нагрузкой, метод сечений

Так, если мы рассматриваем сечение на расстоянии 1 м от начала балки, то общая нагрузка, действующая на рассматриваемую часть балки, составит 3 кг, на расстоянии 2 м — 6 кг и так далее.

Получается, что чем больше расстояние от точки А до рассматриваемого сечения (или от начала координат до точки х), тем большую силу нужно приложить в рассматриваемом сечении, чтобы отсеченная часть балки оставалась в равновесии. Более того, мы видим здесь явную закономерность, которую можно выразить следующим уравнением:

Q = — 3x (545.4.1)

А если присмотреться к формулам (545.1.2) и (545.4.1) повнимательнее, то мы увидим, что поперечная сила есть ничто иное, как дифференциал функции нагрузки. Другими словами, чтобы определить значение поперечных сил в том или ином поперечном сечении, нам нужно проинтегрировать уравнение (545.1.2):

Q = ∫qdx = — ∫3dx + A = — 3x + A (545.4.2)

где А — некая постоянная величина, как это следует из общих правил интегрирования. В данном случае А — это значение опорной реакции. Как именно определяются опорные реакции в зависимости от нагрузки на балку — это отдельная большая тема. Здесь просто отметим, что при равномерно распределенной нагрузке на балку А = В = ql/2. В данном случае при значении нагрузки q = 3 кг/м опорные реакции составят A = B = 3·4/2 = 6 кг.

Теперь у нас есть все необходимые данные для построения эпюры поперечных сил при действии на балку равномерно распределенной нагрузки:

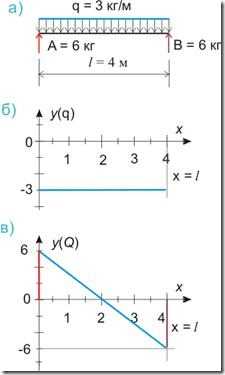
Рисунок 545.4. Равномерно распределенная нагрузка: а) общепринятое обозначение, опорные реакции, б) график функции — равномерно распределенной нагрузки, в) график функции — поперечных сил, действующих в сечениях балки.

 

Сразу отметим важную особенность эпюр поперечных сил, из которой вытекает одно из общих правил построения эпюр:

1. В местах приложения сосредоточенных сил, будь то опорные реакции или любые другие сосредоточенные силы, направленные вертикально, на эпюре «Q» всегда будет резкое изменение. При этом разница значений, определяемая по эпюре, будет равна значению приложенной сосредоточенной силы, а направление изменения будет такое же, как и у приложенной силы.

Подтверждение этой особенности мы видим и на рисунке 545.4.в), где в начале и в конце балки наблюдается скачкообразное изменение значений поперечных сил, равное значению опорных реакций. 

Это правило действует для всех балок вне зависимости от степени статической неопределимости, количества и вида опор. Более того, это правило действует и при построении эпюр поперечных сил для рам.

Построение эпюр изгибающих моментов

Как тонко подметил Архимед, любая сила, приложенная с некоторым плечом относительно рассматриваемой точки, создает вращающий момент. И чем больше плечо, тем больше значение вращающего момента при одном и том же значении приложенной силы.

Это правило рычага действительно и при построении эпюр изгибающих моментов. Вот только моменты называются не вращающими, а изгибающими, но суть от этого не меняется. Так предполагается, что в любом поперечном сечении балки, находящемся на расстоянии х от начала балки (начала координат) могут действовать изгибающие моменты.

Например в нашем случае в начале балки приложена сосредоточенная сила — опорная реакция А = 6 кг, соответственно эта сила будет создавать изгибающий момент Ах, где х — плечо действия силы. При этом равномерно распределенная нагрузка также будет создавать изгибающий момент. А чтобы определить значение этого момента, сначала определяется общее значение нагрузки -qx, что мы и делали при построении эпюры поперечных сил. Общее значение распределенной нагрузки в рассматриваемом сечении можно рассматривать как равнодействующую сосредоточенную силу, а прикладывается эта сила в центре тяжести эпюры нагрузки. Т.е. в этом случае мы рассматриваем эпюру нагрузки, как некое физическое тело, имеющее плотность и соответственно центр тяжести. Впрочем с точки зрения теории сопротивления материалов в этом нет ничего удивительного.

Определить положение центра прямоугольной эпюры нагрузки несложно. Подобными упражнениями мы занимались в школе, когда определяли центр тяжести линейки. И находится этот центр тяжести посредине длины линейки, а в данном случае посредине рассматриваемой части эпюры нагрузки и составляет х/2.Таким образом плечо действия равнодействующей сосредоточенной силы при равномерно распределенной нагрузке составляет х/2. При этом функциональное уравнение изгибающих моментов, необходимое для построения эпюры моментов, будет иметь следующий вид:

M = Ax — qx·x/2 = Ax — qx2/2 (545.5.1)

 

Примерно такой же результат мы получим, если проинтегрируем уравнение поперечных сил:

M = ∫(A — qx)dx = M0 + Ax — qx2/2 (545.5.2) 

Где М0 = 0 — это опять же постоянная интегрирования. В данном случае — значение момента на опоре А. Так как мы рассматриваем однопролетную безконсольную балку на шарнирных опорах, то в этом частном случае значение момента на опоре А равно нулю. Кроме того значение момента на опоре В для шарнирной безконсольной балки также равно нулю, так как шарнирные опоры повороту сечений ни как не препятствуют. Эта особенность в частности используется при определении опорных реакций однопролетной безконсольной балки на шарнирных опорах. Другими словами, зная, что момент на опоре В равен нулю, мы можем определить значение опорной реакции А из уравнения (45.5.2):

МВ = 0 = Аl — ql2/2 (545.5.3)

A = (ql2/2)/l = ql/2 (545.5.4)

В общем случае значение момента в начале координат может быть не равно 0.

А теперь рассмотрим еще одну особенность изгибающих моментов: для рассматриваемого сечения не имеет принципиального значения, какой будет знак у момента, положительный или отрицательный, так как при любом знаке в сечении будет как растягиваемая, так и сжимаемая зона сечения. А вот какая именно зона сечения будет растягиваемой, верхняя или нижняя — имеет большое значение, потому что не все материалы имеют равное сопротивление растяжению и сжатию, а кроме того форма сечения далеко не всегда бывает прямоугольной.

В связи с этим при построении эпюр изгибающих моментов принято следующее правило:

2. Эпюра моментов строится с той стороны, где будет растянутая зона сечения. При этом момент, пытающийся вращать рассматриваемое сечение по часовой стрелке, считается положительным, а против часовой стрелки — отрицательным.

Примечание: это правило не является общепринятым. В некоторых справочниках и учебниках по теории сопротивления материалов положительный момент строится сверху от оси х, что в общем то логично, но при этом получается, что положительный момент там, где сжатая зона сечения. В других он строится с той стороны, где растянутая зона сечения, но при этом может показываться со знаком «-«, если строится снизу от оси х. Но как я уже говорил выше, принципиального значения это не имеет, главное понимать общий смысл изгибающих моментов.

Если мы посмотрим на направление действия опорной реакции А и распределенной нагрузки q (рисунок 545.4), то увидим, что относительно любого из рассматриваемых сечений опорная реакция А пытается вращать это сечение по часовой стрелке, а распределенная нагрузка q — против. Это означает, что функциональное уравнение, описывающее изменение изгибающих моментов по длине балки, составлено у нас правильно.

При этом растянутой будет нижняя зона сечения балки по той причине, что балка прогнется вниз при таком действии нагрузки. Следовательно эпюру моментов в данном случае следует строить снизу от оси координат х.

Теперь у нас есть все данные для построения эпюры изгибающих моментов. Судя по уравнению

(545.5.2) это будет квадратная парабола, а максимальное значение изгибающего момента будет посредине балки, так как нагрузка у нас симметричная, и составит М = 6·2 -3·22/2 = 6 кгм.

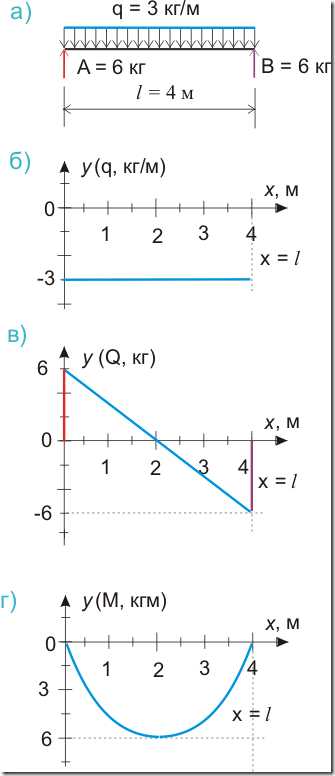
Рисунок 545.5.г) эпюра изгибающих моментов, как график функции у = 6х — 3х2/2

В общем случае, когда нагрузка несимметричная, как показано на рисунках 545.2.а) и б) или на балку действуют несколько распределенных нагрузок, то определить сечение в пролете балки, в котором действует максимальный изгибающий момент. можно, воспользовавшись следующим общим правилом:

3.1. При действии распределенных нагрузок максимальный момент в пролете балки будет в том сечении, в котором значение поперечных сил равно нулю.

Если мы посмотрим на рисунки 545.5.в) и г), то увидим, что это так и есть. Если на балку действуют только сосредоточенные силы, то следует использовать другое правило:

3.2. При действии на балку сосредоточенных сил максимальный момент будет в точке приложения как минимум одной из таких сил.

А вообще в ряде случаев при действии нескольких сосредоточенных сил на балку их, для упрощения расчетов, можно привести к эквивалентной равномерно распределенной нагрузке.

У многопролетных статически неопределимых балок на шарнирных опорах, у балок с жестким защемлением на опорах и у балок с относительно большой длиной консоли максимальный момент может быть не в пролете, а на одной из опор. Тем не менее правило определения момента в пролете по поперечным силам действует и для таких балок.

При построении эпюр изгибающих моментов можно выделить еще несколько общих правил.

4. В точке приложения сосредоточенных сил к балке всегда резко изменяется угол наклона касательной к эпюре моментов «М».

В нашем случае сосредоточенные силы — опорные реакции приложены в начале и в конце балки и если мысленно рассматривать ось х до начала и после конца балки как все ту же балку, то действительно в начале и конце балки мы видим резкое изменение угла наклона касательных, которые можно провести к кривой эпюры моментов в этих точках. 

Это правило действует даже в тех случаях, когда эпюра моментов — не кривая, а ломаная линия. Например, при действии на балку только сосредоточенных сил.

5. В местах приложения к балке внешних изгибающих моментов на эпюре «М» всегда будет резкое изменение. При этом разница значений, определяемая по эпюре, будет равна значению приложенного изгибающего момента.

Как видим данное правило подобно правилу 1, используемому при построении эпюр поперечных сил и в этом нет ничего удивительного, так как закономерности построения графиков функций общие.

Примечание: Касательные и нормальные напряжения, действующие в рассмариваемых поперечных сечениях балки, распределяются не равномерно по высоте сечения балки. Формально для определения максимальных касательных и нормальных напряжений в рассматриваемом сечении требуется дополнительное построение эпюр касательных и нормальных напряжений, но как правило большой необходимости в этом нет, особенно если балка имеет прямоугольное сечение. Какой эти эпюры могут иметь вид, можно посмотреть здесь. Тут лишь упомянем, что на вид эпюры нормальных напряжений

геометрическая форма поперечного сечения ни как не влияет, а на вид эпюры касательных напряжений геометическая форма сечения влияет значительно.

Построение эпюр углов поворота и прогибов

Для дальнейшего расчета балки по второй группе предельных состояний — расчета по деформациям часто требуется построить эпюры углов поворота и прогибов. Начнем с эпюры углов поворота.

Вообще-то более правильно данную эпюру называть «эпюрой тангенсов углов поворота поперечных сечений балки», тем не менее в специализированной литературе принято упрощенное название для этой эпюры, мы тоже не будем нарушать традицию.

В целом значение и углов поворота и прогибов зависит от жесткости балки. Чем больше жесткость ЕI, тем меньше будут углы поворота и прогибы. Более подробно эта тема рассматривается отдельно, здесь лишь отметим, что угол поворота — это дифференциал функции изгибающих моментов:

θ = ∫Мdx (545.6.1)

В нашем случае при действии равномерно распределенной нагрузки на однопролетную балку на шарнирных опорах:

θ = — θ0 + Ах2/2EI — qx3/6EI (545.6.2)

где θ0 — постоянная интегрирования, в данном случае θ0 — угол поворота на опоре А (начальный угол поворота) не равен нулю, так как шарнирные опоры не препятствуют повороту поперечных сечений балки на опорах.

Примечание: Тут может возникнуть вопрос, а почему в данном случае перед начальным углом поворота стоит знак «-«. Объяснение этому можно найти в статье, ссылка на которую дана выше. Здесь лишь сформулируем еще одно правило, используемое при построении эпюр углов поворотов

6. Знак «-» перед начальным углом поворота означает, что угол между касательной к эпюре «θ» и осью х откладывается вниз от оси х (по часовой стрелке).

Соответственно в начале и в конце безконсольной балки с шарнирными опорами мы можем наблюдать резкое изменение значений углов поворота, но это уже даже не правило, а так, общая закономерность. Пойдем дальше.

Прогиб балки — это дифференциал функции углов поворота:

f = ∫θdx (545.7.1)

В данном случае

f = — θх + Ах3/6EI — qx4/24EI (545.7.2)

 

Хотя шарнирные опоры не препятствуют повороту поперечных сечений на опорах, но они препятствуют перемещениям этих сечений вдоль оси у, поэтому в данном случае f0 = 0 и эта постоянная интегрирования в формуле (545.7.2) не приводится. Более того, если нагрузка на балку несимметричная, т.е. углы поворота поперечных сечений на опорах разные, то начальный угол поворота определяется, исходя из того, что прогиб и на опоре А и на опоре В равен нулю, тогда в нашем случае точке В:

fB = 0 = -θ0l + Al3/6EI — ql4/24EI (545.7.3)

θ0 = (ql·l3/(2·6EI) — ql4/24EI)/l = ql3/24EI (545.7.4)

Примечательно, что при определении опорных реакций однопролетной шарнирной балки мы использовали похожую особенность — значения моментов на опорах А и В равны нулю.

На основании этих данных мы можем построить эпюры углов поворота и прогиба балки. При этом значения углов поворота и прогибов будут зависеть, как уже говорилось, от жесткости балки, но в данном случае нас интересует только общий вид эпюр:

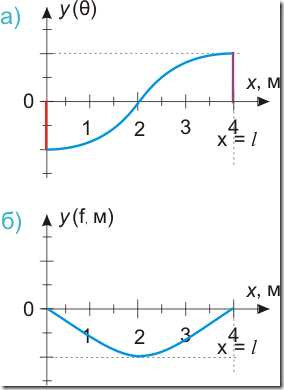
Рисунок 545.6. а) эпюра углов поворота, б) эпюра прогибов — как графики функции.

Как видим, между эпюрами углов поворота и прогибов существует такая же связь, как и между эпюрами поперечных сил и изгибающих моментов. Опять же в этом нет ничего удивительного — это общая закономерность. Тем не не менее одну из этих закономерностей выделим особо:

7. Максимальный прогиб балки на шарнирных опорах будет в том сечении, в котором значение угла поворота равно нулю.

Вот собственно и все, что нужно было сказать по поводу построения эпюр для балки.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

https://verrsus.wordpress.com

http://verrsus-35rus.livejournal.com/

http://steel-c.livejournal.com/

Понравилось это:

Нравится Загрузка…

Похожее

verrsus.wordpress.com

Подробное построение эпюр усилий в балке

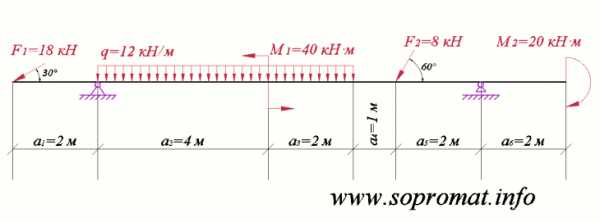
Рис. 1

Дано расчетную схему двухопорной балки (рис. 1) и приложенную к ней внешнюю нагрузку.

Нужно:
1) Определить опорные реакции.
2) Построить эпюры внутренних усилий: эпюру продольных сил (рис. 2, в), поперечных сил (рис. 2, г) и изгибающих моментов (рис. 2, д).

1) Определение опорных реакций.

Спроектируем силы и на ось и (рис. 2, а, б).
Их проекции равны:
кН;
кН;
кН;
кН.

Положительный знак проекции указывает, что ее направление совпадает с положительным направлением соответствующей оси, минус — проекция направлена в отрицательную сторону оси.

На расчетной схеме балки (которая изображена на рис. 2, а) отбрасываем опорные шарниры и заменяем их реакциями в вязях (рис. 2, б). Обозначаем опоры точками и , а соответствующие реакции и . Направление реакций выбираем произвольно, если с уравнений равновесия получим реакцию с отрицательным знаком, то ее начальное направление нужно изменить на противоположное. Используя уравнение статического равновесия (сумма проекций всех сил на оси и равна нулю и сумма моментов всех сил относительно любой точки равна нулю), определяем опорные реакции:

Сумма проекций на ось :
;
;
кН.

Сумма моментов всех сил относительно точки :

;
;
кН.

Сумма моментов всех сил относительно точки :

;
;
кН.

Проверка (сумма проекций всех сил на ось ):
.

Найденные реакции обозначаем на рис. 2,б.

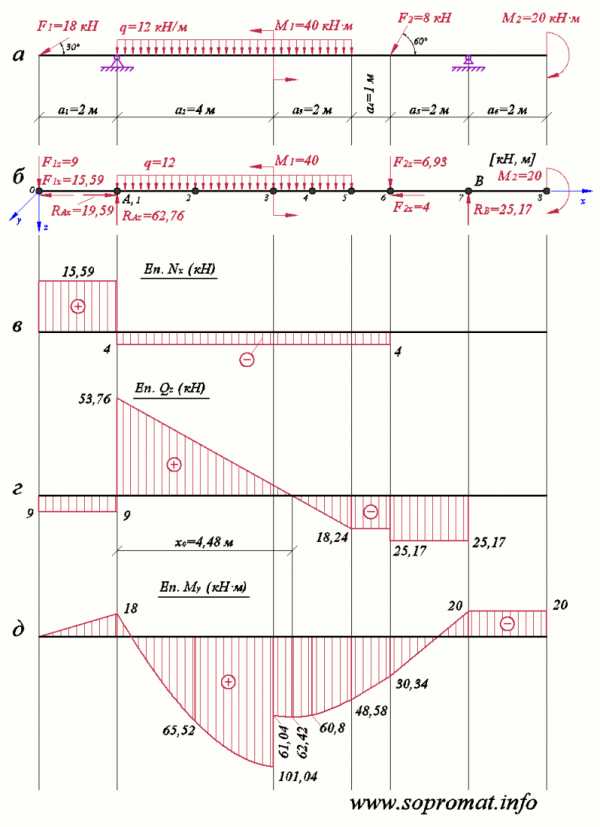
Рис. 2

2) Построение эпюр усилий.

Для нахождения внутренних усилий в характерных точках балки (начало и конец балки, точки приложения сосредоточенных сил и моментов, начало и конец равномерно распределенной нагрузки) будем использовать следующее правило знаков для построения эпюр внутренних усилий. Усилия определяются не в точке, а бесконечно близко к ней (для балки — это левое и правое сечение от характерной точки).

Определение усилий в точке «0»

• Правое сечение (рис. 3).

Рис. 3

Как видно из рис. 3, справа от точки «0» балка разделена на две части (левую, которая изображена на рис. 3 и правую, которую мы отбросили). Это сечение находится бесконечно близко к точке «0», то есть можно принять, что расстояние между сечением и точкой равно нулю. Для плоской задачи в поперечном сечении будут действовать три усилия ( — продольная сила, — поперечная сила и — изгибающий момент). Все усилия направляем так, чтобы они имели положительное направление (в соответствии с правилом знаков).

Для определения усилия , спроектируем все силы на ось :
;
кН.
Откладываем значение усилия на рис. 2, в.

Определяем усилия , проектируем все силы на ось :
;
кН.
Откладываем значение усилия на рис. 2, г.

Усилие , берем сумму моментов всех сил относительно сечения (момент, который вращается вокруг сечения против часовой стрелки, берем со знаком плюс, а по часовой стрелке — со знаком минус):
;
.
Момент относительно точки, от силы, которая проходит через эту точку, равен нулю.
Откладываем значение усилия на рис. 2, д.

В сечении где приложена сосредоточенная продольная сила, на эпюре будет скачок на величину этой силы. Поэтому в таких сечениях значение продольной силы находят слева и справа от точки.

В сечении где приложена сосредоточенная поперечная сила, на эпюре будет скачок на величину этой силы. Поэтому в таких сечениях значение поперечной силы находят слева и справа от точки.

Определение усилий в точке «1»

• Левое сечение (рис. 4).

Рис. 4

Усилие , спроектируем все силы на ось :
;
кН.
Откладываем значение усилия на рис. 2, в.

Усилие , спроектируем все силы на ось :
;
кН.
Откладываем значение усилия на рис. 2, г.

Усилие , сумма моментов всех сил относительно сечения:
;
кН·м.
Откладываем значение усилия на рис. 2, д.

• Правое сечение (рис. 5).

Рис. 5

Усилие , спроектируем все силы на ось :
;
кН.
Откладываем значение усилия на рис. 2, в.

Усилие , спроектируем все силы на ось :
;
кН.
Откладываем значение усилия на рис. 2, г.

Усилие , сумма моментов всех сил относительно сечения:
;
кН·м.
Откладываем значение усилия на рис. 2, д.
Как видим в левом и правом сечении изгибающие моменты равны. То есть в точках где приложена сосредоточенная сила и начинается (или заканчивается) равномерно распределенная нагрузка, изгибающий момент не меняется. В таких точках изгибающий момент будем находить только в одном из сечений (слева или справа от точки).

Определение усилий в точке «2»

• Левое сечение (рис. 6).

Рис. 6

Усилие , спроектируем все силы на ось :
;
кН.

Усилие , спроектируем все силы на ось :
;
кН.

Усилие , сумма моментов всех сил относительно сечения:
;
кН·м.
Откладываем значение усилия на рис. 2, д.

• Правое сечение (рис. 7).

Рис. 7

Усилие , спроектируем все силы на ось :
;
кН.

Усилие , спроектируем все силы на ось :
;
кН.

Усилие , сумма моментов всех сил относительно сечения:
кН·м.

В точке «2» усилия с левой и правой стороны одинаковые. Точка «2» не характерная точка, она нужна только для нахождения изгибающего момента (под равномерно распределенной нагрузкой эпюра моментов изменяется параболой) на этом участке находим минимум три значения на эпюре моментов: в начале участка (т. «1»), в центре (т . «2») и в конце (т. «3»). В точке «4» изгибающий момент будем находить только в одном из сечений (слева или справа от точки).

Усилие не будет меняться до точки «6», то есть в точках «3», «4» и «5» его определять не будем.

Усилие , на участке под равномерно распределенной нагрузкой, будет изменяться прямолинейно (косой линией). Так как на участке от точки «1» до «5» нет сосредоточенных сил, то для построения эпюры поперечных сил на этом участке достаточно найти ее значение в начале (т. «1», что мы уже сделали) и в конце участка (т . «5»).

Понравилась статья! Поддержи проект! Ставь ЛАЙК!

www.sopromat.info

Эпюры в балках

ее приложения. Для распределенной нагрузки, изменяющейся по произ-

вольному закону (рис. 1.6, а) имеем: R = ∫b qy ( z )dz . Вычисление равнодей-

a

ствующей для нагрузок, имеющих постоянную интенсивность (равномерно распределенные нагрузки) значительно упрощается: R = qyl (рис. 1.6, б).

2 ЭПЮРЫ ВНУТРЕННИХ СИЛОВЫХ ФАКТОРОВ

2.1ОБЩИЕ СВЕДЕНИЯ ОБ ЭПЮРАХ

Винженерной практике необходимо четко представлять связь между внешними нагрузками и возникающими в элементах конструкций внутренними силами, напряжениями и перемещениями. Указанные зависимости являются некоторыми функциями координат x, y или z и могут быть изображены на плоскости в виде графиков, называемых эпюрами внутренних силовых факторов, напряжений или перемещений соответственно.

Рассмотрим построение эпюр внутренних силовых факторов, которые являются функциями координаты z, определяющей текущее положе-

ние поперечного сечения бруса: Nz=f(z), Qx=f(z), Qy=f(z), Mx=f (z), My=f (z), Mz=f (z). Графики этих функций, построенные в соответствующем масшта-

бе, называются эпюрами внутренних силовых факторов. Справедливо и другое определение: эпюрой называется график, показывающий изменение внутренних силовых факторов при перемещении поперечного сечения вдоль оси бруса при неизменной внешней нагрузке.

Построение эпюр внутренних силовых факторов необходимо для выполнения прочностных расчетов (подбора необходимых размеров поперечного сечения бруса из условий прочности при соответствующих видах его деформации). Эпюры помогают установить положение «опасных» сечений, где возникают максимальные значения внутренних усилий и, следовательно, действуют экстремальные нормальные или касательные напряжения. Построение эпюр ведется известным методом сечений.

	Мх Nz		Qy	y
			z
	Qy	z	Nz Мх
y

Рисунок 2.1 – Правило знаков ВСФ

Введем следующие правила для определения знаков внутренних силовых факторов (рис. 2.1) для наиболее частого случая загружения бруса, когда все внешние усилия действуют в вертикальной плоскости zOy. Та-

studfiles.net

Построение эпюр для двухопорной балки

Для двухопорной металлической балки, загруженной распределенной нагрузкой, необходимо определить внутренние силовые факторы в поперечных сечениях и построить эпюры поперечных сил и изгибающих моментов.

Порядок решения задачи:

Первым делом находим реакции в опорах данной балки:

Расчет эпюр

Обозначаем участки балки:

Записываем уравнения внутренних силовых факторов для каждого участка и рассчитываем численные значения в характерных сечениях:

Участок 1

\[ (0\le { z }_{ 1 }\le 2м) \]

\[ { Q }_{ y1 }={ R }_{ A }-q{ z }_{ 1 }\\ \]

\[ { M }_{ x1 }={ R }_{ A }{ z }_{ 1 }-\frac { q{ z }_{ 1 }^{ 2 } }{ 2 } \\ \]

\[ при\quad { z }_{ 1 }=0\rightarrow { Q }_{ y1 }=3кН\quad { M }_{ x1 }=0 \]

\[ при\quad { z }_{ 1 }=2м\rightarrow { Q }_{ y1 }=-1кН\quad { M }_{ x1 }=2кНм \]

Определение экстремума

\[ { z }_{ экстр. }=\frac { { R }_{ A } }{ q } =1.5м \]

\[ { при\quad { z }_{ экстр. }=1.5м\rightarrow { Q }_{ y1 }=0\quad { M }_{ x1 }=2.25кНм } \]

Участок 2

\[ (0\le { z }_{ 2 }\le 2м) \]

\[ { Q }_{ y1 }={ -R }_{ B } \]

\[ { M }_{ x1 }={ R }_{ B }{ z }_{ 2 } \]

\[ при\quad { z }_{ 2 }=0\rightarrow { Q }_{ y2 }=-1кН\quad { M }_{ x2 }=0 \]

\[ при\quad { z }_{ 2 }=2м\rightarrow { Q }_{ y2 }=-1кН\quad { M }_{ x2 }=2кНм \]

По полученным значениями строим эпюры внутренних силовых факторов:

sopromats.ru