Эпюра сил: Краткий курс сопротивления материалов

Содержание

Краткий курс сопротивления материалов

Заславский Б. В. Краткий курс сопротивления материалов. Учебник для авиационных специальностей вузов. М.: Машиностроение, 1986. — 328 с.

Изложены основные термины и определения теории сопротивления материалов. Рассмотрены растяжение, сжатие, сдвиг, кручение, изгиб, удар, колебания, устойчивость элементов и систем, статически определимые и неопределимые системы. Приведены методы расчетов: на прочность, за пределами упругости и др. Даны примеры расчетов. Материал изложен в соответствии с учебной программой авиационных специальностей вузов.

4, ФОРМЫ ТЕЛ, РАССМАТРИВАЕМЫХ В СОПРОТИВЛЕНИИ МАТЕРИАЛОВ
1.5. ОПОРНЫЕ УСТРОЙСТВА. ОПОРНЫЕ РЕАКЦИИ
1.6. ОСНОВНЫЕ ГИПОТЕЗЫ О СВОЙСТВАХ МАТЕРИАЛА
1.7. ПОНЯТИЕ О РАСЧЕТНОЙ СХЕМЕ
1.8. ВНУТРЕННИЕ СИЛЫ. МЕТОД СЕЧЕНИЙ
1.9. НАПРЯЖЕНИЕ. ПОНЯТИЕ О НАПРЯЖЕННОМ СОСТОЯНИИ
1.10. НОРМАЛЬНЫЕ И КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ
1.11. ВНУТРЕННИЕ СИЛОВЫЕ ФАКТОРЫ В БРУСЕ
1.12. ВИДЫ ДЕФОРМАЦИЙ БРУСА
ГЛАВА 2. ЦЕНТРАЛЬНОЕ РАСТЯЖЕНИЕ И СЖАТИЕ ПРЯМОГО БРУСА
2.2. ПРОДОЛЬНЫЕ И ПОПЕРЕЧНЫЕ ДЕФОРМАЦИИ БРУСА
2.3. КОЭФФИЦИЕНТ ПОПЕРЕЧНОЙ ДЕФОРМАЦИИ (КОЭФФИЦИЕНТ ПУАССОНА)
2.4. НАПРЯЖЕНИЯ В ПОПЕРЕЧНЫХ СЕЧЕНИЯХ
2.5. НАПРЯЖЕНИЯ В НАКЛОННЫХ СЕЧЕНИЯХ
2.6. ЗАКОН ГУКА ПРИ ОДНООСНОМ РАСТЯЖЕНИИ. ПРИНЦИП НЕЗАВИСИМОСТИ ДЕЙСТВИЯ СИЛ
2.7. УДЛИНЕНИЯ И ПЕРЕМЕЩЕНИЯ
2.8. ОПРЕДЕЛЕНИЕ МЕХАНИЧЕСКИХ СВОЙСТВ МАТЕРИАЛА ПРИ РАСТЯЖЕНИИ
2.9. ДИАГРАММЫ УСЛОВНЫХ И ИСТИННЫХ НАПРЯЖЕНИЙ
2.10. МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ МАТЕРИАЛА
2.11. ЗАКОН РАЗГРУЗКИ И ПОВТОРНОГО НАГРУЖЕНИЯ

2.12. ПЛАСТИЧНЫЕ И ХРУПКИЕ МАТЕРИАЛЫ
2.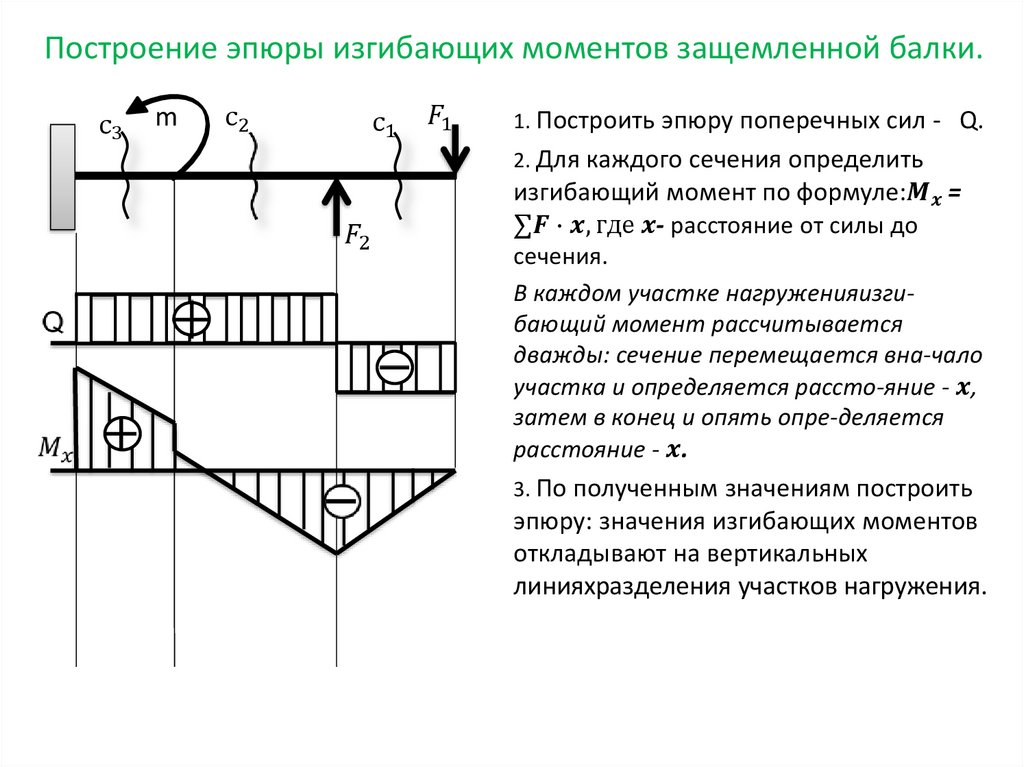

13. МЕХАНИЧЕСКИЕ СВОЙСТВА ПРИ СЖАТИИ
2.14. ВЛИЯНИЕ ТЕМПЕРАТУРЫ НА МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ
2.15. ПОЛЗУЧЕСТЬ. ПОСЛЕДЕЙСТВИЕ И РЕЛАКСАЦИЯ
2.16. ДЛИТЕЛЬНАЯ ПРОЧНОСТЬ
2.17. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
2.18. О РАСЧЕТЕ НА ПРОЧНОСТЬ
2.19. ДВА ТИПА РАСЧЕТОВ НА ПРОЧНОСТЬ
2.20. ЭПЮРЫ НОРМАЛЬНЫХ СИЛ, НОРМАЛЬНЫХ НАПРЯЖЕНИЙ И ПЕРЕМЕЩЕНИЙ
2.21. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ ЗАДАЧИ ПРИ РАСТЯЖЕНИИ И СЖАТИИ
2.22. ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ
2.23. МОНТАЖНЫЕ УСИЛИЯ
2.24. НАПРЯЖЕНИЯ ПРИ ДВУХОСНОМ РАСТЯЖЕНИИ И СЖАТИИ
2.25. ЗАКОН ГУКА ПРИ ДВУХОСНОМ И ТРЕХОСНОМ РАСТЯЖЕНИИ
2.26. ИЗМЕНЕНИЕ ОБЪЕМА ПРИ ТРЕХОСНОМ РАСТЯЖЕНИИ
2.27. УДЕЛЬНАЯ ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ ТРЕХОСНОМ РАСТЯЖЕНИИ И СЖАТИИ
2.28. ЗАКОН ПАРНОСТИ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ
ГЛАВА 3. СДВИГ
3.2. ЧИСТЫЙ СДВИГ
3.3. СВЯЗЬ МЕЖДУ УПРУГИМИ ПОСТОЯННЫМИ Е, G И «МЮ» ДЛЯ ИЗОТРОПНОГО ТЕЛА
3.4. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ СДВИГЕ
ГЛАВА 4. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ
4.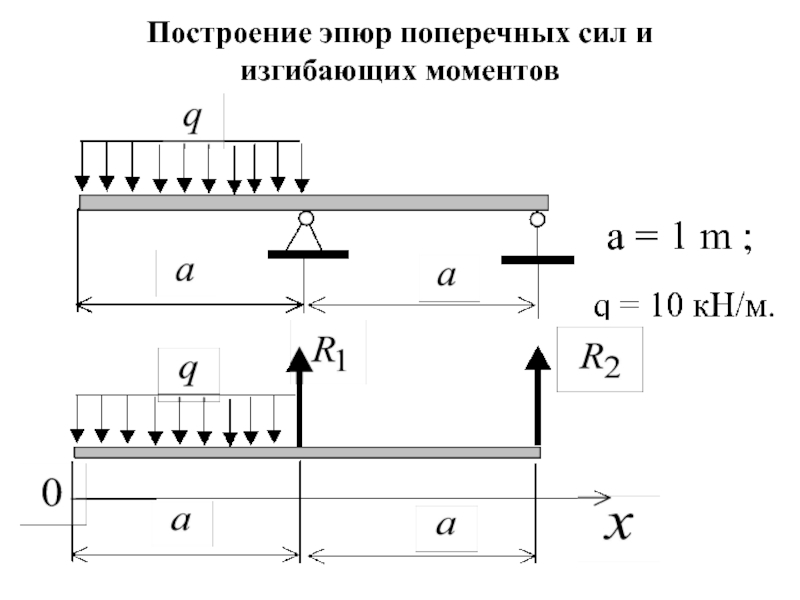

2. ЦЕНТР ТЯЖЕСТИ СЕЧЕНИЯ
4.3. ЗАВИСИМОСТЬ МЕЖДУ МОМЕНТАМИ ИНЕРЦИИ ОТНОСИТЕЛЬНО ПАРАЛЛЕЛЬНЫХ ОСЕЙ
4.4. МОМЕНТЫ ИНЕРЦИИ ПРОСТЕЙШИХ ФИГУР
4.5. ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ СЛОЖНЫХ ФИГУР
4.6. ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПОВОРОТЕ ОСЕЙ КООРДИНАТ
4.7. ГЛАВНЫЕ ОСИ И ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ
4.8. ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ГЛАВНЫХ ОСЕЙ
ГЛАВА 5. КРУЧЕНИЕ
5.2. НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ ПРИ КРУЧЕНИИ ЦИЛИНДРИЧЕСКОГО БРУСА КРУГЛОГО СЕЧЕНИЯ
5.3. НАПРЯЖЕНИЯ В РАЗЛИЧНО ОРИЕНТИРОВАННЫХ СЕЧЕНИЯХ И ХАРАКТЕР РАЗРУШЕНИЯ ПРИ КРУЧЕНИИ БРУСА КРУГЛОГО СЕЧЕНИЯ
5.4. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ КРУЧЕНИИ
5.5. О НАПРАВЛЕНИИ ВЕКТОРА КАСАТЕЛЬНОГО НАПРЯЖЕНИЯ В КОНТУРНЫХ ТОЧКАХ СЕЧЕНИЯ ЦИЛИНДРИЧЕСКОГО БРУСА

5.6. КРУЧЕНИЕ ТОНКОСТЕННОГО БРУСА ЗАМКНУТОГО ПРОФИЛЯ
5.7. КРУЧЕНИЕ БРУСА ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ
5.8. КРУЧЕНИЕ ТОНКОСТЕННОГО БРУСА ОТКРЫТОГО ПРОФИЛЯ
5.9. ОБОБЩЕНИЕ РАСЧЕТНЫХ УРАВНЕНИЙ ДЛЯ БРУСЬЕВ РАЗЛИЧНЫХ СЕЧЕНИЙ
5.10. ЭПЮРЫ КРУТЯЩИХ МОМЕНТОВ, НАПРЯЖЕНИЙ И УГЛОВ ЗАКРУЧИВАНИЯ
5.

11. РАСЧЕТ НА ПРОЧНОСТЬ ПРИ КРУЧЕНИИ
5.12. ЦИЛИНДРИЧЕСКИЕ ВИНТОВЫЕ ПРУЖИНЫ МАЛОГО ШАГА
5.13. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ ЗАДАЧИ ПРИ КРУЧЕНИИ
ГЛАВА 6. ИЗГИБ
6.2. ВНУТРЕННИЕ СИЛОВЫЕ ФАКТОРЫ ПРИ ИЗГИБЕ БРУСА
6.3. ДИФФЕРЕНЦИАЛЬНЫЕ ЗАВИСИМОСТИ ПРИ ИЗГИБЕ
6.4. ЭПЮРЫ ПЕРЕРЕЗЫВАЮЩИХ СИЛ И ИЗГИБАЮЩИХ МОМЕНТОВ
6.5. НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ЧИСТОМ ИЗГИБЕ
6.6. НОРМАЛЬНЫЕ И КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ПОПЕРЕЧНОМ ИЗГИБЕ. ФОРМУЛА ЖУРАВСКОГО
6.7. НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ ТОНКОСТЕННЫХ БАЛОК
6.8. ЦЕНТР ИЗГИБА
6.9. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ ПОПЕРЕЧНОМ ИЗГИБЕ
6.10. РАЦИОНАЛЬНЫЕ ФОРМЫ ПОПЕРЕЧНЫХ СЕЧЕНИЙ
6.11. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ ИЗГИБЕ
6.12. ПЕРЕМЕЩЕНИЯ ПРИ ИЗГИБЕ. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ УПРУГОЙ ЛИНИИ И ЕГО ИНТЕГРИРОВАНИЕ
6.13. ЭНЕРГЕТИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ СЕЧЕНИЙ БАЛОК. ИНТЕГРАЛ МОРА
6.14. СПОСОБ ВЕРЕЩАГИНА
6.15. БАЛКИ ПЕРЕМЕННОГО СЕЧЕНИЯ
ГЛАВА 7. СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ СТЕРЖНЕВЫЕ СИСТЕМЫ
7.2. НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ПРОСТРАНСТВЕННОМ БРУСЕ МАЛОЙ КРИВИЗНЫ.

ИНТЕГРАЛ МОРА
7.3. ПЛОСКИЕ РАМЫ
7.4. ПРОСТРАНСТВЕННЫЕ РАМЫ
7.5. ПЛОСКОПРОСТРАНСТВЕННЫЕ РАМЫ
7.6. ФЕРМЫ
7.7. СМЕШАННЫЕ СИСТЕМЫ
7.8. ОТНОСИТЕЛЬНЫЕ ПЕРЕМЕЩЕНИЯ СЕЧЕНИЙ СТЕРЖНЕВОЙ СИСТЕМЫ
ГЛАВА 8. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СТЕРЖНЕВЫЕ СИСТЕМЫ
8.2. ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ КАНОНИЧЕСКИХ УРАВНЕНИЙ

8.3. ПОСЛЕДОВАТЕЛЬНОСТЬ РЕШЕНИЯ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ ЗАДАЧ
8.4. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ СЕЧЕНИЙ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ
8.5. О РАЦИОНАЛЬНОМ ВЫБОРЕ ОСНОВНОЙ СИСТЕМЫ. ИСПОЛЬЗОВАНИЕ ПРЯМОЙ И ОБРАТНОЙ СИММЕТРИИ
ГЛАВА 9. КОСОЙ ИЗГИБ. ВНЕЦЕНТРЕННОЕ РАСТЯЖЕНИЕ И СЖАТИЕ
9.2. ВНЕЦЕНТРЕННОЕ РАСТЯЖЕНИЕ И СЖАТИЕ
ГЛАВА 10. ОСНОВЫ НАПРЯЖЕННОГО И ДЕФОРМИРОВАННОГО СОСТОЯНИЯ В ТОЧКЕ ТЕЛА
10.3. НАПРЯЖЕНИЯ НА ПРОИЗВОЛЬНО НАКЛОНЕННОЙ К ОСЯМ КООРДИНАТ ПЛОЩАДКЕ
10.4. НОРМАЛЬНЫЕ И КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ НА НАКЛОННОЙ ПЛОЩАДКЕ
10.5. ГЛАВНЫЕ ПЛОЩАДКИ И ГЛАВНЫЕ НАПРЯЖЕНИЯ. ИНВАРИАНТЫ НАПРЯЖЕННОГО СОСТОЯНИЯ
10.6. ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ГЛАВНЫХ ПЛОЩАДОК
10.

7. ЭЛЛИПСОИД НАПРЯЖЕНИЙ
10.8. ЭКСТРЕМАЛЬНЫЕ ЗНАЧЕНИЯ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ И ПЛОЩАДКИ ИХ ДЕЙСТВИЯ

10.9. КРУГОВАЯ ДИАГРАММА НАПРЯЖЕНИЙ (КРУГИ МОРА)
10.10. НАПРЯЖЕНИЯ НА ПЛОЩАДКАХ, РАВНОНАКЛОННЫХ К ГЛАВНЫМ (ОКТАЭДРИЧЕСКИЕ НАПРЯЖЕНИЯ)
10.11. ПОНЯТИЕ О ШАРОВОМ ТЕНЗОРЕ И ДЕВИАТОРЕ НАПРЯЖЕНИЙ
10.12. КЛАССИФИКАЦИЯ НАПРЯЖЕННОГО СОСТОЯНИЯ В ТОЧКЕ ТЕЛА
10.13. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
10.14. ГЛАВНЫЕ НАПРЯЖЕНИЯ И ГЛАВНЫЕ ПЛОЩАДКИ В БРУСЕ
10.15. ДЕФОРМИРОВАННОЕ СССТОЯНИЕ В ТОЧКЕ ТЕЛА. АНАЛОГИЯ МЕЖДУ ЗАВИСИМОСТЯМИ ТЕОРИИ НАПРЯЖЕНИЙ И ТЕОРИИ ДЕФОРМАЦИЙ
10.16. ОБОБЩЕННЫЙ ЗАКОН ГУКА ДЛЯ ИЗОТРОПНОГО ТЕЛА
10.17. УДЕЛЬНАЯ ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ И ЕЕ ДЕЛЕНИЕ НА УДЕЛЬНУЮ ЭНЕРГИЮ ИЗМЕНЕНИЯ ОБЪЕМА И УДЕЛЬНУЮ ЭНЕРГИЮ ИЗМЕНЕНИЯ ФОРМЫ
10.18. ОПРЕДЕЛЕНИЕ ГЛАВНЫХ НАПРЯЖЕНИЙ И ГЛАВНЫХ ДЕФОРМАЦИЙ ПО РЕЗУЛЬТАТАМ ЭКСПЕРИМЕНТА
ГЛАВА 11. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ
11.2. НАЗНАЧЕНИЕ ТЕОРИЙ ПРЕДЕЛЬНОГО СОСТОЯНИЯ
11.3. ТЕОРИЯ НАИБОЛЬШИХ НОРМАЛЬНЫХ НАПРЯЖЕНИЙ
11.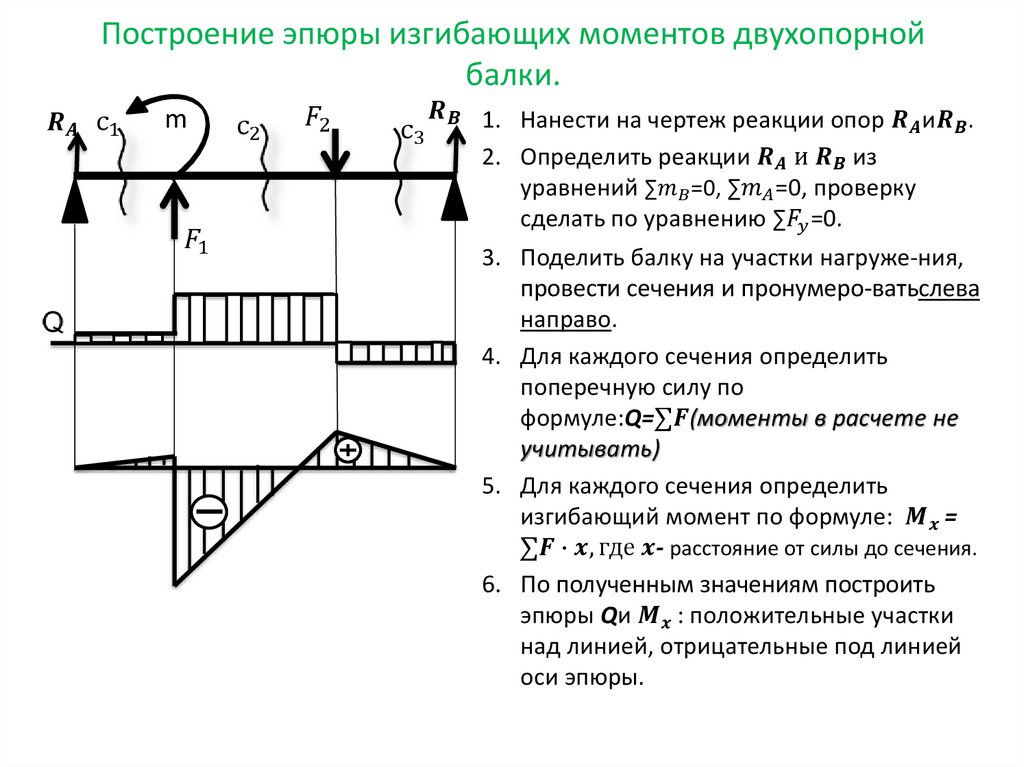

4. ТЕОРИЯ НАИБОЛЬШИХ ОТНОСИТЕЛЬНЫХ УДЛИНЕНИЙ
11.5. ТЕОРИЯ НАИБОЛЬШИХ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ
11.6. ТЕОРИЯ УДЕЛЬНОЙ ЭНЕРГИИ ИЗМЕНЕНИЯ ФОРМЫ
11.7. ТЕОРИЯ МОРА
11.8. СООТНОШЕНИЯ МЕЖДУ ПРЕДЕЛАМИ ТЕКУЧЕСТИ ПРИ ПРОСТОМ РАСТЯЖЕНИИ И ЧИСТОМ СДВИГЕ ПО РАЗЛИЧНЫМ ТЕОРИЯМ
11.9. НЕКОТОРЫЕ ЗАМЕЧАНИЯ О ВЫБОРЕ ТЕОРИИ ПРЕДЕЛЬНЫХ СОСТОЯНИЙ ПРИ РАСЧЕТАХ
11.10. КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ И ЕЕ ВЛИЯНИЕ НА ПРОЧНОСТЬ ПРИ ПОСТОЯННЫХ ВО ВРЕМЕНИ НАПРЯЖЕНИЯХ
11.11. О МЕХАНИКЕ ХРУПКОГО РАЗРУШЕНИЯ
ГЛАВА 12. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ НАПРЯЖЕНИЯХ, ПЕРЕМЕННЫХ ВО ВРЕМЕНИ
12.2. МЕХАНИЗМ УСТАЛОСТНОГО РАЗРУШЕНИЯ
12.3. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
12.4. ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ ПРЕДЕЛА ВЫНОСЛИВОСТИ. ПРЕДЕЛ ОГРАНИЧЕННОЙ ВЫНОСЛИВОСТИ
12.5. ЗАВИСИМОСТЬ ПРЕДЕЛА ВЫНОСЛИВОСТИ ОТ СТЕПЕНИ АСИММЕТРИИ ЦИКЛА. ДИАГРАММА ПРЕДЕЛЬНЫХ АМПЛИТУД
12.6. ВЕРОЯТНОСТНЫЙ ХАРАКТЕР ЯВЛЕНИЯ УСТАЛОСТИ
12.7. МАЛОЦИКЛОВАЯ УСТАЛОСТЬ
12.8. ФАКТОРЫ, ВЛИЯЮЩИЕ НА СОПРОТИВЛЕНИЕ УСТАЛОСТИ
12.9. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ ОДНООСНОМ НАПРЯЖЕННОМ СОСТОЯНИИ И ЧИСТОМ СДВИГЕ (ИЗГИБЕ, РАСТЯЖЕНИИ И КРУЧЕНИИ)
12.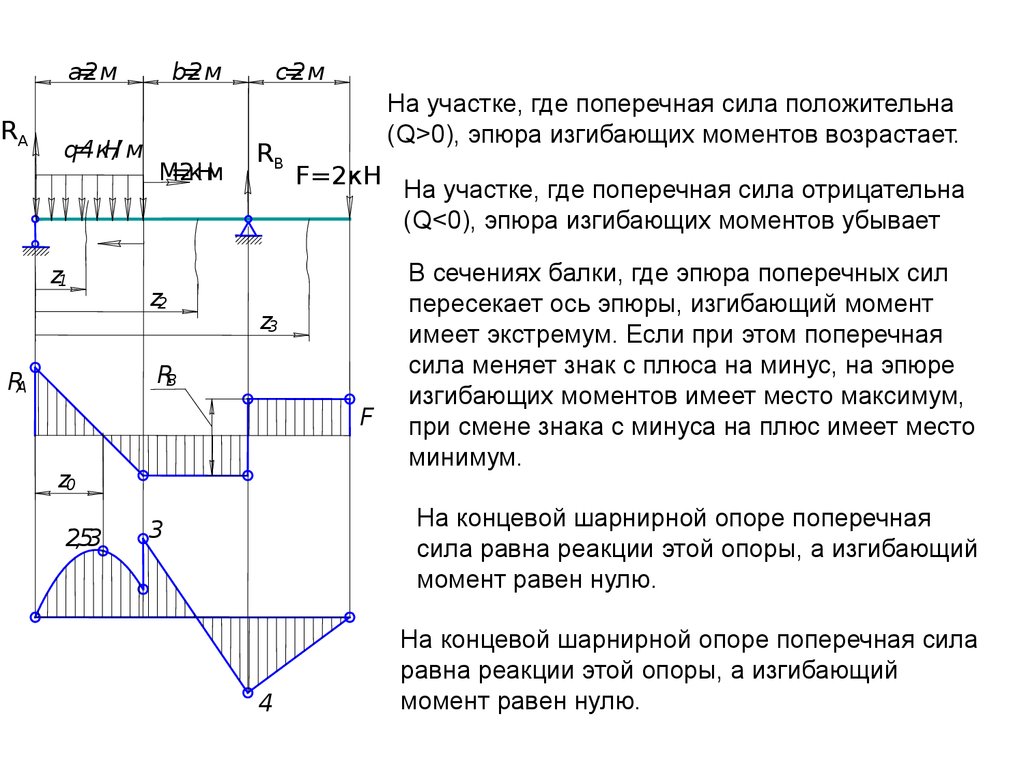

10. РАСЧЕТ НА ПРОЧНОСТЬ ПРИ СЛОЖНОЕ НАПРЯЖЕННОМ СОСТОЯНИИ
12.11. СОПРОТИВЛЕНИЕ УСТАЛОСТИ ПРИ НЕСТАЦИОНАРНЫХ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ
ГЛАВА 13. РАСЧЕТЫ ЗА ПРЕДЕЛАМИ УПРУГОСТИ
13.2. СХЕМАТИЗАЦИЯ ДИАГРАММ РАСТЯЖЕНИЯ
13.3. РАСЧЕТ ПО НАГРУЗКАМ, ИСЧЕРПЫВАЮЩИМ НЕСУЩУЮ СПОСОБНОСТЬ
13.4. РАСЧЕТ БАЛОК ПО НАГРУЗКАМ, ИСЧЕРПЫВАЮЩИМ НЕСУЩУЮ СПОСОБНОСТЬ
13.5. НЕСУЩАЯ СПОСОБНОСТЬ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ БАЛОК И РАМ
13.6. ЧИСТЫЙ УПРУГОПЛАСТИЧЕСКИЙ ИЗГИБ ПРЯМОГО БРУСА
13.7. РАЗГРУЗКА И ОСТАТОЧНЫЕ НАПРЯЖЕНИЯ
ГЛАВА 14. РАСЧЕТ ПРОСТЕЙШИХ ОСЕСИММЕТРИЧНО НАГРУЖЕННЫХ ТОНКОСТЕННЫХ ОБОЛОЧЕК ВРАЩЕНИЯ
14.2. УРАВНЕНИЯ РАВНОВЕСИЯ ЭЛЕМЕНТА СИММЕТРИЧНОЙ БЕЗМОМЕНТНОЙ ОБОЛОЧКИ

14.3. ТЕОРЕМА О ДАВЛЕНИИ НА КРИВОЛИНЕЙНУЮ СТЕНКУ
14.4. РАСЧЕТ СФЕРИЧЕСКИХ И ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК НА НОРМАЛЬНОЕ ДАВЛЕНИЕ ПО БЕЗМОМЕНТНОЙ ТЕОРИИ
ГЛАВА 15. РАСЧЕТ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ, ДВИЖУЩИХСЯ С УСКОРЕНИЕМ
15.2. РАСЧЕТ ПОСТУПАТЕЛЬНО ДВИЖУЩИХСЯ СИСТЕМ
15.3. НАПРЯЖЕНИЯ В ТОНКОСТЕННОМ ВРАЩАЮЩЕМСЯ КОЛЬЦЕ
15.

4. РАСЧЕТ РАВНОМЕРНО ВРАЩАЮЩЕГОСЯ ПРЯМОГО БРУСА
15.5. ВРАЩАЮЩИЕСЯ РАМЫ
ГЛАВА 16. УДАР
16.2. УДАР ПАДАЮЩЕГО ГРУЗА ПО УПРУГОЙ СИСТЕМЕ, МАССА КОТОРОЙ МАЛА ПО СРАВНЕНИЮ С МАССОЙ ГРУЗА
16.3. ПРИВЕДЕННАЯ МАССА. КОЭФФИЦИЕНТ ПРИВЕДЕНИЯ
16.4. УДАР ПО СИСТЕМЕ, МАССА КОТОРОЙ СОИЗМЕРИМА С МАССОЙ УДАРЯЮЩЕГО ГРУЗА
ГЛАВА 17. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ. ПРОДОЛЬНЫЙ ИЗГИБ
17.2. ОПРЕДЕЛЕНИЕ КРИТИЧЕСКОЙ СИЛЫ МЕТОДОМ ИНТЕГРИРОВАНИЯ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ УПРУГОЙ ЛИНИИ СТЕРЖНЯ. ФОРМУЛА ЭЙЛЕРА
17.3. ПРЕДЕЛЫ ПРИМЕНИМОСТИ ФОРМУЛЫ ЭЙЛЕРА
17.4. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ ЗА ПРЕДЕЛАМИ ПРОПОРЦИОНАЛЬНОСТИ. ГРАФИК КРИТИЧЕСКИХ НАПРЯЖЕНИЙ
17.5. ПРАКТИЧЕСКИЕ СПОСОБЫ РАСЧЕТА НА ПРОДОЛЬНЫЙ ИЗГИБ
17.6. ЭНЕРГЕТИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ КРИТИЧЕСКОЙ НАГРУЗКИ
17.7. ДИНАМИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ КРИТИЧЕСКОЙ НАГРУЗКИ
ГЛАВА 18. ПРОДОЛЬНО-ПОПЕРЕЧНЫЙ ИЗГИБ
18.3. ПРИБЛИЖЕННАЯ ФОРМУЛА ДЛЯ ОПРЕДЕЛЕНИЯ ПРОГИБА БАЛКИ ПРИ ПРОДОЛЬНО-ПОПЕРЕЧНОМ ИЗГИБЕ
18.4. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ДЛЯ ИЗГИБАЮЩИХ МОМЕНТОВ
18.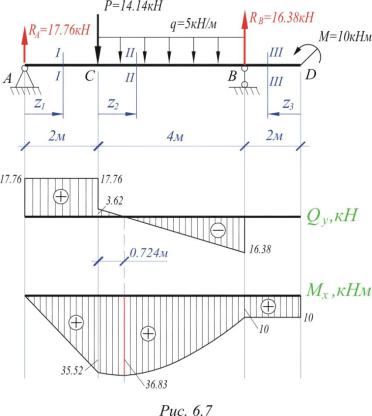

5. РАСЧЕТ НА ПРОЧНОСТЬ ПРИ ПРОДОЛЬНО-ПОПЕРЕЧНОМ ИЗГИБЕ

2.1. Эпюры сил и моментов. Правила, применяемые при построении эпюр

Кисляков Н.И.Прикладная механика Л.3-4. 1101.03.17

Лекция 3-4

Тема.2 Расчеты механизмов на прочность и жесткость

2.1. Эпюры сил и моментов. Правила, применяемые при построении эпюр

2.2. Продольные силы. Эпюры продольных сил

2.3. Крутящие моменты. Эпюры крутящих моментов

2.4. Балки и опоры. Реакции и их вычисление

2.5. Изгиб. Поперечные силы и моменты в сечениях при изгибе

2.6. Построение эпюр Q и M для балок

2.7. Дифференциальные зависимости при изгибе

Тема.2 Расчеты механизмов на прочность и жесткость

Усилия и моменты в разных сечениях одного и того же стержня различны.

Графики (диаграммы), показывающие, как изменяются внутренние усилия при переходе от сечения к сечению, называют эпюрами.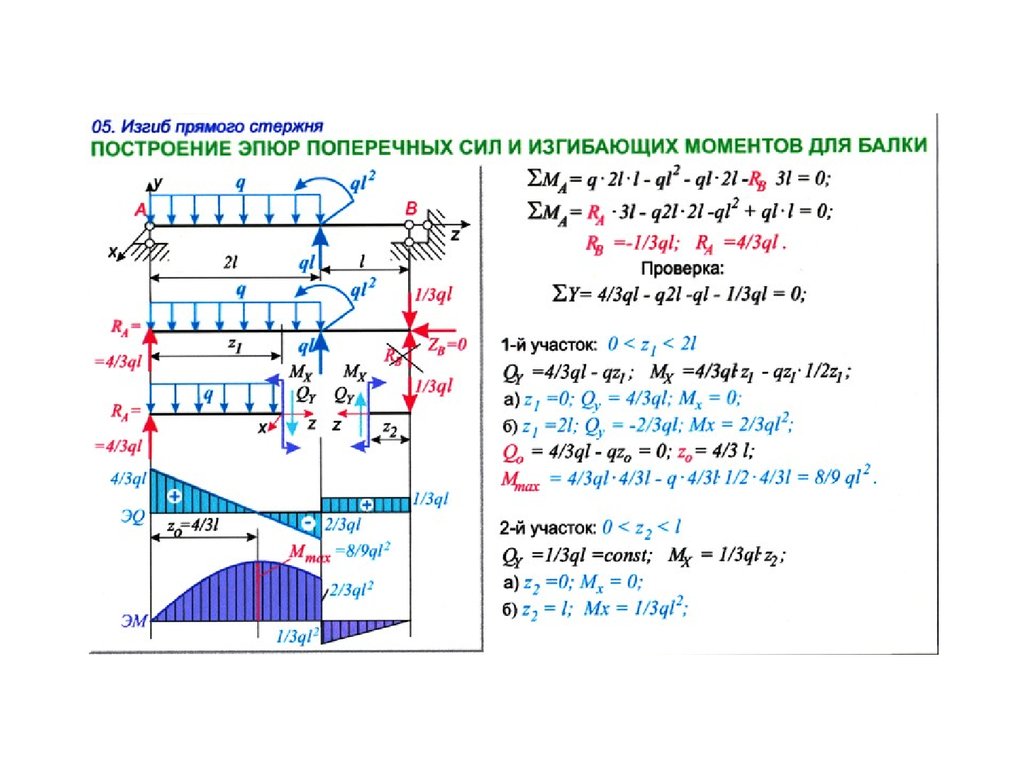

Правила, применяемые при построении эпюр:

1. Ось (базу), на которой строится эпюра, всегда выбирают так, чтобы она была параллельна или просто совпадала с осью стержня.

2. Ординаты эпюры откладывают от оси эпюры по перпендикуляру.

3. Штриховать эпюры принято линиями, перпендикулярными к базе.

4. Для усилий и моментов выбирают некоторый масштаб. Ординаты откладывают строго в масштабе. Кроме того, на эпюрах проставляют числа, показывающие величины характерных ординат, а в поле эпюры в кружочке ставят знак усилия.

Продольная (осевая) сила считается положительной, если она вызывает растяжение, и отрицательной, если вызывает сжатие. Внешние силы сами по себе ни положительны, ни отрицательны, но каждая дает в выражении для N слагаемое определенного знака.

В качестве примера построения эпюр осевых сил рассмотрим стержень (рис. 1), нагруженный в точках А, В и С сосредоточенными силами Р₁ Р₂, Р₃, направленными вдоль оси.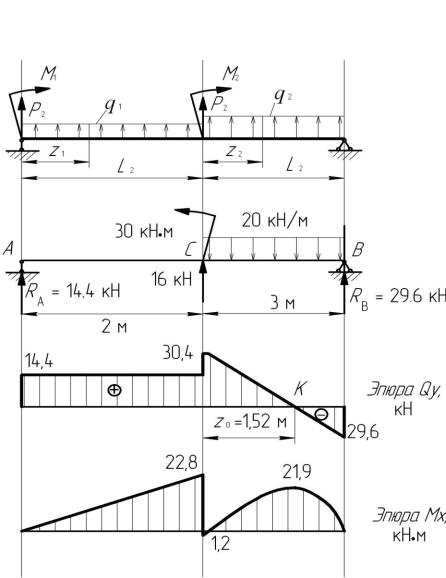

Рис 1 рис 2

Приступая к построению эпюры, стержень разбивают на участки.

Участком называют часть стержня между точками приложения сосредоточенных сил. Если на стержень действует распределенная нагрузка, участком называют часть стержня, в пределах которого распределенная нагрузка изменяется по одному закону. В рассматриваемом примере два участка — 1(АВ) и 2 (ВС).

Чтобы построить эпюры, нужно составить выражения для осевых сил в произвольном сечении каждого участка.

Продольная сила в сечении равна алгебраической сумме проекций на ось бруса сил, взятых по одну сторону от сечения!

Выберем начало координат в крайней левой точке стержня; ось х направим вдоль его оси. В произвольном сечении любого участка на расстоянии х от начала координат находим осевую силу как сумму проекций всех внешних сил, расположенных слева или справа от рассматриваемого сечения:

1 участок (0 х < а) слева: N (х)= = 2000н; справа: N (х)== (5000 — 3000) н = 2000 н.

2 участок (а < х l) слева: N(х) == (2000 — 5000) н = -3000н; справа: N (х) = —P₃ = -3000н.

Поскольку эти величины не зависят от абсцисс сечения, то во всех сечениях первого участка продольная сила N — 2000 н, а для любого сечения второго участка она равна — 3000 н. Откладывая полученные ординаты от оси эпюры, строим эпюру N. Заметим, что штриховка эпюры показывает откладываемые ординаты. В сечениях А, В и С на эпюре получились скачки, равные соответственно 2000, 5000 и 3000 н, т. е. как раз тем силам, которые приложены к стержню в этих сечениях.

Если на стержень действуют только сосредоточенные силы, то линии эпюры параллельны ее оси (эпюра N состоит из прямоугольников и имеет скачки в тех сечениях, где приложены внешние силы). Так, нетрудно убедиться, что для стержня, изображенного на рис. 2, эпюра будет иметь такой вид, как показано на рисунке.

Если стержень расположен вертикально и учитывается его собственный вес, то линия эпюры наклонена к оси (для цилиндрического стержня) или криволинейна (для стержня с непрерывно меняющимися размерами сечения).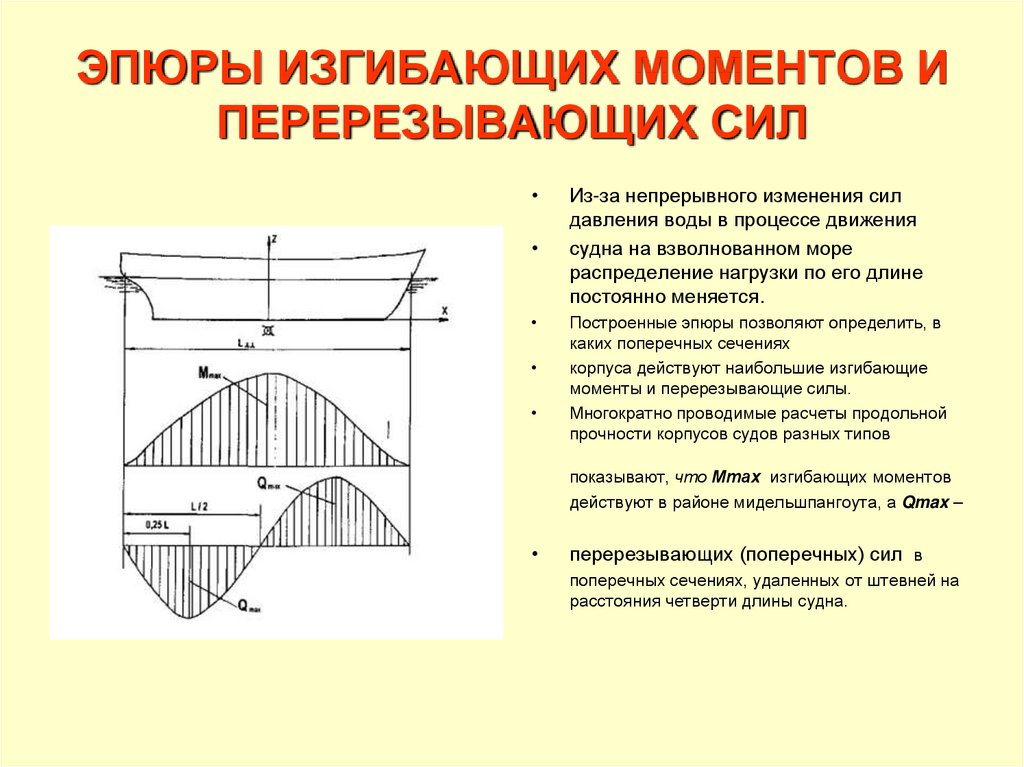

Интерпретация диаграмм силы — физика для старших классов

Все ресурсы по физике для старших классов

6 диагностических тестов 233 практических теста Вопрос дня Карточки Learn by Concept

Справка по физике для старших классов » Силы » Равнодействующая сила » Интерпретация диаграмм сил

Что из следующего представляет силу трения?

Возможные ответы:

Правильный ответ:

Объяснение:

Сила трения всегда будет параллельна поверхности, по которой движется объект. Он будет исходить прямо из центра объекта и направлен в направлении, противоположном движению объекта.

На этой диаграмме V указывает параллельно поверхности и противоположно направлению движения.

Сообщить об ошибке

Что из следующего представляет собой силу тяжести?

Возможные ответы:

Правильный ответ:

Пояснение:

Помните, что на диаграмме сил силы исходят из центра объекта.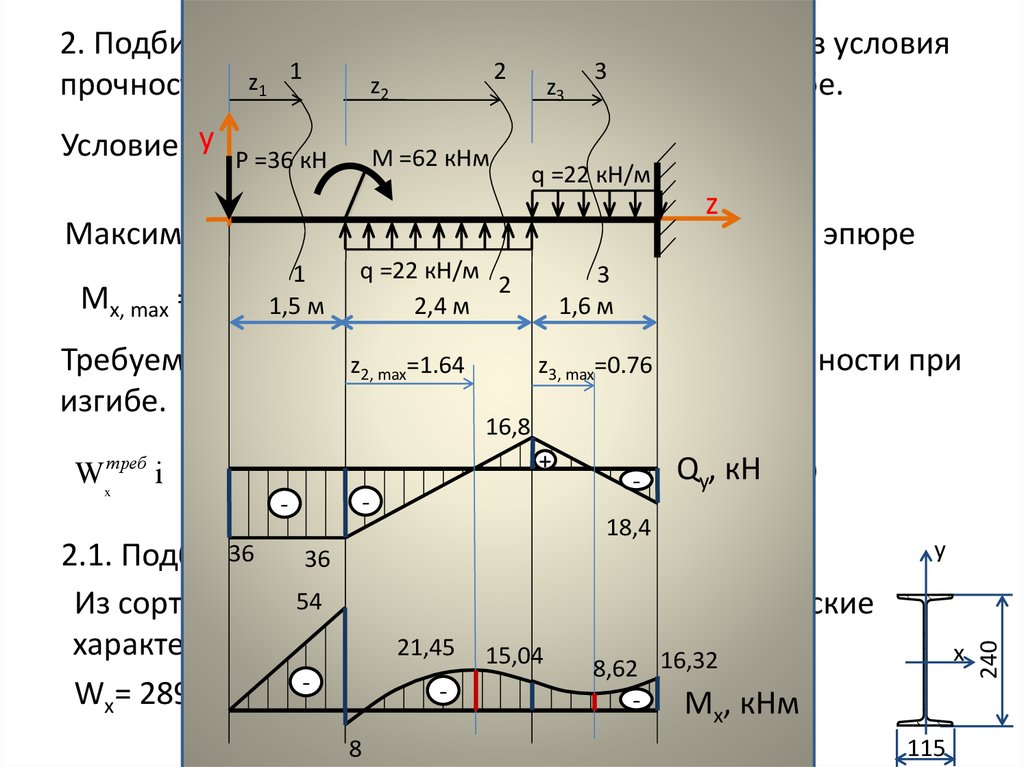 Сила тяжести будет всегда направлена прямо вниз от центра объекта.

На этой диаграмме W направлен прямо вниз.

Сообщить об ошибке

Каково значение угла внутри треугольника, образованного X , W и Y ?

Возможные ответы:

Требуется дополнительная информация

Правильный ответ: 90 005

Пояснение:

При работе в наклонной плоскости, когда мы разбиваем нашу силу тяжести на составные части, угол при вершине этого треугольника будет равен углу наклонной плоскости.

На диаграмме общая сила тяжести равна Вт . X представляет горизонтальную составляющую и параллельна поверхности плоскости. Y представляет собой вертикальную составляющую и перпендикулярна поверхности плоскости. Таким образом, X и Y образуют прямой угол с W в качестве гипотенузы. Повернув этот треугольник так, чтобы прямой угол совпадал с прямым углом наклонной плоскости (между Q и P ), мы видим, что W выравнивается с наклонной поверхностью, а Y выравнивается с основанием, P . На основании этих совмещений угол между W и Y должен быть равен углу между поверхностью и P ; таким образом, .

Сообщить об ошибке

Что из следующего представляет нормальную силу?

Возможные ответы:

-W

Правильный ответ:

Объяснение:

Нормальная сила всегда перпендикулярна поверхности, на которой находится объект, и направлена от этой поверхности.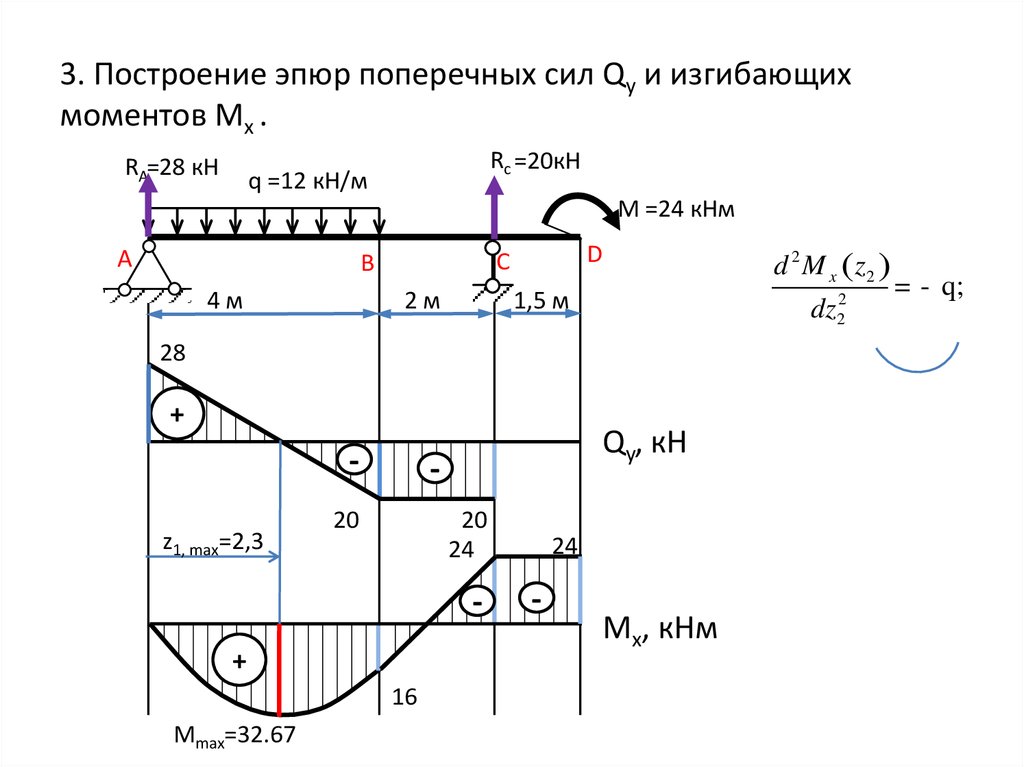

На этой диаграмме Z — единственная сила, направленная перпендикулярно поверхности и направленная вверх. Эта сила должна противодействовать вертикальной силе тяжести, которая будет перпендикулярна поверхности в направлении вниз ( И ).

Сообщить об ошибке

Какое из следующих утверждений неверно?

Возможные ответы:

Правильный ответ:

Объяснение:

На этой диаграмме V представляет силу трения. Уравнение для силы трения: , где — коэффициент трения.

В данном случае Z представляет нормальную силу. Мы можем переписать уравнение трения:

Z можно переписать в терминах угла, но его всегда нужно умножать на коэффициент трения, чтобы получить уравнение для V .

Остальные уравнения верны.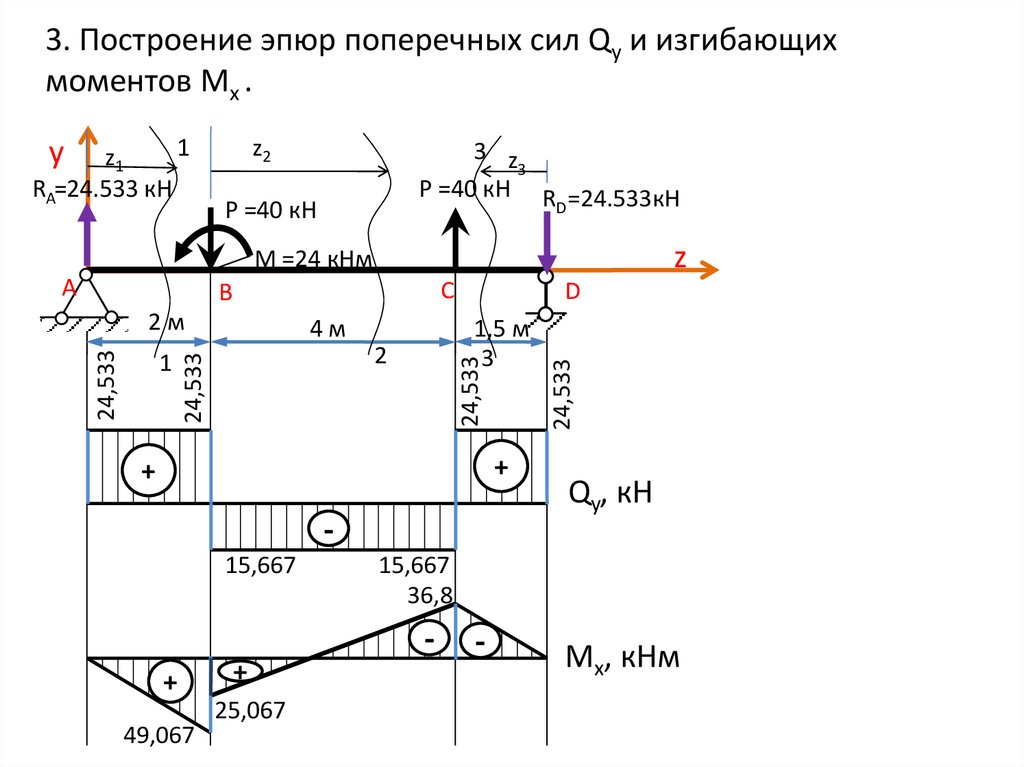

— X и Y образуют прямой угол, поэтому применима теорема Пифагора.

— Z — нормальная сила, которая по определению равна и противоположна вертикальной силе тяжести.

— W — это полная сила тяжести, которая будет равна произведению массы на ускорение свободного падения.

— треугольник, образованный W , X и Y подобен треугольнику, образованному поверхностью, Q и P , а это означает, что эти углы должны быть равны.

Сообщить об ошибке

В соответствии с этой диаграммой силы нормальная сила будет равна какой из следующих величин?

Возможные ответы:

Правильный ответ:

Объяснение:

В этой задаче Y и Z равны, но противоположны друг другу, а Z является нашей нормальной силой.

Если мы сможем найти Y , то мы сможем найти Z .

Мы можем использовать наше понимание тригонометрии, чтобы найти уравнение для Y .

Если подставить угол, то получится:

Поскольку мы вычисляем Y , мы можем умножить обе части на W .

Теперь, когда мы знаем уравнение для Y , мы можем вернуться к нашему исходному уравнению, чтобы найти Z .

Сообщить об ошибке

Какое расстояние проходит объект согласно этой диаграмме?

Возможные ответы:

Требуется дополнительная информация

Правильный ответ:

Требуется дополнительная информация

Пояснение:

Мы не можем узнать расстояние, которое проходит объект. Несмотря на то, что силовая диаграмма помещает наш объект примерно посередине плоскости, мы не знаем положение, где объект начинается или где объект заканчивается. Мы не можем рассчитать изменение расстояния.

Сообщить об ошибке

Что из следующего правильно вычисляет X в пересчете на W ?

Возможные ответы:

Правильный ответ:

Объяснение:

Мы можем использовать наше понимание тригонометрии, чтобы найти эту связь, поскольку X и Y образуют прямой угол.

Если мы подставим угол, мы увидим, что X противоположно, а W является гипотенузой.

Так как мы ищем X , мы можем умножить обе части на W .

Сообщить об ошибке

Как мы можем использовать эту диаграмму для расчета результирующей силы, действующей на объект?

Возможные ответы:

Правильный ответ:

Пояснение:

В этой задаче нам нужно разбить силы на горизонтальную и вертикальную составляющие. Единственная разница с наклонной плоскостью заключается в том, что вы должны перевести горизонтальную плоскость так, чтобы она была параллельна поверхности, по которой движется объект, а вертикальная плоскость должна быть перпендикулярна поверхности, по которой движется объект.

К счастью, это уже сделано на диаграмме, где сила тяжести ( W ) разбита на вертикальную составляющую ( Y ) и горизонтальную составляющую ( X ).

Теперь нам нужно просуммировать силы в каждой плоскости. Силы в вертикальной плоскости будут перпендикулярны поверхности: Z и Y .

Так как Z и Y являются противоположными и равными силами:

В вертикальной плоскости результирующая сила отсутствует. Это имеет смысл, так как мы не ожидаем, что объект будет двигаться перпендикулярно поверхности, по которой он скользит.

Теперь мы можем суммировать горизонтальные силы: В и Х .

Обратите внимание, что X положительное, а V отрицательное. Это потому, что V представляет собой силу трения и противоположна силе X .

Поскольку в вертикальной плоскости силы нет, это дает нашу итоговую результирующую силу: .

Сообщить об ошибке

Уведомление об авторских правах

Все ресурсы по физике для старших классов

6 Диагностические тесты 233 практических теста Вопрос дня Карточки Learn by Concept

Силовые диаграммы — AP Physics 1

Все ресурсы AP Physics 1

7 Диагностические тесты 170 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 Следующая →

AP Physics 1 Справка » Ньютоновская механика » Силы » Основы силы и законы Ньютона » Диаграммы силы

Рассмотрим следующую систему:

Если масса движется вниз по плоскости со скоростью и углом, каков коэффициент кинетического трения между массой и наклоном?

Возможные ответы:

Правильный ответ:

Объяснение:

Прежде чем мы начнем использовать уравнения, нам нужно определить, какие силы действуют на брусок в этой системе.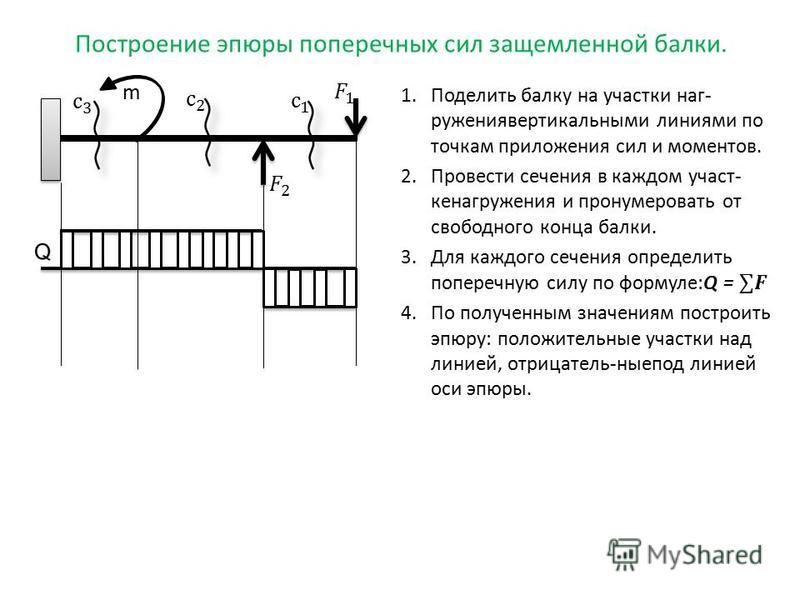 Единственными значимыми силами в этой ситуации являются гравитация и трение. Нам дано ускорение блока, что дает нам инструменты для определения чистой силы.

Используя второй закон Ньютона, мы можем написать:

Сила трения вычитается, потому что она находится в направлении, противоположном движению бруска. Замена выражений на каждую переменную, мы получаем:

Отмена массы и перестройки для коэффициента кинетического трения, мы получаем:

Мы имеем значения для каждой переменной, позволяя нам решить:

55555

Сообщить об ошибке

Рассмотрим следующую систему:

Эта система находится на другой планете, гравитационная постоянная которой отличается от земной. Если угол измеряется, коэффициент кинетического трения равен, а блок ускоряется со скоростью, каково ускорение свободного падения на этой планете?

Возможные ответы:

Правильный ответ:

Объяснение:

В этом сценарии на блок действуют две соответствующие силы: гравитация и трение. Мы можем использовать второй закон Ньютона, чтобы решить эту проблему:

Подставляя выражения для каждой силы, мы получаем:

Исключая массу и переставляя , мы получаем:

Теперь мы можем подставить значения для каждой переменной и решить:

Сообщить об ошибке

На рисунке безмассовая струна соединяет два блока массами 30 кг и 50 кг, которые находятся на плоской поверхности без трения. Сила притягивает блок массой 50 кг, как показано на рисунке. Если сила, действующая на 50-килограммовый блок, равна 100 Н, каково натяжение нити, соединяющей два блока?

Возможные ответы:

Правильный ответ:

Пояснение:

Начните с рисования сил, действующих на каждый блок. Вы также можете нарисовать силу тяжести и нормальную силу для каждого блока, но они были опущены на изображении, потому что они компенсируют друг друга для каждого блока и потому что в этой задаче нет трения.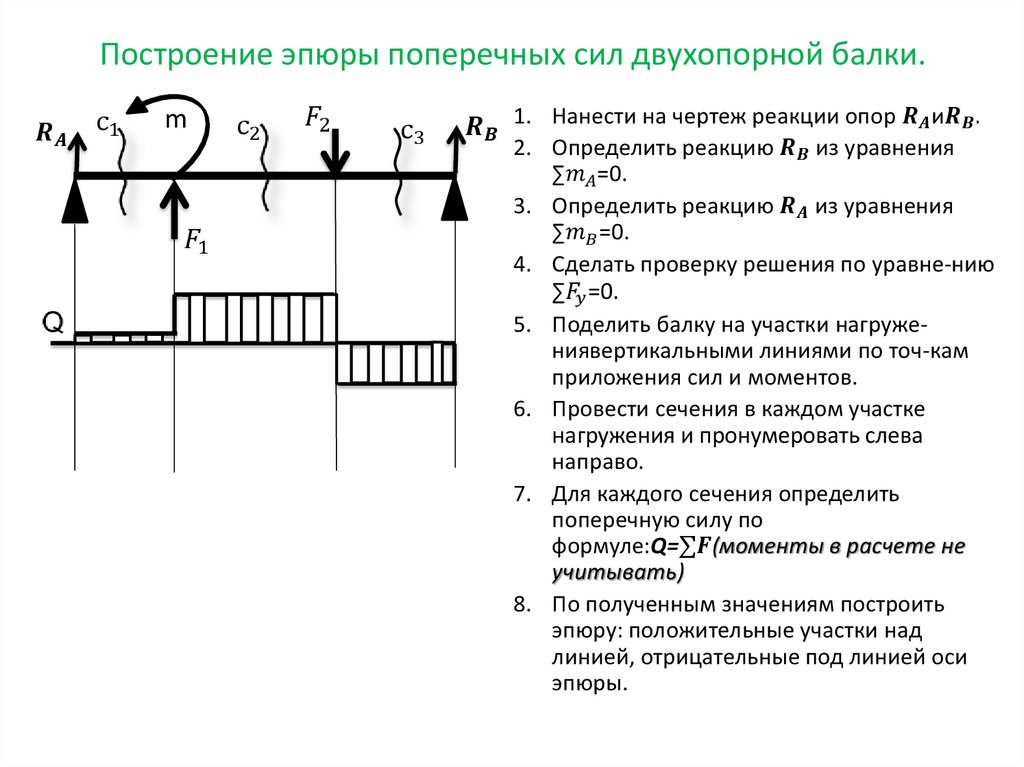

В вопросе нам дано, что сила равна 100 Н. Так как блоки соединены нитью, они будут ускоряться с одинаковой скоростью, и мы можем рассматривать их как систему, которая движется так, как если бы она была единым целым. предмет общей массой 80 кг (30 кг плюс 50 кг). Используйте второй закон Ньютона:

В этой задаче две силы натяжения образуют пару действие/противодействие и поэтому равны по величине, но противоположны по направлению (третий закон Ньютона). Итак:

Мы можем найти ускорение, так как напряжения сокращаются.

Теперь, когда у нас есть ускорение, нам нужно написать новое уравнение, в котором сила натяжения не компенсируется, чтобы мы могли найти натяжение.

Сделайте это, снова используя второй закон Ньютона, за исключением только одного из блоков:

Рассмотрим 30-килограммовый блок. Единственная сила, действующая на 30-килограммовый блок, — это натяжение, а ускорение — это то, что мы нашли выше.

Сообщить об ошибке

Мяч с массой находится на рампе, как показано ниже:

Найдите величину нормальной силы мяча.

Возможные ответы:

Правильный ответ:

Объяснение:

Нормальная сила перпендикулярна плоскости:

Во-первых, нам нужно найти.

Мы можем найти с помощью тригонометрического уравнения, применимого в данном случае. Мы знаем длину стороны, противоположной (5 м), и длину стороны, прилегающей к (10 м), поэтому мы можем использовать следующее уравнение для решения :

Подставляя длины сторон данного треугольника, мы можем найти .

Обратите внимание, что нормальная сила является одной из сторон другого прямоугольного треугольника. Другой катет — это параллельная сила, а гипотенуза — это сила тяжести.

Используя тригонометрию, мы знаем, что

, потому что , или, с точки зрения этой задачи, .

Подставляя известные значения в это уравнение, мы можем найти нормальную силу:

Сообщить об ошибке

Каково ускорение блока выше, если его масса и коэффициент кинетического трения ?

Возможные ответы:

Недостаточно информации

Правильно ответ:

Объяснение:

Составляющая перпендикуляра к уклону равна , где это угол между землей и уклоном.

где – нормальная сила.

Сила трения, действующая в направлении, противоположном движению, составляет:

— коэффициент кинетического трения.

Составляющая, параллельная уклону:

Чистая сила на блоке:

90 005

Сообщить об ошибке

Масса подвешена на двух кабели. Какова величина натяжения левого троса?

Возможные ответы:

Правильный ответ:

Объяснение:

Начните с построения диаграммы сил, действующих на массу в задаче:

Масса сама создает силу тяжести, направленную вниз:

Чтобы масса оставалась неподвижной, силы должны находиться в равновесии. Следовательно, сумма сил в направлениях x и y должна быть равна нулю:

Натяжения x и y можно записать в терминах величины натяжения каждого троса. Начните с направления x:

Поскольку угол одинаков для всех, натяжение в каждом углу должно быть эквивалентным. Используйте это свойство при выполнении баланса сил в направлении Y:

Сообщить об ошибке кабели. Какова величина натяжения в правом кабеле?

Возможные ответы:

Правильный ответ:

Объяснение:

Начните с рисования силовой диаграммы сил, действующих на массу:

Масса сама создает силу гравитации, направленную вниз.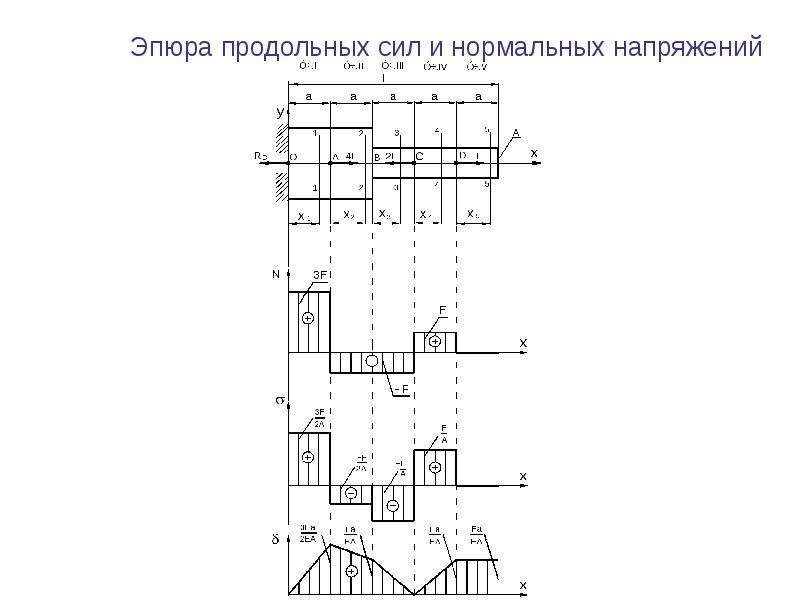

Чтобы масса оставалась неподвижной, силы должны быть в равновесии. Следовательно, сумма сил в направлениях x и y должна быть равна нулю:

Натяжения x и y можно записать в терминах величины натяжения каждого троса. Начните с направления x:

Поскольку угол одинаков для всех, натяжение в каждом углу должно быть эквивалентным. Используйте это свойство при выполнении балансировки сил в направлении Y:

Сообщить об ошибке 9 0005

Груз массой 50 кг поддерживается двумя тросами. Найдите величину натяжения левого троса.

Возможные ответы:

Правильный ответ:

Пояснение:

Начните с построения диаграммы сил, действующих на массу:

Масса сама создает силу гравитации, направленную вниз.

Натяжения x и y можно записать в терминах величины натяжения каждого троса. Начните с направления x:

Поскольку угол одинаков для всех, натяжение в каждом углу должно быть эквивалентным. Используйте это свойство при выполнении баланса сил в направлении y:

Сообщить об ошибке

Что из следующего верно, когда объект достигает терминала скорость?

Возможные ответы:

Правильный ответ:

Объяснение:

При предельной скорости:

Таким образом, по второму закону Ньютона:

Сообщить об ошибке

Масса движется вниз по наклонной плоскости угла с постоянной скоростью, как показано ниже. Коэффициент трения между бруском и наклонной плоскостью определяется выражением .

Каково значение с точки зрения , , , и ?

Возможные ответы:

Правильный ответ:

Объяснение:

Схема свободного тела блока приведена выше. На этот брусок действуют три силы. Во-первых, это вес под действием силы тяжести, который задается как . Во-вторых, нормальная сила плоскости, которая задается как . В-третьих, сила трения, действующая против направления его движения и определяемая как . Мы выбираем систему координат так, чтобы наша ось x совпадала с движением блока вниз по плоскости, а ось y совпадала с направлением нормальной силы. Таким образом, сила трения направлена в отрицательном направлении оси x, а нормальная сила выровнена с положительным направлением оси y. Однако вес не направлен ни по одной из этих осей, поэтому мы разделяем силу на ее компоненты, вдоль отрицательной оси y и вдоль положительной оси x.