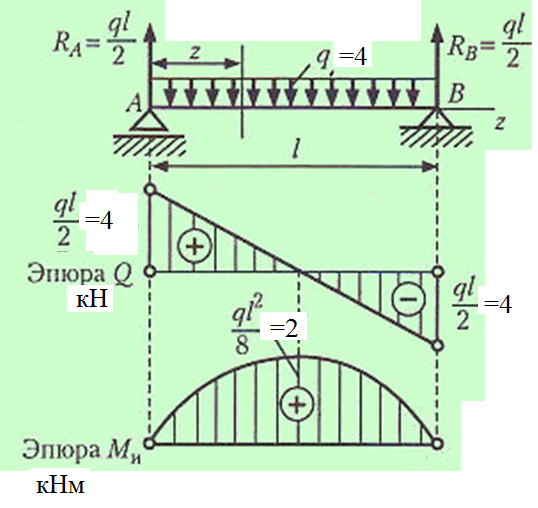
Задача на построение эпюр Q и M в балке

Для балки определить  опорные реакции и построить эпюры изгибающих моментов (М) и поперечных сил (Q).

1. Обозначаем опоры буквами А и В и направляем опорные реакции R_А и R_В.

Составляем уравнения равновесия.

Проверка

Записываем значения R_А и R_В на расчетную схему.

2. Построение эпюры поперечных сил методом сечений. Сечения расставляем на характерных участках (между изменениями). По размерной нитке – 4 участка, 4 сечения.

сеч. 1-1   ход слева.

Сечение проходит по участку с

равномерно распределенной нагрузкой, отмечаем размер z₁ влево от сечения до начала участка. Длина участка 2 м. Правило знаков для Q — см. здесь.

Строим по найденным значением эпюру Q.

сеч. 2-2   ход справа.

Сечение вновь проходит по участку равномерно распределенной нагрузкой, отмечаем размер z₂  вправо от сечения до начала участка. Длина участка 6 м.

Строим эпюру Q.

сеч. 3-3   ход справа.

сеч. 4-4   ход справа.

Строим эпюру Q.

3. Построение эпюры М методом характерных точек.

Характерная точка – точка, сколь-либо заметная на балке. Это точки

А, В, С, D, а также точка К, в которой Q=0 и изгибающий момент имеет экстремум.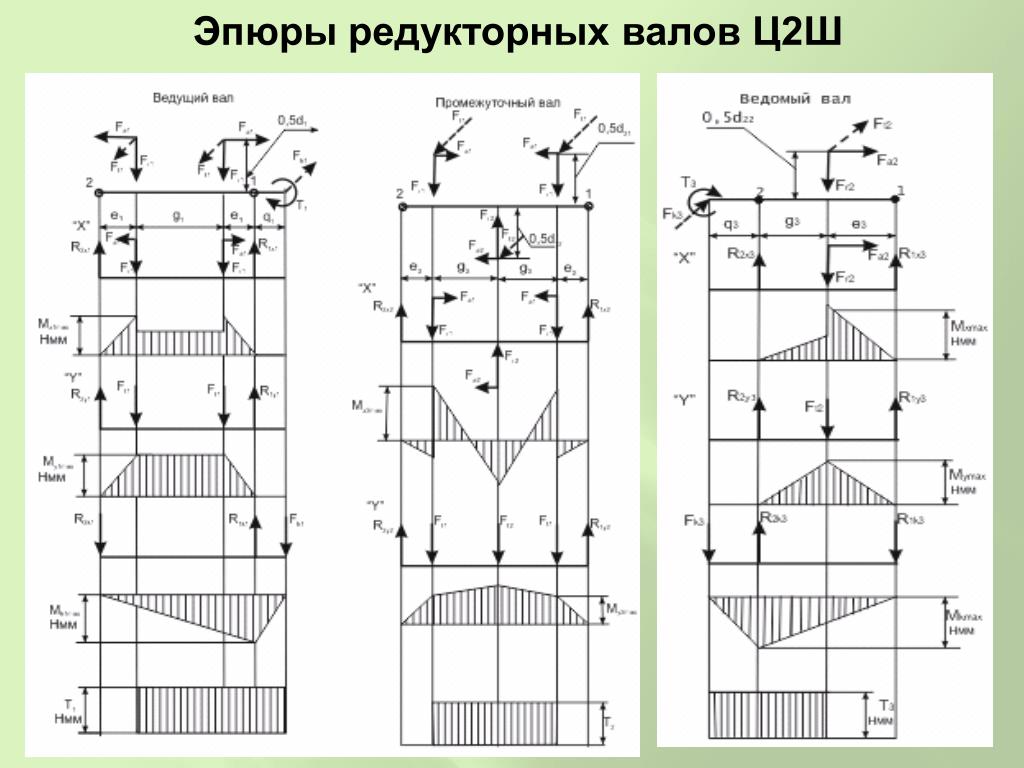 Также в середине консоли поставим дополнительную точку Е, поскольку на этом участке под равномерно распределенной нагрузкой эпюра М описывается кривой линией, а она строится, как минимум, по 3 точкам.

Итак, точки расставлены, приступаем к определению в них  значений изгибающих моментов. Правило знаков — см. здесь.

Участки NA, AD – параболическая кривая (правило «зонтика» у механических специальностей или «правило паруса» у строительных ), участки

DС, СВ – прямые наклонные линии.

Момент в точке D следует определять как слева, так и справа от точки D. Сам момент в эти выражения не входит. В точке D получим два значения с разницей на величину m – скачок на его величину.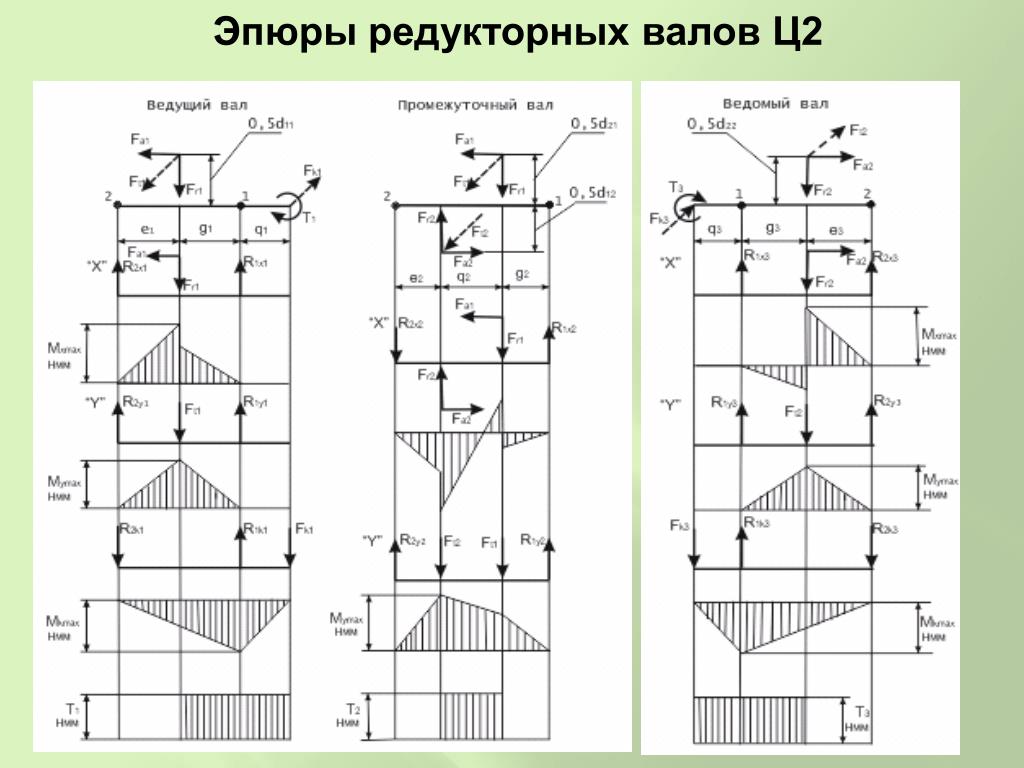

Теперь следует определить момент в точке К (Q=0). Однако сначала определим положение точки К, обозначив расстояние от нее до начала участка неизвестным х.

Т. К принадлежит второму характерному участку, его уравнение для поперечной силы (см. выше)

Но поперечная сила в т. К равна 0, а z₂ равняется неизвестному х.

Получаем уравнение:

Теперь, зная х, определим  момент в точке К с правой стороны.

Строим эпюру М. Построение выполним для механических специальностей, откладывая положительные значения вверх от нулевой линии и используя правило «зонтика».

Пример построения эпюры Q по эпюре М

Признаки правильного вида эпюры Q

1. На прямом элементе без нагрузки по его длине поперечная сила постоянна и эпюра Q имеет прямоугольную форму.

2.В сечении, которое совпадает с действующей поперек оси стержня сосредоточенной силой, ординаты эпюры Q слева и справа от силы имеют скачок, равный величине этой силы.

3.На участке с равномерно распределенной нагрузкой эпюра Q прямолинейна и имеет наклон к оси стержня (рис. 3.11, 3), тангенс угла которого равен интенсивности нагрузки q = dQ / dx =tg β . Нулевому значению

на эпюре Q на участке с равномерно распределенной нагрузкой соответствует экстремальное значение на эпюре M .

Для построения эпюры Q на прямолинейном элементе при отсутствии на нем нагрузки и при действии по его длине равномерно распределенной нагрузки достаточно иметь соответственно одну и две ординаты по концам элемента.

В программе SCAD поперечные силы на КЭ вычисляются минимум в двух концевых сечениях. Поэтому информации для построения эпюры Q достаточно.

Однако иногда у расчетчика возникает необходимость построения эпюры Q по эпюре M вручную. Для этого можно использовать уравнение Q =dM / dx .

Отсюда следует, что на любом КЭ стержня с прямолинейной эпюрой M величина Q будет постоянной и значение Q и знак определятся из выражения (3.2).

Полагая, что на участках прямолинейных эпюр M , приведенных на рис. 3.1, местная система координат направлена так, как показано на рис. 3.2, 3.3. В соответствии с этим поставлены знаки ординат эпюр M . Тогда по формуле (3.2) получим те же величины Q, которые были получены на рис. 3.11 первым способом.

При построении эпюры Q на участках с равномерно распределенной нагрузкой

используют формулу (3.3), полученную по аналогии с формулой (3.1) на основе принципа независимости действия сил.

Поперечные силы Qн,к по этой формуле определяют для крайних сечений элемента (в

узлах «н» и «к» МСК) как сумму ординат Qo	= ±ql / 2 эпюры Qo	для балки, загруженной
н,к
равномерно распределенной нагрузкой (рис. 3.12,а), и ординат		Qн,к(лом) = (M к − M н) / l ,
вызванной опорными моментами M н и Mк, действующими		по концам элемента

(рис. 3.12, б, г):
Q	= ± ql	+ M к −M н .	(3.3)
н,к	2	l

Обратим внимание, что первое слагаемое при нагрузке направленной «вниз» всегда имеет один и тот же вид (см. 3.12,а). Второе слагаемое дает эпюру с постоянными

53

ординатами на всем элементе, но знак этого слагаемого зависит от знаков моментов по концам КЭ. На рис. 3.12,б, г показаны варианты с положительным и отрицательным знаками

второго слагаемого. При этом изменяются суммарные ординаты, сдвигая нулевую ординату суммарной эпюры Q «вправо» при положительном втором слагаемом и «влево» – при

отрицательном (рис. 3.12,в,д).

Пример. Вычислим по формуле (3.3) ординаты эпюры Q на участке с равномерно

54

распределенной нагрузкой на рис. 3.11, позиция 3. При назначенной МСК (см. рис. 3.4, 3.5) M н = −ql 2 / 2 , M к = 0 . Тогда по формуле (3.3) получаем

Qн,к =±ql		ql	.
	+( ql ) =
2	2	0

Результат совпадает с простым определением ординат (см. рис. 3.11, позиция 3).

(3.4)

Qн,к первым способом

3.3. Эпюра продольных сил N

Процедура построения ординат эпюры N

Для построения ординаты эпюры N в каком – либо сечении необходимо:

1.Одним из приведенных ниже способов определить численное значение

продольной силы в сечении и ее знак.

2.Отложить найденное численное значение N в виде ординаты перпендикулярно оси стержня с одной из сторон стержня в соответствии со знаком N .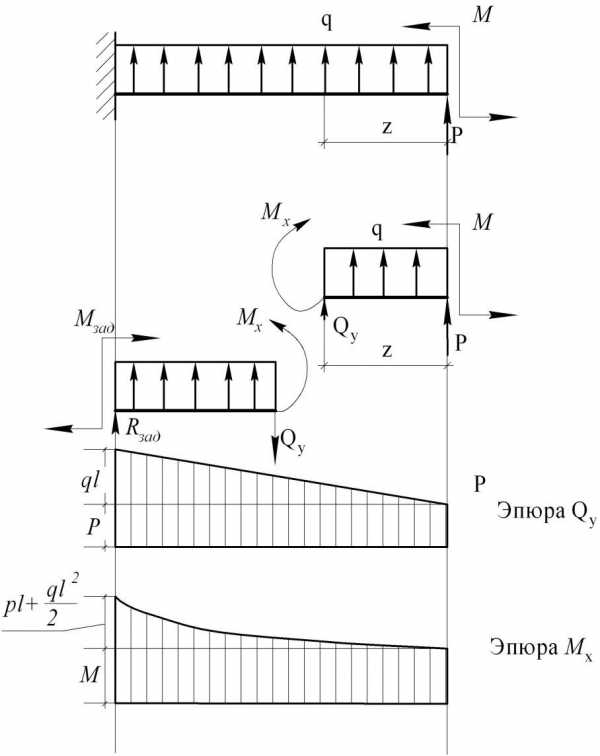

Способ 1. Определение продольной силы в сечении стержня из уравнения равновесия части стержня

слева или справа от сечения Численное значение продольной силы в любом сечении стержня равно

численному значению алгебраической суммы проекций всех внешних сил, действующих на стержневую систему с любой одной из сторон сечения, на касательную к оси стержня.

Растягивающая продольная сила в сечении стержня считается положительной, сжимающая – отрицательной (рис. 3.13).

55

Иными словами, способ 1 состоит в определении N из уравнения

	слева	справа
равновесия	вида ∑Pк,i	= 0 (или ∑Pк,i = 0), где Pк,i – проекция силы с
	i	i
номером i	(i =1, 2,…np )	слева (или справа) от сечения на касательную к оси

стержня со своим знаком по отношению к рассматриваемому поперечному сечению стержня.

Эпюры N для нагрузок, изображенных на рис. 3.1 и 3.11, ординаты которых вычислены этим способом, приведены на рис. 3.14.

Способ 2. Определение продольной силы в сечении стержня из рассмотрения равновесия узлов стержневой системы

Для иллюстрации второго способа рассмотрим узел C на рис. 3.1, позиция 2. Вырежем узел и рассмотрим его равновесие под действием поперечных и продольных сил. Векторы поперечных сил, действующие на узел, найдем по правилу «тупого узла» (рис. 3.15). Продольные силы в двух разрезанных стержнях (с номерами s и r) определятся из двух уравнений равновесия вида ∑ X = 0; ∑Z = 0 .

Рассмотрим теперь некоторый узел с двумя наклонными по отношению друг к другу стержнями (рис. 3.16). Предположим, что поперечные силы,

56

Понимание графиков Q-Q | Библиотека Университета Вирджинии Research Data Services + Sciences

График Q-Q, или график квантилей-квантилей, представляет собой графический инструмент, помогающий нам оценить, правдоподобно ли получен набор данных из некоторого теоретического распределения, такого как нормальное или экспоненциальное. Например, если мы проводим статистический анализ, который предполагает, что наши остатки нормально распределены, мы можем использовать график нормального Q-Q, чтобы проверить это предположение. Это просто визуальная проверка, а не герметичное доказательство, так что это несколько субъективно. Но это позволяет нам сразу увидеть, правдоподобно ли наше предположение, а если нет, то как оно нарушается и какие точки данных способствуют нарушению.

Диаграмма Q-Q — это диаграмма рассеяния, созданная путем сопоставления двух наборов квантилей друг с другом. Если оба набора квантилей взяты из одного и того же распределения, мы должны увидеть точки, образующие примерно прямую линию. Вот пример нормального графика Q-Q, когда оба набора квантилей действительно взяты из нормального распределения.

Что такое «квантили»? Их часто называют «перцентилями». Это точки в ваших данных, ниже которых падает определенная часть ваших данных. Например, представьте себе стандартное нормальное распределение классической колоколообразной кривой со средним значением 0.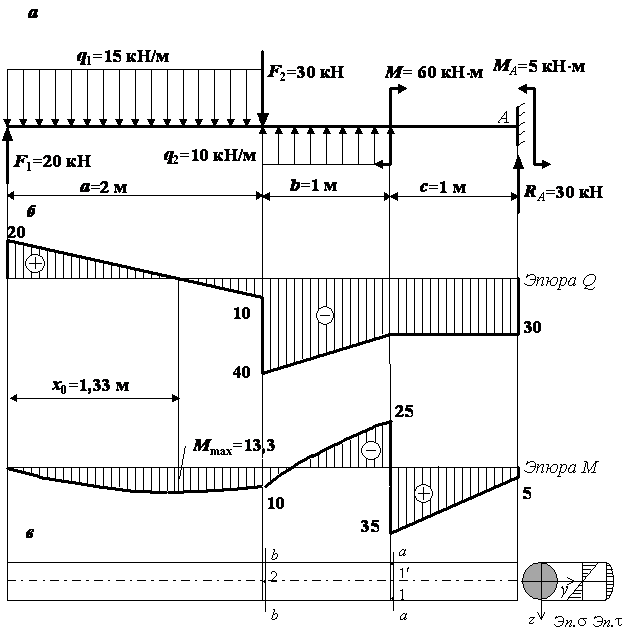 Квантиль 0,5, или 50-й процентиль, равен 0. Половина данных лежит ниже 0. Это пик горба на кривой. 0,95-й квантиль, или 95-й процентиль, составляет около 1,64. 95 процентов данных лежат ниже 1,64. Следующий код R генерирует квантили для стандартного нормального распределения от 0,01 до 0,99 с шагом 0,01:

qнорма (последовательность (0,01, 0,99, 0,01))

 

Мы также можем случайным образом сгенерировать данные из стандартного нормального распределения, а затем найти квантили. Здесь мы генерируем выборку размером 200 и находим квантили от 0,01 до 0,99, используя функцию квантиля :

квантиль (rнорма (200), вероятность = последовательность (0,01, 0,99, 0,01))

 

Таким образом, мы видим, что квантили — это просто ваши данные, отсортированные в порядке возрастания, с различными точками данных, помеченными как точки, ниже которых падает определенная часть данных. Однако стоит отметить, что существует множество способов расчета квантилей. На самом деле функция квантилей в R предлагает 9 различных алгоритмов квантилей! См. справку (квантиль) для получения дополнительной информации.

Графики Q-Q берут ваши выборочные данные, сортируют их в порядке возрастания, а затем строят их в зависимости от квантилей, рассчитанных на основе теоретического распределения. Количество квантилей выбирается в соответствии с размером ваших выборочных данных. В то время как нормальные графики Q-Q чаще всего используются на практике из-за большого количества статистических методов, предполагающих нормальность, графики Q-Q фактически могут быть созданы для любого распределения.

В R есть две функции для создания графиков Q-Q: qqnorm и qqplot .

qqnorm создает нормальный график Q-Q. Вы даете ему вектор данных, и R строит данные в отсортированном порядке по сравнению с квантилями из стандартного нормального распределения. Например, рассмотрим набор данных деревьев , поставляемый с R.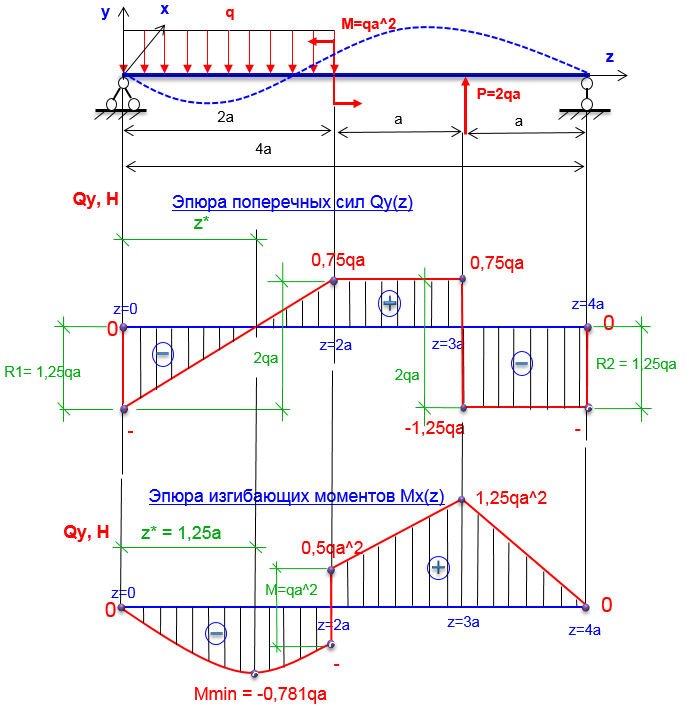 Он обеспечивает измерения обхвата, высоты и объема древесины на 31 срубленном дереве черной вишни. Одна из переменных — Высота . Можем ли мы предположить, что наша выборка высот происходит из населения с нормальным распределением?

qqnorm (деревья $ Высота)

 

Это кажется довольно надежным предположением. Кажется, что точки падают около прямой линии. Обратите внимание, что по оси x отложены теоретические квантили. Это квантили стандартного нормального распределения со средним значением 0 и стандартным отклонением 1.

Функция qqplot позволяет построить график Q-Q для любого распределения. В отличие от функции qqnorm , вы должны предоставить два аргумента: первый набор данных и второй набор данных. Смотрим на randu данные, которые поставляются с R. Это кадр данных, который содержит 3 столбца случайных чисел на интервале (0,1). Случайные числа должны быть распределены равномерно. Поэтому мы можем проверить это предположение, создав график Q-Q отсортированных случайных чисел по сравнению с квантилями из теоретического равномерного (0,1) распределения. Здесь мы создаем график Q-Q для номеров первого столбца, который называется x :

.
y <- qunif(ppoints(длина(randu$x)))
qqplot(randu$x,y)

 

Функция точек генерирует заданное количество вероятностей или пропорций. Мне нужно было такое же количество значений в randu$x , поэтому я дал ему аргумент length(randu$x) , который возвращает 400. Затем функция qunif возвращает 400 квантилей из равномерного распределения для 400 пропорций. . Я сохраняю это в y , а затем строю y против randu$x в функции qqplot . Опять же, мы видим точки, расположенные вдоль прямой линии на графике Q-Q, что является убедительным доказательством того, что эти числа действительно получены из равномерного распределения.

Что делать, если точки не лежат на прямой? Что мы можем сказать о наших данных? Чтобы помочь нам ответить на этот вопрос, давайте сгенерируем данные из одного распределения и построим график относительно квантилей другого. Сначала мы строим распределение с перекосом вправо, распределение хи-квадрат с 3 степенями свободы, в сравнении с нормальным распределением.

qqplot(qnorm(ppoints(30)), qchisq(ppoints(30),df=3))

 

Обратите внимание, что точки образуют кривую, а не прямую линию. Нормальные графики Q-Q, которые выглядят так, обычно означают, что ваши данные выборки искажены.

Затем мы строим распределение с «тяжелыми хвостами» по сравнению с нормальным распределением:

qqplot(qnorm(ppoints(30)), qcauchy(ppoints(30)))

 

Обратите внимание, что точки ложатся вдоль линии в середине графика, но изгибаются на концах. Нормальные графики Q-Q, демонстрирующие такое поведение, обычно означают, что ваши данные имеют более экстремальные значения, чем можно было бы ожидать, если бы они действительно исходили из нормального распределения.

С вопросами или разъяснениями относительно этой статьи обращайтесь в StatLab библиотеки UVA: statlab@virginia. edu

Просмотреть всю коллекцию статей StatLab библиотеки UVA.

Клэй Форд
Консультант по статистическим исследованиям
Библиотека Университета Вирджинии
26 августа 2015 г.

Объяснение графиков Q-Q. Исследуйте возможности графиков Q-Q. | Парас Варшней

«Понимание концепции графиков Q-Q»

Источник: Image Link

В статистике графики Q-Q (квантиль-квантиль) играют очень важную роль для графического анализа и сравнения двух вероятностных распределений путем построения их квантилей относительно каждого другой. Если два распределения, которые мы сравниваем, точно равны, то точки на графике Q-Q будут точно лежать на прямой линии y = x.

«Нарисуй график, нарисуй линию, скажи мне, все ли в порядке!» — Джош Стармер

Да, это так просто. Будучи специалистом по данным или вообще статистиком, вам очень важно знать, является ли распределение нормальным или нет, чтобы применять различные статистические меры к данным и интерпретировать их в гораздо более понятной для человека визуализации, и здесь появляется график Q-Q.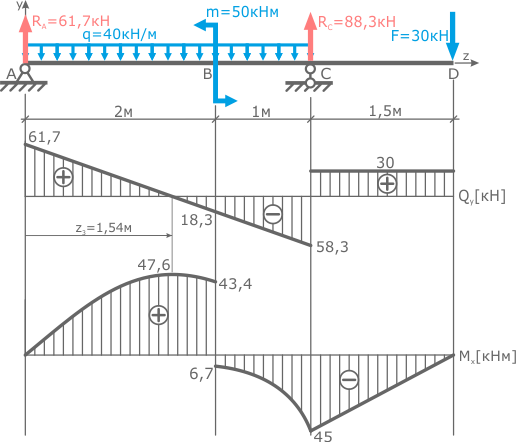 изображение. Самый фундаментальный вопрос, на который отвечает график Q-Q:

Является ли эта кривая нормально распределенной?

Источник: Википедия График Q-Q для нормального распределения

Нормально распределенный, но почему?

Графики Q-Q используются для определения типа распределения случайной величины, будь то распределение Гаусса, равномерное распределение, экспоненциальное распределение или даже распределение Парето и т. д. Вы можете определить тип распределения, используя мощность графика Q-Q, просто глядя на сюжет. В общем, речь идет о нормальных распределениях только потому, что у нас есть очень красивая концепция правила , которое идеально вписывается в нормальное распределение. Итак, мы знаем, какая часть данных лежит в диапазоне первого стандартного отклонения, второго стандартного отклонения и третьего стандартного отклонения. отклонение от среднего. Таким образом, знание того, является ли распределение нормальным, открывает для нас новые возможности, позволяющие легко экспериментировать с данными. Во-вторых, нормальное распределение очень часто встречается в большинстве природных явлений, имеющих обширный масштаб.

Как это работает?

Мы наносим теоретические квантили или в основном известные как стандартная нормальная переменная (нормальное распределение со средним значением = 0 и стандартным отклонением = 1) на оси X и упорядоченные значения для случайной величины, которую мы хотим найти, является ли она Гауссово распределение или нет, по оси Y. Что дает очень красивую и гладкую структуру, подобную прямой линии, из каждой точки, нанесенной на график.

Теперь нам нужно сосредоточиться на концах прямой линии. Если точки на концах кривой, образованной из точек, не падают на прямую линию, а действительно значительно разбросаны по позициям, то мы не можем заключить связь между осями x и y, которая ясно означает, что наши упорядоченные значения, которые мы хотели для расчета не являются нормально распределенными.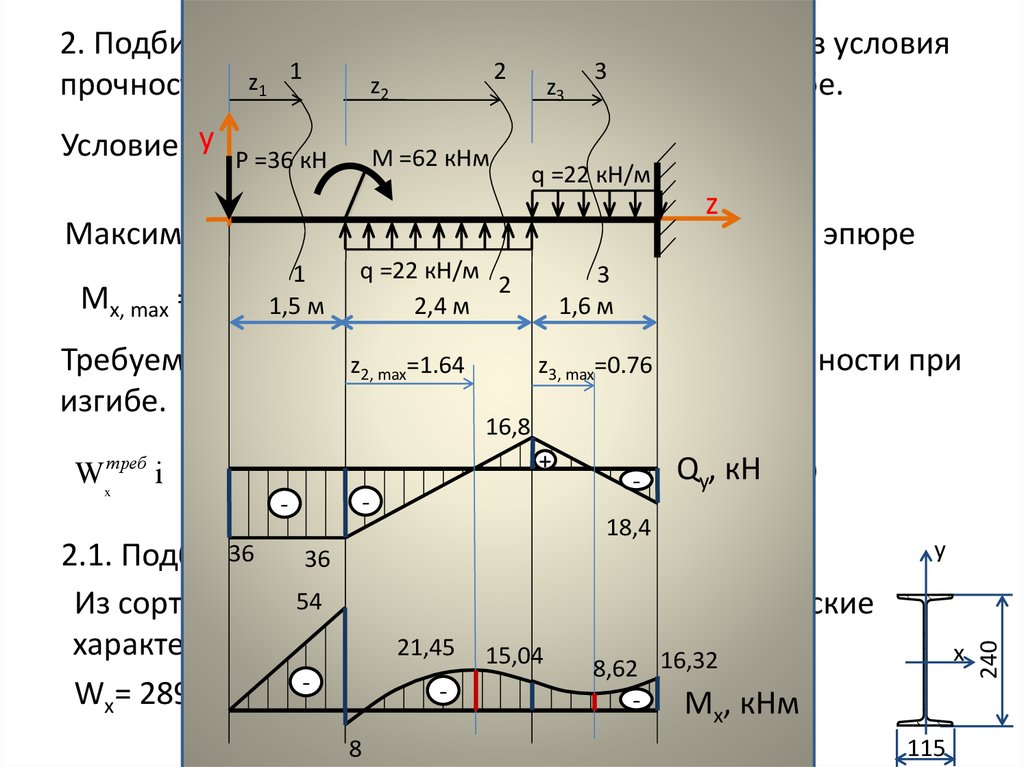

Если все точки, нанесенные на график, точно лежат на прямой линии, то мы можем четко сказать, что это распределение является нормальным, поскольку оно равномерно выровнено со стандартной нормальной переменной, которая является простой концепцией графика Q-Q.

Источник: примеры графика Sherrytowers Q-Q

Перекошенные графики Q-Q

Графики Q-Q также используются для нахождения асимметрии (мера « асимметрии ») распределения. Когда мы откладываем теоретические квантили по оси x и выборочные квантили, распределение которых мы хотим знать, по оси y, мы видим очень своеобразную форму нормально распределенного графика Q-Q для асимметрии. Если нижний конец графика Q-Q отклоняется от прямой линии, а верхний — нет, то мы можем ясно сказать, что распределение имеет более длинный хвост слева от него или просто смещен влево (или смещен отрицательно ), но когда мы видим, что верхний конец графика Q-Q отклоняется от прямой линии, а нижний и следует прямой линии, тогда кривая имеет более длинную до правую сторону и это 90 125 с перекосом вправо 90 126 (или 90 125 90 148 с перекосом в положительную сторону 90 149 90 126 ).

График Q-Q с левым перекосом для нормального распределения График Q-Q с перекосом вправо для нормального распределения

График Q-Q с хвостом

Точно так же мы можем говорить о эксцессе (мера « Хвостатость ») распределения, просто взглянув на его график Q-Q. Распределение с толстым хвостом будет иметь оба конца графика Q-Q, чтобы отклониться от прямой линии, а его центр следует прямой линии, тогда как распределение с тонким хвостом будет формировать график Q-Q с очень меньшим или незначительным отклонением на концах. таким образом, он идеально подходит для нормального распределения.

График Q-Q с толстым хвостом для нормального распределения График Q-Q с тонким хвостом для нормального распределения

Сколько данных нам нужно?

Обратите внимание, что когда количество точек данных значительно меньше, график Q-Q работает не очень точно и не дает окончательного ответа, но когда у нас есть достаточное количество точек данных, а затем мы строим график Q-Q, используя большой набор данных, тогда он дает нам значительный результат, чтобы сделать вывод о любом результате о типе распределения.

Реализация графиков Q-Q в Python

Вот простая реализация построения графика Q-Q в Python.

Реализация графика QQ с использованием statsmodels API

Другая реализация графика QQ с использованием библиотеки Scipy.

Реализация графика Q-Q с использованием script.statsSource: StackExchange Output Q-Q Plot

Узнайте больше о графиках Q-Q

Я определенно рекомендую вам посетить страницу Википедии с графиком Q-Q, на которой есть очень красивое объяснение полной концепции математической работы. позади него, что было бы довольно подавляющим в этой вводной статье. Кроме того, посмотрите видео Джоша Стармера на YouTube, которое наглядно демонстрирует концепцию.

Другие статьи Параса Варшни о науке о данных:

Как оценить производительность модели машинного обучения в Python?

Практический подход к вычислению производительности модели и реализации в Python, охватывающий все математические…

medium.com

Как создать портфолио по науке о данных, которое поможет вам получить работу?

Научитесь создавать сильное портфолио, которое говорит о вас!

medium.