Эпюры Q и М для горизонтальных балок
В обоих случаях поперечная сила взята со знаком минус, потому что эпюра М — нисходящая (при движении слева направо). Следует также обратить внимание на следующую зависимость, вытекающую из формулы (VI.2). На тех участках балки, где изгибающий момент изменяется по параболе (кривая 2-го порядка), поперечная сила изменяется по линейному закону, т. е, эпюра — наклонная прямая (линия 1-го порядка). Там же, где М изменяется по линейному закону, т. е. эпюра М — наклонная прямая, поперечная сила Q постоянна, эпюра — горизонтальная прямая (линия нулевого порядка). Вообще, порядок функции, описывающей закон изменения Q, на единицу ниже порядка функции, выражающей закон изменения М. Это следует непосредственно из формулы (VI.2). [c.141]В сечении балки D, проведенном справа от нагрузки, Q = -j-2,0 — Р = = -+-2,0—4,0 = —2,0 Г это значение сохраняется и на участке DE (на эпюре горизонтальная прямая).
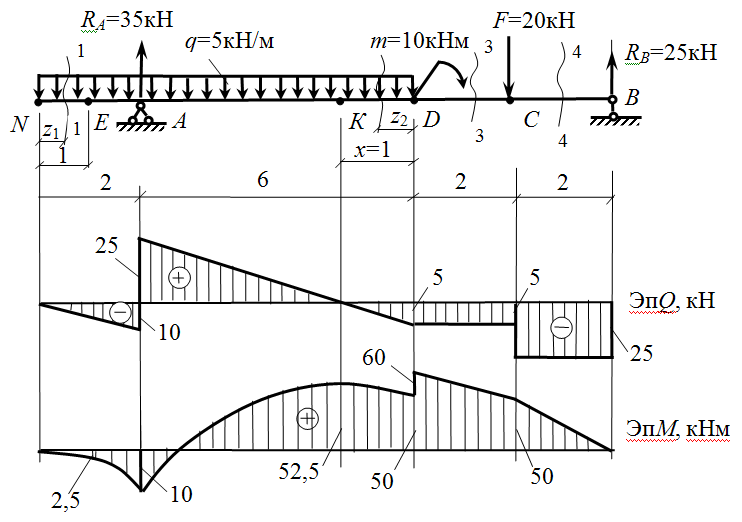
Когда статически неопределимая величина Н найдена, то полную эпюру моментов получают сложением эпюры простой балки СО и эпюры момента, вызванного горизонтальным распором Н. [c.164]
В дальнейшем при построении эпюр изгибающих моментов будем всегда ординаты этих эпюр откладывать в направлении выпуклой стороны бруса, или, как принято говорить, будем строить эпюру на растянутом волокне. Это удобно потому, что эпюра при этом показывает, в какую сторону выгибается брус в той или иной части. Для горизонтальной балки это означает, что положительные моменты откладываются вниз, отрицательные — вверх. [c.130]
Шарнирно-опертая по концам двутавровая балка наклонена под углом 60 к горизонтальной оси и нагружена сосредоточенной вертикальной силой Р = 40 кН, действующей в плоскости симметрии двутавра и приложенной к его полке (см. рисунок). Построить эпюру нормальных напряжений для опасного сечения балки, пренебрегая ее собственным весом.
При действии на балку распределенной нагрузки ее разбивают на части линиями, перпендикулярными геометрической оси балки. Площадь каждой части представляют вектором, приложенным в ее центре тяжести, С помощью этих векторов, как векторов сосредоточенных сил, строят и план сил, и веревочный многоугольник. Полученную полигональную эпюру УИ уточняют путем проведения кривой, вписанной в полигон, а ступенчатую эпюру Q — путем проведения кривой или прямой (в зависимости от порядка распределенной нагрузки), проходящей через точки горизонтальных отрезков ступенчатой эпюры, находящиеся против начала и конца каждой части площади распределенной нагрузки. [c.107]
Балка шарнирно закреплена на опоре А, конец В положен на катки. Сила Р=2 Т. Определить вертикальные и горизонтальные составляющие опорных реакций и построить эпюры усилий,
Построить эпюру касательных напряжений по сечению и вычислить с , и для балки тонкостенного уголкового профиля пролетом /=40 см, изгибаемой силой Р=2Ъ кГ, приложенной в центре изгиба сечения, в двух случаях 1) сила Ру=Р направлена вертикально и 2) сила направлена горизонтально.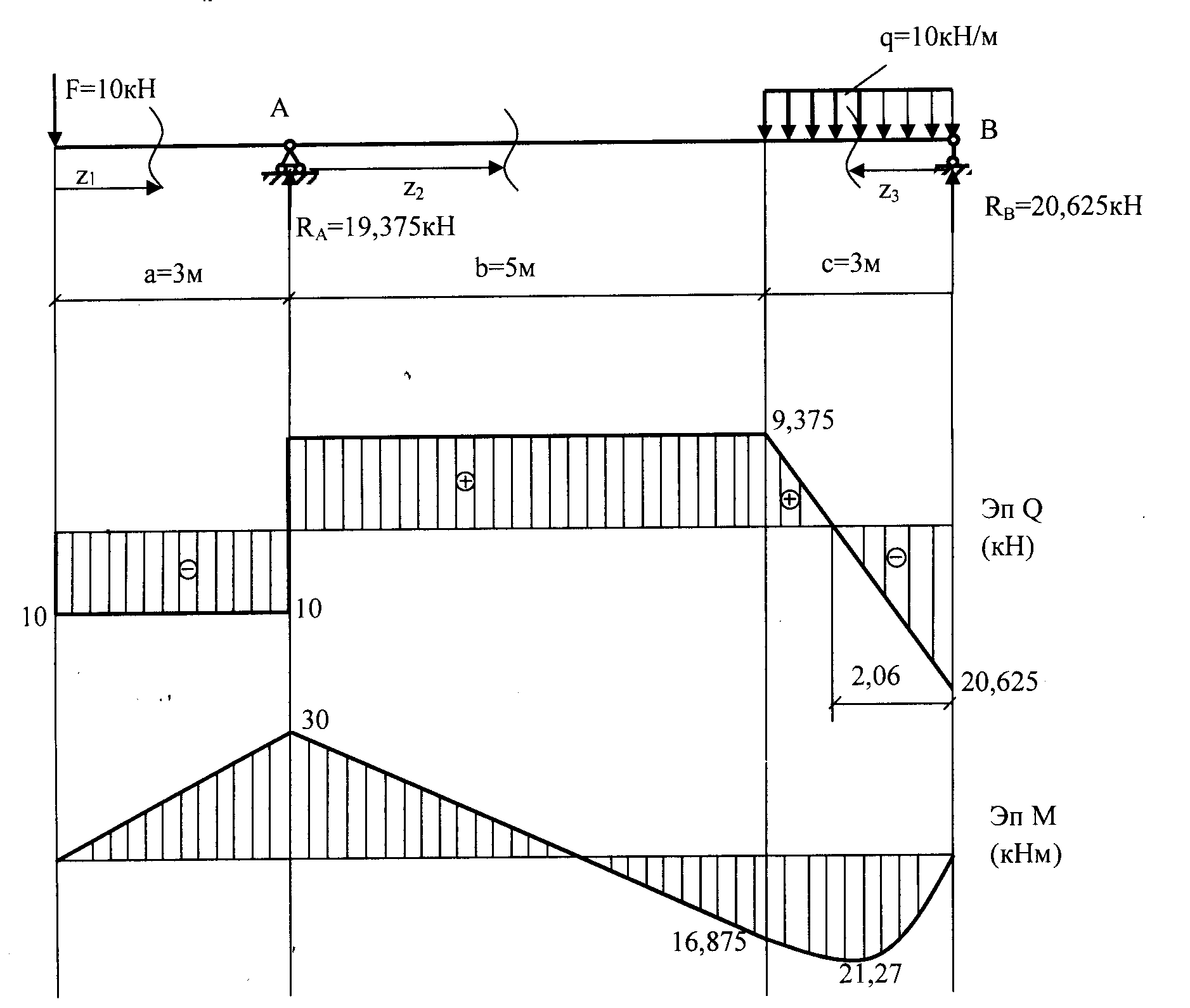 Размеры сечения 6=40 мм, t=2 мм. Указать положение центра изгиба.
[c.116]
Размеры сечения 6=40 мм, t=2 мм. Указать положение центра изгиба.
[c.116]
Ординаты, заключенные между пролетными эпюрами от нагрузки и осью, дают искомую окончательную спрямленную эпюру изгибающих моментов. На рис. 9.9, в суммарная эпюра изгибающих моментов с ординатами, отложенными от горизонтальной оси, заштрихована. При этом эпюра оказывается расположенной со стороны растянутого волокна, т. е. с выпуклой стороны балки. [c.263]
У левого конца балки и до опоры А Q = —2,0Ги эпюра ограничена горизонтальной прямой справа от опоры А Q = — 2 -j А = — 2- -6,8=- -4,8 7 на участке АВ, несущем сплошную равномерно распределенную нагрузку, эпюра Q ограничена наклонной прямой. [c.453]
Касательное напряжение в вертикальной стенке двутавровой балки убывает по мере приближения к горизонтальной полке (рис. 5.12, б). В самой полке плоскость, в которой действуют парные касательные напряжения, должна совпадать с плоскостью полки. Это становится особенно ясным, если вообразить, что толщина йз стремится к нулю. На рис. 5.12, а стрелками показано распределение векторов т по сечению. Соответствующие эпюры, изображающие зависимость величины напряжения от положения волокна, показаны на рис. 5.12, б.
Это становится особенно ясным, если вообразить, что толщина йз стремится к нулю. На рис. 5.12, а стрелками показано распределение векторов т по сечению. Соответствующие эпюры, изображающие зависимость величины напряжения от положения волокна, показаны на рис. 5.12, б.
Еще раз рассмотрим балку прямоугольного поперечного сечения (высоты h, ширины Ь) в условиях поперечного изгиба (рис. 10.2а). Здесь же снизу дана эпюра изгибающих моментов М = М(х). Выделим двумя поперечными сечениями участок балки длиной dx. Этот элемент показан отдельно рядом на рис. 10.2(5. Далее горизонтальным сечением выделим часть этого элемента (рис. 10.2в). Горизонтальное сечение с координатой у проведено выше нейтрального слоя. Эта отсеченная часть имеет высоту ( — г/). Действующие на эту часть усилия показаны схематически на рис. 10.3. По сечениям с равными площадями /4 = у) Ь действуют нормальные напряжения а ц (т + da (рис. 10.3). Приращение напряжения происходит потому, что изменяется изгибающий момент с М яо М + dM (см.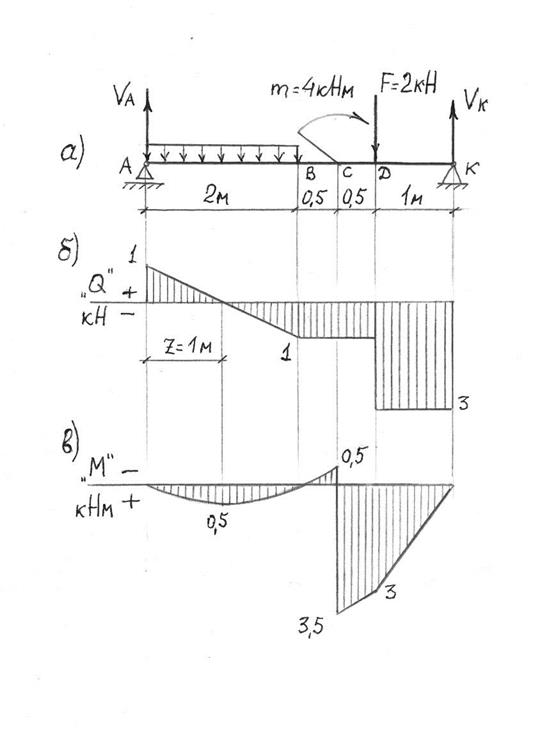 рис. 10.2а). Поэтому равнодействующая N + dN нормальных элементарных усилий (элементарных усилий а dA слева. Равновесие же элемента балки обеспечивается усилием dT (рис. 10.3), направленным направо и являющимся равнодействующим элементарных
[c.173]
рис. 10.2а). Поэтому равнодействующая N + dN нормальных элементарных усилий (элементарных усилий а dA слева. Равновесие же элемента балки обеспечивается усилием dT (рис. 10.3), направленным направо и являющимся равнодействующим элементарных
[c.173]
Результаты вычислений для балки-стенки высотой h = 21 приведены на рис. 29 в виде эпюр нормальных напряжений для двух вертикальных сечений (на опоре и посередине пролета) и нормальных напряжений а у для двух горизонтальных сечений. Нетрудно убедиться, что эти эпюры заметно отличаются от эпюр, получаемых в сопротивлении материалов. [c.84]
Строим эпюру изгибающих моментов в горизонтальной плоскости методом характерных точек. Для балки характерными точками (сечениями) являются точки А, С я В. Определим в этих сечениях значения изгибающих моментов в сечении А — [c.158]
Деревянная балка (рис. 308) изгибается силами Pi = 2 кн ( 200 /сГ) и P Pg=l KH ( 100 кГ). Требуется построить эпюры изгибающих моментов в вертикальной и горизонтальной плоскостях и подобрать прямоугольное сечение балки
 225]
225]
Деревянная балка нагружена, как показано на рис. 314. Для одного яз вариантов, приведенных в табл. 20 , требуется построить эпюры изгибающих моментов в вертикальной и горизонтальной плоскостях определить размеры поперечного [c.230]
В общем случае эпюра поперечных сил может пересекать горизонтальную ось в нескольких местах, и каждой такой точке пересечения на эпюре изгибающих моментов будет соответствовать максимум или минимум. Для того чтобы найти наибольшее по абсолютной величине значение изгибающего момента в балке, необходимо исследовать все эти максимумы или минимумы. [c.135]
Используя соотношения (1) — (о), можно без труда построить эпюры поперечных сил и изгибающих моментов. Эпюра поперечных сил (рис. 4.10, Ь) состоит из двух горизонтальных прямых, соответствующих ненагруженным участкам балки, и [c.137]
На рис. 6.15 показано, как определяются прогибы непризматических балок методом моментных площадей. На рис. 6.15, Ь приведена эпюра изгибающих моментов, а на рис. 6.15, с — эпюра М1(Е1). Площади и статические моменты различных участков эпюры М Е1) можно использовать для нахождения углов поворотов и прогибов. Например, найдем угол поворота на левой опоре и прогиб в середине пролета. В силу симметрии балки касательная к линии прогибов в центре балки С горизонтальна. Поэтому из первой теоремы о моментных площадях следует, что угол поворота 0 на левой опоре равен площади эпюры М1 Е1) на участке между точками Л и С. Таким образом, величина угла поворота определяется следующим выражением
[c.231]
На рис. 6.15, Ь приведена эпюра изгибающих моментов, а на рис. 6.15, с — эпюра М1(Е1). Площади и статические моменты различных участков эпюры М Е1) можно использовать для нахождения углов поворотов и прогибов. Например, найдем угол поворота на левой опоре и прогиб в середине пролета. В силу симметрии балки касательная к линии прогибов в центре балки С горизонтальна. Поэтому из первой теоремы о моментных площадях следует, что угол поворота 0 на левой опоре равен площади эпюры М1 Е1) на участке между точками Л и С. Таким образом, величина угла поворота определяется следующим выражением
[c.231]
Балка с любым направлением сосредоточенных сил, перпендикулярных к оси. Каждую силу раскладывают на составляющие в главных плоскостях балки (или в горизонтальной и вертикальной плоскостях V и Н) и вычерчивают для обеих групп сил отдельные эпюры
На фиг. 25, а показаны эпюры изгибающих моментов, поперечных и продольных сил для лома-НОЙ КОНСОЛИ. Усилия определяются последовательно, начиная от свободного конца. В раме на фиг. 25, б предварительно определяются реакции опор, как для прямой балки, являющейся горизонтальной проекцией данной рамы. На фиг. 25, в показаны
[c.150]
Усилия определяются последовательно, начиная от свободного конца. В раме на фиг. 25, б предварительно определяются реакции опор, как для прямой балки, являющейся горизонтальной проекцией данной рамы. На фиг. 25, в показаны
[c.150]
Итак, для построения эпюры. Q необходимо, перемещаясь вдоль балки слева направо, откладывать под каждой силой уступ в сторону этой силы по ее величине, проводить горизонтальную ступень на участке между силами и спускаться (или подниматься) по наклонной прямой указанного наклона под участком равномерно распределенной нагрузки. [c.136]
Результат, полученный для балки прямоугольного сечения, можно использовать для вычисления касательных напряжений в стенке двутавровой балки. Не останавливаясь на доказательствах, укажем, что в полках двутавровых балок возникают горизонтально направленные касательные напряжения а вертикальные %гу близки к нулю, при этом для вычисления последних формула Журавского неприменима.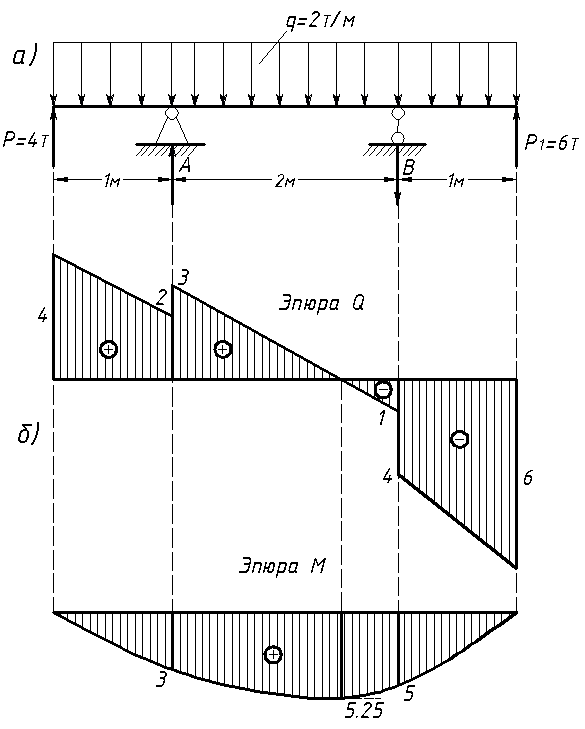 На рис. 7.52 показано направление касательных напряжений в полке и стенках двутаврового профиля и дана эпюра т в стенке I
[c.272]
На рис. 7.52 показано направление касательных напряжений в полке и стенках двутаврового профиля и дана эпюра т в стенке I
[c.272]
Балка с любы и направлением сосредоточенных сил. перпендикулярных оси. Каждую силу раскладывают на составляющие в главных плоскостях балки (или в горизонтальной и вертикальной плоскостях V л Н) к вычерчивают для обеих групп сил отдельные эпюры Q (х) и М х). Геометрическое сложение для отдельных сечений значений Q (х) и соответственно М (х) даёт полную величину поперечных сил и моментов для этих сечений (эпюры суммарных Q и УИ).
Рассмотрим действие сил в раме. На рис. 69, а построены эпюры моментов в статически определимой системе для случая А, а на рис. 70, а — для случая В. Значения свободных (грузовых) членов Дгр помещены в табл. 8 и 10. Найденные величины неизвестных приведены в табл. И. Окончательные эпюры моментов нанесены на рис. 69, б, в и на рис. 70, б, в. Эпюры моментов для случая В построены с учетом силы Xi.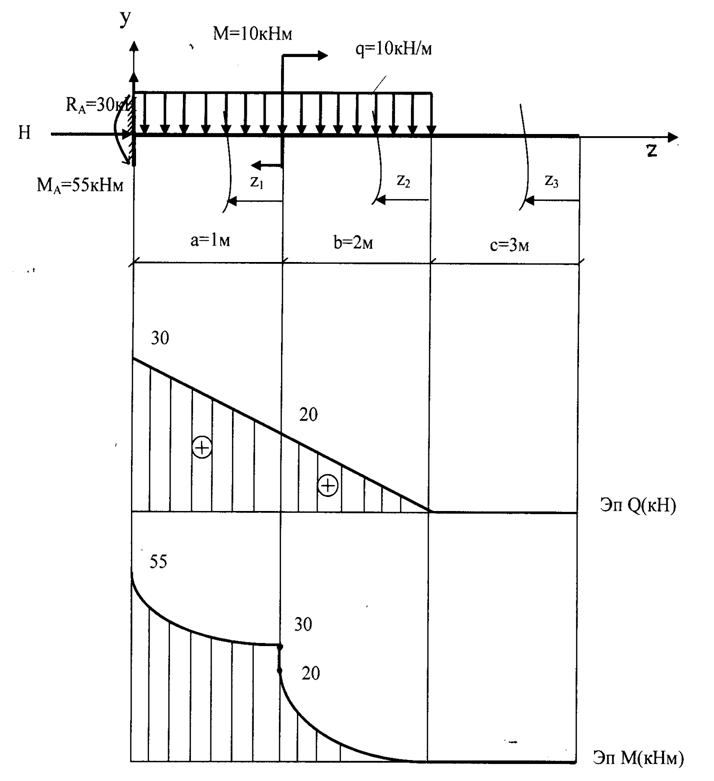 Как видим, в случае А изгибающие моменты в боковине в междурамном креплении в горизонтальной плоскости существенно меньше, чем в случае В. Это объясняется положительным влиянием концевой балки. Возникающая в ней сила Ki противодействует появлению больших моментов за счет привлечения к воспринятию сил в раме-в кривой второй боковины. В этом заключается положительная 108
[c.108]
Как видим, в случае А изгибающие моменты в боковине в междурамном креплении в горизонтальной плоскости существенно меньше, чем в случае В. Это объясняется положительным влиянием концевой балки. Возникающая в ней сила Ki противодействует появлению больших моментов за счет привлечения к воспринятию сил в раме-в кривой второй боковины. В этом заключается положительная 108
[c.108]
Проведём ось абсцисс и -построим эпюру моментов. Заменим эпюру М(х), как нагрузку qf, силами и построим силовой и веревочный многоугольники, не забывая о знаках фиктивных сил. Так как конец А защемлён, то ось абсцисс для балки АВ надо провести так, чтобы она коснулась верёвочного многоугольника под этим сечением, т. е. являлась бы продолжением первой стороны ось абсцисс для второй балки BD определится тем, что в точке С прогиб равен нулю, а в шарнире В обе балки имеют один и тот же прогиб поэтому ось абсцисс второй балки пройдет через точку с пересечения верёвочного многоугольника с вертикалью опоры С и через точку Ь — точку пересечения первой оси абсцисс с вертикалью шарнира В, В нижней части фяг, 310 ординаты прогибов отложены от общей горизонтальной оси абсцисс. [c.387]
[c.387]
Пользуясь эпюрой действительных изгибающих моментов так же, как и для случаев вала, получаем возможность определить необходимую длину горизонтальных листов балки. Определим значения а] для клёпаной балки, подробно разобранной в 98—102. Исходные данные берём из таблицы 21, Подсчёты ведём согласно таблице 21а. [c.394]
Определим опорные реакции и построим эпюру моментов для балки, находящейся (фиг. 356) под действием равномерно распределённой нагрузки q. Сначала изобразим все реакции, которые по устройству опор могут возникнуть в этой балке. Таких реакций может быть на опоре А три вертикальная А, горизонтальная На [c.434]
X в уравнение не входит, следовательно, поперечная сила — величина постоянная по длине левой половины балки. Проведем соответственную горизонтальную прямую и заштрихуем левую часть эпюры поперечных сил. [c.195]
Из всех рассмотренных примеров знаем, что в тех участках балки, где нет нагрузки, изгибающие моменты меняются по закону прямой, эпюра поперечных сил на таких участках, постоянна. Следовательно, для таких участков можно не делать промежуточных разрезов, а находить изгибающие моменты только на границах участков и вершины полученных ординат соединять прямыми. Эпюра поперечных сил на таких участках состоит из отрезков горизонтальных прямых. Изгибающий момент на границе первого участка в точке С найдем, разрезав балку через точку С
[c.211]
Следовательно, для таких участков можно не делать промежуточных разрезов, а находить изгибающие моменты только на границах участков и вершины полученных ординат соединять прямыми. Эпюра поперечных сил на таких участках состоит из отрезков горизонтальных прямых. Изгибающий момент на границе первого участка в точке С найдем, разрезав балку через точку С
[c.211]
Предположим, что материальная точка стремится двигаться по горизонтальной линии, на которой построена эпюра Q, начиная от точки, соответствующей левому концу балки, и кончая точкой, соответствующей правому (рис. 8.23, в). [c.213]
Построенную эпюру моментов можно для большей наглядности спрямить . Для этого проведем горизонтальную прямую и отложим от нее ординаты веревочного многоугольника для наиболее характерных точек положительные — вниз, отрицательные — вверх. Найденные точки соединим прямыми. Получим спрямленную эпюру моментов, т. е. построенную от горизонтальной линии (рис. 8.36, г). На левой половине балки АС, загруженной сплошной нагрузкой, можно ломаную линию заменить вписанной в нее кривой, т. е. немного скруглить вершины.
[c.229]
8.36, г). На левой половине балки АС, загруженной сплошной нагрузкой, можно ломаную линию заменить вписанной в нее кривой, т. е. немного скруглить вершины.
[c.229]
При графическом построении эпюр прогибов и углов наклона масштабы сил и длин, а также полюсное расстояние Н можно выбирать произвольно. Однако для удобства построения полюсное расстояние Н возьмем таким образом, чтобы крайние лучи силового многоугольника были наклонены под углом 45° к горизонтальной оси, тогда построения получаются достаточно четкими. Величины же прогибов и углов наклона в любом сечении определим по формулам (10.68). Для того чтобы построенная графически эпюра прогибов обладала большей наглядностью, необходимо, чтобы условие 1/=1/1 было выполнено, т. е. реальные прогибы балки в любом сечении должны быть численно равны соот-ветствуюш,им ординатам в построенной графически эпюре прогибов. Из этого условия находят полюсное расстояние Н [c.324]
Построим эпюру изгибающих моментов.
 Под балкой (рис. 11.46, г) проведем горизонтальную прямую и отложим вверх отрезки, численно равные опорным изгибающим моментам. Соединим концы пунктирной линией — получим эпюру опорных моментов. К наклонным прямым подвесим ранее построенные эпюры от внешней (пролетной) нагрузки.
[c.372]
Под балкой (рис. 11.46, г) проведем горизонтальную прямую и отложим вверх отрезки, численно равные опорным изгибающим моментам. Соединим концы пунктирной линией — получим эпюру опорных моментов. К наклонным прямым подвесим ранее построенные эпюры от внешней (пролетной) нагрузки.
[c.372]Правила знаков. Во всех задачах этой главы принято считать положительными ) реакции и нагрузки, направленные вверх и вправо б) моменты сил, нращаюш,ие по ходу часовой стрелки в) усилия в сечениях изгибающий момент М, вызывающий сжатие верхних и растяжение нижних волокон элемента горизонтальной балки поперечную силу Q, вызывающую поворот элемента балки по ходу часовой стрелки продольную силу Л/, вызывающую растяжение. Положительные ординаты эпюр усилий откладываются вверх (по оси j/) от горизонтальной оси балки. [c.292]
Изображаем балку с наг рузкой, дейс1вующей в вертикальной (рис. 5.5, 6) и горизонтальной (рис. 5 5, в) плоскостях. Определяем реакции и строим эпюры а. Му.
[c.156]
Му.
[c.156]
Нагрузка, вызывающая изгиб балки в горизонтальной плоскости xOz, и эпюры изгибаюи их моментов Му представлены на рис. 5.7, в. [c.159]
Для балки корытного сечения с сосредоточенными площадями стрингеров (рис. к задаче 4.143), пользуясь площадями Т эпюры 5, найти момент инерции сечения относительно горизонтальной центральной оси и положение центра и згиба D без учета влияния площади сечения стенок (1), и с учетом этой площади (2). [c.117]
ИЗ сечений будет иметь точку приложения посредине расстояния между центрами тяжести горизонтальных и отогнутых стержней в этом сечении. Множество точек приложения этих равнодействующих представляет собой квадратную параболу (пунктир на рис. 13.32, б), а( х )инно-эквивалентную (сжатую по вертикали в два раза) той, по которой расположены отогнутые стержни. В каждом поперечном сечении действует сила (равнодействующая усилий во всех стержнях арматуры), имеющая эксцентриситет, равный расстоянию от точки пересечения параболы, изображенной пунктиром, с поперечным сечением балки, до оси. Вследствие наличия эксцентриситета указанная сила в каждом из сечений создает изгибающий момент, противоположный по направлению тому, который вызывается внешней нагрузкой. Эпюра этих изгибающих моментов, созданных предварительным напряжением балки, как и от нагрузки, также представляет собой квадратную параболу, но имеет противоположный знак. Чем больше величина суммарной силы натяжения стержней арматуры, тем пропорционально больше все ординаты эпюры изгибающих моментов, вызванных предварительным напряжением балки. Можно подобрать величину суммарной силы такой, чтобы эпюры М > и с точностью до знака оказались тождественными Мч = М «.
[c.313]
Вследствие наличия эксцентриситета указанная сила в каждом из сечений создает изгибающий момент, противоположный по направлению тому, который вызывается внешней нагрузкой. Эпюра этих изгибающих моментов, созданных предварительным напряжением балки, как и от нагрузки, также представляет собой квадратную параболу, но имеет противоположный знак. Чем больше величина суммарной силы натяжения стержней арматуры, тем пропорционально больше все ординаты эпюры изгибающих моментов, вызванных предварительным напряжением балки. Можно подобрать величину суммарной силы такой, чтобы эпюры М > и с точностью до знака оказались тождественными Мч = М «.
[c.313]
Балка с любым направлением с о с р е д о г о ч е и н ы X сил. 1] е р п е и д и к у л я р и ы х i о с и. К а-ждую силу раскладывают на o raikiiiio-щие в главных плоскостях балки (ил1 ij горизонтальной и вертикальной плоскостях V и Н) и вычерчивают для обеих групп сил отдельные эпюры Q q( ) Геометрическое сло-
[c.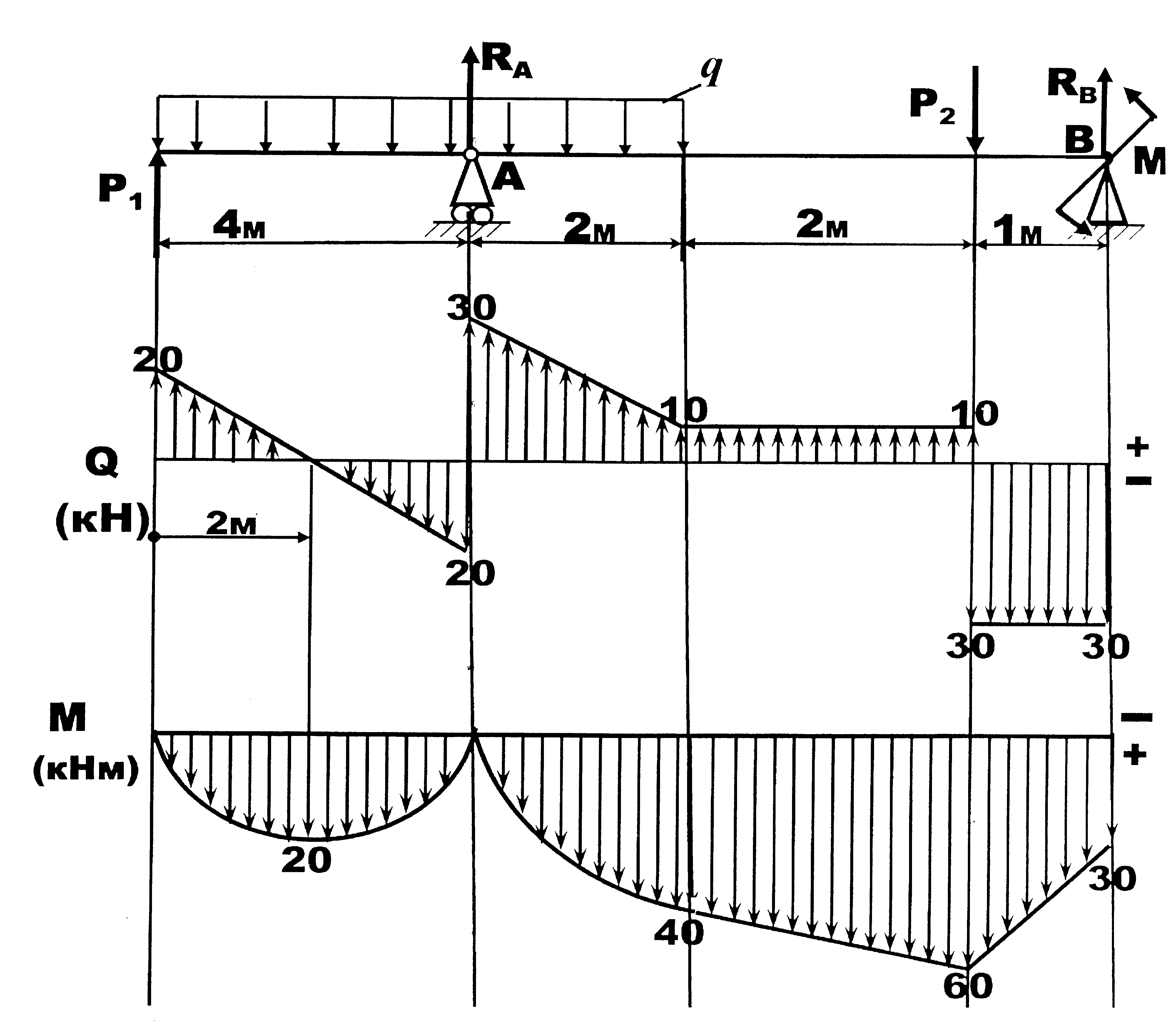 53]
53]
Балка П-образного профиля (размеры даны в мм) подвергается изгибу в вертикальной плоскости xz. В опасном сечении Qmax = 12 т, М ах = 5 тм. Опредблить величину наибольших нормальных и касателвных напряжений, построить эпюры распределения касательных напряжений по высоте стенок и Ху по ширине горизонтальной полки. Выяснить, в каких точках и по каким площадкам касательные напряжения будут наибольшими. [c.161]
Максимальный прогиб балки возникает в точке Е, где касательная к линии прогибов горизонтальна. Угол 0 между касательными в точках Л и Е равен площади участка эпюры моментов между точками Л и (показанной в последней части рисунка), деленной на жесткость при изгибе Н/. Этот угол долижем быть такой же, как и угол 0д, поскольку тангенс угла наклона втотке равен нулю. Отсюда получаем [c.224]
Проведем по длине третьего участка горизонтальную линию гз, продолжение которой проходит через точку с. Ординаты этой прямой дадут поперечную силу для третьего участка балки, она будет отрицательна и откладывается вниз от оси. На этом построение эпюры р заканчивается, остается только заштриховать полученную эпюру 1тпрдг51, что и сделано на рис. 8.35.
[c.228]
На этом построение эпюры р заканчивается, остается только заштриховать полученную эпюру 1тпрдг51, что и сделано на рис. 8.35.
[c.228]
Правила контроля эпюр
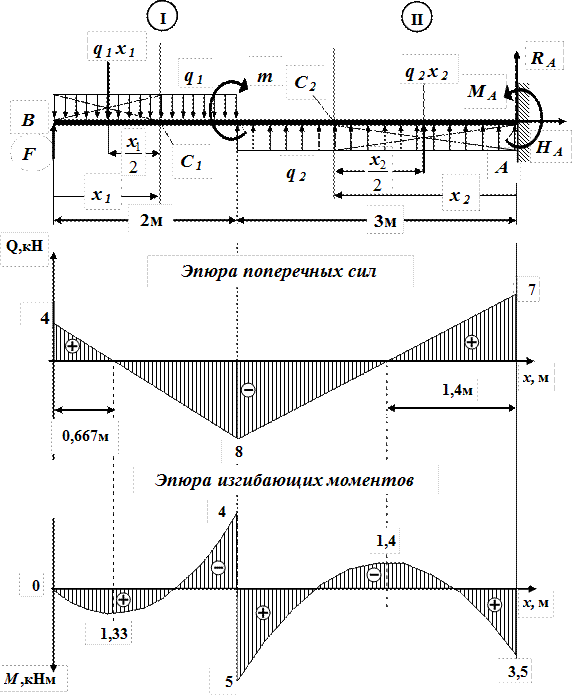
Строим эпюру Q. Для этого двигаемя вдоль оси z балки слева-направо по расчетной схеме.На левой границе 1-го участка приложена (вниз) сила YA = 36,67 кН, поэтому делаем скачек (вниз) на 36,67 (ОТ НУЛЯ. начинаем с нуля — можно думать, что есть ненагруженный хвостик балки слева от опоры А, где M=0, Q=0).
Теперь находимся в пределах 1-го участка. Распределенная нагрузка на нем равна нулю, поэтому Q — постоянна и равна -36,67 кН на всем участке.
Теперь пересекаем границу со 2-м участком. На этой границе нет сосредоточенных сил, поэтому нет скачка.
Движемся по 2-му участку. Здесь приложена постоянная распределенная нагрузка q= 20 кН/м (вверх), поэтому здесь эпюра Q — наклонная прямая (возрастание слева-направо). Приращение Q по формуле (22) = площади = 20кН/м*3м = 60кН.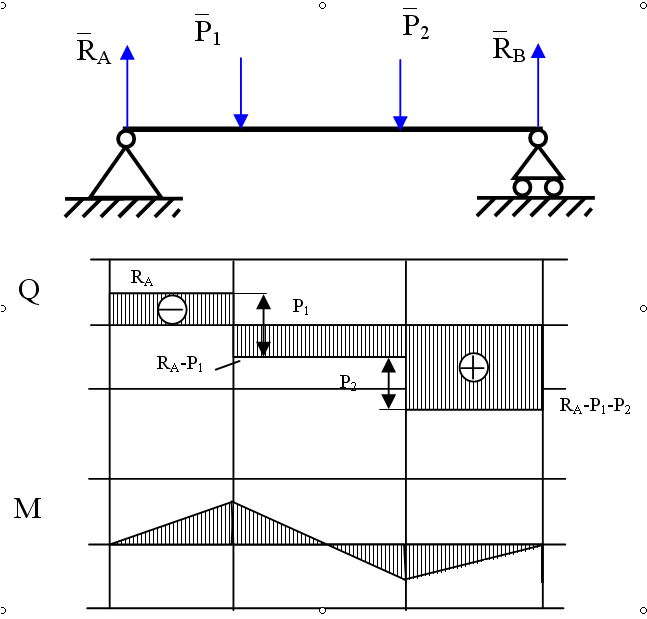 То есть на правой границе 2-го участка Q = -36,67 + 60 = 23,34кН.
То есть на правой границе 2-го участка Q = -36,67 + 60 = 23,34кН.
Пересекаем границу с 3-м участком. Здесь тоже нет состредоточенной силы, поэтому нет и скачка.
Движемся по 3-му участку. На участке q=0, поэтому Q постоянна, т е равна значению, которое было на левой границе, т е 23,33 кН.
Пересекаем правую границу 3-го участка. Здесь приложена (вниз) сила YB = 23,33 кН (реакция правой опоры). Поэтому эпюра Q делает скачек вниз (и приходит к нулевому значению. Это обязательно — для проверки).
Строим эпюру M. Для этого двигаемя вдоль оси z балки слева-направо по расчетной схеме.На левой границе 1-го участка пара сил (внешняя нагрузка) не приложена, поэтому эпюра M на 1-м участке начинается от нуля — можно думать, что есть ненагруженный хвостик балки слева от опоры А, где M=0, Q=0)
Теперь мы находимся в пределах 1-го участка. На нем Q — постоянна и равна -36,67 кН, поэтому эпюра M — Наклонная прямая на всем участке. Приращение M на участке вычислим как площадь прямоугольника на эпюре
Q = -36,67*2= -73,34 кНм. Механики откладывают на эпюре M -73,34 — вниз, строители — вверх.
Механики откладывают на эпюре M -73,34 — вниз, строители — вверх.
Теперь пересекаем границу 2-го участка. Здесь нет приложена пара сил M=80 кНм, поэтому скачок = 80 кНм. «Направление» скачка (то есть его рисунок-зигзаг) для механиков совпадает с рисунком пары M. Для строителей — наоборот. Возможно, проще рассуждать о приращении +80 (это для всех) и откладывать соответственно (у механиков — вверх, у строителей — вниз).
Движемся по 2-му участку. Здесь приложена постоянная распределенная нагрузка q= 20 кН/м (вверх), поэтому здесь эпюра M — парабола. Эпюра Q пересекает ось z на расстоянии 36,67/20 = 1,83 м. Чтобы найти экстремальное значеине M, найдем вначале приращение момента от левой границы 2-го участка до точки эккстремума. Это — пдощадь треугольника на эпюре Q = 36,57*1,83/2=33,55. Приращение отрицательно, так как Q здесь отрицательно.
M_экстр = 6,67 — 33,55 = -26,9 кНм. Значение M на правой границе = -26,9 + 23,33*1,17/2= -13,3 кНм.
.
Пересекаем границу с 3-м участком.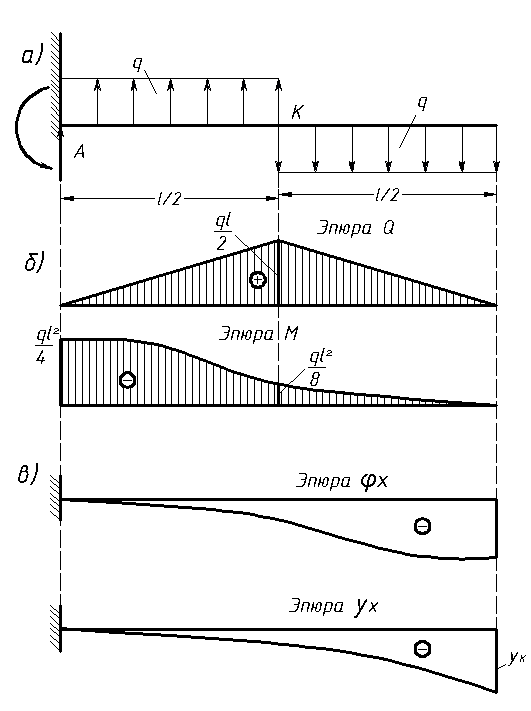 Здесь тоже — пара сил M = 80, направленная противоположно предыдущей. Соответственно, скачек будет противоположный, поэтому в начале 3-го участка M = -93,35 кНм.
Движемся по 3-му участку. На участке Q=+23,33 кН — постоянна, поэтому эпюра M — наклонная прямая, M возрастает (алгебраически) слева-направо. Приращение M на участке равно площади соответствующего прямоугольника на эпюре Q и равно = +23,33*4 = 93,3. Поэтому значение M на правой границе 3-го участка = -93,3 + 93,3 = 0.
Здесь тоже — пара сил M = 80, направленная противоположно предыдущей. Соответственно, скачек будет противоположный, поэтому в начале 3-го участка M = -93,35 кНм.
Движемся по 3-му участку. На участке Q=+23,33 кН — постоянна, поэтому эпюра M — наклонная прямая, M возрастает (алгебраически) слева-направо. Приращение M на участке равно площади соответствующего прямоугольника на эпюре Q и равно = +23,33*4 = 93,3. Поэтому значение M на правой границе 3-го участка = -93,3 + 93,3 = 0.
Пересекаем правую границу 3-го участка. Здесь не приложена пара сил. Поэтому если далее есть ненагруженный хвостик балки, то на нем M=0 (Это всегда должно соблюдаться, как проверка)
Построение эпюр Q и М для более сложных случаев нагрузки
Содержание:
Построение эпюр Q и М для более сложных случаев нагрузки
- Графики Q и M для более сложных случаев нагрузки. Изучив общие приемы построения сюжета и его характеристики, перейдем к решению более сложных задач.
 Рассмотрим, как вычислить Q и M, когда на балку действует непрерывно неравномерно распределенная нагрузка.- Фигура. 165. Тор изменяется по длине луча, в зависимости от x (рис. 165). Другими словами, q является функцией x или q-q (x). Боковые силы и изгибающие моменты также становятся некоторыми функциями от x: M=M{x) и Q=Q(x). Кривая adceb, представляющая закон изменения q (x), называется грузовой линией, а область, ограниченная этой кривой, — грузовой зоной. Вычислите Q и M для
Рассмотрим, как вычислить Q и M, когда на балку действует непрерывно неравномерно распределенная нагрузка.- Фигура. 165. Тор изменяется по длине луча, в зависимости от x (рис. 165). Другими словами, q является функцией x или q-q (x). Боковые силы и изгибающие моменты также становятся некоторыми функциями от x: M=M{x) и Q=Q(x). Кривая adceb, представляющая закон изменения q (x), называется грузовой линией, а область, ограниченная этой кривой, — грузовой зоной. Вычислите Q и M для
любого сечения балки, взятого на расстоянии Xj от свободного края. Если рассматривать поперечные силы как сумму элементарных сил q (x)•dx, приложенных к левой отрезной части балки, и заменить суммирование интегралом、: Дио= — у)(Х). (12.12) Здесь W (XJ) показывает часть грузового пространства, расположенную с левой стороны отсека съемки C-C. Изгибающий момент того же сечения равен сумме моментов фундаментальной силы q (x) rfx, действующей на отрезную часть балки, а результирующий момент r (q) равен сумме моментов rfx.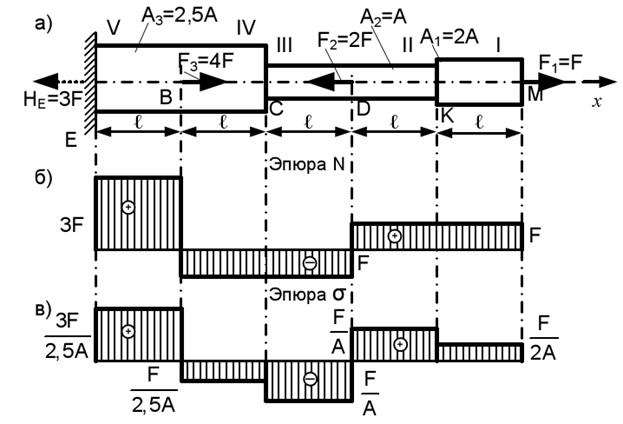 M (x0= — R q * x r= — co (Xi)•x r. (12.13)другими словами, изгибающий момент от неравномерно р
M (x0= — R q * x r= — co (Xi)•x r. (12.13)другими словами, изгибающий момент от неравномерно р
аспределенной нагрузки равен произведению площади нагрузки§ 73] построение Q и M для более сложных случаев Плотины, стойки, усиленные- Людмила Фирмаль
На одной стороне поперечного сечения-расстояние от центра тяжести участка до рассматриваемого участка (в результате плеча). П р и М EP48. Рассмотрим построение участка под действием непрерывной нагрузки, которая изменяется по длине балки по законам треугольника(рис. 166). Такая нагрузка поддерживает давление воды или грунта под рабочей балкой, например, щие стенки бака стойки предназначены для хранения жидкости. Аналогично инерционная сила нагружается на шатуны парового двигателя и двигателя внутреннего сгорания. Величина этой нагрузки определяется вертикальной qQ, которая является наибольшей
прочностью нагрузки (кг/м). Реакция=0; определите реакции A и B, а чтобы найти A, составьте уравнение момента около точки B.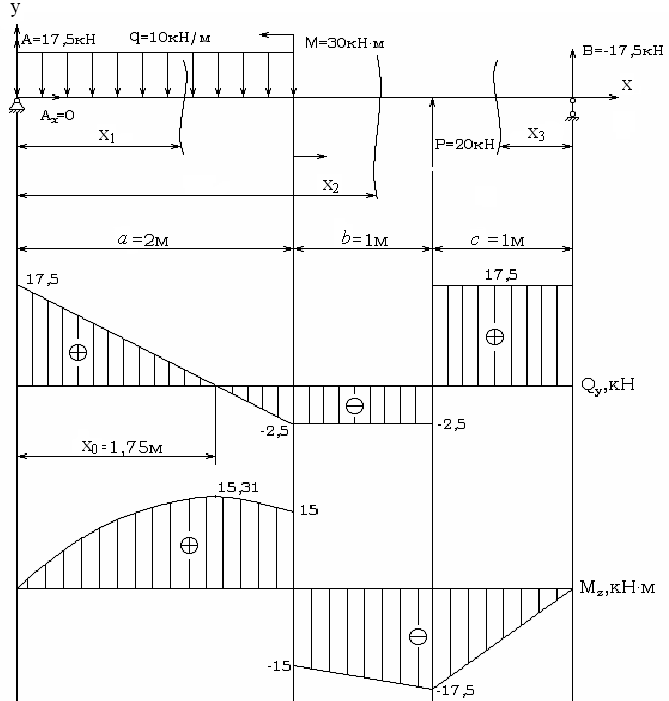 s: X3=0z=P = 2g, j>x s=0z-P+qc=2 + 2 • 2 =6 тонн. Полная диаграмма поперечных сил, построенная по трем уравнениям, полученным таким образом, показана на рисунке. Из графика 168 видно, что Shah0=8.8 t (абсолютное значение) в сечении левой опоры B. Теперь перейдем
s: X3=0z=P = 2g, j>x s=0z-P+qc=2 + 2 • 2 =6 тонн. Полная диаграмма поперечных сил, построенная по трем уравнениям, полученным таким образом, показана на рисунке. Из графика 168 видно, что Shah0=8.8 t (абсолютное значение) в сечении левой опоры B. Теперь перейдем
к созданию фигуры изгибающего момента с использованием тех же трех сечений. Момент 1-1: L41=AXi (уравнение линии) силы, приложенной к левой обрезанной части относительно центра тяжести сечения. В x1=0L41=0;в x t=Aa = AA=7,2 * 2=14,4 TLE для второго участка (a x2Z):=Ah3—q (x2-a) X ’ 2%=Ah3— ~ ——02.18)§ 73] участок 2 4 7 для Q и / или более сложных случаев Это уравнение параболы, для его построения необходимо дать переменной x2 не менее трех значений: x s=A M2=AA-Mi=-1;1 • 2 — 16 = — 1,6 TM\pri=Z Ma=Al-Mo-q= 7,2 • 10 — 16 — — = — 8 теперь TM вычисляет MA для точки,
в которой MA достигает максимального значения x2, то есть точки, в которой график Q проходит через ноль. Исследуя уравнение момента на максимуме, находим: <Да2 Подставляя это в уравнение M2, machm a=Axa-Ma-q= 7,2 • 5,6 — 16,0 — (5’^— = 11,3 ТМ.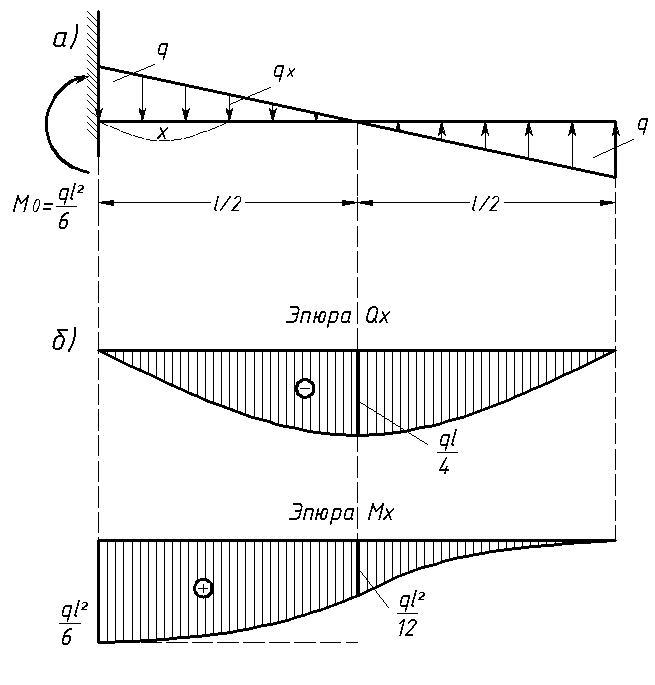 По полученным трем значениям момента строится параболическая кривая, выражающая закон изменения момента во втором сечении (для повышения точности построения). Для получения представления изгибающего момента рассматривается правосторонняя отсекающая часть балки. Правильный момент силы относительно центра тяжести в разделе 3-3 равен: qxj2 • (12.19) Это уравнение (парабола) вычисляется по формуле: x8=0m3=0; Значение 0С: С Х8=7.. ПК ФС2 £ 2 2 2 — 2 2 • 22 Восемь. — 3TM; AC2 2•22>X3=Mz= — Pc— 2 2 * 2 — = — 8ТМ.
По полученным трем значениям момента строится параболическая кривая, выражающая закон изменения момента во втором сечении (для повышения точности построения). Для получения представления изгибающего момента рассматривается правосторонняя отсекающая часть балки. Правильный момент силы относительно центра тяжести в разделе 3-3 равен: qxj2 • (12.19) Это уравнение (парабола) вычисляется по формуле: x8=0m3=0; Значение 0С: С Х8=7.. ПК ФС2 £ 2 2 2 — 2 2 • 22 Восемь. — 3TM; AC2 2•22>X3=Mz= — Pc— 2 2 * 2 — = — 8ТМ.
Значение M8 в верхней секции опоры B совпадает со значением, найденным перед MA в той же секции. График изгибающего момента состоит из рисунка. Как видно из графика, это 168, max M=14.4 t (выше аналитического максимума L12). Кстати, как и на рисунке. На участке, где 164, применяется набор сил A1o, участок L4 имеет скачок со значением LT0. П р и М Е Р51. Рассмотрим построение графиков M и Q для системы балок(рис. 169), состоящая из основной консольной балки ABC и подвесной балки CD, соединенных шарниром C).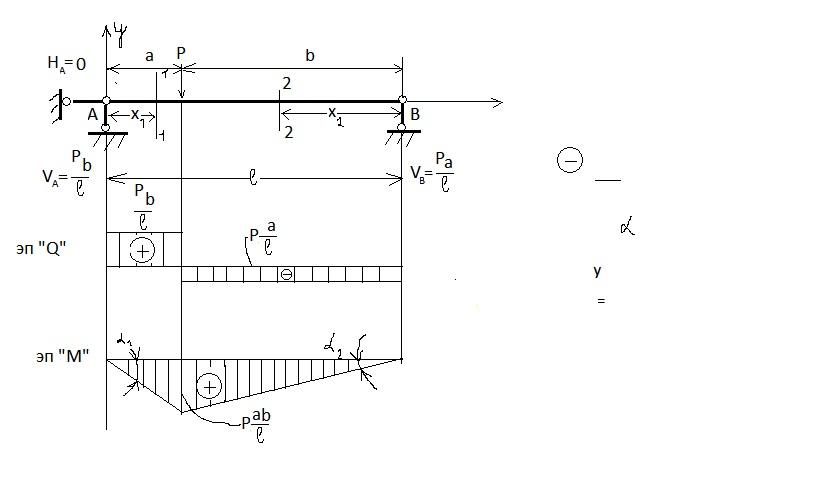 Чтобы построить сюжет, мы находим реакцию в луче. Как использовать 169, система луча, мы можем только написать 3, Все объявление луча 4 поддерживают реакцию D, H A, B и D. It может иметь ту же формул
Чтобы построить сюжет, мы находим реакцию в луче. Как использовать 169, система луча, мы можем только написать 3, Все объявление луча 4 поддерживают реакцию D, H A, B и D. It может иметь ту же формул
у равновесия. Четвертое уравнение не допускает передачи моментов, так как позволяет части луча (AC) вращаться относительно другой (CD). В последнем случае необходимо, чтобы сумма моментов для точки С силы, приложенной слева или справа от этого шарнира, была равна нулю.248 испытание[гл. ДВЕНАДЦАТЫЙ Другими словами, для поддержания равновесия балки изгибающий момент в шарнире должен быть равен нулю. Это дополнительное требование делает рекламный луч статически определяемым. Определение реакции начинается с расчета НД Если суммировать проекцию всех сил на ось луча до нуля, то H A=0. 1) сведите сумму всех силовых моментов о точке а к нулю;2) сведите сумму всех силовых моментов о точке D к нулю; или\3) сведите сумму всех силовых моментов о точке а к нулю. Решая систему этих трех уравнений, можно получить все три
неизвестные реакции: I, B, D, но легко определить эти реакции, разложив пучок ad на простейшие. — =6 тонн, s::=7 4=».-. После определения реакции он снова воспроизводит пучок как имеющий все силы и реакции, определяя момент и боковые силы, как в обычном случае. Испытанием будет
— =6 тонн, s::=7 4=».-. После определения реакции он снова воспроизводит пучок как имеющий все силы и реакции, определяя момент и боковые силы, как в обычном случае. Испытанием будет
равенство нулевого момента на шарнире C участка элемента и боковой силы, на которую шарнир C не является точкой отрыва секции, если к нему не приложена внешняя сила, показанная на рисунке. 169§ 73] построение Q и M для более сложных случаев Рисунок 2 4 9 Определите опорную реакцию для построения графика Q и M отдельно для каждой подвески и главной балки, а также способ отсчета значений полученных значений Q и M от общей оси X. П р и М EP52. Балка со сломанной осью, обычно называемая рамкой, строится с помощью Q и M (рис. 171). Горизонтальный стержень Солнца называется болтом и называется вертикальным стержнем рамы. Перекладина и стойка соединены
жестким узлом с, образуя непрерывную систему. Мы переходим к узлу жесткости рамы. Порядок графиков Q и M для таких систем не меняется. Для определения эталонной реакции поставим уравнение равновесия: 2^=0; qh-H A=0, Или Или A=B, З М А=&,^ — В1=, 0, Или 2-4^ 2/ 2 • 2 — 8 ′ И- Для поперечины, O^x^Z, поперечный изгибающий момент M (x)=BX=. 1 2′ — Боковая сила Q (y)=q-y; изгибающий момент M (y)= Значения вертикальных осей участков Q и M приведены в таблице 19. Соответствующие графики Q и M состоят из цифр. 172.
1 2′ — Боковая сила Q (y)=q-y; изгибающий момент M (y)= Значения вертикальных осей участков Q и M приведены в таблице 19. Соответствующие графики Q и M состоят из цифр. 172.
Смотрите также:
6.3 Дифференциальные зависимости при изгибе
6.3 Дифференциальные зависимости при изгибе
Выделим на участке балки с произвольной нагрузкой в месте, где нет сосредоточенных сил и моментов, малый элемент dz. Так как вся балка находится в равновесии, то и элемент dz будет находиться в равновесии под действием приложенных к нему поперечных сил, изгибающих моментов и внешней нагрузки. Поскольку Qy и Mx в общем случае меняются вдоль оси балки, то в сечениях элемента dz будут возникать поперечные силы Qy и Qy+ dQy, а также изгибающие моменты Mx и Mx+dMx.
Из условия равновесия выделенного элемента получим:
, следовательно
; (6. 5)
5)
, следовательно
(6.6)
Рекомендуемые файлы
Шлюзовое окно закрыто щитом треугольной формы шириной a = 2 м. За щитом воды нет, а глубина воды перед ним – h2 = 6 м, при этом горизонт воды перед щитом совпадает с его вершиной. Определить силу гидростатического давления и положение центра давления
Физика
Для горизонтального трубопровода, размеры которого указаны на схеме, определить расход Q при заданном избыточном давлении M = 0,4 МПа и уровне воды в резервуаре h = 5 м. Коэффициент сопротивления вентиля ξ = 4 и сопла ξ = 0,06 (сжатие струи на выходе
Физика
Физика, 12 вариант, задача 4, подробно, принято на макс. балл
Физика
ЗАДАЧА 2 Вариант 7 ПРИНЯТОЕ
Физика
Расход воды при температуре 10˚ C в горизонтальной трубе кольцевого сечения, состоящей из двух концентрических оцинкованных стальных труб (при Δ=0,15 мм ), Q=0,0075 м3/с. Внутренняя труба имеет наружный диаметр d=0,075 м, а наружная труба имеет внутр
Физика
Насос производительностью 18 м3/ч забирает воду из колодца по трубе диаметром d = 100 мм. Определить высоту установки насоса h, при условии, что наибольший вакуум в трубе не превышает 60 кПа.
Определить высоту установки насоса h, при условии, что наибольший вакуум в трубе не превышает 60 кПа.
Физика
Первое из двух записанных уравнений дает условие
(6.7)
Из второго уравнения, пренебрегая слагаемым как бесконечно малой величиной второго порядка, найдем
(6.8)
Рассматривая полученные выражения, совместно можем получить
(6.9)
Полученные соотношения называют дифференциальными зависимостями Д.И. Журавского при изгибе.
Если Вам понравилась эта лекция, то понравится и эта — Религиозный туризм в исламе.
Анализ дифференциальных зависимостей при изгибе позволяет установить некоторые особенности (правила) построения эпюр изгибающих моментов и поперечных сил:
— на участках, где нет распределенной нагрузки q, эпюры Q ограничены прямыми, параллельными базе, а эпюры М — наклонными прямыми;
— на участках, где к балке приложена распределенная нагрузка q, эпюры Q ограничены наклонными прямыми, а эпюры М — квадратичными параболами. При этом, если эпюру М строим «на сжатом волокне», то выпуклость параболы будет направлена против направления действия q, а экстремум будет расположен в сечении, где эпюра Q пересекает базовую линию;
При этом, если эпюру М строим «на сжатом волокне», то выпуклость параболы будет направлена против направления действия q, а экстремум будет расположен в сечении, где эпюра Q пересекает базовую линию;
— в сечениях, где к балке прикладывается сосредоточенная сила, на эпюре Q будут скачки на величину и в направлении данной силы, а на эпюре М — перегибы, острием направленные в направлении действия этой силы;
— в сечениях, где к балке прикладывается сосредоточенный момент, на эпюре Q изменений не будет, а на эпюре М — скачок на величину этого момента;
— на участках, где Q>0, момент М возрастает, а на участках, где Q<0, момент М убывает.
Сопромат.in.ua: Изгиб: определение внутренних усилий
Изгиб — (англ. bending, flexure) вид деформации, при котором происходит искривление осей прямых брусьев (балок) или изменение кривизны осей кривых брусьев. Брус, работающий на изгиб, называется балкой. Изгиб связан с возникновением в поперечных сечениях бруса изгибающих моментов. Прямой изгиб возникает в случае, когда изгибающий момент в данном поперечном сечении бруса действует в плоскости, проходящей через одну из главных центральных осей инерции этого сечения. В случае, когда плоскость действия изгибающего момента в данном поперечном сечении бруса не проходит ни через одну из главных осей инерции этого сечения, называется косым.
Изгиб связан с возникновением в поперечных сечениях бруса изгибающих моментов. Прямой изгиб возникает в случае, когда изгибающий момент в данном поперечном сечении бруса действует в плоскости, проходящей через одну из главных центральных осей инерции этого сечения. В случае, когда плоскость действия изгибающего момента в данном поперечном сечении бруса не проходит ни через одну из главных осей инерции этого сечения, называется косым.
Если при прямом или косом изгибе в поперечном сечении бруса действует только изгибающий момент, то соответственно имеется чистый прямой или чистый косой изгиб. Если в поперечном сечение действует также и поперечная сила, то имеется поперечный прямой или поперечный косой изгиб.
Часто термин «прямой» в названии прямого чистого и прямого поперечного изгиба не употребляют и их называют соответственно чистым изгибом и поперечным изгибом.
Дифференциальные зависимости при изгибе
$$q = – {dQ _y\over dz}; \qquad Q _y = {dM_x\over dz} $$
Из этих уравнений следует
$$q = – {d^2M _x\over dz^2} $$
Здесь ось z направлена вдоль центральной оси балки.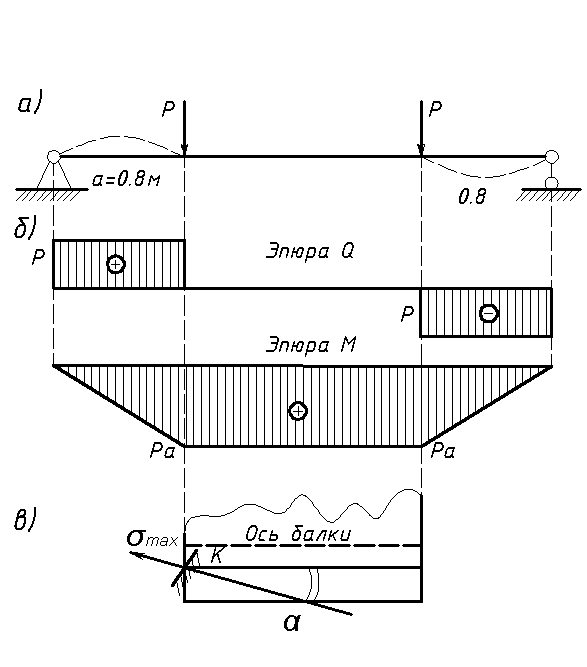
Правило знаков
Правило знаков для поперечной силы
Поперечная сила считается положительной, если она стремится повернуть элемент балки по ходу часовой стрелки.
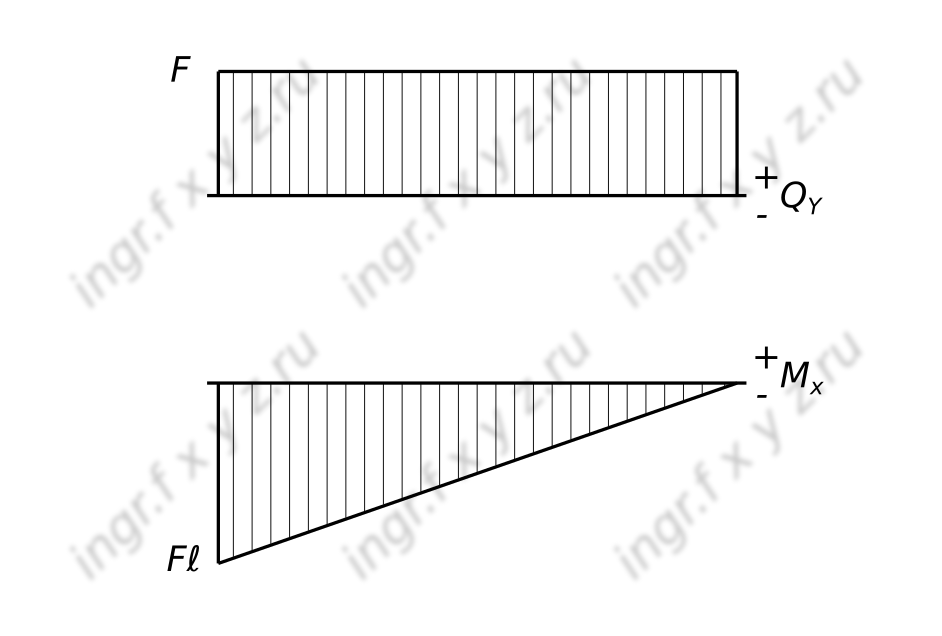
При построении эпюры поперечной силы положительные значения поперечной силы откладываются вверх от горизонтальной базовой линии, а отрицательные – вниз.
Правило знаков для изгибающих моментов.
Изгибающий момент принимается положительным, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части, изгибает элемент балки так, что нижние волокна оказываются растянутыми, т.е. ось балки искривляется выпуклостью вниз.
Нужно учесть, что при построении эпюры изгибающего момента в строительных и транспортных ВУЗах принято откладывать положительный момент вниз ( со стороны растянутого волокна), а в машиностроительных ВУЗах — вверх (положительный момент откладывается со стороны сжатого волокна).Усилия в балке определяют методом сечений.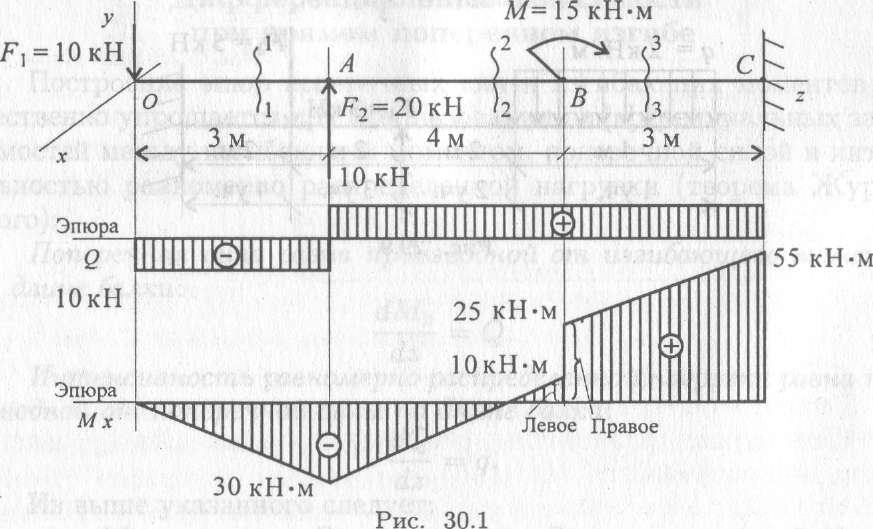
Общий ход определения усилий и построения эпюр
- Определяем опорные реакции
- Намечаем характерные сечения балки.
- Определяем поперечную силу и изгибающий момент в каждом характерном сечении.
- По найденным значениям поперечной силы и изгибающих моментов строим эпюры .
Правила контроля правильности эпюр Q и M (Q
y и Mx)- Эпюра Qy является прямолинейной на всех участках.
- Эпюра M (Mx) является криволинейной (квадратная парабола) на участке под равномерно распределенной нагрузкой, и прямолинейная на всех остальных участках.
- Под точкой приложения сосредоточенной силы (реакции) на эпюре Qy обязательно должен быть скачок (разрыв) на величину этой силы (реакции). Аналогично, под точкой приложения сосредоточенного момента на эпюре Mx обязательно будет скачок на величину момента.
- Если на участке под распределенной нагрузкой эпюра Qy пересекает ось, то эпюра Mx в этом сечении имеет экстремум.
- На участках с поперечной силой одного знака эпюра моментов Mx имеет одинаковую монотонность. Так, если Qy > 0 эпюра моментов убывает слева направо; при Qy > 0 эпюра Mx возрастает слева направо.
- Порядок линии на эпюре Qy всегда на единицу меньше, чем на эпюре изгибающих моментов. То есть, если эпюра моментов Mx – квадратная парабола, то эпюра поперечных сил Qy на этом участке – наклонная прямая; если эпюра Mx – наклонная прямая, то эпюра Qy на этом участке – прямая, параллельная оси; если Mx постоянная (прямая, параллельная оси), то на этом участке Qy = 0.
Связанные статьи
метки: внутренние усилия, изгиб
Колонки для ГХ GsBP®-PLOT-Q, GS-Tek | ВВР
Положения и условия
Спасибо, что посетили наш сайт. Настоящие условия использования применимы к веб-сайтам США, Канады и Пуэрто-Рико («Веб-сайт»), которыми управляет VWR («Компания»).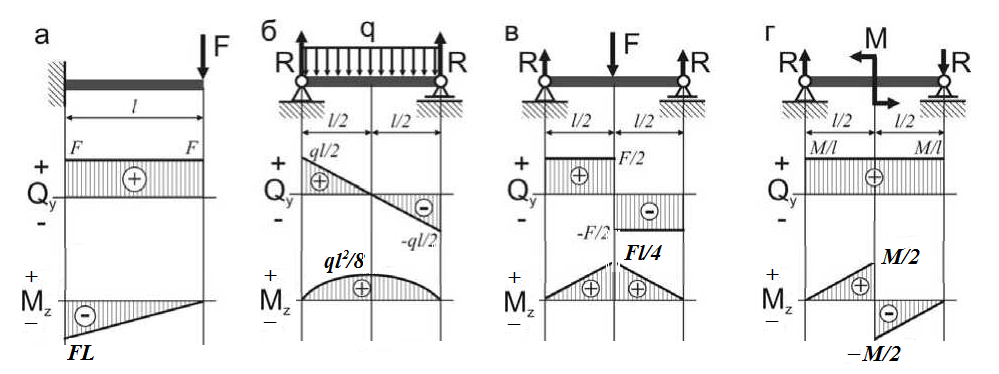 Если вы заходите на веб-сайт из-за пределов США, Канады или Пуэрто-Рико, посетите соответствующий международный веб-сайт, доступный по адресу www.vwr.com, для ознакомления с применимыми условиями. На всех пользователей веб-сайта распространяются следующие условия использования веб-сайта (данные «Условия использования»).Пожалуйста, внимательно прочитайте настоящие Условия использования перед доступом к любой части веб-сайта или его использованием. Получая доступ к веб-сайту или используя его, вы подтверждаете, что прочитали, поняли и согласны соблюдать настоящие Условия использования с периодическими изменениями, а также Политику конфиденциальности Компании, которая настоящим включена в настоящие Условия. использования. Если вы не хотите соглашаться с настоящими Условиями использования, не открывайте и не используйте какую-либо часть веб-сайта.
Если вы заходите на веб-сайт из-за пределов США, Канады или Пуэрто-Рико, посетите соответствующий международный веб-сайт, доступный по адресу www.vwr.com, для ознакомления с применимыми условиями. На всех пользователей веб-сайта распространяются следующие условия использования веб-сайта (данные «Условия использования»).Пожалуйста, внимательно прочитайте настоящие Условия использования перед доступом к любой части веб-сайта или его использованием. Получая доступ к веб-сайту или используя его, вы подтверждаете, что прочитали, поняли и согласны соблюдать настоящие Условия использования с периодическими изменениями, а также Политику конфиденциальности Компании, которая настоящим включена в настоящие Условия. использования. Если вы не хотите соглашаться с настоящими Условиями использования, не открывайте и не используйте какую-либо часть веб-сайта.
Компания может пересматривать и обновлять настоящие Условия использования в любое время без предварительного уведомления, разместив измененные условия на веб-сайте.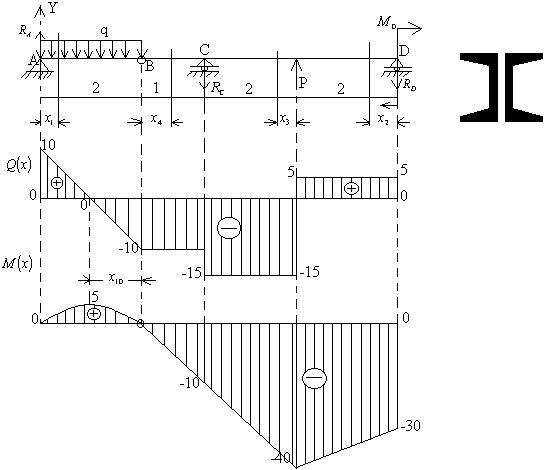 Ваше дальнейшее использование веб-сайта означает, что вы принимаете и соглашаетесь с пересмотренными Условиями использования. Если вы не согласны с Условиями использования (в которые время от времени вносятся поправки) или недовольны Веб-сайтом, вашим единственным и исключительным средством правовой защиты является прекращение использования Веб-сайта.
Ваше дальнейшее использование веб-сайта означает, что вы принимаете и соглашаетесь с пересмотренными Условиями использования. Если вы не согласны с Условиями использования (в которые время от времени вносятся поправки) или недовольны Веб-сайтом, вашим единственным и исключительным средством правовой защиты является прекращение использования Веб-сайта.
Использование на месте
Информация, содержащаяся на этом веб-сайте, предоставляется только в информационных целях. Несмотря на то, что на момент публикации информация считается верной, вы должны самостоятельно определить ее пригодность для вашего использования.Не все продукты или услуги, описанные на этом веб-сайте, доступны во всех юрисдикциях или для всех потенциальных клиентов, и ничто в настоящем документе не предназначено в качестве предложения или ходатайства в какой-либо юрисдикции или любому потенциальному клиенту, если такое предложение или продажа не соответствуют требованиям.
Покупка товаров и услуг
Настоящие Положения и условия применяются только к использованию Веб-сайта.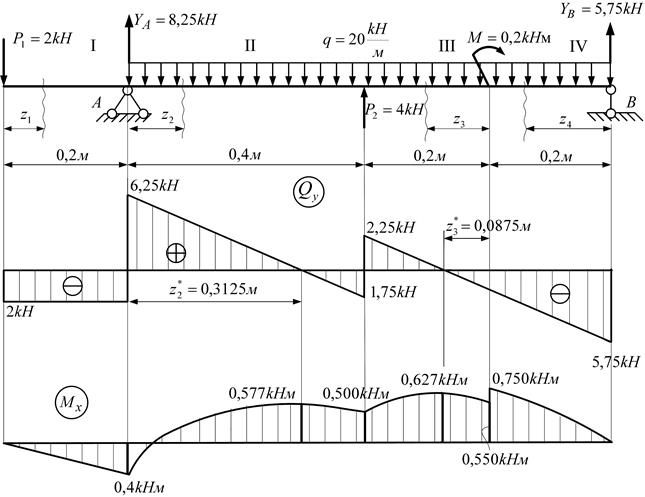 Обратите внимание, что условия, касающиеся обслуживания, продажи продуктов, рекламных акций и других связанных с этим мероприятий, можно найти на странице https://us.vwr.com/store/content/externalContentPage.jsp?path=/en_US/about_vwr_terms_and_conditions.jsp, и эти положения и условия регулируют любые покупки продуктов или услуг у Компании.
Обратите внимание, что условия, касающиеся обслуживания, продажи продуктов, рекламных акций и других связанных с этим мероприятий, можно найти на странице https://us.vwr.com/store/content/externalContentPage.jsp?path=/en_US/about_vwr_terms_and_conditions.jsp, и эти положения и условия регулируют любые покупки продуктов или услуг у Компании.
Интерактивные функции
Веб-сайт может содержать доски объявлений, чаты, группы новостей, форумы, сообщества, личные веб-страницы, календари и/или другие средства обмена сообщениями или средствами связи, предназначенные для того, чтобы вы могли общаться с широкой общественностью или с группой ( совместно именуемые «Функция сообщества»).Вы соглашаетесь использовать Функцию сообщества только для публикации, отправки и получения сообщений и материалов, которые являются надлежащими и связаны с конкретной Функцией сообщества. Вы соглашаетесь использовать Веб-сайт только в законных целях.
A.
В частности, вы соглашаетесь не делать ничего из следующего при использовании функции сообщества:
1. Порочить, оскорблять, преследовать, преследовать, угрожать или иным образом нарушать законные права (такие как право на неприкосновенность частной жизни и публичность) других лиц.
2. Публиковать, публиковать, загружать, распространять или распространять любые неуместные, богохульные, клеветнические, нарушающие авторские права, непристойные, непристойные или незаконные темы, имена, материалы или информацию.
3. Загружать файлы, содержащие программное обеспечение или другие материалы, защищенные законами об интеллектуальной собственности (или правами на неприкосновенность частной жизни или публичное использование), если только вы не владеете правами на них или не контролируете их, или не получили все необходимые согласия.
4. Загружать файлы, содержащие вирусы, поврежденные файлы или любое другое подобное программное обеспечение или программы, которые могут нарушить работу чужого компьютера.
5. Перехват или попытка перехвата электронной почты, не предназначенной для вас.
6. Рекламировать или предлагать продать или купить какие-либо товары или услуги для любых деловых целей, если такая Функция сообщества специально не разрешает такие сообщения.
7. Проводить или рассылать опросы, конкурсы, финансовые пирамиды или письма счастья.
8. Загружайте любой файл, опубликованный другим пользователем Элемента сообщества, о котором вы знаете или должны были бы знать, что он не может быть законно распространен таким образом или что у вас есть договорные обязательства по сохранению конфиденциальности (несмотря на его доступность на веб-сайте).
9. Фальсифицировать или удалять любые указания на авторство, юридические или другие надлежащие уведомления, обозначения прав собственности или ярлыки происхождения или источника программного обеспечения или других материалов, содержащихся в загружаемом файле.
10. Искажать связь с каким-либо лицом или организацией.
11.Участвовать в любых других действиях, которые ограничивают или препятствуют чьему-либо использованию Веб-сайта или которые, по определению Компании, могут нанести вред Компании или пользователям Веб-сайта или привлечь их к ответственности.
12. Нарушать любые применимые законы или правила или нарушать любой кодекс поведения или другие правила, которые могут применяться к какой-либо конкретной функции сообщества.
13. Собирать или иным образом собирать информацию о других, включая адреса электронной почты, без их согласия.
B. Вы понимаете и признаете, что несете ответственность за любой контент, который вы отправляете, вы, а не Компания, несете полную ответственность за такой контент, включая его законность, надежность и уместность. Если вы публикуете от имени или от имени вашего работодателя или другого лица, вы заявляете и гарантируете, что вы уполномочены делать это. Загружая или иным образом передавая материал в любую область Веб-сайта, вы гарантируете, что этот материал принадлежит вам или находится в общественном достоянии, или иным образом свободен от имущественных или других ограничений, и что вы имеете право размещать его на Веб-сайте.
Кроме того, загружая или иным образом передавая материалы в любую область веб-сайта, вы предоставляете Компании безотзывное, безвозмездное право во всем мире публиковать, воспроизводить, использовать, адаптировать, редактировать и/или изменять такие материалы любым способом, в любые средства массовой информации, известные в настоящее время или обнаруженные в будущем, во всем мире, в том числе в Интернете и всемирной паутине, в рекламных, коммерческих, коммерческих и рекламных целях, без дополнительных ограничений или компенсации, если это не запрещено законом, и без уведомления, проверки или одобрения.
C. Компания оставляет за собой право, но не берет на себя никакой ответственности, (1) удалять любые материалы, размещенные на веб-сайте, которые Компания по своему собственному усмотрению считает несовместимыми с вышеизложенными обязательствами или иным образом неуместными по любой причине. ; и (2) прекратить доступ любого пользователя ко всему Веб-сайту или его части.
Тем не менее, Компания не может ни просматривать все материалы до их размещения на Веб-сайте, ни гарантировать незамедлительное удаление нежелательных материалов после их публикации.Соответственно, Компания не несет ответственности за какие-либо действия или бездействие в отношении передач, сообщений или контента, предоставленных третьими лицами. Компания оставляет за собой право предпринимать любые действия, которые она сочтет необходимыми для защиты личной безопасности пользователей данного веб-сайта и общественности; однако Компания не несет ответственности перед кем-либо за выполнение или невыполнение действий, описанных в этом параграфе.
D. Несоблюдение вами положений (A) или (B) выше может привести к прекращению вашего доступа к Веб-сайту и может подвергнуть вас гражданской и/или уголовной ответственности.
Специальное примечание о материалах сообщества
Любой контент и/или мнения, загруженные, выраженные или представленные через любую функцию сообщества или любой другой общедоступный раздел веб-сайта (включая защищенные паролем области), а также все статьи и ответы на вопросы, кроме контента, явно разрешенного Компании, являются исключительно мнением и ответственностью физического или юридического лица, представляющего их, и не обязательно отражают мнение Компании. Например, любое рекомендуемое или предлагаемое использование продуктов или услуг, доступных от Компании, которое публикуется через Функция сообщества, не является признаком одобрения или рекомендации со стороны Компании. Если вы решите следовать любой такой рекомендации, вы делаете это на свой страх и риск.
Например, любое рекомендуемое или предлагаемое использование продуктов или услуг, доступных от Компании, которое публикуется через Функция сообщества, не является признаком одобрения или рекомендации со стороны Компании. Если вы решите следовать любой такой рекомендации, вы делаете это на свой страх и риск.
Ссылки на сторонние сайты
Веб-сайт может содержать ссылки на другие веб-сайты в Интернете. Компания не несет ответственности за содержание, продукты, услуги или практику любых сторонних веб-сайтов, включая, помимо прочего, сайты, связанные с Веб-сайтом или с него, сайты, размещенные на Веб-сайте, или рекламу третьих лиц, и не делает заявлений относительно их качество, содержание или точность.Наличие ссылок с веб-сайта на любой сторонний веб-сайт не означает, что мы одобряем, одобряем или рекомендуем этот веб-сайт. Мы отказываемся от всех гарантий, явных или подразумеваемых, в отношении точности, законности, надежности или достоверности любого контента на любом стороннем веб-сайте. Использование вами сторонних веб-сайтов осуществляется на ваш страх и риск и регулируется условиями использования таких веб-сайтов.
Использование вами сторонних веб-сайтов осуществляется на ваш страх и риск и регулируется условиями использования таких веб-сайтов.
Права собственности на контент
Вы признаете и соглашаетесь с тем, что все содержимое Веб-сайта (включая всю информацию, данные, программное обеспечение, графику, текст, изображения, логотипы и/или другие материалы), а также его дизайн, выбор, сбор, размещение и сборка являются являются собственностью Компании и защищены законами США и международными законами об интеллектуальной собственности.Вы имеете право использовать содержимое веб-сайта только в личных целях или в законных деловых целях. Вы не можете копировать, изменять, создавать производные работы, публично демонстрировать или выполнять, переиздавать, хранить, передавать, распространять, удалять, удалять, дополнять, добавлять, участвовать в передаче, лицензировать или продавать любые материалы в Интернете. сайта без предварительного письменного согласия Компании, за исключением: (а) временного хранения копий таких материалов в оперативной памяти, (б) хранения файлов, которые автоматически кэшируются вашим веб-браузером для целей улучшения отображения, и (в) печати разумного количество страниц веб-сайта; при условии, что в каждом случае вы не изменяете и не удаляете какие-либо уведомления об авторских правах или других правах собственности, включенные в такие материалы.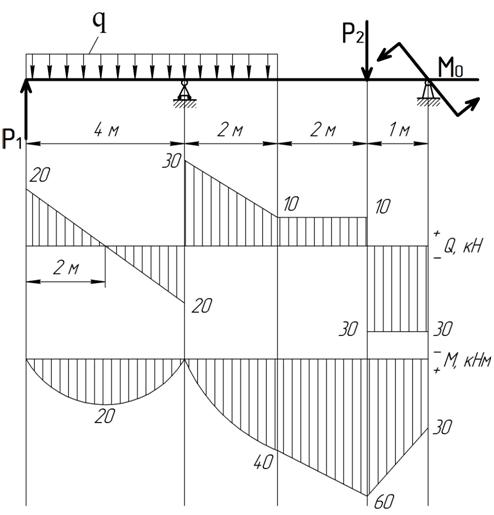 Ни название, ни какие-либо права интеллектуальной собственности на какую-либо информацию или материалы на Веб-сайте не передаются вам, а остаются за Компанией или соответствующим владельцем такого контента.
Ни название, ни какие-либо права интеллектуальной собственности на какую-либо информацию или материалы на Веб-сайте не передаются вам, а остаются за Компанией или соответствующим владельцем такого контента.
Товарные знаки
Название и логотип Компании, а также все соответствующие названия, логотипы, названия продуктов и услуг, встречающиеся на Веб-сайте, являются товарными знаками Компании и/или соответствующих сторонних поставщиков. Их нельзя использовать или повторно отображать без предварительного письменного согласия Компании.
Отказ от ответственности
Компания не несет никакой ответственности за материалы, информацию и мнения, представленные на Веб-сайте или доступные через него («Контент сайта»). Вы полагаетесь на Контент Сайта исключительно на свой страх и риск. Компания отказывается от какой-либо ответственности за травмы или убытки, возникшие в результате использования любого Контента Сайта.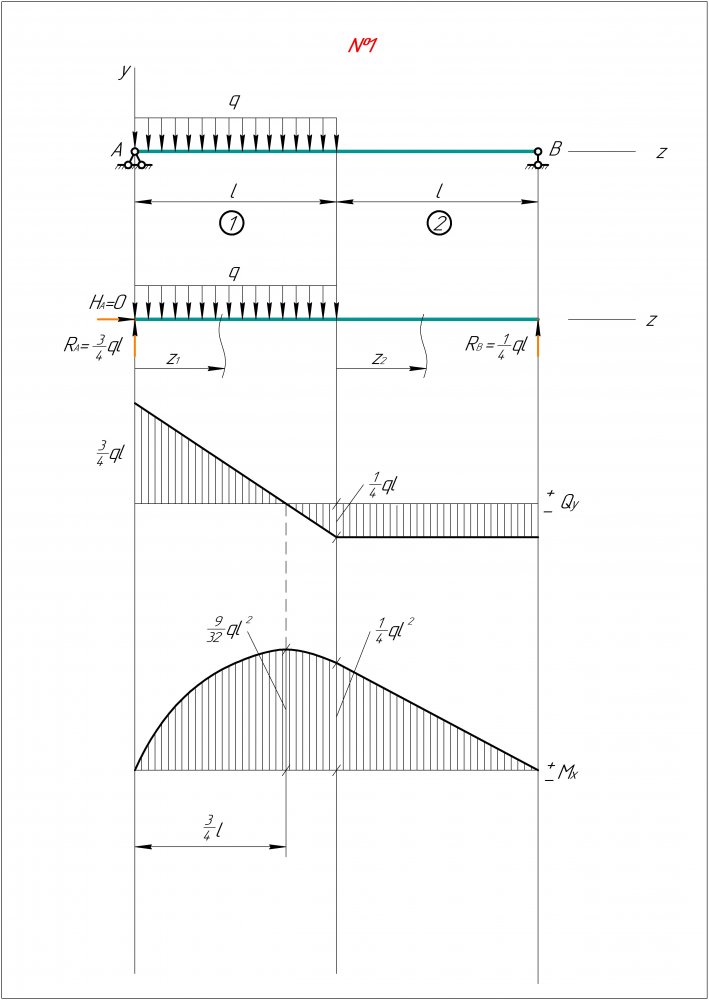
ВЕБ-САЙТ, СОДЕРЖИМОЕ САЙТА, ПРОДУКТЫ И УСЛУГИ, ПРЕДОСТАВЛЯЕМЫЕ НА ВЕБ-САЙТЕ ИЛИ ДОСТУПНЫЕ ЧЕРЕЗ ЕГО, ПРЕДОСТАВЛЯЮТСЯ НА УСЛОВИЯХ «КАК ЕСТЬ» И «КАК ДОСТУПНО», СО ВСЕМИ ОШИБКАМИ.НИ КОМПАНИЯ, НИ ЛЮБОЕ СВЯЗАННОЕ С КОМПАНИЕЙ ЛИЦО НЕ ДАЕТ НИКАКИХ ГАРАНТИЙ ИЛИ ЗАЯВЛЕНИЙ В ОТНОШЕНИИ КАЧЕСТВА, ТОЧНОСТИ ИЛИ ДОСТУПНОСТИ ВЕБ-САЙТА. В ЧАСТНОСТИ, НО НЕ ОГРАНИЧИВАЯ ВЫШЕИЗЛОЖЕННОЕ, НИ КОМПАНИЯ, НИ ЛЮБОЕ СВЯЗАННОЕ С КОМПАНИЕЙ ЛИЦО НЕ ГАРАНТИРУЕТ И НЕ ЗАЯВЛЯЕТ, ЧТО ВЕБ-САЙТ, СОДЕРЖИМОЕ САЙТА ИЛИ УСЛУГИ, ПРЕДОСТАВЛЯЕМЫЕ НА ВЕБ-САЙТЕ ИЛИ ЧЕРЕЗ ВЕБ-САЙТ, БУДУТ ТОЧНЫМИ, НАДЕЖНЫМИ, БЕЗОШИБОЧНЫМИ ИЛИ БЕСПЕРЕБОЙНЫМИ; ЧТО ДЕФЕКТЫ БУДУТ ИСПРАВЛЕНЫ; ЧТО ВЕБ-САЙТ ИЛИ СЕРВЕР, КОТОРЫЙ ДЕЛАЕТ ЕГО ДОСТУПНЫМ, НЕ СОДЕРЖАТ ВИРУСОВ ИЛИ ДРУГИХ ВРЕДНЫХ КОМПОНЕНТОВ; ИЛИ ЧТО ВЕБ-САЙТ БУДЕТ ОТВЕЧАТЬ ВАШИМ ПОТРЕБНОСТЯМ ИЛИ ОЖИДАНИЯМ.КОМПАНИЯ ОТКАЗЫВАЕТСЯ ОТ ВСЕХ ГАРАНТИЙ ЛЮБОГО РОДА, ЯВНЫХ ИЛИ ПОДРАЗУМЕВАЕМЫХ, ВКЛЮЧАЯ ЛЮБЫЕ ГАРАНТИИ КОММЕРЧЕСКОЙ ПРИГОДНОСТИ, ПРИГОДНОСТИ ДЛЯ ОПРЕДЕЛЕННОЙ ЦЕЛИ И НЕНАРУШЕНИЯ ПРАВ.
НИ ПРИ КАКИХ ОБСТОЯТЕЛЬСТВАХ КОМПАНИЯ, ЕЕ ЛИЦЕНЗИАРЫ ИЛИ ПОДРЯДЧИКИ НЕ НЕСУТ ОТВЕТСТВЕННОСТИ ЗА ЛЮБОЙ УЩЕРБ ЛЮБОГО РОДА, ПО ЛЮБОЙ ПРАВОВОЙ ТЕОРИИ, ВОЗНИКШИЙ ИЗ ИЛИ В СВЯЗИ С ИСПОЛЬЗОВАНИЕМ ВАМИ ИЛИ НЕВОЗМОЖНОСТЬЮ ИСПОЛЬЗОВАНИЯ ВЕБ-САЙТА, СОДЕРЖИМОГО САЙТА, ЛЮБЫЕ УСЛУГИ, ПРЕДОСТАВЛЯЕМЫЕ НА ИЛИ ЧЕРЕЗ ВЕБ-САЙТ ИЛИ ЛЮБОЙ ССЫЛОЧНЫЙ САЙТ, ВКЛЮЧАЯ ЛЮБЫЕ ПРЯМЫЕ, КОСВЕННЫЕ, СЛУЧАЙНЫЕ, ОСОБЫЕ, КОСВЕННЫЕ ИЛИ ШТРАФНЫЕ УБЫТКИ, ВКЛЮЧАЯ, ПОМИМО ПРОЧЕГО, ТРАВМЫ, УПУЩЕННУЮ ПРИБЫЛЬ ИЛИ УЩЕРБ В РЕЗУЛЬТАТЕ ЗАДЕРЖКИ, ПЕРЕРЫВА В ОБСЛУЖИВАНИИ , ВИРУСЫ, УДАЛЕНИЕ ФАЙЛОВ ИЛИ ЭЛЕКТРОННЫХ СООБЩЕНИЙ, ИЛИ ОШИБКИ, УПУЩЕНИЯ ИЛИ ДРУГИЕ НЕТОЧНОСТИ НА ВЕБ-САЙТЕ ИЛИ СОДЕРЖИМОМ САЙТА ИЛИ УСЛУГАХ, НЕЗАВИСИМО ОТ НЕБРЕЖНОСТИ СО СТОРОНЫ КОМПАНИИ И БЫЛА ИЛИ НЕ УВЕДОМЛЕНА КОМПАНИЯ О ВОЗМОЖНОСТИ ЛЮБОЙ ТАКОЙ УЩЕРБ, ЕСЛИ НЕ ЗАПРЕЩЕНО ПРИМЕНИМЫМ ЗАКОНОДАТЕЛЬСТВОМ.
Возмещение убытков
Вы соглашаетесь ограждать и ограждать Компанию и ее должностных лиц, директоров, агентов, сотрудников и других лиц, связанных с Веб-сайтом, от любых и всех обязательств, расходов, убытков и издержек, включая разумные гонорары адвокатов, вытекающих из любое нарушение вами настоящих Условий использования, использование вами веб-сайта или любых продуктов, услуг или информации, полученных с веб-сайта или через него, ваше подключение к веб-сайту, любой контент, который вы отправляете на веб-сайт через любую Функция сообщества или нарушение вами каких-либо прав другого лица.
Применимое законодательство; Международное использование
Настоящие условия регулируются и толкуются в соответствии с законами штата Пенсильвания без учета каких-либо принципов коллизионного права. Вы соглашаетесь с тем, что любой иск по закону или справедливости, который возникает из настоящих Условий использования или относится к ним, будет подан исключительно в суды штата или федеральные суды, расположенные в Пенсильвании, и настоящим вы соглашаетесь и подчиняетесь личной юрисдикции таких судов для целей судебного разбирательства любого такого действия.
Настоящие Условия использования применимы к пользователям в США, Канаде и Пуэрто-Рико. Если вы заходите на веб-сайт из-за пределов США, Канады или Пуэрто-Рико, посетите соответствующий международный веб-сайт, доступный по адресу www.vwr.com, для ознакомления с применимыми условиями. Если вы решите получить доступ к этому веб-сайту из-за пределов указанной юрисдикции, а не использовать доступные международные сайты, вы соглашаетесь с настоящими Условиями использования и тем, что такие условия будут регулироваться и толковаться в соответствии с законами Соединенных Штатов и штата. Пенсильвании, и что мы не делаем заявлений о том, что материалы или услуги на этом веб-сайте подходят или доступны для использования в этих других юрисдикциях.В любом случае, все пользователи сами несут ответственность за соблюдение местного законодательства.
Общие условия
Настоящие Условия использования, в которые время от времени могут вноситься поправки, представляют собой полное соглашение и понимание между вами и нами, регулирующее использование вами Веб-сайта. Наша неспособность осуществить или обеспечить соблюдение какого-либо права или положения Условий использования не означает отказ от такого права или положения. Если какое-либо положение Условий использования будет признано судом компетентной юрисдикции недействительным, вы, тем не менее, соглашаетесь с тем, что суд должен приложить усилия для реализации намерений сторон, отраженных в этом положении, и других положений Условия использования остаются в полной силе.Ни курс дел или поведение между вами и Компанией, ни какие-либо торговые практики не должны рассматриваться как изменяющие настоящие Условия использования. Вы соглашаетесь с тем, что независимо от любого закона или закона об обратном, любой иск или основание для иска, вытекающие из или связанные с использованием Сайта или Условий использования, должны быть поданы в течение одного (1) года после такого требования или основания. действия возникло или будет навсегда запрещено. Любые права, прямо не предоставленные в настоящем документе, сохраняются за Компанией и для нее.
Наша неспособность осуществить или обеспечить соблюдение какого-либо права или положения Условий использования не означает отказ от такого права или положения. Если какое-либо положение Условий использования будет признано судом компетентной юрисдикции недействительным, вы, тем не менее, соглашаетесь с тем, что суд должен приложить усилия для реализации намерений сторон, отраженных в этом положении, и других положений Условия использования остаются в полной силе.Ни курс дел или поведение между вами и Компанией, ни какие-либо торговые практики не должны рассматриваться как изменяющие настоящие Условия использования. Вы соглашаетесь с тем, что независимо от любого закона или закона об обратном, любой иск или основание для иска, вытекающие из или связанные с использованием Сайта или Условий использования, должны быть поданы в течение одного (1) года после такого требования или основания. действия возникло или будет навсегда запрещено. Любые права, прямо не предоставленные в настоящем документе, сохраняются за Компанией и для нее. Мы можем прекратить ваш доступ или приостановить доступ любого пользователя ко всему Сайту или его части без предварительного уведомления за любое поведение, которое мы, по нашему собственному усмотрению, считаем нарушением любого применимого закона или наносящим ущерб интересам другого пользователя. , стороннего поставщика, поставщика услуг или нас. Любые вопросы, касающиеся настоящих Условий использования, следует направлять на адрес [email protected].
Мы можем прекратить ваш доступ или приостановить доступ любого пользователя ко всему Сайту или его части без предварительного уведомления за любое поведение, которое мы, по нашему собственному усмотрению, считаем нарушением любого применимого закона или наносящим ущерб интересам другого пользователя. , стороннего поставщика, поставщика услуг или нас. Любые вопросы, касающиеся настоящих Условий использования, следует направлять на адрес [email protected].
Жалобы на нарушение авторских прав
Мы уважаем интеллектуальную собственность других и просим наших пользователей делать то же самое.Если вы считаете, что ваша работа была скопирована и доступна на Сайте таким образом, что это представляет собой нарушение авторских прав, вы можете уведомить нас, предоставив нашему агенту по авторским правам следующую информацию:
электронная или физическая подпись лица, уполномоченного действовать от имени владельца авторского права;
описание защищенной авторским правом работы, права на которую были нарушены в соответствии с вашим заявлением;
указание URL-адреса или другого конкретного места на Сайте, где находится материал, который, по вашему мнению, нарушает авторские права;
ваш адрес, номер телефона и адрес электронной почты;
ваше заявление о том, что вы добросовестно полагаете, что оспариваемое использование не разрешено владельцем авторских прав, его агентом или законом; и
ваше заявление, сделанное под страхом наказания за лжесвидетельство, о том, что приведенная выше информация в вашем уведомлении является точной и что вы являетесь владельцем авторских прав или уполномочены действовать от имени владельца авторских прав.
С нашим агентом для уведомления о нарушении авторских прав на Сайте можно связаться по адресу: [email protected].
Визуализация и построение орбит и плотностей
Бесплатная программа визуализации с открытым исходным кодом IQmol (www.iqmol.org) предоставляет графический пользовательский интерфейс для Q-Chem, который можно использовать в качестве построителя молекулярной структуры, как инструмент для локальной или удаленной отправки заданий Q-Chem, и как инструмент визуализации плотностей и молекулярных орбиталей. Кроме того, Q-Chem может генерировать данные об орбитах и плотности в форматах, подходящих для построения графиков с помощью различных сторонних программ визуализации.
10.6.1 Визуализация орбиталей с помощью MolDen и MacMolPlt
По запросу Q-Chem создаст входной файл для MolDen, бесплатной программы молекулярной визуализации [482, 483]. MolDen можно использовать для просмотра шарико-стержневых молекулярных моделей (включая пошаговую визуализацию оптимизации геометрии), молекулярных орбиталей, нормальных мод колебаний и спектров колебаний.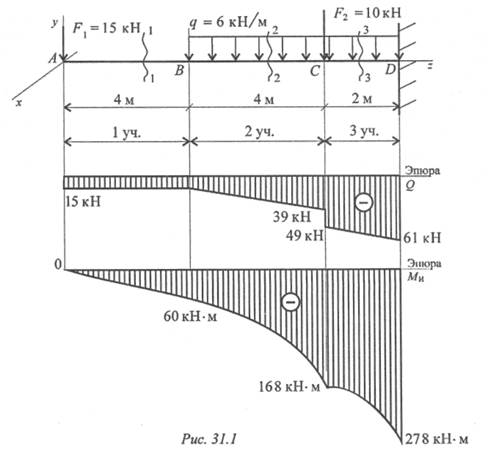 MolDen также содержит мощный матричный редактор Z . В сочетании с Q-Chem орбитальная визуализация через MolDen в настоящее время поддерживается для функций , , и (чистых или декартовых), а также для чистых функций.После установки MOLDEN_FORMAT на TRUE Q-Chem добавит входной файл в формате MolDen в конец файла журнала Q-Chem. Поскольку в некоторых версиях MolDen возникают трудности с анализом самого файла журнала Q-Chem, мы рекомендуем пользователю вырезать и вставлять отформатированную MolDen часть файла журнала Q-Chem в отдельный файл для чтения MolDen.
MolDen также содержит мощный матричный редактор Z . В сочетании с Q-Chem орбитальная визуализация через MolDen в настоящее время поддерживается для функций , , и (чистых или декартовых), а также для чистых функций.После установки MOLDEN_FORMAT на TRUE Q-Chem добавит входной файл в формате MolDen в конец файла журнала Q-Chem. Поскольку в некоторых версиях MolDen возникают трудности с анализом самого файла журнала Q-Chem, мы рекомендуем пользователю вырезать и вставлять отформатированную MolDen часть файла журнала Q-Chem в отдельный файл для чтения MolDen.
MOLDEN_FORMAT
Запрашивает входной файл в формате MolDen, содержащий информацию из задания Q-Chem.
ТИП:
ПО УМОЛЧАНИЮ:
ОПЦИИ:
True
Добавить входной файл MolDen в конец выходного файла Q-Chem.
РЕКОМЕНДАЦИЯ:
Файлы в формате MolDen также могут быть прочитаны MacMolPlt, другой бесплатной программой визуализации [484, 485]. MacMolPlt генерирует орбитальные изоконтурные поверхности намного быстрее, чем MolDen, однако в MacMolPlt эти поверхности доступны только для декартовых гауссовских базисных функций, i.е. , PURECART = 2222 , что может отличаться от значения по умолчанию.
Пример 10.212 Создание файла MolDen для визуализации молекулярных орбиталей.
$молекула
0 1
О
Н 1 0,95
Н 1 0,95 2 104,5
$конец
$rem
МЕТОД hf
ОСНОВА cc-pvtz
PRINT_ORBITALS true (по умолчанию печатается 5 виртуальных орбиталей)
MOLDEN_FORMAT верно
$конец
Для оптимизации геометрии и расчета частоты колебаний достаточно установить для параметра MOLDEN_FORMAT значение TRUE , и соответствующая информация о геометрии или нормальном режиме автоматически появится в разделе MolDen файла журнала Q-Chem.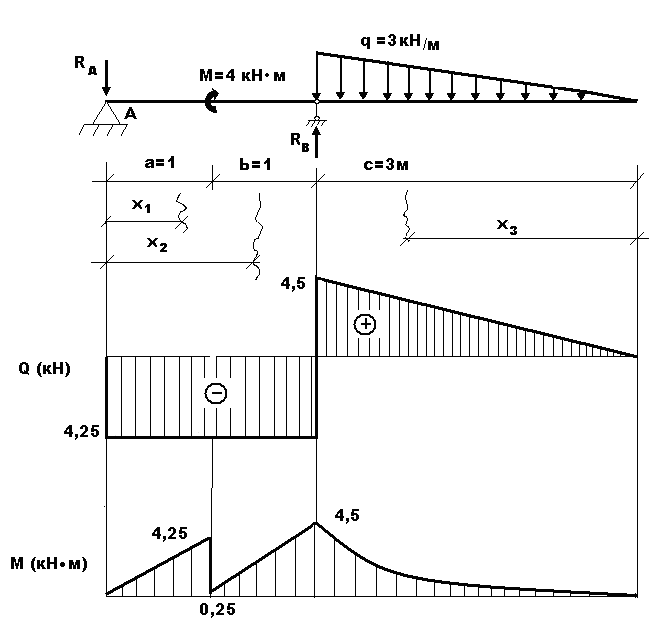
Пример 10.213 Создание файла MolDen для пошаговой оптимизации геометрии.
$молекула
0 1
О
Н 1 0,95
Н 1 0,95 2 104,5
$конец
$rem
ТИП РАБОТЫ опт
МЕТОД hf
БАЗИС 6-31Г*
MOLDEN_FORMAT верно
$конец
10.6.2 Визуализация естественных переходных орбиталей
Для возбужденных состояний, рассчитанных с использованием методов CIS, RPA или TDDFT, построение орбиталей естественного перехода (NTO), как описано в разделе 6.11.2, запрашивается с использованием переменной $rem NTO_PAIRS . Эта переменная также определяет количество пар NTO дырка/частица, которые выводятся для каждого возбужденного состояния. Хотя общее количество пар дырка/частица равно количеству занятых МО, обычно только очень небольшое количество этих пар (часто только одна пара) имеет значительные амплитуды. (Дополнительные NTO большой амплитуды могут встречаться в случаях сильной электронной связи между несколькими хромофорами [110]. )
)
NTO_PAIRS
Управляет записью пар дырка/частица NTO для возбужденного состояния.
ТИП:
ПО УМОЛЧАНИЮ:
ОПЦИИ:
Запись пар NTO на возбужденное состояние.
РЕКОМЕНДАЦИЯ:
Если активировано (), для каждого состояния будет напечатано как минимум две пары NTO.Увеличьте значение, если желательны дополнительные NTO.
Когда NTO_PAIRS , Q-Chem создаст NTO в формате MolDen. NTO зависят от состояния в том смысле, что каждое возбужденное состояние имеет свои собственные NTO, поэтому для каждого возбужденного состояния требуется отдельный файл MolDen. Эти файлы записываются в рабочий каталог задания в подкаталог с именем NTOs , поэтому для получения NTO необходимо сохранить рабочий каталог с помощью параметра –save , описанного в разделе 2. 7. Выходные файлы в каталоге NTOs имеют очевидное соглашение об именах файлов. «Дырчатые» НТО (представляющие собой линейные комбинации занятых МО) печатаются в файлы MolDen в порядке возрастания важности, при этом соответствующие амплитуды возбуждения заменяют канонические собственные значения МО. (Это только соглашение о форматировании; амплитуды возбуждения не связаны с собственными значениями МО.) За дырками следуют NTO «частиц», которые представляют возбужденный электрон и представляют собой линейные комбинации виртуальных МО.Они написаны в порядке убывания амплитуды. Чтобы облегчить различение двух наборов в файлах MolDen, амплитуды дырок указаны с отрицательными знаками, в то время как соответствующий NTO для возбужденного электрона имеет ту же амплитуду с положительным знаком.
7. Выходные файлы в каталоге NTOs имеют очевидное соглашение об именах файлов. «Дырчатые» НТО (представляющие собой линейные комбинации занятых МО) печатаются в файлы MolDen в порядке возрастания важности, при этом соответствующие амплитуды возбуждения заменяют канонические собственные значения МО. (Это только соглашение о форматировании; амплитуды возбуждения не связаны с собственными значениями МО.) За дырками следуют NTO «частиц», которые представляют возбужденный электрон и представляют собой линейные комбинации виртуальных МО.Они написаны в порядке убывания амплитуды. Чтобы облегчить различение двух наборов в файлах MolDen, амплитуды дырок указаны с отрицательными знаками, в то время как соответствующий NTO для возбужденного электрона имеет ту же амплитуду с положительным знаком.
Из-за способа построения NTO (см. Раздел 6.11.2) анализ NTO доступен только тогда, когда количество виртуальных орбиталей превышает количество занятых орбиталей, что может быть не так для минимальных базисных наборов.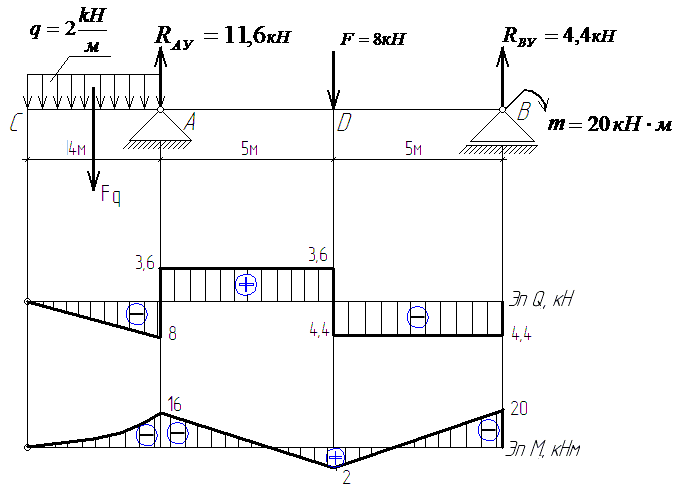
Пример 10.214 Генерация естественных переходных орбиталей в формате MolDen для нескольких возбужденных состояний урацила.
$молекула
0 1
N -2,181263 0,068208 0,000000
С -2,927088 -1,059037 0,000000
N -4,320029 -0,
10.6.3 Генерация объемных данных с использованием
$графиков Самый простой способ визуализации плотности заряда и молекулярных орбиталей, которые оценивает Q-Chem, — это графический пользовательский интерфейс, подобный описанному в предыдущем разделе.Альтернативная процедура, часто полезная для создания высококачественных изображений для публикации, заключается в оценке определенных плотностей и орбиталей на заданной пользователем сетке точек. Это достигается вызовом опции $plots , которая сама активируется запросом IANLTY = 200.
Это достигается вызовом опции $plots , которая сама активируется запросом IANLTY = 200.
Формат ввода $plots описан ниже. Он позволяет отображать молекулярные орбитали, плотности основного состояния SCF и плотности возбужденных состояний, полученные из расчетов CIS, RPA или TDDFT/TDA или TDDFT.Также в связи с возбужденными состояниями также могут быть нанесены либо переходные плотности, плотности присоединения / отсоединения, либо естественные переходные орбитали (на тех же уровнях теории, что и выше).
По умолчанию выводом команды $plots является один (или несколько) ASCII-файлов в рабочем каталоге с именами plot.mo , и т. д. . Затем результаты должны быть визуализированы с помощью сторонней программы, способной создавать трехмерные графики. (Некоторые предложения даны в Разделе 10.6.4.)
Примером использования опции $plots является следующая колода ввода:
Пример 10.215 Задание, которое оценивает H HOMO и LUMO на сетке вдоль оси связи. Результат построения графика находится в файле ASCII с именем plot.mo, в котором для каждой точки сетки перечислены , , , а также значение каждого запрошенного MO.
Результат построения графика находится в файле ASCII с именем plot.mo, в котором для каждой точки сетки перечислены , , , а также значение каждого запрошенного MO.
$молекула
0 1
Н 0,0 0,0 0,35
Н 0,0 0,0 -0,35
$конец
$rem
МЕТОД hf
ОСНОВА 6-31г**
ИАНЛТИ 200
$конец
$сюжеты
Нанесите на линию HOMO и LUMO.
1 0.0 0.0
1 0,0 0,0
15 -3,0 3,0
2 0 0 0
1 2
$конец
Общий формат для раздела $plots входной панели Q-Chem.
$plots
Одна строка комментария
Спецификация трехмерной сетки точек в 3 строках:
Строка с 4 целыми числами, указывающими, сколько элементов строить:
Необязательная строка со списком целых чисел МО для оценки (только если )
МО(1) МО(2) МО()
Необязательная строка с целочисленным списком плотностей для оценки (только если )
Rho(1) Rho(2) Rho()
Необязательный строка с целочисленным списком плотностей перехода (только если )
Trans(1) Trans(2) Trans()
Необязательная строка с состояниями для плотностей отрыва/прикрепления (если )
DA(1) DA(2) DA()
$end
Строка 1 раздела ключевых слов $plots зарезервирована для комментариев.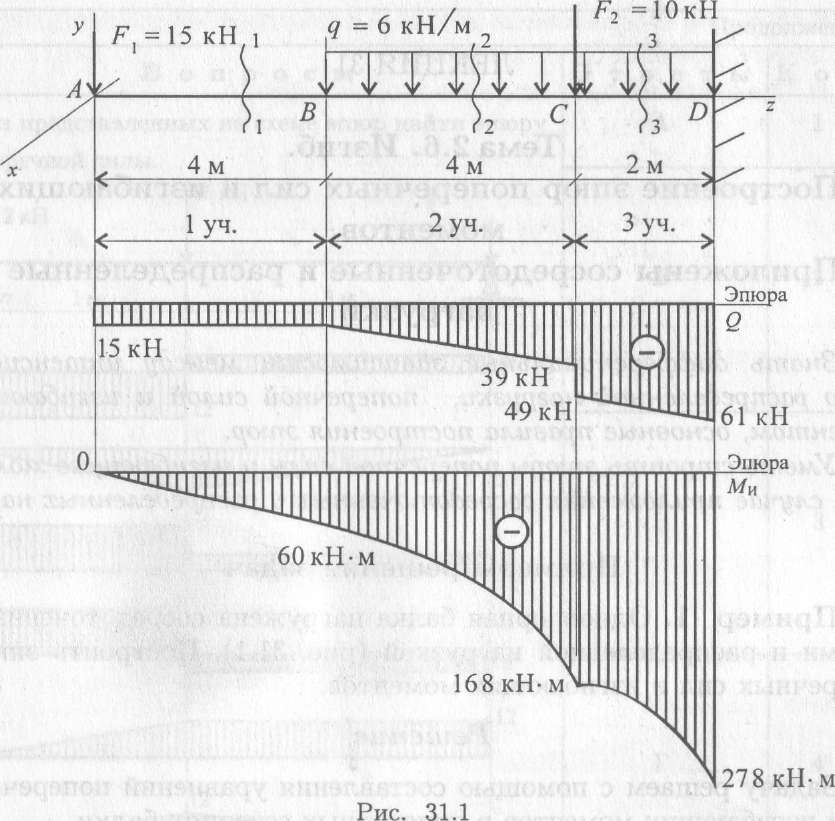 В строках 2–4 указано количество точек одного измерения и диапазон сетки (обратите внимание, что диапазоны координат указаны в ангстремах, а все выходные данные — в атомных единицах). Строка 5 должна содержать 4 неотрицательных целых числа, указывающих количество: молекулярных орбиталей (), плотности электронов (), плотности перехода и плотности присоединения/отсоединения (), чтобы рассчитать значения сетки.
В строках 2–4 указано количество точек одного измерения и диапазон сетки (обратите внимание, что диапазоны координат указаны в ангстремах, а все выходные данные — в атомных единицах). Строка 5 должна содержать 4 неотрицательных целых числа, указывающих количество: молекулярных орбиталей (), плотности электронов (), плотности перехода и плотности присоединения/отсоединения (), чтобы рассчитать значения сетки.
В последних строках указывается, какие МО, плотности электронов, плотности переходов и состояния присоединения/отсоединения CIS должны быть нанесены на график (строка может быть оставлена пустой или удалена, если количество элементов для построения равно нулю).Молекулярные орбитали пронумерованы; плотности электронов пронумерованы, где 0 = основное состояние, 1 = первое возбужденное состояние, 2 = второе возбужденное состояние, и т. д. ; и прикрепить/отсоединить указанное от состояния.
По умолчанию все выходные данные печатаются в файлы в рабочем каталоге, перезаписывая любой существующий файл с таким же именем.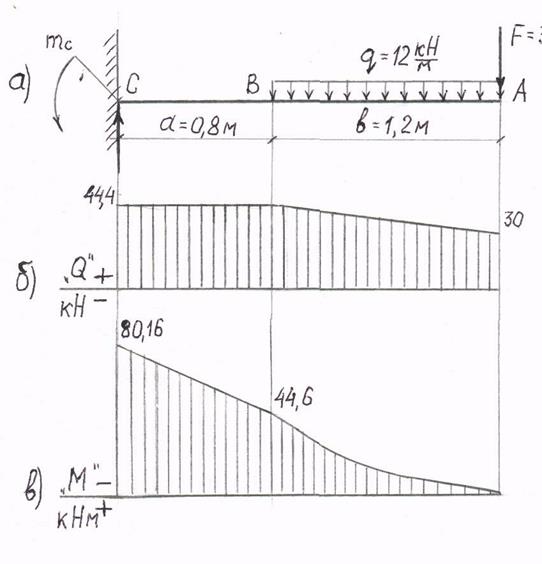
Молекулярные орбитальные данные печатаются в файл с именем plot.mo ;
плотности нанесены на графика.вф ;
ограниченный нерасслабленный анализ привязанности/отделения отправляется на plot.attach.alpha и
plot.detach.alpha ;неограниченный нерасслабленный анализ привязанности/отрыва отправляется на plot.attach.alpha ,
plot.detach.alpha , plot.attach.beta и plot.detach.beta ;анализ ограниченной расслабленной привязанности/отстраненности нанесен на график .attach.rlx.alpha и
plot.detach.rlx.alpha ; и, наконец,неограниченный анализ расслабленной привязанности/отстраненности отправляется на plot.attach.rlx.alpha ,
plot.detach.rlx.alpha , plot.attach.rlx.beta и plot.detach .rlx.бета .
Вывод печатается в атомарных единицах, где сначала координаты, а затем значение элемента, как показано ниже:
x1 y1 z1 a1 a2 ... АН x2 y1 z1 b1 b2 ... bN ...
Вместо стандартной одно-, двух- или трехмерной декартовой сетки пользователь может захотеть отобразить орбитали или плотности в наборе точек сетки по своему выбору. Такие точки задаются с помощью входной секции $grid , формат которой представляет собой просто декартовы координаты всех указанных пользователем точек сетки:
х1 у1 z1 х2 у2 з2 ...
Секция $plots по-прежнему должна быть указана, как описано выше, но если присутствует секция ввода $grid , то эти указанные пользователем точки сетки переопределяют точки, указанные в секции $plots .
Утилита Q-Chem $plots позволяет пользователю строить графики плотности перехода и плотности отсоединения/присоединения непосредственно из амплитуд, сохраненных в результате предыдущего расчета, без необходимости решать пост-SCF (CIS, RPA, TDA или TDDFT) снова уравнения. Чтобы воспользоваться этой функцией, необходимо использовать тот же рабочий каталог Q-Chem, а для переменной SKIP_CIS_RPA $rem должно быть установлено значение TRUE .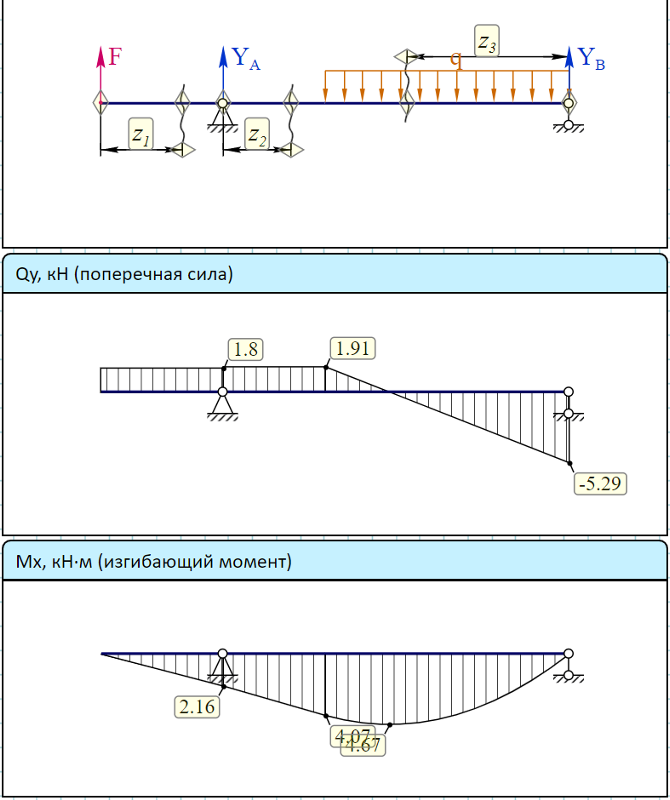 Чтобы еще больше сократить время вычислений, SCF_GUESS $rem можно установить на READ .
Чтобы еще больше сократить время вычислений, SCF_GUESS $rem можно установить на READ .
SKIP_CIS_RPA
Пропускает решение уравнений CIS, RPA, TDA или TDDFT для анализа волновой функции.
ТИП:
ПО УМОЛЧАНИЮ:
ОПЦИИ:
РЕКОМЕНДАЦИЯ:
Установите значение true, чтобы ускорить генерацию данных графика, если те же расчетные файлы были запущены ранее с файлами временных данных.
10.6.4 Прямое создание файлов «кубов»
В качестве альтернативы формату вывода, описанному выше, все данные $plots могут быть выведены непосредственно в подкаталог с именем plots в рабочем каталоге задания, который поэтому должен быть сохранен с использованием параметра –save . описано в Разделе 2.7. Данные построения в этом подкаталоге записываются не в формате plot.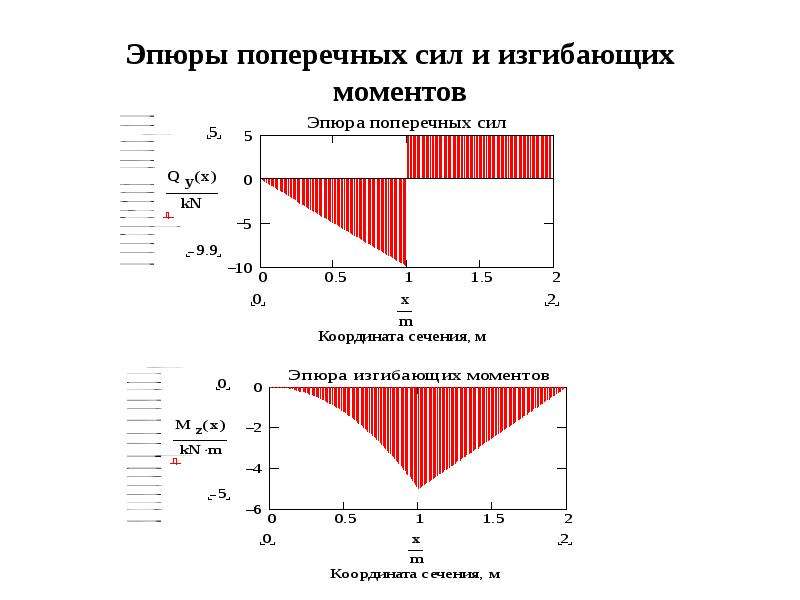 * , описанном выше, а в форме так называемого «кубического» файла, по одному для каждой запрашиваемой орбитали или плотности.Формат «куб» является стандартным для объемных данных и состоит из небольшого заголовка, за которым следуют орбитальные значения или значения плотности в каждой точке сетки в формате ASCII. (Полную спецификацию формата см. в Ref. Herbert:2015a.) Поскольку координаты сетки сами по себе не распечатываются (их расположение подразумевается из информации, содержащейся в заголовке), каждый отдельный файл куба намного меньше, чем соответствующий график .* файл был бы. Кубические файлы могут быть прочитаны многими стандартными (и свободно доступными) графическими программами, включая MacMolPlt [484, 485] и VMD [487, 488].VMD, в частности, рекомендуется для создания высококачественных изображений для публикации. Файлы куба для MO и плотностей, запрошенные в разделе $plots , запрашиваются путем установки MAKE_CUBE_FILES на TRUE с разделом $plots , указанным в разделе 10.
* , описанном выше, а в форме так называемого «кубического» файла, по одному для каждой запрашиваемой орбитали или плотности.Формат «куб» является стандартным для объемных данных и состоит из небольшого заголовка, за которым следуют орбитальные значения или значения плотности в каждой точке сетки в формате ASCII. (Полную спецификацию формата см. в Ref. Herbert:2015a.) Поскольку координаты сетки сами по себе не распечатываются (их расположение подразумевается из информации, содержащейся в заголовке), каждый отдельный файл куба намного меньше, чем соответствующий график .* файл был бы. Кубические файлы могут быть прочитаны многими стандартными (и свободно доступными) графическими программами, включая MacMolPlt [484, 485] и VMD [487, 488].VMD, в частности, рекомендуется для создания высококачественных изображений для публикации. Файлы куба для MO и плотностей, запрошенные в разделе $plots , запрашиваются путем установки MAKE_CUBE_FILES на TRUE с разделом $plots , указанным в разделе 10. 6.3.
6.3.
MAKE_CUBE_FILES
Запрашивает создание файлов куба для MO, NTO или NBO.
ТИП:
ПО УМОЛЧАНИЮ:
ОПЦИИ:
ЛОЖЬ
Не создавать кубические файлы.
ИСТИНА
Создание кубических файлов для MO и плотностей.
NTOS
Создание файлов куба для NTO.
NBOS
Создание файлов куба для NBO.
РЕКОМЕНДАЦИЯ:
PLOT_SPIN_DENSITY
Запросы генерации спиновых плотностей и .
ТИП:
ПО УМОЛЧАНИЮ:
ОПЦИИ:
ЛОЖЬ
Не создавать файлы куба плотности вращения.
ИСТИНА
Создание файлов куба плотности вращения.
РЕКОМЕНДАЦИЯ:
Установите значение TRUE , если в дополнение к общей плотности требуются значения плотности вращения.Требуется, чтобы параметр MAKE_CUBE_FILES также был установлен на TRUE , и чтобы в секции ввода $plots запрашивалась одна или несколько общих плотностей. Затем также будут генерироваться соответствующие спиновые плотности.
Следующий пример иллюстрирует создание кубических файлов для плотности основного и возбужденного состояния, включая соответствующие плотности спина. В этом примере подкаталог plots временного каталога задания должен содержать файлы с именами dens.N.cube (общая плотность для состояния , где или 1 соответствует основному и первому возбужденному состоянию соответственно), dens_alpha.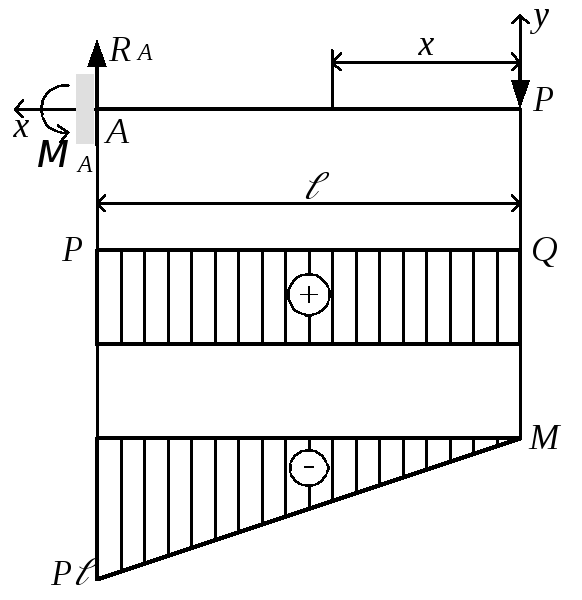 N.cube и dens_beta.N.cube (и для каждого состояния) и dens_spin.N.cube (для каждого state.)
N.cube и dens_beta.N.cube (и для каждого состояния) и dens_spin.N.cube (для каждого state.)
Пример 10.216 Создание файлов куба плотности и спиновой плотности для основного и первого возбужденного состояния радикала HOO.
$молекула
0 2
Н 1,004123 -0,180454 0,000000
О -0,246002 0,596152 0,000000
О -1.312366 -0,230256 0,000000
$конец
$rem
plot_spin_density правда
make_cube_files верно
scf_convergence 8
метод b3lyp
основа 6-31+Г*
cis_n_roots 1
$конец
$сюжеты
информация о сетке и запрос на построение 2 плотностей
20 -5,0 5,0
20 -5,0 5,0
20 -5,0 5,0
0 2 0 0
0 1
$конец
Файлы куба также доступны для естественных переходных орбиталей (разделы 6.11.2 и 10.6.2) путем установки MAKE_CUBE_FILES на NTOS , хотя в этом случае процедура несколько сложнее из-за состояния- специфика этих величин.Файлы куба для NTO генерируются только для одного возбужденного состояния, идентификатор которого указывается с помощью CUBEFILE_STATE .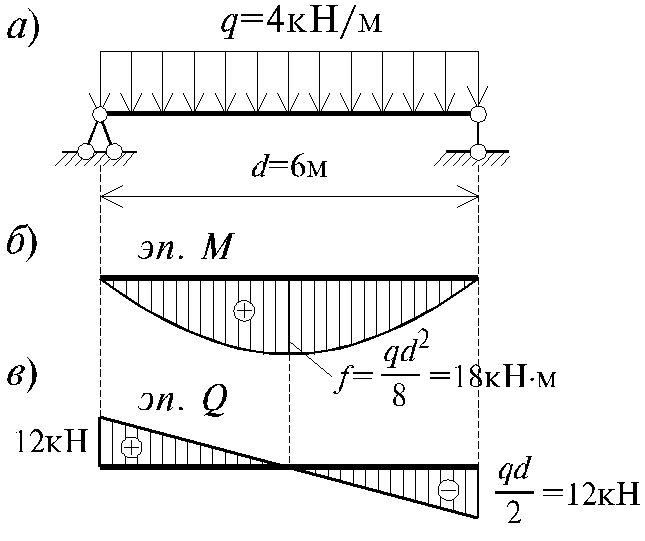 Кубические файлы для дополнительных состояний легко получить с помощью последовательности заданий Q-Chem, в которых второе (и последующие) задания считывают конвергентную информацию об основном и возбужденном состояниях, используя SCF_GUESS и SKIP_CIS_RPA .
Кубические файлы для дополнительных состояний легко получить с помощью последовательности заданий Q-Chem, в которых второе (и последующие) задания считывают конвергентную информацию об основном и возбужденном состояниях, используя SCF_GUESS и SKIP_CIS_RPA .
CUBEFILE_STATE
Определяет, какое возбужденное состояние используется для создания кубических файлов
ТИП:
ПО УМОЛЧАНИЮ:
ОПЦИИ:
Создание кубических файлов для возбужденного состояния th
РЕКОМЕНДАЦИЯ:
Дополнительным усложнением является способ указать, какие NTO будут выводиться в виде файлов куба.Когда для MAKE_CUBE_FILES установлено значение TRUE , это указывается в разделе $plots таким же образом, как МО задаются для построения графиков.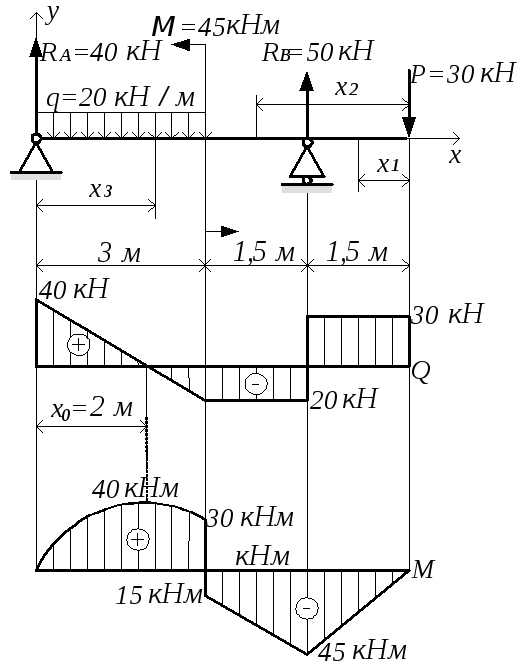 Однако необходимо понимать порядок, в котором хранятся NTO. Для системы с -спиновыми МО занятые NTO хранятся в порядке возрастания амплитуды, так что ‘-й занятый NTO является наиболее важным. Затем виртуальные NTO сохраняются в порядке уменьшения важности . Согласно этому соглашению, самая высокая занятая амплитуда возбуждения NTO (HONTO) и самая низкая незанятая амплитуда возбуждения NTO (LUNTO) всегда является наиболее значимой для любого конкретного возбужденного состояния.Таким образом, орбитали и представляют самую важную пару NTO, а орбитали и представляют собой вторую по значимости пару NTO, и т. д. .
Однако необходимо понимать порядок, в котором хранятся NTO. Для системы с -спиновыми МО занятые NTO хранятся в порядке возрастания амплитуды, так что ‘-й занятый NTO является наиболее важным. Затем виртуальные NTO сохраняются в порядке уменьшения важности . Согласно этому соглашению, самая высокая занятая амплитуда возбуждения NTO (HONTO) и самая низкая незанятая амплитуда возбуждения NTO (LUNTO) всегда является наиболее значимой для любого конкретного возбужденного состояния.Таким образом, орбитали и представляют самую важную пару NTO, а орбитали и представляют собой вторую по значимости пару NTO, и т. д. .
Пример 10.217 Создание кубических файлов для возбуждения HONTO-to-LUNTO второго синглетного возбужденного состояния урацила. Обратите внимание, что для урацила.
$молекула
0 1
N -2,181263 0,068208 0,000000
С -2,927088 -1,059037 0,000000
N -4,320029 -0,
 ..
КУБФАЙЛ_СОСТОЯНИЕ 2 ! ...для 2-го возбужденного состояния
$конец
..
КУБФАЙЛ_СОСТОЯНИЕ 2 ! ...для 2-го возбужденного состояния
$конец
Файлы кубов для орбиталей естественных связей (для основного состояния или любого возбужденного состояния CIS, RPA или TDDFT) можно создать практически таким же образом, установив MAKE_CUBE_FILES равным NBOS и используя CUBEFILE_STATE для выбора желаемого электронного состояния. CUBEFILE_STATE = 0 выбирает NBO в основном состоянии. Конкретные NBO для построения выбираются с использованием раздела $plots с учетом того, что Q-Chem хранит NBO в порядке убывания заполнения, при этом все NBO со спинами предшествуют любым NBO со спинами в случае неограниченного вычисления SCF.(Для основных состояний обычно имеется один сильно занятый NBO для каждого электрона.) Файлы куба NBO сохраняются в подкаталоге plots рабочего каталога задания. Последнее предостережение: чтобы получить файлы куба NBO, пользователь должен указать параметр AONBO в разделе $nbo , как показано в следующем примере.
Пример 10.218 Генерация кубических файлов для NBO первого возбужденного состояния .
$rem
МЕТОД СНГ
ОСНОВА СС-ПВТЗ
CIS_N_ROOTS 1
CIS_TRIPLETS ЛОЖЬ
НБО 2! NBO в основном и возбужденном состоянии
MAKE_CUBE_FILES NBOS! генерировать файлы куба NBO...
КУБФАЙЛ_СОСТОЯНИЕ 1 ! ... для первого возбужденного состояния
$конец
$нбо
АОНБО
$конец
$молекула
0 1
О
Н 1 0,95
Н 1 0,95 2 104,5
$конец
$сюжеты
Постройте 5 NBO с высокой занятостью, по одному для каждого альфа-электрона
40 -8,0 8,0
40 -8,0 8,0
40 -8,0 8,0
5 0 0 0
1 2 3 4 5
$конец
10.6.5 Графики NCI
Мы реализовали графики нековалентного взаимодействия (NCI) от группы Weitao Yang [489, 490]. Для создания этих графиков можно установить для переменной PLOT_REDUCED_DENSITY_GRAD $rem значение TRUE (см.в примере ввода в каталоге $QC/samples ).
Ошибка неработающей ссылки
ЕСЕ 1250-001 Весна 2018 г.
Авторизоваться
Приборная панель
Календарь
Входящие
История
Помощь
- Мой Dashboard
- ECE 1250-001 Весна 2018 г.
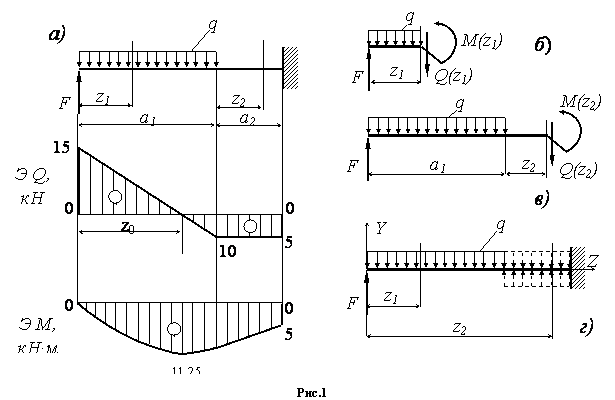
- Главная
- Назначения
- стр.
- Pages
- Syllabus
- Media Gallery
- My Media
- Office 365
- Adobe Creative Cloud
- Conexed
- Zoom
- Курс Обратная связь
К сожалению, вы нашли неработающую ссылку!
Колонки VP-HayeSep Q PLOT
Дивинилбензол высокой чистотыПОДОБНЫЕ ФАЗЫ
HP-PLOT Q, CP-PoraPLOT Q, Rt-Q Bond, Supel Q PLOT, AT-Q
ОСНОВНЫЕ ПРИМЕНЕНИЯ
Растворители, углеводороды, спирты, соединения серы, остаточные растворители, галогенированные углеводороды
HayeSep D представляет собой более чистую форму пористого полимера HayeSep Q и имеет сходные
характеристики удержания. HayeSep D более высокой чистоты дает колонки PLOT с
превосходные эксплуатационные характеристики по сравнению с производимыми с HayeSep Q.
В течение нескольких лет мы использовали HayeSep D более высокой степени очистки для изготовления HayeSep D/Q.
столбцы СЮЖЕТ. Наши колонки HayeSep D/Q сопоставимы с колонками других производителей.
производители колонн Q-типа. Мы сохранили оба названия продуктов для наших клиентов.
удобство.
HayeSep D более высокой чистоты дает колонки PLOT с
превосходные эксплуатационные характеристики по сравнению с производимыми с HayeSep Q.
В течение нескольких лет мы использовали HayeSep D более высокой степени очистки для изготовления HayeSep D/Q.
столбцы СЮЖЕТ. Наши колонки HayeSep D/Q сопоставимы с колонками других производителей.
производители колонн Q-типа. Мы сохранили оба названия продуктов для наших клиентов.
удобство.
| Материал | ID | Длина | мкм df | Артикул № |
|---|---|---|---|---|
| Плавленый кварц | 0,32 мм | 15 метров | 10 | КФС-PQ1532-100 |
| 30 метров | 10 | КФС-PQ3032-100 | ||
| 0,53 мм | 15 метров | 20 | КФС-PQ1553-200 | |
| 30 метров | 20 | КФС-PQ3053-200 |
Квантильный график — обзор
7.
 3.2
Оценка подгонки параметрических семейств
3.2
Оценка подгонки параметрических семействСначала мы обсудим частный случай семейств место-масштаб, которые включают в себя нормальные и экспоненциальные семейства. Этот метод также можно применять для проверки соответствия моделей, которые могут быть преобразованы в семейства в масштабе местоположения. Например, логнормальные модели и модели Вейбулла могут быть преобразованы в семейства в масштабе местоположения путем применения к данным логарифмического преобразования.
Как мы уже отмечали, в модели масштаба местоположения F0([x-µ|/σ) график Q–Q является приблизительно линейным с наклоном 1/σ и точкой пересечения -µ/σ.Таким образом, мы можем оценить гипотезу местоположения-масштаба, проверив, следует ли график Q-Q некоторой линейной конфигурации без указания наклона и точки пересечения линии. Таким образом, мы можем использовать тот же график Q-Q без каких-либо изменений, чтобы проверить соответствие всего семейства местоположений-масштабов cdfs . Заметим также, что нам не нужно оценивать неизвестные параметры µ и σ.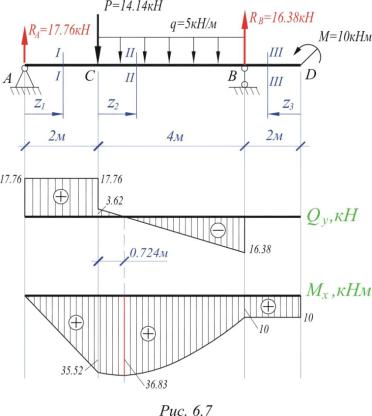 Эти свойства делают использование графика Q – Q особенно привлекательным. Рассмотрим некоторые важные частные случаи семейств пространственного масштаба.
Эти свойства делают использование графика Q – Q особенно привлекательным. Рассмотрим некоторые важные частные случаи семейств пространственного масштаба.
Однопараметрическая экспоненциальная модель с cdf 1-exp(-kr) представляет собой масштабное семейство. Это естественно возникает в области надежности и других приложениях, где интерес сосредотачивается на частоте отказов (или скорости затухания). Экспоненциальное распределение характеризуется тем, что оно имеет постоянную частоту отказов (или скорость затухания). Построение экспоненциального графика Q – Q уже обсуждалось в предыдущем разделе. При экспоненциальности график должен быть приблизительно линейным с наклоном λ и точкой пересечения 0.
Если экспоненциальная модель не соответствует данным, естественным следующим шагом является рассмотрение более общей модели Вейбулла с cdf 1−exp(−[x/α]β) для некоторых α>0 и β>0. Это семейство распределений включает экспоненциальную модель как частный случай, когда β=1.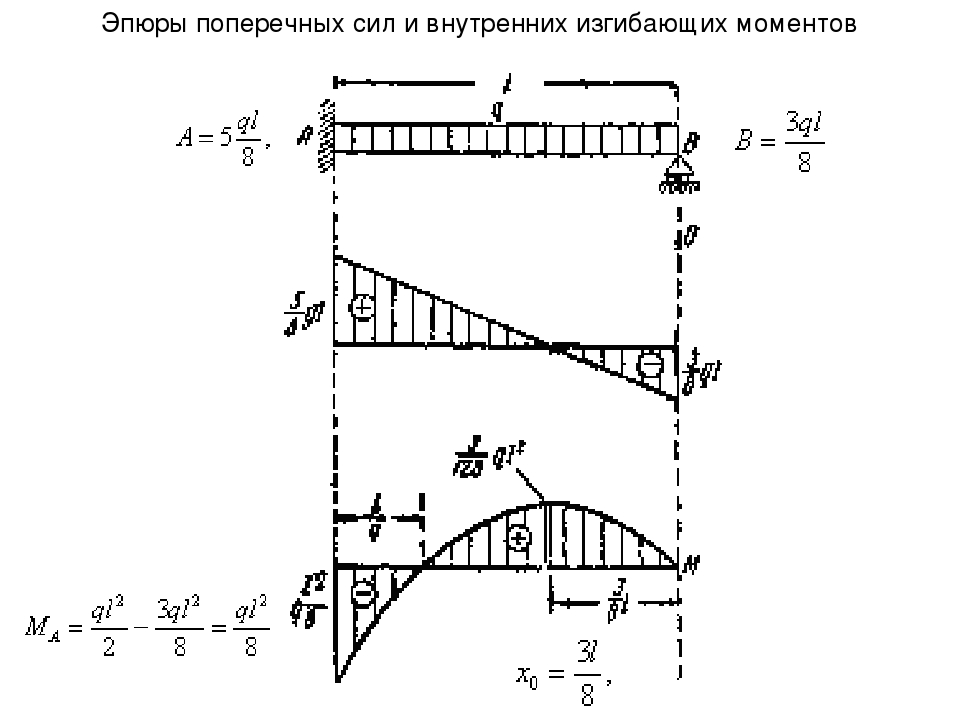 Это гибкое семейство, которое можно использовать для моделирования различных задач. Семейство Вейбулла не является семейством в масштабе местоположения, но его можно превратить в одно, применив логарифмическое преобразование. В частности, если Y имеет распределение Вейбулла, то X = log( Y ) имеет распределение наименьшего экстремального значения (SEV), которое представляет собой семейство масштабов местоположения с параметром местоположения µ = log (α) и масштабом параметр σ=β-1.Таким образом, график Q – Q с X(i)=log(Y(i)) и F0-1(pi)=log[-log(1-pi)] можно использовать для оценки соответствия моделей Вейбулла. В модели Вейбулла график будет линейным с наклоном 1/σ=β и точкой пересечения -µ/σ=βlog(α). В частности, если верна экспоненциальная модель, линия будет иметь наклон 1. Рекомендации, обсуждавшиеся в предыдущем подразделе, можно использовать для интерпретации отклонений от линейности.
Это гибкое семейство, которое можно использовать для моделирования различных задач. Семейство Вейбулла не является семейством в масштабе местоположения, но его можно превратить в одно, применив логарифмическое преобразование. В частности, если Y имеет распределение Вейбулла, то X = log( Y ) имеет распределение наименьшего экстремального значения (SEV), которое представляет собой семейство масштабов местоположения с параметром местоположения µ = log (α) и масштабом параметр σ=β-1.Таким образом, график Q – Q с X(i)=log(Y(i)) и F0-1(pi)=log[-log(1-pi)] можно использовать для оценки соответствия моделей Вейбулла. В модели Вейбулла график будет линейным с наклоном 1/σ=β и точкой пересечения -µ/σ=βlog(α). В частности, если верна экспоненциальная модель, линия будет иметь наклон 1. Рекомендации, обсуждавшиеся в предыдущем подразделе, можно использовать для интерпретации отклонений от линейности.
Нормальное распределение играет центральную роль в статистике, и оценка того, принадлежит ли данное распределение нормальному семейству, является часто возникающей проблемой.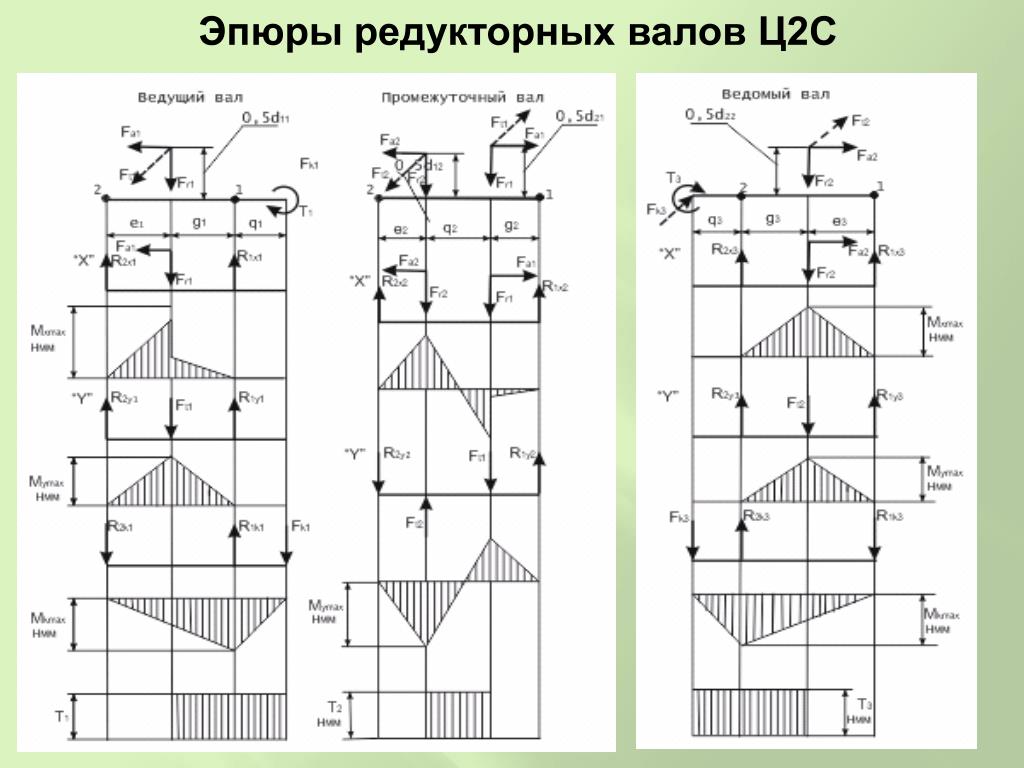 Кроме того, логнормальное распределение оказалось полезным при моделировании данных с тяжелыми хвостами, таких как данные разведки нефти и газа и экологические данные о качестве воздуха. Нормальный график Q–Q получается, если принять F0(x) в (7.7) за стандартную нормаль cdf Φ(x). При нормальной модели график будет приблизительно линейным с наклоном 1/σ и точкой пересечения -µ/σ. График Q – Q для оценки логнормальности получают, сначала логарифмируя данные, а затем используя нормальный график Q – Q.
Кроме того, логнормальное распределение оказалось полезным при моделировании данных с тяжелыми хвостами, таких как данные разведки нефти и газа и экологические данные о качестве воздуха. Нормальный график Q–Q получается, если принять F0(x) в (7.7) за стандартную нормаль cdf Φ(x). При нормальной модели график будет приблизительно линейным с наклоном 1/σ и точкой пересечения -µ/σ. График Q – Q для оценки логнормальности получают, сначала логарифмируя данные, а затем используя нормальный график Q – Q.
Пример
Как мы уже видели, рисунок 3(a) представляет собой экспоненциальный график Q–Q для данных об отказах механического устройства. Поскольку никакая линия, проходящая через начало координат, не соответствует данным, мы можем сделать вывод, что экспоненциальная модель не подходит для этого набора данных. График кажется нелинейным с выпуклой формой, что предполагает модель Вейбулла как возможную альтернативу. График Вейбулла Q-Q на рисунке 3(b) приблизительно линейный, что позволяет предположить, что модель Вейбулла правдоподобна.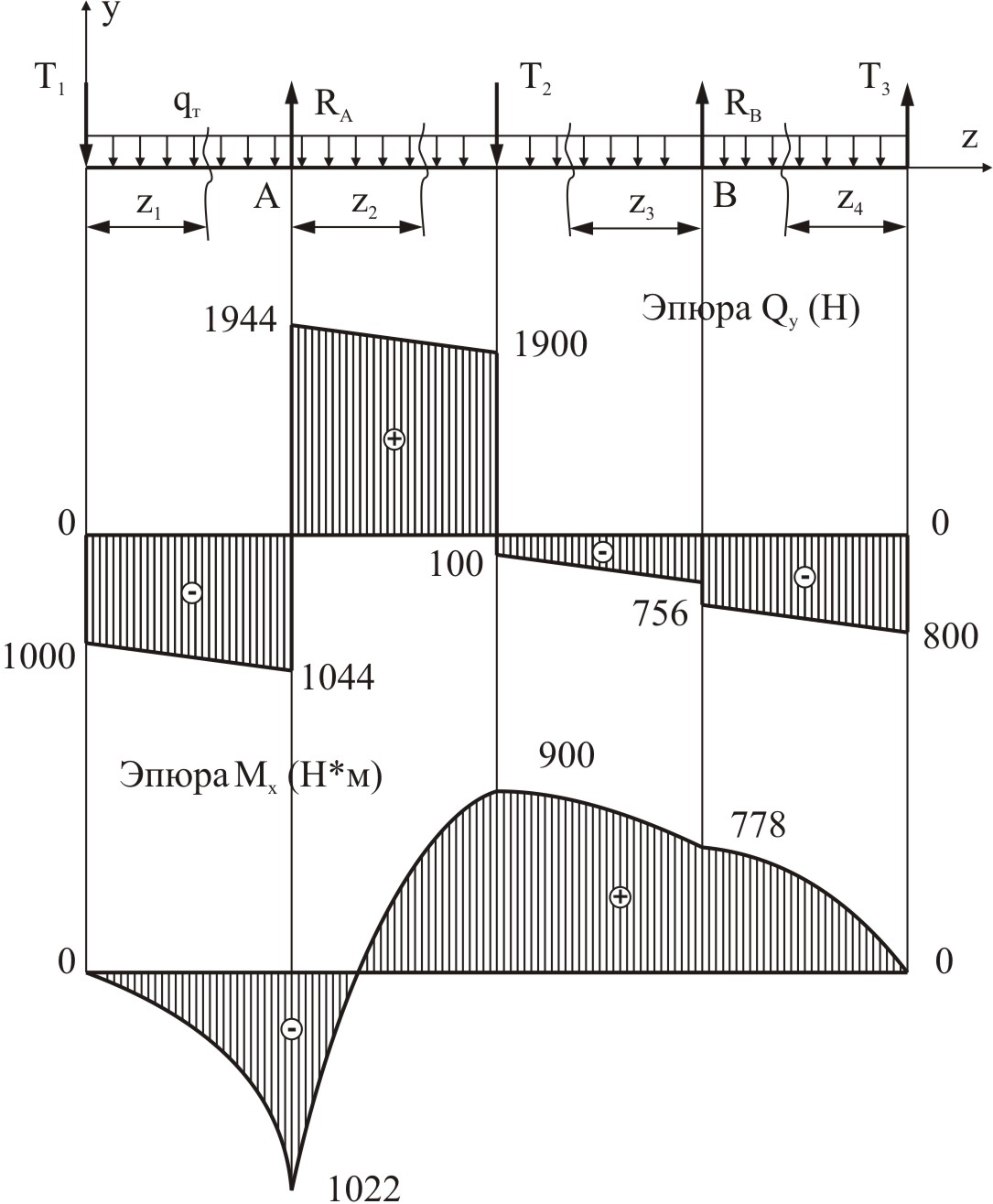 Логнормальный график Q – Q показан на рисунке 3(c) и предполагает, что логнормальная модель может быть немного лучше.
Логнормальный график Q – Q показан на рисунке 3(c) и предполагает, что логнормальная модель может быть немного лучше.
Чтобы распространить метод построения графика Q–Q на более общие параметрические семейства, такие как бета или гамма, мы должны сначала оценить неизвестные параметры θ . Для оценки этих параметров можно использовать метод максимального правдоподобия, который будет обсуждаться в главе 8. После получения оценки θ график Q–Q для оценки сложной гипотезы (7.). В соответствии с нулевой гипотезой график должен быть приблизительно линейным с наклоном 1 и точкой пересечения 0. Отклонения от линейности можно интерпретировать, используя рекомендации, обсуждавшиеся в последнем разделе.
| 1.
Исследовательский анализ данных 1.3. Методы ЭДА 1.3.3. Графические приемы: Алфавитный
| |||
| Цель: Проверить, могут ли два набора данных соответствовать одному и тому же распределению | График квантиль-квантиль (qq) — это графический метод.
для определения того, получены ли два набора данных из популяций с
общий дистрибутив. График qq представляет собой график квантилей первых данных. против квантилей второго набора данных. Под квантилем мы понимаем долю (или процент) баллов ниже заданного значения. То есть квантиль 0,3 (или 30%) это точка, в которой 30% процентов данных падают ниже и 70% падают выше этого значения. Также наносится опорная линия под углом 45 градусов. Если два
наборы исходят из популяции с таким же распределением,
точки должны падать примерно вдоль этой опорной линии.То
больше отклонение от этой опорной линии, тем больше
доказательства для вывода о том, что два набора данных пришли
из популяций с разным распределением. Преимущества графика q-q:
График q-q похож на вероятностный график. Для график вероятности, квантили для одной из выборок данных заменяются квантилями теоретического распределение. | ||
| Пробный участок | Этот график qq
набор данных JAHANMI2.
| ||
| Определение: квантилей для набора данных 1 в сравнении с квантилями для набора данных 2 | График q-q формируется:
Обе оси указаны в единицах соответствующих наборов данных.То есть фактический уровень квантиля не отображается.
Для данной точки на графике qq мы знаем
что уровень квантиля одинаков для обеих точек,
но не то, чем на самом деле является этот квантильный уровень. Если наборы данных имеют одинаковый размер, график q-q по сути, график отсортированного набора данных 1 против отсортированный набор данных 2. Если наборы данных не имеют одинакового размера, квантили обычно выбираются в соответствии с отсортированные значения из меньшего набора данных, а затем квантили для большего набора данных интерполируются. | ||
| вопросов | График q-q используется для ответа на следующие вопросы:
| ||
| Важность: Проверить наличие общего дистрибутива | Когда есть две выборки данных, часто желательно
чтобы узнать, верно ли предположение об общем распределении
оправдано. Если это так, то оценщики местоположения и масштаба могут
объединить оба набора данных, чтобы получить оценки общего местоположения
и масштаб. Если две выборки различаются, также полезно получить
некоторое понимание различий. График qq может
дать более полное представление о характере различий
чем аналитические методы, такие как хи-квадрат
и двухвыборочные тесты Колмогорова-Смирнова. Если это так, то оценщики местоположения и масштаба могут
объединить оба набора данных, чтобы получить оценки общего местоположения
и масштаб. Если две выборки различаются, также полезно получить
некоторое понимание различий. График qq может
дать более полное представление о характере различий
чем аналитические методы, такие как хи-квадрат
и двухвыборочные тесты Колмогорова-Смирнова. | ||
| Связанные методы | Бигистограмма T-тест F-тест 2-выборочный критерий хи-квадрат 2-выборочный критерий Колмогорова-Смирнова | ||
| Практический пример | График квантиль-квантиль демонстрируется на керамическая прочность тематическое исследование данных. | ||
| Программное обеспечение | Графики Q-Q доступны в некоторых статистических
программные продукты. Если количество точек данных в двух выборках одинаково,
должно быть относительно легко написать макрос в статистическом
программы, которые не поддерживают график q-q. Если число
точек не равны, запись макроса для графика q-q может
быть трудным. Если количество точек данных в двух выборках одинаково,
должно быть относительно легко написать макрос в статистическом
программы, которые не поддерживают график q-q. Если число
точек не равны, запись макроса для графика q-q может
быть трудным. | ||
Диаграммы прямоугольной формы
Чтобы понять сюжеты типа «ящик с усами», вы должны понять медианы и квартили набора данных.
Медиана — это среднее число набора данных или среднее значение двух средних чисел (если имеется четное количество точек данных).
Медиана ( Вопрос 2 ) делит набор данных на две части: верхний набор и нижний набор. То нижний квартиль ( Вопрос 1 ) — медиана нижней половины, а верхний квартиль ( Вопрос 3 ) является медианой верхней половины.
Пример:
Находить
Вопрос
1
,
Вопрос
2
, и
Вопрос
3
для следующего набора данных и нарисуйте график в виде прямоугольника и усов.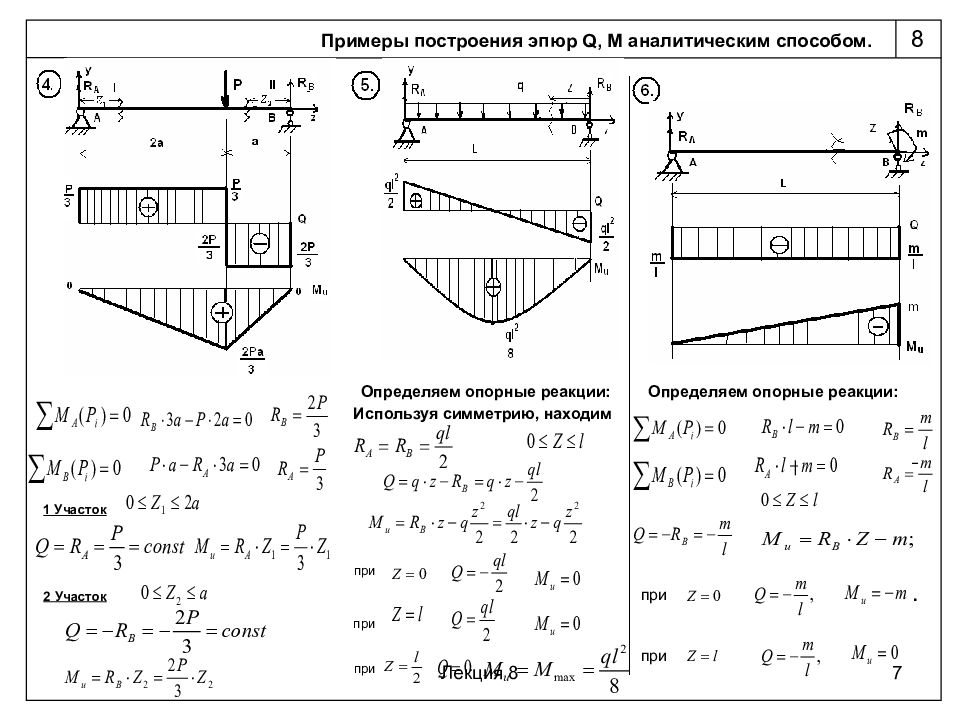
{ 2 , 6 , 7 , 8 , 8 , 11 , 12 , 13 , 14 , 15 , 22 , 23 }
Есть 12 точки данных.Средние два 11 и 12 . Итак, медиана, Вопрос 2 , является 11,5 .
«Нижняя половина» набора данных — это набор { 2 , 6 , 7 , 8 , 8 , 11 } . Медиана здесь 7,5 . Так Вопрос 1 знак равно 7,5 .
«Верхняя половина» набора данных — это набор
{
12
,
13
,
14
,
15
,
22
,
23
}
.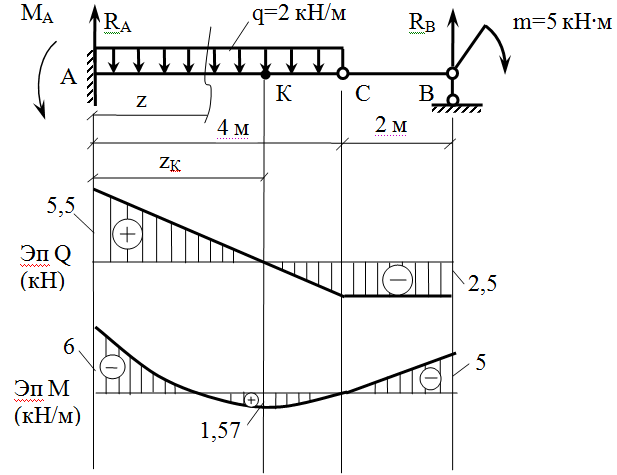 Медиана здесь
14,5
. Так
Вопрос
3
знак равно
14,5
.
Медиана здесь
14,5
. Так
Вопрос
3
знак равно
14,5
.
На графике «ящик с усами» отображаются значения Вопрос 1 , Вопрос 2 , и Вопрос 3 , наряду с экстремальными значениями набора данных ( 2 и 23 , в таком случае):
На графике «коробка с усами» показана «коробка» с левым краем в Вопрос 1 , правый край в Вопрос 3 , «середина» коробки в Вопрос 2 (медиана) и максимум и минимум как «усы».
Обратите внимание, что график делит данные на
4
равные части. Левый ус представляет дно
25
%
данных, левая половина поля представляет второй
25
%
, правая половина прямоугольника представляет третий
25
%
, а правый ус представляет вершину
25
%
.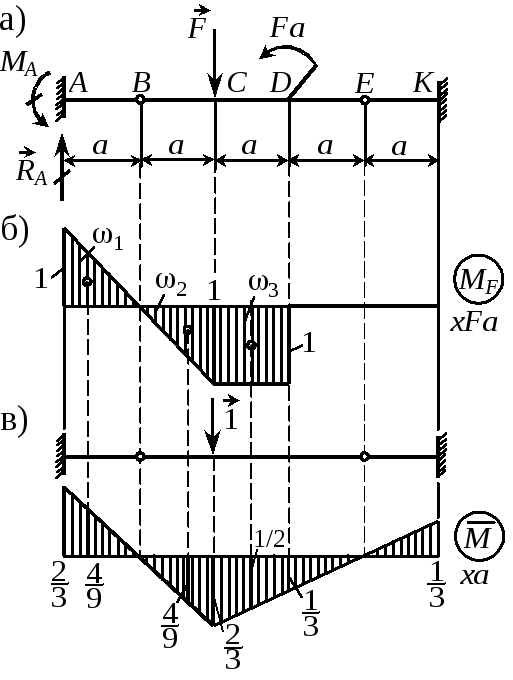
Выбросы
Если значение данных очень далеко от квартилей (намного меньше, чем Вопрос 1 или намного больше, чем Вопрос 3 ), его иногда обозначают выброс .Вместо того, чтобы показывать с помощью усов графика «ящик с усами», выбросы обычно показываются в виде отдельных точек на графике.
Стандартное определение выброса — это число меньше
Вопрос
1
или больше, чем
Вопрос
3
более чем
1,5
раз
межквартильный диапазон
(
IQR
знак равно
Вопрос
3
−
Вопрос
1
).
То есть выброс — это любое число меньше
Вопрос
1
−
(
1.5
×
IQR
)
или больше, чем
Вопрос
3
+
(
1,5
×
IQR
)
.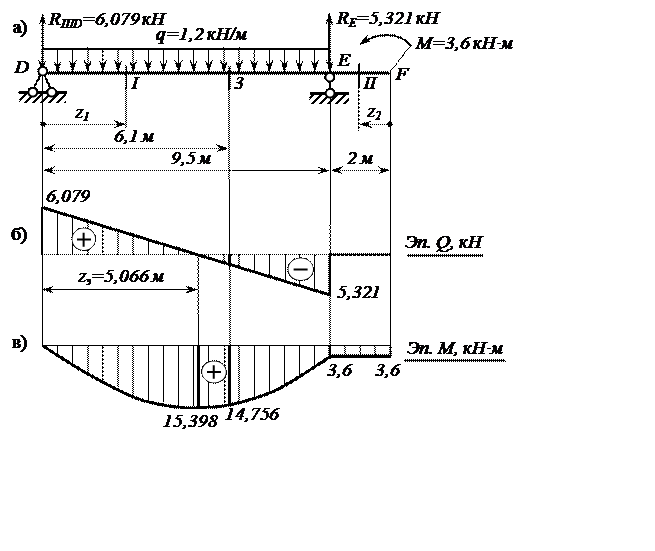
Пример:
Находить Вопрос 1 , Вопрос 2 , и Вопрос 3 для следующего набора данных. Определите любые выбросы и нарисуйте график типа «ящик с усами».
{ 5 , 40 , 42 , 46 , 48 , 49 , 50 , 50 , 52 , 53 , 55 , 56 , 58 , 75 , 102 }
Есть
15
значения, расположенные в порядке возрастания. Так,
Вопрос
2
это
8
й
точка данных,
50
.
Так,
Вопрос
2
это
8
й
точка данных,
50
.
Вопрос 1 это 4 й точка данных, 46 , и Вопрос 3 это 12 й точка данных, 56 .
Межквартильный диапазон IQR является Вопрос 3 − Вопрос 1 или 56 − 47 знак равно 10 .
Теперь нам нужно найти, есть ли значения меньше, чем
Вопрос
1
−
(
1,5
×
IQR
)
или больше, чем
Вопрос
3
+
(
1,5
×
IQR
)
.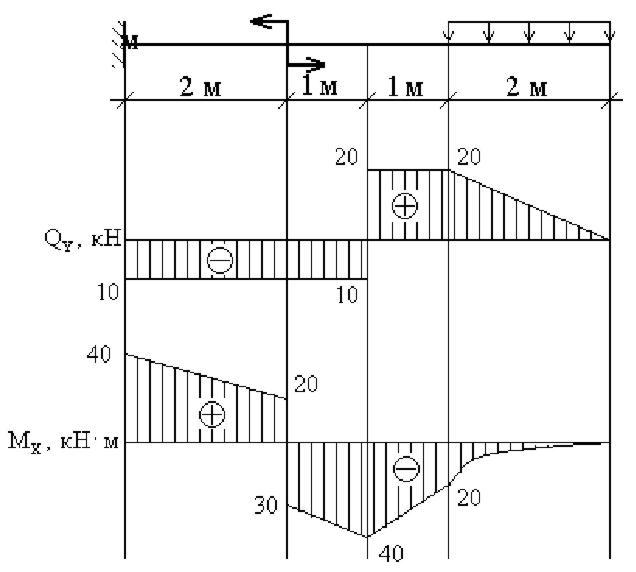
Вопрос 1 − ( 1,5 × IQR ) знак равно 46 − 15 знак равно 31
Вопрос 3 + ( 1.5 × IQR ) знак равно 56 + 15 знак равно 71
С 5 меньше чем 31 и 75 и 102 больше, чем 71 , Есть 3 выбросы.
График коробки и усов, как показано. Обратите внимание, что 40 и 58 показаны как концы усов, а выбросы нанесены отдельно.
.
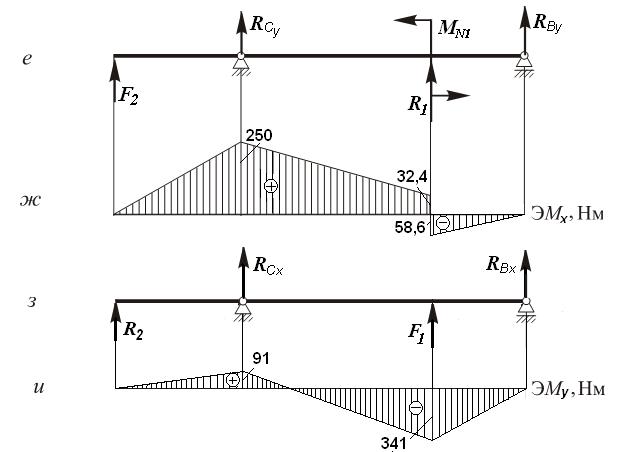
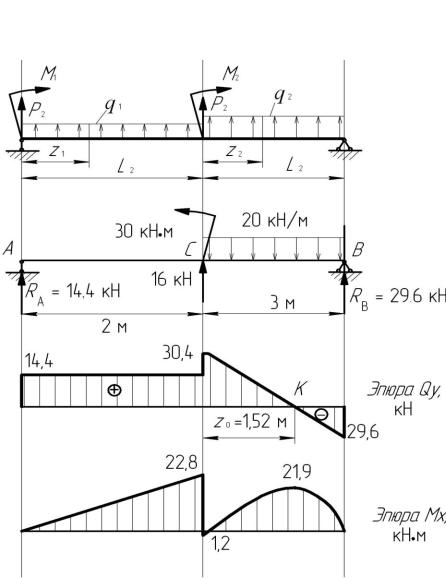
 3.3.24.
3.3.24.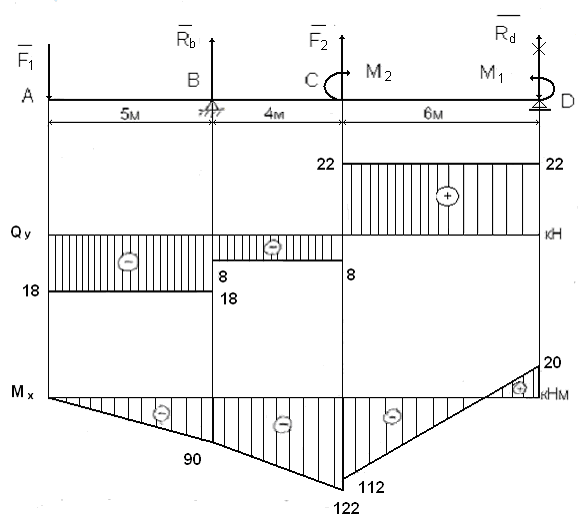
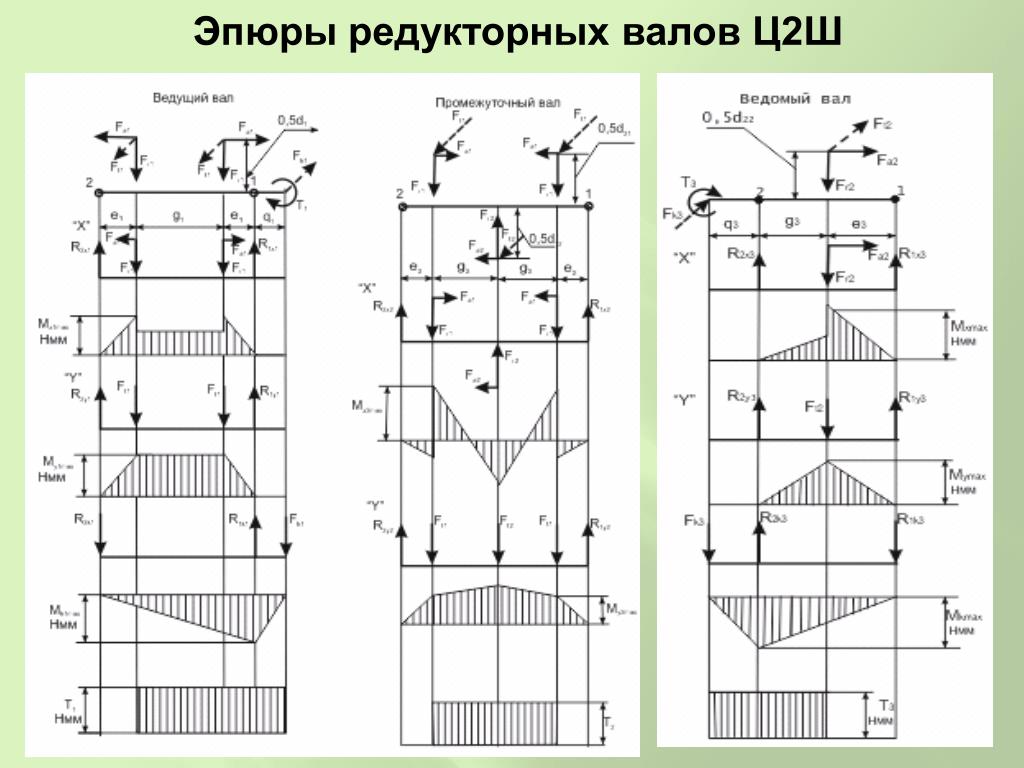 DAT
показывает, что
DAT
показывает, что