Эпюра внутренних сил для продольно распределенной нагрузки

Пример решения задачи построения эпюры внутренних продольных сил N_z для стержня с продольно распределенной нагрузкой q.

Задача

Рассчитать значения внутренних продольных сил N и построить их эпюру для стержня к которому приложены сосредоточенная сила и продольная равномерно распределенная нагрузка

для дальнейшего расчета на прочность.

Другие примеры решений >
Помощь с решением задач >

Пример решения

Предыдущий пункт решения задачи:

• Расчет опорной реакции в заделке стержня.

Рассматриваемый стержень имеет два силовых участка, обозначим их цифрами I и II.

Для расчета внутренних сил на них воспользуемся методом сечений.

Начнем с первого силового участка BC.
Мысленно рассекаем участок в произвольном месте между сечениями B и C.

Выбираем для рассмотрения левую часть стержня, так как к ней приложено меньшее количество нагрузок.

Внутренняя сила на I силовом участке равна сумме внешних сил (с учетом правила знаков при растяжении-сжатии) приложенных к рассматриваемой отсеченной части стержня:

Так как на данном участке нет распределенной нагрузки, полученное значение N_I будет одинаковым для всех сечений первого участка.

Другие видео

Переходим на второй силовой участок CD.
Проведя сечение,

рассматриваем правую часть стержня.

На данном участке есть распределенная нагрузка поэтому необходимо показать расстояние от границы участка до рассматриваемого сечения обозначив его переменной z₂.

Интервал возможных значений переменной z₂ лежит в пределах от 0 до 50см, т.е. 0 ≤ z₂ ≤ 0,5м.

Выражение для расчета N_II

В полученном выражении переменная z₂ в первой степени, следовательно, зависимость линейная.

Рассчитаем значения внутренней силы N_II на границах участка при z₂=0 и z

2=0,5м.

По полученным данным строим эпюру N.

На I участке в соответствии с выбранным масштабом откладываем вниз от базовой линии значение 30 кН и проводим горизонтальную линию в пределах участка.

На II участке было получено 2 значения. Переменная z₂ откладывалась от правой границы участка (сечения D) поэтому под сечением D где z₂=0 ставим точку на базовой линии.

Под сечением C где z₂=0,5м откладываем значение 20кН.

Полученные точки соединяем прямой линией, проставляем знаки, заштриховываем и проверяем построенную эпюру.

Другие примеры решения задач >

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

---

НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ

На нашем сайте можно бесплатно скачать:

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Сохранить или поделиться с друзьями

---

Заказать решение

---

Поиск формул и решений задач

Задача 7 | ПроСопромат.

ру

Построение  эпюр М и Q в балке на двух опорах с определенными опорными реакциями. Построение методом характерных точек.

1. Построение эпюры Q_у.  Из теоретического курса известно, что на участке балки с равномерно распределенной нагрузкой эпюра Q_у ограничивается наклонной прямой, а на участке, на котором нет распределенной нагрузки, — прямой, параллельной оси, поэтому для построения эпюры поперечных сил достаточно определить значения Q_у в начале и конце каждого участка. В сечении, соответствующем точке приложения сосредоточенной силы, поперечная сила должна быть вычислена чуть левее этой точки (на бесконечно близком расстоянии от нее) и чуть правее ее; поперечные силы в таких местах обозначаются соответственно  .

Строим эпюру Q_у методом характерных точек, ходом слева. Для большей наглядности отбрасываемую часть балки на первых порах рекомендуется закрывать листом бумаги. Характерными точками для двухопорной балки (рис. а) будут точки C и D – начало и конец распределенной нагрузки, а также  A   и B – точки приложения опорных реакций, E– точка приложения сосредоточенной силы. Проведем мысленно ось y перпендикулярно оси балки через точку С и не будем менять ее положение, пока не пройдем всю балку от C до E. Рассматривая левые отсеченные по характерным точкам части балки, проецируем на ось y действующие на данном участке силы с соответствующими знаками. В результате получаем:

Для проверки правильности определения поперечной силы в сечениях можно пройти балку аналогичным образом, но с правого конца. Тогда отсеченными будут правые части балки. Результат должен получиться тот же. Совпадение результатов может служить контролем построения эпюры Q_у. Проводим нулевую линию под изображением балки и от нее в принятом масштабе откладываем найденные значения поперечных сил с учетом знаков в соответствующих точках. Получим эпюру Q_у (рис. б).

Построив эпюру, обратите внимание на следующее: эпюра под распределенной нагрузкой изображается наклонной прямой, под ненагруженными участками — отрезками, параллельными нулевой линии, под сосредоточенной силой на эпюре образуется скачок, рав­ный значению силы. Если наклонная линия под распределенной на­грузкой пересекает нулевую линию, отметьте эту точку, то это точка экстремума, и она является теперь для нас характерной, согласно дифференциальной зависимости между Q_у и М_x, в этой точке момент имеет экстремум и его нужно будет определить при построении эпюры изгибающих моментов.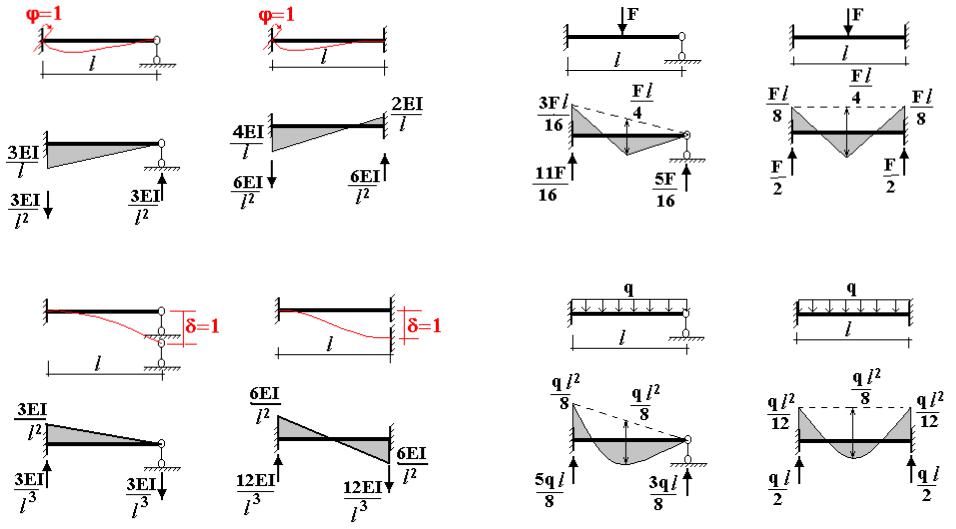 В нашей задаче это точка К. Сосредоточенный момент на эпю­ре Q_у себя никак не проявляет, так как сумма проекций сил, образую­щих пару, равна нулю.

2. Построение эпюры моментов.Строим эпюру изгибающих моментов, как и поперечных сил, ме­тодом характерных точек, ходом слева. Известно, что на участке балки с равномерно распределенной нагрузкой эпюра изгибающих моментов очерчивается кривой линией (квадратичной параболой), для построения которой надо иметь не менее трех точек и, следовательно, должны быть вычислены значе­ния изгибающих моментов в начале участка, конце его и в одном проме­жуточном сечении. Такой промежуточной точкой лучше всего взять сечение, в кото­ром эпюра Q_у пересекает нулевую линию, т.е. где Q_у= 0. На эпюре М в этом сечении должна находиться вершина параболы. Если же эпюра Q_у не пересекает нулевую линию, то для построения эпюры М следует на данном участке взять дополнительную точку, к примеру, в середине участка (начала и конца действия распределенной нагрузки), помня, что выпуклостью парабола всегда обращена вниз, если на­грузка действует сверху вниз (для строительных специальностей). Существует правило «дождя», которое очень помогает при построении параболической части эпю­ры М.  Для строителей это правило выглядит следующим образом: представьте, что распределенная нагрузка — это дождь, подставьте под него зонт в перевернутом виде, так чтобы дождь не стекал, а собирался в нем. Тогда выпуклость зонта будет обращена вниз. Точно так и бу­дет выглядеть очертание эпюры моментов под распределенной нагрузкой. Для механиков существует так называемое  правило «зонта». Распределенная нагрузка представляется дождем, а очертание эпюры должно напоминать очертания зонтика. В данном примере эпюра построена для строителей.

Если требуется более точное построение эпюры, то должны быть вычислены значения изгибающих моментов в нескольких промежуточ­ных сечениях. Условимся для каждого такого участка изгибающий момент сначала определить в произвольном сечении, выражая его через расстояние х от какой-либо точки. Затем, давая расстоянию х ряд значений, получим значения изгибающих моментов в соответствую­щих сечениях участка. Для участков, на которых нет распределенной нагрузки, изгибающие моменты определяют в двух сечениях, соот­ветствующих началу и концу участка, так как эпюра М на таких участках ограничивается прямой. Если к балке приложен внешний сосредоточенный момент, то обязательно надо вычислять изгибающий момент чуть левее места приложения сосредоточенного момента и чуть правее его.

Для двухопорной балки характерные точки следующие: C и D – начало и конец распределенной нагрузки; А – опора балки; В – вторая опора балки и точка приложения сосредоточенного момента; Е – правый конец балки; точка К, соответствующая сечению балки, в котором Q_у = 0.

Ход слева. Правую часть до рассматриваемого сечения мысленно отбрасываем (возьмите лист бумаги и прикройте им отбрасываемую часть балки). Находим сумму моментов всех сил, действующих слева от сечения относительно рассматриваемой точки. Итак,

Прежде чем определить момент в сечении К, необходимо найти расстояние х=АК. Составим выражение для поперечной силы в данном сечении и приравняем его к нулю (ход слева):

Это расстояние можно найти также из подобия треугольников KLN и KIG на эпюре Q_у (рис.б).

Определяем момент в точке К:

Пройдем оставшуюся часть балки ходом справа.

Как видим, момент в точке D при ходе слева и справа получился одинаковый – эпюра замкнулась. По найденным значениям строим эпюру. Положительные значения откладываем вниз от нулевой линии, а отрицательные – вверх (см. рис. в).

Построение диаграмм сдвига и момента

Опубликовано 21 июля 2021 г. Автор: Abigail Stason

Решить реакции

1)      Нарисуйте свободное тело балки, показав фактические распределенные нагрузки.

2)      Начертите второе свободное тело, заменив любые распределенные нагрузки эквивалентными сосредоточенными нагрузками. Величина нагрузок может быть рассчитана по их площадям и помещена в их центроиды, как указано в таблице ниже. Обратите внимание, что показанные области относятся только к перечисленным уравнениям. Таким образом, площадь для 3x ²  + 2x нет в списке! Кроме того, нулевые концы парабол, кубиков и т. д. являются вершинами  (т. е. форма начинается с нулевого наклона). Площади не указаны ни для каких других условий.

3)      Суммируйте моменты левой реакции, чтобы определить правую реакцию.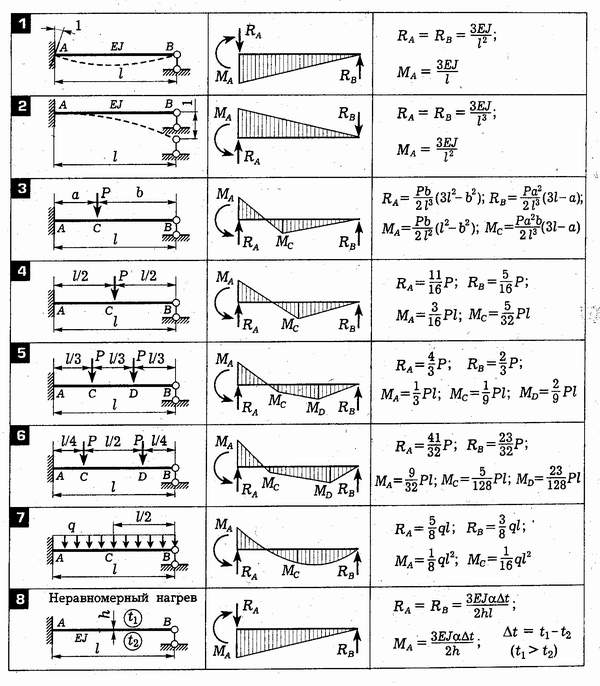 Затем суммируйте моменты о правильной реакции, чтобы определить другую реакцию. Затем просуммируйте вертикальные силы для проверки результатов.

4)      Сотрите вторую диаграмму нагрузки с заменой распределенных нагрузок. Он используется только для решения реакций.

Чтобы построить диаграмму сдвига

1)      Под первой диаграммой нагрузки проведите вертикальные линии на каждой сосредоточенной нагрузке, на каждом сосредоточенном моменте и на обоих концах каждой распределенной нагрузки.

2)      Начиная с левого края рисунка, делайте все, что вам говорят нагрузки. Если вы пересечете нагрузку нулевой ширины (сосредоточенную нагрузку), двигающуюся ВНИЗ, площадь под этой нагрузкой (ее величина) сместит диаграмму сдвига ВНИЗ на величину этой нагрузки на расстоянии нулевой ширины. (Замените ВНИЗ на ВВЕРХ, если это уместно.) Таким образом, после прохождения сосредоточенной нагрузки значение диаграммы сдвига должно мгновенно измениться на величину нагрузки и в направлении, на которое направлена ​​нагрузка.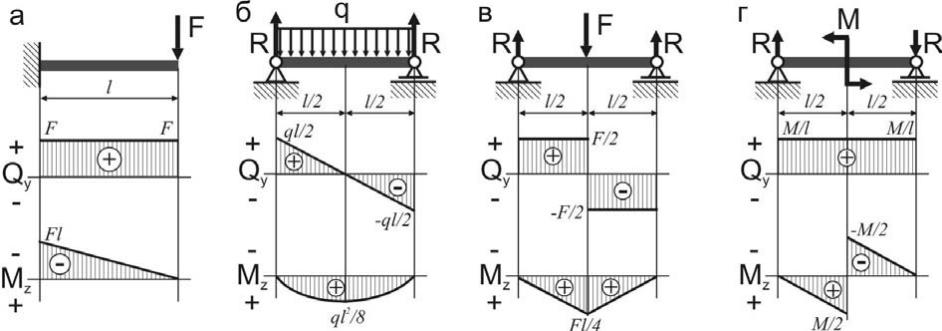

3)      Если вы пересекаете распределенную нагрузку, идущую ВНИЗ, величина под этой распределенной нагрузкой (ее площадь) сместит диаграмму сдвига ВНИЗ на эту величину, превышающую базовый размер распределенной нагрузки. (Замените ВНИЗ на ВВЕРХ, если это необходимо.) Таким образом, после того, как вы закончите прохождение по ширине распределенной нагрузки, значение диаграммы сдвига изменится на величину распределенной нагрузки и в направлении, на которое направлена ​​нагрузка. Распределенные нагрузки, направленные вниз, смещают диаграмму сдвига вниз и наоборот.

4)      Форма диаграммы нагрузки будет определять форму диаграммы сдвига непосредственно ниже. Форма диаграммы нагрузки всегда меняется на следующую форму, показанную в таблице «Площади и центроиды» выше. Таким образом, если нагрузка представляет собой прямую горизонтальную линию, форма диаграммы сдвига будет представлять собой прямую наклонную линию. Если диаграмма нагрузки представляет собой параболу, то диаграмма сдвига будет кубической.

5)      Вы можете сказать, должна ли треугольная диаграмма нагрузки «превратиться» в «тощую» параболу или в «толстую» параболу, используя исчисление: значение в любой точке любой диаграммы «превращается» (интегрируется) в наклон следующей диаграммы. Таким образом, если вы видите нагрузку с нулевой величиной где-либо на балке, вы должны увидеть наклон с нулевой величиной на диаграмме сдвига в этой же точке. Если вы видите небольшие нагрузки, то они должны «превратиться» в диаграммы сдвига с «малыми» уклонами. Если вы видите большие нагрузки, они должны «превратиться» в большие уклоны на диаграмме сдвига.

6)      Поскольку сосредоточенные моменты не имеют сил «вверх-вниз», они не вызывают никакого изменения величины диаграммы сдвига в точках приложения. Это не означает, что они не влияют на диаграмму сдвига, потому что они влияют. Они влияют на него, изменяя реакции, что, в свою очередь, влияет на диаграмму сдвига. Таким образом, вы не увидите никаких изменений на диаграмме сдвига в точке приложения сосредоточенного момента.

Построение моментной диаграммы

1)      Под диаграммой сдвига проведите вертикальные линии в каждой интересующей точке, в том числе каждый раз, когда диаграмма сдвига пересекает ось, и в сосредоточенные моменты.

2)      Начиная с левого края фигуры, делайте все, что вам говорят ножницы. Если вы пересекаете распределенный сдвиг, идущий ВНИЗ, величина под этим распределенным сдвигом (его площадь) сдвинет диаграмму моментов ВНИЗ на эту величину по сравнению с базовым размером распределенного сдвига. (Замените ВНИЗ на ВВЕРХ, когда это необходимо.) Таким образом, после того, как вы закончите рассмотрение ширины распределенного сдвига, значение диаграммы моментов изменится на величину распределенного сдвига и в направлении, указанном сдвигом. Поскольку области сдвига не будут иметь маленьких стрелок, указывающих вверх или вниз, как это было на диаграммах нагрузки, используйте области сдвига выше оси как положительные (толкает диаграмму моментов вверх), а области сдвига ниже оси как отрицательные (толкает диаграмму моментов вниз). )

3)      Форма диаграммы сдвига будет предсказывать форму диаграммы моментов непосредственно ниже. Форма диаграммы сдвига всегда меняется на следующую форму, показанную в таблице «Площади и центроиды» выше. Таким образом, если сдвиг представляет собой прямую наклонную линию, форма диаграммы сдвига будет параболой. Если диаграмма сдвига представляет собой параболу, то диаграмма моментов будет кубической.

4)      С помощью исчисления можно определить, должна ли треугольная диаграмма сдвига «превратиться» в «тощую» параболу или в «толстую» параболу: значение в любой точке любой диаграммы «превращается» (интегрируется) в наклон следующей диаграммы. Таким образом, если вы видите сдвиг с нулевой величиной где-либо на балке, вы должны увидеть наклон с нулевой величиной на диаграмме моментов в этой же точке. Если вы видите небольшие сдвиги, они должны «превратиться» в диаграммы моментов с «малыми» наклонами. Если вы видите большие сдвиги, они должны «превратиться» в большие уклоны на диаграмме моментов.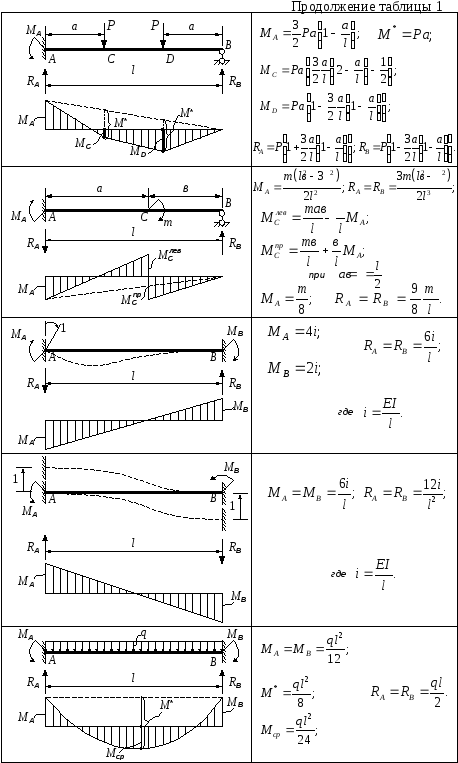

5)      Концентрированные моменты заставляют величину моментной диаграммы «прыгать» в точках их приложения. Внешние моменты, действующие по часовой стрелке на балку, заставляют внутренний момент в балке справа от точки приложения становиться положительным (или более положительным, чем если бы момент не был приложен). Таким образом, внешние моменты, действующие по часовой стрелке на балку, вызывают диаграмма моментов, чтобы мгновенно «подпрыгнуть» от текущего значения. Величина, на которую «подпрыгивает» диаграмма момента, является величиной приложенного момента. Моменты против часовой стрелки заставляют диаграмму моментов «прыгать вниз». Таким образом, вы получаете интересный эффект, заключающийся в том, что «положительные» внешние моменты (используя ваше соглашение о знаках статики) вызывают «отрицательные» скачки на диаграмме моментов (используя ваше соглашение о знаках конструкции балки). Опять же, вы должны рисовать свои диаграммы слева направо. для применения этих правил.

Filed Under: Uncategorized

СИЛА НА ПЕРЕРЕЗ И ИЗГИБАЮЩИЙ МОМЕНТ

11 сентября 2021 г. 21 апреля 2023 г.

СИЛА НА СДВИГ определяется как алгебраическая сумма всех вертикальных сил либо с левой, либо с правой стороны сечения.

ИЗГИБАЮЩИЙ МОМЕНТ определяется как алгебраическая сумма моментов всех сил слева или справа от сечения.

 

ЗНАК УСЛОВИЙ:

• Сдвиг по часовой стрелке будет принят как положительный , а сдвиг против часовой стрелки будет принят как отрицательный .

• Изгибающий момент, вызывающий вогнутость вверх , будет принят как положительный и будет называться провисающим изгибающим моментом.

• Изгибающий момент, вызывающий выпуклость вверх , будем считать отрицательным и будем называть Изгибающий момент.

 

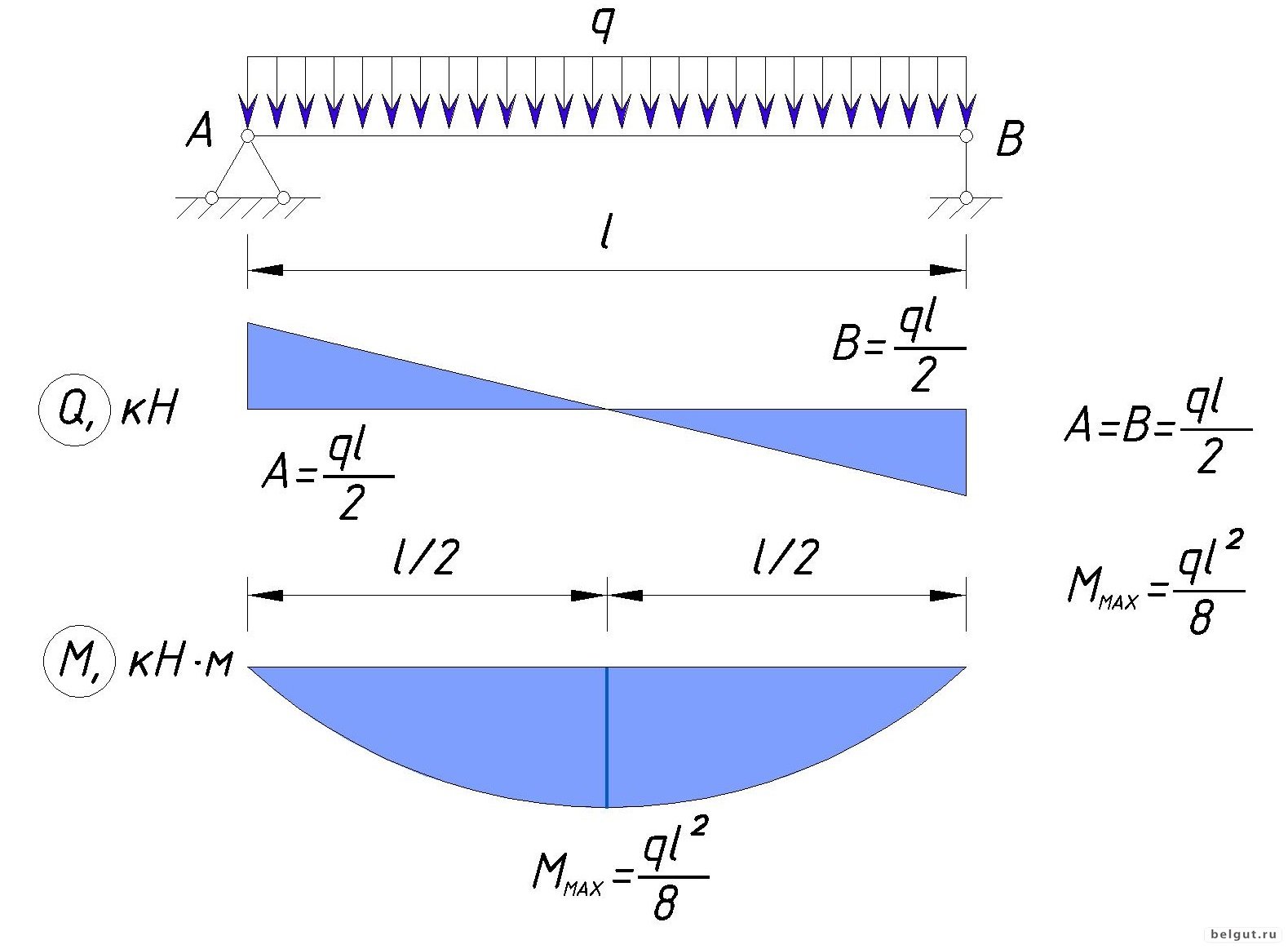
ДИАГРАММА ПЕРЕСЕЧНОЙ СИЛЫ:

Это графическое изображение изменения поперечной силы по длине балки. Ордината SFD в любом сечении дает значение поперечной силы в этом сечении из-за фиксированных положений нагрузки на балку.

Диаграмма силы сдвига будет Прямоугольная между ТОЧЕЧНАЯ НАГРУЗКА.

Диаграмма поперечной силы

будет Треугольная между РАВНОМЕРНО РАСПРЕДЕЛЕННАЯ НАГРУЗКА.

Диаграмма поперечной силы

будет Параболической между РАВНОМЕРНО ИЗМЕНЯЮЩЕЙСЯ НАГРУЗКОЙ.

 

ДИАГРАММА ИЗГИБАЮЩЕГО МОМЕНТА:

Это графическое изображение; представление изменения изгибающего момента по длине балки. Ордината BMD в любом сечении дает значение изгибающего момента в этом сечении из-за фиксированных положений нагрузки на балку.

Диаграмма изгибающего момента будет Треугольная между ТОЧЕЧНАЯ НАГРУЗКА.

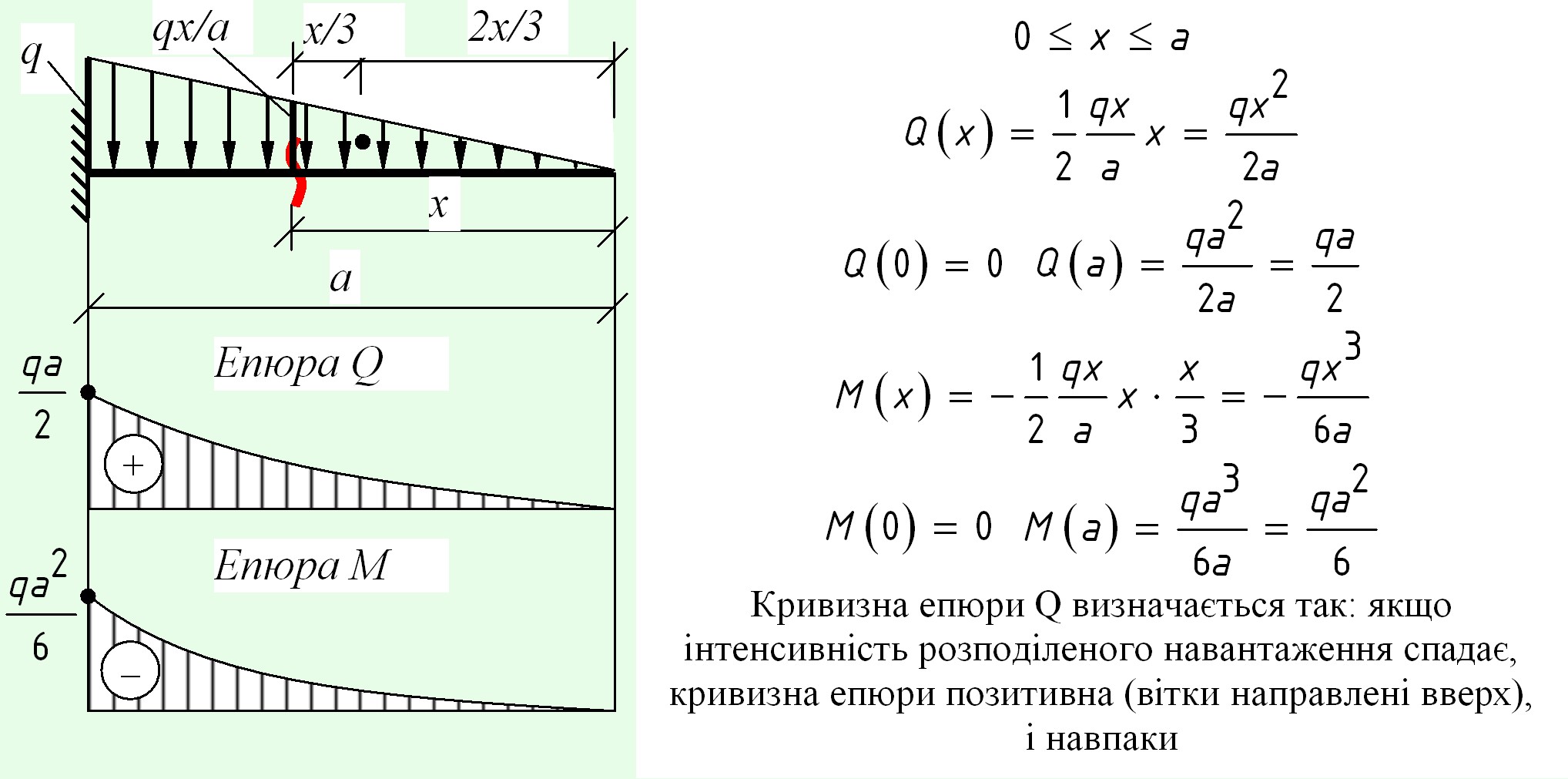
Диаграмма изгибающего момента будет Параболическая между РАВНОМЕРНО РАСПРЕДЕЛЕННАЯ НАГРУЗКА.

Диаграмма изгибающего момента

будет гиперболической между РАВНОМЕРНО ИЗМЕНЯЮЩЕЙСЯ НАГРУЗКОЙ.

 

СВОЙСТВА ДИАГРАММЫ СИЛЫ ПЕРЕСЕЧЕНИЯ:

• Диаграмма силы сдвига состоит из прямоугольника , если балка нагружена точечными нагрузками.

• Диаграмма поперечной силы состоит из наклонной линии для участка, на который действует равномерно распределенная нагрузка .

• Диаграмма поперечной силы состоит из параболической кривой для участка, на который действует треугольное или трапециевидное распределение нагрузки .

• Диаграмма поперечной силы состоит из кубических кривых для участка, на который действует распределение параболической нагрузки .

• Сила сдвига не изменяется в точке приложения пары .

 

СВОЙСТВА ДИАГРАММЫ ИЗГИБАЮЩЕГО МОМЕНТА:

• Диаграмма изгибающего момента состоит из наклонных линий для балки, нагруженной точечными нагрузками.

• Диаграмма изгибающего момента состоит из параболической кривой для участка, на который действует равномерно распределенная нагрузка .

• Диаграмма изгибающего момента кубической кривой или кривой третьей степени для участка, на который действует равномерно изменяющаяся нагрузка .

• Диаграмма изгибающего момента состоит из кривой четвертой степени , если распределение нагрузки является параболическим.

• Изгибающий момент максимален, когда поперечная сила равна нулю или меняет знак.

• Изгибающий момент резко в точке приложения пары.

 

ТОЧКА КОНТРАФЛЕКСА:

 

 

Изгибающие моменты противоположной природы всегда вызывают искривление балок в противоположных направлениях. В балке, если изгибающий момент меняет знак в точке, где сама точка имеет нулевой изгибающий момент, балка меняет кривизну в этой точке нулевого изгибающего момента, и эта точка называется точкой обратного изгиба. Таким образом, в точке обратного изгиба луч изгибается в противоположном направлении. Точка обратного изгиба называется точкой изгиба или виртуальным шарниром.

 

ИСПОЛЬЗОВАНИЕ ДИАГРАММЫ СИЛЫ ПЕРЕСЕЧЕНИЯ И ДИАГРАММЫ ИЗГИБАЮЩЕГО МОМЕНТА:

• Каждая конструкция пытается сопротивляться деформации, развивая внутреннее сопротивление (сдвиг, момент и/или изгибающий момент). Однако свойства тела будут определять, какое сопротивление будет оказано нагрузке.

• Например,
  • Балка из бетонного материала имеет очень высокое сопротивление сдвигу. Однако он очень слаб в напряжении.
  • Стальная балка обладает высокой устойчивостью как к сдвигу, так и к изгибу. Однако он очень дорог по сравнению с бетоном.

• Следовательно, при проектировании балки из бетона находим точки максимальных значений SFD и BMD. Эти значения, в свою очередь, дают нам представление о типе материала и геометрии, которые нам нужно обеспечить, чтобы противостоять деформации (или разрушению в целом). Поскольку бетон очень дешевый, мы стараемся обеспечить его как можно больше. Однако он слаб в напряжении.

 

• Следовательно, для зон максимального изгибающего момента (которые мы находим в BMD) мы предоставляем стальную арматуру. Мы также находим зоны максимальной силы сдвига (от SFD). Если значения силы сдвига превышают способность (сопротивление) бетона, мы предлагаем стальные скобы для сопротивления сдвигу, чтобы противостоять дополнительному сдвигу.

• Та же концепция применима и к столбцам.