Эпюра изгибающих моментов M консольной балки (Видео)
Выберите предметМеханикаТеоретическая механикаСопротивление материаловТеория машин и механизмовДетали машинВысшая математикаФизикаНачертательная геометрияИнформатикаАвиационная и ракетно-космическая техникаАвтоматизация технологических процессовАвтоматика и управлениеАрхитектура и строительствоБазы данныхВысшая математикаГеометрияГидравликаДетали машинИздательское делоИнформатикаИнформационная безопасностьИнформационные технологииМатериаловедениеМашиностроениеМеталлургияМетрологияМеханикаМорская техникаНаноинженерияНачертательная геометрияПолиграфияПриборостроение и оптотехникаПрограммированиеПроцессы и аппаратыРабота на компьютереРадиофизикаСопротивление материаловТелевидениеТеоретическая механикаТеория вероятностейТеория машин и механизмовТеплоэнергетика и теплотехникаТехнологические машины и оборудованиеТехнология продовольственных продуктов и товаровТранспортные средстваФизикаХолодильная техникаЧертежиЧерчениеЭлектроника, электротехника, радиотехникаЭнергетическое машиностроениеЯдерная энергетика и теплофизикаЯдерные физика и технологииАнализ хозяйственной деятельностиАнтикризисное управлениеБанковское делоБизнес-планированиеБухгалтерский учет и аудитВнешнеэкономическая деятельностьГостиничное делоГосударственное и муниципальное управлениеДеловой этикетДеньгиИнвестицииИнновационный менеджментКредитЛогистикаМаркетингМеждународные рынкиМенеджментМенеджмент организацииМикро-, макроэкономикаНалогиОрганизационное развитиеПроизводственный маркетинг и менеджментПромышленный маркетинг и менеджментСервисСтандартизацияСтатистикаСтратегический менеджментСтрахованиеТаможенное делоТеория управленияТовароведениеТорговое делоТуризмУправление персоналомФинансовый менеджментФинансыЦенообразование и оценка бизнесаЭконометрикаЭкономикаЭкономика предприятияЭкономика трудаЭкономическая теорияЭкономический анализАрхеологияАстрономияБезопасность жизнедеятельностиБиологияБиотехнологияВетеринарияВоспроизводство и переработка лесных ресурсовГеографияГеодезияГеологияГидрометеорологияЕстествознаниеКартография и геоинформатикаМедицинаНефтегазовое делоПочвоведениеПриродообустройство и водопользованиеСельское и рыбное хозяйствоХимияХирургияЭкологияБиблиотечно-информационная деятельностьДизайнДокументоведение и архивоведениеЖурналистикаИскусствоИсторияКонфликтологияКриминалистикаКультурологияЛитератураЛогикаМеждународные отношенияМузыкаПедагогикаПолитологияПраво и юриспруденцияПсихологияРежиссураРеклама и PRРелигияСвязи с общественностьюСоциальная работаСоциологияСтрановедениеТеатроведениеФизическая культураФилософияЭтикаЯзыки (переводы)Языкознание и филология
Выберите вид работы…Решение задачКонтрольная работаКурсовая работаПомощь на экзаменеОтветы на вопросыОтчёт по практикеЧертёжДипломная работаРефератМонографияБизнес-планТворческая работаЭссеСочиненияРецензияДокладНабор текстаМагистерская диссертацияКандидатская диссертацияСтатьяЛабораторная работаПереводПрезентацииПовышение уникальности текстаДругое
isopromat.ru
Часть 1. Построение эпюры поперечной силы и изгибающего момента на консольной балке
Что такое консольная балка, и какие особенности существуют при построении эпюр на такой схеме?
Консольной называют такую балку, у которой один конец закреплен в жесткой заделке, а другой свободен от закрепления. Построение эпюр производят на основе алгоритма экспресс метода по характерным сечениям, но при этом есть рекомендация : строить эпюры в определенном направлении – от свободного конца к заделке, всегда оставляя часть со свободным концом для вычисления значений внутренних силовых факторов в характерном сечении. А зачем ? Затем, чтобы не определять реактивных усилий в заделке, экономя время на решение задачи.
1.3.3. Пример решения задачи
Задача
Для данной консольной балки построить эпюры поперечной силы Qy и изгибающего момента Мх.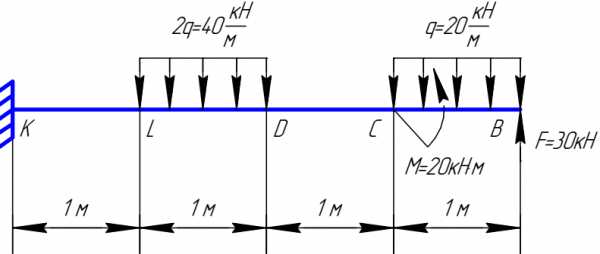
РЕШЕНИЕ
Итак, строить эпюры будем, не определяя реактивных усилий в заделке. Направление построения примем со свободного конца к заделке, т.е. от точки B к точке К. Начинаем построение с эпюры поперечной силы Qy.
Построение эпюры Qy
Под расчетной схемой проведем базу для эпюры и разделим ее на участки. Для этого обозначим буквами характерные сечения: B, C, D, L, K. Таким образом на схеме и, соответственно, на базе получилось четыре участка: BC, CD, DL и LK.
Ый участок (BC)
Правая граница участка т. B: имеется сосредоточенная сила F=30 кН, от которой на эпюре должен быть скачок на величину 30кН. Знак скачка определим, поворачивая силу по ходу построения эпюры, т.е. справа налево. Сила поворачивается против часовой стрелки, поэтому откладываем ординату 30 кН вниз, в отрицательную сторону.
Состояние по длине участка: весь участок загружен распределенной нагрузкой, поэтому на эпюре будет наклонная прямая с угловым коэффициентом, равным q=20кН/м, а поскольку направление вектора q противоположно направлению силы F, наклонная прямая пойдет вверх, в положительную область значений Qy.
Правая граница участка т. С: определим величину силы, на которую произойдет изменение поперечной силы за счет действия распределенной нагрузки на участке, умножив q на длину участка 1 м, получим 20кН. Величина поперечной силы в т. «С» определится как сумма: -F +q×1м=-10кН. Отложим это значение вниз от базы, т.е. со знаком «–». Соединим ординаты на левой и правой границе участка наклонной прямой.
Ой участок (CD)
Правая граница участка т. C: сосредоточенная сила отсутствует, а на сосредоточенный момент М=30кНм поперечная сила не реагирует. Следовательно, значение поперечной силы -10кН не изменится.
Состояние по длине участка: участок пустой, ничем не загружен, поэтому на эпюре должна быть прямая, параллельная базе. Проведем ее до левой границы участка.
Левая граница участка т. D: Значение такое же, как и на правой границе, т.е. -10кН.
Ий участок (DL)
Правая граница участка т. D: Сосредоточенная сила отсутствует, поэтому значение поперечной силы -10кН не изменится.
Состояние по длине участка: участок загружен равномерно распределенной нагрузкой интенсивностью 2q=40кН/м. Поэтому на эпюре должна быть наклонная прямая с угловым коэффициентом, равным +2q=40кН/м. Почему +40кн/м . Потому, что стрелки интенсивности поворачиваются по часовой стрелке при движении по участку справа налево.
Левая граница участка т. L: определим величину силы, на которую произойдет изменение Q
Ый участок (LK)
Правая граница участка т. L: сосредоточенная сила отсутствует, т.е. значение поперечной силы 30 кН не изменится.
Состояние по длине участка: участок пустой, ничем не загружен, поэтому на эпюре должна быть прямая, параллельная базе. Проведем ее до левой границы участка.
Левая граница участка т. K: Значение такое же, как на правой границе, т.е. 30кН.
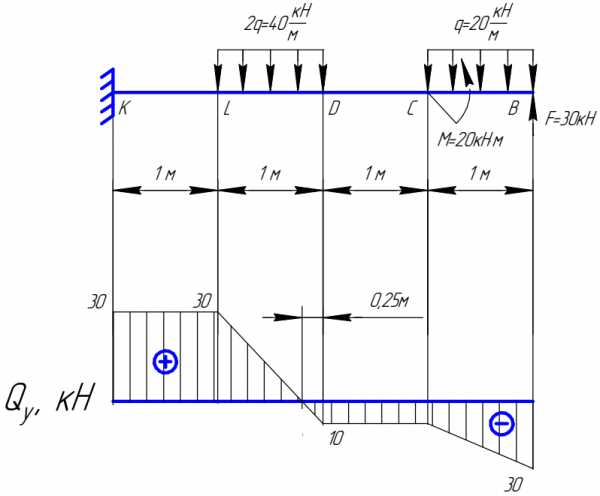
Построение эпюры изгибающего момента Мх
Ый участок (BC)
Правая граница участка т. B: Отсутствует сосредоточенный внешний момент, поэтому скачка в начале участка не будет. Начинаем эпюру момента с нуля.
Состояние по длине участка: участок загружен равномерно распределенной нагрузкой, поэтому на эпюре будет квадратичная парабола, выпуклостью вверх, навстречу действию нагрузки. Для определения наличия экстремума анализируем эпюру поперечной силы этого участка. Наклонная прямая на эпюре Qy не пересекает базу, т.е. внутри участка не принимает нулевое значение. Это говорит о том, что экстремума на параболе не будет. Такие параболы строят по двум значениям в граничных точках участка.
Левая граница участка т. C: Определим значение внутреннего изгибающего момента в т. C по части балки BC в табличной форме:
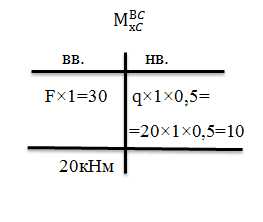
Полученную величину момента 20кНм откладываем в точке C выше базы и соединяем с нулем в т. B параболой без экстремума, направляя выпуклость вверх.
Ой участок (CD)
Правая граница участка т. C: здесь находится сосредоточенный момент М=20кНм, который вызовет на эпюре скачок, равный 20кНм. Знак скачка определим по направлению действия момента. По ходу построения эпюры внешний момент направлен в сторону верхних волокон, поэтому откладываем скачок вверх и получим 40кНм.
Состояние по длине участка: участок пустой, ничем не загружен, поэтому на эпюре момента должна быть наклонная прямая с угловым коэффициентом Qy=-10кН этого участка.
Левая граница участка т. D: Величину внутреннего момента в точке D определим с использованием табличной формы по всей части балки BD.
По двум значениям момента, полученным в точках C и D, строим наклонную прямую.
Ий участок (DL)
Правая граница участка т.D: сосредоточенный момент отсутствует, поэтому значение момента 50кНм не изменится.
Состояние по длине участка: участок загружен равномерно распределенной нагрузкой интенсивностью 2q=40кН/м. Поэтому должна быть квадратичная парабола выпуклостью вверх навстречу действию 2q. Наличие экстремума определяем по эпюре поперечной силы этого участка. Очевидно, что в точке пересечения наклонной прямой на эпюре Qy квадратичная парабола будет иметь экстремальное значение. Определим расстояние от точки D до точки экстремума. Для этого величину, отсекаемую наклонной прямой в точке D, поделим на угловой коэффициент этой наклонной прямой, равный 2q=40кН/м: 10кН/40кНм/м=0,25 м. Обозначим соответствующее сечение на расчетной схеме буквой S. Вычислим величину экстремума по части балки BS, используя табличную форму.
Левая граница участка т. L: определим величину момента по части балки BL, используя табличную форму.
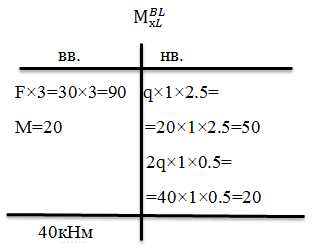
По значениям момента, полученным в трех точках участка, строим параболу.
Ый участок (LK)
Правая граница участка т. L: сосредоточенный внешний момент отсутствует, т.е. значение 40кНм, полученное в данной точке в конце предыдущего участка не изменится.
Состояние по длине участка: участок пустой, ничем не загружен, поэтому на эпюре должна быть наклонная прямая с угловым коэффициентом, равным Qy=30кН данного участка.
Левая граница участка т. K: значение внутреннего момента вычислим по всей балке BK, используя табличную форму.
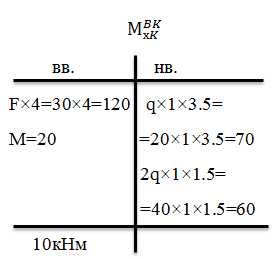
Полученную величину момента 10кНм на верхних волокнах откладываем в точке K выше базы и соединяем наклонной прямой со значением в точке L.
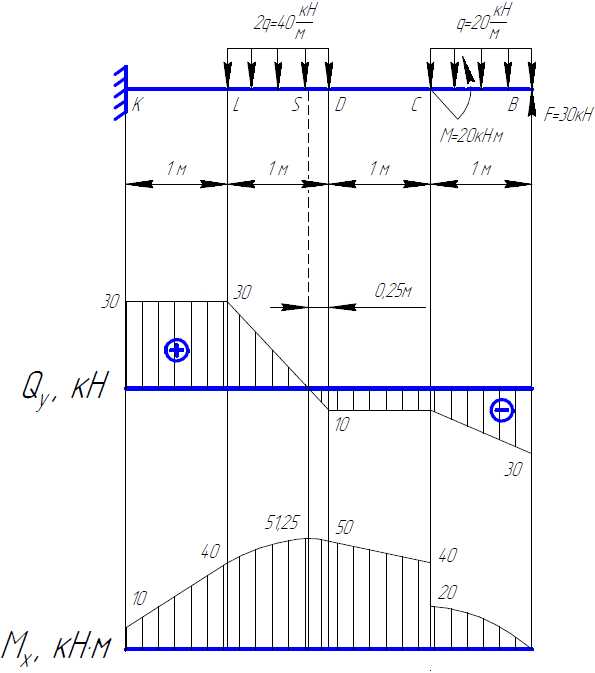
Правильность построенных эпюр проверим, используя дифференциальную зависимость слева направо в пределах каждого участка. Участки KL и LS: Qy>0, Mx↑; участки SD, DC и CD: Qy<0, Mx↓. Анализ показал полное соответствие поведения функции изгибающего момента дифференциальной зависимости.
Эпюры построены.
1.3.4. Задача для самостоятельного решения на занятии
Для данной расчетной схемы построить эпюры поперечной силы и изгибающего момента, используя основные закономерности и определяя значения внутренних силовых факторов в характерных сечениях.
cyberpedia.su
1.4 Построение эпюр крутящих моментов
Крутящий моментв сечении численно равен алгебраической сумме внешних моментов, приложенных по одну сторону от рассматриваемого сечения, относительно продольной оси Z.
Правило знаков для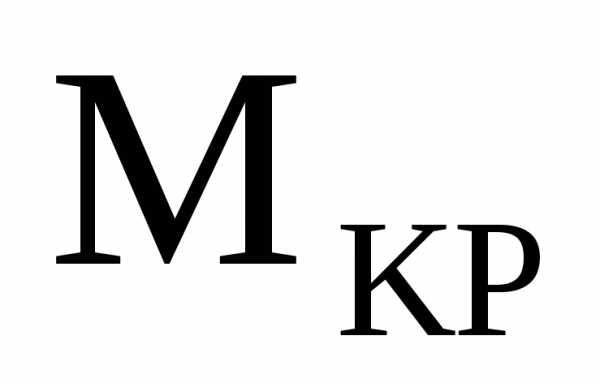 
:
условимся считать крутящий момент в
сечении положительным, если при взгляде
на сечение со стороны рассматриваемой
отсеченной части внешний момент виден
направленным против движения часовой
стрелки и отрицательным — в противном
случае.
Пример 2.Построить эпюру крутящих моментов для жестко защемленного стержня (рис.5,а).
Порядок расчета.
Следует отметить, что алгоритм и принципы построения эпюры крутящих моментов полностью совпадают с алгоритмом и принципами построения эпюры продольных сил.
1.Намечаем характерные сечения.
2.Определяем крутящий момент в каждом характерном сечении.
3.По найденным значениям строим эпюру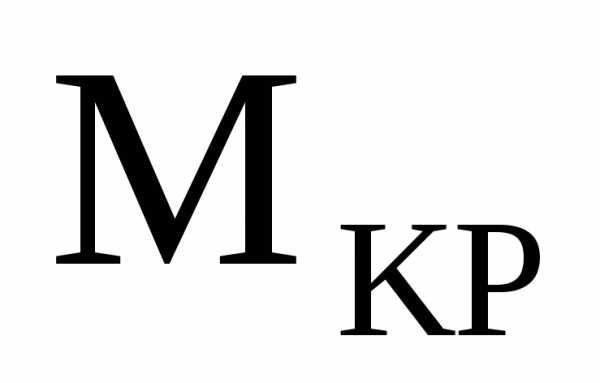 
(рис.5,б).
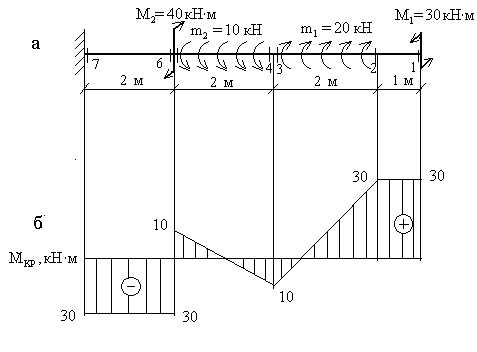
Рис. 5
1.6 Правила контроля эпюри
Для эпюр продольных сил и крутящих моментов характерны определенные закономерности, знание которых позволяет оценить правильность выполненных построений.
Эпюры
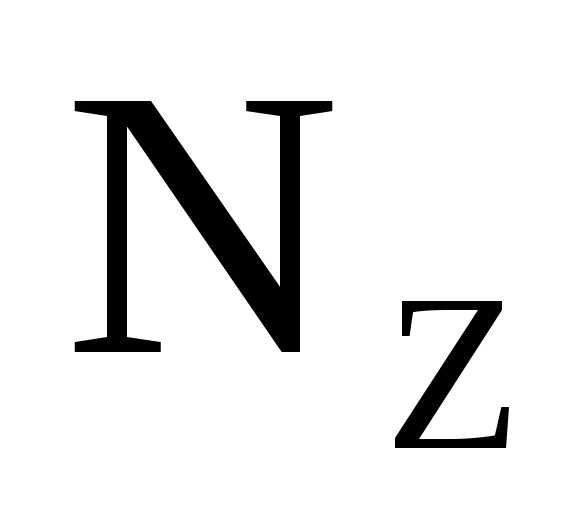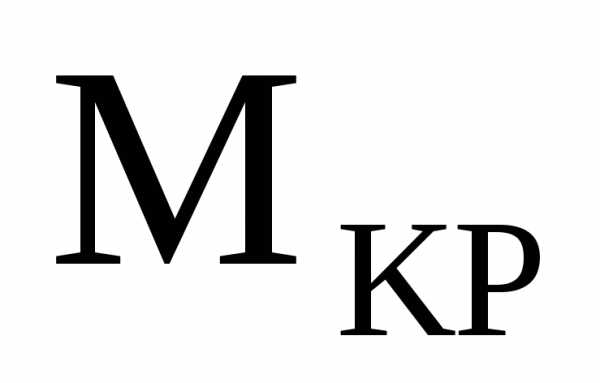ивсегда прямолинейные.На участке, где нет распределенной нагрузки, эпюра
()
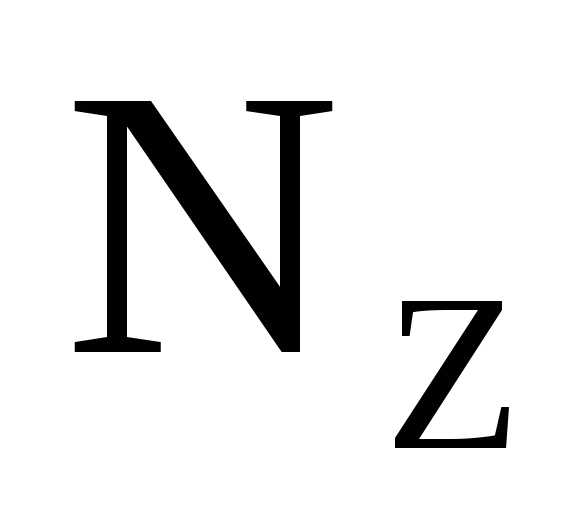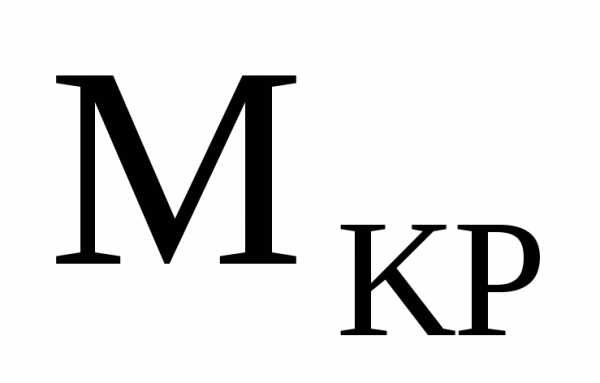— прямая, параллельная оси; а на участке
под распределенной нагрузкой — наклонная
прямая.Под точкой приложения сосредоточенной силы на эпюре
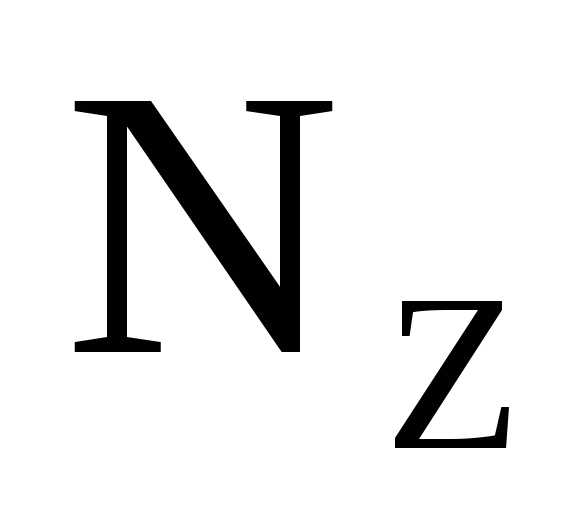обязательно должен быть скачок на
величину этой силы, аналогично под
точкой приложения сосредоточенного
момента на эпюребудет скачок на величину этого момента.
и
всегда прямолинейные.
(
)
— прямая, параллельная оси; а на участке
под распределенной нагрузкой — наклонная
прямая.
обязательно должен быть скачок на
величину этой силы, аналогично под
точкой приложения сосредоточенного
момента на эпюре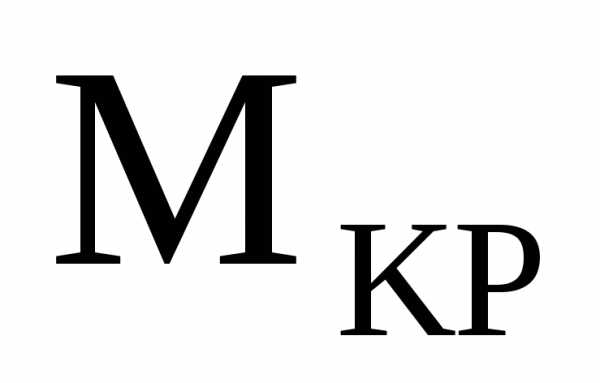
будет скачок на величину этого момента.1.7 Построение эпюр поперечных сили изгибающих моментовв балках
Стержень, работающий на изгиб, называется балкой. В сечениях балок, загруженных
вертикальными нагрузками, возникают,
как правило, два внутренних силовых
фактора — поперечная сила
и изгибающий момент
.
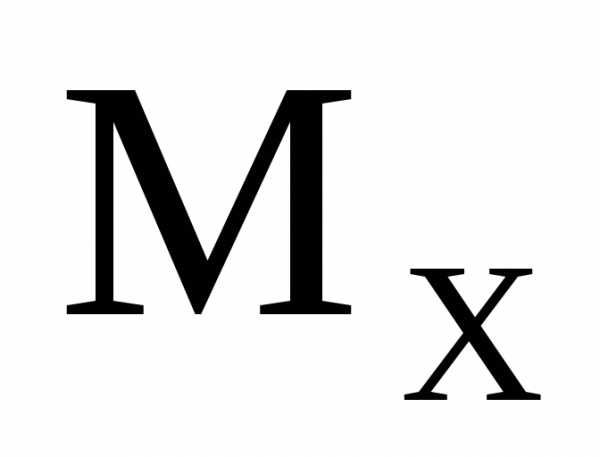Поперечная силав сечении численно равна алгебраической сумме проекций внешних сил, приложенных по одну сторону от рассматриваемого сечения, на поперечную (вертикальную) ось.
Правило знаков для 
:условимся считать поперечную силу в
сечении положительной, если внешняя
нагрузка, приложенная к рассматриваемой
отсеченной части, стремится повернуть
данное сечение по часовой стрелке и
отрицательной — в противном случае.
Схематически это правило знаков можно представить в виде
Изгибающий момент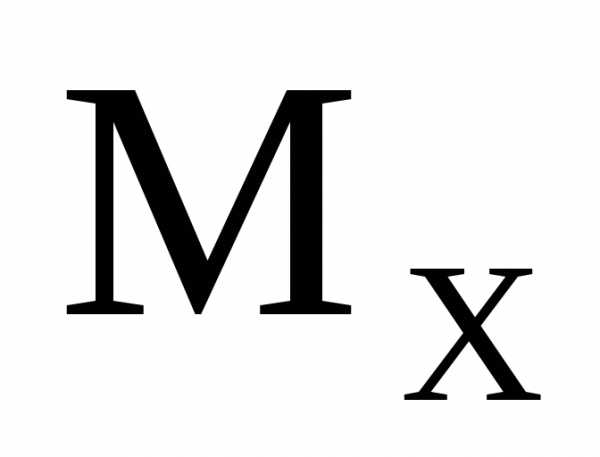
в сечении численно равен алгебраической
сумме моментов внешних сил, приложенных
по одну сторону от рассматриваемого
сечения, относительно оси x , проходящей
через данное сечение.
Правило знаков для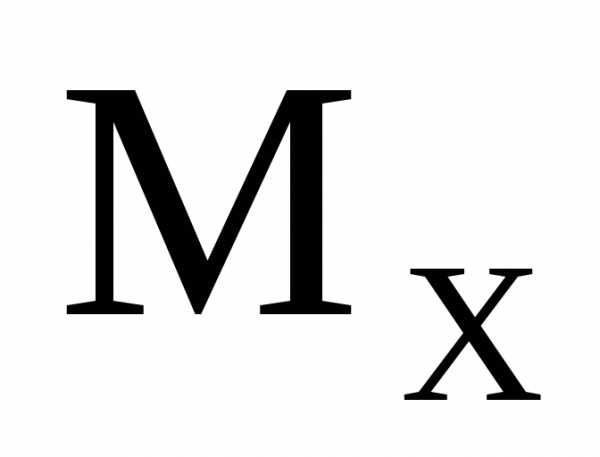
:
условимся считать изгибающий момент
в сечении положительным, если внешняя
нагрузка, приложенная к рассматриваемой
отсеченной части, приводит к растяжению
в данном сечении нижних волокон балки
и отрицательной — в противном случае.
Схематически это правило знаков можно представить в виде:
Следует отметить, что при использовании
правила знаков для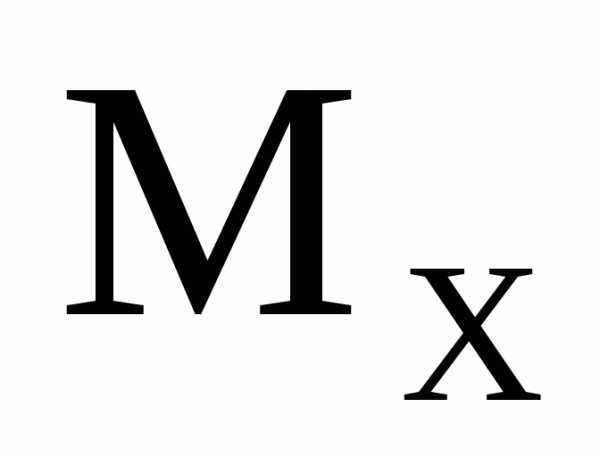 
в указанном виде, эпюра
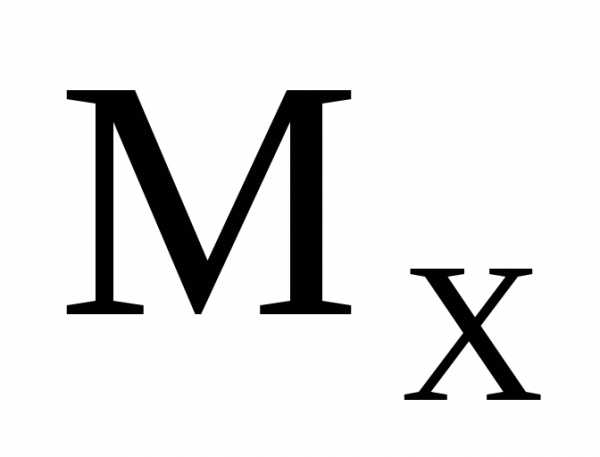всегда оказывается построенной со
стороны сжатых волокон балки.
1.8 Консольные балки
При построении эпюр 
и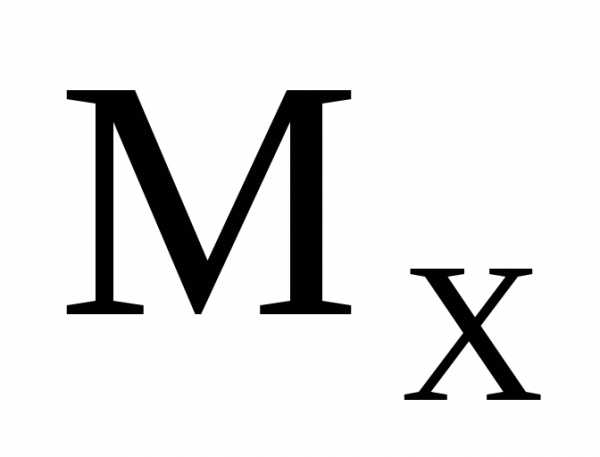
в
консольных, или жестко защемленных,
балках нет необходимости (как и в
рассмотренных ранее примерах) вычислять
опорные реакции, возникающие в жесткой
заделке, но выбирать отсеченную часть
нужно так, чтобы заделка в нее не
попадала.
Пример 3.Построить эпюры
и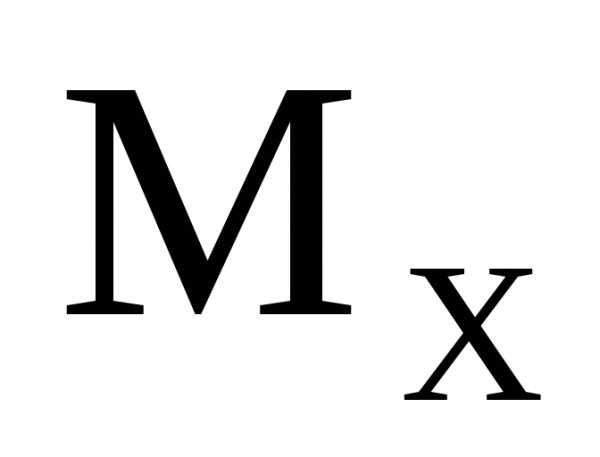
(рис.6).
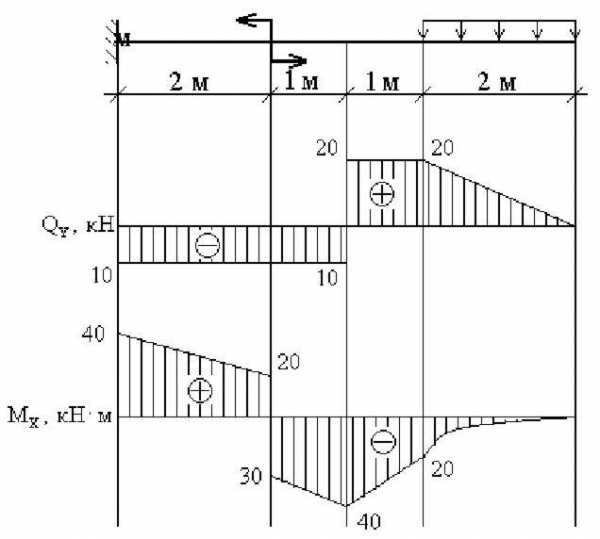
Рис. 6
Порядок расчета.
Намечаем характерные сечения.
Определяем поперечную силу в каждом характерном сечении.
По вычисленным значениям строим
эпюру 
.
3. Определяем изгибающий момент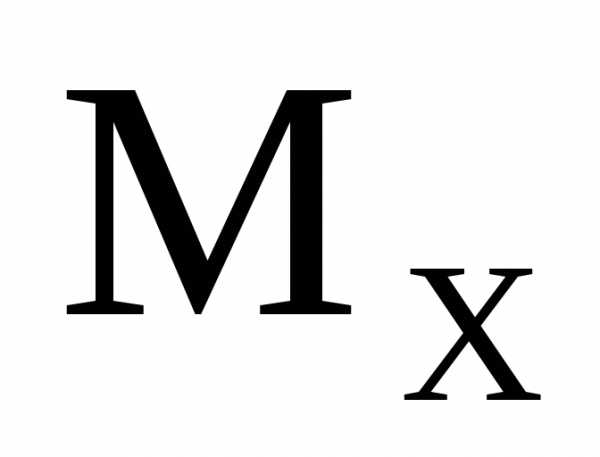 
в каждом характерном сечении.
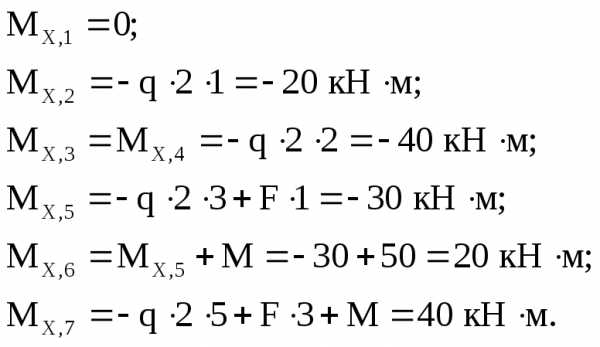
По вычисленным значениям строим эпюру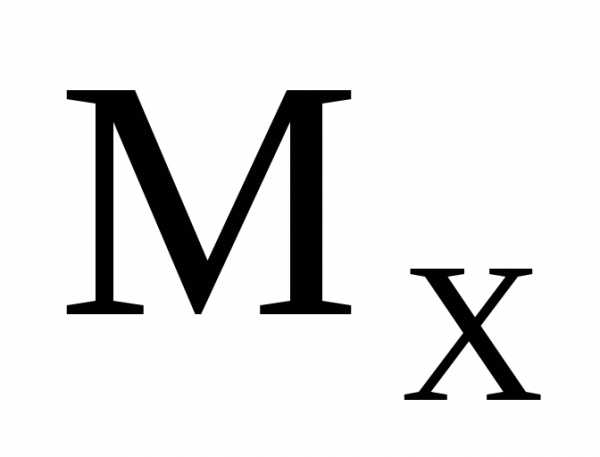 
,
причем, на участке под распределенной
нагрузкой эпюра будет криволинейной
(квадратная парабола). Выпуклость кривой
на этом участке всегда обращена навстречу
распределенной нагрузке.
studfiles.net
Часть 1. Построение эпюры поперечной силы и изгибающего момента на консольной балке
Что такое консольная балка, и какие особенности существуют при построении эпюр на такой схеме?
Консольной называют такую балку, у которой один конец закреплен в жесткой заделке, а другой свободен от закрепления. Построение эпюр производят на основе алгоритма экспресс метода по характерным сечениям, но при этом есть рекомендация : строить эпюры в определенном направлении – от свободного конца к заделке, всегда оставляя часть со свободным концом для вычисления значений внутренних силовых факторов в характерном сечении. А зачем ? Затем, чтобы не определять реактивных усилий в заделке, экономя время на решение задачи.
1.3.3. Пример решения задачи
Задача
Для данной консольной балки построить эпюры поперечной силы Qy и изгибающего момента Мх.
РЕШЕНИЕ
Итак, строить эпюры будем, не определяя реактивных усилий в заделке. Направление построения примем со свободного конца к заделке, т.е. от точки B к точке К. Начинаем построение с эпюры поперечной силы Qy.
Построение эпюры Qy
Под расчетной схемой проведем базу для эпюры и разделим ее на участки. Для этого обозначим буквами характерные сечения: B, C, D, L, K. Таким образом на схеме и, соответственно, на базе получилось четыре участка: BC, CD, DL и LK.
Ый участок (BC)
Правая граница участка т. B: имеется сосредоточенная сила F=30 кН, от которой на эпюре должен быть скачок на величину 30кН. Знак скачка определим, поворачивая силу по ходу построения эпюры, т.е. справа налево. Сила поворачивается против часовой стрелки, поэтому откладываем ординату 30 кН вниз, в отрицательную сторону.
Состояние по длине участка: весь участок загружен распределенной нагрузкой, поэтому на эпюре будет наклонная прямая с угловым коэффициентом, равным q=20кН/м, а поскольку направление вектора q противоположно направлению силы F, наклонная прямая пойдет вверх, в положительную область значений Qy.
Правая граница участка т. С: определим величину силы, на которую произойдет изменение поперечной силы за счет действия распределенной нагрузки на участке, умножив q на длину участка 1 м, получим 20кН. Величина поперечной силы в т. «С» определится как сумма: -F +q×1м=-10кН. Отложим это значение вниз от базы, т.е. со знаком «–». Соединим ординаты на левой и правой границе участка наклонной прямой.
Ой участок (CD)
Правая граница участка т. C: сосредоточенная сила отсутствует, а на сосредоточенный момент М=30кНм поперечная сила не реагирует. Следовательно, значение поперечной силы -10кН не изменится.
Состояние по длине участка: участок пустой, ничем не загружен, поэтому на эпюре должна быть прямая, параллельная базе. Проведем ее до левой границы участка.
Левая граница участка т. D: Значение такое же, как и на правой границе, т.е. -10кН.
Ий участок (DL)
Правая граница участка т. D: Сосредоточенная сила отсутствует, поэтому значение поперечной силы -10кН не изменится.
Состояние по длине участка: участок загружен равномерно распределенной нагрузкой интенсивностью 2q=40кН/м. Поэтому на эпюре должна быть наклонная прямая с угловым коэффициентом, равным +2q=40кН/м. Почему +40кн/м . Потому, что стрелки интенсивности поворачиваются по часовой стрелке при движении по участку справа налево.
Левая граница участка т. L: определим величину силы, на которую произойдет изменение Qy за счет действия распределенной нагрузки на участке, умножив 2q на длину участка 1 м, получим 40кН. Величина поперечной силы в т. «L» определится как сумма: -F +q ×1м +2q×1м=-10+40=30кН. Отложим это значение вверх от базы, т.е. со знаком «+». Соединим ординаты на левой и правой границе участка наклонной прямой.
Ый участок (LK)
Правая граница участка т. L: сосредоточенная сила отсутствует, т.е. значение поперечной силы 30 кН не изменится.
Состояние по длине участка: участок пустой, ничем не загружен, поэтому на эпюре должна быть прямая, параллельная базе. Проведем ее до левой границы участка.
Левая граница участка т. K: Значение такое же, как на правой границе, т.е. 30кН.
Построение эпюры изгибающего момента Мх
Ый участок (BC)
Правая граница участка т. B: Отсутствует сосредоточенный внешний момент, поэтому скачка в начале участка не будет. Начинаем эпюру момента с нуля.
Состояние по длине участка: участок загружен равномерно распределенной нагрузкой, поэтому на эпюре будет квадратичная парабола, выпуклостью вниз, в сторону действия нагрузки. Для определения наличия экстремума анализируем эпюру поперечной силы этого участка. Наклонная прямая на эпюре Qy не пересекает базу, т.е. внутри участка не принимает нулевое значение. Это говорит о том, что экстремума на параболе не будет. Такие параболы строят по двум значениям в граничных точках участка.
Левая граница участка т. C: Определим значение внутреннего изгибающего момента в т. C по части балки BC в табличной форме:
Полученную величину момента 20кНм откладываем в точке C ниже базы и соединяем с нулем в т. B параболой без экстремума, направляя выпуклость вних.
Ой участок (CD)
Правая граница участка т. C: здесь находится сосредоточенный момент М=20кНм, который вызовет на эпюре скачок, равный 20кНм. Направление скачка определим, как противоположное направлению действия момента. По ходу построения эпюры внешний момент направлен в сторону верхних волокон, поэтому откладываем скачок вниз и получим 40кНм.
Состояние по длине участка: участок пустой, ничем не загружен, поэтому на эпюре момента должна быть наклонная прямая с угловым коэффициентом Qy=-10кН этого участка.
Левая граница участка т. D: Величину внутреннего момента в точке D определим с использованием табличной формы по всей части балки BD.
По двум значениям момента, полученным в точках C и D, строим наклонную прямую.
Ий участок (DL)
Правая граница участка т.D: сосредоточенный момент отсутствует, поэтому значение момента 50кНм не изменится.
Состояние по длине участка: участок загружен равномерно распределенной нагрузкой интенсивностью 2q=40кН/м. Поэтому должна быть квадратичная парабола выпуклостью вниз в сторону действия 2q. Наличие экстремума определяем по эпюре поперечной силы этого участка. Очевидно, что в точке пересечения наклонной прямой на эпюре Qy квадратичная парабола будет иметь экстремальное значение. Определим расстояние от точки D до точки экстремума. Для этого величину, отсекаемую наклонной прямой в точке D, поделим на угловой коэффициент этой наклонной прямой, равный 2q=40кН/м: 10кН/40кНм/м=0,25 м. Обозначим соответствующее сечение на расчетной схеме буквой S. Вычислим величину экстремума по части балки BS, используя табличную форму.
Левая граница участка т. L: определим величину момента по части балки BL, используя табличную форму.
По значениям момента, полученным в трех точках участка, строим параболу.
Ый участок (LK)
Правая граница участка т. L: сосредоточенный внешний момент отсутствует, т.е. значение 40кНм, полученное в данной точке в конце предыдущего участка не изменится.
Состояние по длине участка: участок пустой, ничем не загружен, поэтому на эпюре должна быть наклонная прямая с угловым коэффициентом, равным Qy=30кН данного участка.
Левая граница участка т. K: значение внутреннего момента вычислим по всей балке BK, используя табличную форму.
Полученную величину момента 10кНм на нижних волокнах откладываем в точке K ниже базы и соединяем наклонной прямой со значением в точке L.
Правильность построенных эпюр проверим, используя дифференциальную зависимость слева направо в пределах каждого участка. Участки KL и LS: Qy>0, Mx↓; участки SD, DC и CD: Qy<0, Mx↑. Анализ показал полное соответствие поведения функции изгибающего момента дифференциальной зависимости.
Эпюры построены.
1.3.4. Задача для самостоятельного решения на занятии
Для данной расчетной схемы построить эпюры поперечной силы и изгибающего момента, используя основные закономерности и определяя значения внутренних силовых факторов в характерных сечениях.
Рекомендуемые страницы:
lektsia.com
Расчет консольной балки (жесткая заделка слева), построение эпюр
Определение опорных реакций
1. Согласно схеме решения задач статики определяем, что для нахождения неизвестных реакций необходимо рассмотреть равновесие балки.
2. На балку наложена связь в точке A (слева) типа жесткая заделка, поэтому освобождаем балку, заменив действие связи реакциями (HA, RA, MA).
3. Определим реакции опор в соответствии с уравнениями равновесия балки: ∑Fx = 0, ∑Fy = 0, ∑MA = 0.
∑Fx = 0: HA + P1*cos(30) = 0
∑Fy = 0: RA - q1*1.8 - P1*sin(30) = 0;
∑MA = 0: MA - q1*1.8*(1.8/2) + M1 - 3*P1*sin(30) = 0;
4. Решаем полученную систему уравнений, находим неизвестные :
HA = - P1*cos(30) = - 7*0.8660 = -6.06 (кН), так как реакция отрицательна, на расчетной схеме направим ее в противоположную сторону.
RA = q1*1.8 + P1*sin(30) = 2*1.8 + 7*sin(30) = 7.10 (кН)
MA = q1*1.8*(1.8/2) - M1 + 3*P1*sin(30) = 2*1.8*(1.8/2) - 19 + 3*7*sin(30) = -5.26 (кН*м), так как момент отрицателен, на расчетной схеме направим его в противоположную сторону.
5. Сделаем проверку, составив дополнительное моментное уравнение отоносительно свободного конца балки:
- 3*RA - MA + q1*1.8*(1.2+1.8/2) + M1 + 0*P1*sin(30) = - 3*7.10 - 5.26 + 2*1.8*(1.2+1.8/2) + 19.00 + 0*7*sin(30) = 0
Построение эпюр
Рассмотрим 1-й участок 0 ≤ x1 < 1.8Продольная сила N:Рассмотрим 2-й участок 1.8 ≤ x2 < 2.4
N(x1) = HA
Значения N на краях участка:
N1(0) = 6.06 = 6.06 (кН)
N1(1.80) = 6.06 = 6.06 (кН)
Поперечная сила Q:
Q(x1) = + RA - q1*(x1 - 0)
Значения Q на краях участка:
Q1(0) = + 7.10 - 2*(0 - 0) = 7.10 (кН)
Изгибающий момент M:
M(x1) = + RA*(x1) + MA - q1*(x1)2/2
Значения M на краях участка:
M1(0) = + 7.10*(0) + 5.26 - 2*(0 - 0)2/2 = 5.26 (кН*м)
Продольная сила N:Рассмотрим 3-й участок 2.4 ≤ x3 < 3
N(x2) = HA
Значения N на краях участка:
N2(1.80) = 6.06 = 6.06 (кН)
N2(2.40) = 6.06 = 6.06 (кН)
Поперечная сила Q:
Q(x2) = + RA - q1*(1.8 - 0)
Значения Q на краях участка:
Q2(1.80) = + 7.10 - 2*(1.8 - 0) = 3.50 (кН)
Q2(2.40) = + 7.10 - 2*(1.8 - 0) = 3.50 (кН)
Изгибающий момент M:
M(x2) = + RA*(x2) + MA - q1*(1.8 - 0)*[(x2 - 1.80) + (1.80 - 0)/2]
Значения M на краях участка:
M2(1.80) = + 7.10*(1.80) + 5.26 - 2*1.8*(0 + 0.90) = 14.80 (кН*м)
M2(2.40) = + 7.10*(2.40) + 5.26 - 2*1.8*(0.60 + 0.90) = 16.90 (кН*м)
Продольная сила N:
N(x3) = HA
Значения N на краях участка:
N3(2.40) = 6.06 = 6.06 (кН)
N3(3) = 6.06 = 6.06 (кН)
Поперечная сила Q:
Q(x3) = + RA - q1*(1.8 - 0)
Значения Q на краях участка:
Q3(2.40) = + 7.10 - 2*(1.8 - 0) = 3.50 (кН)
Q3(3) = + 7.10 - 2*(1.8 - 0) = 3.50 (кН)
Изгибающий момент M:
M(x3) = + RA*(x3) + MA - q1*(1.8 - 0)*[(x3 - 1.80) + (1.80 - 0)/2] - M1
Значения M на краях участка:
M3(2.40) = + 7.10*(2.40) + 5.26 - 2*1.8*(0.60 + 0.90) - 19 = -2.10 (кН*м)
M3(3) = + 7.10*(3) + 5.26 - 2*1.8*(1.20 + 0.90) - 19 = 0 (кН*м)
Расчет произведен при помощи онлайн-сервиса SOPROMATGURU.RU
sopromatguru.ru
Построение эпюр бесплатно. Консольная балка со знакопеременной нагрузкой
Определение опорных реакций
1. Согласно схеме решения задач статики определяем, что для нахождения неизвестных реакций необходимо рассмотреть равновесие балки.
2. На балку наложена связь в точке A (справа) типа жесткая заделка, поэтому освобождаем балку, заменив действие связи реакциями (HA, RA, MA).
3. Определим реакции опор в соответствии с уравнениями равновесия балки: ΣFx = 0, ΣFy = 0, ΣMA = 0.
ΣFx = 0: HA = 0
ΣFy = 0: - (U1справа *1.47)/2 + RA = 0;
ΣMA = 0: - (U1слева *1.03/2) * (3 - 1.03 + (2/3)*1.03) + (U1справа *1.47/2) * (3 - 2.5 + (1/3)*1.47) + MA = 0;
4. Решаем полученную систему уравнений, находим неизвестные :
HA = 0 (кН)
RA = (U1справа *1.47)/2 = - (35*1.03)/2 + (50*1.47)/2 = 18.75 (кН)
MA = (U1слева *1.03/2) * (3 - 1.03 + (2/3)*1.03) - (U1справа *1.47/2) * (3 - 2.5 + (1/3)*1.47) = + (U1слева *1.03/2) * (3 - 1.03 + (2/3)*1.03) - (U1справа *1.47/2) * (3 - 2.5 + (1/3)*1.47) = 11.46 (кН*м)
5. Сделаем проверку, составив дополнительное моментное уравнение отоносительно свободного конца балки:
(U1слева *1.03/2) * (1.03 - (2/3)*1.03) - (U1справа *1.47/2) * (2.5 - (1/3)*1.47) + 3*RA + MA = (U1слева *1.03/2) * (1.03 - (2/3)*1.03) - (U1справа *1.47/2) * (2.5 - (1/3)*1.47) + 3*18.75 + 11.46 = 0
Построение эпюр
Рассмотрим 1-й участок 0 ≤ x1 < 2.5Поперечная сила Q:Рассмотрим 2-й участок 2.5 ≤ x2 < 3
Q(x1) = + (U1слева *1.03)/2 - (U1справа *(x - 1.03)/1.47*(x - 1.03))/2
Значения Q на краях участка:
Q1(0) = + ([(35 - 35*(1.03 - 0)/1.03)*(0 - 0)]/2 + 35*(1.03 - 0)/1.03*(0 - 0)) = 0 (кН)
Q1(2.50) = + (35*1.03)/2 - (50*(2.5 - 1.03)/1.47*(2.50 - 1.03))/2 = -18.75 (кН)
Изгибающий момент M:
M(x1) = - (U1слева *1.03)/2*(x - 1.03 + (2/3)*1.03) + (U1справа *(x - 1.03)/1.47*(x - 1.03))/2*(x - 1.03)*(1/3)
Значения M на краях участка:
M1(0) = + ([(35 - 35*(1.03 - 0)/1.03)*(0 - 0)]/2*(0 - 0)*(2/3) + 35*(1.03 - 0)/1.03*(0 - 0)*(0 - 0)*(1/2)) = 0 (кН*м)
M1(2.50) = - (35*1.03)/2*(2.50 - 1.03 + (2/3)*1.03) + (50*(2.5 - 1.03)/1.47*(2.50 - 1.03))/2*(2.50 - 1.03)*(1/3) = 20.83 (кН*м)
Поперечная сила Q:
Q(x2) = + (U1слева *1.03)/2 - (U1справа *1.47)/2
Значения Q на краях участка:
Q2(2.50) = + (35*1.03)/2 - (50*(2.5 - 1.03)/1.47*(2.50 - 1.03))/2 = -18.75 (кН)
Q2(3) = + (35*1.03)/2 - (50*1.47)/2 = -18.75 (кН)
Изгибающий момент M:
M(x2) = - (U1слева *1.03)/2*(x - 1.03 + (2/3)*1.03) + (U1справа *1.47)/2*(x - 2.5 + (1/3)*1.47)
Значения M на краях участка:
M2(2.50) = - (35*1.03)/2*(2.50 - 1.03 + (2/3)*1.03) + (50*(2.5 - 1.03)/1.47*(2.50 - 1.03))/2*(2.50 - 1.03)*(1/3) = 20.83 (кН*м)
M2(3) = - (35*1.03)/2*(3 - 1.03 + (2/3)*1.03) + (50*1.47)/2*(3 - 2.5 + (1/3)*1.47) = 11.46 (кН*м)
Расчет произведен при помощи онлайн-сервиса SOPROMATGURU.RU
sopromatguru.ru
Построение эпюр изгибающих моментов и поперечных сил , подбор поперечного размера балки.
Ниже приведено условие и решение задачи. Закачка решения в формате doc начнется автоматически через 10 секунд.
Для схем балок 1 и 2 требуется :
1) Вычертить расчётные схемы, указав числовые значения размеров и нагрузок ;
2) Вычислить опорные реакции (схема 2) и проверить их ;
3) Составить аналитические выражения изменения изгибающего момента Mx и поперечной силы Qy на всех участков балок ;
4) Построить эпюры изгибающих моментов Mx и поперечных сил Qy, указав значения ординат во всех характерных сечениях участков балок ;
5) Руководствуясь эпюрами изгибающих моментов, вычертить приблизительный вид изогнутых осей балок ;
6) Определить положения опасных сечений и из условия прочности подобрать поперечные размеры балок :
a) для схемы 1 – круг диаметром d при допускаемом напряжении [σ]=280 МПа (сталь) ;
б) для схемы 2 – двутавровое (ГОСТ 8239-72) при допускаемом напряжении [σ]=200 МПа (сталь).
Дано : схема 1 — № 7 ; схема 2 — № 4 ; c/a=1.8 ; P/qa=1.8 ; m/qa2=0.8 ; a=2 м ; q=11 кН/м.
Решение.
а) Схема 1.
Расчётная схема.
P=1.8qa=1.8×11×2=39.6 кН ; m=0.8qa2=0.8×11×22=35.2 кН·м ; c=1.8a=1.8×2=3.6 м.
Эпюры поперечных сил и изгибающих моментов строим методом сечений. Определим выражения для поперечных сил и изгибающих моментов на каждом из участков балки. Балка имеет два участка. Обозначим zi – расстояние от левого конца балки до некоторого сечения.
На участке AB : 0≤z1≤a
Q1=-P+qz1 ; M1=-Pz1+0.5qz12
На участке BC : a≤z2≤c+a
Q2=-P+qz2 ; M2=-Pz2+m+0.5qz22
Вычислим поперечные силы и изгибающие моменты в характерных сечениях балки.
На участке AB : при z1=0 ;
QA=-P=-39.6 кН ; MA=0 кН·м.
при z1=a ;
QлB=-P+qa= -39.6+11×2=-17.6 кН ;
MлB=-Pa+0.5qa2=-39.6×2+0.5×11×22= -57.2 кН·м.
На участке BC : при z2=a ; QпрB
easyhelp.su