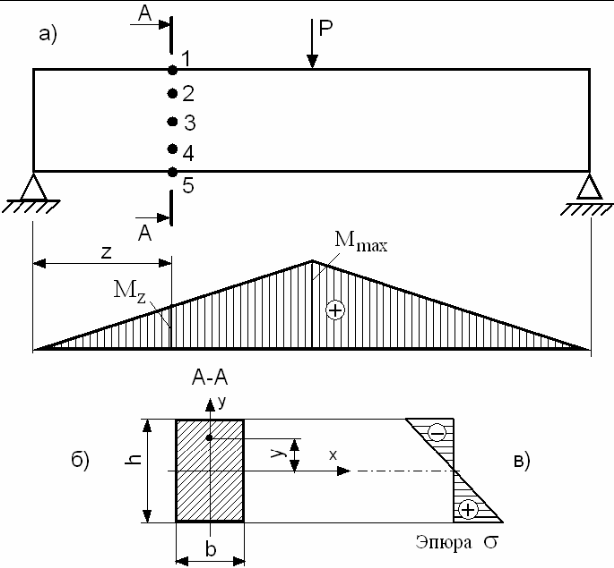
Определение изгибающих моментов и поперечных сил. Построение эпюр
Рассматривая построенные для трех разобранных примеров эпюры, нетрудно подметить определенную связь между эпюрами изгибающих моментов и поперечных сил поперечная сила Q (х) представляет собой про- а изводную от изгибающего момента УИ зг (х) по длине балки. Это можно доказать следу-ющим образом. [c.137]На рис. 4.8 показано построение эпюр изгибающих моментов и поперечных сил на примере стержня, защемленного одним концом. Такого рода стержни называются консолями. В данном случае с правой стороны на стержень не наложены связи, и изгибающие моменты и поперечные силы в любом сечении могут быть найдены без предварительного определения реакций. [c.164]
Выводы о взаимосвязи эпюр М и Q между собой и с внешней нагрузкой позволяют обходиться без составления уравнений изгибающих моментов и поперечных сил для каждого участка балки.
Нормальные и касательные напряжения, возникающие в поперечных сечениях балки, зависят соответственно от величин изгибающих моментов М и поперечных сил Q. Поэтому для определения наиболее опасных сечений, т. е. таких, в которых появляются наибольшие напряжения, необходимо знать изменения моментов и поперечных сил по длине всей балки. Обычно для большей наглядности эти изменения величин УИ и Q по длине балки представляют графически. Такие графики изменения М и Q называются эпюрами изгибающих моментов и поперечных сил.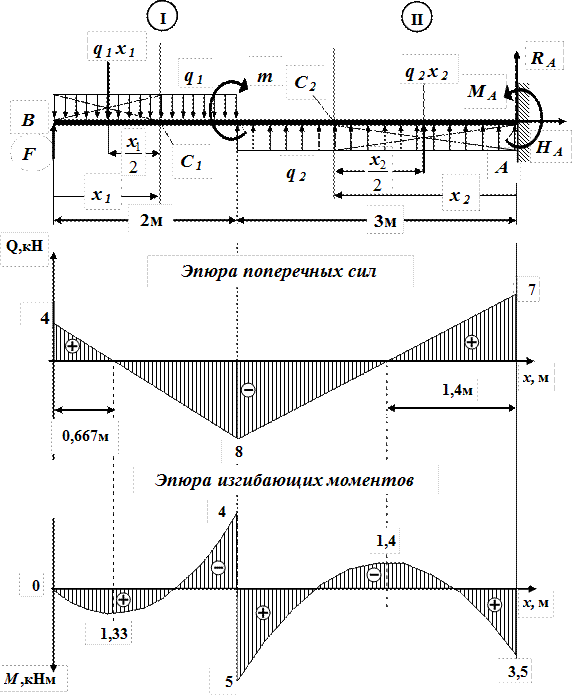
Эпюра—это график, построенный, в определенном масштабе и наглядно показывающий изменение величины изгибающих моментов и поперечных сил вдоль оси стержня или балки.
Итак, при вычислении перемещений в стержневых системах необходимо производить перемножение эпюр изгибающих и крутящих моментов, нормальных и поперечных сил, построенных от заданных нагрузок, на соответствующие эпюры, построенные от вспомогательных нагрузок. Так же как и в балках, при определении линейных перемещений пользуются силами Р = 1, а при определении угловых перемещений — моментами Ж = 1.
[c.406]
Так же как и в балках, при определении линейных перемещений пользуются силами Р = 1, а при определении угловых перемещений — моментами Ж = 1.
[c.406]
Рассматривая все построенные выше эпюры, нетрудно подметить определенную закономерную связь между эпюрами изгибающих моментов и эпюрами поперечных сил. Судя по виду эпюр, поперечная сила Q представляет собой производную от изгибающего момента М по длине бруса. Докажем, что эта закономерность действительно имеет место. [c.123]
Определению потенциальной энергии предшествует анализ внутренних силовых факторов, возникающих в брусе. Этот анализ производится, как известно, при помощи метода сечений и завершается построением эпюр изгибающих и крутящих моментов, а, в тех случаях, когда это необходимо — построением эпюр нормальных и поперечных сил. [c.168]
Графический способ построения изогнутой оси балки основан на полном совпадении процесса вычисления изгибающего момента М и поперечной силы С с процессом вычисления прогиба у и угла наклона ф.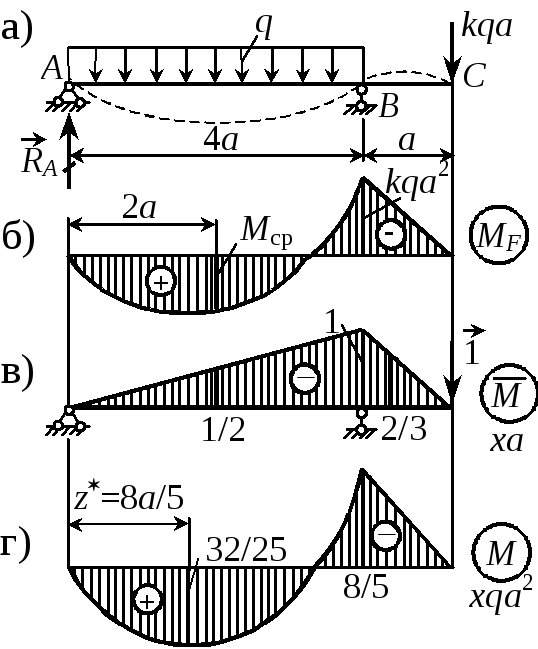 Для определения прогиба у и угла наклона ф в каком-либо сечении балки необходимо построить действительную эпюру изгибающих моментов и, загрузив ею фиктивную балку, найти величины /И и С в этом сечении. Поделив эти величины на жесткость EJ, получим прогиб у и угол наклона ф в рассматриваемом сечении балки. Эпюры М п Q можно построить также графически с помощью веревочного и силового многоугольников. Совершенно аналогично можно построить и эпюры М и С, которые представляют собой EJ—кратные законы распределения прогибов и углов наклона по длине балки. Величины фиктивного изгибающего момента и фиктивной поперечной силы в любом сечении балки определим по формулам
Для определения прогиба у и угла наклона ф в каком-либо сечении балки необходимо построить действительную эпюру изгибающих моментов и, загрузив ею фиктивную балку, найти величины /И и С в этом сечении. Поделив эти величины на жесткость EJ, получим прогиб у и угол наклона ф в рассматриваемом сечении балки. Эпюры М п Q можно построить также графически с помощью веревочного и силового многоугольников. Совершенно аналогично можно построить и эпюры М и С, которые представляют собой EJ—кратные законы распределения прогибов и углов наклона по длине балки. Величины фиктивного изгибающего момента и фиктивной поперечной силы в любом сечении балки определим по формулам
Рассматривая основные понятия и определения, мы без доказательства утверждали, что при прямом изгибе возникают поперечная сила и изгибающий момент. Теперь необходимо привести соответствующие обоснования. Надо изобразить на доске произвольным образом нагруженную (в главной плоскости) двухопорную балку, определить реакции и, применив метод сечений, убедиться, что в произвольном поперечном сечении балки возникают поперечная сила Qy и изгибающий момент Мх.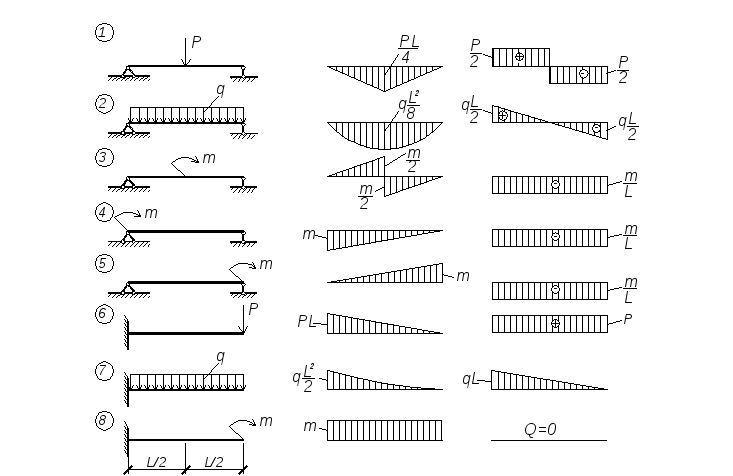 Остальные четыре внутренних силовых фактора тождественно равны нулю. Естественно, на этой стадии ознакомления с поперечной силой и изгибающим моментом обозначения Q и М снабжаются соответствующими индексами в дальнейшем при построении эпюр от этих индексов можно будет отказаться.
[c.121]
Остальные четыре внутренних силовых фактора тождественно равны нулю. Естественно, на этой стадии ознакомления с поперечной силой и изгибающим моментом обозначения Q и М снабжаются соответствующими индексами в дальнейшем при построении эпюр от этих индексов можно будет отказаться.
[c.121]
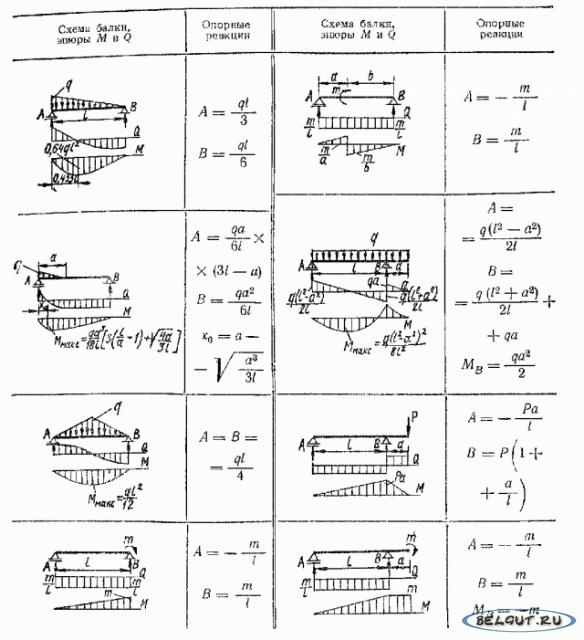
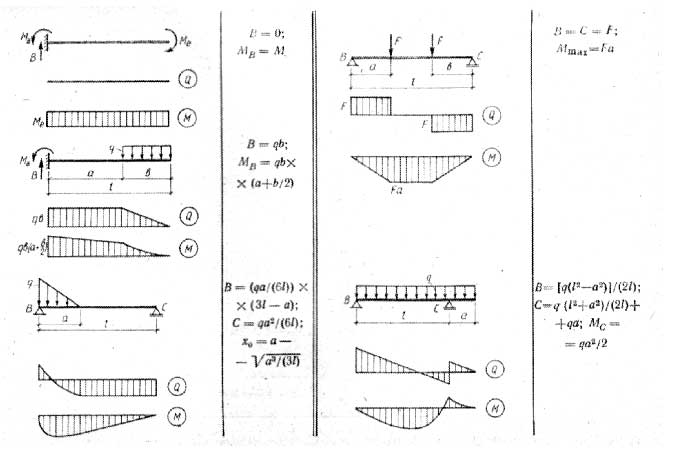
Построение эпюр. Графики изменения поперечных сил и изгибающих моментов вдоль центральной оси балки называются эпюрами. При построении эпюр поперечных сил и изгибающих моментов в большинстве случаев следует начинать с определения реакций опор. [c.146]
Построение эпюр QnM позволяет определить внутренние усилия в любом сечении балки, которые складываются из нормальных и касательных напряжений, возникающих в этом сечении при изгибе. Обратимся к вопросу об определении этих напряжений. Выше мы выяснили, что поперечная сила в сечении складывается из элементарных касательных усилий, а изгибающий момент — из нормальных, приводящихся к парам. Если на некотором участке балки поперечная сила Q отсутствует, т.
Для определенности при построении эпюр поперечных сил и изгибающих моментов установим для них правила знаков. [c.226]
В заделке возникают три реакции (На, Яа, Л а), независимых уравнений статики для плоской системы сил также три. Следовательно, имеем статически определимую систему все реакции определяются из статических уравнений. Однако для консольной балки провести решение можно без определения реакций опор. Для этого нужно, используя метод сечений, начинать построение эпюр со свободного конца балки. Из рис. 5.8, а видно, что балка имеет только один расчетный участок. Выбираем на этом участке произвольное сечение (обозначено волнистой линией) на расстоянии г от свободного конца балки и рассмотрим отдельно часть балки, расположенную справа от сечения. Поскольку вся балка находится в равновесии, то в равновесии должна находиться и эта часть балки — это будет в том случае, если в месте разреза приложить внутренние усилия, отражающие действие отброшенной левой части на оставшуюся правую часть.
Иэ рис. 128 показано построение эпюр изгибающих моментов и поперечных сил на примере балки, защемленной одним конном. Такого рода балки называются обычно консолями. В денном случае с правой стороны на балку не [ аложено связей и определение изгибающих моментов и поперечных сил в любом сечении может быть произведено без предварительного определения реакций.
Эпюры Мх и Qx. Графики изменения ш длнн балки изгибающих моментов н поперечных сил во всех поперечных сечениях называются эпюрами внутренних усилий. При построении эпюр Мх и Qx исходят из определений внутренних усилий й правил их знаков. Общие правила, облегчающие построение эпюр если на участке балки нет внешних нагрузок, то эпюры и Qx линейные (причем прямая эпюры Q — параллельна нулевой линии этой эпюрьг) если на участке действует равномерно распределенная нагрузка, то эпадра Мх — нелинейная— квадратная парабола. При этом в сечениях, где поперечная сила, изменяясь линейно, меняет знак, изгибающий момент достигает максимума или минимума точке приложения сосредоточенной силы на эпюре поперечных сил соответствует скачок на величину этой силы, а на впюре изгибающих моментов — перелом линии в точках приложения сосредоточенных моментов эпюра поперечных сил не меняется, а на эпюре изгибающих моментов наблюдается скачок ва величину сосредоточенного момента.
[c.79]
При этом в сечениях, где поперечная сила, изменяясь линейно, меняет знак, изгибающий момент достигает максимума или минимума точке приложения сосредоточенной силы на эпюре поперечных сил соответствует скачок на величину этой силы, а на впюре изгибающих моментов — перелом линии в точках приложения сосредоточенных моментов эпюра поперечных сил не меняется, а на эпюре изгибающих моментов наблюдается скачок ва величину сосредоточенного момента.
[c.79]
Традиционно тему Изгиб , как уже говорилось выше, считают центральной, наиболее важной и трудной в курсе сопротивления материалов. В настоящее время в связи с существенным сокращением программы эта тема, пожалуй, утратила свое главенствующее положение, уступив его теме Растяжение и сжатие . Действительно, по ныне действующей пограмме в этой теме остался практически один вопрос — расчеты на прочность при изгибе (по нормальным напряжениям). Правда, для его изучения требуется уделить значительное внимание вспомогательному вопросу — построению эпюр поперечных сил и изгибающих моментов. Определенные трудности, которые испытывают учащиеся, овладевая техникой построения этих эпюр, приводят к тому, что многие преподаватели продолжают считать эту тему наиболее серьезной, а может быть, и наиболее трудной. Эти трудности обусловлены либо недостаточно твердыми знаниями по статике твердого тела, либо нерациональной методикой обучения построению эпюр. Конечно, из сказанного не следует, что процесс обучения не требует затраты времени, даже при рациональной методике надо затратить 5—6 часов для того, чтобы добиться успеха, но это время расходуется на приобретение навыков, а не на преодоление каких-то фактически несуществующих трудностей.
Определенные трудности, которые испытывают учащиеся, овладевая техникой построения этих эпюр, приводят к тому, что многие преподаватели продолжают считать эту тему наиболее серьезной, а может быть, и наиболее трудной. Эти трудности обусловлены либо недостаточно твердыми знаниями по статике твердого тела, либо нерациональной методикой обучения построению эпюр. Конечно, из сказанного не следует, что процесс обучения не требует затраты времени, даже при рациональной методике надо затратить 5—6 часов для того, чтобы добиться успеха, но это время расходуется на приобретение навыков, а не на преодоление каких-то фактически несуществующих трудностей.
Рассмотрим, например, вал, изображенный на рис. 31, а, где показаны также диаметры вала и действующие нагруяки. Эпюра моментов 1К) уч,ается путем построения силового многоугольника (рис. 34, б) и соответствующего веревочного многоугольника (рис. 34, в). Для определения численного значения изгибающего момента в произвольном поперечном сечении необходимо лишь измерить соответствующую ординату на эпюре моментов в масштабе длин чертежа и умножить ее на полюсное расстояние к, измеренное в масштабе сил силового многоугольника (в нашем случае А = 36200 кг). Для получения кривой изгиба необходимо построить второй веревочный многоугольник при этом построенная ранее эпюра моментов рассматривается как фиктивная эпюра нагрузки. Для учета переменности поперечного сечения вала интенсивность этой фиктивной нагрузки в каждом сечении умножается на где /р —момент
[c.42]
Для получения кривой изгиба необходимо построить второй веревочный многоугольник при этом построенная ранее эпюра моментов рассматривается как фиктивная эпюра нагрузки. Для учета переменности поперечного сечения вала интенсивность этой фиктивной нагрузки в каждом сечении умножается на где /р —момент
[c.42]
Не удается найти страницу | Autodesk Knowledge Network
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}}/500 {{l10n_strings.TAGS}} {{$item}} {{l10n_strings. PRODUCTS}}
{{l10n_strings.DRAG_TEXT}}
PRODUCTS}}
{{l10n_strings.DRAG_TEXT}}
{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.LANGUAGE}} {{$select.selected.display}}{{article.content_lang.display}}
{{l10n_strings.AUTHOR}}{{l10n_strings. AUTHOR_TOOLTIP_TEXT}}
AUTHOR_TOOLTIP_TEXT}}
Правила контроля эпюр при плоском изгибе
При плоском поперечном изгибе возникает два ВСФ поперечная сила и изгибающий момент (если Qy, то Mx, так как сила по Y сгибает плоскость Х). Рассмотрим подробнее правило знаков для изгибающего момента. Если момент сжимает верхние волокна, то он считается положительным. Положительная эпюра откладывается сверху. Значит, если сжимаются верхние волокна, то эпюра сверху. Если момент сжимает нижние волокна, то он
должен быть скачок (ступенька) на величину и направление этого момента.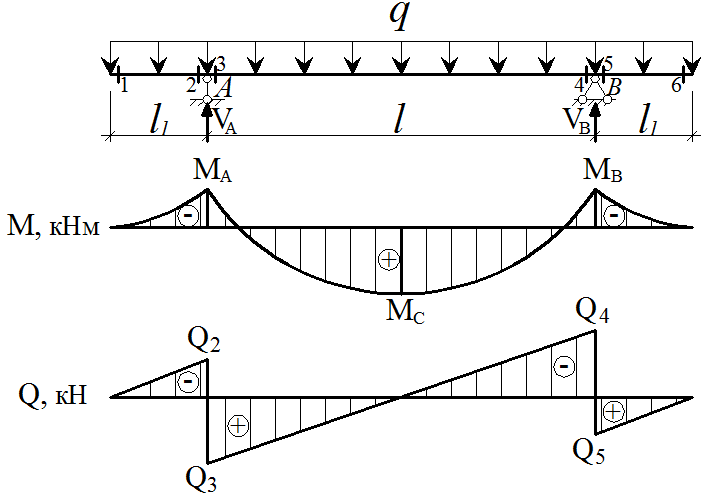
3. На концах балки внутренний момент должен быть
равен нулю, если нет внешнего момента.
4. В промежуточном шарнире изгибающий момент
равен нулю, поэтому эпюра Мх в шарнире должна пройти через ноль, т.е. пересечь ось.
5. На участке, на котором приложена равномерно распределенная нагрузка, эпюра Qy – наклонная прямая линия, а эпюра Мх – парабола.
6. На участке, на котором эпюра Qy – положительна,
эпюра Мх возрастает, Qy отрицательна – Мх убывает, Qy равна нулю – Мх постоянная прямая.
7. В сечении, в котором эпюра Qy пересекает ось,
эпюра Мх обязательно имеет экстремум.
Шестое и седьмое правила являются следствием теоремы
Журавского, согласно которой поперечная сила есть первая
производная от изгибающего момента по координате:
считается отрицательным. Отрицательная эпюра откладывается
снизу. Значит, если сжимаются нижние волокна, то эпюра снизу.
Отсюда следует, что эпюра момента всегда оказывается со стороны сжатых волокон. Поэтому говорят, что эпюра изгибающего момента строится на сжатом волокне. Это можно считать тоже правилом знаков для случая, когда определить, где нижние, а где верхние волокна невозможно.
Запишем 7 правил, применяя которые можно проконтролировать правильность построения эпюр.
1. В сечении, в котором приложена внешняя сосредоточенная сила, на эпюре внутренней силы Qy должен быть скачок (ступенька) на величину и направление этой силы.
2. В сечении, в котором приложен внешний сосредоточенный момент, на эпюре внутреннего момента Mx
2.6. Примеры построения эпюр ВСФ
при плоском изгибе
Пример 8. Построим эпюры ВСФ для балки, изображенной на рис.7, с.9. Опорные реакции для нее мы вычислили в примере 1.
l, q – заданы, RA = RB = 0,5 ql
Для вычисления ВСФ применяем метод сечений. Балка
содержит всего один участок. В произвольном месте на этом
В произвольном месте на этом
участке проведем сечение. Начало координат расположим,
например, в точке А.
Чтобы показать, что сечение проведено действительно в произвольном месте участка, покажем, что расстояние до сечения есть величина переменная «Z» (рис.28) , которая может принимать любое значение в диапазоне 0 £ Z £ l.
Теперь отбросим правую часть балки и вычислим ВСФ в сечении, применяя метод сечений.
Поперечная сила в сечении равна сумме двух внешних сил, оставшихся в левой части бруса – это сосредоточенная сила
RA и сила, возникающая от действия распределенной нагрузки q.
Опорная реакция в уравнение будет подставлена со
знаком «+» в соответствии с правилом знаком для Qy (рис. 25), а распределенная нагрузка – со знаком минус.
Полная сила от действия нагрузки рассчитывается как площадь прямоугольника: высота фигуры q, а ширина –
расстояние от т. В до сечения, т.е. Z (рис.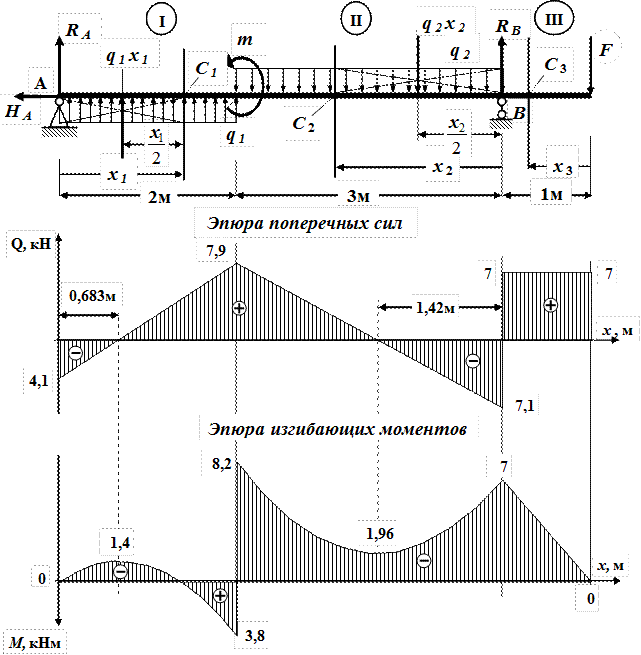 29).
29).
Тогда Qy = RВ – q×Z = 0,5 q×l – q×Z .
Записанное уравнение является уравнением прямой, так
как переменная Z находится в степени 1.
Рис.29. Схема для расчета ВСФ к примеру 8
Чтобы построить прямую, нужно вычислить значение функции в двух точках. За такие точки удобно принять начало и конец участка. Тогда
Qy | = 0,5 ql
| Z= 0
Qy | = 0,5 ql
| Z= l
Далее вычисляем внутренний момент.
В соответствии с методом сечений внутренний момент
равен сумме всех внешних моментов. В нашем случае такими моментами являются два момента: момент, создаваемый опорной реакцией и момент, создаваемый распределенной нагрузкой.
Момент силы НВ равен 0, так как эта сила проходит через сечение и плечо ее равно нулю.
Момент от силы RB равен произведению этой силы на плечо, т.е. на расстояние от т.В до сечения. В нашем случае это расстояние обозначено как Z (рис.29).
Запишем: M(RB) = RB × Z
Знак этого момента будет положительным, так как момент этой силы изгибает балку так, что сжимаются верхние волокна балки (рис.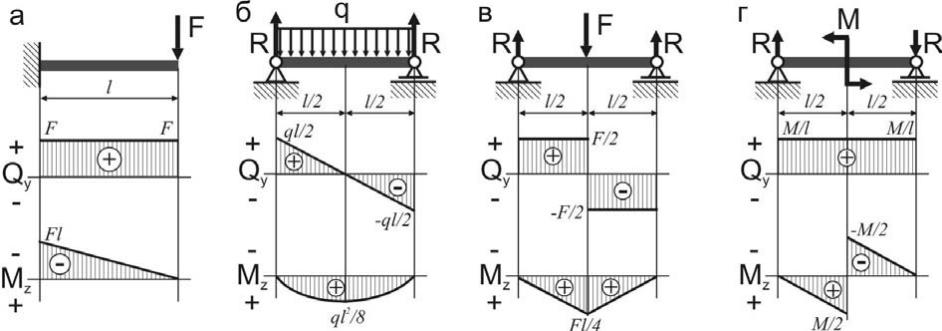 30а).
30а).
нагрузки без учета опоры изгиб будет таким, как показано на рис.30 б.
Величина момента от распределенной нагрузки
вычисляется как произведение полной силы на плечо.
Полная сила рассчитывается как площадь
сжатие
растяж.
Mx Mx
прямоугольника Q = q × Z. Плечо этой силы отсчитывается как расстояние от сечения, в котором вычисляется внутренний момент до центра тяжести прямоугольника, т.е. половина расстояния Z. Тогда величина момента станет q× Z× Z/2, а весь внутренний момент Mx = RВ × Z – q× Z2/2.
|
RB растяж. Z
Z сжатие
|
а б
Рис. 30. Пояснения к выбору знака момента
30. Пояснения к выбору знака момента
Момент, создаваемый распределенной нагрузкой будет отрицательным, т.к. он изгибает балку так, что сжимаются нижние волокна балки (рис.30б).
Теперь посмотрим на рис.31. Этот рисунок показывает,
что, кажется, от равномерно распределенной нагрузки балки
изогнется так, что произойдет сжатие верхних волокон, а значит, знак его будет положительный. Это наиболее часто встречающаяся ошибка в работах студентов. Изгиб, показанный на рис. 31, возникает в том случае, если слева в т.В есть опора, или эквивалентная замена опоры – опорная реакция RВ.
Таким образом, изгиб, показанный на этом рисунке,
возникает при совместном действии двух моментов – момента от опорной реакции и распределенной нагрузки. Применяя метод сечений, мы рассматриваем каждый момент в отдельности, а результат складываем. Поэтому при действии распределенной
Рис. 31. Схема, показывающая сжатие волокон при совместном действии моментов.
Переменная (координата вдоль оси балки) находится в степени 2 (в квадрате), следовательно, записанное уравнение является уравнением параболы. Знак «–» перед Z/2 говорит о том, что ветви параболы направлены вниз (парабола выпуклостью вверх).
Для построения этой параболы необходимо вычислить
значение момента на границах участка, т.е. в точках с координатами 0 м и l м.
По значениям вычисленных величин на границах
участков строим эпюры внутренней поперечной силы и изгибающего момента. Эпюры принято подписывать и указывать значения в характерных точках – на границах участков, точек экстремумов и т.д. В рассматриваемом примере эпюры будут выглядеть так, как показано на рис.32.
Для поперечной силы, отложенные две точки, соединяем
прямой линией в соответствии с полученным уравнением. Значения изгибающего момента на концах балки оказались равны 0. Эти две точки с нулевыми значениями соединяем параболической линией в соответствии с полученным уравнением изгибающего момента. При этом нужно учитывать, что ветви параболы прогибаются вниз. Таким образом, линию можно провести только в том, случае, если у нее есть экстремум, в данном случае максимум. Максимум приходится на середину балки. Об этом говорит то, что эпюра поперечной силы в середине пересекает ось и в соответствии с правилом контроля эпюр № 7, эпюра момента действительно должна иметь экстремум.
Эти две точки с нулевыми значениями соединяем параболической линией в соответствии с полученным уравнением изгибающего момента. При этом нужно учитывать, что ветви параболы прогибаются вниз. Таким образом, линию можно провести только в том, случае, если у нее есть экстремум, в данном случае максимум. Максимум приходится на середину балки. Об этом говорит то, что эпюра поперечной силы в середине пересекает ось и в соответствии с правилом контроля эпюр № 7, эпюра момента действительно должна иметь экстремум.
Эпюра изгибающего момента в соответствии с правилом знаков должна располагаться со стороны сжатого волокна, т.е.
сверху (рис.31).
Максимум на эпюре Мх вычисляется с помощью записанного ранее уравнения момента, подставляя вместо координаты Z координату середины балки, т.е. l/2.
Рис.32. Эпюры поперечной силы
и изгибающего момента к примеру 8
Построив эпюры, можно определить опасное сечение
Таким сечением является сечение, в котором изгибающий момент наибольший по абсолютному значению.
В нашем случае опасным сечением является сечение,
расположенное посередине балки, где изгибающий момент максимален.
RA P1 P2 RВ
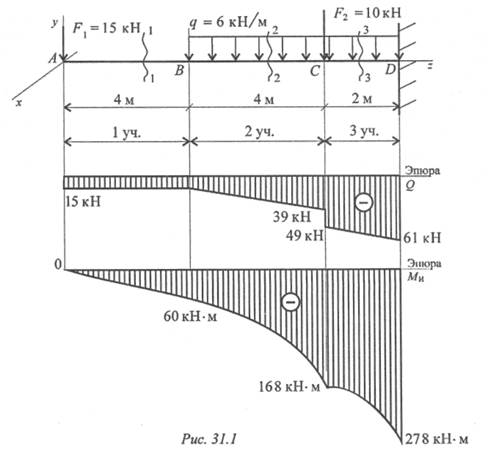
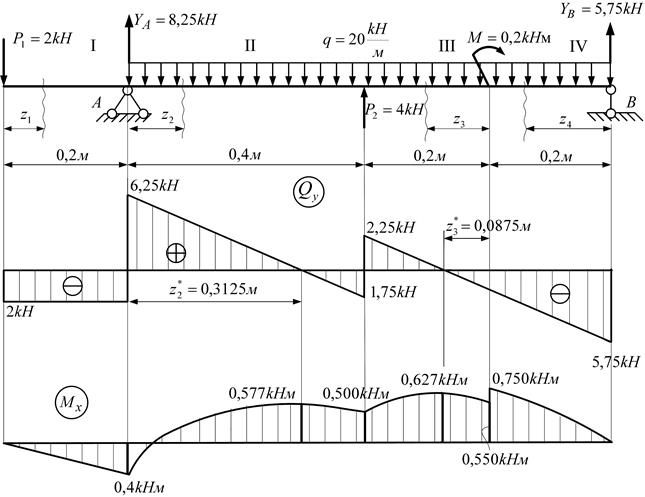
Пример 9. Построим эпюры внутренних силовых факторов для балки, рассмотренной в примере 2. Опорные реакции к этому моменту уже известны.
Рассматриваемая балка имеет три участка длиной 1 м, 8 м и 1 м. На каждом участке проведем сечение в произвольном месте участка.
Первый участок 0 £ Z1 £ 1.
Уравнения поперечной силы приравнивает внутреннюю
силу единственной внешней силе:
Qy = RA = 1,1 – уравнение прямой постоянной линии.
Для ее построения не нужно считать значения
поперечной силы на концах участка.
Mх = RA× Z1 = 1,1× Z1 – уравнение прямой линии,
наклонной по отношению к оси.
Для ее построения нужно вычислить значения на концах участка.
Второй участок 1 £ Z2 £ 9.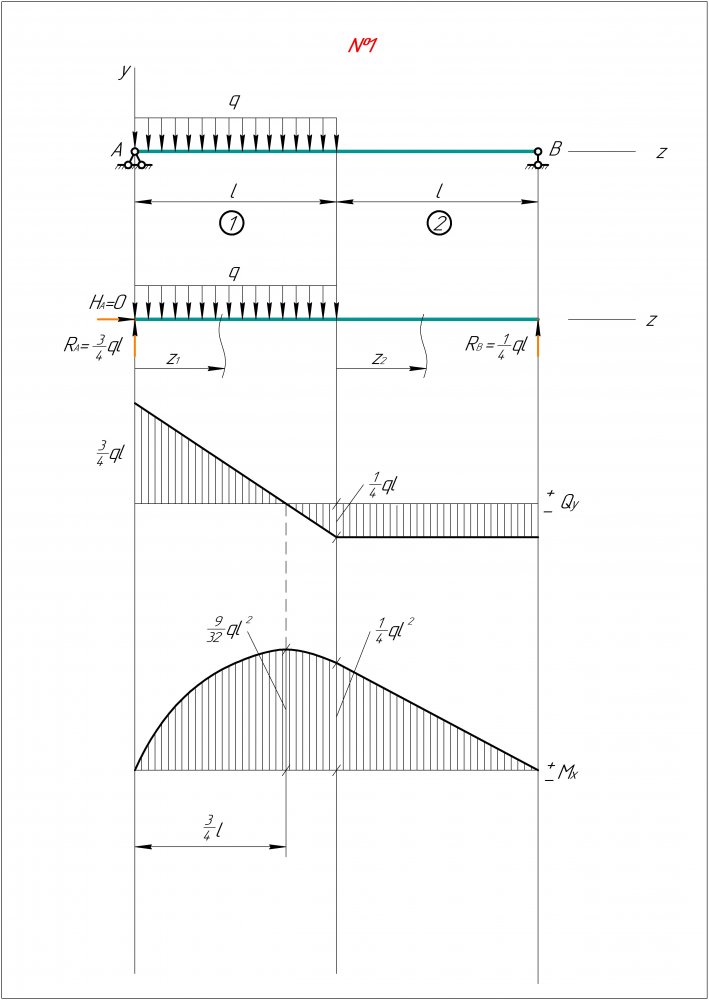
Уравнение внутренней поперечной силы составляется как
сумма двух внешних поперечных сил:
Qy = RA – P1 = 1,1 – 1 = 0,1 – уравнение прямой постоянной линии.
1,1
Рис.33. Эпюры поперечной силы
Мх,
кН*м
Уравнения моментов можно составить так:
Mх = RA× Z2 P1× (Z2 — 1)= 1,1× Z + 1 – Z2 = 0,1× Z2 + 1
Плечо силы Р1 можно вычислить как разность длин двух
отрезков: отрезка длиной Z2 и полной длины первого участка,
т.е. 1 м. (рис.33).
и изгибающего момента к примеру 9
Полученное уравнение представляет собой уравнение наклонной прямой линии и для ее построения нужны две точки – начало и конец участка.
M x |Z =1= 1,1
M x |Z =9 = 0,1 × 9 + 1 = 1,9 .
RA
Третий участок рассмотрим с правой стороны. Начало
координат расположим в точке В. Тогда 0 £ Z3 £ 1.
Запишем уравнения.
Qy= — RB = — 1,9 это уравнение прямой горизонтальной линии. Знак минус потому, что выбрана правая часть балки (см.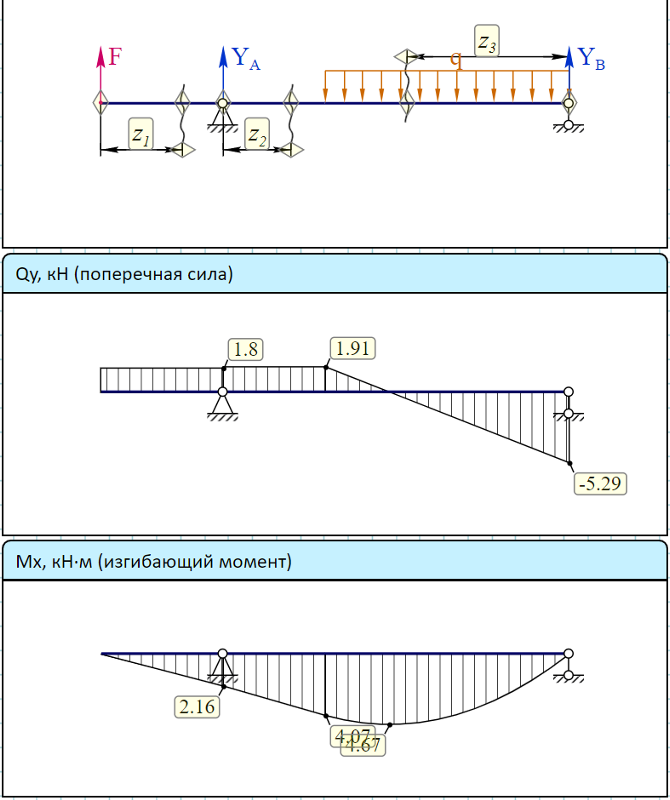 правила знаков для Qy).
правила знаков для Qy).
Mх = RB× Z3 = 1,9× Z3 это уравнение наклонной прямой
линии.
M x |Z =0 = 0
|
M x |Z =1= 1,9 .
По данным этих расчетов строим эпюры. Результат построения эпюр показан на рис. 33. Из анализа эпюр следует,
что опасным сечением является сечение, расположенное в точке приложения сосредоточенной силы Р2, там, где эпюра изгибающего момента максимальна.
|
|
|
Пример 10. Построим эпюры ВСФ для задачи, рассмотренной в примере 3. Опорные реакции на данный момент уже известны.
Построим эпюры ВСФ для задачи, рассмотренной в примере 3. Опорные реакции на данный момент уже известны.
Решение задачи показано на рис. 34.
I участок 0 £ Z1 £ 3.
Q y = R A = 62
уравнение горизонтальной прямой линии.
M x = R A × Z1 M A = 62 × Z1 403
наклонной прямой линии.
— уравнение
Момент опорной реакции считается положительным,
потому что от его действия сжимаются верхние волокна.
Сосредоточенный момент МА изгибает балку так, что сжимаются нижние волокна и поэтому его знак отрицательный.
Рис.34. Эпюры ВСФ для примера 10
M x |Z =0 = — 403
II участок 3 £ Z2 £ 6.
M x |Z =3 = 217 .
расстояние до сечения есть величина переменная и лежащая в диапазоне от 0 до 4 м.
Поперечная сила рассчитывается как сумма всех внешних
Q y = R A q( Z 2 3 ) = 62 10( Z 2 3 )
наклонной прямой линии.
— уравнение
сил отсеченной левой части бруса. В качестве внешней силы здесь имеется только часть равномерной нагрузки.
В качестве внешней силы здесь имеется только часть равномерной нагрузки.
Qy |Z = 3 = 62
Qy |Z =6 = 32 .
Кроме того, обратите внимание на то, что правила знаков
Обратите внимание, как вычисляется полная сила от распределенной нагрузки. Площадь прямоугольника есть произведение высоты q на ширину (Z – 3).
Уравнение внутреннего момента составляем путем
для поперечной силы выбирается наоборот.
Q y = +q × Z 3 .
Это уравнение наклонной линии. Строим его по двум
точкам:
сложения 3 внешних моментов:
Z 3
Q y |Z =0 = 0
Q y |Z =4 = 40 .
M x = R A
× Z 2
M A
q( Z
2
3 ) 2 =
2
Внутренний момент равен сумме двух внешних моментов
– сосредоточенного момента М и момента от распределенной
= 62 × Z 2
403 5( Z
2
3 )2 .
нагрузки q. Чтобы определить знак момента М, представьте брус
с отверстием, в которое вставлен стержень и концы стержня
Это уравнение отличается от уравнения изгибающего
момента на первом участке тем, что добавляется еще один
внешний момент – момент от распределенной нагрузки. Знак этого момента отрицательный, потому что от его действия сжимаются нижние волокна бруса.
Знак этого момента отрицательный, потому что от его действия сжимаются нижние волокна бруса.
Представленное уравнение есть уравнение прямой
наклонной линии.
подвергаются воздействию пары сил. В результате возникает
рычаг, который изогнет балку и можно будет легко увидеть сжатие волокон и знак этого момента (рис.35).
В нашем случае момент сжимает верхние волокна и,
значит, подставляется в уравнение со знаком «+». А вот момент
от распределенной нагрузки сжимает нижние волокна и,
следовательно, будет отрицательным.
M x |Z =0 = — 217
M x |Z =3 = — 76 . Z 2
Для вычисления момента от распределенной нагрузки сначала вычисляется полная сила как произведение высоты
Тогда M x = — q 3 + M
2
= — 5 × Z
2 + 4 .
3
нагрузки Q на ширину (Z-3). Потом она умножается на плечо.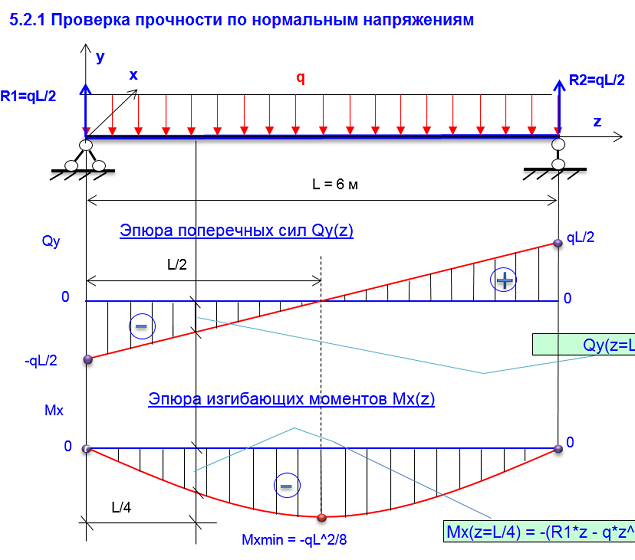
Плечо отсчитывается как расстояние от сечения до середины приложения нагрузки, где расположен ее центр тяжести и равен половине ширины отрезка (Z – 3).
III участок балки 0 £ Z3 £ 4 м.
Третий участок рассмотрен с правой части балки. Начало
координат при этом переносится в т.В. Следовательно,
Момент от нагрузки считается в 2 этапа. Сначала
определяется полная сила как произведение Q на ширину
отрезка Z, потом результат умножается на расстояние до центра тяжести прямоугольника под линией нагрузки, т.е. на половину отрезка Z. В результате переменная оказывается в степени 2 и уравнение становится уравнением параболы, ветви которой
направлены вниз (перед квадратом Z находится знак минус).
Значения на границах участка:
задаче не 3, а только 2 участка – АВ и АС. На участке АВ
сечение можно провести в любом месте до шарнира или после.
M х |Z =0 = 4
M x |Z =4 = 4 5 × 4 2 = 76 .
Если на отрезке АВ выбрать 2 участка, т.е. до шарнира и после,
то это не повлияет на правильность решения задачи. Добавление
По вычисленным значениям строим эпюры сил и
моментов (рис. 34).
Из эпюр следует, что опасным сечением является сечение
на левом конце балки, закрепленное с помощью жесткой заделки, т.е. в т.А, где эпюра внутреннего изгибающего момента
нового участка усложнит и увеличит время решения задачи.
Эпюры, получившиеся при решении этой задачи показаны на рис. 36.
I участок 0 £ Z1 £ l.
Qy = RВ – q×Z1 = 0,25 q×L – q× Z1 – прямая наклонная линия.
по абсолютному значению максимальна. Наибольшее значение
изгибающего момента Мх = 403 кН*м. Наибольшее значение
Q y |Z =0 = 0,25ql
Q y |Z =l = 0,25ql ql = — 0,75ql .
поперечной силы Qy = 62 кН оказалось в том же сечении.
M x = RB Z1 qZ 2 / 2 = 0,25ql Z1 qZ 2 / 2 .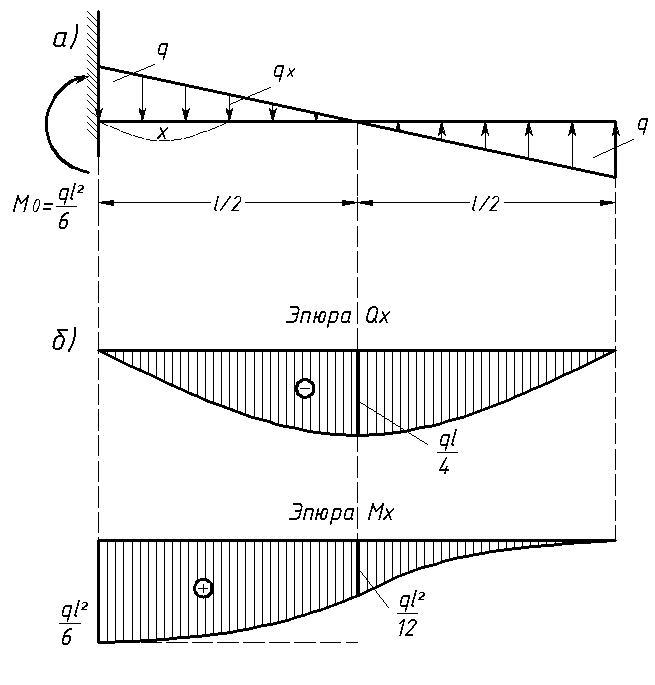
1 1
Это уравнение параболы, ветви вниз. Строим по двум точкам на границах участка.
M x |Z =0 = 0
M x |Z =l
= 0,25ql 2 q l 2
2
= — 0,25ql 2
линии.
II участок 0 £ Z2 £ l.
Qy = — Rc + q× Z2 – это уравнение прямой наклонной
Q y |Z =0 = — 0,25ql
Q y |Z =l = — 0,25ql + ql = 0,75ql .
Уравнение изгибающего момента:
Mx = RС Z 2
Z 2
q 2 = 0,25ql Z
2 2
Z 2
q 2 .
2
Рис. 35. Определение знака сосредоточенного момента.
Это уравнение параболы, ветви вниз. Строим по двум
точкам на границах участка.
Пример 11. Построим эпюры поперечной силы и
M x |Z =0 = 0
M x |Z =l
= 0,25ql 2 q l
2
= — 0 ,25ql 2 .
изгибающего момента для балки, рассмотренной в примере 4.
Опорные реакции определены.
Рассматриваемая балка состоит из двух участков.
Промежуточный шарнир не дает границы участка, так как в этой точке не появляется новой силы или момента. Поэтому в нашей
Вычислим экстремумы эпюры моментов. Экстремумы определяются на основе правила контроля эпюр №7, в основе которого лежит теорема Журавского о дифференциальных зависимостях при плоском изгибе. Прочитайте еще раз это
правило. Чтобы определить максимум, приравняем уравнение поперечной силы к нулю и, решив его, определим расстояние до пересечения этой линией оси.
Сначала для второго участка.
Qy = — Rc + q× Z2 = 0, Z2 = Rc / q = 0,25 ql / q = 0,25 l.
Таким образом, расстояние от правого конца балки до
точки, в которой поперечная сила равна нулю и соответственно
RВ q RА RС
HВ
L L
эпюра Мх имеет экстремум, равно 0,25 l.
Далее эту координату подставляем в уравнение
изгибающего момента, чтобы вычислить величину момента в
этой точке.
Таким же образом вычисляется экстремум на первом
участке. Попробуйте вычислить его самостоятельно. Его величина окажется равной величине экстремального момента на втором участке.
В результате наибольший по абсолютной величине
момент возникает в т.А – на средней опоре и его величина равна
0,25ql2. Таким образом, опасное сечение соответствует т.В для заданной балки.
Применяя 7 правил контроля эпюр при плоском изгибе,
определим, насколько безошибочно мы решили задачу.
В сечении А на эпюре Qy возникает скачок (ступенька).
1/32
3/4
1/4
1/32
Mx, ql
Ее величина должна равняться силе, приложенной в данной точке, т.е. RB = 6/4 ql = (3/4 – (-3/4)) ql = 6/4 ql.
На схеме заданной балки сосредоточенных моментов нет, поэтому эпюра Мх на границах участков во всех точках должна совпадать (ступеней быть не должно). Это правило выполняется.
На концах балки изгибающий момент должен быть равным 0, если здесь нет внешних сосредоточенных моментов.
Это правило в нашем случае также выполняется.
Рис.36. Эпюры ВСФ для примера 11
В промежуточном шарнире эпюра Мх должна пересекать ось, так как момент в шарнире равен 0. Правило выполняется.
На участках, где приложена равномерно распределенная
нагрузка, эпюра Qy должна быть прямой наклонной линией, а эпюра Мх – параболой. Это правило на обоих участках балки выполняется.
До координаты 0,25l эпюра Qy – положительна, значит, эпюра Мх должна возрастать. Далее до координаты опоры А эпюра сил отрицательна и эпюра момента убывает.
На втором участке по длине 0,75l эпюра поперечной силы положительна и эпюра внутреннего момента возрастает.
И на последнем отрезке Qy < 0, поэтому Мх возрастает. Таким образом, контроль правильности на основе дифференциальных зависимостей между поперечной силой и изгибающим моментом также выполняется.
В сечениях с координатами 0,25l и 1,75l эпюра Qy пересекает ось, поэтому эпюра Мх в этих точках имеет экстремум, в данном случае максимум.
Контроль правильности построения эпюр ВСФ по всем 7
пунктам выполняется. Ошибок в расчетах и построении нет.
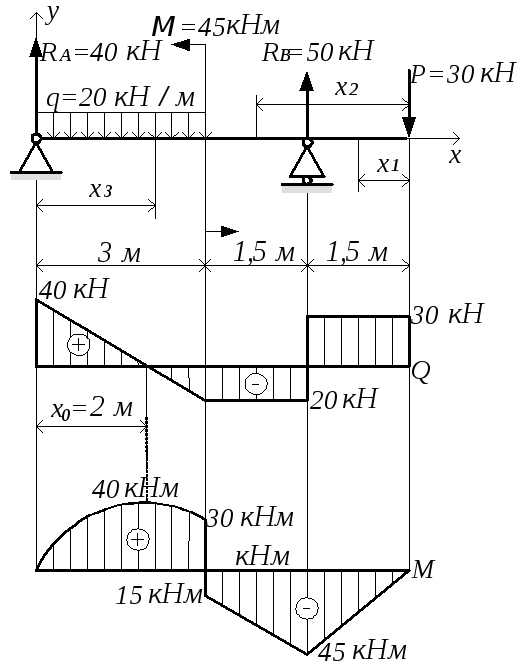
Пример 12. Построим эпюры внутренних сил и моментов для балки, рассмотренной в примере 5. Опорные реакции на данный момент уже определены.
Рассматриваемая балка включает в себя 4 участка.
Границами участков являются точки приложения сосредоточенных и моментов. Кроме того, границей участка является точка начала распределенной нагрузки или точка завершения такой нагрузки. Вообще, правило выбора границы участка связано с уравнениями ВСФ. На разных участках уравнения ВСФ должны быть различны. Если сечение, проведенное рядом с предыдущим, дает абсолютно одинаковые уравнения всех ВСФ, то это означает, что сечение проведено на том же самом участке. Уравнения изменяются тогда, когда происходят изменения во внешних нагрузках. В данном примере граница второго и третьего участков случайно совпали с месторасположением шарнира.
На каждом из четырёх участков проведем одно сечение.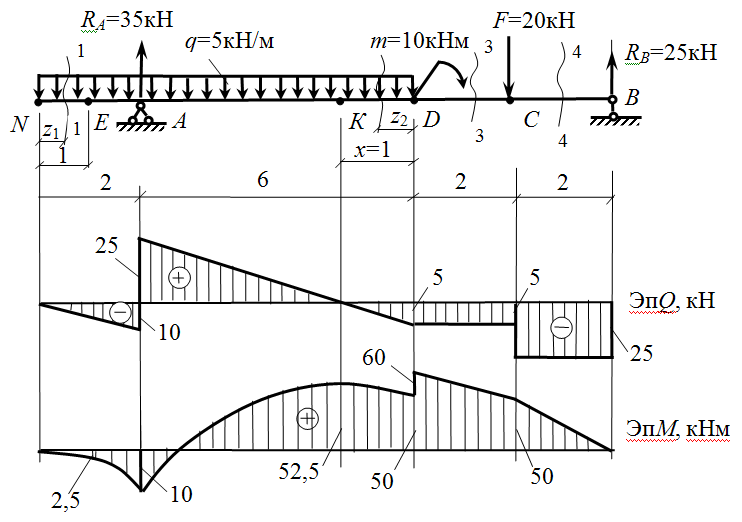
Пронумеруем их в порядке следования слева направо. При
вычислении ВСФ в первом сечении удобнее отбросить правую часть бруса, так как она сложнее.
Рис.37. Эпюры ВСФ для примера 12
То же самое касается второго участка. А вот третий и четвертый участки лучше рассматривать справа.
Решение задачи показано на рис.37.
I участок 0 £ Z1 £ 3.
Qy = RA = 30 – уравнение горизонтальной прямой.
Mx = RA × Z1 – MA = 30× Z1 – 165
Получено уравнение наклонной прямой. Вычисляем
значения на границах.
Особо обратите внимание на то, как вычисляется момент от распределенной нагрузки.
Чтобы вычислить силу от q интенсивность нагрузки
Mx |z =0 = — 165
Mx |z =3 = — 75
умножается на длину отрезка, по которому она приложена. В
II участок 3 £ Z2 £ 6.
Qy = RA + P – q(Z2 – 3) = 30 + 10 – 10 (Z2 – 3) =
=40 – 10 (Z2 – 3)–это уравнение наклонной прямой.
данном случае это будет 3 м. Далее эту силу умножают на плечо.
Далее эту силу умножают на плечо.
Плечом является расстояние от середины отрезка, по которому приложена нагрузка до сечения. Чтобы вычислить это
Q y |Z =3 = 40
Q y |Z =6 = 10
расстояние нужно от всего расстояния от правого конца балки
до сечения, т.е. Z, вычесть половину от отрезка длиной 3 м, т.е.
Mx = RA × Z2 – MA + P × (Z2 – 3) – q(Z2 – 3)2 / 2= 30×Z2 – 165
+ 10 (Z2 – 3) – 5× (Z2 – 3)2.
1,5 м.
В итоге получено уравнение наклонной прямой.
Получено уравнение параболы, ветви вниз. Вычисляем
Вычисляем значения на границах.
значения на границах.
M x |Z =3 = 30
M x |Z =6 = 0 .
M x |Z =3 = — 75
M x |Z =6 = 0
На 4-ом участке эпюра сил пересекает ось. Значит, эпюра
Так как участки выбраны последовательно, а сечение IV
участка мы рассматриваем с противоположного конца, то
сначала запишем уравнения для IV участка.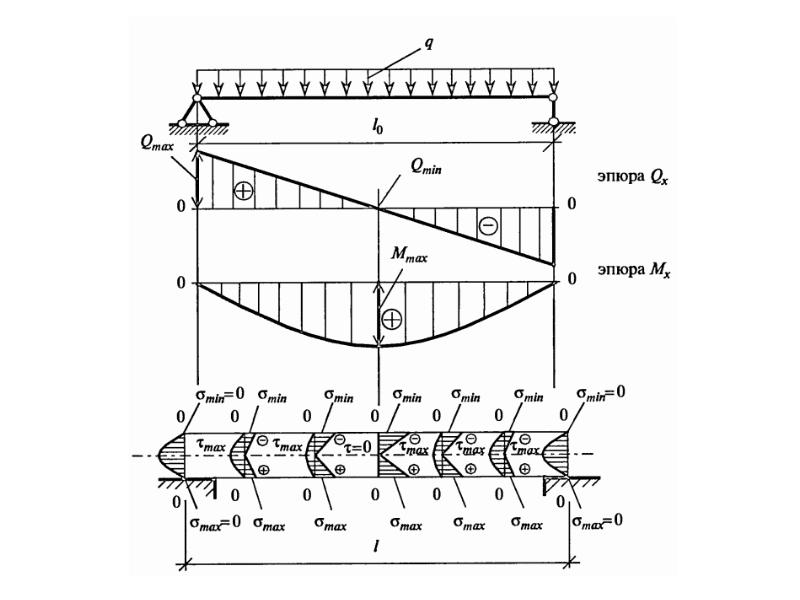
IV участок 0 £ Z4 £ 3.
Qy = — RB + q × Z4 = — 20 + 10 × Z4 – уравнение наклонной прямой.
изгибающего момента здесь должна иметь экстремум. Чтобы вычислить его приравняем уравнение поперечной силы к нулю.
Qy = — RB + q × Z4 = — 20 + 10 × Z4 = 0. Отсюда определим точку пересечения: Z4 = 20 / 10 = 2 (м).
Подставим эту координату в уравнение изгибающего
Q y |Z =3 = — 20
Q y |Z =6 = 10 .
2
момента: M x |Z =2 = 20 × 2 5 × 2 2 = 20 .
Mx = RB× Z4 – q× Z42 / 2= 20× Z – 5× Z4 .
Получено уравнение параболы, ветви вниз. Вычисляем
значения на границах.
Проанализировав эпюры, определяем наибольший изгибающий момент Мх = 165 кН*м и опасное сечение, которое находится на левой опоре (в жесткой заделке).
M x |Z =0 = 0
M x |Z =3 = 15 .
Применяя 7 правил контроля эпюр при плоском изгибе,
III участок 3 £ Z3 £ 6.
Qy = — RB + q× 3 = — 20 + 10 × 3 = 10 – уравнение горизонтальной прямой.
Mx = RB × Z3 + M – q × 3× (Z3 – 1,5) =
= 20× Z3 + 15 + 10× 3× (Z3 – 1,5).
определим, насколько безошибочно мы решили задачу. В
сечении с координатой Z = 3м приложена сосредоточенная сила Р, поэтому на эпюре сил возникает скачок на направление вверх на величину 10 кН. Эпюра поднимается с 30 кН до 40 кН.
В остальных точках на эпюре сил скачков не должно быть.
В сечении с продольной координатой Z = 9 м приложен сосредоточенный момент М = 15 кН*м. Поэтому в этой точке на
эпюре моментов возникает скачок по направлению момента, т.е. вниз, на величину этого момента. В результате эпюра Мх падает с величины 30 кН*м до 15 кН*м, т.е. на 15 кН*м. В других точках эпюра Мх не должна иметь скачков.
На концах балки изгибающий момент равен 0. На левом
конце у нас это условие не выполняется. Но здесь именно так и должно быть – в этом сечении приложен внешний сосредоточенный момент МА. На правом же конце Мх = 0.
На правом же конце Мх = 0.
В промежуточном шарнире момент должен быть равным
нулю, поэтому эпюра Мх в сечении с координатой Z = 6 м пересекает ось.
На 2 и 4 участках к брусу приложена равномерно распределенная нагрузка. Поэтому на этих участках эпюра сил –
прямая наклонная линия, а эпюра моментов – парабола. На 1 и 3 участках тогда эпюра Qy – постоянная прямая, а эпюра Мх – наклонная прямая.
Проверим участки возрастания-убывания эпюры моментов. На всех отрезках, где эпюра сил положительна, эпюра
Мх возрастает, где эпюра сил отрицательна – эпюра Мх убывает.
Таким образом, правило контроля эпюр, основанное на применении теоремы Журавского Qy = (Mx) /, выполняется.
На эпюре Мх имеется единственный экстремум в точке с координатой Z = 10 м именно там, где эпюра поперечной силы пересекает ось.
В результате проверки можно сделать вывод о том, что эпюры внутренних силовых факторов для заданной балки
построены правильно.
Пример 13.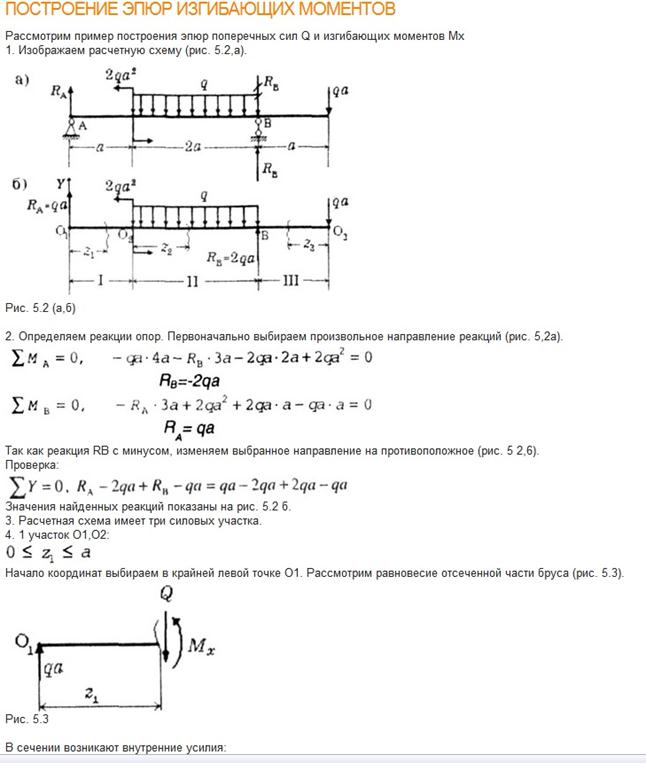 Построим эпюры внутренней силы и внутреннего момента для балки, рассмотренной в примере 6. Опорные реакции в том же примере уже определены.
Построим эпюры внутренней силы и внутреннего момента для балки, рассмотренной в примере 6. Опорные реакции в том же примере уже определены.
Эпюры ВСФ для этой балки показаны на рис.38.
Рассматриваемая балка включает 5 участков. На каждом из 5 участков проводим по одному сечению. Каждое сечение разрезает балку на 2 части – левую и правую. При вычислении внутренних силовых факторов одна из частей отбрасывается.
При рассмотрении 1, 2, 3 сечений лучше отбрасывать
правые части бруса.
При рассмотрении 4 и 5 сечений отбрасывать нужно
левые части.
Рассмотрим 1 сечение. Это сечение проводится на
произвольном расстоянии от начала координат, которое расположено в т.А. Чтобы показать, что сечение проводится на произвольном расстоянии, обозначим это расстояние переменной величиной Z. Оно может принимать любое значение в диапазоне от 0 до 3 м.
I участок 0 £ Z1 £ 3 м.
Внутренняя сила в сечении равна единственной внешней
силе RA с учетом знака.
Qy = RA = 2,5 кН – это уравнение прямой, которая
параллельна оси. Для ее построения нет необходимости расчета
силы на концах участка.
Внутренний момент в сечении равен единственному внешнему моменту, имеющемуся на участке. Таким моментом является момент, создаваемый сосредоточенной силой RA. Эта сила приложена на расстоянии Z от сечения и поэтому создает момент равный произведению силы на плечо:
Mx = RA× Z1 = 2,5× Z1.
Момент этой опорной реакции считается положительным
потому, что в результате изгиба, вызванного этим моментом,
сжимаются верхние волокна балки (см. правило знаков для Мх).
Записанное уравнение является уравнением прямой
наклонной по отношению к оси линией. Для ее построения необходимы 2 точки. Удобно использовать в качестве этих точек границы данного участка.
II участок 3 £ Z2 £ 6.
Начало координат (точку 0) оставили в т.А поэтому левой
границей 2-го участка будет точка с координатой 3 м.
Внутренняя поперечная сила равна теперь уже сумме
двух внешних поперечных сил – RA и силе, создаваемой нагрузкой q. Опорная реакция в уравнение Qy подставляется со
знаком «+», а нагрузка q со знаком минус (см. правило знаков).
Чтобы вычислить полную силу, возникающую от
действия нагрузки нужно вычислить площадь прямоугольной фигуры, возникающей под линией интенсивности q. Таким образом, высоту прямоугольника q нужно умножить на ширину, равную (Z – 3 м).
Qy = RA + Р – q(Z2 – 3)=2,5 – 10(Z2 – 3 м) – это уравнение прямой наклонной к оси линии и для ее построения требуются две точки:
Рис.38. Эпюры ВСФ для примера 13
Эти 2 точки соединим прямой линией.
В сечении внутренний изгибающий момент равен сумме трех внешних моментов относительно точки, в которой провели сечение (рис. 39).
Момент RA рассчитывается как произведение этой силы на плечо, т.е. на Z2.
Плечо силы Р можно вычислить как разность длины двух
отрезков: (Z2 – 3 м).
Для расчета момента, создаваемого распределенной
нагрузкой, следует выполнить уже два действия:
1) вычислить от нагрузки полную силу Q = q (Z2 – 3 м). Эта сила приложена в центр тяжести фигуры, образуемой линией интенсивности нагрузки, т.е. прямоугольника;
2) определить плечо. Плечо этой силы равно половине отрезка (Z2 – 3 м).
Момент от этой силы Q:
Рис.39. Расчет ВСФ на 2-ом участке бруса
Таким образом, уравнение внутреннего момента, составленное с учетом правила знаков для Мх будет выглядеть так:
( Z 2 3 )2
M x = R A × Z 2 + P × ( Z 2 3 ) q × 2 =
Рис.40. Расчет ВСФ на 3-м участке
III участок 6 £ Z3£ 9.
Начало координат (точку 0) оставили в т.А, поэтому
левой границей 3-го участка будет точка с координатой 6 м.
Вычисляем Qy в проведенном сечении. В соответствии с методом сечений она равна сумме всех внешних сил, которые остались в левой части бруса.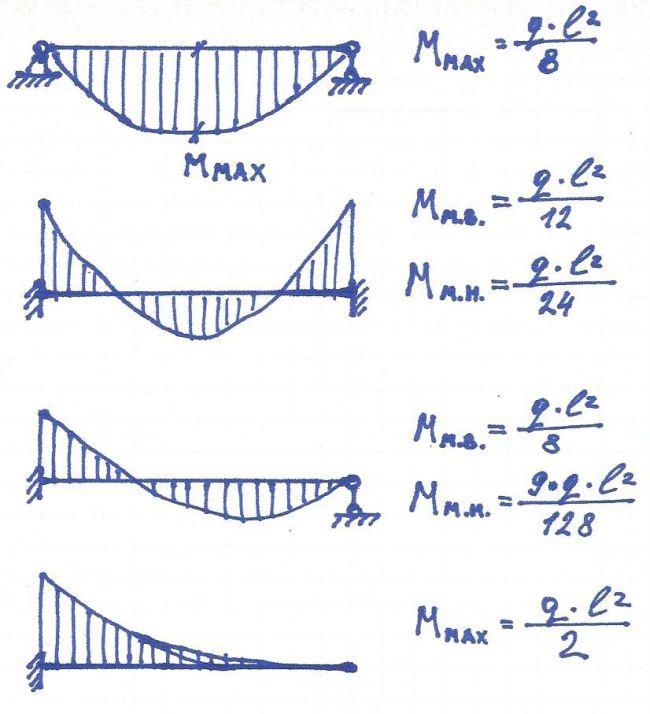 Таких сил здесь 3.
Таких сил здесь 3.
Qy = RA + P – q× 3 = 17,5.
Особо обратите внимание на то, что распределенная
нагрузка здесь приложена по длине 3 м – сечение проводится за
точкой, в которой нагрузка завершается. Поэтому записанное
уравнение является уравнением постоянной прямой.
Внутренний момент равен сумме трёх внешних моментов
Записанное уравнение является уравнением параболы,
ветви вниз.
Вычислим значения момента на границах участка.
– от сосредоточенных сил RA и Р и, распределенной нагрузки q. Плечо опорной реакции равно длине всего отрезка Z3. Плечо силы Р вычисляется как разность (Z3 – 3 м).
Для расчета момента от распределенной нагрузки нужно сначала вычислить полную силу Q = q × 3 м. Эта сила приложена в центр тяжести прямоугольника и, плечо можно определить как расстояние от сечения до этой точки. По рис.40 вычисляем плечо как разность длин (Z3 – 4,5 м). Для определения знаков этих трёх моментов рассмотрим рис. 41, на котором наглядно
41, на котором наглядно
Знак момента силы положительный, потому что при изгибе балки от него сжимаются верхние волокна. Однако величина самой силы RС отрицательна, поэтому в итоге в уравнении все равно появляется минус перед моментом опорной реакции. Момент М считается положительным, потому что от его действия сжимаются верхние волокна балки.
изображен изгиб балки от каждой нагрузки и растяжение-сжатие волокон.
Тогда уравнение внутреннего момента запишется так:
M x = R A × Z 3 + P( Z 3 3 ) q × 3( Z 3 4,5 ) =
= 2,5Z 3 + 10( Z 3 3 ) 10 × 3( Z 3 4,5 ).
Далее это уравнение можно упростить или оставить
таким же. Записанное уравнение является уравнением прямой наклонной линии. Обратите внимание, что степень, в которой находится переменная Z, является единицей.
Вычислим момент на границах участка:
Рассмотрим 5 участок.
M x |Z =9 = — 7 ,5 .
Рис. 41. Пояснения к расчету
Перенесем начало координат в т.В и направим координатную ось справа налево. Тогда расстояние от начала координат до сечения есть величина переменная, которая может принимать любое значение из диапазона: V участок 0 £ Z5 £ 5 м
Внутренняя сила рассчитывается как сумма всех внешних
сил, оставшихся после отбрасывания левой части:
Qy = Rc = ( 33) = 33 кН – прямая постоянная линия.
Знак силы отрицательный потому, что сила направлена
вверх в соответствии с правилом знаков для Qy при выборе правой части бруса.
знаков внешних моментов
Рассмотрим последний 4 участок. Начало координат оставим в т.С. Тогда IV участок 5 £ Z4 £ 8м.
Этот участок очень похож на 2-ой участок. Поэтому
отдельно зарисовывать не будем. Если что-то не вполне понятно, можно рассмотреть рис. 39.
Qy = RС – RB + q × (Z4 – 5) = (33) — 80,5 + 10 × (Z4 – 5) =
= 47,5 + 10 × (Z4 – 5)
Внутренний момент Мх равен единственному внешнему моменту:
Mx = RС× Z5 + M = 33× Z5 + 15 – прямая наклонная линия.
Q y |Z =5 = — 47 ,5
Q y |Z =8 = — 47 ,5 + 10 × 3 = — 17 ,5
( Z 5 )2
правильным, значит методы построения эпюр ВСФ при плоском
M = R
× Z + R ( Z
5 ) q × 4 =
изгибе вы освоили. При построении эпюр внимательно
x С 4 B 4 2
проводите линии, соединяющие точки на границах участков.
= — 33 × Z4
+ 80,5( Z4
5 ) 5( Z4
5 )2
При определении перемещения сечений балки с помощью
энергетических методов, вам предстоит вычислять площади
фигур под эпюрами изгибающего момента. Если линия
M x |Z =5 = — 150
M x |Z =8 = — 7 ,5 .
проведена неправильно, будет вычисляться площадь совсем не
Точки на эпюре сил соединяем по прямой, а на эпюре моментов – по параболе, ветви вниз.
Вычислим максимум на 2 участке.
Приравняем к нулю уравнение поперечной силы
Qy = RA + Р – q × (Z2 – 3) = 0
Отсюда Z* = 3 + (RA + Р)/ q = 3 + (2,5 + 10) / 10 = 4,25 м.
Подставляем это расстояние в уравнение изгибающего
момента:
той фигуры, которая должна быть. В результате, вся задача
будет решена неправильно.
M x = R A × Z 2 + P( Z 2 3 ) q ×
= 2,5 × 4,25 + 10 ×( 4,25 3 ) 10 ×
( Z 2 3 )2
2
( 4,25 3 )2
2
=
= 3,3
Самостоятельно проверьте правильность построения эпюр с помощью 7 правил контроля (см. предыдущую задачу).
Для того чтобы закрепить методы построения эпюр
ВСФ, решите самостоятельно 3 задания – 3, 4, 5 и сравните с
правильным решением.
Задания 4, 5, 6
Постройте эпюры ВСФ для балок из задания 1, 2, 3. На рис. 42, 43, 44 приводятся результаты, которые вы должны получить. Закройте пособие и не открывайте эту страницу до тех пор, пока не получите решения. Сравните результат с ответом. Проанализируйте ошибки, если они есть.
Далее приводятся эпюры ВСФ заданий для
самостоятельного решения. Если ваше решение совпадает с
Если ваше решение совпадает с
Правильное решение
Рис.44. Эпюры ВСФ для балки задания 3
Контрольные вопросы
1. Какой объект принято называть брусом?
2. Какой объект принято называть оболочкой?
3. Какой брус принято называть стержнем?
4. Какой брус принято называть балкой?
5. Какой брус принято называть валом?
6. Какие силы называют активными?
7. Какие силы считают сосредоточенными?
8. Как вычислить полную силу от равномерно распределенной по отрезку нагрузки?
9. Как можно вычислить момент, создаваемый распределенной нагрузкой?
10. Как можно вычислить опорные реакции?
11. Как вычислить опорные реакции для балки, имеющей
промежуточный шарнир?
12. Сколько уравнений равновесия можно составить для
плоской системы?
13. Сколько уравнений равновесия можно составить для
пространственной системы?
14. В чем заключается смысл уравнений равновесия?
В чем заключается смысл уравнений равновесия?
15. Какие силы называются внутренними?
16. Что представляют собой внутренние силовые
факторы?
17. Сколько внутренних силовых факторов может
возникнуть при самой сложной деформации?
18. Какая деформация считается простой?
19. Какая деформация считается сложной?
20. Как можно определить вид деформации?
21. Какая деформация называется осевым растяжениемсжатием?
22. Какая деформация называется чистым сдвигом?
23. Какая деформация называется чистым кручением?
24. Какая деформация называется чистым изгибом?
25. В чем состоит суть метода сечений?
26. Сформулируйте правило знаков для внутренней
продольной силы.
27. Сформулируйте правило знаков для внутреннего
изгибающего момента.
28. Сформулируйте правило знаков для крутящего
момента.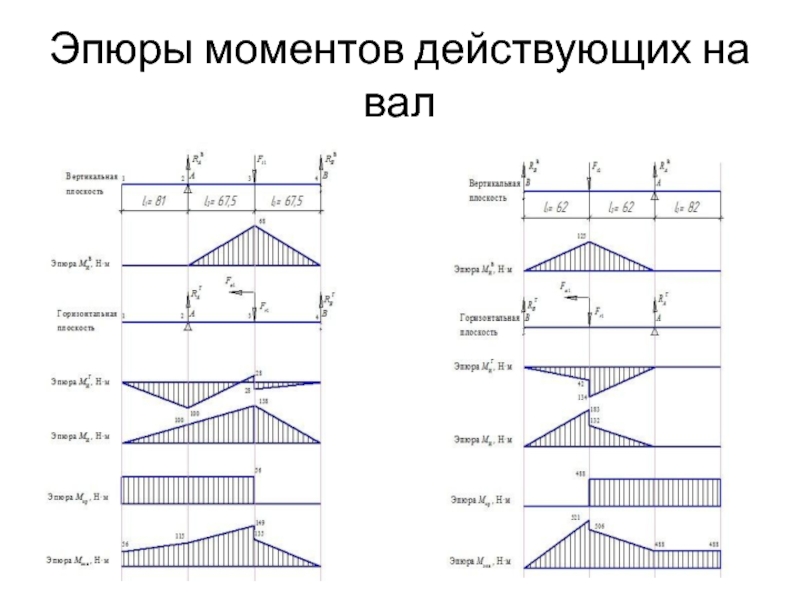
29. Сформулируйте правило знаков для поперечной силы.
30. Что представляет собой шарнирно-подвижная опора?
31. Что представляет собой шарнирно неподвижная
опора?
32. Что представляет собой жесткая заделка?
Список дополнительной литературы
1. Степин, П.А. Сопротивление материалов: учебник /
П.А. Степин . М.: Высш. школа, 1988. –367 с.
2. Феодосьев, В.И. Сопротивление материалов: учебник./
В.И. Феодосьев М.: Изд-во МГТУ им. Н.Э. Баумана, 2001. –
592с.
Материал взят из книги Построение эпюр внутренних силовых факторов при плоском изгибе балки (Сабанаев И.А.)
Эпюры моментов и поперечных сил
Эпюры моментов и поперечных сил
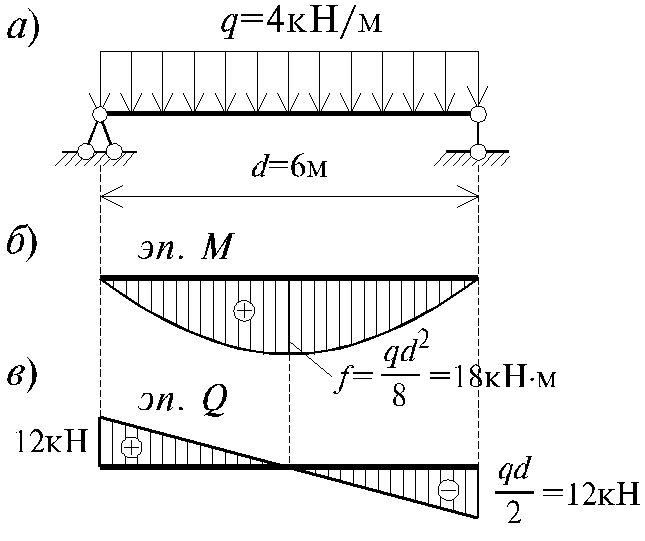
Полную картину распределения поперечных сил и изгибающих моментов по длине балки можно получить, построив эпюры сил и моментов.
Рассмотрим методику построения эпюр для некоторых простейших случаев нагружения.
На рис. 14.3 показана консольная балка, нагруженная двумя равными поперечными силами. Чтобы получить эпюры сил и моментов на участке а рассмотрим произвольное сечение I-I на этом участке.
Действуя, как показано выше, получим:
Рис. 14.3.
Так как 0 £ x1£ a, то 0 £ МИ£ Fa. В соответствии с этим, эпюра поперечных сил на участке а представляет собой горизонтальную линию, отстоящую от оси на положительную величину F. Эпюра изгибающих моментов – это наклонная прямая, ордината которой равна нулю в начале участка и Fa – в конце.
Для получения эпюр на участке b рассмотрим произвольное сечение II-II на этом участке. Поперечная внутренняя сила Q равна алгебраической сумме внешних сил слева от сечения, внутренний изгибающий момент MИ равен алгебраической сумме моментов внешних сил F относительно центра сечения:
Значит, на участке b поперечная сила отсутствует, а изгибающий момент постоянен, положителен и равен Fa.
На рис. 14.4 показана однопролетная двухопорная балка с двумя шарнирными опорами, допускающими поворот сечения балки при изгибных деформациях.
Причем, левая опора является шарнирно-неподвижной, а правая – шарнирно-подвижной, допускающей поступательное смещение вдоль опорной плоскости. Это бывает необходимо для компенсации возможного изменения длины балки при изгибных или температурных деформациях. Так устанавливаются и длинные валы машин – один из подшипников таких валов может смещаться в осевом направлении, так как не закреплен жестко.
Рис. 14.4.
Балка нагружена поперечной силой F. При такой расчетной схеме необходимо сначала определить реакции в опорах RA и RB. Ракцию RA найдем, приравняв нулю сумму моментов сил относительно точки В:
Отсюда:
(14. 1)
1)
Реакцию RB найдем, приравняв нулю сумму моментов относительно точки А:
Откуда:
(14.2)
Теперь, для получения эпюр поперечных сил и изгибающих моментов, аналогично предыдущему, рассматриваем сечение I-I на участке а:
Причем, так как 0 £ x1£ a, то 0 £ МИ£ RAa. В соответствии с этим, эпюра поперечных сил на участке а представляет собой горизонтальную линию, отстоящую от оси на положительную величину RA. Эпюра изгибающих моментов – это наклонная прямая, ордината которой равна нулю в начале участка и RAa – в конце.
В сечении II-II на участке b (с учетом (14.1) и (14.2)):
Здесь а £ х2£ а + b, следовательно (с учетом (16.1)) RAа £ MИ£ 0. Значит, эпюра поперечных сил на участке b представляет собой горизонтальную линию, отстоящую от оси на отрицательную величину -RA. Эпюра изгибающих моментов – это наклонная прямая, ордината которой равна RAa в начале участка и нулю – в конце.
Эпюра изгибающих моментов – это наклонная прямая, ордината которой равна RAa в начале участка и нулю – в конце.
На рис. 14.5 показана однопролетная двухопорная балка, нагруженная изгибающим моментом М. Сначала определяем реакции в опорах RA и RB.
Ракцию RA найдем, приравняв нулю сумму моментов сил относительно точки В:
Отсюда:
(14.3)
Реакцию RBнайдем, приравняв нулю сумму моментов относительно точки А:
Рис. 14.5.
Откуда:
Теперь, для получения эпюр поперечных сил и изгибающих моментов, аналогично предыдущему, рассматриваем сечение I-I на уча- стке а:
Причем, так как 0 £ x1£ a, то 0 £ МИ£ RAa.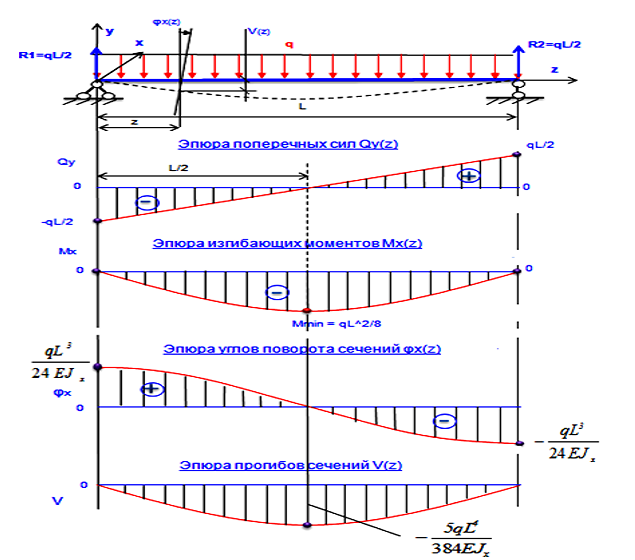 В соответствии с этим, эпюра поперечных сил на участке а представляет собой горизонтальную линию, отстоящую от оси на положительную величину RA. Эпюра изгибающих моментов – это наклонная прямая, ордината которой равна нулю в начале участка и RAa – в конце.
В соответствии с этим, эпюра поперечных сил на участке а представляет собой горизонтальную линию, отстоящую от оси на положительную величину RA. Эпюра изгибающих моментов – это наклонная прямая, ордината которой равна нулю в начале участка и RAa – в конце.
В сечении II-II на участке b (с учетом (14.1) и (14.2)):
Здесь а £ х2£ а + b, следовательно (с учетом (14.3) -RAb £ MИ£ 0. Эпюра поперечных сил на участке b представляет собой горизонтальную линию, отстоящую от оси на положительную величину RA, так же, как на участке а. Эпюра изгибающих моментов – это наклонная прямая, ордината которой равна -RAb в начале участка и нулю – в конце.
Мы не можем найти эту страницу
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings. ADD_COLLECTION_DESCRIPTION}}
ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.ЯЗЫК}} {{$select.selected.display}} {{article. content_lang.display}}
content_lang.display}}
{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}Схемы пучков
Варианты нагрузки/сочетания
Выберите желаемое загружение, комбинацию нагрузок или конверт.
Этап строительства, применимый для вывода анализа этапа строительства, определяется в разделе «Выбор этапа строительства для отображения» или «Панель инструментов этапа». Щелкните справа, чтобы ввести новые или изменить существующие сочетания нагрузок. (См. «Варианты нагрузки/сочетания»)
Примечание
Когда результаты выводятся в максимальных, минимальных и всех значениях в таких случаях, как движущиеся нагрузки, осадки опор, анализ динамики во времени и сочетания нагрузок огибающей, при выборе «все» создаются диаграммы балок, отображаемые в абсолютных значениях сил на стержнях, независимо от знаков сил на стержнях.Чтобы создать диаграммы балок, отражающие знаки, установите флажок «Учитывать знаки в типе сочетания нагрузок оболочки» «все» в меню «Инструменты»> «Установка»> «Среда»> «Результаты».
Шаг
Укажите шаг, для которого должны быть получены результаты анализа. Шаг определяется в геометрическом нелинейном анализе как Шаг нагрузки, а дополнительные шаги определяются на этапах строительства мостов или анализа теплоты гидратации.
Примечание
Этап строительства, применимый для выходных данных анализа этапа строительства, определяется в разделе «Выбор этапа строительства для отображения» или «Панель инструментов этапа».
Макс./мин. Диаграмма
Абсолютные максимальные значения огибающей можно проверить на диаграмме луча.
Примечание
Если выбран Envelope/all, активируется ‘Max/Min Diagram’. Если флажок не установлен, создается диаграмма с абсолютными максимальными значениями Envelope.
КомпонентыВыберите нужный компонент силы стержня из следующих: Деталь: выберите конкретную деталь, для которой будут создаваться силы-члены.Эта функция активируется, когда детали определены в составном сечении для этапа строительства. Fx: осевая сила в локальном направлении x элемента Примечание Mx: Крутящий момент относительно локальной оси x элемента Fy: поперечная сила в локальном направлении элемента по оси Y Fz: поперечная сила в локальном направлении z элемента Fyz: поперечные силы, Fy и Fz отображаются одновременно My: Изгибающий момент относительно локальной оси Y элемента Mz: Изгибающий момент относительно локальной оси Z элемента Myz: Изгибающий момент, My и Mz отображаются одновременно Мб: Бимомент Мт: крутящий момент МВт: Момент деформации Показать усилие фермы: параметр вывода для одновременного создания усилий элементов фермы Только усилие фермы: параметр вывода для создания усилия только элемента фермы
Опции дисплея Точно: отображение усилий на стержнях, рассчитанных в процессе детального анализа, по всей длине каждого элемента балки, включая оба конечных узла. Примечание 5 точек: отображение сил стержня, рассчитанных как в конечных узлах, так и в четвертях каждого элемента балки. Диаграмма представлена путем соединения 5 точек. Без заливки: отображать только контур, представляющий величины сил элементов. Line Fill: отображение диаграммы, заполненной цветными линиями. Сплошная заливка: отображение диаграммы, заполненной цветными поверхностями. Шкала: Масштаб чертежа для сил членов. |
Тип дисплея
Определите тип отображения следующим образом:
Контур | Отображение усилий элементов балки в контуре. |
Диапазоны: определение диапазонов контура. : Назначить диапазон цветового распределения контура. С помощью этой функции можно назначить определенные цвета для определенных диапазонов. Примечание Количество цветов: Назначьте количество цветов, которые будут включены в контур (выберите один из 6, 12, 18, 24 цветов) Цвета: назначение или управление цветами контура. Таблица цветов: Назначьте тип цветов. : Управление цветами по зонам в контуре. Обратный контур: установите флажок, чтобы изменить последовательность изменения цвета в контуре. Contour Line: Назначьте цвет граничной линии контура Край элемента: Назначьте цвет краев элемента при отображении контура Параметры контура: укажите параметры представления контура Контурная заливка Градиентная заливка: отображение цветового градиента (затенения) в контуре. Draw Contour Lines: Отображение цветовых границ в контуре. Рисование только контурной линии Моно-линия: отображение границ контура монохромным цветом. Контурная аннотация Интервал: Укажите интервал легенды или аннотации. Грубый контур (быстрее) (для большой пластины или сплошной модели) Выдавливание |
Деформация | Показать деформированную форму модели. |
Масштабный коэффициент деформации Тип деформации Узловая деформация: отображение деформированной формы, отражающей только узловые смещения. Реальная деформация: Отображение подробной формы деформации, рассчитанной вдоль сечений между обоими концами балочных элементов вместе с узловыми смещениями. Real Displacement (Auto-Scale off): Истинная деформация конструкции представлена графически без увеличения или уменьшения. Относительное смещение: деформация конструкции графически представлена относительно минимального узлового смещения, которое установлено на «0» |
Значения | Отображение усилий элементов балки в числовых значениях. |
Decimal Points: Назначить десятичные точки для отображаемых чисел Exp.: Выразить в виде экспонент Min & Max: отображение максимального и минимального значений Abs Max: отображение абсолютного максимального значения Max: отображение только максимального значения Min: отображение только минимального значения Limit Scale(%): настройка экрана отображать предел для сил стержня относительно выбранного максимального или минимального значения Установить ориентацию: отображать ориентацию числовых значений Примечание |
Легенда | Отображать различные ссылки, относящиеся к результатам анализа, справа или слева от рабочего окна. |
Положение легенды: положение легенды в окне дисплея Тип значения ранга: укажите тип значений в легенде и количество десятичных знаков. |
Анимация | Динамическое моделирование сил балочных элементов. |
Режим анимации: определите тип анимации для результатов анализа. Анимация контура: возможность изменить цвет контура, представляющего переход, в соответствии с величиной изменения Повторить половину/полный цикл: выбрать цикл повторения для динамического представления перехода Примечание Параметры AVI: введите параметры, необходимые для создания окна анимации. Бит на пиксель: Количество битов на пиксель для создания окна по умолчанию для анимации : Назначение метода сжатия данных изображения Кадров за полупериод (3~300): Количество кадров для имитации полупериода Кадров в секунду (5~60): количество кадров в секунду для представления динамического моделирования Вариант этапа строительства: выберите параметры анимации при выполнении анализа этапа строительства. Stage Animation: анимация по этапам строительства Current Stage-Step: анимация по шагам на текущем этапе строительства From ~ To: начальные и конечные этапы строительства или шаги для анимации |
Недеформированный | Перекрытие недеформированной и деформированной формы модели. |
Зеркальный | «Зеркальный» позволяет пользователю расширить результаты анализа, полученные для половинной или четвертной модели, в результаты для полной модели путем отражения плоскостей. |
Отражение половинной модели Отражение четверти модели Зеркальное отражение по : Укажите плоскость (плоскости) отражения, указав плоскость и координату в направлении, перпендикулярном плоскости в GCS. |
Быстрый просмотр | Отображение подробной диаграммы силы луча для элемента в отдельном окне.
|
Элемент: введите номер элемента, для которого генерируются силы стержня. Или щелкните поле ввода и соответствующий элемент в представлении модели. Вариант нагрузки: выберите нужный вариант нагрузки или комбинацию нагрузок. Выберите Загрузить/Шаг/Компенс. Шаг: Укажите шаг, для которого должны быть созданы результаты анализа. Компонент: выберите нужный компонент силы элемента. Значение результата Отображение усилий стержня на I-конце и J-конце, а также максимальные и минимальные значения выбранного элемента. Значение: переместите курсор мыши на диаграмме, чтобы отобразить силы стержня в соответствующей позиции. Общая длина: отображение длины элемента. |
Расположение секции вывода
Назначьте местоположения сечений, в которых возникают усилия элементов балки в числовых значениях.
I: отображение усилия на стержне в начальном узле (N1) балочного элемента.
Центр: отображение усилия на стержне в центре балочного элемента.
Дж: отображение усилия на стержне в конечном узле (N2) балочного элемента.
Abs Max: максимальные абсолютные значения сил стержней среди 5 точек (4-секционных) балочных элементов отображаются в центрах балочных элементов.
Мин./Макс.: минимальные и максимальные усилия на стержнях отображаются в числовом виде в соответствующих местах среди 5 точек (4-секционных) балочных элементов.
Все: Силы стержня на i-конце, в центре и j-конце отображаются в числовом виде.
Генерация пакетного вывода ( , )
Учитывая типы результатов расчета для графических выходных данных, сгенерируйте последовательно графические выходные данные для выбранных вариантов нагрузки и комбинаций. Создается общее количество файлов, равное произведению количества отмеченных элементов в трех столбцах диалогового окна ниже.
Назначьте базовое имя файла, под которым сохраняются типы результатов (данные выбора в диалоговом окне «Формирование пакетного вывода» для графических выходов). | |
Укажите базовые файлы для выполнения пакетной генерации выходных данных, этапы строительства, загружения (комбинации), шаги и т. д. в следующем диалоговом окне. |
Сохраненная информация строки меню: здесь перечислены базовые файлы. Выберите базовые имена файлов для пакетного вывода.
: Удалить все базовые файлы, выбранные с помощью мыши.
При проведении анализа этапов строительства перечисляются все этапы строительства.Мы просто выбираем этапы интересов, которые будут включены в пакетный вывод. Если расчет стадии строительства не выполняется, столбец в диалоговом окне становится неактивным и отображает условия нагрузки (сочетания).
Этапы
Производится вывод результатов всех этапов строительства. Этапы строительства перечислены ниже.
Нагрузки конечной ступени
Выводятся результаты только для финальной стадии. Этапы строительства перечислены ниже.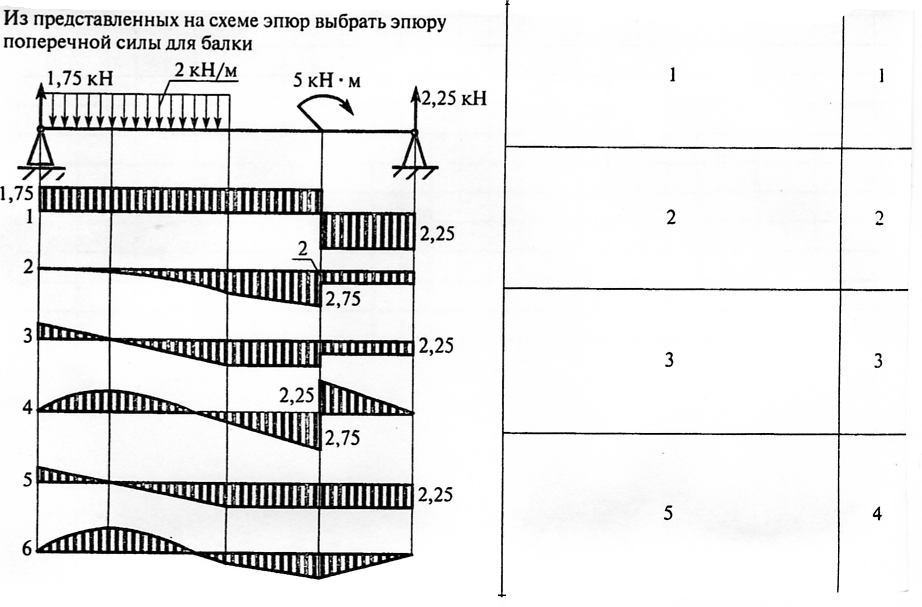 Если анализ стадии строительства не выполняется, то перечисляются условия нагрузки (сочетания).
Если анализ стадии строительства не выполняется, то перечисляются условия нагрузки (сочетания).
Использование Сохранено
Примените только (сохраненный) шаг или условие загрузки (комбинации), выбранное во время создания каждого базового файла.
Этап LCase/LComb
При выполнении анализа этапа строительства выводятся автоматически сгенерированные условия нагрузки этапа строительства и дополнительно введенные сочетания нагрузок этапа строительства. Проверяйте только те условия загрузки (комбинации), которые будут использоваться для создания пакетных выходных данных.Этот столбец становится неактивным, если выбрано «Нагрузки на конечной стадии» или если анализ стадии строительства не выполняется.
Ступенчатая опция
Укажите этапы, для которых будут получены выходные данные при выполнении анализа стадии строительства или геометрического нелинейного анализа больших перемещений.
Сохраненный шаг: используйте только те шаги, которые использовались для создания базовых файлов
Все шаги: Используйте все шаги
Опции вывода
Тип выходного файла
Выберите тип графического файла: BMP или EMF.
Автоматическое описание: В левом верхнем углу графических выходных данных, созданных в пакетном режиме, автоматически генерируются и включаются примечания, такие как типы и компоненты результатов анализа, этапы и этапы построения, условия нагрузки (комбинации) и т. д. Размер шрифта , цвет, тип и т. д. можно изменить, нажав кнопку .
Выходной путь
Укажите путь для сохранения графических файлов, которые будут создаваться в пакетном режиме.
Префикс файла: укажите префикс создаваемых графических файлов.Имена файлов будут состоять из «Префикс»_»Базовое имя файла»_»Загрузить комбинацию».bmp(emf) или «Префикс»_»Базовое имя файла»_»Этап»_»Этап LCase»_»Шаг». БМП(ЭДС).
: Создать указанный пакет графических файлов, отражающий содержимое диалогового окна.
/
Создавать содержимое данных, введенных в диалоговом окне «Основные файлы и создание пакетного вывода», в файле двоичного типа (fn.bog). Нажмите кнопку и выберите файл fn. bog, чтобы использовать тот же формат вывода.
bog, чтобы использовать тот же формат вывода.
Примечание
Импорт/экспорт имеет смысл только для разных проектов.В заданной структурной модели базовые файлы автоматически сохраняются и перечисляются.
Отображение диаграммы изгибающего момента — ОЗУ | Вики STAAD — РАМ | СТАД
| Применяется к | |||
| Продукт(ы): | СТАД.Про | ||
| Версия(и): | Все | ||
| Окружающая среда: | Н/Д | ||
| Площадь: | Отображение диаграммы изгибающего момента | ||
| Подрайон: | Н/Д | ||
| Автор оригинала: | Группа технической поддержки Bentley | ||
Как отобразить диаграмму изгибающего момента и значения на этой диаграмме, силы сдвига или осевые силы?
Сначала вы должны проанализировать файл. Выберите «Анализ» в верхней строке меню Staad.Pro. Выберите опцию «Анализ». После этого нажмите «Выполнить анализ» в нижней части диалогового окна небольшого окна.
Выберите «Анализ» в верхней строке меню Staad.Pro. Выберите опцию «Анализ». После этого нажмите «Выполнить анализ» в нижней части диалогового окна небольшого окна.
После завершения анализа файла нажмите кнопку «Готово».
Далее мы переходим в режим постобработки для графического просмотра сил и результатов.
Чтобы войти в режим постобработки, выберите «Режим» в верхней строке меню и выберите «Постобработка». Помните, что если ваш анализ не завершен, вы не сможете получить доступ к режиму постобработки.
По умолчанию диаграмма отклонения всегда открывается на экране постобработки Staad.Pro.
Чтобы просмотреть диаграммы изгибающих моментов, выберите страницу Балка с левой стороны. В верхней строке меню выберите «Результаты» — «Просмотреть значение». В разделе «Диапазоны» выберите «Все». (Кнопка All означает, что диаграмма изгибающего момента будет отображаться для всех стержней.)
На вкладке «Результаты балки» вы увидите параметры «Изгиб», «Сдвиг», «Аксиальный», «Смещение» и «Напряжения».
Сделайте правильный выбор.
Нажмите кнопку Аннотировать. Затем нажмите на кнопку закрытия.
Вот группа других вариантов просмотра BMD, SFD
Чтобы просмотреть диаграмму изгибающего момента для отдельных стержней, перейдите на страницу Балка > Графики слева и нажмите на любой стержень, и справа отобразятся диаграммы BMD, SFD и осевой силы для стержня.
В качестве альтернативы вы также можете дважды щелкнуть любой элемент, чтобы открыть окно запроса и перейти на вкладку «Изгиб при сдвиге», чтобы просмотреть диаграммы изгибающего момента или поперечной силы для этого элемента.
Что такое диаграмма свободных моментов? – М.В.Организинг
Что такое диаграмма свободных моментов?
Диаграммы сдвига и изгибающего момента — это аналитические инструменты, используемые в сочетании со структурным расчетом для облегчения проектирования конструкции путем определения значения поперечной силы и изгибающего момента в заданной точке элемента конструкции, например балки.
Как поддерживать консольную балку?
Консольные балки не требуют поддержки с противоположной стороны.Отрицательный изгибающий момент, создаваемый в консольных балках, помогает противодействовать создаваемым положительным изгибающим моментам. Консольные балки могут быть легко сконструированы.
Где выйдет из строя консольная балка?
Если материал однородный, то разрушение произойдет там, где момент и сдвиг максимальны, то есть на фиксированной концевой опоре. Если под «провалом» вы подразумеваете недопустимо большой прогиб, то он будет на свободном конце кантилевера.
Как рассчитать силу балки?
Mc = Fc x dc.Момент по часовой стрелке равен произведению силы по часовой стрелке на горизонтальное расстояние от точки равновесия. Рассчитайте моменты против часовой стрелки (Ma), используя формулу для момента: Ma = Fa x da.
Как создать балку вручную?
Конструкция ручной балки
- БАЛОЧНАЯ КОНСТРУКЦИЯ.
- 1.
 ДАННЫЕ.
ДАННЫЕ. - 2. ЭФФЕКТИВНЫЙ ПРОЛЕТ БАЛКИ:
- 3.РАЗМЕР БАЛКИ:
- Коэффициент нагрузки = 23,694 кН/м, коэффициент BM = Wl2/8 = 30,89 кН/м.
- 7.ПРОВЕРКА НА СДВИГ:
- 8. АРМИРОВАНИЕ НА СДВИГ:
- 9.ПРОВЕРЬТЕ НА ИЗГИБ:
Как рассчитать момент?
момент = F x d Перпендикулярное расстояние от оси до силы d = 0,50 м. Это момент по часовой стрелке. Сила будет вращать объект по часовой стрелке вокруг оси вращения. Важно помнить, что расстояние d — это перпендикулярное расстояние от точки опоры до линии действия силы (см. схему).
Как рассчитать SFD и BMD?
Диаграмма поперечной силы и изгибающего момента свободно опертой балки
- Начертите диаграмму поперечной силы и изгибающего момента свободно опертой балки, несущей точечную нагрузку.Как показано на рисунке ниже.
- Обе реакции будут равны.
- Когда свободно опертая балка воспринимает точечные нагрузки.
- Сила сдвига между (B – C) = S.
 F (B – C) = 1000 – 2000.
F (B – C) = 1000 – 2000.
Что такое диаграмма BMD?
Диаграмма изгибающего момента представляет собой графическое представление изменения изгибающего момента по длине балки и обозначается аббревиатурой B.M.D.
Какая польза от SFD и BMD?
Диаграммы сдвига и изгибающего момента — это аналитические инструменты, используемые в сочетании со структурным расчетом для облегчения проектирования конструкции путем определения значения поперечной силы и изгибающего момента в заданной точке элемента.
Что такое пример изгибающего момента?
В механике твердого тела изгибающий момент представляет собой реакцию, возникающую в элементе конструкции, когда к элементу прилагается внешняя сила или момент, вызывающий изгиб элемента. Наиболее распространенным или простейшим конструктивным элементом, подверженным изгибающим моментам, является балка.
Что такое диаграмма SF и BM?
Диаграмма поперечной силы и диаграмма изгибающего момента строятся путем нанесения положения поперечного сечения балочного элемента по оси X и соответствующих значений поперечных сил и изгибающих моментов по оси Y. На важных участках балки координатные точки нанесены по длине балки.
На важных участках балки координатные точки нанесены по длине балки.
Что такое сдвиг и момент?
Силы сдвига возникают, когда две параллельные силы действуют несогласованно друг с другом. Изгибающие моменты — это силы вращения внутри балки, вызывающие изгиб. В любой точке балки изгибающий момент представляет собой сумму: каждой внешней силы, умноженной на расстояние, перпендикулярное направлению силы.
Что такое единица СИ для изгибающего момента?
Объяснение: Момент — это произведение силы и перпендикулярного расстояния, а изгибающий момент — это алгебраическая сумма моментов, отнятых слева или справа от сечения, следовательно, изгибающий момент в единицах СИ такой же, как и момент i.е кНм.
Как найти сдвиг и момент?
Как решить задачу о сдвиге и моменте
- Введение. Решение задачи о сдвиге и моменте.
- Шаг 1: Нарисуйте свободную диаграмму тела.
- Шаг 2: Решите суммы сил и моментов.
- Шаг 3.
 Нарисуйте сечение балки.
Нарисуйте сечение балки. - Шаг 4: Нарисуйте еще одну часть балки.
- Шаг 5: Нарисуйте диаграмму сдвига и момента.
- Шаг 6: Подсказка.
- Шаг 7: ответы.
Пример силы сдвига?
Сила сдвига – это сила, приложенная перпендикулярно поверхности в противовес смещенной силе, действующей в противоположном направлении. Когда элемент конструкции разрушается при сдвиге, две его части толкаются в разные стороны, например, при разрезании ножницами листа бумаги.
Каков максимальный изгибающий момент?
Объяснение: Максимальный изгибающий момент возникает в балке, когда поперечная сила в этом сечении равна нулю или меняет знак, поскольку в точке обратного изгиба изгибающий момент равен нулю.Такой изгибающий момент называется провисающим изгибающим моментом или положительным изгибающим моментом.
Что такое статика момента?
В статике моменты — это эффекты (силы), вызывающие вращение. Скалярный расчет (для двух измерений): Чтобы рассчитать момент относительно точки O в скалярных расчетах, вам потребуется величина силы и перпендикулярное расстояние от точки O до линии действия силы F.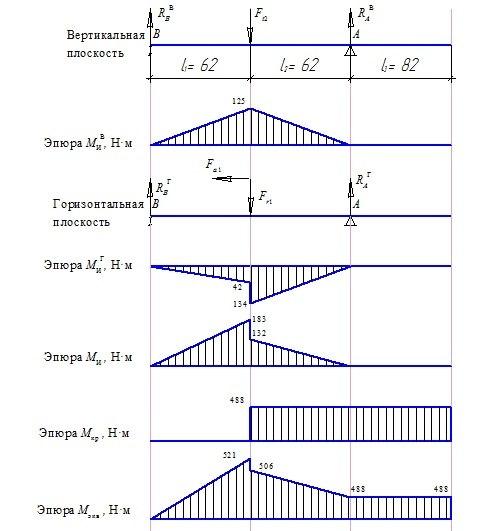
Как узнать, направлен ли момент по часовой или против часовой стрелки?
Моменты
- Момент против часовой стрелки действует вниз слева, а момент по часовой стрелке действует вниз справа.
- Перпендикулярное расстояние — это кратчайшее расстояние между точкой опоры и линией действия силы.
Как узнать, какая у меня лицензия CW или CCW?
Вы можете определить перспективу конца вала, просто подняв мотор перед собой и направив вал на себя. Если вал направлен на вас и вращается вправо, ваш двигатель вращается по часовой стрелке или CWSE. Если вал вращается влево, ваш двигатель вращается против часовой стрелки, или CCWSE.
Что означает момент по часовой стрелке?
Моменты по часовой стрелке: Если сила стремится повернуть или повернуть тело по часовой стрелке, момент силы называется моментом по часовой стрелке.
Какой знак используется для момента по часовой стрелке?
Направление момента противоположно направлению силы. Соглашение таково: моменты по часовой стрелке положительны. моменты против часовой стрелки отрицательны.
Соглашение таково: моменты по часовой стрелке положительны. моменты против часовой стрелки отрицательны.
Диаграмма изгибающего момента — форма и кривизна
Изгибающий момент требуется для расчета балки и также для расчета наклон и отклонение луча.Следующие примеры будут проиллюстрировать, как написать уравнение изгибающего момента для различных типов нагрузки, а затем построить диаграммы изгибающих моментов.Случай I Изгибающий момент точечная нагрузка
Изгибающий момент от точки нагрузка является произведением нагрузки и ее перпендикулярного расстояния от суть момента. как показано ниже.
Рассмотрим кантилевер, на который воздействует точечная нагрузка на свободный конец.
Изгибающий момент на закрепленном конце = W х л = ВЛ
Изгибающий момент M x при расстояние x от свободного конца = W x х = Wx
Это уравнение прямой и
построенная диаграмма изгибающего момента на приведенном выше рисунке показывает, что изменение
изгибающий момент по пролету кантилевера представляет собой прямую.
Случай II Изгибающий момент равномерно распределенная нагрузка
Изгибающий момент от равномерно распределенная нагрузка (udl) составляет равна интенсивности нагрузки х длина груза Икс расстояние его центра от точки момента, как показано на следующие примеры.
Изгибающий момент на закрепленном конце = 10 х 2 х 1= 20 кНм
Изгибающий момент M x при расстояние «х» от свободного конца = 10 х (х) х (х/2) = 0.5 х 2
которая является функцией второй степени «x» и, следовательно, параболический.
Случай III Изгибающий момент из-за равномерно изменяющаяся нагрузка
Изгибающий момент от переменной нагрузки равен равна площади диаграммы нагрузки x расстояние от его центра тяжести с точки зрения момента.
Форма диаграммы изгибающего момента, обусловленная к равномерно меняющейся нагрузке представляет собой кубическую параболу.
Случай IV Изгибающий момент от пара
Изгибающий момент в сечении из-за
пара равна величине пары и в том же смысле
как пара.
ДИАГРАММА ПЕРЕСЕЧНОЙ СИЛЫ И ИЗГИБАЮЩЕГО МОМЕНТА ДЛЯ ОДНООПОРНОЙ БАЛКИ С ВНЕЦЕНТРИЧНОЙ ТОЧЕЧНОЙ НАГРУЗКОЙ
Мы обсуждали значение и важность Шира. сила и изгибающий момент и знак соглашения для поперечной силы и изгибающего момента в наших последних сообщениях.Мы также обсудили диаграммы поперечной силы и изгибающего момента для свободно опертой балки с точечной нагрузкой, действующей в средней точке нагруженной балки во время наши предыдущие посты.Сегодня мы увидим здесь концепцию рисования сдвига диаграммы сил и изгибающих моментов для свободно опертой балки с эксцентриком точечная нагрузка с помощью этого поста.
Давайте посмотрим на следующий рисунок, у нас есть один луч AB длиной L и балка свободно опирается или опирается на опорах с обоих концов.
 И поэтому отображаемый луч указывает на
свободно опертая балка AB и длина L.
И поэтому отображаемый луч указывает на
свободно опертая балка AB и длина L. Предположим, что одна точечная нагрузка W равна действующий на балку на расстоянии a от конца A или на расстоянии b от конец B, как показано на следующем рисунке. Нагрузка W действует в точке C, которая не является серединой нагруженной балки AB, но и точка C находится на расстоянии a от конца A или на расстоянии b от конца B.
Прежде всего, напомним важные моменты для построения диаграммы поперечной силы и изгибающего момента.Теперь всегда помните, что нам придется сначала определить силы реакции на каждом служба поддержки.
Предположим, что R A и R B — силы реакции на концевой опоре A и концевой опоре B соответственно, и мы будет использовать понятие равновесия, чтобы определить значение этих силы реакции. ƩF X =0, ƩF Y =0, ƩM =0,
Теперь мы имеем значения сил реакции при
конец A и конец B, и это, как указано выше. Определим теперь значение
поперечная сила и изгибающий момент во всех критических точках.
Определим теперь значение
поперечная сила и изгибающий момент во всех критических точках.
Рассмотрим одну секцию ХХ на
расстояние x от конца A между A и C, как показано на следующем рисунке. Позволять
Предположим, что F X представляет собой поперечную силу в сечении XX, а изгибающий момент равен
М Х на секции ХХ.
Перерезывающая сила здесь будет положительной, и мы может ссылаться на почтовый знак условные обозначения для поперечной силы и изгибающего момента, чтобы понять знак поперечной силы, который определяется здесь.
Как мы уже обсуждали, поперечная сила будет постоянной между двумя вертикальными нагрузками или мы также можем сказать, что если между двумя точками нет нагрузки, то поперечная сила будет постоянным и будет представлен горизонтальной линией.

Поэтому здесь можно сказать, что сдвиг сила между A и C будет постоянной и будет иметь положительное значение Wb/L.
Теперь предположим, что если бы мы рассмотрели сечение ХХ между С и В и на расстоянии х от конца А. Снова будем нужно напомнить основы графиков поперечной силы и изгибающего момента и мы сможем рассчитать поперечную силу в сечении ХХ. F X = W (b/L-1) = W (b-L/L) Поэтому здесь можно сказать что сила сдвига между C и B будет постоянной и будет иметь отрицательную значение, т. е. -Ва/л. Мы должны отметить это здесь что поперечная сила в точке C изменяется от + Wb/L до – Wa/L.Теперь у нас есть информация относительно поперечной силы во всех критических точках, т.е. Перерезывающая сила в точке A, F A = + Вб/л Перерезывающая сила в точке B, F B = -Ватт/л
Сила сдвига в точке C, F C = сдвиг
сила изменяется от + Wb/L до – Wa/L.
Теперь мы можем нарисовать здесь диаграмму поперечной силы
и это показано здесь на следующем рисунке.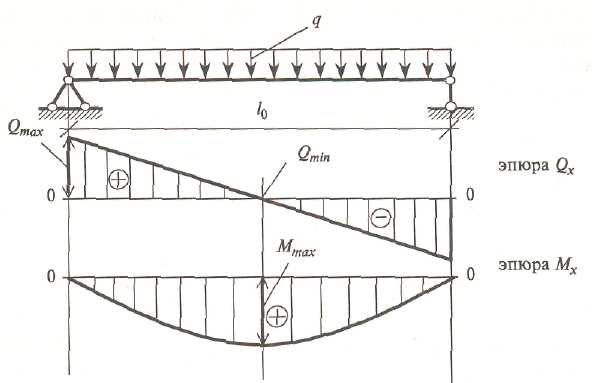
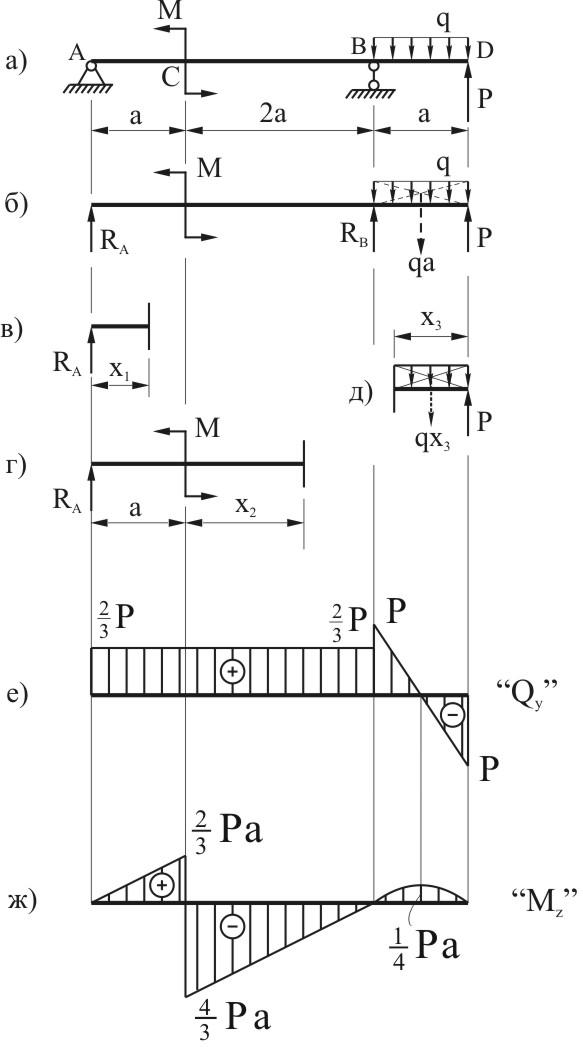 У Вас есть какие-то предложения? Пожалуйста, напишите в комментарии
коробка Артикул: Прочность материала, Р. К. Бансал.
У Вас есть какие-то предложения? Пожалуйста, напишите в комментарии
коробка Артикул: Прочность материала, Р. К. Бансал.Мы увидим еще одну важную тему, а именно диаграммы поперечной силы и изгибающего момента для свободно опертая балка с равномерно распределенной нагрузкой в категория прочности материала.
Также читать сообщить об этом объявленииОсвоение диаграмм поперечной силы и изгибающего момента
Каждая лекция разработана и прочитана с учетом моего опыта преподавания в университете в области проектирования конструкций . Стиль преподавания подходит для всех типов учащихся с материалом, разработанным с помощью нарисованных от руки заметок и набросков. Студентам предлагается участвовать в каждой лекции, активно делая свои собственные записи во время каждой видеолекции… здесь нет «смерти от PowerPoint»! Прежде чем углубляться в рабочие примеры, мы сосредоточимся на закреплении основ.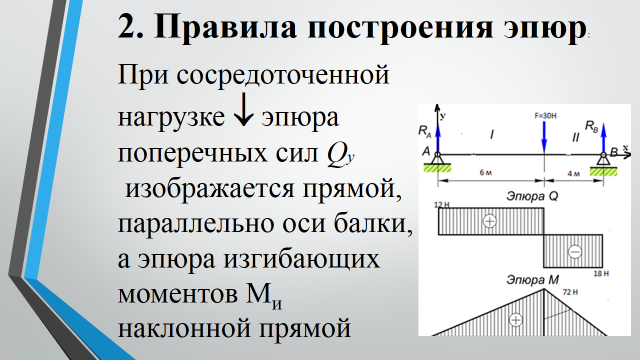
ОБНОВЛЕНИЕ КУРСА . Я только что добавил в курс необязательный побочный проект, в котором мы создаем калькулятор диаграмм поперечной силы и изгибающего момента с использованием Python . Практика действительно важна для закрепления навыков, которые вы получите на этом курсе. Но у вас быстро закончатся вопросы-примеры, и здесь вам может пригодиться калькулятор. Если вы не интересуетесь Python и не хотите создавать калькулятор, не проблема, просто посмотрите первое видео, чтобы узнать, как его использовать, и загрузите его в качестве учебного пособия.
Если вы последуете всем лекциям и попробуете все рабочие примеры, то к концу курса у вас будет отличное понимание этого важного навыка гражданского строительства!
Раздел 1: Обзор основ
Прежде чем мы углубимся в детали диаграмм поперечной силы и изгибающего момента, сначала нам нужно сделать небольшую уборку. Мы проясним несколько предположений, применимых к нашему анализу, и убедимся, что вы можете определить опорные реакции для статически определимых конструкций.
Раздел 2: Понимание внутренних изгибающих моментов
В этом разделе мы начинаем закладывать основы вашего понимания изгибающих моментов. Мы начинаем с рассмотрения того, как изгибающий момент связан с состоянием напряжения внутри конструкции — мы пытаемся ответить на вопрос «, что изгибающий момент говорит нам о состоянии напряжения в конструкции?» .
Затем мы увидим, как принцип равновесия позволяет нам определить внутренний изгибающий момент в любой точке конструкции.Это хорошо подготовит нас к тому, чтобы начать думать о том, как изгибающий момент изменяется вдоль конструкции.
Мы завершим этот раздел несколькими работающими примерами, чтобы убедиться, что вы понимаете все, что мы обсуждали в этом разделе.
Раздел 3: Понимание внутренних сил сдвига
Все, что мы сделали для изгибающих моментов, теперь мы собираемся сделать для поперечных сил:
отношение касательного напряжения к поперечной силе
разрезание конструкции для выявления внутренней поперечной силы соглашение о знаках
Как всегда, мы подтвердим, что вы все поняли, выполнив несколько рабочих примеров.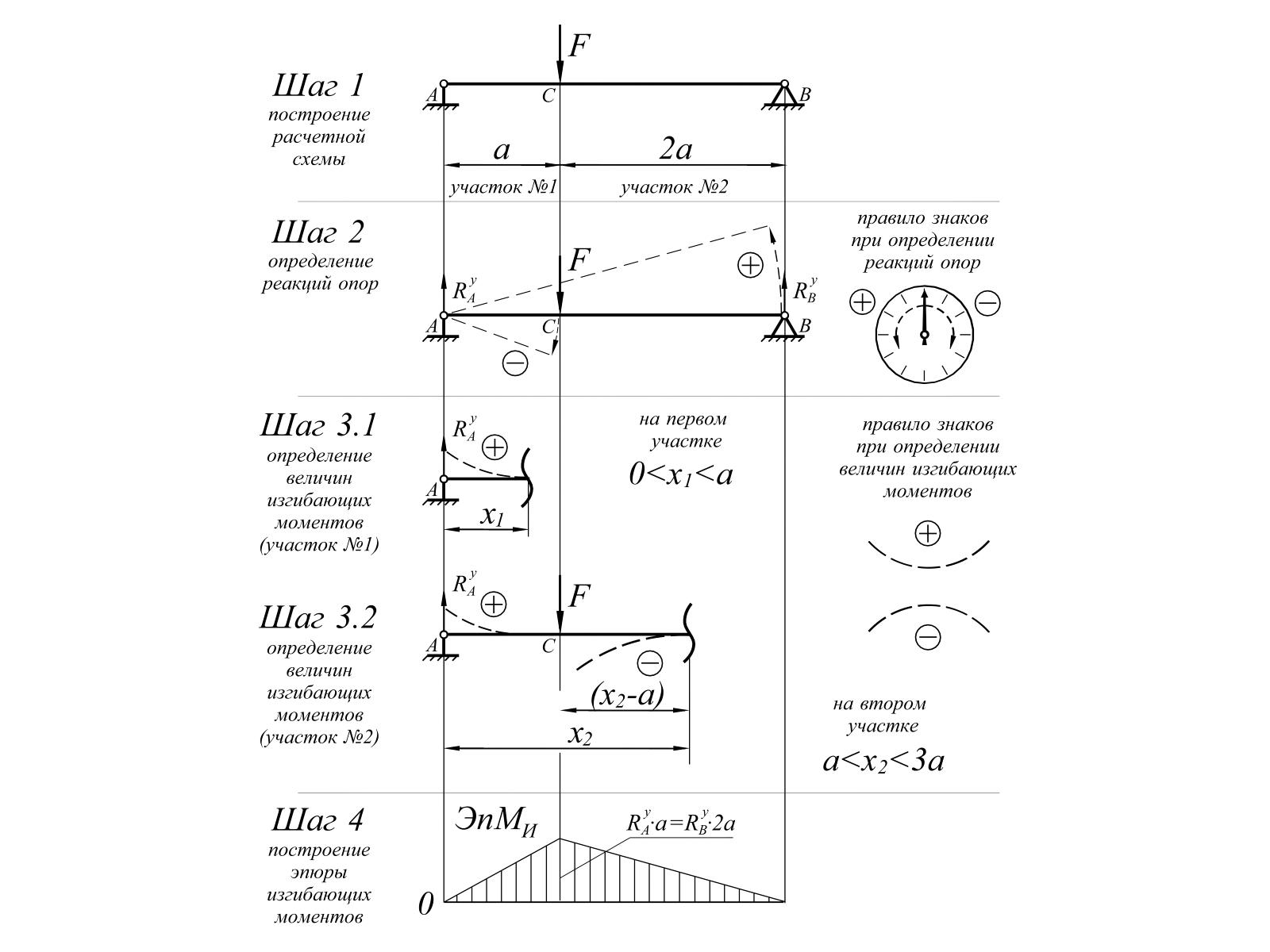
Раздел 4: Дифференциальные зависимости между нагрузкой, поперечной силой и изгибающим моментом
В этом разделе мы поднимаем наше понимание на новый уровень. Мы собираемся установить отношения (и правила), которые позволят нам систематически строить диаграммы изгибающего момента и поперечной силы — каждый раз со 100% точностью. К тому времени, когда вы закончите этот раздел, вы поймете, как можно систематически разрабатывать эти диаграммы, обеспечивая успех каждый раз .
Разделы 5 и 6: Объединение всего воедино — рабочие примеры
В этих последних двух разделах мы закрепим все, что вы уже узнали. Помните, что структурный анализ, как и любой другой навык, только улучшается с практикой. Применяя здесь все, что вы узнали из предыдущих 4 разделов, вы обеспечиваете внедрение навыков.
В разделе 5 мы начнем с уже знакомой темы, рассмотрев балочные конструкции. В разделе 6 мы нанесем то, что вы узнали, на структуры фреймов, что значительно расширит возможности применения инструментов и методов, которые вы разработали в этом курсе!
На этом этапе вы можете уверенно анализировать любую статически определимую конструкцию, с которой вам, вероятно, придется столкнуться в ходе учебы или карьеры в области гражданского строительства.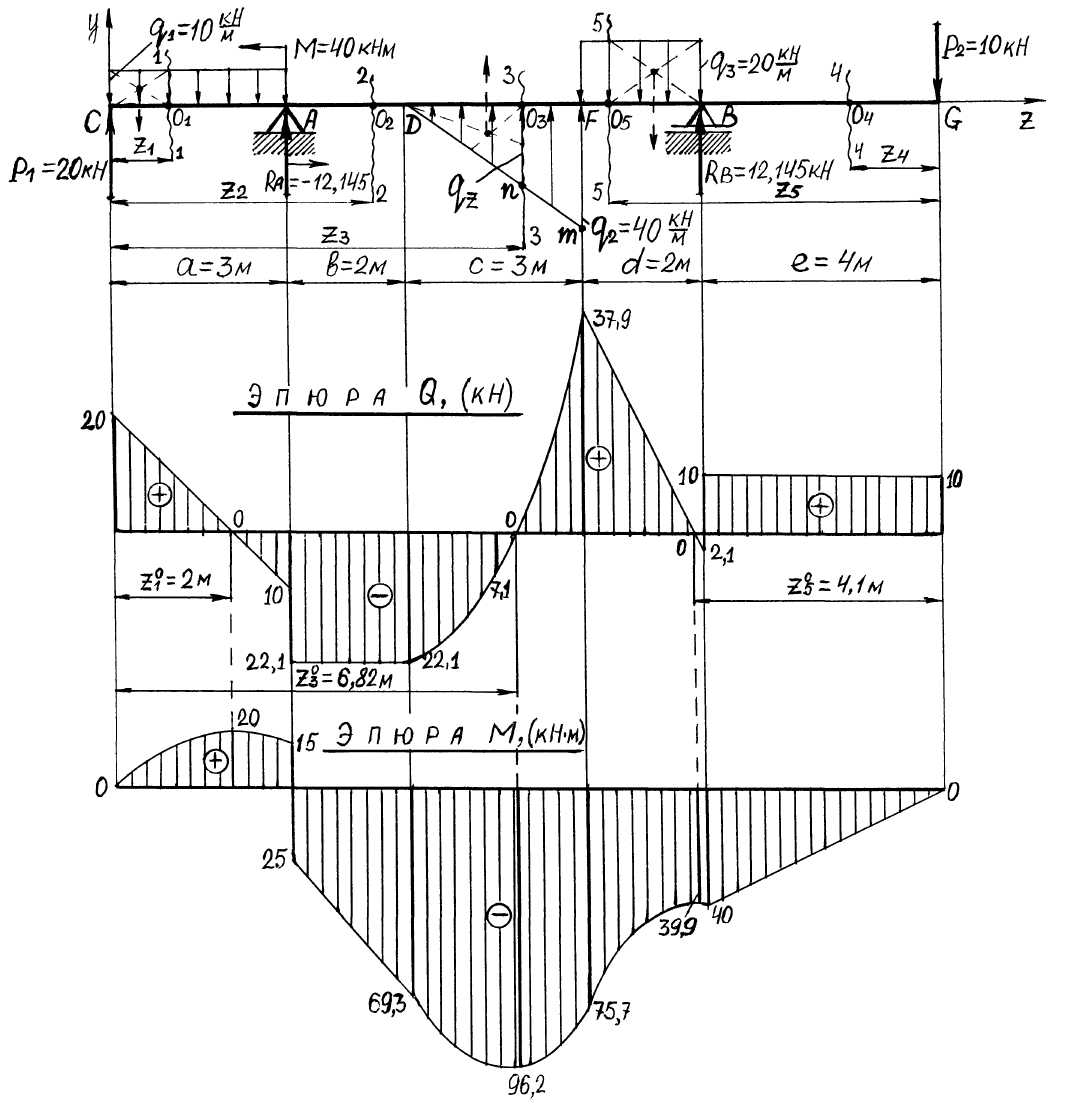
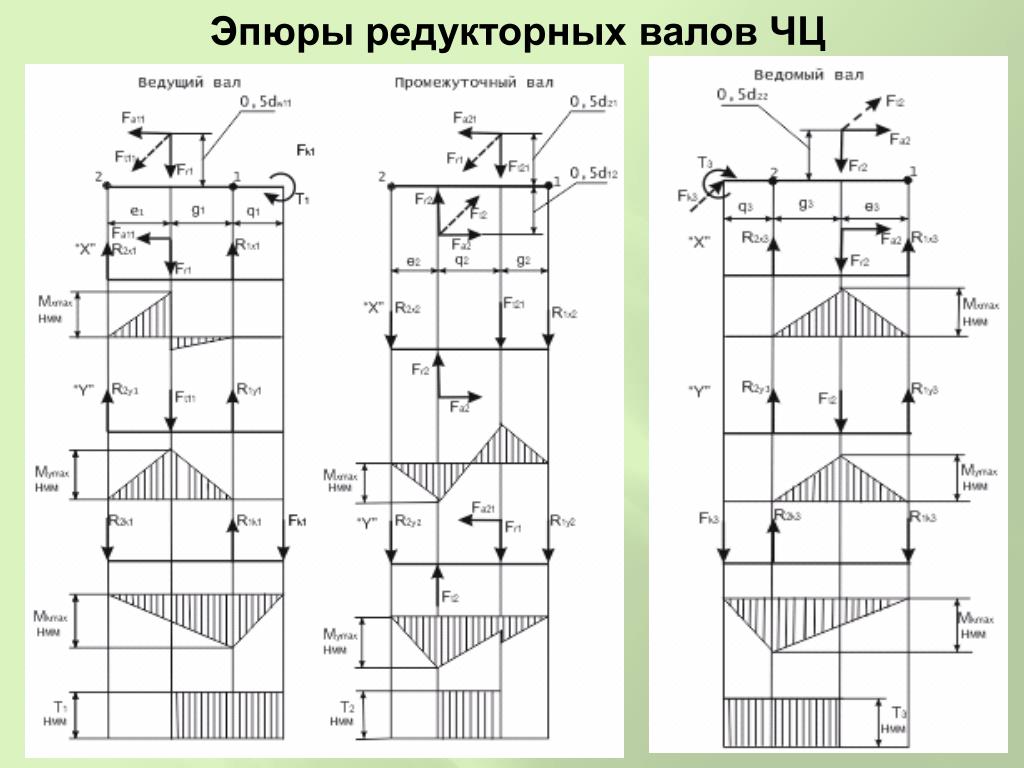 Если выбрано осевое усилие (Fx) и установлен флажок «Только усилие фермы», создаются усилия только на элемент фермы.
Если выбрано осевое усилие (Fx) и установлен флажок «Только усилие фермы», создаются усилия только на элемент фермы.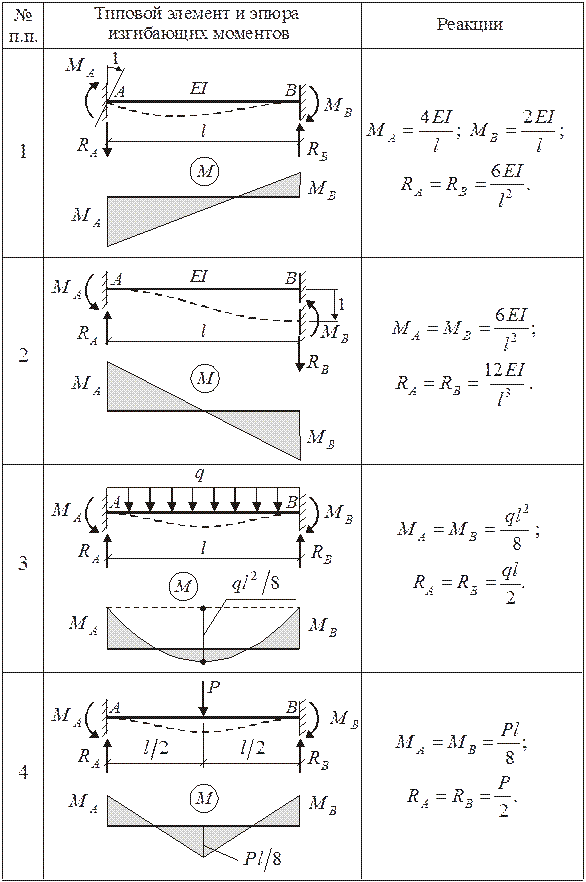
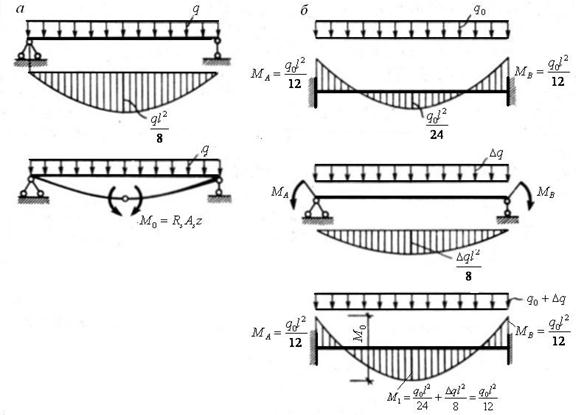

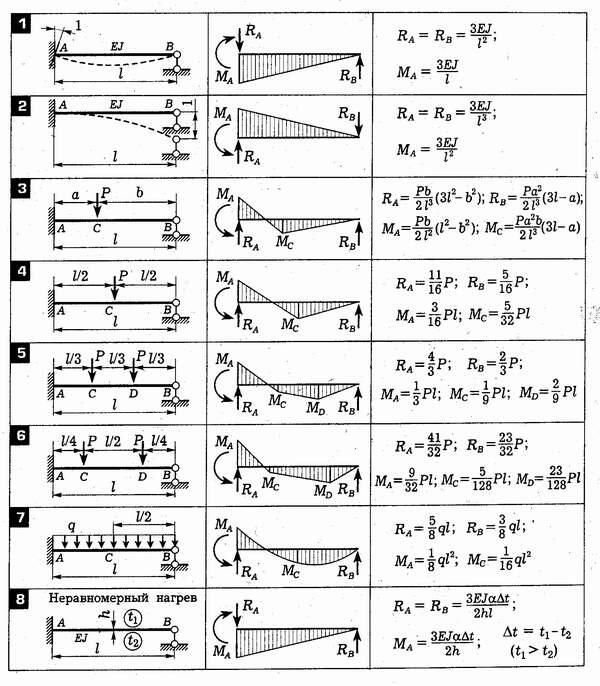 Точно так же этот параметр нельзя применять одновременно к случаям, когда параметр «Скрытый» используется для отображения толщин пластинчатых элементов или параметр «Оба» используется для представления сил (напряжений) верхнего и нижнего стержня.
Точно так же этот параметр нельзя применять одновременно к случаям, когда параметр «Скрытый» используется для отображения толщин пластинчатых элементов или параметр «Оба» используется для представления сил (напряжений) верхнего и нижнего стержня. Этот параметр обычно используется для геометрического нелинейного анализа, отражающего большое смещение.
Этот параметр обычно используется для геометрического нелинейного анализа, отражающего большое смещение.