Проверка правильности построения эпюры продольной силы.
1. В точке приложения сосредоточенной силы на эпюре будет скачок на величину этой силы.
2. Если на участке нет распределенной нагрузки, то эпюра продольной силы очерчивается прямой линией, параллельной оси.
3. Если на участке действует равномернораспределенная нагрузка, то эпюра очерчивается прямой наклонной линией, в соответствии с формулой
(2.2) (2.3)
2 .2 Построение эпюры крутящего момента
Эпюрой крутящего момента называется графическое изображения закона его изменения по длине бруса.
Брус круглого поперечного сечения, работающий на кручение, называется валом.
Кручение — это такой
вид деформации, при котором в поперечном
сечении стержня возникает только один
внутренний силовой фактор – крутящий
момент (Мz),
а остальные внутренние силовые факторы
равны нулю.
. (2.4)
Правило знаков. Крутящий момент считается положительным, если при взгляде в торец отсеченной части он направлен по часовой стрелке (рис 2.5).
Рис.2.5
Порядок построения эпюры Мz и её проверка аналогичны тому же для продольной силы N.
Пример № 2.3. Для вала, находящегося под действием внешних сосредоточенных моментов М1, М2, М3 и М4построить эпюру крутящего момента.
Рис.2.6 К примеру №2.3
Внешние моменты делят вал на три участка, начнем рассматривать их с левого конца:
Эпюра
строится под расчетной схемой.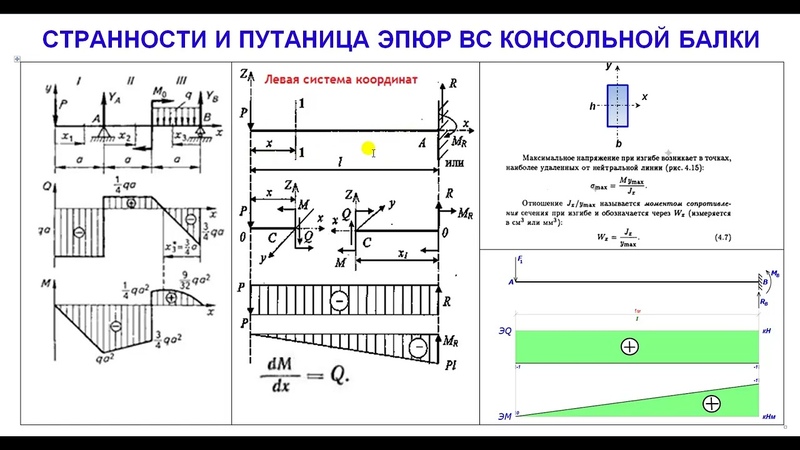
Проводится
проверка правильности построения эпюры
(см. рис. 2.6).
2.3 Построение эпюр поперечной силы Qу и изгибающего момента Мx
Если в поперечном сечении балки под действием внешних сил возникает только изгибающий момент, а остальные пять внутренних силовых фактора равны нулю, то изгиб называется чистым.
Если же в поперечном сечении балки наряду с изгибающим моментом действует так же поперечная сила Q, то изгиб называется поперечным.
Обычно все балки имеют хотя бы одну ось симметрии. Если плоскость действия внешних сил совпадает с осью симметрии балки, то изгиб называется плоским.
При плоском поперечном изгибе в сечениях бруса возникают два силовых фактора — поперечная сила
Рис 2.7
Брус,
работающий на изгиб, называется балкой.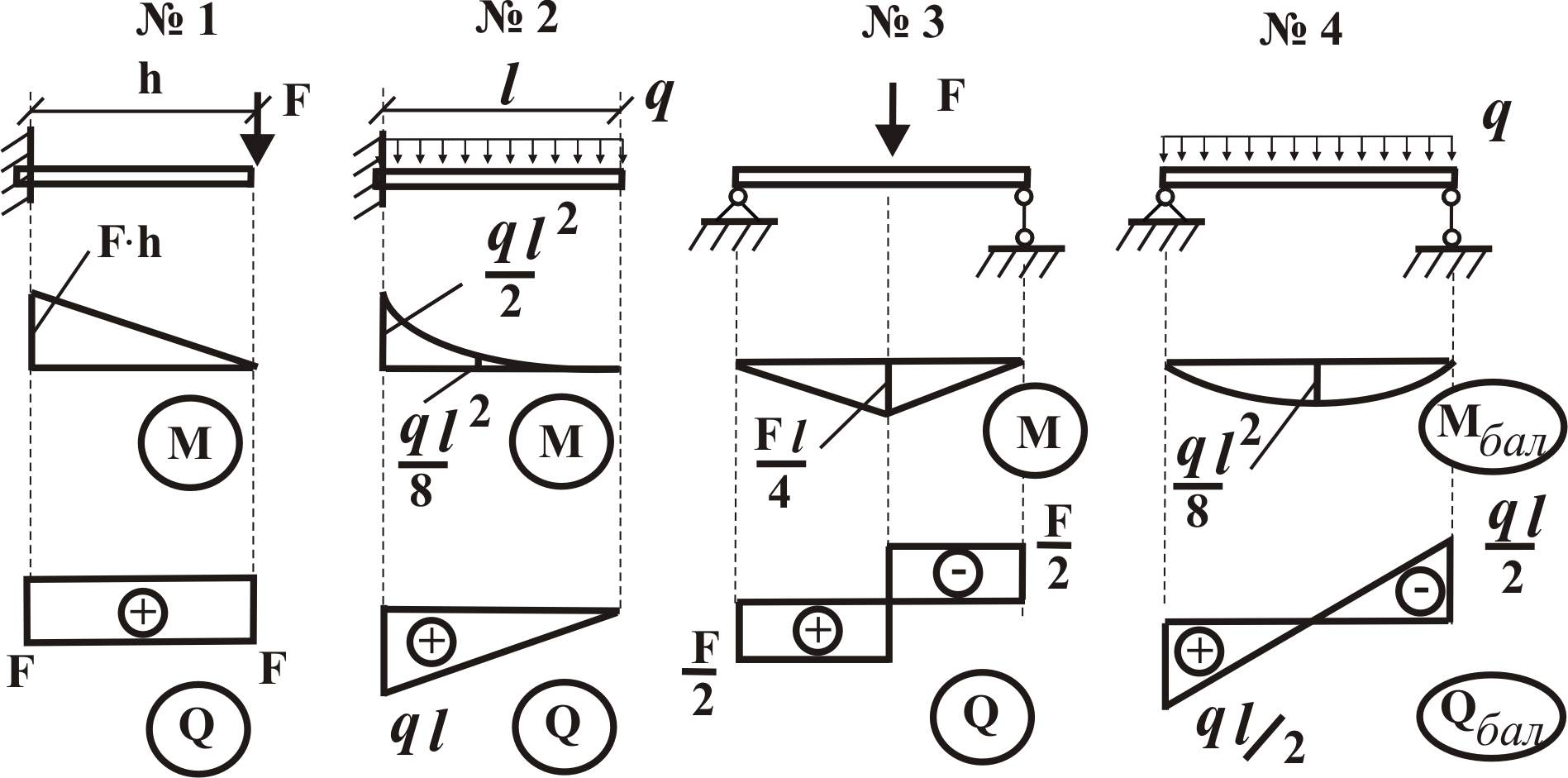
На рисунке 2.8 показана однопролетная
консольная балка,
т.е. балка со свободным концом, и реакции
в опорах, возникающие от действия внешних
сил.
Рис. 2.8
Правило знаков.
Поперечная сила считается положительной, если она вращает элемент балки относительно внутренней нормали по часовой стрелке (рис.2.9).
Рис. 2.9
Изгибающий момент считается положительным, если он растягивает нижние волокна балки и сжимает верхние (рис.2.10).
Рис.2.10
Поперечная сила и изгибающий момент в сечении балки определяются с помощью метода сечений (п. 1.3) в соответствии с выражениями:
(2.5)
. (2.6)
Эти
зависимости используются для построения
эпюр Qуи МХи контроля
правильности построенных эпюр.
Правила контроля эпюр
Ранее, здесь мы получили формулы (2),(4) зависимости поперечной силы Q от распределенной нагрузки q и изгибающего момента M от поперечной силы Q. Из этих дифференциальных зависимостей следуют:
Правила контроля эпюр Q и M — для грузовых участков.
Эти правила (закономерности) выполняются в пределах каждого грузового участка (но не на границах).- Из ф.(2) следует:
— если на участке q=0, то Q — постоянная величина (константа). — если на участке q=Const, то Q линейно зависит от продольной координаты (z), т е эпюра Q на этом участке — наклонная прямая. Более того, если q > 0 (т е направлена вверх), то поперечная нагрука возрастает (увеличивается при изменении z слева — направо). — если на участке q изменяется по линейному закону, то Q — по квадратичному (парабола). - Аналогичные выводы следуют из ф.(4):
— если на участке Q=0, то M — постоянная величина (константа).
— если на участке Q=Const, то M линейно зависит от продольной координаты (z), т е эпюра M на этом участке — наклонная прямая. Более того, если Q > 0 (т е направлена вверх), то M возрастает (увеличивается в алгебраическом смысле, т е с учетом знака +- при изменении z слева — направо). При этом у МЕХАНИКОВ эпюра имеет «положительный» наклон (как / ), а у СТРОИТЕЛЕЙ — «отрицательный» (как \ )
— если на участке Q изменяется по линейному закону, то M — по квадратичному (парабола).
Для определения направления выпуклости этой параболы СТРОИТЕЛИ пользуются правилом ветра и паруса: если вообразить, что ветер дует в направлении q, то выпуклость паруса совпадает с выпуклостью эпюры M. Все связанное с эпюрой М у МЕХАНИКОВ наоборот (механики откладывают значения на эпюре М на сжатой стороне изогнутого бруса, строители — наоборот, на растянутой. Правило знаков +- М для балки совпадают, но графики — эпюры М строятся наоборот (зеркально отражая относительно продольной оси).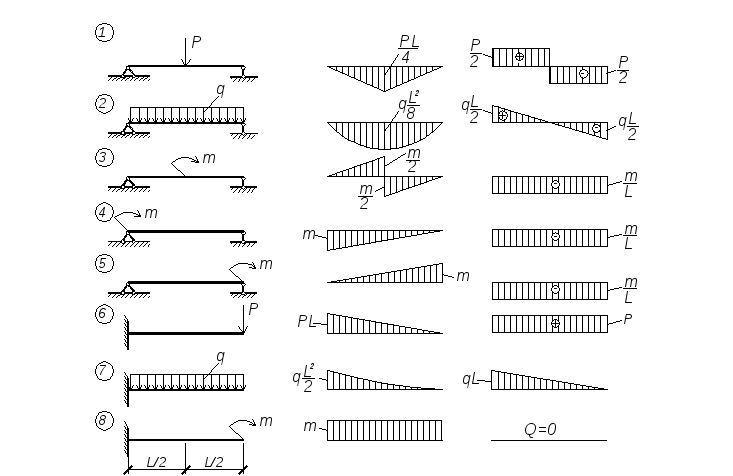
Если наклонная эпюра Q пересекает ось z, то в этом сечении M экстремально (т к 1-я производная = 0). Для определения координаты экстремума М см нижнюю часть рис 6.
Правила контроля (продолжение):
Площадь эпюры q на участке, определяемая по расчетной схеме, равна приращению Q на этом же участке.Площадь эпюры Q на участке, определяемая по эпюре Q, равна приращению M на этом участке.
Более того, можно определить и знак приращения: если q положительна, т е направлена вверх, то Q возрастает (значение на правом краю больше, чем на левом (например: 2 больше чем -6)). Для отрицательного q, естественно, наоборот.
Если площадь эпюры Q положительна, то значение M на правом краю участка алгебраически больше, чем на левом (например: 2 больше чем -6)
Формулы (22), (23) на рис 11 — это следствие из формул (2),(4) главы «Деформации, внутренние силы, внутренние силовые факторы. Эпюры ВСФ».
По формулам (22), (23) можно легко вычислять приращение значений Q и M (соответственно) на каждом грузовом участке.
Правила контроля эпюр Q и M — для границ грузовых участков
Вышеизложенные правила позволяют строить эпюры Q и M для балок без вычислений, изложеных в Примере
Пример: построение эпюр Q и M для балки (рис 4 и 6) на основе правил контроля
- Откройте рис 6 в отдельном окне, отрегулируйте размеры окна и удерживайте его на экране одновременно с этим описанием, чтобы видеть эпюры. Считаем, что опорные реакции уже определены и грузовые участки размечены.
- Строим эпюру Q. Для этого двигаемя вдоль оси z балки слева-направо по расчетной схеме.
На левой границе 1-го участка приложена (вниз) сила YA = 36,67 кН, поэтому делаем скачек (вниз) на 36,67 (ОТ НУЛЯ. начинаем с нуля — можно думать, что есть ненагруженный хвостик балки слева от опоры А, где M=0, Q=0).
Теперь находимся в пределах 1-го участка. Распределенная нагрузка на нем равна нулю, поэтому Q — постоянна и равна -36,67 кН на всем участке.
Теперь пересекаем границу со 2-м участком. На этой границе нет сосредоточенных сил, поэтому нет скачка.
Движемся по 2-му участку. Здесь приложена постоянная распределенная нагрузка q= 20 кН/м (вверх), поэтому здесь эпюра Q — наклонная прямая (возрастание слева-направо). Приращение Q по формуле (22) = площади = 20кН/м*3м = 60кН. То есть на правой границе 2-го участка Q = -36,67 + 60 = 23,34кН.
Пересекаем границу с 3-м участком. Здесь тоже нет состредоточенной силы, поэтому нет и скачка.
Движемся по 3-му участку. На участке q=0, поэтому Q постоянна, т е равна значению, которое было на левой границе, т е 23,33 кН.
Пересекаем правую границу 3-го участка. Здесь приложена (вниз) сила YB = 23,33 кН (реакция правой опоры). Поэтому эпюра Q делает скачек вниз (и приходит к нулевому значению. Это обязательно — для проверки).
- Строим эпюру M. Для этого двигаемя вдоль оси z балки слева-направо по расчетной схеме.
На левой границе 1-го участка пара сил (внешняя нагрузка) не приложена, поэтому эпюра M на 1-м участке начинается от нуля — можно думать, что есть ненагруженный хвостик балки слева от опоры А, где M=0, Q=0)
Теперь мы находимся в пределах 1-го участка.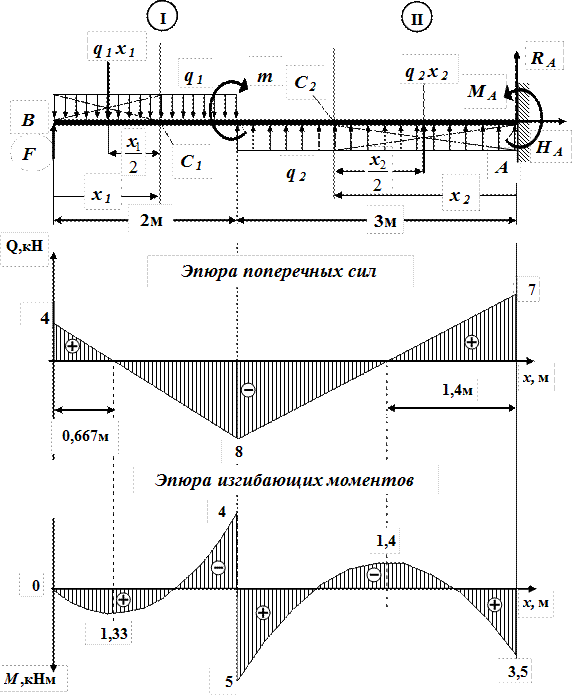 На нем Q — постоянна и равна -36,67 кН, поэтому эпюра M — Наклонная прямая на всем участке. Приращение M на участке вычислим как площадь прямоугольника на эпюре
Q = -36,67*2= -73,34 кНм. Механики откладывают на эпюре M -73,34 — вниз, строители — вверх.Теперь пересекаем границу 2-го участка. Здесь нет приложена пара сил M=80 кНм, поэтому скачок = 80 кНм. «Направление» скачка (то есть его рисунок-зигзаг) для механиков совпадает с рисунком пары M. Для строителей — наоборот. Возможно, проще рассуждать о приращении +80 (это для всех) и откладывать соответственно (у механиков — вверх, у строителей — вниз).
Движемся по 2-му участку. Здесь приложена постоянная распределенная нагрузка q= 20 кН/м (вверх), поэтому здесь эпюра M — парабола. Эпюра Q пересекает ось z на расстоянии 36,67/20 = 1,83 м. Чтобы найти экстремальное значеине M, найдем вначале приращение момента от левой границы 2-го участка до точки эккстремума. Это — пдощадь треугольника на эпюре Q = 36,57*1,83/2=33,55.
На нем Q — постоянна и равна -36,67 кН, поэтому эпюра M — Наклонная прямая на всем участке. Приращение M на участке вычислим как площадь прямоугольника на эпюре
Q = -36,67*2= -73,34 кНм. Механики откладывают на эпюре M -73,34 — вниз, строители — вверх.