Задание 2. Построение линии пересечения плоскостей
По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Стоимость и возможные формы обучения (очно или дистанционно) смотрите разделе Цены.Подробнее о репетиторстве.
2.1. Условие задания
По заданным координатам точек А, В, С, D, E, F (Таблица 2) построить горизонтальную и фронтальную проекции треугольников ∆АBC и ∆DEF, найти линию их пересечения и определить видимость элементов треугольников.
2.2. Пример выполнения задания № 2
Второе задание представляет комплекс задач по темам:
1. Ортогональное проецирование, эпюр Монжа, точка, прямая, плоскость: по известным координатам шести точек А, В, С, D, E, F построить горизонтальную и фронтальную проекции 2-х плоскостей, заданных ∆АBC и ∆DEF;
2. Плоскости общего и частного положения, пересечение прямой и плоскости, пересечение плоскостей, конкурирующие точки: построить линию пересечения заданных плоскостей и определить видимость их элементов.
Построить горизонтальные и фронтальные проекции заданных плоскостей ∆АBC и ∆DEF (Рисунок 2.1).
Для построения искомой линии пересечения заданных плоскостей необходимо:
1. Выбрать одну из сторон треугольника и построить точку пересечения этой стороны с плоскостью другого треугольника: на Рисунке 2.1 построена точка М пересечения прямой EF c плоскостью ∆АBC; для этого прямую EF заключают во вспомогательную горизонтально-проецирующую плоскость δ;
2. Построить фронтальную проекцию 1222 линии пересечения плоскости δ с плоскостью ∆АBC;
3. Найти фронтальную проекцию М2 искомой точки М на пересечении фронтальную проекцию 1222 с фронтальной проекцией E2F2 прямой EF;
4. Найти горизонтальную проекцию М1 точки М с помощью линии проекционной связи;
5. Аналогично построить вторую точку N, принадлежащую искомой линии пересечения заданных плоскостей: заключить во фронтально-проецирующую плоскость β прямую ВС; найти линию пересечения 34 плоскости с плоскостью ∆DEF; на пересечении линии 34 и прямой ВС найти точку N;
6. Определить с помощью конкурирующих точек, для каждой плоскости отдельно, видимые участки треугольников.
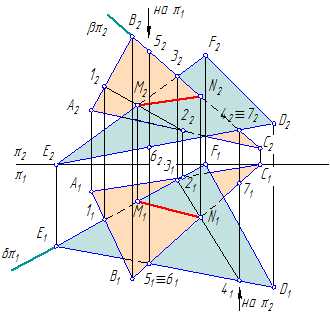
Рисунок 2.1 – Построение линии пересечения двух плоскостей, заданных треугольниками
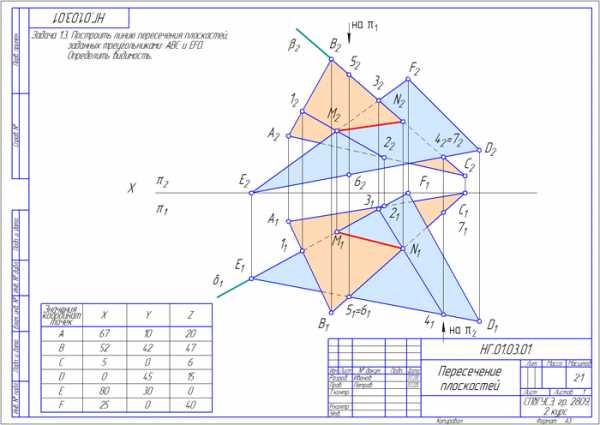
Рисунок 2.2 – Пример оформления задания 2
Видеопример выполнения задания №2
2.3. Варианты задания 2
Таблица 2– Значения координат точек
| Вариант | Координаты (x, y, z) вершин треугольников | |||||
|---|---|---|---|---|---|---|
| А | В | С | D | E | F | |
| 1 | 20; 65; 30 | 40; 15; 65 | 80; 30; 35 | 15; 35; 70 | 70; 75; 80 | 35; 0; 0 |
| 2 | 75; 75; 5 | 60; 20; 60 | 20; 10; 40 | 30; 55; 50 | 90; 50; 35 | 60; 5; 10 |
| 3 | 0; 30; 75 | 30; 65; 15 | 80; 25; 15 | 45; 65; 75 | 95; 40; 0 | 10; 0; 10 |
| 4 | 90; 5; 70 | 65; 60; 15 | 15; 15; 20 | 25; 45; 70 | 95; 60; 35 | 65; 10; 0 |
| 5 | 30; 0; 10 | 70; 15; 15 | 15; 55; 16 | 70; 55; 60 | 5; 30; 60 | 20; 0; 0 |
| 6 | 20; 25; 0 | 60; 5; 80 | 90; 75; 40 | 0; 60; 60 | 75; 80; 70 | 90; 10; 0 |
| 7 | 0; 60; 20 | 20; 10; 60 | 85; 10; 20 | 50; 70; 65 | 75; 35; 0 | 10; 0; 5 |
| 8 | 10; 20; 15 | 55; 70; 5 | 80; 20; 45 | 20; 60; 55 | 100; 35; 20 | 60; 10; 5 |
| 9 | 0; 50; 10 | 60; 70; 70 | 80; 10; 10 | 20; 10; 70 | 90; 50; 60 | 60; 85; 0 |
| 10 | 85; 70; 10 | 25; 20; 25 | 90; 10; 60 | 15; 70; 65 | 105; 10; 45 | 70; 0; 0 |
| 11 | 25; 5; 25 | 60; 60; 5 | 95; 20; 50 | 36; 45; 55 | 105; 45; 60 | 70; 0; 0 |
| 12 | 95; 30; 65 | 15; 15; 10 | 70; 80; 5 | 35; 70; 70 | 115; 80; 55 | 85; 20; 0 |
| 13 | 20; 5; 60 | 50; 60; 5 | 90; 15; 30 | 60; 60; 60 | 100; 5; 10 | |
| 14 | 10; 5; 70 | 80; 20; 25 | 40; 65; 10 | 70; 70; 70 | 0; 35; 60 | 30; 5; 0 |
| 15 | 20; 45; 55 | 60; 70; 10 | 90; 10; 60 | 20; 0; 10 | 95; 20; 10 | 75; 60; 75 |
| 16 | 5; 10; 60 | 40; 65; 10 | 70; 5; 40 | 70; 50; 75 | 0; 70; 45 | 15; 0; 5 |
| 17 | 10; 45; 5 | 90; 5; 10 | 50; 70; 70 | 15; 5; 50 | 95; 15; 65 | 60; 70; 0 |
| 18 | 65; 20; 70 | 0; 20; 15 | 50; 70; 5 | 15; 60; 55 | 90; 60; 40 | 60; 5; 5 |
| 19 | 20; 20; 70 | 50; 50; 10 | 70; 10; 30 | 80; 60; 70 | 5; 40; 60 | 25; 0; 10 |
| 20 | 85; 10; 45 | 70; 50; 0 | 20; 20; 10 | 55; 60; 60 | 0; 0; 60 | 75; 0; 0 |
| 21 | 0; 70; 60 | 30; 10; 80 | 70; 15; 20 | 60; 50; 70 | 0; 0; 50 | 15; 70; 5 |
| 22 | 0; 70; 25 | 45; 10; 70 | 90; 30; 20 | 65; 60; 70 | 90; 10; 15 | 15; 0; 15 |
| 23 | 10; 20; 40 | 50; 60; 10 | 75; 10; 40 | 75; 60; 75 | 5; 70; 55 | 35; 0; 0 |
| 24 | 10; 10; 10 | 90; 80; 20 | 65;10;60 | 15; 70; 65 | 100; 70; 40 | 80; 10; 0 |
| 25 | 60; 65; 10 | 0; 10; 25 | 85; 5; 60 | 20; 65; 60 | 105; 35; 35 | 55; 0; 0 |
| 26 | 10; 70; 20 | 50; 10; 60 | 90; 25; 10 | 70; 65; 45 | 5; 35; 55 | 25; 0; 50 |
| 27 | 10; 5; 70 | 40; 70; 10 | 90; 5; 40 | 100; 55; 25 | 25; 65; 80 | 50; 0; 0 |
| 28 | 0; 50; 5 | 25; 0; 60 | 85; 10; 15 | 50; 50; 50 | 90; 0; 55 | 20; 0; 0 |
| 29 | 10; 70; 10 | 40; 10; 50 | 80; 20; 20 | 80; 55; 55 | 10; 50; 70 | 20; 0; 0 |
| 30 | 75; 70; 20 | 10; 35; 10 | 60; 20; 60 | 20; 70; 70 | 100; 60; 50 | 75; 5; 0 |
Подробнее о репетиторстве.
cadinstructor.org
ПОЯСНЕНИЯ К ВЫПОЛНЕНИЮ ЭПЮРА 2 — МегаЛекции
(нахождение истинной величины сечения способом замены плоскостей проекций)
Задача 1
В первой задаче контрольной работы требуется построить линию пересечения пирамиды с плоскостью и определить видимость пирамиды относительно секущей плоскости, а также секущей плоскости относительно пирамиды.
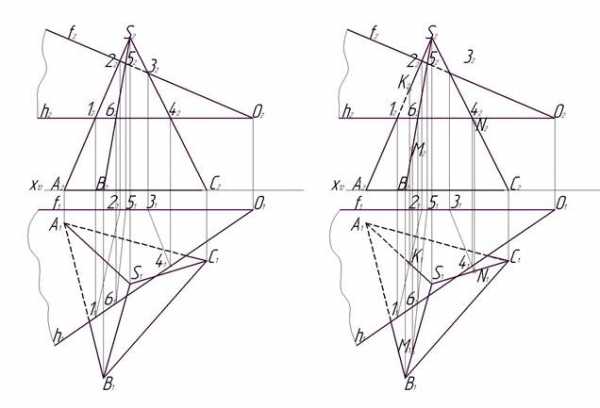
Рис. 10. Этап 1 Рис. 11. Этап 2
Этап 1 (рис.10). В данной задаче дана пирамида SАВС и секущая плоскость, представленная двумя пересекающимися в точке О прямыми, одна из которых, по заданию, является фронталью (f), а другая горизонталью (h).
Для построения линии пересечения, необходимо сначала найти точки пересечения ребер пирамиды секущей плоскостью. Построение начнем с фронтальной плоскости проекций. Определим точку пересечения горизонтали h3 c ребром S2А2 – это точка 12. Найдем горизонтальную проекцию точки 12 на горизонтальной проекции горизонтали – это точка 11. Теперь найдем точку пересечения фронтальной проекции фронтали f2 c ребром S2А2 и ее проекцию на горизонтальной плоскости проекций – это будут точки 22 и 21.
Аналогичным способом находим точки 32 и 42, рассматривая при этом пересечение прямых f2 и h3 c ребром S2C2 на фронтальной плоскости проекций и затем находя проекции точек на горизонтальной плоскости проекций – 31 и 41.
Точно также определяем точки пересечения прямых f2 и h3 с ребром S2B2 – это точки 52 и 62, а затем находим их соответствующие проекции на горизонтальной плоскости проекций – это точки 51 и 61. На горизонтальной плоскости проекций соединяем прямыми отрезками точки 11 и 21; 31 и 41; 51 и 61.
Этап 2 (рис.11). Следующий этап построения заключается в нахождении точек пересечения построенных отрезков с ребрами пирамиды на горизонтальной плоскости проекций. Рассмотрим отрезок 1121. Он пересекает ребро S1А1 в точке К1. Находим фронтальную проекцию точки К1 на фронтальной плоскости проекций на ребре S2А2, используя проекционную связь – это будет точка К2.
Для того, чтобы построить точку пересечения отрезка 3141 с ребром S1С1, необходимо продолжить отрезок 3141 за пределы точки 41. Точку пересечения обозначим N1. Найдем соответствующую проекцию этой точки на фронтальной плоскости проекций на ребре S2С2 и обозначим ее N2.
Аналогично поступим и с отрезком 5161. Продолжим его за пределы точки 61 и обозначим точку пересечения этой прямой с ребром S1В1. Это точка М1. Построим ее фронтальную проекцию на ребре S2В2 – это будет точка М2.
Таким образом, мы получили точки пересечения ребер пирамиды с секущей плоскостью.
Этап 3 (рис.12). На рисунке 12 показан дальнейший ход решения задачи. Для удобства его объяснения мы убрали линии предыдущих построений, оставив только точки пересечения ребер пирамиды с секущей плоскостью, но студентам этого делать не нужно – следует выполнять последующие построения, не убирая предыдущих.

Рис. 12. Этап 3
Соединим точки К1, М1 и N1 на горизонтальной плоскости проекций, а также точки К2, М2 и N2 на фронтальной плоскости проекций.
Теперь мы будем делать построения на фронтальной плоскости проекций. Продолжим f2О2 на произвольную длину за пределы О2 и проведем к f2О2 перпендикулярную прямую. Этим действием мы задали новую плоскость проекций π4, перпендикулярную к фронтальной плоскости проекций π2. Обозначим ее ось — Х2,4.
Из точек К2, М2 и N2 проведем линии, перпендикулярные оси Х2,4 (пока произвольной длины).
На линии, проведенной из точки К2, начиная от оси Х2,4, отложим отрезок a, равный расстоянию от оси Х1,2 до К1 (на горизонтальной плоскости проекций). Полученную точку обозначим К4.
На линии, проведенной из точки N2, начиная от оси Х2,4, отложим отрезок b, равный расстоянию от оси Х1,2 до N1 (на горизонтальной плоскости проекций). Полученную точку обозначим N4.
На линии, проведенной из точки М2, начиная от оси Х2,4, отложим отрезок с, равный расстоянию от оси Х1,2 до М1 (на горизонтальной плоскости проекций). Полученную точку обозначим М4.
Точки К4, N4 и М4 соединим. Если построение сделано правильно, то должна получиться прямая линия.
Если кратко раскрыть смысл выполненных построений, то он заключается в том, что мы ввели новую плоскость проекций для того, чтобы сечение, представленное треугольником К2М2N2, заняло проецирующее положение относительно новой плоскости π4 и спроецировалось в прямую линию.
При определении видимости фигур нужно мысленно представить пирамиду и секущую плоскость в пространстве и, сопоставляя горизонтальную и фронтальную проекции, определить, какая часть пирамиды закрыта плоскостью, а какая часть плоскости закрыта пирамидой.
Задача 2
Этап 4 (рис.13). Мы подошли к последнему этапу выполнения эпюра 2. В этой задаче нужно построить истинную величину сечения. Для этого нам снова нужно ввести новую плоскость проекций, пусть это будет плоскость П5. Параллельно построенной прямой К4N4М4 проведем прямую на любом расстоянии. Это будет ось Х4,5. Из точек К4, N4 и М4 проведем перпендикуляры на эту ось и продолжим их на произвольную длину.
На перпендикуляре, проведенном из точки К4, от оси Х4,5 отложим отрезок l1, равный расстоянию от оси Х2,4 до точки К2. Обозначим точку К5.
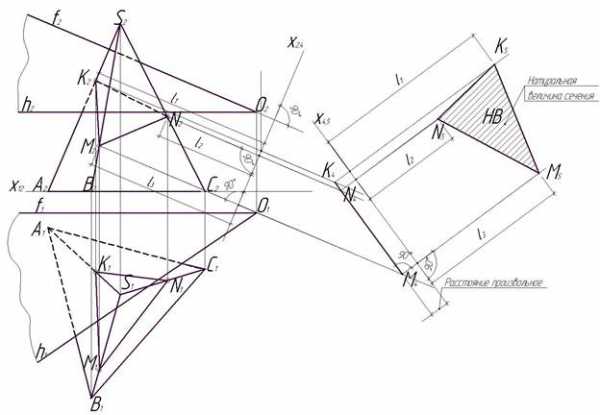 Рис. 13. Этап 4
Рис. 13. Этап 4
На перпендикуляре, проведенном из точки N4, от оси Х4,5 отложим отрезок l2, равный расстоянию от оси Х2,4 до точки N2. Обозначим точку N5.
На перпендикуляре, проведенном из точки M4, от оси Х4,5 отложим отрезок l3, равный расстоянию от оси Х2,4 до точки М2. Обозначим точку М5. Соединим полученные точки К5, N5 и М5.
Δ К5N5М5 – является натуральной величиной сечения пирамиды SАВС, полученного при пересечении ее секущей плоскостью, представленной двумя пересекающимися в точке О прямыми, одна из которых является фронталью (f), а другая горизонталью (h).
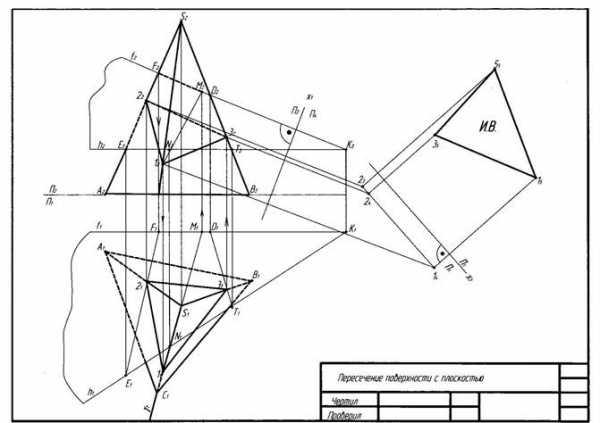
Рис. 14. Пример выполнения эпюра №2
ЭПЮР №2
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
Эпюр №2
ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТИ С ПЛОСКОСТЬЮ (пример 2)
Содержание эпюра. Даны пирамида и плоскость, заданная следами, требуется:
задача 1 – построить линию пересечения пирамиды с плоскостью и определить видимость фигур;
задача 2 – определить истинную величину сечения.
Образец выполнения эпюра №2 представлен на рисунке 18.
Пояснения к выполнению эпюра 2
(нахождение истинной величины сечения способом замены плоскостей проекций)
Задача 1
В первой задаче данного примера требуется построить линию пересечения пирамиды с плоскостью, заданной следами, а также определить видимость пирамиды относительно секущей плоскости, а также секущей плоскости относительно пирамиды.
Этап 1 (рис.15). Решение задачи начнем на горизонтальной плоскости проекций. Здесь к горизонтальному следу заданной плоскости (β1) проведем (в произвольной точке) линию, перпендикулярную этому горизонтальному следу. Эта линия будет осью новой плоскости проекций π4, обозначим ее Х1,4. Теперь опустим перпендикуляры из точек А1, В1, С1 и S1 на ось Х1,4. Получим точки В4, А4, С4 и О4. Это точки основания пирамиды в новой плоскости проекций. У пирамиды есть вершина – S, которую мы еще не построили. Это можно сделать следующим образом: от точки О4 продолжим перпендикуляр вниз и на нем отложим отрезок h, равный расстоянию от S2O2 на фронтальной плоскости проекций.
Рис. 15. Этап 1
Соединив точки А4, В4, С4 и S4, получим проекцию пирамиды во введенной плоскости П4. Теперь нужно построить в этой плоскости след секущей плоскости. Для этого на фронтальном следе β2 в любом месте ставим точку и обозначаем ее 12. Опускаем перпендикуляр из точки 12 на ось Х1,2 и получаем точку 22. Из точки 22 параллельно горизонтальному следу β1 проводим прямую до пересечения с осью Х1,4. Точку пересечения обозначим 24. Продолжим прямую 2224 за границу точки 24 на произвольную величину. На этой прямой отложим расстояние 2414, равное отрезку 1222, взятого с фронтальной плоскости проекций. Точку 14 соединим с точкой пересечения горизонтального следа β1 и осью плоскости проекций Х1,4.
Этим построением мы перевели секущую плоскость β в проецирующее положение, которое дает нам новые возможности в последующем построении сечения.
Рис. 16. Этап 2
Этап 2 (рис.16). Проецирующее положение секущей плоскости β4 дало нам возможность определить точки пересечения секущей плоскости и пирамиды. Это точки К4 и М4. Перенесем их проекции на горизонтальную плоскость проекций, используя проекционные связи (эти линии параллельны горизонтальному следу секущей плоскости – β1). На ребре S1C1 найдем точку К1, а на ребре А1S1 – точку М1. Еще две точки сечения (N2 и D2) мы найдем на горизонтальном следе секущей плоскости β1. Это точки ее пересечения с основанием пирамиды (со сторонами А1В1 и В1С1).
Соединив точки N1, M1, K1и D1, мы получим искомое сечение на горизонтальной плоскости проекций.
Найдем теперь точки этого сечения на фронтальной плоскости проекций. Для этого, опять используя проекционные связи, перенесем полученные точки на соответствующие им ребра во фронтальной проекции. Обозначим точки N2, M2, K2, D2 и соединим их отрезками.
Для определения видимости фигур нужно представить их в пространстве и, используя логику, можно прийти к выводу, что верхняя часть пирамиды закрывает секущую плоскость, мы ее не видим, по той же причине нам не видна сторона сечения М2К2.
Задача 2
На завершающем этапе задания необходимо построить натуральную величину найденного сечения. Для этого снова введем новую плоскость проекций.
Этап 3 (рис.17). Для того, чтобы ввести новую плоскость проекций, параллельно следу β4 на произвольном расстоянии от него, проведем прямую линию – это будет ось новой плоскости проекций, обозначим ее Х4,5. Из точек М4, К4, N4 и D4 (точки N4 и D4 мы перенесли с горизонтальной проекции на ось Х1,4 и они совпали в одной точке) опустили перпендикуляры на ось Х4,5 и продолжили их на произвольную длину. На этих перпендикулярах (от оси Х4,5) отложили отрезки, равные расстояниям от оси Х1,4 до соответствующим им проекциям точек на горизонтальной плоскости проекций. Например, расстояние a – это расстояние от оси Х1,4 до точки К1, расстояние b – от оси Х1,4 до точки D1, расстояние c – от оси Х1,4 до точки N1, расстояние d – от оси Х1,4 до точки М1.
Рис. 17. Этап 3
Так как точки N4 и D4 по построению совпали, то они расположились на одной прямой. Обозначим полученные точки N5, M5, K5, D5. Соединив их отрезками, мы получим натуральную величину сечения пирамиды, плоскостью β, которая задана следами.
Рис. 18. Пример выполнения эпюра №2 (пример 2)
studfiles.net
Эпюра Монжа | Начертательная геометрия
онлайн
Эпюра Монжа или комплексный чертеж — это чертеж, составленный из двух или более связанных между собой ортогональных проекций геометрической фигуры.
Пользоваться пространственным макетом для отображения ортогональных проекций геометрических фигур неудобно ввиду его громоздкости, а также из-за того, что при его переносе на лист бумаги, на плоскостях H и W происходит искажение формы и размеров проецируемой фигуры. Поэтому вместо изображения на чертеже пространственного макета используется эпюра Монжа.
Эпюра Монжа получается преобразованием пространственного макета путем совмещения плоскостей H и W с фронтальной плоскостью проекций V: — для совмещения плоскости H с V поворачиваем ее на 90 градусов вокруг оси x в направлении движения часовой стрелки. На рисунке, для наглядности, плоскость H повернута на угол чуть меньший 90 градусов, при этом ось y, принадлежащая горизонтальной плоскости проекции, после поворота совпадает с осью z; — после совмещения горизонтальной плоскости, поворачиваем вокруг оси z также на угол 90 градусов профильную плоскость в направлении противоположном движению часовой стрелки. При этом ось y, принадлежащая профильной плоскости проекции, после поворота совпадает с осью x.
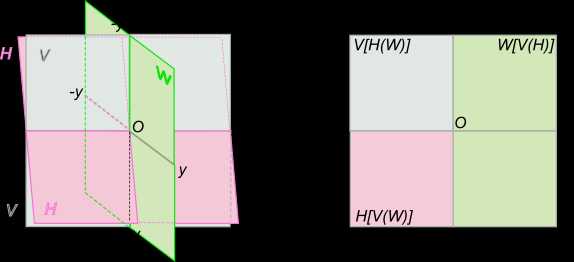
Эпюра Монжа
После преобразования пространственный макет примет вид, показанный на рисунке. На этом рисунке указана также последовательность взаимного положения пол плоскостей проекций, так запись V[H(W)] указывает, что в этой части эпюра Монжа (ограниченного положительным направлением осей x и z) ближе к нам находится верхняя левая пола фронтальной плоскости проекции V, за ней располагается задняя левая пола горизонтальной плоскости проекции H, далее следует верхняя задняя пола профильной плоскости W.
Так как плоскости не имеют границ, то в совмещенном положении (на эпюре) эти границы не показывают, нет необходимости оставлять надписи, указывающие положение пол плоскостей проекций. Излишне также напоминать, где отрицательное направление координатных осей. Тогда, в окончательном виде эпюра Монжа, заменяющая чертеж пространственного макета примет вид, показанный на рисунке.

Эпюра Монжа
Эпюра Монжа может быть выполнена с помощью: — обычных чертежных инструментов и приспособлений: Чертежные инструменты; Чертежные принадлежности и приборы; — Программы для построения (рисования) эпюра Монжа: Выполнение чертежа в графическом редакторе.
В качестве примера оформления эпюра Монжа предлагаем решение задачи на построение равнобедренного прямоугольного треугольника ABC:
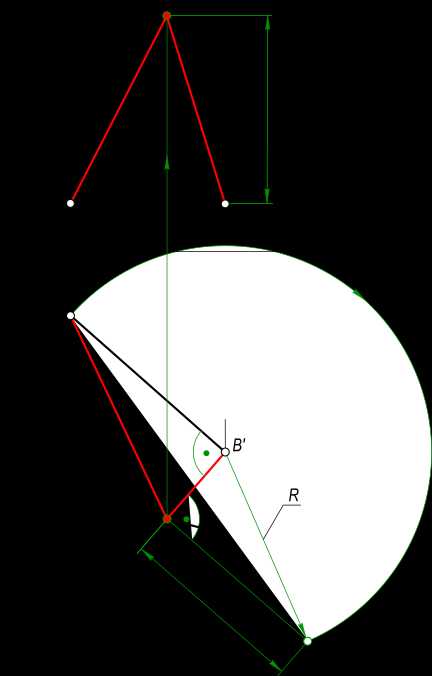
Эпюра Монжа
— в черном цвете отображается известное по условию задачи; — в зеленом цвете отображаются все построения которые ведут к решению задачи; — в красном цвете отображается найденные искомые задачи. По условию задачи заданы проекции треугольника ABC(A`B`C`, A»B»…»). Для решения задачи необходимо найти недостающую проекцию C».
Эпюры контрольных графических работ представлены в: Альбом графических работ по начертательной геометрии.
+
ngeo.fxyz.ru
Методическое пособие «Эпюр № 1выполнено на основе учебного пособия
Оглавление
Оглавление 3
ВВЕДЕНИЕ 4
1.ОБЩИЕ УКАЗАНИЯ 4
2.МЕТОДИКА РЕШЕНИЯ ЭПЮРА 4
3.ПОСЛЕДОВАТЕЛЬНОСТЬ ВЫПОЛНЕНИЯ ЭПЮРА 6
ПРИЛОЖЕНИЕ 1 16
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 18
ВВЕДЕНИЕ
Методическое пособие «Эпюр № 1выполнено на основе учебного пособия А. И. Образцова, изданного в 1953 году.
Данное пособие предназначено для оказания помощи студентам при выполнении графической работы «Эпюр №1» по курсу «Начертательная геометрия».
Цель работы — научиться строить линию пересечения заданных плоских фигур, определять видимость этих фигур на проекциях.
Графическая работа «Эпюр №1» является первым самостоятельным заданием студента по дисциплине «Начертательная геометрия». Для выполнения этой работы студент должен изучить следующие разделы начертательной геометрии: «Точка и прямая», «Плоскость», «Взаимное положение прямой и плоскости», «Взаимное положение двух плоскостей».
ОБЩИЕ УКАЗАНИЯ
Графическая работа «Эпюр №1» выполняется в масштабе 1:1 на формате А3 (297420 мм). В правом нижнем углу формата А3 студент выполняет основную надпись – форма 1 по ГОСТ 2.104-68. Пример заполнения основной надписи приведен в Приложении I. В левом верхнем углу формата выполняется дополнительная графа 26 (1470 мм). Пример выполнения графической работы дан в Приложении I.
В соответствии с ГОСТ 2.303-68 задание выполняется следующими типами линий:
— линии видимого контура толщиной S, равной 0,60,8 мм;
— линии построения – сплошные тонкие, толщиной от до ;
— линии невидимого контура – штриховые, толщиной от до ;
— следы вспомогательных плоскостей-посредников изображаются разомкнутыми линиями, длиной 8-10 мм, толщиной от 1,5 S до 2S.
МЕТОДИКА РЕШЕНИЯ ЭПЮРА
Вариант задания включает в себя три различные геометрические плоские фигуры:
— фигура № 1 задана координатами трех точек, фигура № 2 (многоугольник) полностью задана координатами трех точек и оставшимися точками, у которых одна из координат заменяется условием их принадлежности к плоской фигуре № 2;
— фигура № 3 занимает проецирующее положение (фронтально-проецирующее или горизонтально-проецирующее) и задается очерком в виде кольца, серпа, круга или его части.
Выполнение эпюра состоит из графического решения нескольких задач:
достроить недостающую проекцию многоугольника;
построить проекции линии пересечения треугольника АВС и многоугольника;
построить проекции линии пересечения: треугольника с плоскостью частного положения; многоугольника с плоскостью частного положения;
определить видимость элементов фигур на чертеже, считая фигуры непрозрачными.
Исходные данные заданы численными значениями координат и сведены в таблицу № 1.
ПОСЛЕДОВАТЕЛЬНОСТЬ ВЫПОЛНЕНИЯ ЭПЮРА
Для выполнения графической работы студенту необходимо решить ряд задач.
Задача 1. Построение исходного чертежа многоугольника (рис. 1).
Горизонтальная проекция многоугольника ABCDE задана полностью, а фронтальная проекция только тремя проекциями точек АВЕ. Необходимо достроить фронтальную проекцию точек С , D. При построении недостающей проекции заданного многоугольника необходимо соблюдать условие принадлежности точек данной фигуры к плоскости. Чтобы точки С, D лежали в плоскости, определенной тремя точками А, В и Е, необходимо, чтобы они находились на прямых, лежащих в этой плоскости. Этими прямыми являются диагонали АС, АD и ВЕ, горизонтальные проекции которых можно построить (рис. 1а).


а) б)
Рис. 1. Построение исходного чертежа многоугольника:
а— построение недостающих проекций вершин многоугольника; б— пропорциональное деление отрезка BE
На фронтальной проекции пятиугольника проводят проекцию диагонали ВЕ. В плоскости пятиугольника лежат точки пересечения диагоналей К и М, горизонтальные проекции которых К и М имеются, а фронтальные проекции получаются в результате пересечения линий проекционной связи, проведенных из К и М, с диагональю ВЕ. По двум точкам строятся фронтальные проекции других двух диагоналей АК и АМ, на них должны лежать проекции точек С и D, которые определяются по их горизонтальным проекциям.
В случае, если линия совпадает по направлению с линией проекционной связи или круто наклонена к оси проекций, то недостающая проекция точки строится из условия пропорционального деления отрезка: если точка делит отрезок на пропорциональные части, то проекция этой точки делит проекции этого отрезка в том же отношении. На рис. 1б нужно построить горизонтальную проекцию точки М. Из проекции точки В проводят линию под углом меньше 90 к ВЕ и на ней от проекции точки В откладывают отрезки равные ВМ и ВЕ. Соединяют Е и Е и параллельно этому направлению проводят от М линию до пересечения с ВЕ. Получают искомую горизонтальную проекцию М.
Задача 2. Построить точку пересечения прямой MN с плоскостью треугольника АВС.
Если прямая линия не параллельна плоскости, то она пересекает эту плоскость в действительной точке (см. рис. 2).

Рис. 2. Построение точки пересечения прямой с плоскостью
Алгоритм решения задачи:
1) Через заданную прямую MN проводим вспомогательную плоскость-посредник , перпендикулярную фронтальной плоскости проекций. Следовательно, на фронтальной плоскости проекций V все точки плоскости-посредника будут проецироваться в прямую линию, совпадающую с фронтальной проекцией прямой MN.
2) Находим линию пересечения вспомогательной плоскости-посредника с заданной плоскостью треугольника АВС. На чертеже линия (1,2).
3) Находим искомую точку пересечения К прямой MN с плоскостью треугольника АВС. Она определяется как пересечение искомой прямой с найденной линией пересечения вспомогательной плоскости-посредника с плоскостью треугольника АВС.
Определение видимости на чертеже.
В начертательной геометрии плоскости считаются непрозрачными, поэтому необходимо на проекциях определить видимость.
Для определения видимости на чертеже используем метод конкурирующих точек, сущность которого заключается в выборе двух скрещивающихся прямых.
Для определения видимости на фронтальной плоскости проекций V поступают так. Выбираем две скрещивающиеся прямые ВС и МN, фронтальные проекции которых пересекаются в точках 1 и 3. По горизонтальной проекции определяем, что проекция точки 3, лежащая на проекции прямой MN, будет закрывать проекцию точки 1, лежащую на проекции прямой ВС, т. к она будет ближе к наблюдателю. На чертеже направление взгляда наблюдателя показано стрелкой. Следовательно, на фронтальной плоскости проекций проекция МN будет закрывать проекцию ВС. Границей видимости является проекция точки пересечения К.
Для определения видимости на горизонтальной плоскости проекций Н выбираем две скрещивающиеся прямые АС и MN, горизонтальные проекции которых пересекаются в точках 4 и 5. По фронтальной проекции определяем, что проекция точки 5, лежащая на проекции прямой МN, будет закрывать проекцию точки 4, лежащую на проекции прямой АС, т. к. она будет ближе к наблюдателю. На чертеже направление взгляда наблюдателя показано стрелкой. Следовательно, на горизонтальной плоскости проекций проекция MN будет закрывать проекцию АС. Границей видимости является проекция точки пересечения К.
Задача 3. Построение линии пересечения двух плоскостей, одна из которых занимает частное положение.
Даны две плоскости: плоскость ∆АВС – плоскость общего положения, плоскость ∆DЕК – плоскость частного положения, которая расположена перпендикулярно фронтальной плоскости проекций (рис. 3).
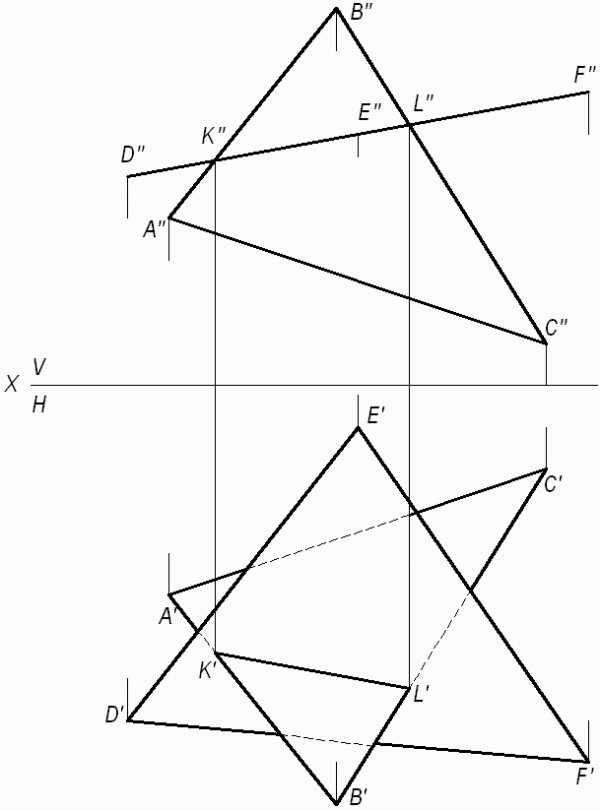
Рис. 3. Построение
линии пересечения двух плоскостей, одна
из которых занимает
частное положение
Фронтальная проекция ∆DЕК совпадает с фронтальным следом плоскости и фронтальной проекцией линии пересечения треугольников.
(KL) линия пересечения двух треугольников. Проекции этой линии пересечения – фронтальную и горизонтальную строят исходя из свойства принадлежности точек K и L сторонам (АВ) и (ВС), соответственно. Видимость треугольников на горизонтальной плоскости проекций определяем методом конкурирующих точек, рассмотренном в задаче 2.
Задача 4. Построение линии пересечения двух плоскостей общего положения.
Даны две плоскости общего положения, заданные треугольниками АВС и DЕК. Построить линию пересечения двух треугольников, определить видимость треугольников на проекциях.
Прямая линия, получаемая при взаимном пересечении двух плоскостей, определяется двумя точками, каждая из которых одновременно принадлежит обеим плоскостям. Общие точки определяются решением основной позиционной задачи начертательной геометрии – построение точки пересечения прямой с плоскостью (см. рис. 2).
Для решения данной задачи проводят вспомогательные плоскости-посредники частного положения (проецирующие плоскости). Решение задачи приведено на рис. 4.
Алгоритм решения задачи:
1. Определяют первую точку линии пересечения двух треугольников – точку М.
1.1. Фронтально-проецирующая плоскость проведена через сторону DК и задана на чертеже фронтальным следом V.
1.2. Плоскость пересекает плоскость треугольника АВС по прямой (1,2), на чертеже строят две проекции этой прямой.
1.3. Прямая (1,2) пересекает сторону DК в точке М, строят две проекции точки М и М.
2. Определяют вторую точку искомой линии пересечения двух треугольников – точку N.
2.1. Горизонтально-проецирующая плоскость проведена через сторону АВ и задана на чертеже горизонтальным следом Н.
2.2. Плоскость пересекает плоскость треугольника DЕК по прямой (3,4), на чертеже строят две проекции этой прямой.
2.3. Прямая (3,4) пересекает АВ в точке N, строят две проекции точки N и N.
Плоскости треугольников АВС и DЕК пересекаются по прямой MN.
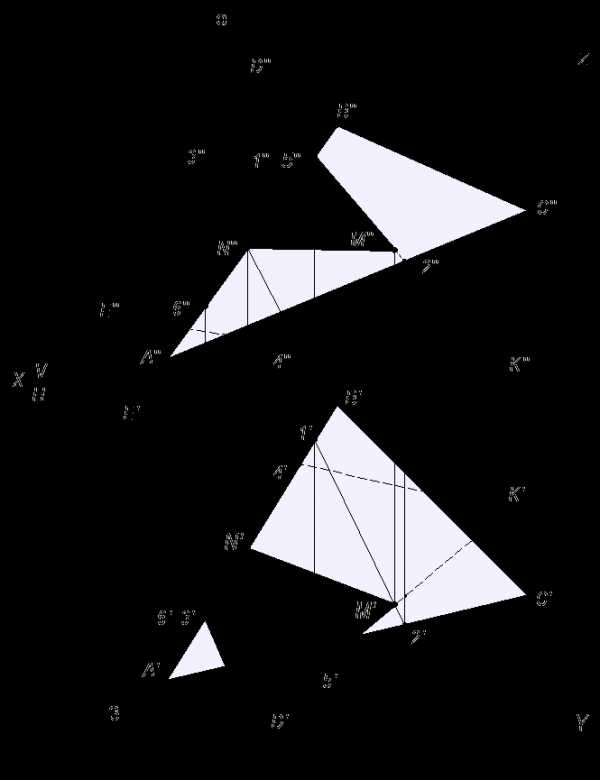
Рис. 4. Построение линии пересечения двух треугольников
3. Видимость плоских фигур на проекциях определяют методом конкурирующих точек.
Для определения видимости на фронтальной плоскости проекций V выбираем две скрещивающиеся прямые DK и AB, фронтальные проекции которых пересекаются в точках 1 и 5. По горизонтальной проекции определяем, что проекция точки 5, лежащая на проекции прямой DK, будет закрывать проекцию точки 1, лежащую на проекции прямой АВ, т. к. она будет ближе к наблюдателю. Следовательно, на фронтальной плоскости проекция DK будет закрывать проекцию AB. Границей видимости является проекция линии пересечения MN.
Для определения видимости на горизонтальной плоскости проекций Н выбираем две скрещивающиеся прямые АВ и DЕ, горизонтальные проекции которых пересекаются в точках 3 и 6. По фронтальной проекции определяем, что проекция точки 3, лежащая на проекции прямой DЕ, будет закрывать проекцию точки 6, лежащую на проекции прямой AB, т.к. она будет ближе к наблюдателю. Следовательно, на горизонтальной плоскости проекция DЕ будет закрывать проекцию АВ. Границей видимости является проекция линии пересечения NM.
Задача 5. Построить две проекции линии пересечения плоскости общего положения, заданной следами и плоскости общего положения, заданной параллельными прямыми а и b.
Для решения данной задачи проводят вспомогательные плоскости-посредники частного положения (плоскости уровня), пересекающие заданные плоскости по прямым, недостающие проекции которых легко строятся и пересекаются в пределах чертежа.
Графическое решение задачи приведено на рис. 5.

Рис. 5. Построение линии пересечения двух плоскостей
Вспомогательная горизонтальная плоскость-посредник γ задана следом γV и пересекает плоскость по горизонтали, проходящей через точку 3, а плоскость по горизонтали (1, 2). Горизонтальные проекции этих горизонталей пересекаются в точке К. Строят фронтальную проекцию точки К, используя свойство принадлежности точки прямой линии. Точка К принадлежит обеим плоскостям и . Вторая точка N, общая для двух плоскостей и , определяется второй вспомогательной плоскостью-посредником частного положения δ (на чертеже задана следом δV). Искомая прямая (КN) является линией пересечения двух плоскостей и .
ПРИЛОЖЕНИЕ 1

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Гордон В.О., Семенцов-Огиевский М. А. Курс начертательной геометрии. Учеб. пособие. М.: Высшая школа. 2007.272 с.
2. Самохвалов Ю. И. Начертательная геометрия. Учебное пособие. Екатеринбург: Изд-во УГГУ. 2011. 121 с.
3. Самохвалов Ю. И., Шангина Е. И. Начертательная геометрия. Инженерная графика. Учебно-методическое пособие. Екатеринбург: Изд-во УГГУ. 2011. 96 с.
gigabaza.ru
ПОЯСНЕНИЯ К ВЫПОЛНЕНИЮ ЭПЮРА 1 — МегаЛекции
Задача 1
В первой задаче контрольной работы требуется найти расстояние от точки D до плоскости треугольника ABC. Кратчайшее расстояние от точки до плоскости есть перпендикуляр, опущенный из данной точки на эту плоскость.
Этап 1(рис. 1). Для решения этой задачи необходимо, прежде всего, провести горизонталь (h3) из какой-нибудь вершины треугольника ABC на фронтальной плоскости проекций (П2) и фронталь (f1) – на горизонтальной плоскости проекций (П1) из любой вершины ΔАВС, удобной для этого построения. Обозначив точку пересечения фронтали со стороной ΔАВС на горизонтальной плоскости проекций точкой 11, нужно найти ее проекцию (по проекционной связи) на фронтальной проекции ΔАСВ, это будет точка 12.
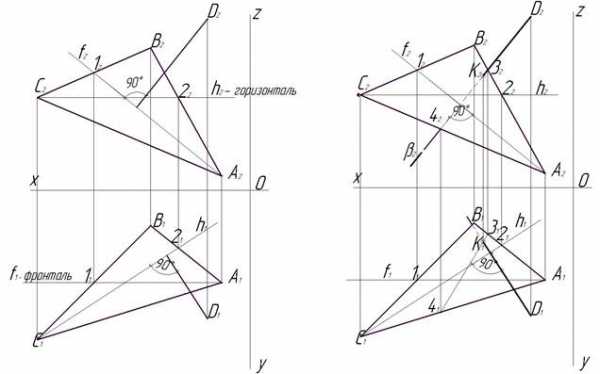
Рис. 1 Этап 1 Рис. 2 Этап 2
Таким же образом находятся точки 22 и 21, используя горизонталь (h3). Из точки D2 опускаем ⊥ (перпендикуляр) на f2 (отрезок А212) и из точки D1 опускаем ⊥ на h2 (отрезок С1 21).
Этап 2 (рис. 2). Необходимо найти основание перпендикуляра как точку пересечения прямой DK и плоскости, заданной ΔАВС. Для этого продолжаем перпендикуляр из точки D2 (на фронтальной плоскости проекций) до пересечения со стороной А2С2 – обозначаем точку 42. Пересечение перпендикуляра со стороной А2В2 дает нам точку 32. Заключаем прямую 4232 во вспомогательную проецирующую плоскость β2, это действие дает нам возможность найти проекцию отрезка 4232 на горизонтальной плоскости проекций (П1) в плоскости ΔАВС – это отрезок 4131. Находим точку пересечения отрезка 4131 с перпендикуляром, опущенным из точки D1 и обозначаем ее К1. Используя проекционную связь, находим точку К2 на перпендикуляре, который опущен из точки D2. Таким образом, мы нашли точку пересечения перпендикуляра, опущенного из точки D на плоскость, заданную ΔАВС, на обеих проекциях.
Этап 3 (рис. 3). Следующий этап выполнения задания содержит в себе нахождение натуральной величины перпендикуляра DК.
Это действие можно проводить на любой из плоскостей проекций, мы выбираем горизонтальную плоскость и начинаем построение с восстановления перпендикуляра к отрезку D1К1 в точке D1 (пока произвольной длины). Переходим на фронтальную плоскость проекций и находим расстояние от точки К2 до D2 как разность их высот по отношению к оси Х. Найденное расстояние откладываем на восстановленном перпендикуляре к отрезку D1К1 в точке D1 на горизонтальной плоскости проекций. Отмечаем точку D0. Точку D0 соединяем с точкой К1. Отрезок D0К1 – является натуральной (истинной) величиной перпендикуляра DК к плоскости, заданной ΔАВС. Этот способ нахождения истинной величины расстояния от точки, лежащей вне плоскости, до плоскости называется способом прямоугольного треугольника.
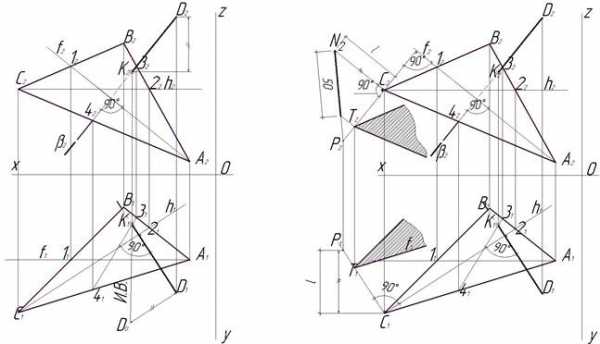
Рис. 3 Этап 3 Рис. 4 Этап 4
Задача 2
Этап 4 (рис. 4). На этом этапе необходимо решить вторую задачу эпюра 1, т.е. построить плоскость, параллельную плоскости, заданной треугольником АВС, и отстоящую от неё на 50 мм. Построение начинаем с того, что через любую вершину ΔАВС проводим линию параллельную перпендикуляру DК. На фронтальной плоскости (П2) эта линия будет // (параллельна) D2К2, а на горизонтальной плоскости (П1) — // D1К1. Отмечаем во фронтальной плоскости проекций (П2) на только что проведенной // перпендикуляру D2К2 линии через вершину С2 любую произвольную точку Р2. Находим ее проекцию на горизонтальной плоскости проекций (П1) на линии, проведенной через точку С1 параллельно перпендикуляру D1К1. Методом прямоугольного треугольника находим натуральную величину отрезка С2Р2. Для этого необходимо найти и измерить разность расстояний от точек С1 и Р1 до оси Х. На рис. 4 это расстояние обозначено буквой l. Теперь нужно возвратиться на фронтальную проекцию и провести перпендикуляр в точке С2 к отрезку С2Р2. На нем отложить отрезок l и конечную точку N2 соединить с точкой Р2. Полученный отрезок N2P2 и будет натуральной величиной отрезка С2Р2. Именно на отрезке N2P2 от точки N2 нужно отложить расстояние, равное 50 мм, и из конечной точки провести линию параллельную отрезку N2С2, которая пересечет отрезок С2Р2 в точке Т2 (бывают случаи, когда истинная величина отрезка С2Р2, т.е. отрезок N2С2, меньше, чем требуемое по условию задачи расстояние 50мм. Это не должно смущать студента, так как отрезок N2P2 можно продолжить за точку Р2, также как отрезок С2Р2).
Теперь, когда точка Т2, которая отстоит от плоскости ΔАВС на 50мм, найдена, нужно найти ее горизонтальную проекцию, используя проекционную связь. Точка Т1 будет располагаться на отрезке С1Р1. Далее необходимо задать плоскость, параллельную ΔАВС, используя свойство параллельности плоскостей, смысл, которого в следующем: если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны. Возьмем две, пересекающиеся в точке С2, стороны С2В2 и С2А2 и через точку Т2 проведем прямые, одна из которых параллельна С2В2, а другая — С2А2. Ограничим угол В2С2А2 волнистой линией. Это будет плоскость, заданная двумя, пересекающимися в точке Т2, прямыми, параллельная ΔАВС. На горизонтальной плоскости проекций через точку Т1 проведем одну прямую, параллельную стороне С1В1, а другую прямую – параллельную С1А1. Полученный угол В1С1А1 ограничим волнистой линией. Таким образом, мы получили горизонтальную проекцию плоскости, параллельную ΔАВС, которая образована двумя пересекающимися прямыми.
Задача 3
В задаче 3 искомая плоскость, перпендикулярная к заданной, должна содержать в себе заданную прямую и перпендикуляр, опущенный из любой точки этой прямой на заданную плоскость. Точки пересечения заданной прямой и перпендикуляра определяют линию пересечения искомой и заданной плоскостей. Видимость плоскостей определяется при помощи конкурирующих точек скрещивающихся прямых, принадлежащих этим плоскостям.
Этап 5 (рис.5). Построения, выполняемые на этапе 5, повторяют построения, выполненные на этапах 1 и 2 и заключаются в построении перпендикуляров из точек D1 и D2 на проекции плоскости, заданной ΔАВС. Дело в том, что плоскость, которая должна пересечь ΔАВС, по условию задачи ей перпендикулярна, значит, одна из сторон новой плоскости, заданной скрещивающимися прямыми, должна являться перпендикуляром к ΔАВС. Точки К1 и К2 являются точками пересечения перпендикуляров, опущенных из точек D1 и D2 на горизонтальную и фронтальную плоскости ΔАВС. Эти точки являются началами отрезков, по которым будет проходить пересечение двух плоскостей. Но для построения плоскости необходимо ввести в наш чертеж точки Е1 и Е2.
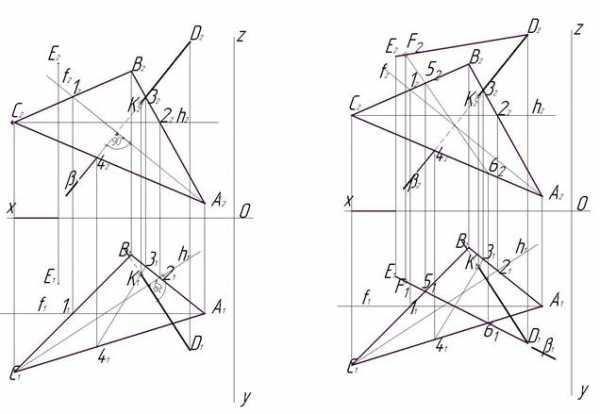
Рис.5. Этап 5 Рис. 6. Этап 6
Этап 6 (рис.6). На горизонтальной проекции через прямую D1 Е1 задаем секущую плоскость b и отмечаем точки пересечения D1 Е1 с ΔА1В1С1 — 51 и 61. Находим их соответствующие проекции на фронтальной плоскости – 52 и 62. Точки 52 и 62 соединяем между собой и продолжаем этот отрезок до пересечения с прямой Е2D2. Получили точку F2.
Этап 7 (рис.7). Соединяем точки F2 и К2 на фронтальной плоскости проекций, а также точки F1 и К1 на горизонтальной плоскости проекций. Отрезки F2 К2 и F1К1 – являются линиями пересечения заданной плоскости ΔАВС и искомой, перпендикулярной заданной.
Этап 8 (рис.8). На последнем этапе необходимо определить видимость пересечения двух плоскостей. Это можно определить, используя метод конкурирующих точек скрещивающихся прямых, которым принадлежат эти точки.
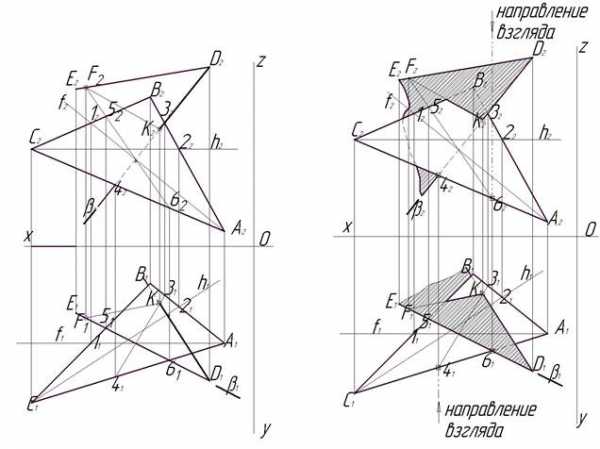
Рис.7. Этап 7 Рис. 8 Этап 8
Возьмем точку 61, в которой скрещиваются прямые С1А1 и Е1D1, и подымем проекционную связь на фронтальную плоскость проекций. По этой проекционной связи проследим сверху вниз расположение прямых С2А2 и Е2D2. Нас интересует, какая из этих прямых встретится на нашем пути (сверху вниз) раньше. Первой мы встречаем прямую Е2D2, а затем прямую С2А2. Из этого можно сделать вывод, что на горизонтальной проекции из двух рассматриваемых скрещивающихся прямых выше лежит прямая Е1D1. Это значит, что в этой плоскости проекций плоскость, заданная пересекающимися прямыми Е1D1 и К1D1,находится выше плоскости, заданной ΔАВС, значит, в этом месте она будет видимой до линии пересечения F1К1, а ΔАВС – невидимым.
Чтобы определить видимость пересекающихся плоскостей на фронтальной плоскости проекций, возьмем точку 42. В этой точке скрещиваются прямые С2А2 и D242. Опустим проекционную связь из этой точки на горизонтальную проекцию. И проследим, какая из прямых С1А1 и D141 встретится нам раньше, если смотреть на них снизу вверх. Как видно из чертежа, первой встречается С1А1, а затем D141. Это говорит о том, что на фронтальной проекции (с которой мы начинали свое исследование) ΔАВС, которому принадлежит прямая С1А1, будет видимым, плоскость, заданная пересекающимися прямыми Е1D1 и К1D1, – невидимой. Для более наглядного изображения нужно заштриховать одну из пересекающихся плоскостей и показать невидимые стороны плоскостей пунктирной линией.
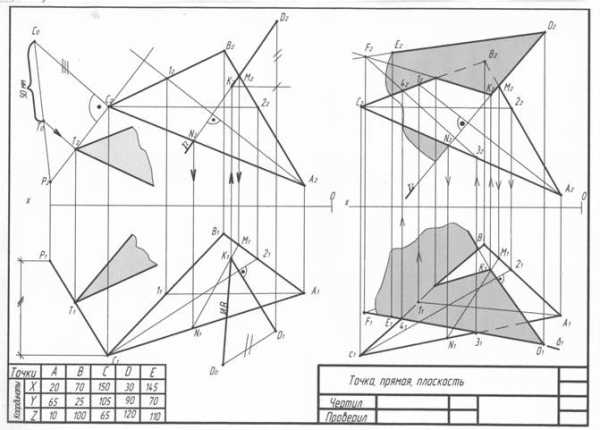
Рис.9. Пример выполнения эпюра №1
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
2.8 Основные варианты перемножения эпюр
Очевидно, что разнообразие приложенных нагрузок и геометрических схем конструкций приводит к различным, с точки зрения геометрии, перемножаемым эпюрам. Для реализации правила Верещагина нужно знать площади геометрических фигур и координаты их центров тяжести. На рис.29 представлены некоторые основные варианты, возникающие в практических расчетах.
Для перемножения эпюр сложной формы их необходимо разбивать на простейшие. Например, для перемножения двух эпюр, имеющих вид трапеции, нужно одну из них разбить на треугольник и прямоугольник, умножить площадь каждого из них на ординату второй эпюры, расположенную под соответствующим центром тяжести, и результаты сложить. Аналогично поступают и для умножения криволинейной трапеции на любую линейную эпюру.
Если указанные выше действия проделать в общем виде, то получим для таких сложных случаев формулы, удобные для использования в практических расчетах (рис.30). Так, результат перемножения двух трапеций (рис.30,а):
(2.21)
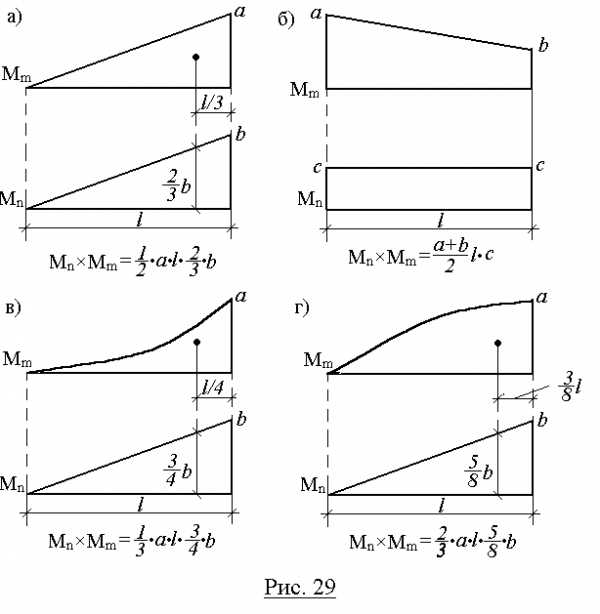
Рис. 29
По формуле (2.21) можно перемножить и эпюры, имеющих вид «перекрученных» трапеций (рис.30,б), но при этом произведение ординат, расположенных по разные стороны от осей эпюр, учитывается со знаком минус.
Если одна из перемножаемых эпюр очерчена по квадратной параболе (что соответствует нагружению равномерно распределенной нагрузкой), то для перемножения со второй (обязательно линейной) эпюрой ее рассматривают как сумму (рис.30,в) или разность (рис.30,г) трапециидальной и параболической эпюр. Результат перемножения в обоих случаях определяется формулой:
(2.22)
но значение f при этом определяется по-разному (рис. 30, в, г).
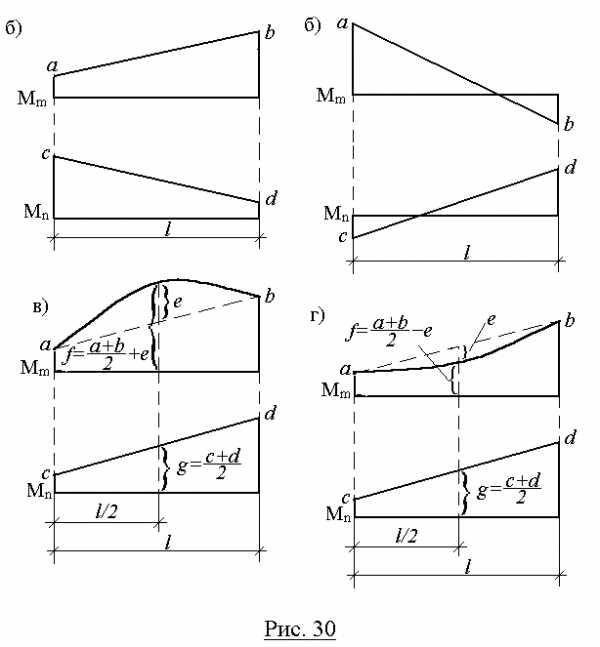
Рис. 30
Возможны случаи, когда ни одна из перемножаемых эпюр не является прямолинейной, но хотя бы одна из них ограничена ломаными прямыми линиями. Для перемножения таких эпюр их предварительно разбивают на участки, в пределах каждого из которых по крайней мере одна эпюра являетя прямолинейной.
Рассмотрим использование правила Верещагина на конкретных примерах.
Пример 15.Определить прогиб в середине пролета и угол поворота левого опорного сечения балки, нагруженной равномерно распределенной нагрузкой (рис.31,а), способом Верещагина.
Последовательность расчета способом
Верещагина – такая же, как и в методе
Мора, поэтому рассмотрим три состояния
балки: грузовое – при действии
распределенной нагрузки q; ему
соответствует эпюра Mq(рис.31,б),
и два единичных состояния — при действии
силы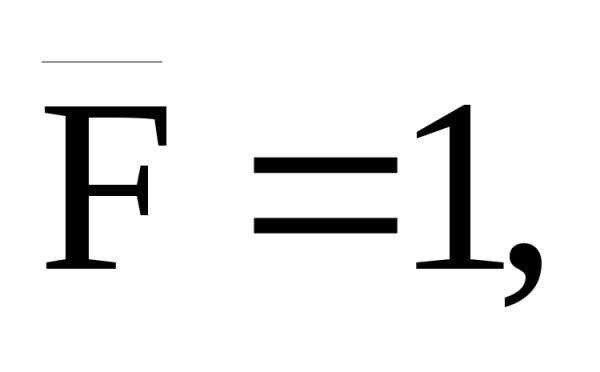 приложенной в точке С (эпюра
приложенной в точке С (эпюра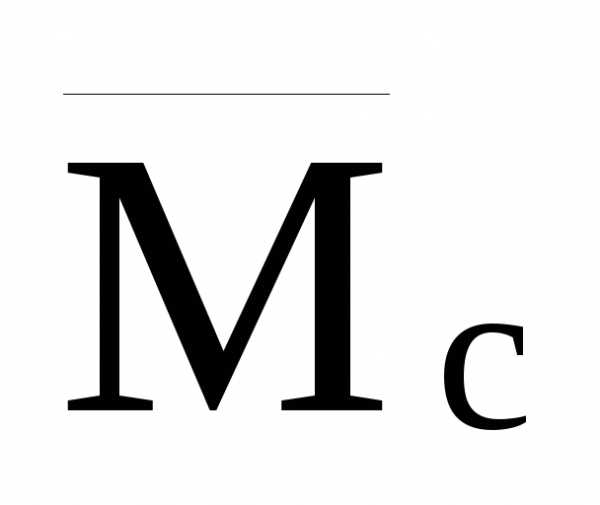 ,
рис.31,в), и момента
,
рис.31,в), и момента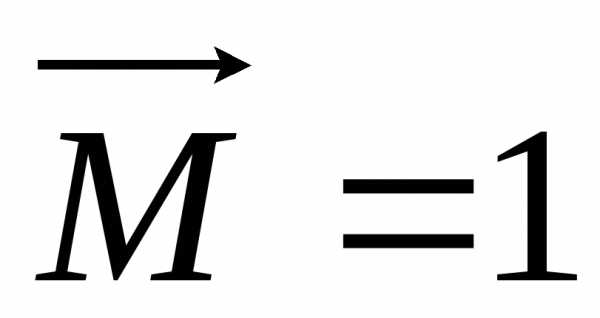 ,
приложенного в точке В (эпюра
,
приложенного в точке В (эпюра ,
рис.31,г).
,
рис.31,г).
Прогиб балки в середине пролета:
.
Аналогичный результат был получен
ранее методом Мора (см. пример 13). Следует
обратить внимание на тот факт, что
перемножение эпюр выполнялось для
половины балки, а затем, в силу симметрии,
результат удваивался. Если же площадь
всей эпюры Mqумножить на
расположенную под ее центром тяжести
ординату эпюры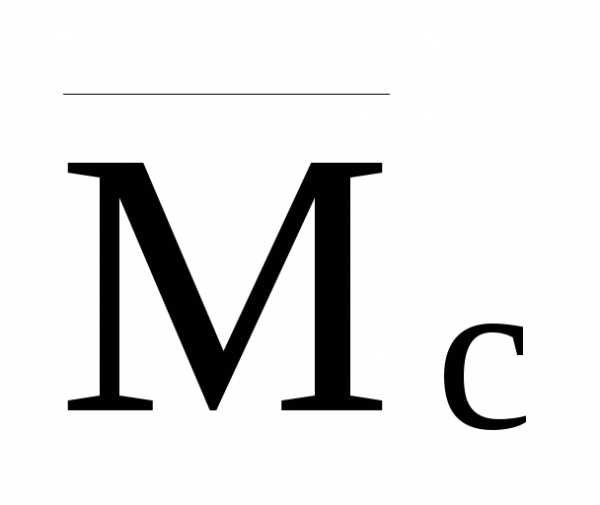 (
(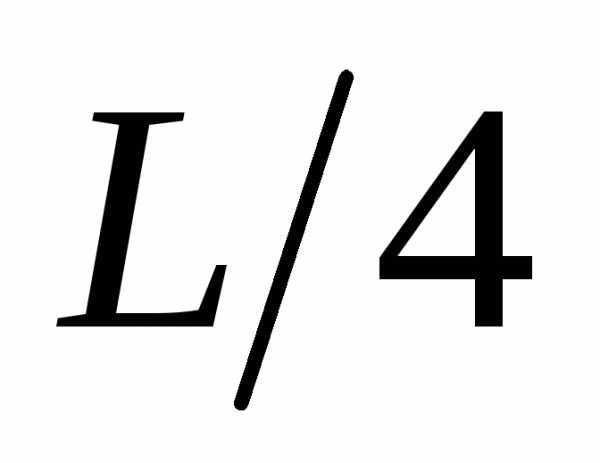 на
рис.31,в), то величина перемещения будет
совершенно иной и неправильной так как
эпюра
на
рис.31,в), то величина перемещения будет
совершенно иной и неправильной так как
эпюра ограничена ломаной линией. На
недопустимость такого подхода уже
указывалось выше.
ограничена ломаной линией. На
недопустимость такого подхода уже
указывалось выше.
А при вычислении угла поворота сечения
в точке В можно площадь эпюры Mqумножить на расположенную под ее центром
тяжести ординату эпюры (
(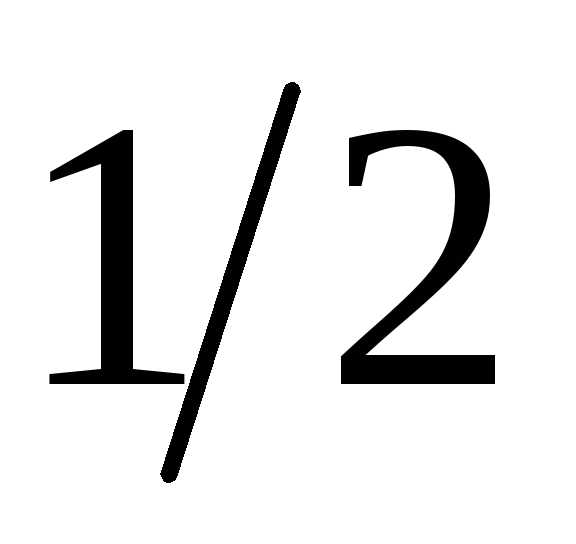 ,
рис.31,г), так как эпюра
,
рис.31,г), так как эпюра ограничена прямой линией:
ограничена прямой линией:
Этот результат также совпадает с результатом, полученным ранее методом Мора (см. пример 13).
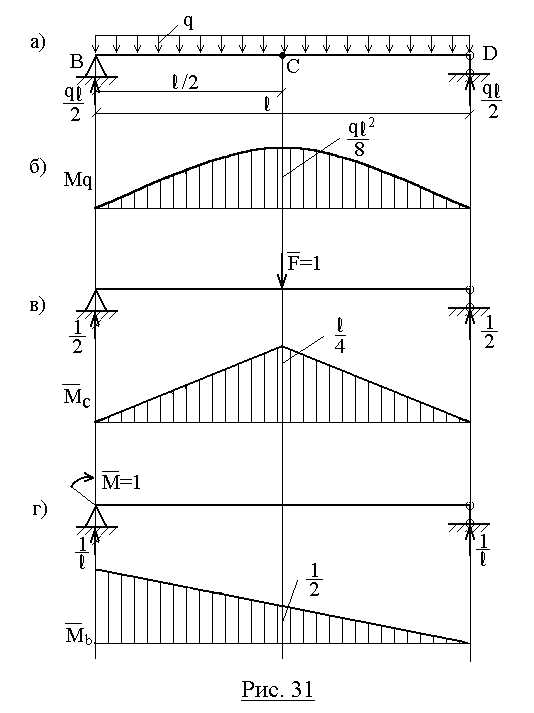
Рис. 31
Пример 16.Определить горизонтальное и вертикальное перемещения точки А в раме (рис.32,а).
Как и в предыдущем примере, для решения
задачи необходимо рассмотреть три
состояния рамы: грузовое и два единичных.
Эпюра моментов MF, соответствующая
первому состоянию, представлена на
рис.32,б. Для вычисления горизонтального
перемещения прикладываем в точке А по
направлению искомого перемещения (т.е.
горизонтально) силу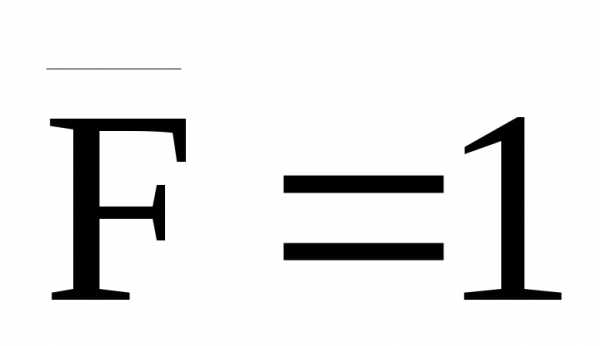 ,
а для вычисления вертикального
перемещения силу
,
а для вычисления вертикального
перемещения силу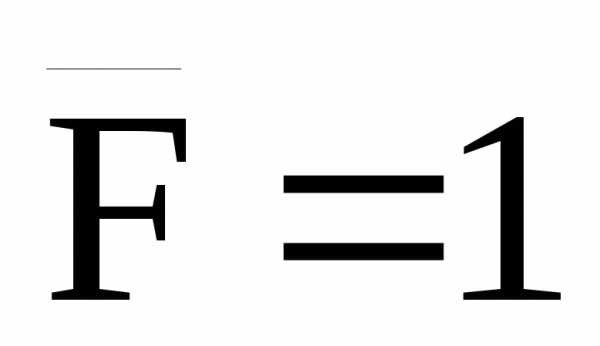 прикладываем вертикально (рис.32,в,д).
Соответствующие эпюры
прикладываем вертикально (рис.32,в,д).
Соответствующие эпюры и
и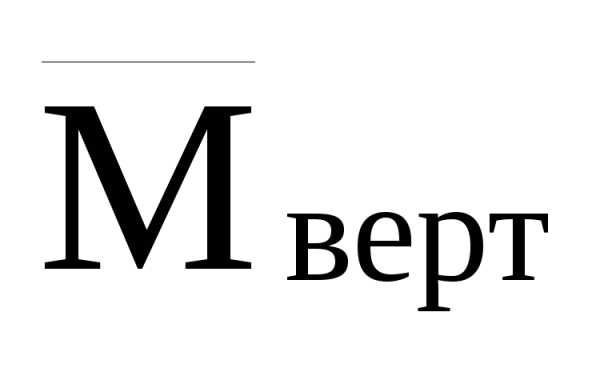 показаны на рис.32,г,е.
показаны на рис.32,г,е.
Горизонтальное перемещение точки А:
При вычислении 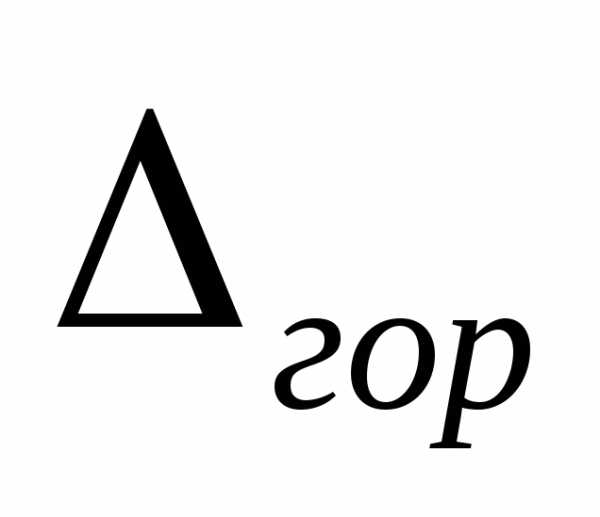 на участке АВ трапеция (эпюра MF)
разбита на треугольник и прямоугольник,
после чего треугольник с эпюры
на участке АВ трапеция (эпюра MF)
разбита на треугольник и прямоугольник,
после чего треугольник с эпюры «умножен»
на каждую из этих фигур. На участке ВС
криволинейная трапеция разделена на
криволинейный треугольник и прямоугольник,
а для перемножения эпюр на участке СД
использована формула (2.21).
«умножен»
на каждую из этих фигур. На участке ВС
криволинейная трапеция разделена на
криволинейный треугольник и прямоугольник,
а для перемножения эпюр на участке СД
использована формула (2.21).
Знак » — «, полученный при вычислении 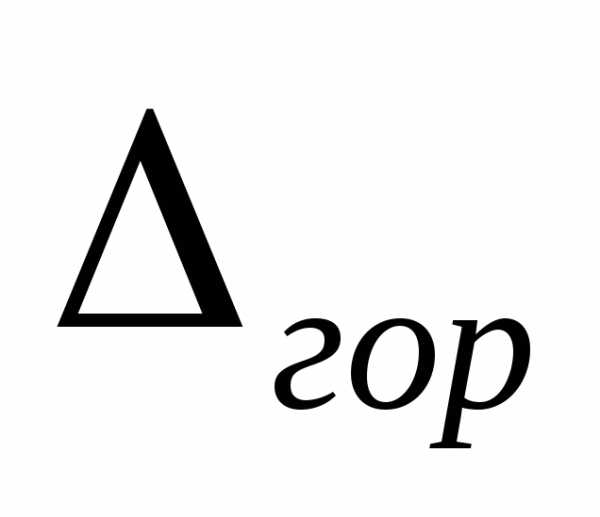 ,
означает, что точка А перемещается по
горизонтали не влево (в этом направлении
приложена сила
,
означает, что точка А перемещается по
горизонтали не влево (в этом направлении
приложена сила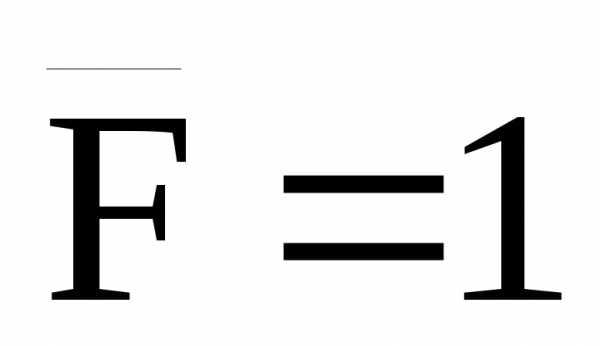 ),
а вправо.
),
а вправо.
Вертикальное перемещение точки А:
Здесь знак » — » означает, что точка А перемещается вниз, а не вверх.
Отметим, что единичные эпюры моментов,
построенные от силы 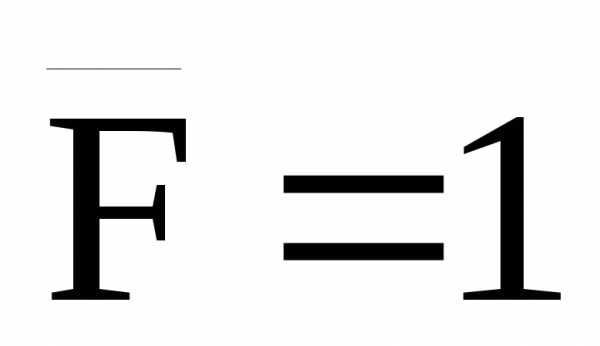 ,
имеют размерность длины, а единичные
эпюры моментов построенные от момента
,
имеют размерность длины, а единичные
эпюры моментов построенные от момента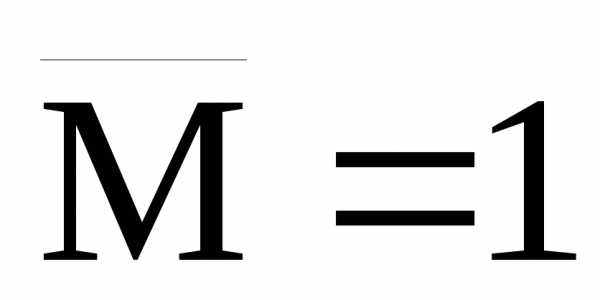 ,
являются безразмерными.
,
являются безразмерными.
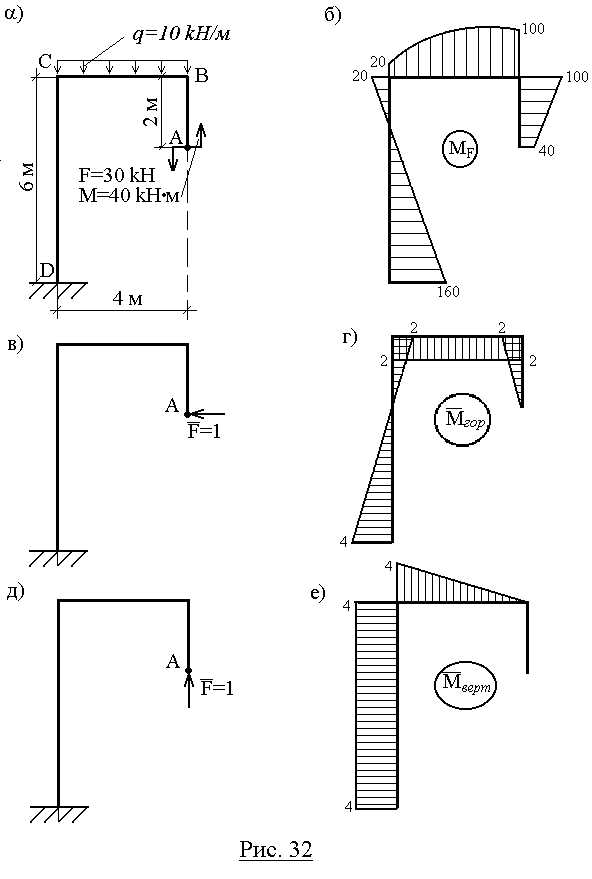
Рис.32
Пример 17.Определить вертикальное перемещение точки А плоско-пространственной системы (рис.33,а).
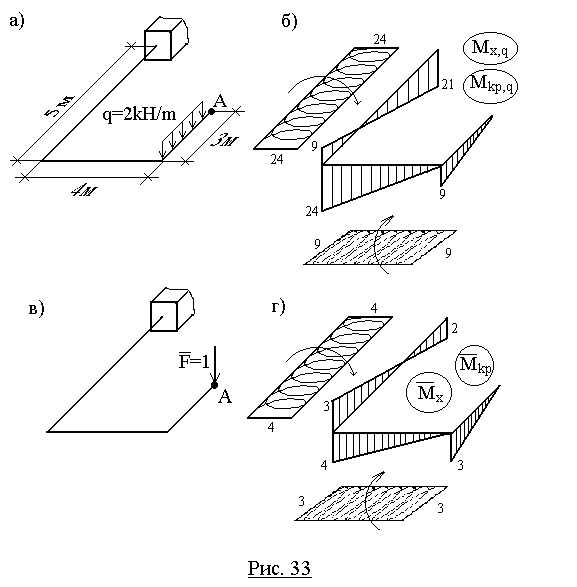
Рис.23
Как известно (см. гл.1), в поперечных сечениях стержней плоско-пространственной системы возникают три внутренних силовых фактора: поперечная сила Qy, изгибающий момент Mxи крутящий момент Mкр. Так как влияние поперечной силы на величину перемещения незначительно (см. пример 14, рис.27), то при вычислении перемещения методом Мора и Верещагина из шести слагаемых остаются только два.
Для решения задачи построим эпюры
изгибающих моментов Mx,qи крутящих
моментов Мкр,qот внешней нагрузки
(рис.33,б), а затем в точке А приложим силу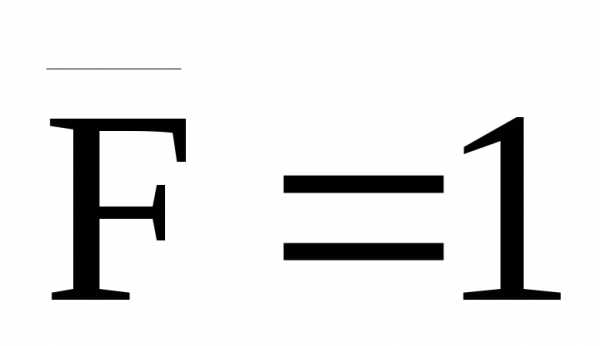 по направлению искомого перемещения,
т.е. вертикального (рис.33,в), и построим
единичные эпюры изгибающих моментов
по направлению искомого перемещения,
т.е. вертикального (рис.33,в), и построим
единичные эпюры изгибающих моментов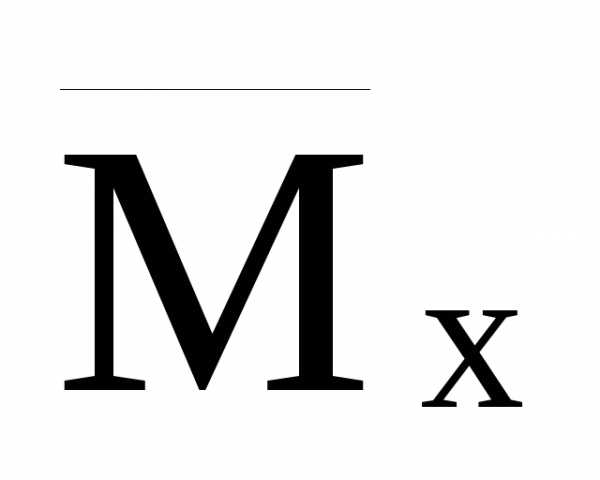 и крутящих моментов
и крутящих моментов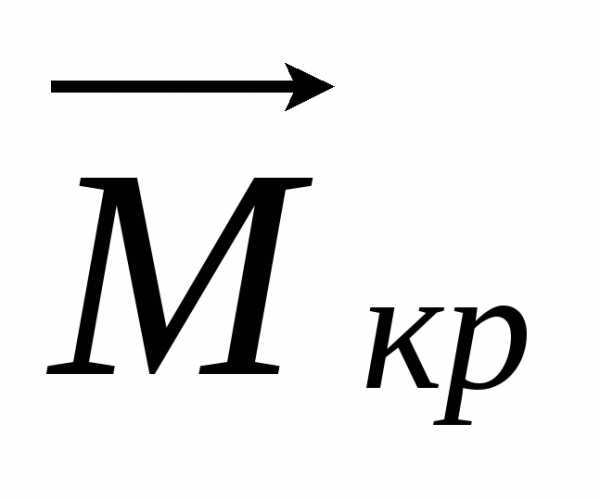 (рис.33,г).
Стрелками на эпюрах крутящих моментов
показаны направления закручивания
соответствующих участков
плоско-пространственной системы.
(рис.33,г).
Стрелками на эпюрах крутящих моментов
показаны направления закручивания
соответствующих участков
плоско-пространственной системы.
Вертикальное перемещение точки А:
При перемножении эпюр крутящих моментов произведение берется со знаком «+», если стрелки, указывающие направление кручения, сонаправленны, и со знаком » — » – в противном случае.
studfiles.net