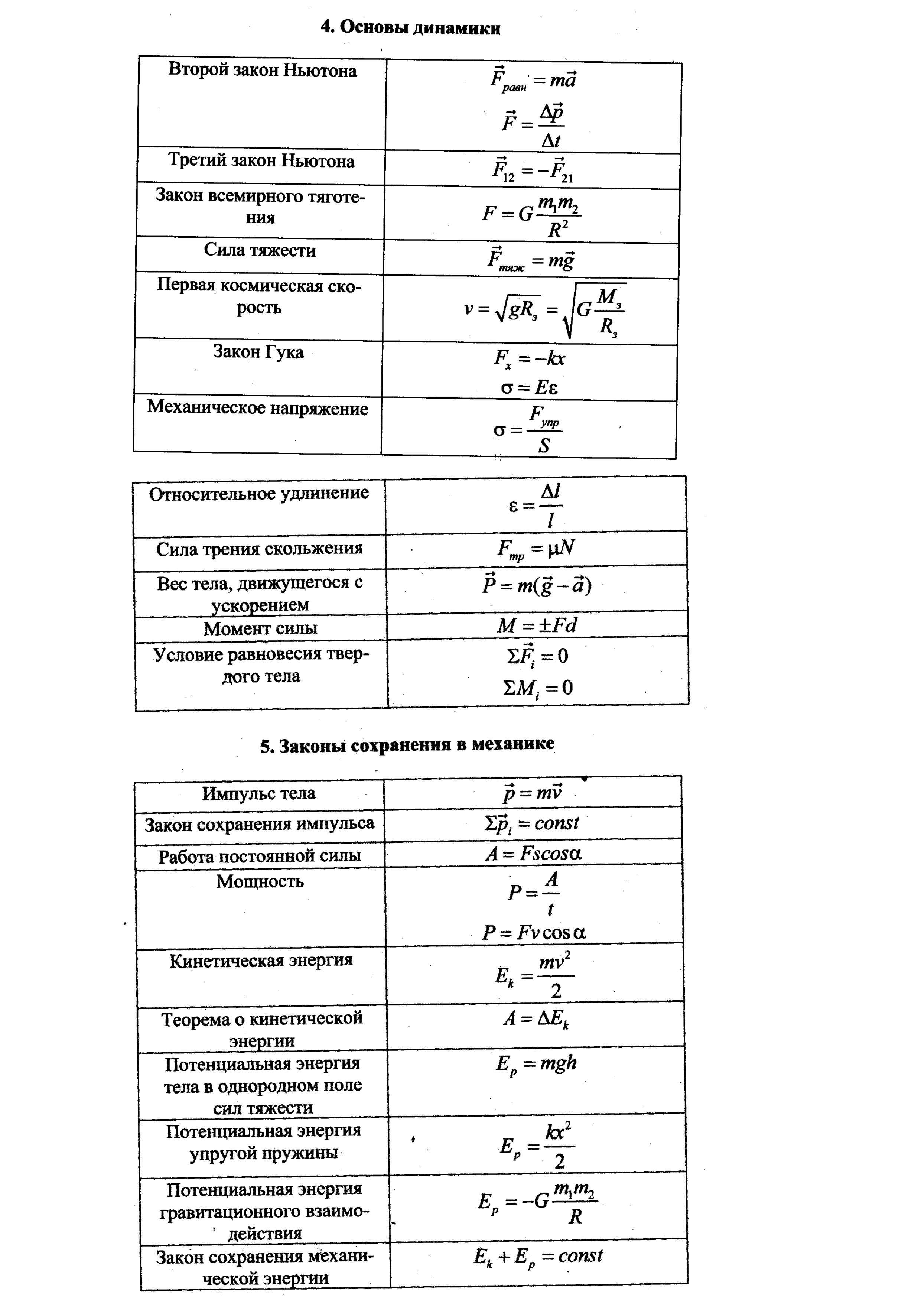
Основные формулы по всем разделам физики

Шпаргалка

• формат jpg
• размер 149.22 КБ
• добавлен 14 января 2011 г.

Здесь представлены самые основные формулы, которые могут понадобиться студенту при сдачи экзамена по физике. Разделы: кинематика, динамика, электростатика, квантовая физика, ядерная физика и другие.
Один этот самый лист.

Похожие разделы

1. Абитуриентам и школьникам
2. ВНО / ЗНО
3. ЗНО по физике

1. Абитуриентам и школьникам
2. ЕГЭ
3. ЕГЭ по физике

1. Абитуриентам и школьникам
2. ОГЭ / ГИА / ДПА
3. ОГЭ / ГИА / ДПА по физике

1. Абитуриентам и школьникам
2. Физика

1. Академическая и специальная литература
2. Механика
3. Механика жидкостей и газов

1. Академическая и специальная литература
2. Педагогика
3. Методики преподавания
4. Методика преподавания физики

1. Академическая и специальная литература
2. Радиоэлектроника
3. Антенная и СВЧ техника
4. Электромагнитные поля и волны

1. Академическая и специальная литература
2. Радиоэлектроника
3. Радиофизика

1. Учебные планы, программы и нормативная документация
2. Для средней школы
3. Физика

1. Учебные планы, программы и нормативная документация
2. Физика

Смотрите также

Шпаргалка

• формат pdf
• размер 1. 58 МБ
• добавлен 21 января 2012 г.

М.: РИОР, 2009. — 32 с. В шпаргалке приведены все основные формулы и определения по физике. Рекомендуется всем изучающим и сдающим физику в школах, средних и высших учебных заведениях.

Билеты и вопросы

• формат docx
• размер 207.3 КБ
• добавлен 22 июня 2011 г.

Страниц101, билетов 47, включает в себя вопросы по квантовому, термодинамическому, механическому разделам физики, примеры решения задач, базовые формулы,

Билеты и вопросы

• формат jpg
• размер 6. 22 МБ
• добавлен 13 марта 2009 г.

Файл содержит 10 билетов за 3 семестр по физики. Билет включает в себя тестовые вопросы по следующим разделам физики: квантовая природа излучения; элементы квантовой физики атомов, молекул и твердых тел; элементы физики атмного ядра и элементарных частиц; 2009 годrn

• формат doc
• размер 127.5 КБ
• добавлен 20 июня 2010 г.

Для всех учебных заведений, содержит оптику, статику, электродинамику, и другие разделы физики в 8 страницах, отличная помощница на экзамене, сделана лично мной, в свое время мне очень помогла.

• формат pdf
• размер 1.95 МБ
• добавлен 06 октября 2011 г.

На 10 страницах приведены всё основные формулы по физике. Может пригодиться студенту при подготовке к экзамену, контрольной работе или просто для освежения памяти по следующим разделам: Кинематика. Динамика. Законы сохранения. Работа и мощность. Статика и гидростатика. Тепловые явления. Электростатика. Постоянный ток. Магнитные явления. Колебания и волны. Оптика.

Шпаргалка

• формат doc
• размер 136.87 КБ
• добавлен 24 января 2009 г.

Формулы по курсу физики: Механике, молекулярной физике и термодинамике, электричеству и магнетизму, колебаниям и волнам, оптике, квантовой природе излучения, элементам квантовой физики атомов, молекул и твёрдых тел, элементам физики атомного ядра и элементарных частиц.

• формат doc
• размер 25.36 КБ
• добавлен 14 июня 2009 г.

Основные формулы на 7 небольших листках(5х8) (от кинематики и динамики до квантовой физики). Формат:rar-doc- 25 Кб содержит формулы по следующим разделам. Кинематика. Динамика. Законы сохранения энергии. Механика жидкостей. Основы МКТ. Термодинамика. Колебания и волны. Электростатика. и др.

Шпаргалка

• формат gif
• размер 1.03 МБ
• добавлен 07 августа 2010 г.

6 изображений, готовых к печати. Распечатать и вырезать готовые странички. Шпоры содержат формулы и основные понятия по всему курсу физики. Оглавление: Кинематика Вращательное движение Динамика Жидкости и газы Закон Гука Основы термодинамики Основы М. К. Т. Тепловое расширение Поверхностное натяжение Законы идеальных газов Тепловые двигатели Влажность Мех. колебания и волны Электростатика Постоянный электр. ток Электромагнетизм Оптика, атомная…

• формат doc
• размер 27.87 КБ
• добавлен 25 мая 2009 г.

Содержит формулы курса физики. Содержание: Механика. Молекулярная физика. Электричество. Колебания и волны.

Шпаргалка

• формат doc
• размер 194.92 КБ
• добавлен 31 января 2009 г.

Весь теоретический материал по всем разделам физики и формулы. Например, Механика — кинематика. Молекулярная физика. — Тепловые явления. Механическое движение механическим движением называется изменение положения тела (в пространстве) относительно других тел (с течением времени).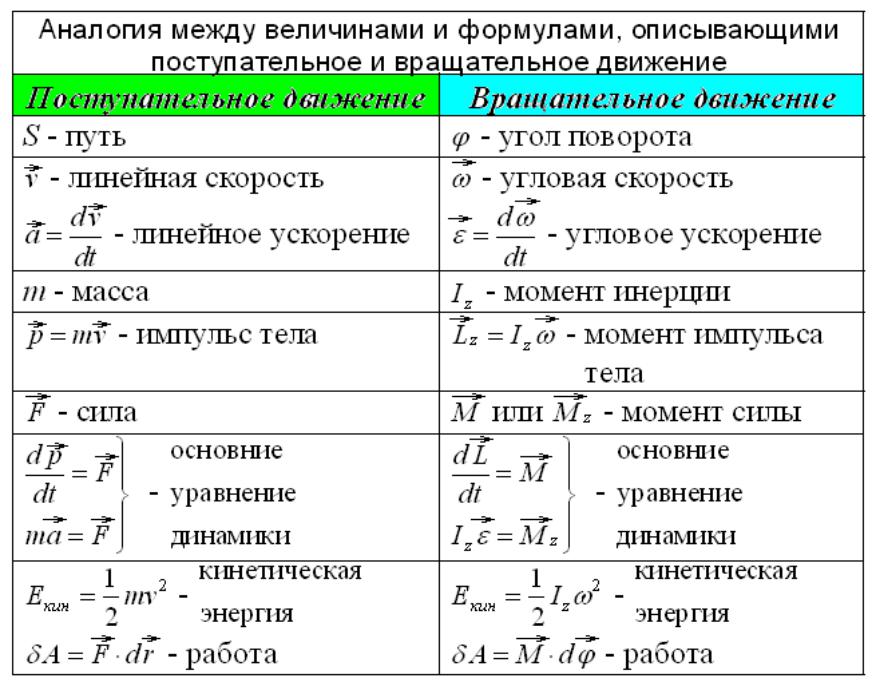

Относительность движения.

50 основных формул по физике с пояснением

Оглавление

Время чтения:  6 минут

2 535

Основа изучения физики, заключается в изучении основных ее законов, формул, определений. В данном материале, мы подробно разберем основные разделы физики и ее формулы.

Основные формулы по электрике, подразделяются на следующие категории:

Формулы электрического тока

Электромагнитная индукция

Возникновение электрического тока, поля, поляризации. Изменение магнитного поля во времени или при движении в магнитном поле.

Ток индукции — процесс, вызванный электродвижущей силой. Основоположником является Майкл Фарадей. Величина индукции не зависит от изменения потока или самого магнитного поля.

Формулы:

Электромагнитные колебания/ Характеризуются изменениями напряжения в индукции магнитного поля.

К электромагнитным колебаниям относятся следующие значения:

• микроволны;
• радиоволны;
• рентген лучи и другие.

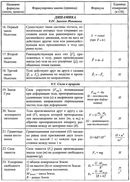
Основные формулы электромагнитных колебаний

Магнитное поле электрического тока

Действует на движущиеся заряды тела, обладающие магнитным полем. Это особенный вид материи, который осуществляет взаимодействие между зарядами или телами, у которых есть свойство магнитного поля.

Постоянный электрический ток

Данный ток не изменяется, даже если меняет свое значение время и направление движения. Для тока характерны, наиболее известные законы физики: закон Ома, Джоуля-Ленца.

Электрические заряды можно наблюдать в:

• металах, а именно частицах свободных электронов;
• ионы, катионы в электролите;
• в различных газах в виде катионов;
• в вакуумной системе;
• полупроводники.

Электростатика

Возникает вследствие взаимодействия электрических частиц с друг другом. Все электростатические вычисления в основном отталкиваются, от закона Кулона.

Примером электростатики является: притяжение воздушного шара к шерсти или бумаги в принтере друг к другу.

Основные формулы раздела механики

Кинематика прямолинейного движения

Движение, при котором материальная точка за одинаковое время, совершает равное количество оборотов. Когда скорость материальной точки непостоянна, то в промежутки времени она изменяется на одну и туже величину.  

Формулы:

Кинематика криволинейного движения

Направление скорости при данном движении всегда направлено по касательной, относительно траектории движения. Криволинейное движение, сумма прямолинейного движения и по окружностям различных радиусов. Изменение наблюдается и по направлению и величине значения.

Динамика

Основные причины изменения механического движения, являются основой изучения динамики. Данный раздел механики тесно связан с кинематикой и постоянно в решении задач с ней взаимодействует.

Статика

Статика занимается понятием нагрузки на тело, которое создают иные тела и момента силы. Решение задач по статике, выражается построением эпюр.

Гидростатика

Данному разделу, характерно изучение характеристик, связанных с понятием жидкости. Закон Паскаля, Архимеда, являются основой гидростатики.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Формулы для определения: работы, энергии, мощности

Основные формулы термодинамики и молекулярной физики

Колебания и волны в физике

Раздел физики, занимающийся физическими явлениями. Которым характерны циклическим изменением величин в пространстве. Движение и состояние системы, повторяются во времени.

Основные формулы молекулярной физики

Данный раздел, согласно названию, изучает все что тесно связано с молекулярным строением тел.  Для молекулярной физики характерно определение, как молярная масса.

Основные формулы термодинамики

Главным определение этого раздела, является понятие температуры и свойства, которые с ней связаны.

Основные формулы оптической физики

Основное определение для оптической — это свет. Все его основные свойства и характеристики. Его взаимодействие с различными веществами. Создание инструментов, для его использования.

Основные формулы элементов теории относительности

Теория, которая изучает пространственно-временные характеристики для физических, и не только, тел. Основателем считается, ученый Альберт Эйнштейн.

Основные формулы световых квантов

Заучить все перечисленные формулы, будет довольно непросто. Однако, изучить и запомнить основные из них, нужно обязательно. Большинство формул, выражаются одна с одной и если рассмотреть их внимательно, то можно без труда это понять.

Без простых основ, изучать физику, невозможно, потому что практически все разделы, так или иначе между собой взаимосвязаны.

Уравнение движения — определение, вывод, примеры и часто задаваемые вопросы

Физика — это отрасль науки, изучающая материю, ее основные составы, движение, поведение в пространстве и времени, а также их отношения с энергией и силой.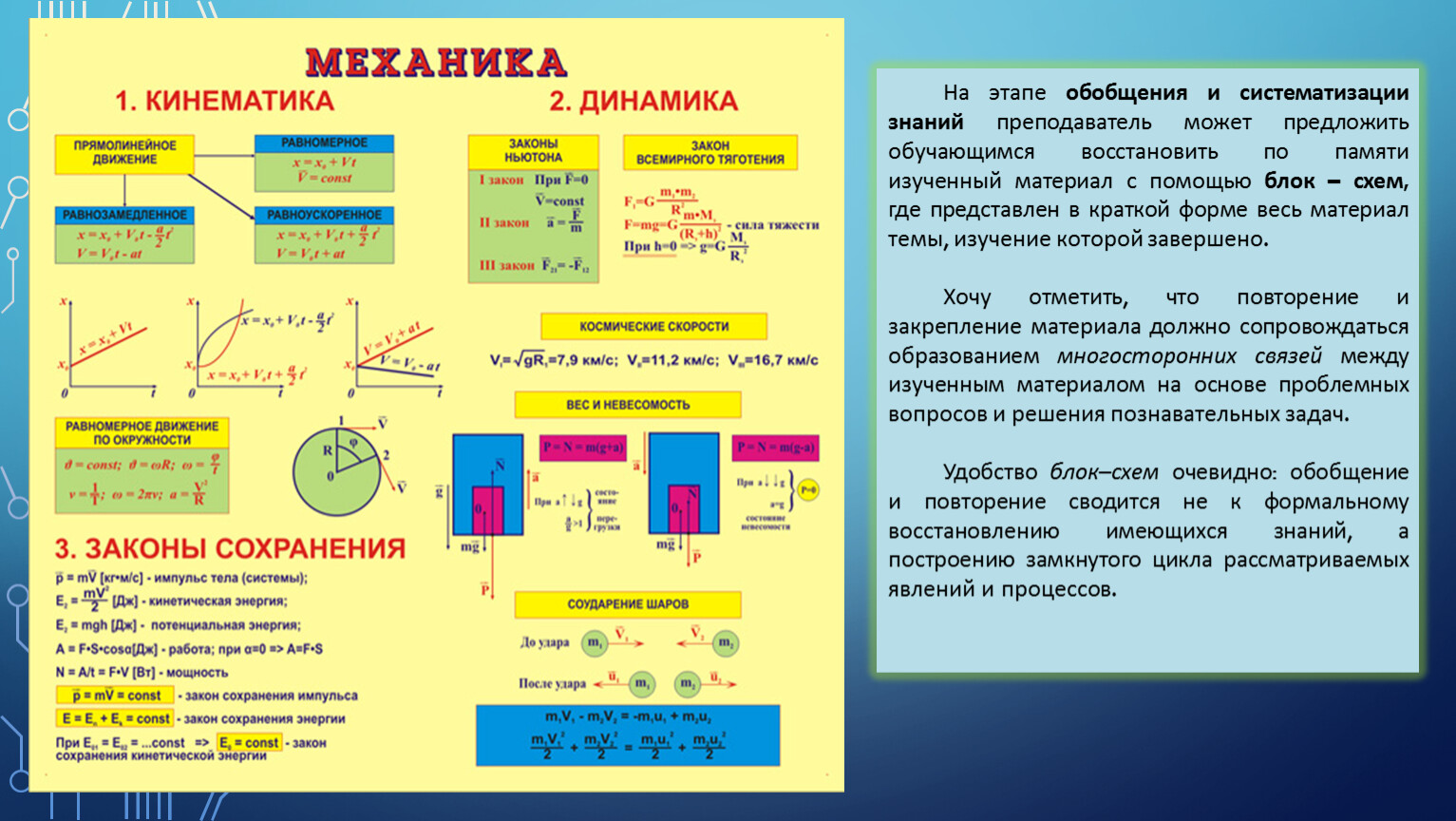 Физика — это огромная область для изучения, поэтому она делится на множество частей в зависимости от области, на которой она сосредоточена. Механика — раздел, изучающий движение тел под действием сил, а также отношения между различными силами, действующими телами друг на друга в системе.

Сэр Исаак Ньютон; который считается отцом механики, был первым, кто дал фундаментальные физические законы, касающиеся объектов и их движения. Он сформулировал три уравнения движения объекта и опубликовал их в своей книге «Philosophiae Naturalis Principia Mathematica», которая считается отправной точкой в ​​истории классической механики.

Уравнения движения

В 1687 году сэр Исаак Ньютон опубликовал свою книгу, и в этой книге он написал о своем понимании движения в физическом мире как о законе движения Ньютона. Эти законы вместе с опубликованными уравнениями дали миру понимание движения объектов, а также их пересечения друг с другом.

Уравнения движения — это математические уравнения, которые объясняют поведение физической системы во времени. Они используются для описания движения объектов и систем в терминах динамических переменных. Проще говоря, уравнения движения используют математические функции для описания поведения физической системы.

Сэр Исаак Ньютон дал три уравнения движения. Эти уравнения широко известны как первое, второе и третье уравнения движения, и они подробно описаны ниже.

Первое уравнение движения

Первое уравнение движения; которое обеспечивает связь между начальной и конечной скоростью, временем и ускорением, выглядит следующим образом:

 

Второе уравнение движения

Второе уравнение движения;

 

Третье уравнение движения

Третье уравнение движения; которая обеспечивает связь между начальной и конечной скоростью, ускорением и перемещением, выглядит следующим образом:

 

В приведенных выше уравнениях v — конечная скорость (единица измерения — метр в секунду), u — начальная скорость (единица измерения — метр в секунду), a — ускорение (единица измерения — метр в секунду ² ), s — смещение (единицы-метры), t — время (единицы-секунды).

Вывод уравнения движения

Мы можем вывести уравнение движения, используя три следующих метода:

• Графический метод
• Алгебраический метод
• Расчетный метод

Вывод первого уравнения движения

Графический метод

90 002  

Так как наклон графика скорость-время представляет собой ускорение.

Наклон графика = AB/BC

Согласно графику

AB = v-u и BC=t

⇒ a =(v-u)/t

⇒ at =v-u

⇒ v = и+ат

Алгебраическим методом

Как мы знаем, ускорение определяется как скорость изменения скорости, поэтому, если скорость изменяется от u до v за время t, то

a = изменение скорости/затраченное время

⇒ a = (v-u)/t

⇒ at = v-u

⇒ v = u+at

Расчетным методом

По определению ускорения оно определяется как скорость изменения в скорости.

Математически это может быть выражено как:

a = dv/dt

Умножение DT с обеих сторон,

⇒ ADT = DV

Интегрируя с обеих сторон, мы получаем (предел DV составляет u -v, а предел DT составляет от 0 до T)

⇒ at = V — V — V u

⇒ v = u + at

Вывод второго уравнения движения

Графическим методом

9000 2  

Площадь под графиком — перемещение тела.

Пройденное расстояние (с) = Площадь OADC = Площадь OADC + Площадь ABD

⇒ s = (AD × BD × 1/2) + (OA × OC)

По графику

OA = u, OC = t, AD = t, BD = v-u × at × 1/2) + ut

⇒ s = ut + at/2

Алгебраическим методом

конечное и начальное положение, и задается произведение средней скорости и затраченного времени

, что может быть математически представлено как s = (u+v)/2×t. . .(и)

Из первого уравнения движения v=u+at

Уравнение (i) становится

s = (u+u+at)/2×t

⇒ s = (2u+at)/2×t

⇒ s = ut+at ² /2 

Расчетным методом

Поскольку скорость известна как скорость изменения смещения, 9000 3

v=ds/dt

Умножить dt на обе стороны,

⇒ ds = vdt

Из первого уравнения движения, подставив v=u+at

ds = (u+at)dt

⇒ ds = udt+atdt

Интегрирование обеих сторон (предел ds от 0 до s и предел dt от 0 до t)

Вывод третьего уравнения движения 9004 9

Графическим методом

 

Площадь под графиком представляет собой перемещение тела.

Площадь под графиком = Площадь трапеции OABC

⇒ s = (1/2) × ((Сумма параллельных сторон) × Высота

⇒ s = 1/2 x (OA + CB) x OC

Из графика

OA = u, CB = v, OC = t

⇒ s = 1/2 x (u + v) x t

Из первого уравнения движения мы знаем, что t = (v – u )/ a

⇒ s = 1/2 x ((u + v) × (v – u))/a

⇒ s = 1/2 x (v + u) × (v – u)/a

⇒ s = (v ² – u ² )/2a

⇒ 2as = v ² – u ²

⇒  v ² = и ² + 2ас

Алгебраическим методом

Поскольку смещение является кратчайшим расстоянием между конечным и начальным положением и определяется произведением средней скорости и затраченного времени

, что может быть математически представлено как s = (u+v)/2 × т . . .(i)

Преобразовывая первое уравнение движения, мы получаем t = (v-u)/a

Подставляя t = (v-u)/a в уравнение (i), получаем

s = (u+v )/2×(v-u)/a

⇒ 2as = (v+u)(v-u)

⇒ 2as = v ² -u ²

⇒ v ² =u ² +2as

Расчетным методом 9 0049

Поскольку скорость известна как скорость изменения смещения,

v =дс/дт . . .(i)

, а ускорение определяется как скорость изменения скорости.

а = dv/dt . . .(ii)

Из (i) и (ii) получаем

a ds/dt = v dv/dt

⇒ a ds = v dv

Интегрируя обе части, получаем( предел ds равен 0 до s, а предел dv — от u до v)

Решенные примеры уравнения движения

Пример 1: Махеш бросает мяч в горизонтальном направлении. Если мяч проходит 60 метров за 4 секунды, они вычисляют ускорение.

Ответ: 

Поскольку тело брошено, это означает, что начальная скорость равна нулю.

⇒ u = 0

Расстояние, пройденное мячом, равно смещению.

⇒ с = 80 метров

Период времени t = 4 с.

Используя уравнение, s = ut + at ² /2

⇒ 80 = 0(4) + a(4) ² /2

⇒ 80 = 8a

⇒ а=10 м/ s ²

Следовательно, ускорение тела после этого равно 10 м/с ² .

Пример 2: Тело движется с постоянным ускорением 10 м/с ² . Если начальная скорость тела 5 м/с, то какой будет его скорость через 2 с?

Ответ:

Ускорение тела 10 м/с ²

⇒ a = 10 м/с ²

Начальная скорость 5 м/с.

⇒  u = 5 м/с

Период времени 2 сек.

⇒ t = 2 с

Используя уравнение, v = u + at

⇒ v = 5 + 10(2)

⇒ v = 5 + 20

⇒ v = 25 м/с

Следовательно, скорость тела через 2 с равна 25 м/с.

Пример 3: Тело движется с постоянным ускорением 10 м/с ² . Чему будет равно его перемещение, если начальная скорость тела 5 м/с, а конечная скорость 105 м/с?

Ответ:

Ускорение тела 10 м/с ² .

⇒ a = 10

Начальная скорость 5 м/с.

⇒ u = 5 м/с

Конечная скорость 105 м/с.

⇒ v = 105 м/с

Используя уравнение, v ² – u ² = 2as

⇒ 105 ² – 5 ² = 2(10)(с)

⇒  с = (11025 – 25)/20

⇒  с = 550 с

Следовательно, период времени равен 550 секунд.

Пример 4. Каково будет перемещение тела, если начальная и конечная скорости равны 20 и 70 м/с соответственно за 5 секунд?

Ответ:

Начальная скорость 20 м/с.

⇒ u = 20 м/с

Конечная скорость 170 м/с.

⇒ v = 70 м/с

Период времени 5 сек.

⇒  t = 5 с

Используя уравнение, s = (1/2) (v + u)t

⇒ s = (0,5) (70 + 20)(5)

⇒ s = 550 метров

Следовательно, перемещение тела равно 550 метрам.

Пример 5: Автомобиль движется со скоростью 50 м/с, когда водитель видит человека, переходящего дорогу, притормаживает, и автомобиль останавливается через 4 секунды. Вычислите расстояние, пройденное автомобилем.

Ответ:

Начальная скорость 50 м/с.

⇒ u = 50 м/с

Конечная скорость равна 0 м/с.

⇒ v = 0 м/с

Период времени составляет 4 секунды.

⇒ t = 4s

Используя уравнение, s = (1/2)(v + u)t

⇒ s = (0,5)(50 + 0)(4)

⇒ s = 100 метров

Следовательно, перемещение тела равно 100 м.

Пример 6: автомобиль замедляется со скоростью 6 м/с ² . Какое расстояние проедет автомобиль, если начальная скорость 20 м/с, а время остановки автомобиля 3 секунды?

Ответ:

Замедление тела равно 6 м/с ²

⇒ a = 6

Начальная скорость 20 м/с.

⇒ u= 20 м/с

Период времени составляет 3 секунды.

⇒ t = 3 с

Используя уравнение, s = ut – at ² /2

⇒ s = 20(3) + 6(3) ² /2

⇒ s = 60+27

⇒ s = 87 м

Следовательно, перемещение тела равно 87 м.

Часто задаваемые вопросы по уравнениям движения

Вопрос 1: Что такое уравнения движения?

Решение:

три уравнения 047 v ² – u ² = 2as

вместе называются уравнениями движения.

Вопрос 2: Что представляет площадь под графиком скорость-время?

Ответ:

Площадь под графиком скорость-время представляет собой ускорение объекта, для которого построен график.

Вопрос 3: Что представляет площадь под графиком перемещение-время?

Ответ:

Площадь под графиком смещения-времени представляет величину смещения объекта, для которого построен график.

Вопрос 4: Что представляет собой наклон графика перемещение-время?

Решение:

Наклон графика перемещение-время представляет собой скорость объекта, для которого построен график.

Вопрос 5: Что представляет собой наклон графика зависимости скорости от времени?

Решение:

Наклон графика зависимости скорости от времени представляет собой ускорение объекта, для которого построен график.

Счет, математика и статистика — Набор академических навыков

Уравнения движения (механика)

ContentsToggle Главное меню 1 Уравнения движения 2 Проверьте себя 3 Внешние ресурсы

Уравнения движения

90 002 Уравнения движения, также известные как уравнения SUVAT, используются, когда ускорение $a$ постоянно. Они известны как уравнения СУВАТ, потому что содержат следующие переменные: $s$ — расстояние, $u$ — начальная скорость, $v$ — скорость в момент времени $t$, $a$ — ускорение и $t$ — время. {-1} }$, когда прекращает ускорение. 9{-1} }$. С какой скоростью он двигался, когда вышел из самолета?

Решение

Из вопроса мы знаем, что \begin{align} s &= ?\\ u &= ?\\ v &= 40\\ a &= 9.8\\ t &= 4.05 \end{align} Мы хотите найти $u$, начальную скорость, из значений, которые у нас есть. Уравнение, которое у нас есть, которое включает $u$, $v$, $a$ и $t$, имеет вид \[v = u + at.\]. Однако его нужно изменить, чтобы сделать $u$ объектом уравнения. Это дает \[u = v — at.\] При подстановке известных нам значений мы получаем \begin{align} u &= v — at,\\ &= 40 — \left(9{-1} }$, каково расстояние в $\mathrm{m}$ от $A$ до $B$?

Решение

Из вопроса мы знаем значения некоторых переменных. Лучше всего записать то, что мы знаем, в виде списка \begin{align} s &= ?\\ u &= 5\\ v &= 10\\ a &= ?\\ t &= 6 \end{align} Из списка значений, которые мы знаем, нам нужно использовать уравнение $s = \left(\frac{u+v}{2}\right)t$, чтобы найти $s$. При подстановке получаем: \begin{align} s& = \left(\frac{u+v}{2}\right)t,\\ &= \left(\frac{5 + 10}{2}\right) \times 6,\\ &=45 \mathrm{m}. \end{align} Расстояние от $A$ до $B$ равно $45 \mathrm{m}$. 9{-1} }. \end{align} Для $t$ имеем \begin{align} \frac{2}{3} \mathrm{minute} & = \frac{2}{3} \times 60\mathrm{s}, \\ & = 40\mathrm{s}. \end{align} Теперь мы можем записать то, что мы знаем, в список \begin{align} s &= ?\\ u &= 0\\ v &= \frac{50}{3} \\ a &= ? \\ t &= 40 \end{align} Обратите внимание, что $u=0$, потому что автомобиль начинает движение в состоянии покоя. Из списка значений, которые мы знаем, нам нужно использовать уравнение $s = \left(\frac{u+v}{2}\right)t$, чтобы найти $s$. При подстановке получаем: \begin{align} s& = \left(\frac{u+v}{2}\right)t,\\ &= \left(\frac{0 + 5/3}{2}\ справа) \times 40,\\ &=\frac{100}{3} \mathrm{m}. \end{align} Расстояние от $A$ до $B$ равно $\frac{100}{3}\mathrm{m}$. 9{-1} }$ при внезапном торможении. Автомобиль проходит $40\mathrm{m}$ при торможении, а затем останавливается. Каково было ускорение автомобиля при торможении?

Решение

Как и в случае с предыдущими вопросами, лучше сначала перечислить, что мы знаем \begin{align} s &= 40\\ u &= 22\\ v &= 0\\ a &= ?\\ t &= ? \end{align} Мы знаем, что конечная скорость должна быть $v=0$, так как в вопросе говорится, что машина останавливается.