Движение по окружности. Угол поворота и угловая скорость
Радиан Угловая скорость Линейная скорость Частота и период вращения Движение тела по окружности можно описывать тем же способом, которым пользуются при описании прямолинейного движения. Но часто более удобным оказывается другой способ, с которым мы сейчас ознакомимся.
рис. 1
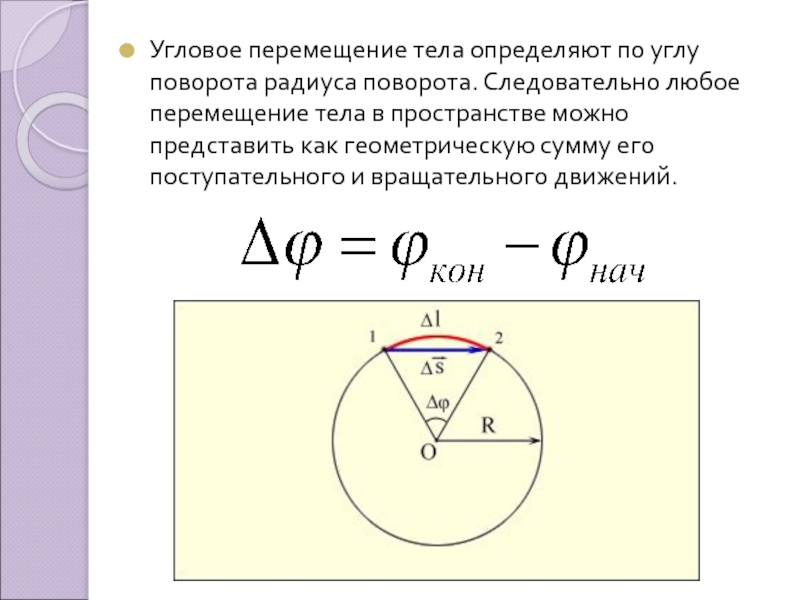
Представим себе, что некоторое тело движется по окружности радиусом $r$ (рис. 1). Проведем из центра $O$ окружности радиус к какой-нибудь точке тела $A$ и будем следить не только за самим телом, но и за радиусом, проведенным к нему. Мы увидим, что, по мере того как тело движется, радиус поворачивается. Если, например, тело за промежуток времени $t$ переместилось из точки $A$ в точку $B$, то за это же время радиус повернулся на угол $\phi$. Этот угол мы будем называть углом поворота радиуса. О движении тела можно, следовательно, сказать, во-первых, что тело за промежуток времени $t$ прошло путь $l$ по дуге $AB$ окружности, во-вторых, что оно совершило перемещение $\vec{s}$, модуль которого равен длине хорды $AB$, и, в-третьих, что радиус, проведенный к телу, совершил поворот на угол $\phi$.
По какой бы окружности ни двигалось тело, при равных углах поворота радиуса равны и отношения длины дуги к радиусу. Поэтому и сами углы можно измерять величиной этого отношения
$\phi = \frac{l}{r}$.
При таком измерении углов за единицу измерения угла удобно принять не градус, а угол, соответствующий дуге, длина которой $l$ равна радиусу $r$, потому что тогда угол $\phi$ будет равен единице. Такая единица измерения угла сейчас общепринята в науке, и называют ее радианом (сокращенно рад).
Радиан — это угол между двумя радиусами круга, вырезающий на окружности дугу, длина которой равна радиусу.
Легко установить связь между градусом и радианом.Когда тело (или точка) совершит один полный оборот по окружности радиусом $r$, то длина пройденной дуги будет равна $2 \pi r$. Поэтому величина угла в радианах равна:
$\phi = \frac{2 \pi r}{r} = 2 \pi рад \approx 6,28 рад$.
Следовательно, один оборот — это поворот радиуса на угол в $2 \pi$ рад.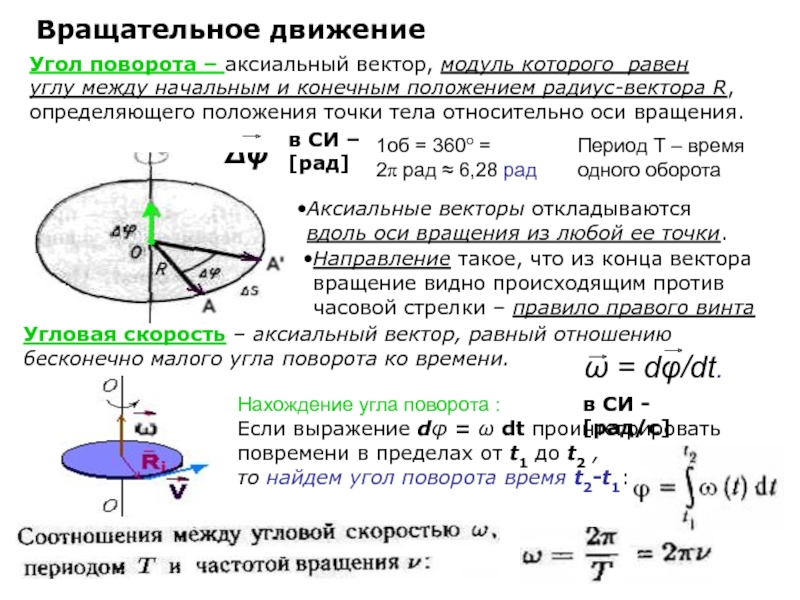 { \prime}$.
{ \prime}$.
Таким образом, длина дуги, пройденной телом, и угол поворота радиуса, проведенного к нему, связаны формулой
$l = r \phi$.
Скорость равномерного движения тела по окружности тоже можно выражать в угловых единицах. Для этого используют понятие угловой скорости.
Под угловой скоростью мы будем понимать отношение угла поворота радиуса, проведенного к телу, к промежутку времени, в течение которого совершен этот поворот.
Угловую скорость обозначают греческой буквой $\omega$ (омега), так что$\omega = \frac{ \phi }{t}$.
Так как здесь угол $\phi$ выражен в радианах, а время $t$ в секундах, та угловая скорость $\omega$ измеряется в радианах в секунду (рад/сек).
В отличие от угловой скорости скорость $v$, измеряемую отношением длины пути $l$ ко времени $t$ и выражаемую в метрах в секунду, называют линейной скоростью. Между угловой скоростью $\omega$ и линейной скоростью $v$ очень простая связь. Если в выражение для угловой скорости подставить вместо $\phi$ его значение $\frac{l}{r}$, то мы получим: $\omega = \frac{l}{rt}$,
Так как в свою очередь $l = vt$, то $\omega = \frac{v}{r}$, или $v = \omega r$.
Линейная скорость точки равна произведению угловой скорости на радиус окружности, по которой происходит движение.
Скорость движения тела по окружности часто выражают также числом оборотов в единицу времени. Легко связать угловую скорость с числом оборотов е единицу Бремени. Действительно, при одном обороте радиус поворачивается на угол в $2 \pi$ рад. Значит, совершив в единицу времени, например, $n$ оборотов, радиус повернется на угол $2 \pi n$ рад. Поэтому угловая скорость $\omega$ и число оборотов е единицу времени $n$ связаны выражением$\omega = 2 \pi n$.
Число оборотов в единицу времени ($n$) обычно называют также частотой вращения. Величина, обратная частоте, определяет время, за которое тело делает один оборот. Это время называют периодом вращения и обозначают буквой $T$:
$T = \frac{1}{n} = \frac{2 \pi }{ \omega }$.Физика. 8 класс
Физика. 8 класс
ОглавлениеГлава 1. Общие сведения о движении§ 1. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ. МАТЕРИАЛЬНАЯ ТОЧКА § 2. ПОЛОЖЕНИЕ ТОЧКИ (ТЕЛА) В ПРОСТРАНСТВЕ § 3. ПЕРЕМЕЩЕНИЕ § 4. ПОНЯТИЕ О ВЕКТОРАХ. ВЕКТОР ПЕРЕМЕЩЕНИЯ. КООРДИНАТЫ ТЕЛА § 5. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: СЛОЖЕНИЕ ВЕКТОРОВ § 6. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: ВЫЧИТАНИЕ ВЕКТОРОВ § 7. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР § 8. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ § 9.  ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДВИЖЕНИЯ ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДВИЖЕНИЯ§ 10. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ § 11. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ (ПРОДОЛЖЕНИЕ) § 12. ЕДИНИЦЫ ИЗМЕРЕНИЙ ДЛИНЫ И ВРЕМЕНИ Глава 2. Прямолинейное неравномерное движение § 13. СРЕДНЯЯ СКОРОСТЬ § 14. МГНОВЕННАЯ СКОРОСТЬ § 15. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ § 16. НАПРАВЛЕНИЕ УСКОРЕНИЯ § 17. ПЕРЕМЕЩЕНИЕ ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ § 18. СРЕДНЯЯ СКОРОСТЬ ПРИ ПРЯМОЛИНЕЙНОМ РАВНОУСКОРЕННОМ ДВИЖЕНИИ. СВЯЗЬ МЕЖДУ ПЕРЕМЕЩЕНИЕМ И СКОРОСТЬЮ § 19. ИЗМЕРЕНИЕ УСКОРЕНИЯ § 20. СВОБОДНОЕ ПАДЕНИЕ ТЕЛ § 21. ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ Глава 3. Криволинейное движение § 22. ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ § 23. УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ § 24. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГОЛ ПОВОРОТА И УГЛОВАЯ СКОРОСТЬ § 26. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА § 27. ОБ ОТНОСИТЕЛЬНОСТИ ДВИЖЕНИЯ ТЕЛА ПРИ ВРАЩЕНИИ СИСТЕМЫ ОТСЧЕТА Динамика Глава 4.  Законы движения Законы движения§ 28. ТЕЛА И ИХ ОКРУЖЕНИЕ. ПЕРВЫЙ ЗАКОН НЬЮТОНА § 29. ПОЧЕМУ ВОЗНИКАЮТ УСКОРЕНИЯ § 30. ВЗАИМОДЕЙСТВИЕ TEЛ. УСКОРЕНИЯ ТЕЛ ПРИ ИХ ВЗАИМОДЕЙСТВИИ § 31. ИНЕРТНОСТЬ ТЕЛ § 32. МАССА ТЕЛ § 33. МАССА ЛУНЫ § 34. СИЛА § 35. ВТОРОЙ ЗАКОН НЬЮТОНА § 36. ВТОРОЙ ЗАКОН НЬЮТОНА (продолжение) § 37. ИЗМЕРЕНИЕ СИЛ. ДИНАМОМЕТР § 38. ТРЕТИЙ ЗАКОН НЬЮТОНА § 39. ЗНАЧЕНИЕ ЗАКОНОВ НЬЮТОНА Глава 5. Силы природы § 40. ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ § 41. СИЛА УПРУГОСТИ § 42. СИЛА ВСЕМИРНОГО ТЯГОТЕНИЯ § 43. ПОСТОЯННАЯ ВСЕМИРНОГО ТЯГОТЕНИЯ § 44. СИЛА ТЯЖЕСТИ § 45. ВЕС ТЕЛ § 46. ИЗМЕРЕНИЕ МАССЫ ТЕЛ ВЗВЕШИВАНИЕМ § 47. МАССА ЗЕМЛИ § 48. СИЛА ТРЕНИЯ. ТРЕНИЕ ПОКОЯ § 49. СИЛА ТРЕНИЯ СКОЛЬЖЕНИЯ § 50. СИЛА СОПРОТИВЛЕНИЯ, ВОЗНИКАЮЩАЯ ПРИ ДВИЖЕНИИ ТЕЛА В ЖИДКОСТИ ИЛИ В ГАЗЕ Глава 6. Применение законов движения § 51. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ УПРУГОСТИ § 52. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: НАЧАЛЬНАЯ СКОРОСТЬ ТЕЛА РАВНА НУЛЮ ИЛИ ПАРАЛЛЕЛЬНА СИЛЕ ТЯЖЕСТИ § 53.  ВЕС ТЕЛА, ДВИЖУЩЕГОСЯ С УСКОРЕНИЕМ ВЕС ТЕЛА, ДВИЖУЩЕГОСЯ С УСКОРЕНИЕМ§ 54. НЕВЕСОМОСТЬ § 55. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ПОД УГЛОМ К ГОРИЗОНТУ § 56. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ГОРИЗОНТАЛЬНО § 57. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ПЕРВАЯ КОСМИЧЕСКАЯ СКОРОСТЬ § 58. ДВИЖЕНИЕ ПЛАНЕТ § 59. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ ТРЕНИЯ § 60. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ НЕСКОЛЬКИХ СИЛ § 61. ПАДЕНИЕ ТЕЛА В ГАЗЕ ИЛИ В ЖИДКОСТИ § 62. НАКЛОН ТЕЛ ПРИ ДВИЖЕНИИ НА ПОВОРОТАХ § 64. ВСЕГДА ЛИ ВЕРНЫ ЗАКОНЫ МЕХАНИКИ НЬЮТОНА Равновесие тел Глава 7. Элементы статики § 65. РАВНОВЕСИЕ ТЕЛ ПРИ ОТСУТСТВИИ ВРАЩЕНИЯ § 66. РАВНОВЕСИЕ ТЕЛА С ЗАКРЕПЛЕННОЙ ОСЬЮ. МОМЕНТ СИЛЫ § 67. ПРАВИЛО МОМЕНТОВ § 68. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ § 69. РАВНОВЕСИЕ ТЕЛ НА ОПОРАХ Законы сохранения в механике Глава 8. Закон сохранения импульса § 70.  СИЛА И ИМПУЛЬС СИЛА И ИМПУЛЬС§ 71. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА § 72. РЕАКТИВНОЕ ДВИЖЕНИЕ Глава 9. Механическая работа и мощность § 74. ПОЧЕМУ РАБОТА ОПРЕДЕЛЯЕТСЯ КАК ПРОИЗВЕДЕНИЕ § 75. БОЛЕЕ ОБЩЕЕ ОПРЕДЕЛЕНИЕ РАБОТЫ § 76. РАБОТА, СОВЕРШАЕМАЯ СИЛАМИ, РАВНОДЕЙСТВУЮЩАЯ КОТОРЫХ НЕ РАВНА НУЛЮ. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ § 77. РАБОТА СИЛЫ ТЯЖЕСТИ § 78. РАБОТА СИЛЫ УПРУГОСТИ § 79. РАБОТА СИЛЫ ТРЕНИЯ § 80. МОЩНОСТЬ Глава 10. Закон сохранения энергии § 82. РАБОТА ТЕЛА И ИЗМЕНЕНИЕ ЕГО СОСТОЯНИЯ. ПОНЯТИЕ ОБ ЭНЕРГИИ § 83. ПОТЕНЦИАЛЬНАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ § 84. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГО ДЕФОРМИРОВАННОГО ТЕЛА § 85. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ТЕЛА, НАХОДЯЩЕГОСЯ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ § 36. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ § 87. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ § 88. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И СИЛА ТРЕНИЯ § 89. ПРЕВРАЩЕНИЕ ЭНЕРГИИ И ИСПОЛЬЗОВАНИЕ МАШИН § 90. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ § 91. СТОЛКНОВЕНИЕ ТЕЛ § 92. ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ.  ЗАКОН БЕРНУЛЛИ ЗАКОН БЕРНУЛЛИ§ 93. О ЗНАЧЕНИИ ЗАКОНОВ СОХРАНЕНИЯ Заключение Лабораторные работы 1. Определение ускорения тела при равноускоренном движении 2. Определение коэффициента трения скольжения 3. Изучение движения тела по параболе 5. Определение центра тяжести плоской пластины Ответы к упражнениям |
6.1 Угол поворота и угловая скорость – Физика
Раздел Цели обучения
К концу этого раздела вы сможете делать следующее:
- Описывать угол поворота и связывать его с его линейным аналогом
- Опишите угловую скорость и свяжите ее с ее линейным эквивалентом
- Решение задач на угол поворота и угловую скорость
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:
- (4) Научные концепции.
 Учащийся знает и применяет законы, управляющие движением, в различных ситуациях. Ожидается, что студент:
Учащийся знает и применяет законы, управляющие движением, в различных ситуациях. Ожидается, что студент:- (C) анализировать и описывать ускоренное движение в двух измерениях, используя уравнения, включая примеры снарядов и кругов.
Основные термины раздела
| Градусы | Радианные меры |
|---|---|
| 30∘30∘ | π6π6 |
| 60∘60∘ | π3π3 |
| 90∘90∘ | π2π2 |
| 120∘120∘ | 2π32π3 |
| 135∘135∘ | 3π43π4 |
| 180∘180∘ | ππ |
Стол 6.1 Обычно используемые углы в градусах и радианах
Угловая скорость
Поддержка учителей
Поддержка учителей
[BL] Просмотр перемещения, скорости, скорости, ускорения.
[AL] Спросите учащихся, изменяется ли скорость при равномерном круговом движении. А как насчет скорости? А ускорение?
Как быстро вращается объект? Мы можем ответить на этот вопрос, используя понятие угловой скорости. Сначала рассмотрим угловую скорость (ω)(ω) — скорость изменения угла поворота. В форме уравнения угловая скорость равна
ω=ΔθΔt,ω=ΔθΔt,6,2
, что означает, что угловой поворот (Δθ)(Δθ) происходит за время ΔtΔt. Если объект поворачивается на больший угол поворота за заданное время, он имеет большую угловую скорость. Единицами угловой скорости являются радианы в секунду (рад/с).
Теперь давайте рассмотрим направление угловой скорости, а значит мы теперь должны называть его угловой скоростью. Направление угловой скорости вдоль оси вращения. Для объекта, вращающегося по часовой стрелке, угловая скорость направлена от вас вдоль оси вращения. Для объекта, вращающегося против часовой стрелки, угловая скорость указывает на вас вдоль оси вращения.
Угловая скорость (ω) представляет собой угловую версию линейной скорости v . Тангенциальная скорость – это мгновенная линейная скорость объекта, находящегося во вращательном движении . Чтобы получить точное соотношение между угловой скоростью и тангенциальной скоростью, снова рассмотрим ямку на вращающемся компакт-диске. Эта яма движется по дуге (Δs)(Δs) за короткое время (Δt)(Δt), поэтому ее тангенциальная скорость равна
v=ΔsΔt.v=ΔsΔt.6.3
Из определения угла поворота Δθ=ΔsrΔθ=Δsr видно, что Δs=rΔθΔs=rΔθ . Подставляя это в выражение для v , получаем
v=rΔθΔt=rω.v=rΔθΔt=rω.
Уравнение v=rωv=rω говорит, что тангенциальная скорость v пропорциональна расстоянию r от центра вращения. Следовательно, тангенциальная скорость больше для точки на внешнем краю компакт-диска (с большими r ), чем для точки ближе к центру компакт-диска (с меньшими r ). Это имеет смысл, потому что точка, расположенная дальше от центра, должна пройти большую длину дуги за то же время, что и точка, расположенная ближе к центру. Обратите внимание, что обе точки по-прежнему будут иметь одинаковую угловую скорость, независимо от их расстояния от центра вращения. См. рисунок 6.4.
Это имеет смысл, потому что точка, расположенная дальше от центра, должна пройти большую длину дуги за то же время, что и точка, расположенная ближе к центру. Обратите внимание, что обе точки по-прежнему будут иметь одинаковую угловую скорость, независимо от их расстояния от центра вращения. См. рисунок 6.4.
Рисунок 6.4 Точки 1 и 2 поворачиваются на один и тот же угол (ΔθΔθ), но точка 2 перемещается на большую длину дуги (Δs2Δs2), поскольку она находится дальше от центра вращения.
Поддержка учителей
Поддержка учителей
[AL] Объясните, что период времени ΔtΔt в уравнении, определяющем тангенциальную скорость ( v=ΔsΔtv=ΔsΔt ), должен быть коротким, чтобы дугу, описываемую движущимся объектом, можно было аппроксимировать прямой линией. Это позволяет нам определить направление тангенциальной скорости как касательное к окружности. Это приближение становится все более точным по мере того, как ΔtΔt становится все меньше.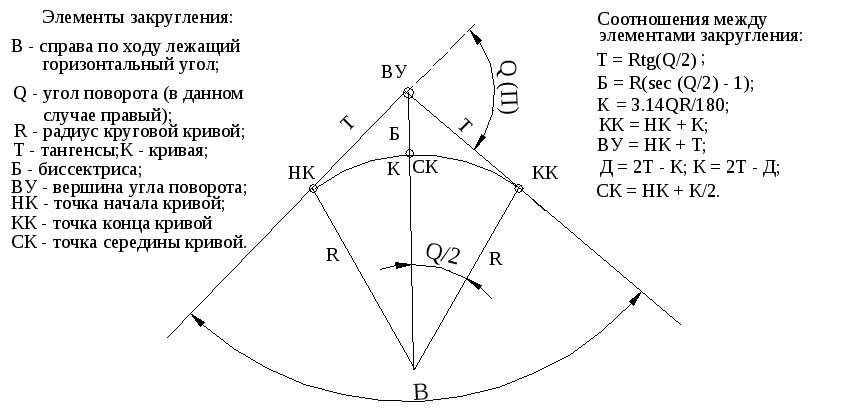
Теперь рассмотрим другой пример: шина движущегося автомобиля (см. рис. 6.5). Чем быстрее вращается шина, тем быстрее движется автомобиль — большое ωω означает большое против , потому что v=rωv=rω. Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью ωω, создаст для автомобиля большую линейную (тангенциальную) скорость v, . Это связано с тем, что больший радиус означает, что более длинная дуга должна касаться дороги, поэтому автомобиль должен двигаться дальше за то же время.
Рисунок
6,5
Автомобиль, движущийся со скоростью v, вправо, имеет шину, вращающуюся с угловой скоростью ωω. Скорость протектора шины относительно оси составляет v , такая же, как если бы автомобиль был поднят на домкрат и колеса крутились, не касаясь дороги. Непосредственно под осью, где шина касается дороги, протектор шины движется назад относительно оси с тангенциальной скоростью v=rωv=rω, где r — радиус шины. Поскольку дорога неподвижна относительно этой точки шины, автомобиль должен двигаться вперед с линейной скоростью против . Большая угловая скорость шины означает большую линейную скорость автомобиля.
Поскольку дорога неподвижна относительно этой точки шины, автомобиль должен двигаться вперед с линейной скоростью против . Большая угловая скорость шины означает большую линейную скорость автомобиля.
Однако бывают случаи, когда линейная скорость и тангенциальная скорость не эквивалентны, например, когда колеса автомобиля крутятся на льду. В этом случае линейная скорость будет меньше тангенциальной скорости. Из-за отсутствия трения под шинами автомобиля по льду длина дуги, по которой перемещаются протекторы шин, больше, чем линейное расстояние, по которому движется автомобиль. Это похоже на бег на беговой дорожке или вращение педалей на велотренажере; вы буквально никуда не денетесь.
Советы для успеха
Угловая скорость ω и тангенциальная скорость v являются векторами, поэтому мы должны указать величину и направление. Направление угловой скорости находится вдоль оси вращения и указывает от вас для объекта, вращающегося по часовой стрелке, и к вам для объекта, вращающегося против часовой стрелки. В математике это описывается правилом правой руки. Тангенциальная скорость обычно описывается как восходящая, нисходящая, левая, правая, северная, южная, восточная или западная, как показано на рис. 6.6.
В математике это описывается правилом правой руки. Тангенциальная скорость обычно описывается как восходящая, нисходящая, левая, правая, северная, южная, восточная или западная, как показано на рис. 6.6.
Рисунок 6,6 Поскольку муха на краю старой виниловой пластинки движется по кругу, ее мгновенная скорость всегда направлена по касательной к кругу. В этом случае направление угловой скорости находится на странице.
Смотреть физику
Связь между угловой скоростью и скоростью
В этом видео рассматриваются определение и единицы измерения угловой скорости, а также их связь с линейной скоростью. Он также показывает, как конвертировать между оборотами и радианами.
Для объекта, движущегося по круговому пути с постоянной угловой скоростью, изменится ли линейная скорость объекта, если радиус пути увеличится?
Да, потому что тангенциальная скорость не зависит от радиуса.

Да, потому что тангенциальная скорость зависит от радиуса.
Нет, так как тангенциальная скорость не зависит от радиуса.
Нет, так как тангенциальная скорость зависит от радиуса.
Решение задач на угол поворота и угловую скорость
Снап Лаборатория
Измерение угловой скорости
В этом упражнении вы создадите и измерите равномерное круговое движение, а затем сопоставите его с круговыми движениями с разными радиусами.
- Одна струна (длина 1 м)
- Один предмет (резиновая пробка с двумя отверстиями) для привязки к концу
- Один таймер
Процедура
- Привязать объект к концу строки.
- Раскачивайте объект по горизонтальному кругу над головой (раскачивание с запястья). Важно, чтобы круг был горизонтальным!
- Поддерживайте постоянную скорость объекта при его раскачивании.
- Таким образом измерьте угловую скорость объекта. Измерьте время в секундах, за которое объект совершает 10 оборотов. Разделите это время на 10, чтобы получить угловую скорость в оборотах в секунду, которую вы можете преобразовать в радианы в секунду.
- Какова примерная линейная скорость объекта?
- Переместите руку вверх по веревке так, чтобы длина веревки составила 90 см. Повторите шаги 2–5.
- Переместите руку вверх по веревке так, чтобы ее длина составила 80 см. Повторите шаги 2–5.
- Переместите руку вверх по веревке так, чтобы ее длина составила 70 см.
 Повторите шаги 2–5.
Повторите шаги 2–5. - Переместите руку вверх по веревке так, чтобы ее длина составила 60 см. Повторите шаги 2–5
- Переместите руку вверх по веревке так, чтобы ее длина составила 50 см. Повторите шаги 2–5
- Построить графики зависимости угловой скорости от радиуса (т.е. длины струны) и линейной скорости от радиуса. Опишите, как выглядит каждый график.
Если медленно раскачивать объект, он может вращаться со скоростью менее одного оборота в секунду. Каковы были бы обороты в секунду для объекта, который делает один оборот за пять секунд? Какова будет его угловая скорость в радианах в секунду?
Объект будет вращаться со скоростью \frac{1}{5}\,\text{об/с}. Угловая скорость объекта будет \frac{2\pi}{5}\,\text{rad/s}.
Объект будет вращаться со скоростью \frac{1}{5}\,\text{об/с}.
 Угловая скорость объекта будет \frac{\pi}{5}\,\text{рад/с}.
Угловая скорость объекта будет \frac{\pi}{5}\,\text{рад/с}.Объект будет вращаться со скоростью 5\,\text{об/с}. Угловая скорость объекта будет 10\pi\,\text{rad/s}.
Объект будет вращаться со скоростью 5\,\text{об/с}. Угловая скорость объекта будет 5\pi\,\text{rad/s}.
Теперь, когда у нас есть понимание концепций угла поворота и угловой скорости, мы применим их к реальным ситуациям башни с часами и вращающейся шины.
Рабочий пример
Угол поворота часовой башни
Часы на часовой башне имеют радиус 1,0 м. а) На какой угол поворачивается часовая стрелка часов, когда она движется с 12 часов дня до 12 часов дня. до 15:00? (b) Какова длина дуги по внешнему краю часов между часовой стрелкой в эти два времени?
до 15:00? (b) Какова длина дуги по внешнему краю часов между часовой стрелкой в эти два времени?
Стратегия
Мы можем вычислить угол поворота, умножив полный оборот (2π2π радиан) на долю 12 часов, покрываемых часовой стрелкой при переходе от 12 к 3. Зная угол поворота, мы можем найти длину дуги, переформулировав уравнение Δθ=ΔsrΔθ=Δsr, поскольку радиус задан.
Решение задачи (a)
При переходе от 12 к 3 часовая стрелка покрывает 1/4 из 12 часов, необходимых для совершения полного оборота. Следовательно, угол между часовой стрелкой в положении 12 и 3 равен 14×2πrad=π214×2πrad=π2 (т. е. 90 градусов).
Решение (б)
Преобразовывая уравнение
Δθ=Δsr,Δθ=Δsr,6,4
получаем
Δs=rΔθ.Δ с=rΔθ.6,5
Подстановка известных значений дает длину дуги
Δs=(1,0 м)(π2рад)=1,6 мΔs=(1,0 м)(π2рад)=1,6 м6,6
Dis обсуждение
Мы смогли отбрасывать радианы из окончательного решения в часть (b), потому что на самом деле радианы безразмерны. Это связано с тем, что радиан определяется как отношение двух расстояний (радиуса и длины дуги). Таким образом, формула дает ответ в метрах, как и ожидалось для длины дуги.
Это связано с тем, что радиан определяется как отношение двух расстояний (радиуса и длины дуги). Таким образом, формула дает ответ в метрах, как и ожидалось для длины дуги.
Рабочий пример
Как быстро вращается автомобильная шина?
Рассчитайте угловую скорость автомобильной шины радиусом 0,300 м, когда автомобиль движется со скоростью 15,0 м/с (около 54 км/ч). См. рисунок 6.5.
Стратегия
В этом случае скорость протектора шины относительно оси шины равна скорости автомобиля относительно дороги, поэтому мы имеем v = 15,0 м/с. Радиус шины равен r = 0,300 м. Поскольку мы знаем v и r , мы можем изменить уравнение v=rωv=rω, чтобы получить ω=vrω=vr и найти угловую скорость.
Решение
Чтобы найти угловую скорость, мы используем соотношение: ω=vrω=vr .
Подстановка известных величин дает
ω=15,0 м/с0,300 м=50,0 рад/с.ω=15,0 м/с0,300 м=50,0 рад/с.6,7
Обсуждение
Когда мы отбрасываем единицы измерения в приведенном выше расчете, мы получаем 50,0/с (т. е. 50,0 в секунду, что обычно записывается как 50,0 с -1 ). Но угловая скорость должна иметь единицы рад/с. Поскольку радианы безразмерны, мы можем подставить их в ответ для угловой скорости, потому что мы знаем, что движение является круговым. Также обратите внимание, что если бы землеройная машина с гораздо большими шинами, скажем, радиусом 1,20 м, двигалась с той же скоростью 15,0 м/с, ее шины вращались бы медленнее. Они будут иметь угловую скорость
ω=15,0 м/с1,20м=12,5рад/сω=15,0м/с1,20м=12,5рад/с6,8
Практические задачи
1.Чему равен угол в градусах между часовой и минутной стрелками часов, показывающих 9 часов утра?
- 0°
- 90°
- 180°
- 360°

Какова приблизительная длина дуги между часовой и минутной стрелками часов, показывающих 10:00, если радиус часов равен 0,2 м?
- 0,1 м
- 0,2 м
- 0,3 м
- 0,6 м
Проверьте свое понимание
3.Что такое круговое движение?
Круговое движение — это движение объекта по линейной траектории.
Круговое движение — это движение объекта по зигзагообразной траектории.
Круговое движение — это движение объекта по круговой траектории.
Вариант D сбивает с толку как дистрактор

Что подразумевается под радиусом кривизны при описании вращательного движения?
- Радиус кривизны — это радиус кругового пути.
- Радиус кривизны — это диаметр кругового пути.
- Радиус кривизны — это длина окружности кругового пути.
- Радиус кривизны – это площадь кругового пути.
Что такое угловая скорость?
Угловая скорость – это скорость изменения диаметра кругового пути.
Угловая скорость – это скорость изменения угла, образуемого круговой траекторией.
Угловая скорость – это скорость изменения площади кругового пути.

Угловая скорость — это скорость изменения радиуса кругового пути.
Какое уравнение определяет угловую скорость ω, если r — радиус кривизны, θ — угол, t — время?
\omega = \frac{\Delta\theta}{\Delta{t}}
\omega = \frac{\Delta{t}}{\Delta\theta}
\omega = \frac{\Delta{r}}{\Delta{t}}
\omega = \frac{\Delta{t}}{\Delta{r}}

Найдите три примера объекта, движущегося по кругу.
искусственный спутник Земли, гоночный автомобиль, движущийся по круговой гоночной трассе, и волчок, вращающийся вокруг своей оси
искусственный спутник на орбите Земли, гоночный автомобиль, движущийся по круговой гоночной трассе, и мяч, привязанный к веревке, раскачивается по кругу вокруг головы человека
Земля вращается вокруг своей оси, гоночный автомобиль движется по круговой гоночной трассе, а мяч, привязанный к веревке, раскручивается по кругу вокруг головы человека
Земля, вращающаяся вокруг своей оси, лопасти работающего потолочного вентилятора и волчок, вращающийся вокруг своей оси
Какова относительная ориентация векторов радиуса и тангенциальной скорости объекта при равномерном круговом движении?
Вектор тангенциальной скорости всегда параллелен радиусу окружности, по которой движется объект.
Вектор тангенциальной скорости всегда перпендикулярен радиусу окружности, по которой движется объект.
Вектор тангенциальной скорости всегда находится под острым углом к радиусу окружности, по которой движется объект.
Вектор тангенциальной скорости всегда находится под тупым углом к радиусу окружности, по которой движется объект.

Поддержка учителей
Поддержка учителей
Используйте вопросы Проверьте свое понимание , чтобы оценить, справляются ли учащиеся с целями обучения этого раздела. Если учащиеся борются с определенной задачей, формирующее оценивание поможет определить, какая цель вызывает проблему, и направит учащихся к соответствующему содержанию.
6.1 Угол вращения и угловая скорость – Колледж физики главы 1-17
6 Равномерное круговое движение и гравитация
Резюме
- Задайте длину дуги, угол поворота, радиус кривизны и угловую скорость.
- Рассчитайте угловую скорость вращения колеса автомобиля.
В главе 2 «Кинематика» мы изучали движение по прямой и ввели такие понятия, как перемещение, скорость и ускорение. В главе 3 «Двумерная кинематика» речь шла о движении в двух измерениях. Движение снаряда — это частный случай двумерной кинематики, в котором объект проецируется в воздух, подвергаясь действию силы гравитации, и приземляется на расстоянии. В этой главе мы рассмотрим ситуации, когда объект не приземляется, а движется по кривой. Начнем изучение равномерного кругового движения с определения двух угловых величин, необходимых для описания вращательного движения.
Движение снаряда — это частный случай двумерной кинематики, в котором объект проецируется в воздух, подвергаясь действию силы гравитации, и приземляется на расстоянии. В этой главе мы рассмотрим ситуации, когда объект не приземляется, а движется по кривой. Начнем изучение равномерного кругового движения с определения двух угловых величин, необходимых для описания вращательного движения.
Когда объекты вращаются вокруг некоторой оси — например, когда CD (компакт-диск) на рис. 1 вращается вокруг своего центра — каждая точка объекта движется по дуге окружности. Рассмотрим линию от центра компакт-диска к его краю. Каждая яма, используемая для записи звука вдоль этой линии, проходит под одним и тем же углом за одно и то же время. Угол поворота представляет собой величину поворота и аналогичен линейному расстоянию. Мы определяем угол поворота [латекс]\boldsymbol{\Delta\theta}[/латекс] как отношение длины дуги к радиусу кривизны:
[латекс]\boldsymbol{\Delta\theta\:=}[/latex][латекс]\boldsymbol{\frac{\Delta{s}}{r}}. [/latex]
[/latex]
Длина дуги [latex]\boldsymbol{\Delta{s}}[/latex] — это расстояние, пройденное по окружности, как показано на рисунке 2. Обратите внимание, что [latex]\boldsymbol{r}[/latex] равно радиус кривизны кругового пути.
Мы знаем, что для одного полного оборота длина дуги равна длине окружности радиуса [латекс]\boldsymbol{r}.[/latex]Длина окружности равна [латекс]\boldsymbol{2\pi{r }}.[/latex]Таким образом, за один полный оборот угол поворота равен
[латекс]\boldsymbol{\Delta\theta\:=}[/латекс][латекс]\boldsymbol{\frac{2\pi{r}}{r}}[/latex][латекс]\boldsymbol{= \:2\пи}. 0}[/латекс]в круге или одном обороте, соотношение между радианами и градусами, таким образом, равно 90}.[/латекс]
0}[/латекс]в круге или одном обороте, соотношение между радианами и градусами, таким образом, равно 90}.[/латекс]
Как быстро вращается объект? Мы определяем угловую скорость [латекс]\boldsymbol{\omega}[/латекс] как скорость изменения угла. В символах это
[латекс]\boldsymbol{\omega\:=}[/латекс][латекс]\boldsymbol{\frac{\Delta\theta}{\Delta{t}}},[/latex]
, где угловой поворот[латекс]\boldsymbol{\Delta\theta}[/latex]происходит за время[латекс]\boldsymbol{\Delta{t}}.[/latex]Чем больше угол поворота в данном время, тем больше угловая скорость. Единицами угловой скорости являются радианы в секунду (рад/с).
Угловая скорость[латекс]\boldsymbol{\omega}[/latex]аналог линейной скорости[латекс]\boldsymbol{v}.[/latex]Чтобы получить точное соотношение между угловой и линейной скоростью, мы снова рассмотрим яму на вращающемся компакт-диске. Эта яма перемещается на длину дуги [латекс]\boldsymbol{\Delta{s}}[/latex]за время[латекс]\boldsymbol{\Delta{t}},[/latex] и поэтому имеет линейную скорость
[латекс]\boldsymbol{v\:=}[/латекс][латекс]\boldsymbol{\frac{\Delta{s}}{\Delta{t}}}. [/latex]
[/latex]
Из [латекс]\boldsymbol{\Delta\theta=\frac{\Delta{s}}{r}}[/latex] мы видим, что [латекс]\boldsymbol{\Delta{s}=r\Delta\theta }.[/latex]Подстановка этого выражения в выражение для[latex]\boldsymbol{v}[/latex] дает
[латекс]\boldsymbol{v\:=}[/латекс][латекс]\boldsymbol{\frac{r\Delta\theta}{\Delta{t}}}[/latex][латекс]\boldsymbol{= \:г\омега}.[/латекс]
Мы записываем это отношение двумя разными способами и получаем два разных понимания:
[латекс]\boldsymbol{v=r\omega\textbf{или}\omega\:=}[/latex][латекс]\boldsymbol{\frac{v}{r}}.[/latex]
Первое соотношение в [latex]\boldsymbol{v=r\omega\textbf{ или }\omega\:=\frac{v}{r}}[/latex] утверждает, что линейная скорость[latex]\boldsymbol{ v}[/latex]пропорциональна расстоянию от центра вращения, таким образом, она является наибольшей для точки на ободе (самая большая[latex]\boldsymbol{r}[/latex]), как и следовало ожидать. Мы также можем назвать эту линейную скорость[latex]\boldsymbol{v}[/latex]точки на ободе тангенциальная скорость . Второе соотношение в [latex]\boldsymbol{v=r\omega\textbf{ или }\omega\:=\frac{v}{r}}[/latex] можно проиллюстрировать, рассмотрев шину движущегося автомобиля. Обратите внимание, что скорость точки на ободе шины равна скорости[латекс]\жирныйсимвол{v}[/латекс]автомобиля. См. рис. 4. Таким образом, чем быстрее движется автомобиль, тем быстрее вращается шина. ]\boldsymbol{v=r\omega}.[/latex]Аналогично, шина большего радиуса, вращающаяся с той же угловой скоростью ([latex]\boldsymbol{\omega}[/latex]), будет производить большую линейную скорость ( [латекс]\boldsymbol{v}[/латекс]) для автомобиля.
Второе соотношение в [latex]\boldsymbol{v=r\omega\textbf{ или }\omega\:=\frac{v}{r}}[/latex] можно проиллюстрировать, рассмотрев шину движущегося автомобиля. Обратите внимание, что скорость точки на ободе шины равна скорости[латекс]\жирныйсимвол{v}[/латекс]автомобиля. См. рис. 4. Таким образом, чем быстрее движется автомобиль, тем быстрее вращается шина. ]\boldsymbol{v=r\omega}.[/latex]Аналогично, шина большего радиуса, вращающаяся с той же угловой скоростью ([latex]\boldsymbol{\omega}[/latex]), будет производить большую линейную скорость ( [латекс]\boldsymbol{v}[/латекс]) для автомобиля.
 Большая угловая скорость шины означает большую скорость автомобиля.
Большая угловая скорость шины означает большую скорость автомобиля.Пример 1: Как быстро вращается автомобильная шина?
Рассчитайте угловую скорость автомобильной шины радиусом 0,300 м, когда автомобиль движется со скоростью [latex]\boldsymbol{15,0\textbf{ м/с}}[/latex](около[latex]\boldsymbol{54\textbf{ км /ч}}[/латекс]). См. рис. 4.
Стратегия
Поскольку линейная скорость обода шины равна скорости автомобиля, мы имеем[latex]\boldsymbol{v=15.0\textbf{ м/с}}.[ /latex]Радиус шины равен[latex]\boldsymbol{r=0,300\textbf{м}}.[/latex]Знание[latex]\boldsymbol{v}[/latex]и[latex]\ boldsymbol{r},[/latex]мы можем использовать второе соотношение в[latex]\boldsymbol{v=r\omega,\:\omega=\frac{v}{r}}[/latex]для вычисления углового скорость.
Решение
Для расчета угловой скорости воспользуемся следующим соотношением: r}}.[/latex]
Замена известных,
[латекс]\boldsymbol{\omega\:=}[/latex][латекс]\boldsymbol{\frac{15. 0\textbf{м/с}} {0.300\textbf{ м}}}[/latex][latex]\boldsymbol{=\:50.0\textbf{ рад/с}}.[/latex]
0\textbf{м/с}} {0.300\textbf{ м}}}[/latex][latex]\boldsymbol{=\:50.0\textbf{ рад/с}}.[/latex]
Обсуждение
Когда мы отменяем единицы в приведенном выше расчете, получаем 50,0/с. Но угловая скорость должна иметь единицы рад/с. Поскольку радианы на самом деле безразмерны (радианы определяются как отношение расстояния), мы можем просто вставить их в ответ для угловой скорости. Также обратите внимание, что если бы землеройная машина с гораздо большими шинами, скажем, радиусом 1,20 м, двигалась с той же скоростью 15,0 м/с, ее шины вращались бы медленнее. Они будут иметь угловую скорость
[латекс]\boldsymbol{\omega=(15,0\textbf{м/с})/(1,20\textbf{м})=12,5\textbf{рад/с}}.[/latex]
Оба [латекс]\boldsymbol{\omega}[/latex] и [латекс]\boldsymbol{v}[/latex] имеют направления (следовательно, они являются угловой и линейной скоростями , соответственно). Угловая скорость имеет только два направления относительно оси вращения — либо по часовой стрелке, либо против часовой стрелки. Линейная скорость касается траектории, как показано на рисунке 5.
Линейная скорость касается траектории, как показано на рисунке 5.
ЭКСПЕРИМЕНТ 9 ДЛЯ ДОМА0793
Привяжите предмет к концу веревки и раскачивайте его по горизонтальному кругу над головой (раскачивая на запястье). Поддерживайте постоянную скорость при раскачивании объекта и измеряйте угловую скорость движения. Какова примерная скорость объекта? Определите точку рядом с вашей рукой и выполните соответствующие измерения, чтобы рассчитать линейную скорость в этой точке. Определите другие круговые движения и измерьте их угловые скорости.
Рисунок 5. Поскольку объект движется по кругу, здесь муха на краю старомодной виниловой пластинки, ее мгновенная скорость всегда касается окружности. Направление угловой скорости в этом случае – по часовой стрелке.
ИССЛЕДОВАНИЯ PHET: РЕВОЛЮЦИЯ БОЖЬЕЙ КОРОВКИ
Рис. 6. Революция божьей коровки Присоединяйтесь к божьей коровке в исследовании вращательного движения. Вращайте карусель, чтобы изменить ее угол, или выберите постоянную угловую скорость или угловое ускорение.

 Мы обсудим конкретно круговое движение и вращение. Круговое движение — это когда объект движется по круговой траектории. Примеры кругового движения включают гоночный автомобиль, мчащийся по круговой кривой, игрушку, прикрепленную к веревке, которая качается по кругу вокруг вашей головы, или круговое петля-петля на американских горках. Вращение — это вращение вокруг оси, проходящей через центр масс объекта, например, Земля, вращающаяся вокруг своей оси, колесо, вращающееся вокруг своей оси, вращение торнадо на пути разрушения или вращение фигуриста во время выступление на Олимпиаде. Иногда объекты будут вращаться во время кругового движения, например Земля, вращающаяся вокруг своей оси, вращаясь вокруг Солнца, но мы сосредоточимся на этих двух движениях отдельно.
Мы обсудим конкретно круговое движение и вращение. Круговое движение — это когда объект движется по круговой траектории. Примеры кругового движения включают гоночный автомобиль, мчащийся по круговой кривой, игрушку, прикрепленную к веревке, которая качается по кругу вокруг вашей головы, или круговое петля-петля на американских горках. Вращение — это вращение вокруг оси, проходящей через центр масс объекта, например, Земля, вращающаяся вокруг своей оси, колесо, вращающееся вокруг своей оси, вращение торнадо на пути разрушения или вращение фигуриста во время выступление на Олимпиаде. Иногда объекты будут вращаться во время кругового движения, например Земля, вращающаяся вокруг своей оси, вращаясь вокруг Солнца, но мы сосредоточимся на этих двух движениях отдельно.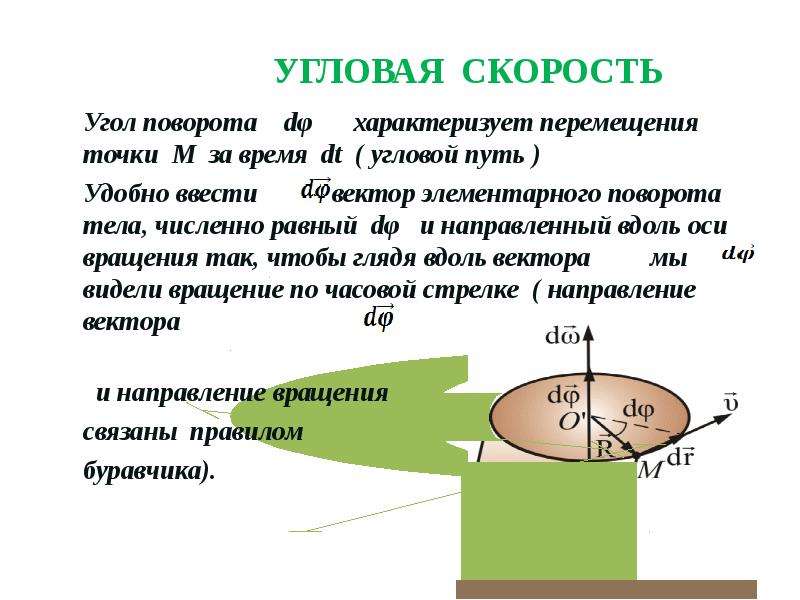 Объясните, что вращение Земли слегка эллиптическое, хотя и очень близкое к круговому.
Объясните, что вращение Земли слегка эллиптическое, хотя и очень близкое к круговому.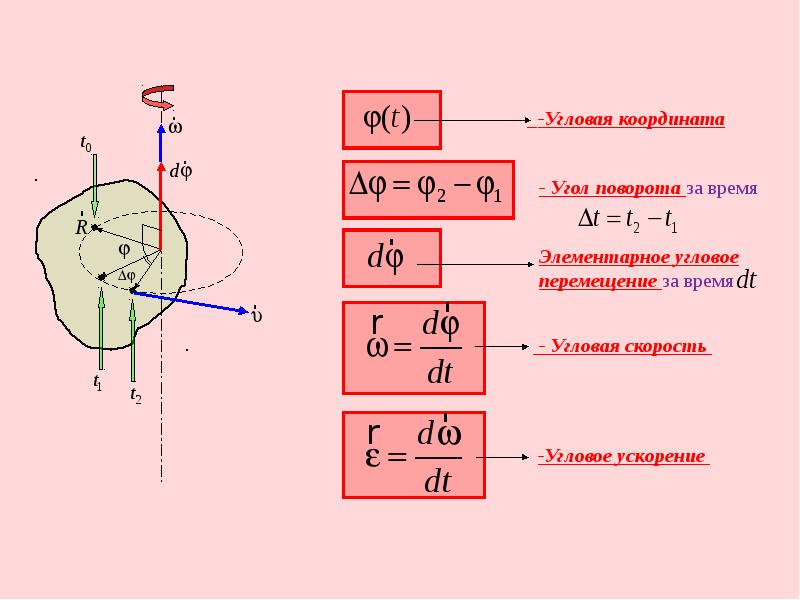 Радиус кривизны, r , является радиусом кругового пути. Оба показаны на рис. 6.3.
Радиус кривизны, r , является радиусом кругового пути. Оба показаны на рис. 6.3. Мы можем преобразовать радианы, обороты и градусы, используя соотношение
Мы можем преобразовать радианы, обороты и градусы, используя соотношение