Построение эпюр
Определение 1
Эпюра — это графическое изображение нагрузок и напряжений по всей длине бруса, используемое для визуального анализа напряженности, а также распределения нагрузок по всей длине бруса.
Эпюру можно построить на основании следующих параметров: внутренних сил (продольных и поперечных), крутящих и изгибающих моментов, напряжений (нормальных и касательных) и перемещений.
Процесс построения эпюр
Процесс построения эпюры стандартизирован и осуществляется по определенным правилам. Это сделано для общего понимания графиков всеми участниками производственного процесса.
Сначала строится нулевая линия. С левой стороны от линии пишется символическое название эпюры: $N$ — продольные силы, $Q$ — поперечные силы, $Mиз$ — изгибающие моменты, $T$ или $Mкр$ — вращающие момент, $σ$ и $τ$ — нормальное и касательное напряжения. Название сопровождается единицей измерения в соответствии с параметром (наименованием эпюры), например, $МПа$ — мегапаскаль.
Затем определяются границы силовых участков, то есть таких участков, где силовой фактор (деформация) остается постоянным или изменяется в рамках одной закономерности. Зачастую, границы силовых участков представляют собой сечения с приложенной внешней нагрузкой. Обозначение границ на эпюре реализуется в виде тонких вертикальных линий.
Замечание 1
Если брус обладает сложной объемной формой, то границы определяют аналитически.
Далее эпюра масштабируется. Масштаб выбирается в соответствии с предварительным просчетом отображаемого фактора по всем контрольным сечениям (КС) бруса.
После выбора масштаба и построения внешнего контура эпюры КС присваиваются значения фактора без указания знака (“$+$” и “$–$”). Факторы с положительными значениями чертятся над нулевой линией, а с отрицательными под.
В области с положительными значениями на самом широком участке пишется знак “$+$” и обводится кружком, а с отрицательными выполняется также операция, но указывается знак “$–$”. Можно поставить знаки справа и слева от “$0$”, при этом кружками они обводится не будут.
Определение знака фактора
Знак фактора определяется направлением внутренних силовых факторов и действием деформации. Например, нагрузке продольного типа, направленной на сжатие присваивается знак “$–$”, а на растяжение “$+$”.
Если вращение “отсеченной” части бруса осуществляется против часовой стрелки, то крутящий момент будет со знаком “$+$”, а по часовой стрелке знаком “$–$”. При рассмотрении поперечной силы $Q$, смотрим вертикальную плоскость, если она направлена вниз, то знак “$–$” (вверх “$+$”), а также учитываем поворот балки по часовой “$+$” и против часовой “$–$” .
Пример построения
Построим эпюры для простой двухоппорной балки с распределенной нагрузкой и действующей силой $F$=$10 кН$ и длиной $8$ $м$.
Начертим расчетную схему и укажем все нагрузки и значения:
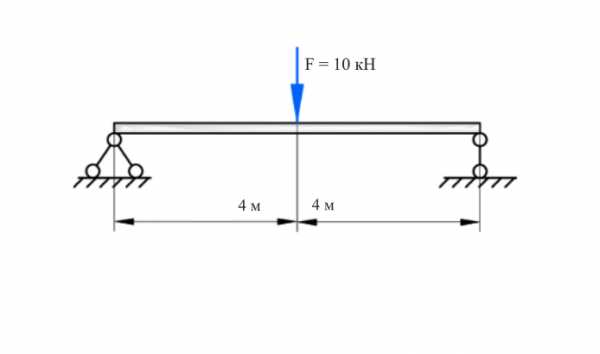
Рисунок 1. Расчетная схема двухопорной балки. Автор24 — интернет-биржа студенческих работ
Определим реакции опор ($R$) в данном случае реакция для каждой точки будет равна половине приложенной, силы, так части балки равны по длине (нагрузка распределена).
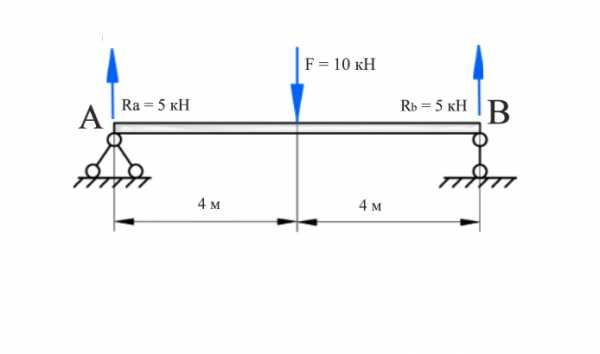
Рисунок 2. Реакции опор $Ra$ и $Rb$. Автор24 — интернет-биржа студенческих работ
Обозначаем границы участков балки.
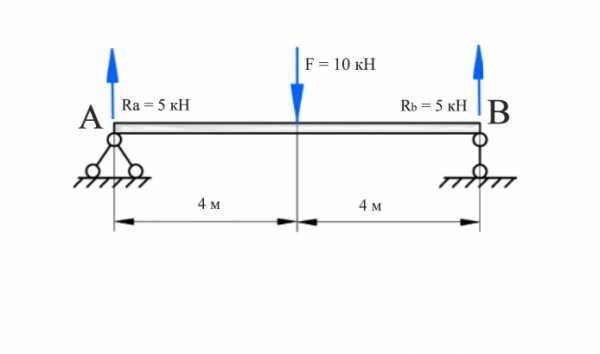
Рисунок 3. Границы участков балки. Автор24 — интернет-биржа студенческих работ
На первом участке отметим произвольное сечение и назовем его буквой $D$. Оно расположено на расстоянии $z1$ от левого торца балки. Относительно этого сечения записываем законы, описывающие изменения поперечных сил и изгибающих моментов, в рамках участка.
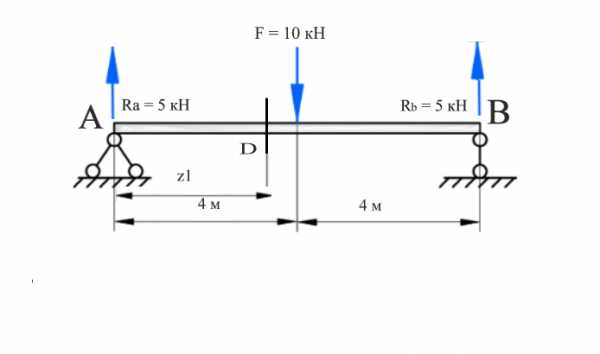
Рисунок 4. Произвольное сечение D. Автор24 — интернет-биржа студенческих работ
Запишем уравнение для поперечной силы. Поворот реакции $Ra$ выполняется по часовой стрелке, поэтому уравнение имеет вид:
$Qy_1 = Ra = 10 кН$
Обозначим границы, указав значение поперечной силы на графике, и начертим эпюру.
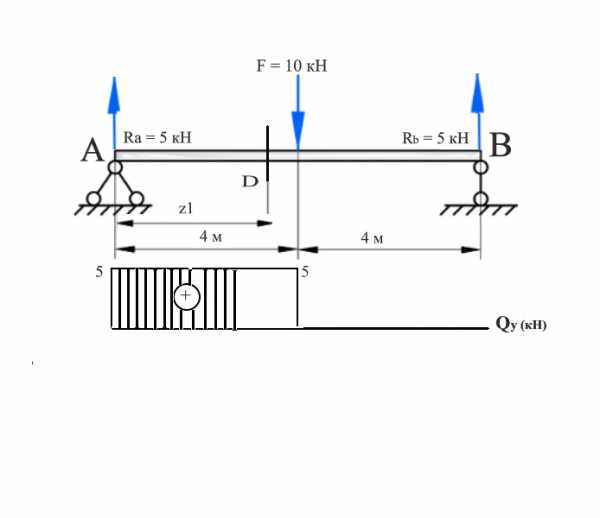
Рисунок 5. Эпюра поперечной силы. Автор24 — интернет-биржа студенческих работ
Запишем уравнение для изгибающего момента. В данном случае момент силы направлен на растяжение, поэтому укажем знак “$+$”, поэтому уравнение имеет вид:
$Mx_1 = Ra • z_1$
Из уравнения видно, что изменения изгибающего момента будут происходить, в соответствии с линейным законом, и зависеть от координаты $z_1$.
Замечание 2
Изображение эпюров со стороны растянутых волокон (показано в примере) характерно для инженерно-строительной практики. В механике эпюра чертится со стороны сжатых волокон.
Рассчитаем эпюру этого участка, подставив в уравнение координаты $z_1 = 0$ (начало участка) и $z_2 = 4$ (конец участка), а затем построим ее.
$Mx_1(z_1 = 0) = Ra • z_1 = 5 • 0 = 0$
$Mx_1 (z_1 = 4) = Ra • z_1 = 5 • 4 = 20$
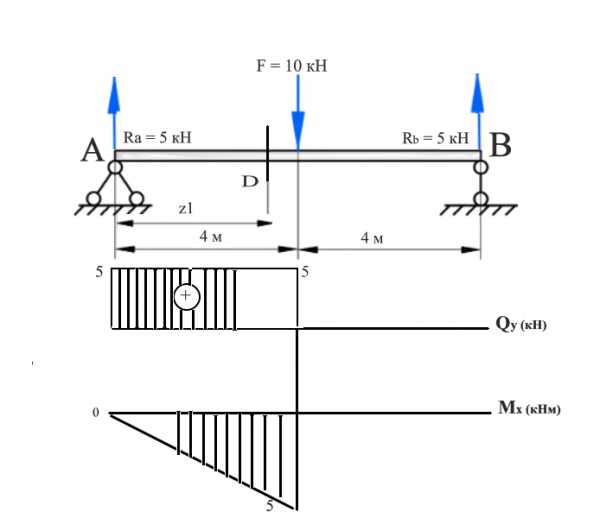
Рисунок 6. Эпюра изгибающего момента. Автор24 — интернет-биржа студенческих работ
Выполним расчеты для второго участка балки:
$Qy_2 = – Rb = –10 кН$
$Mx_2 = Rb • z_2$
$Mx_2 (z_2 = 0) = Rb • z_2 = 5 • 0 = 0$
$Mx_2 (z_2 = 4) = Rb • z_2 = 5 • 4 = 20$
Начертим окончательную версию эпюры.
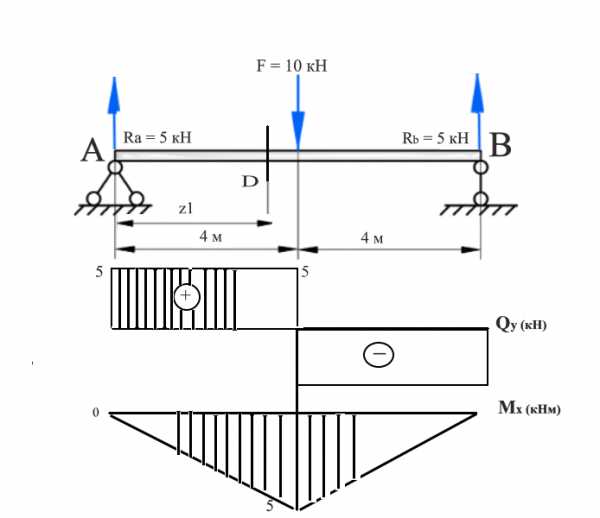
Рисунок 7. Полноценная эпюра рассматриваемой балки. Автор24 — интернет-биржа студенческих работ
spravochnick.ru
16.Что такое изгибающий момент, поперечная ,продольная силы? Что такое эпюра внутренних усилий, что показывает каждая ордината на эпюре?
Изгибающий момент, поперечная сила, продольная сила— внутренние усилия возникающие от действия внешних нагрузок ( изгиб, поперечная внешняя нагрузка ,растяжение-сжатие).
Эпюры -графики изменения внутренних усилий вдоль продольной оси стержня, построенные в определённом масштабе.
Ордината на эпюре показывает значение внутреннего усилия в данной точке оси сечения.
17.Изгибающий момент. Правила (порядок) построения эпюры изгибающих моментов.
Изгибающий момент— внутреннее усилие возникающее от действия внешней нагрузки( изгиба , внецентренного сжатия –растяжения).
Порядок построения эпюры изгибающих моментов:
1.Определение опорных реакций данной конструкции.
2.Определение участков данной конструкции ,в пределах которых изгибающий момент будет изменяться по одному и тому же закону.
3.Произвести сечение данной конструкции в окрестности точки , которая разделяет участки.
4.Отбросить одну из частей конструкции, разделённой пополам.
5.Найти момент ,который уравновесит действие на одну из оставшихся частей конструкции всех внешних нагрузок и реакций связи.
6.Нанести значение этого момента, с учётом знака и выбранного масштаба, на эпюру.
Вопрос № 18.Поперечная сила. Построение эпюры поперечных сил, используя эпюру изгибающих моментов.
Поперечная сила Q –внутреннее усилие возникающее в стержне под воздействием внешней нагрузки( изгиб, поперечная нагрузка). Поперечная сила направлена перпендикулярно оси стержня.
Эпюра поперечных сил Q строится исходя из следующей дифференциальной зависимости: ,т.е. Первая производная от изгибающего момента по продольной координате равна поперечной силе.
Знак поперечной силы определяется исходя из следующего положения:
Если нейтральная ось конструкции на эпюре моментов поворачивается к оси эпюры по часовой стрелке, то эпюра поперечных сил имеет знак плюс, если против- минус.
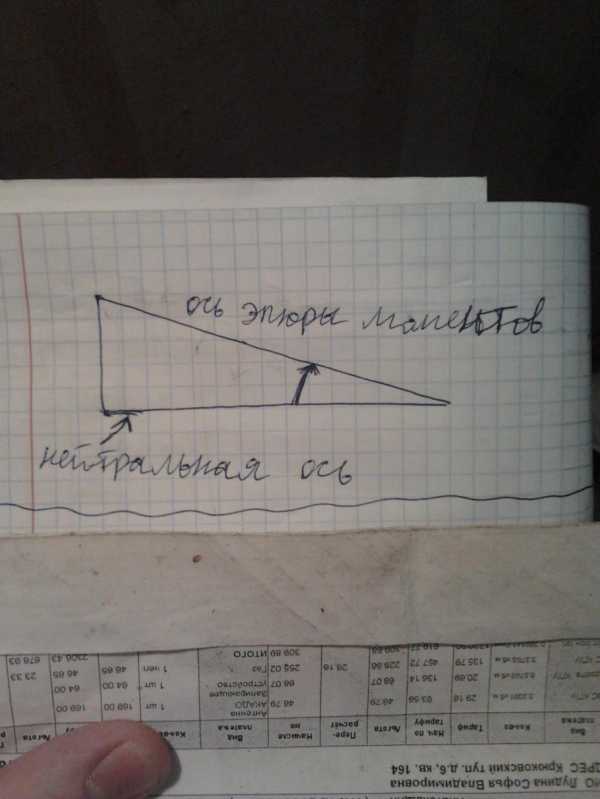
В зависимости от эпюры M эпюра Q может принимать тот или иной вид:
1.если эпюра моментов имеет вид прямоугольника , то эпюра поперечных сил равна нулю.
2.Если эпюра моментов представляет собой треугольник , то эпюра поперечных сил имеет вид прямоугольника.
3.Если эпюра моментов имеет вид квадратной параболы , то эпюра поперечных сил имеет треугольника и строится по следующему принципу
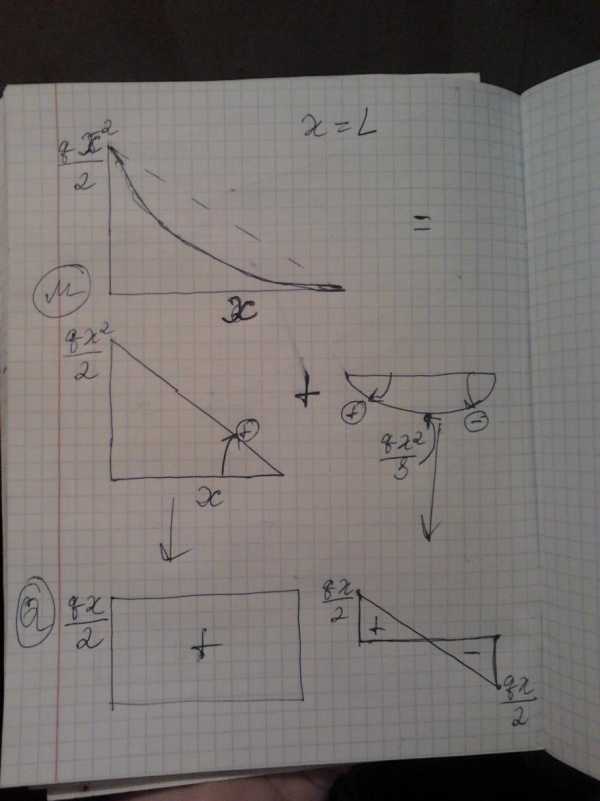
Вопрос №19 . Продольная сила. Метод построения эпюры продольных сил используя эпюру поперечных сил. Правило знаков.
Полольная сила N- внутреннее усилие возникающее вследствие центрального и внецентренного растяжения-сжатия. Продольная сила направлена вдоль оси стержня.
Для того что бы построить эпюру продольных усилий нужно:
1.Вырезать узел данной конструкции. Если мы имеем дело с одномерной конструкцией , то сделать сечение на интересующем нас участке этой конструкции.
2.Снять с эпюры Q значения усилий действующих в непосредственной близости от вырезанного узла.
3.Дать направление векторам поперечных сил, исходя из того какой знак имеет данное поперечное усилие на эпюре Q по следующим правилам: если поперечная сила имеет на эпюре Q знак плюс , то её нужно направить так , что бы она вращала данный узел по часовой стрелке, если поперечная сила имеет знак минус –против часовой стрелки. Если внешняя сила проложена к узлу , то её нужно оставить и рассматривать узел вместе с ней.
4.Уравновесить узел продольными усилиями N.
5.Правило знаков для N:если продольная сила направлена к сечению , то она имеет знак минус ( работает на сжатие).если продольная сила направлена от сечения , она имеет знак плюс ( работает на растяжение).
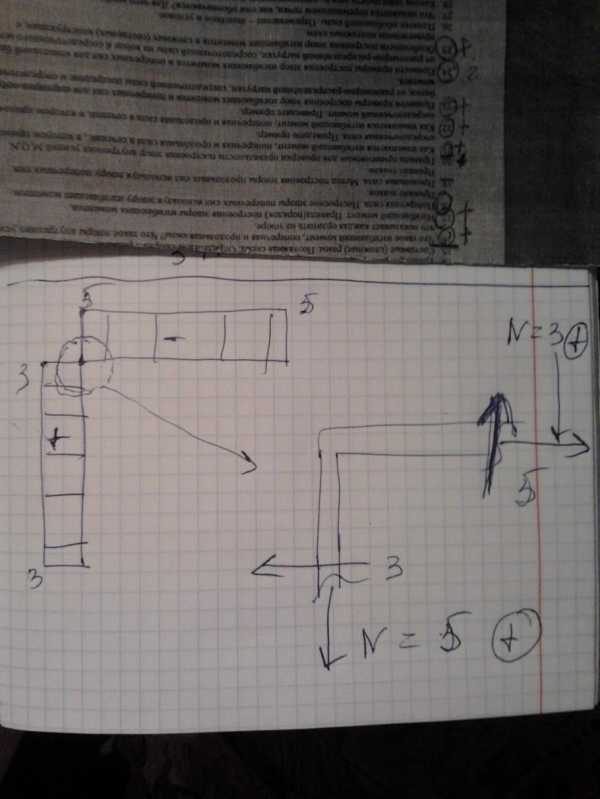
Вопрос № 20.Правилаприменяемые для проверки правильности построения эпюр внутренних усилий M,Q,N.
1. В сечении, где приложена сосредоточенная сила F, на эпюре Q будет скачок, равный значению этой силы и направленный в ту же сторону (при построении эпюры слева направо), а эпюра М будет иметь перелом, направ- ленный в сторону действия силы F.
2. В сечении, где приложен сосредоточенный изгибающий момент на эпюре М, будет скачок, равный значению момента М; на эпюре Q изменений не будет. При этом направление скачка будет вниз (при построении эпюры слева направо), если сосредоточенный момент действует по ходу часовой стрелки, и вверх, если против хода часовой стрелки.
3.Если
на
участке, где имеется равномерно
распределенная нагрузка, поперечная
сила в одном из сечений равна нулю
(Q=M’=0),
то изгибающий момент в этом сечении
принимает экстремальное значение
М
4.Для проверки правильности построения эпюры М можно использовать метод вырезания узлов. При этом момент приложенный в узле нужно при вырезании узла оставлять.
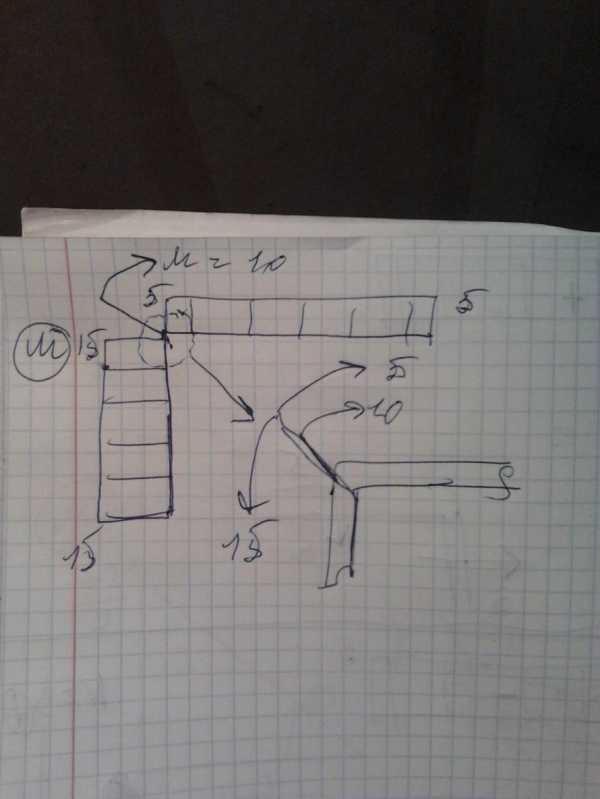
Правильность построения эпюр Q и M можно проверить, дублируя метод вырезания узлов методом сечений и наоборот.
studfiles.net
52.Основные правила построения эпюр поперечных сил и изгибающих моментов
52.Основные правила построения эпюр поперечных сил и изгибающих моментов.

1.7 ПОСТРОЕНИЕ ЭПЮР ПОПЕРЕЧНЫХ СИЛ И ИЗГИБАЮЩИХ МОМЕНТОВ В БАЛКАХ Стержень, работающий на изгиб, называется балкой. В сечениях балок, загруженных вертикальными нагрузками, возникают, как правило, два внутренних силовых фактора — поперечная сила и изгибающий момент . Поперечная сила в сечении численно равна алгебраической сумме проекций внешних сил, приложенных по одну сторону от рассматриваемого сечения, на поперечную (вертикальную) ось. Правило знаков для : условимся считать поперечную силу в сечении положительной, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части, стремится повернуть данное сечение по часовой стрелке и отрицательной — в противном случае. Схематически это правило знаков можно представить в виде Изгибающий момент в сечении численно равен алгебраической сумме моментов внешних сил, приложенных по одну сторону от рассматриваемого сечения, относительно оси x , проходящей через данное сечение. Правило знаков для : условимся считать изгибающий момент в сечении положительным, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части, приводит к растяжению в данном сечении нижних волокон балки и отрицательной — в противном случае. Схематически это правило знаков можно представить в виде: Следует отметить, что при использовании правила знаков для в указанном виде, эпюра всегда оказывается построенной со стороны сжатых волокон балки. 1.8 КОНСОЛЬНЫЕ БАЛКИ При построении эпюр и в консольных, или жестко защемленных, балках нет необходимости (как и в рассмотренных ранее примерах) вычислять опорные реакции, возникающие в жесткой заделке, но выбирать отсеченную часть нужно так, чтобы заделка в нее не попадала.
studfiles.net
Пример построения эпюры Q по эпюре М
Признаки правильного вида эпюры Q
1.На прямом элементе без нагрузки по его длине поперечная сила постоянна и эпюра Q имеет прямоугольную форму.
2.В сечении, которое совпадает с действующей поперек оси стержня сосредоточенной силой, ординаты эпюры Q слева и справа от силы имеют скачок, равный величине этой силы.
3.На участке с равномерно распределенной нагрузкой эпюра Q прямолинейна и имеет наклон к оси стержня (рис. 3.11, 3), тангенс угла которого равен интенсивности нагрузки q = dQ / dx =tg β . Нулевому значению
на эпюре Q на участке с равномерно распределенной нагрузкой соответствует экстремальное значение на эпюре M .
Для построения эпюры Q на прямолинейном элементе при отсутствии на нем нагрузки и при действии по его длине равномерно распределенной нагрузки достаточно иметь соответственно одну и две ординаты по концам элемента.
В программе SCAD поперечные силы на КЭ вычисляются минимум в двух концевых сечениях. Поэтому информации для построения эпюры Q достаточно.
Однако иногда у расчетчика возникает необходимость построения эпюры Q по эпюре M вручную. Для этого можно использовать уравнение Q =dM / dx .
Отсюда следует, что на любом КЭ стержня с прямолинейной эпюрой M величина Q будет постоянной и значение Q и знак определятся из выражения (3.2).
Полагая, что на участках прямолинейных эпюр M , приведенных на рис. 3.1, местная система координат направлена так, как показано на рис. 3.2, 3.3. В соответствии с этим поставлены знаки ординат эпюр M . Тогда по формуле (3.2) получим те же величины Q, которые были получены на рис. 3.11 первым способом.
При построении эпюры Q на участках с равномерно распределенной нагрузкой
используют формулу (3.3), полученную по аналогии с формулой (3.1) на основе принципа независимости действия сил.
Поперечные силы Qн,к по этой формуле определяют для крайних сечений элемента (в
узлах «н» и «к» МСК) как сумму ординат Qo | = ±ql / 2 эпюры Qo | для балки, загруженной |
н,к |
|
|
равномерно распределенной нагрузкой (рис. 3.12,а), и ординат | Qн,к(лом) = (M к − M н) / l , | |
вызванной опорными моментами M н и Mк, действующими | по концам элемента | |
(рис. 3.12, б, г): |
|
|
|
Q | = ± ql | + M к −M н . | (3.3) |
н,к | 2 | l |
|
|
|
Обратим внимание, что первое слагаемое при нагрузке направленной «вниз» всегда имеет один и тот же вид (см. 3.12,а). Второе слагаемое дает эпюру с постоянными
studfiles.net
Проверки построения эпюр Q и М по дифференциальным зависимостям
Проверка или контроль построения эпюр. Следует хорошо усвоить дифференциальные зависимости между интенсивностью распределенной нагрузки, поперечной силой и изгибающим моментом, что позволит быстро и правильно строить эпюры. Как проверить эпюры Q и М ? Необходимо запомнить следующие правила (проверки построения эпюр):
- На участке балки, где отсутствует распределенная нагрузка, эпюра Qy – прямая,параллельная базовой линии, а эпюра Мх — наклонная прямая.
- Под сосредоточенной силой на эпюре Qy наблюдается скачок, численно равный приложенной внешней силе, а на эпюре Мх – излом.
- В точке приложения сосредоточенной пары сил (момента) на эпюре момента происходит скачок на размер момента этой пары, а эпюра Qy не претерпевает изменений.
- На участке действия равномерно распределенной нагрузки эпюра Qy выражается наклонной прямой, а эпюра Мх – параболой, обращенной выпуклостью навстречу действию распределенной нагрузки.
- На участках балки, где эпюра Q положительна, изгибающий момент с увеличением координаты z увеличивается, и, наоборот, там, где Q < 0, изгибающий момент уменьшается.
- Если на участке действия распределенной нагрузки эпюра Q пересекает базовую линию, то в этом сечении изгибающий момент принимает экстремальное значение.
- Если на границе действия распределенной нагрузки не приложено сосредоточенных сил, то на эпюре Qy участок, параллельный оси абсцисс, переходит в наклонный без скачка, а параболическая и наклонная части эпюры Мх сопрягаются плавно без изгиба.
- Изгибающий момент в концевых сечениях балки всегда равен нулю, за исключением случая, когда в концевом сечении действует сосредоточенная пара сил. В этом случае изгибающий момент в концевом сечении балки равен моменту действующей пары сил.
- В сечении, соответствующем заделке, Qy и Мх численно равны опорной реакции и реактивному моменту заделки.
Пример балки, на которой наглядно можно проверить правильность построения эпюр по дифференциальным зависимостям. Эпюра М построена на растянутых волокнах.
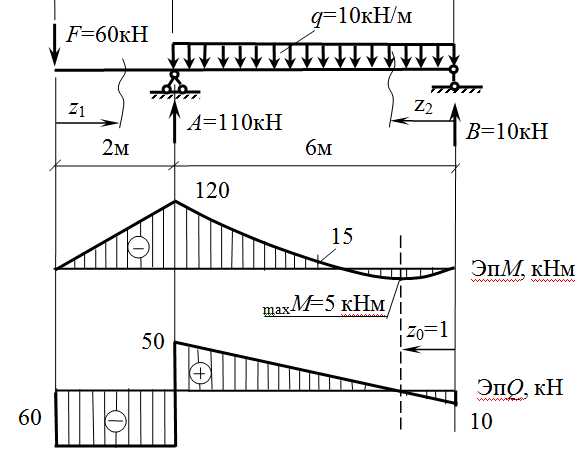
При построении эпюр изгибающих моментов рекомендуется придерживаться существующей традиции:
— если это балка является строительной конструкцией, то эпюра моментов строится на «растянутых» волокнах (положительные моменты откладываются вниз, отрицательные – вверх),
— а если балка является объектом машиностроения, то наоборот: эпюра моментов строится на «сжатых» волокнах (положительные моменты откладываются вверх, отрицательные – вниз).
Запись опубликована автором admin в рубрике Изгиб.prosopromat.ru