Прямой чистый изгиб стержня (Лекция №19)

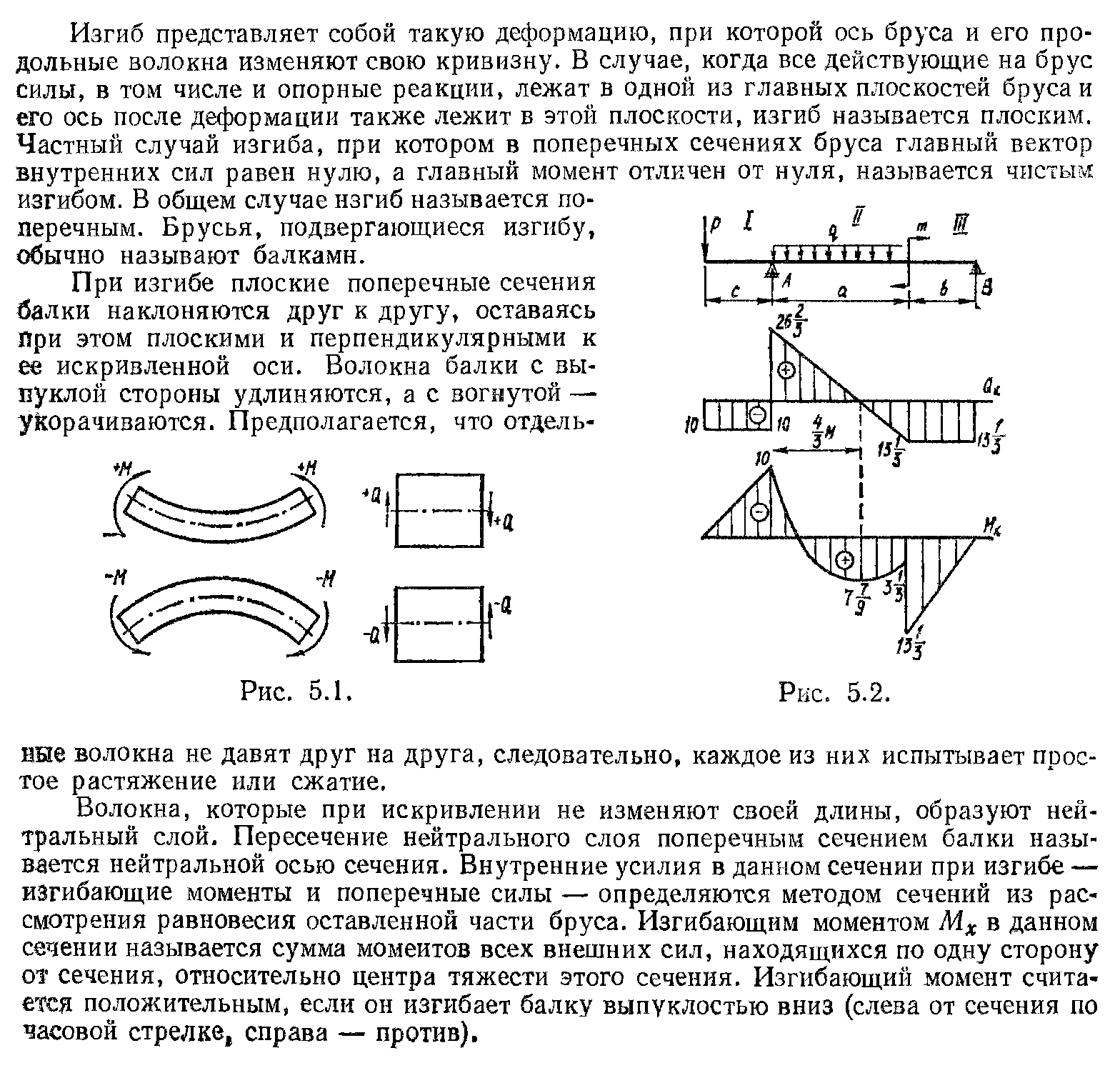
   При прямом чистом изгибе в поперечном сечении стержня возникает только один силовой фактор — изгибающий момент М_х (рис. 1). Так как Q_y=dM_x/dz=0, то M_x=const и чистый прямой изгиб может быть реализован при загружении стержня парами сил, приложенными в торцевых сечениях стержня. Поскольку изгибающий момент M_х по определению равен сумме моментов внутренних сил относительно оси Ох с нормальными напряжениями его связывает выкающее из этого определения уравнение статики

.

   Сформулируем предпосылки теории чистого прямого изгиба призматического стержня. Для этого проанализируем деформации модели стержня из низкомодульного материала, на боковой поверхности которого нанесена сетка продольных и поперечных рисок (рис. 2). Поскольку поперечные риски при изгибе стержня парами сил, приложенными в торцевых сечениях, остаются прямыми и перпендикулярными к искривленным продольным рискам, это позволяет сделать вывод о выполнении

гипотезы плоских сечений, которая, как показывает решение этой задачи методами теории упругости, перестает быть гипотезой, становясь точным фактом — законом плоских сечений. Замеряя изменение расстояний между продольными рисками, приходим к выводу о справедливости гипотезы о ненадавливании продольных волокон .

   Ортогональность продольных и поперечных рисок до и после деформирования (как отражение действия закона плоских сечений) указывает также на отсутствие сдвигов, касательных напряжений в поперечных и продольных сечениях стержня.

Рис.1. Связь внутреннего усилия и напряжения

 

Рис.2. Модель чистого изгиба

 

   Таким образом, чистый прямой изгиб призматического стержня сводится к одноосному растяжению или сжатию продольных волокон напряжениями (индекс

г в дальнейшем опускаем). При этом часть волокон находится в зоне растяжения (на рис. 2 это—нижние волокна), а другая часть—в зоне сжатия (верхние волокна). Эти зоны разделены нейтральным слоем (п—п), не меняющим своей длины, напряжения в котором равны нулю. Учитывая сформулированные выше предпосылки и полагая, что материал стержня линейно-упругий, т. е. закон Гука в этом случае имеет вид: , выведем формулы для кривизны нейтрального слоя (—радиус кривизны) и нормальных напряжений . Предварительно отметим, что постоянство поперечного сечения призматического стержня и изгибающего момента (M_х=сonst), обеспечивает постоянство радиуса кривизны нейтрального слоя по длине стержня (рис. 3, а), нейтральный слой (п—п) описывается дугой окружности.

   Рассмотрим призматический стержень в условиях прямого чистого изгиба (рис. 3, а) с поперечным сечением, симметричным относительно вертикальной оси

Оу. Это условие не отразится на конечном результате (чтобы прямой изгиб был возможен, необходимо совпадение оси Оу с главной осью инерции поперечного сечения, которая и является осью симметрии). Ось Ox поместим на нейтральном слое, положение которого заранее неизвестно.

а) расчетная схема, б) деформации и напряжения

Рис.3. Фрагмент чистого изгиба бруса

 

   Рассмотрим вырезанный из стержня элемент длиной dz, который в масштабе с искаженными в интересах наглядности пропорциями изображен на рис. 3, б. Поскольку интерес представляют деформации элемента, определяемые относительным смещением его точек, одно из торцевых сечений элемента можно считать неподвижным. Ввиду малости считаем, что точки поперечного сечения при повороте на этот угол перемещаются не по дугам, а по соответствующим касательным.

Вычислим относительную деформацию продольного волокна АВ, отстоящего от нейтрального слоя на у:

.

Из подобия треугольников С00₁ и 0₁ВВ₁ следует, что

.

   Продольная деформация оказалась линейной функцией расстояния от нейтрального слоя, что является прямым следствием закона плоских сечений

(1)

Тогда нормальное напряжение, растягивающее волокно АВ, на основании закона Гука будет равно

(2)

   Эта формула не пригодна для практического использования, так как содержит две неизвестные: кривизну нейтрального слоя и положение нейтральной оси

Ох, от которой отсчитывается координата у. Для определения этих неизвестных воспользуемся уравнениями равновесия статики. Первое выражает требование равенства нулю продольной силы

(3)

Подставляя в это уравнение выражение (2)

и учитывая, что , получаем, что

   Интеграл в левой части этого уравнения представляет собой статический момент поперечного сечения стержня относительно нейтральной оси Ох, который может быть равным нулю только относительно центральной оси. Поэтому нейтральная ось Ох проходит через центр тяжести поперечного сечения.

   Вторым уравнением равновесия статики является, связывающее нормальные напряжения с изгибающим моментом (который легко может быть выражен через внешние силы и поэтому считается заданной величиной). Подставляя в уравнение связки выражение для. напряжений, получим:

и учитывая, что где J_x—главный центральный момент инерции относительно оси Ох, для кривизны нейтрального слоя получаем формулу

(4)

   Кривизна нейтрального слоя является мерой деформации стержня при прямом чистом изгибе.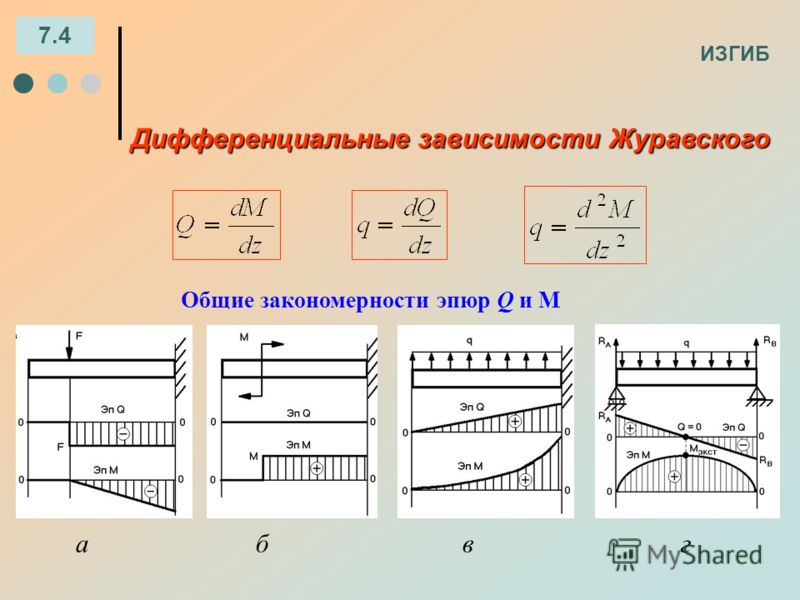 тем меньше, чем больше величина EJ_х, называемая жесткостью поперечного сечения при изгибе (по аналогии с жесткостью поперечного сечения при растяжении EF).

Подставляя (4) в (2), получаем формулу для нормальных напряжений в виде

(5)

Рис.4. Распределение нормальных напряжений

 

которая была впервые получена Ш. Кулоном в 1773 году. Для согласования знаков изгибающего момента М_х и нормальных напряжений в правой части формулы (5) ставится знак минус, так как при M_х>0 нормальные напряжения при y>0 оказываются сжимающими. Однако в практических расчетах удобнее, не придерживаясь формального правила знаков, определять напряжения по модулю, а знак ставить по смыслу. Нормальные напряжения при чистом изгибе призматического стержня являются линейной функцией координаты у и достигают наибольших значений в волокнах, наиболее удаленных от нейтральной оси (рис. 4), т. е.

   Здесь введена геометрическая характеристика , имеющая размерность м³ и получившая название

момента сопротивления при изгибе. Поскольку при заданном M_х напряжения max ? тем меньше, чем больше W_x, момент сопротивления является геометрической характеристикой прочности поперечного сечения изгибе. Приведем примеры вычисления моментов сопротивления для простейших форм поперечных сечений. Для прямоугольного поперечного сечения (рис. 5, а) имеем J_х=bh³/12,y_max = h/2 и W_x = J_x/y_max = bh²/6. Аналогично для круга (рис. 5,a J_x=d⁴/64, y_max=d/2) получаем W_x=d³/32, для кругового кольцевого сечения (рис. 5, в), у которого

получаем

Итак, максимальные нормальные напряжения в сечении с изгибающим моментом M_х определяются по формуле

(6)

Рис.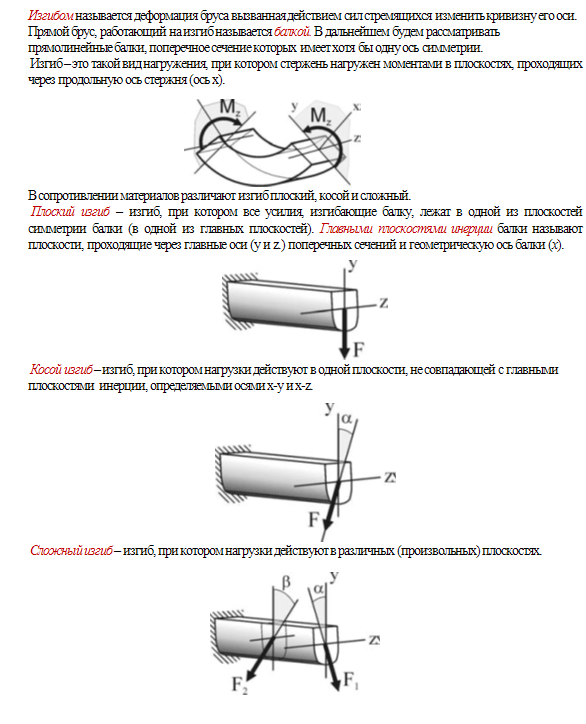 5. Конфигурации поперечных сечений бруса

 

   Этой формулой удобно пользоваться для расчета балок пластичного материала в упругой области, одинаково работающего на растяжение и сжатие. Поскольку знак напряжения в этом случае не имеет значения, напряжения вычисляются по модулю, и условие прочности при изгибе балки в форме призматического стержня получает вид

где max M_х—максимальное значение изгибающего момента (легко определяемое по его эпюре), — допускаемое напряжение на простое растяжение (сжатие). Напомним, что чистый изгиб балки сводится к растяжению и сжатию ее волокон (неравномерному в отличие от деформации растяжения (сжатия) призматического стержня, при котором ).

Рис.6. Модель изгиба хрупкого материала

 

   При расчете балок из хрупких материалов следует различать наибольшие растягивающие max и наибольшие сжимающие напряжения (рис. 6.), которые также определяются по модулю непосредственно и сравниваются с допускаемыми напряжениями на растяжение и сжатие . 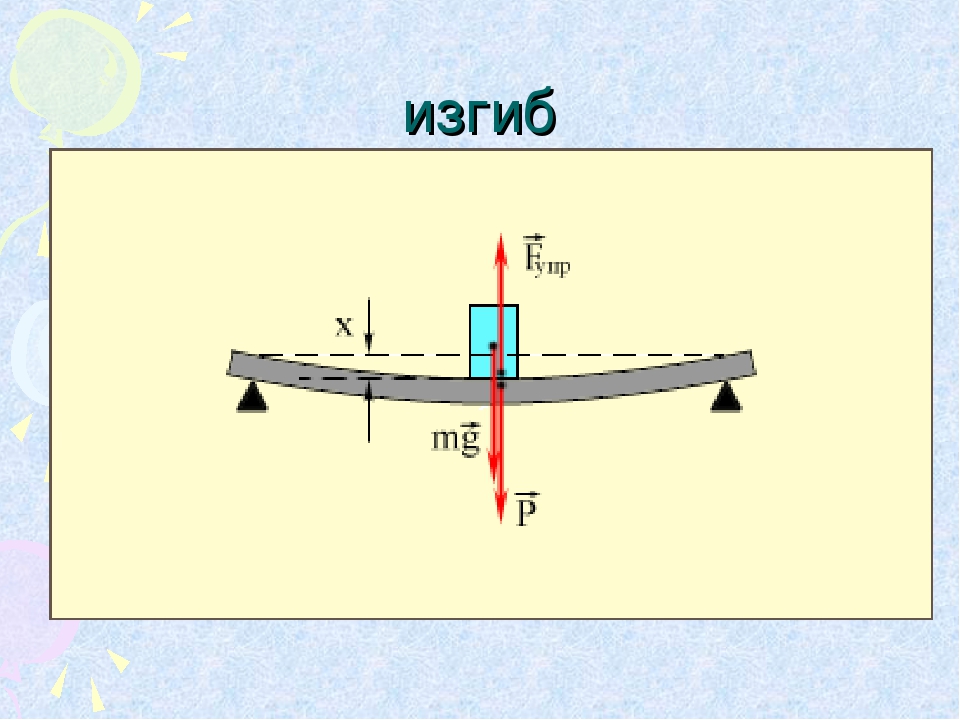Условие прочности в этом случае будет иметь вид:

.

Дальше…

Чистый изгиб. определение нормальных напряжений

Содержание:

Чистый изгиб. определение нормальных напряжений

• Чистый изгиб. Определение нормы Напряжение Как уже говорилось выше, в сечении балки в момент изгиба возникает изгибающий момент и поперечная сила. При исследовании напряженного состояния удобнее начинать с особого случая, когда боковая сила равна нулю. Таким образом, в центральной части балки, показанной на рисунке. 203, чей собственный вес игнорируется, имеет чистый

изгиб:момент по длине этого участка не изменяет своей величины, и нет никакой боковой силы. Изучите закон распределения напряжений в поперечном сечении балки при чистом изгибе и сможете найти максимальное напряжение. Сначала рассмотрим балку, имеющую поперечное сечение по крайней мере с одной осью симметрии, совпадающей с силовой плоскостью.

Таким образом, одна из инерционных осей находится на плоскости изгиба, а другая Людмила Фирмаль

перпендикулярна ей. Для решения этой задачи необходимо привлечь условие деформации в дополнение к статическому условию, которое может быть сформулировано только на основе экспериментального наблюдения. На стороны балки 224if наносят сетку в виде продольных и поперечных линий(рис. После того, как деформация изгиба произошла, обнаруживается, что продольная линия принимает криволинейную форму, а поперечная линия становится

прямой. Участок 0 Участок М Это обстоятельство указывает на то, что при изгибе и растяжении гипотеза о плоском поперечном сечении справедлива. Это ги Рис 204А Эта гипотеза вместе с уравнениями статики позволяет решить задачу определения напряжений при чистом изгибе.’ Рассмотрим элементы балки длиной DX после деформации- 225) — кривая фиг. 205, а). Две смежные секции наклонены, образуя угол между ними. В этих условиях верхние волокна сжимаются, а нижние растягиваются. Волокна, которые

• лежат на определенной высоте, остаются неповрежденными, мы называем их нейтральными. О площади поперечного сечения(рис. 205, в) поверхность, на которой присутствуют нейтральные волокна, образует след нейтрального Луча Oh. Радиус кривизны нейтрального волокна равен оси o, где сечение rotates.It обозначается продольными волокнами и деформируется таким же образом. Для удобства рассуждения на рисунке. 205, б, волокна получают условное изображение деформированных элементов, остающихся на прямой линии. Верхние волокна сжимались, а нижние растягивались.

Согласно этой фигуре, относительное удлинение волокна АА на расстоянии от нейтрального слоя легко установить, что каждый состоит из двух сегментов АИ, равных значению y, следовательно, суммарному удлинению любого волокна. Это будет ДГ/ч-Уду. Но так как YH-rblr, относительное удлинение этого волокна М Х1 Если предположить, что отдельные волокна не прижимаются друг к другу, то каждое из них подпадает под условие простого растяжения (или сжатия). В этом случае для перехода от расширения g к напряжению

o можно использовать простую крюковую зависимость. а=ее= — у.(8.8) П’ Во-первых, мы устанавливаем положение нейтральной линии, Людмила Фирмаль

которая измеряет расстояние y. для этого мы используем тот факт, что результат основной нормальной силы Ayr (т. е. нормальной силы) в поперечном сечении при чистом изгибе равен нулю: Н=] * Эр=0, Г Или I Ом V = 0. Х Р тт Е Но так как умножение-не ноль, но в то же время оно может быть П 2 26винести для знака интеграла(поскольку он не зависит от интегральной переменной), а затем уменьшить его UIR=0. Е Полученный Интеграл представляет собой статический момент площади поперечного сечения относительно нейтральной оси выхлопного газа и равен нулю только тогда, когда ось проходит через центроид сечения. Исходя из этого, можно сказать, что нейтральная ось чистого, прямого изгиба стержня проходит через центр тяжести сечения. Рассмотрим моменты внутренних сил относительно

нейтральной оси. Для этого вычислите сумму моментов основной внутренней силы<z (1P) для этой оси и уравняйте ее с изгибающими моментами: Мг=(ОС?7) У. Е Если вместо напряжения o подставить его значение по формуле (8.8)、 Интегралом, входящим в это уравнение, является момент инерции поперечного сечения стержня) HRM= п Так… Где найти кривизну нейтрального слоя: — (8.9) П Подставляя это выражение в выражение(8.8), можно, наконец, (8.10)) Формула(8.10) позволяет определить напряжение в любой точке горизонтальной линии поперечного сечения пучка, удаленной от нейтральной оси на расстояние Y. график, Закон изменения напряжений на высоте 227 интервала называется диаграммой напряжений. Для риса. 205 g

показывает график давления при чистом изгибе. Самое высокое напряжение-это точка, в которой значение y принимает наибольшее значение, то есть самое дальнее волокно. При выводе формулы (8.10) мы предположили, что поперечное сечение стержня симметрично относительно оси Oh. Однако это предположение было сделано только для удобства рассуждений. Получается, что формула (8.10) может быть использована для любого поперечного сечения, но при этом предполагается, что одна из главных осей инерции находится в плоскости нагрузки. Чтобы доказать последнее утверждение, мы приравниваем к нулю момент инерции всех основных внутренних

сил относительно оси OU. Это следует UGR=0. п Поскольку известно, что это значение равно центробежному моменту инерции сечения, ось Y и ось g являются главными осями. Для симметричного поперечного сечения, учитываемого при выводе, оси y и d являются главными центральными осями. Для других поперечных сечений плоскость груза должна быть параллельна центральной оси.

Смотрите также:

Изгиб чистый — Энциклопедия по машиностроению XXL

ПРЯМОЙ ИЗГИБ ЧИСТЫЙ И ПОПЕРЕЧНЫЙ  [c.201]

Рассмотрим наиболее простой случай изгиба — чистый, прямой изгиб бруса прямоугольного сечения.  [c.252]

Тщательные исследования точности и сходимости решения были проведены в работе [57], где изучалось влияние числа контурных точек на точность решения, причем результаты расчетов методом расширения заданной системы сравнивались с известными точными решениями для чистого изгиба, чистого сдвига и т. д. Проведенные сравнения указали на хорошую сходимость решения даже при небольшом числе контурных точек.  [c.158]

Эта формула выведена для частного случая среза. Она применима и для других видов плоского напряженного состояния i[54]. Выведенные Нейбером формулы позволяют определять упругие коэффициенты концентрации напряжений для внешних мелких и глубоких плоских и асимметричных выточек, внутренних отверстий, а также для выточек с острыми углами при различных видах напряженного состояния (чистое растяжение, чистый изгиб, чистый сдвиг, чистое кручение).  [c.131]

Как задача о кручении стержня, так и задача об изгибе (чистом и поперечном) решается не только для условий чисто упругой работы материала, но и применительно к упруго-пластической стадии его работы, а также применительно к работе стержня при указанных на него воздействиях, если материал обладает свойством вязкоупругости.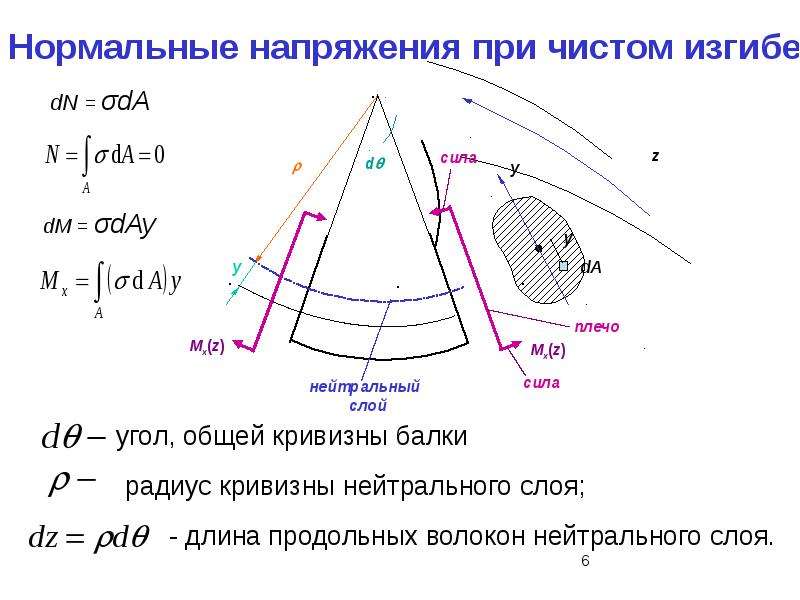  [c.8]

Мх (в силу ТОГО, что изгиб чистый) и Е1х (в силу того, что рассматривается призматический брус). Постоянство вдоль оси балки величины Кд.= 1/р (кривизны) означает, что изогнутой осью призматической балки при чистом изгибе является дуга окружности. Во-вторых, чем больше величина Е1х, тем меньше рх- Вследствие этого Е1X естественно назвать жесткостью стержня при изгибе. Этот фактор имеет физико-геометрическую природу. Множитель Е характеризует жесткость материала, а множитель Iх— жесткость балки, обусловленную геометрическими свойствами сечения (чем больше 1х, тем жестче балка). Линейку значительно труднее согнуть в ее плоскости, нежели расположив плашмя (рис. 12.8).  [c.110]

Энергия потенциальная 316 —при изгибе чистом — Энергия потенциальная 313  [c.979]

Испытания на усталость выполняют при разных напряженных состояниях образцов изгиб — чистый или консольный повторно-переменное растяжение — сжатие комбинированное сложнонапряженное состояние и т. д. Разрушение металлов при их усталости отличается от разрушения при однократных или повторяемых малое число раз нагрузках и характеризуется следующими особенностями [2, ПО, 147]  [c.441]

Такой случай изгиба, при котором поперечная сила в сечениях, перпендикулярных к оси балки, обращается в нуль, называется чистым изгибом. Чистый изгиб осуществим, если система внешних сил, приложенных к некоторому участку балки, приводится к парам сил (см., например, рис. 130). На практике, однако, чистый изгиб возможен лишь в случаях, когда собственный вес балки достаточно мал по сравнению с величинами приложенных к ней внешних сил и им можно пренебречь.  [c.215]

Рис. 6.8. Картина усталости при изгибе чистого никеля в вакууме [14) а —23°.С. ASo = 0.07%. N/Wf = 5% б —SSO G. Де = 0.12 %, JV/Nf = 1 % в

Основные положения, характеризующие деформацию чистого изгиба. Исследование напряженного состояния балок мы начнем с простейшего случая, так называемого чистого изгиба. Чистый изгиб есть частный случай изгиба, при котором в  [c.161]

Если все поперечные сечения какого-либо участка бруса испытывают чистый прямой изгиб, то весь этот участок находится в состоянии чистого изгиба. Другие участки этого же бруса могут находиться в состоянии поперечного прямого изгиба, чистого косого изгиба или поперечного косого изгиба.  [c.228]

При поперечном косом изгибе (как плоском, так и пространственном) в поперечных сечениях бруса возникают четыре внутренних силовых фактора поперечные силы и и изгибающие моменты Л1х, и Му. При чистом косом изгибе поперечные силы отсутствуют. Для расчетов на прочность и жесткость практически безразлично, будет ли изгиб чистым или поперечным, так как влияние поперечных сил, как правило, не учитывают.  [c.334]

ДЕФОРМАЦИЯ ИЗГИБА. НАПРЯЖЕННОЕ СОСТОЯНИЕ ПРИ ИЗГИБЕ. ПОПЕРЕЧНЫЙ ИЗГИБ. ЧИСТЫЙ ИЗГИБ  [c.326]

В. Изгиб чисто вязкой балки под действием постоянной осевой  [c.341]

Чистый изгиб……… Чистый цилиндрический изгиб. …………. 3.576 М 1,282 М 3,В10 М 4,280 М 1.998 М  [c.362]

Изгиб чистый — Расчет напряжений 26 Износостойкость — Классификация сопряжений по условиям изнашивания 41 — Расчет 41 — 46  [c.236]

ПИЧ — плоский изгиб чистый ШАЛ Пк — поковка  [c.29]

Изгиб называется чистым, если н сечении балки возникает только изгибающий момент Му 2,  [c.28]

Установка для испытания на ползучесть трубчатых образцов при изгибе и кручении. Одновременное нагружение образца изгибающим и крутящим моментами обеспечивается тем, что оси нагружающей балки 3 и образца J скрещиваются под некоторым углом (рис. 36). Рычаги 4 расположены под прямым углом к оси образца. Перемещающиеся опоры 2 дают возможность получать различный по величине изгибающий момент, в том числе и равный нулю. Изменение плеча рычага 4 позволяет регулировать величину крутящего момента Мкр, причем в случае приложения нагрузки в точке рычага, лежащей на оси образца (/i = 0), Мкр = 0. Таким образом, изменяя точку приложения нагрузки и места расположения опор, можно получать три вида нагружения чистый изгиб, чистое кручение и комбинированное нагружение с различными отношениями. Мкр//Иизг. В установке опоры выполнены в виде шариков, уложенных в полукольцевую канавку. Это дает возможность контакта опоры и захвата по линии окружности, что очень важно для создания изгибающего момента. В то же время при таком исполнении опор захват легко вращается, не препятствуя передаче крутящего момента на образец.  [c.42]

Наряду с функциональной автономностью температурная камера конструктивно связана с испытательной машиной или прибором. Учитывая это, камеры группируют в зависимости от вида испытаний к разрывным и универсальным машинам к машинам для испытаний на ползучесть, длительную прочность, релаксацию к машинам для испытаний на усталость при растяжении, сжатии или знакопеременных циклах растяжения-сжатня к машинам для испытаний на усталость при изгибе (чистом, консольном, вращающихся образцов) к машинам для испытаний на ударную прочность.  [c.278]

Существует два способа испытания на изгиб. Чистый (круговой) изгиб (рис. I, а) с нагружением образца через жесткую траверсу двумя силами Р/2, приложенными на одинаковых расстояниях (плечах) от опор, при этом эпюра изгибающих моментов имеет форму трапеции, на длине / изгибающий момент М постоянен п оп-вен (Р/2)а. Испытание на изгиб сосредоточенной силой, приложенной в середине проле-  [c.37]

Другие решения, полученные впервые Нейбером, относятся к пространственной полости в виде эллипсоида вращения в цилиндре при чистом изгибе, чистом сдвиге и крученин. Соответствующие формулы и графики содержатся в [В 14].  [c.294]

Таким образом, при одновременном изгибе и кручении в поперечном сечении вала учитывают только два внутренних силов кх фактора — изгибающий момент и крутящий момент Поперечной силой пренебрегают, полагая изгиб чистым (рис. 162, а).  [c.259]

Предел про ности при статическом изгибе чистых смол и композиционных пластмасс, так же как и при растяжении, примерно одинаков и лежит в пределах 400—800 kFJ m- за искл очешгем иескольких видов термопластов (вини-пластовых прессованных плит и др. ). Наибольшую прочность на изгиб имеют стеклотекстолиты и древесно-слоистые пластмассы.  [c.109]

Рассмотрим балку с одинаковыми по ее длине речными сечениями, имеющими вертикальную ось симм (левая и правая части сечения при наложении совпадз рис. 3.10. Пусть на концы балки действуют внешние м ты М, изгибающие ее в вертикальной плоскости. Тако нагружения, при котором в поперечных сечениях возн только изгибающий момент, называется чистым изгибом. чистом изгибе сечение А—А, расположенное на середине д балки после приложения момента М остается плоским, следует из условия симметрии — точки этого сечения не 1 смещаться влево или вправо, так как обе стороны равно ны. Если теперь рассмотреть [7, 19] сечение Б—Б, рас женное посередине левой (или правой) половины балки, Т( него можно сделать такое же заключение, и т. д. Таким (  [c.38]

Рассмотрим простейший случай изгиба — чистый изгиб, прн котором в поперечных сечениях стержня действует только изгибаюший момент. Например, в условиях чистого изгиба работают участки стержней [c.71]

It). Какие напряжения возникают п поперечных сечениях балок при чистом изгибе 1ю какому закону они изменяются Какие точки сечения балок ярляются самыми нагруженными (опасными)  [c.64]

Как выглядит «проектиророчный расчет» при чистом изгибе Какие ifjopMbi сечения балок являются рациональными при чистом изгибе  [c.64]

---

Прикладная механика (1977) — [ c.153 ]

Сопротивление материалов (1988) — [ c.132 ]

Сопротивление материалов (1970) — [ c.19 , c.113 , c.124 ]

Сопротивление материалов 1986 (1986) — [ c.259 , c.261 ]

Сопротивление материалов (1999) — [ c.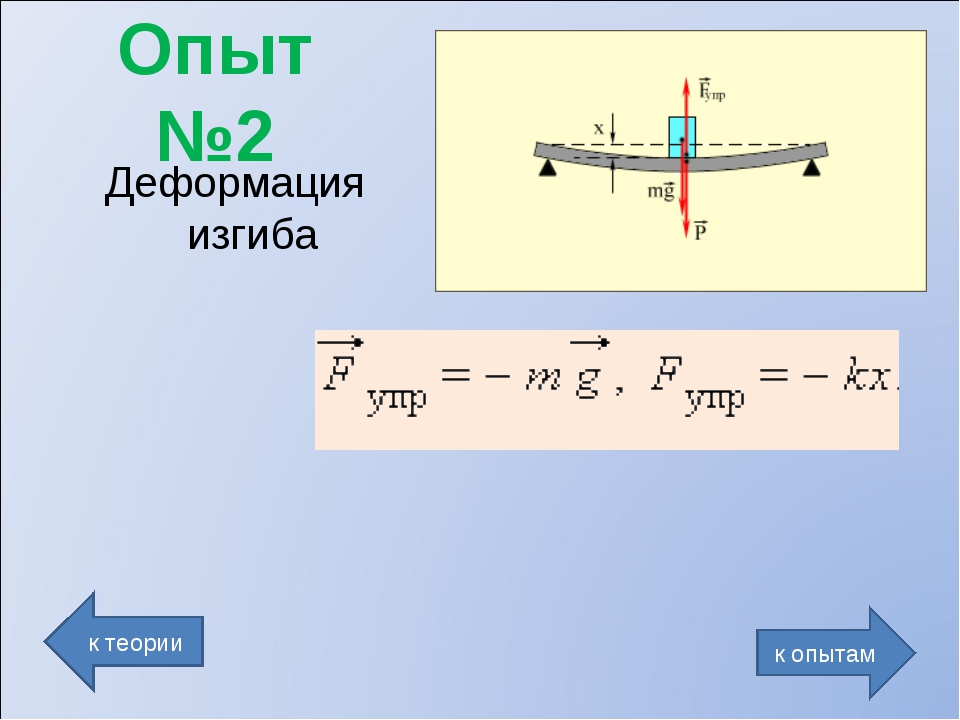 23 , c.157 ]

Сопротивление материалов (1986) — [ c.20 , c.133 ]

Теоретическая механика (1970) — [ c.106 , c.603 ]

Прикладная механика твердого деформируемого тела Том 1 (1975) — [ c.36 , c.58 ]

Сопротивление материалов (1976) — [ c.215 , c.224 ]

Сопротивление материалов (1959) — [ c.123 , c.248 ]

История науки о сопротивлении материалов (1957) — [ c.164 ]

Пластинки и оболочки (1966) — [ c. 45 , c.50 , c.55 , c.56 , c.60 , c.72 , c.359 ]

Механика материалов (1976) — [ c.145 , c.310 ]

Краткий курс сопротивления материалов Издание 2 (1977) — [ c.161 ]

Сопротивление материалов Издание 6 (1979) — [ c.115 ]

Сопротивление материалов Издание 13 (1962) — [ c.258 , c.323 ]

Композиционные материалы (1990) — [ c.226 , c.227 ]

Сопротивление материалов Издание 8 (1998) — [ c. 19 , c.154 , c.156 , c.175 ]

Сопротивление материалов (1964) — [ c.197 ]

Сопротивление материалов (1962) — [ c.164 ]

Технический справочник железнодорожника Том 2 (1951) — [ c.53 ]

Сопротивление материалов Том 1 Издание 2 (1965) — [ c.85 , c.194 , c.305 ]

---

Чистый изгиб балки прямоугольного сечения

Пример 16.5. Рассмотрим известную задачу сопротивления материалов — чистый изгиб балки прямоугольного сечения единичной ширины (рис. 16.8).  [c. 337]

Главная часть научной работы Сен-Венана относится к математической теории упругости, и о ней будет сказано далее. Но он внес многое также и в элементарное учение о сопротивлении материалов, в особенности в теорию изгиба стержней ). Он первый исследовал точность допущений, лежащих в основе теории изгиба, а именно 1) поперечные сечения балки остаются при ее деформировании плоскими и 2) продольные волокна балки при этом не оказывают давления друг на друга, находясь в состоянии простого осевого растяжения или сжатия. Он доказывает, что оба эти допущения строго выполняются лишь в случае чистого изгиба, когда на балку действуют две равные, противоположно направленные пары, приложенные по концам. Исследуя чистый изгиб балки прямоугольного сечения (рис. 63, а), он показывает, что изменения  [c.164]

В качестве примера рассмотрим чистый изгиб балки прямоугольного сечения, высотой h, шириной Ь. Положим, что поперечные сечения остаются в процессе изгиба плоскими и что материал обладает одинаковыми свойствами при растяжении и при сжатии, так что нейтральная линия проходит через центр тяжести поперечного сечения. Пусть о а о обозначает наибольшее напряжение, а а —напряжение на расстоянии у от нейтральной оси. Тогда из уравнения (с) находим  [c.448]

Сначала рассмотрим простейший случай — чистый изгиб балки прямоугольного сечения и определим для него предельный момент (рис. 13.7).  [c.430]

Для чистого изгиба балки прямоугольного сечения  [c.143]

При чистом изгибе балки прямоугольного поперечного сечения и последующей разгрузке возникли остаточные напряжения (рис. а). Проверить, что после нагружения балки с указанными остаточными напряжениями такими же моментами противополож-  [c.143]

Изгиб. В случае чистого изгиба бруса прямоугольного сечения, когда изгибающий момент по длине балки не изменяется, можно считать, что материал находится в одноосном напряженном состоянии, на выпуклой стороне балки волокна растянуты, а на вогнутой — сжаты.  [c.96]

Уравнение (V.20) устанавливает связь между хрупкой прочностью при чистом изгибе балки прямоугольного поперечного сечения и кручении круглого стержня. Надо полагать, что при переходе к одноосному растяжению и чистому сдвигу, которые можно рассматривать как предельные случаи изгиба и кручения, когда  [c.144]

Рассмотрим участок балки прямоугольного сечения, который находится в состоянии чистого изгиба. На рис. 11.4.1, а показан участок балки до приложения изгибающих моментов, а на рис. 11.4.1, в — с приложенными моментами. Нанесем на балку две риски АВ и СО, отстоящие друг от друга на расстоянии с1х.  [c.186]

Поперечный изгиб. При поперечном изгибе, кроме нормальных напряжений ст , в балке возникают касательные напряжения т . Соотношение между нормальными и касательными напряжениями зависит от отношения высоты балки к ее длине. Для длинных балок величина касательных напряжений мала по сравнению с нормальными. Поэтому в рассматриваемой задаче касательными напряжениями будем пренебрегать, считая балку достаточно длинной. Тогда решение (12.4), полученное для чистого изгиба, будет пригодно и для поперечного изгиба, только изгибающий момент будет теперь переменной величиной, зависящей от координаты 2. Переменной же величиной вдоль оси стержня будет и высота упругой зоны Из формулы (12.4) для балки прямоугольного сечения находим зависимость высоты упругой зоны от изгибающего момента М  [c.275]

Балка прямоугольного сечения имеет переменный по высоте модуль упругости, изменяющийся по закону Еу.В(1 2 У /Н). Определить грузоподъемность балки при чистом изгибе, если ( О- 1 — I 0 ). 80 МПа.  [c.70]

Рис. 12.3. Характер деформации балки прямоугольного поперечного сечения при чистом изгибе л) балка.до деформации с сеткой линий, нанесенных на ее поверхности, и нагрузка, вызывающая чистый изгиб б) балка, испытавшая чистый изгиб в) поперечное сечение балки прямоугольного сечения, испытавшей изгиб г) балка, загруженная моментами на торцах, создаваемыми нагрузкой, распределенной не по линейному закону 3) характер деформации балки, изображенной на фиг.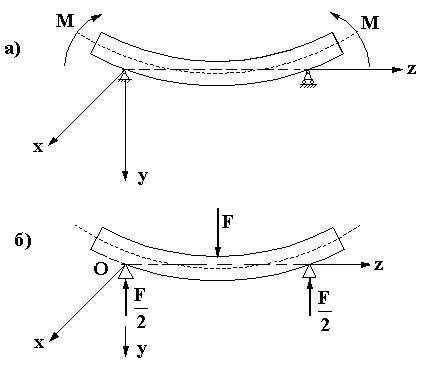 г е) поперечное сечение около торца (после деформации) в балке, изображенной на фиг. г.

Балка прямоугольного сечения при чистом изгибе, имеющая круглое отверстие с центром на оси (фиг. 3).  [c.405]

Некоторое приближенное представление о тех изменениях в распределении напряжений, которые возникают вследствие швов расширения, можно получить при сравнении явлений, которые возникают в простой балке прямоугольного сечения при чистом изгибе с явлениями, возникающими в балке при наличии в ней поперечных надрезов. i  [c.407]

При назначении надлежащих размеров поперечных сечений в стальных конструкциях иногда бывает необходимо учитывать не только те нагрузки, при которых материал начинает обнаруживать текучесть, но и такие, под действием которых сооружение окончательно теряет несущую способность, совершенно разрушаясь. Анализ свидетельствует, что если два сооружения спроектированы с одним и тем же коэффициентом запаса относительно предела текучести, то они могут характеризоваться весьма различными коэффициентами запаса в отношении полного разрушения. Рассмотрим, например, чистый изгиб балки и положим, что материал ее—сталь—следует закону Гука до предела текучести, с превышением же этого предела—удлиняется без упрочнения при этих условиях распределения напряжений, показанные на рис. 200, а и 200, б, будут отражать два предельных состояния 1) начало текучести и 2) полное разрушение. Соответствующие изгибающие моменты для прямоугольного поперечного сечения (рис. 200, в) определяются из следующих формул  [c.508]

Если на боковой поверхности балки прямоугольного сечения нанести поперечные риски и подвергнуть балку чистому изгибу,  [c.146]

Произведенный анализ- напряженного состояния изогнутой балки прямоугольного сечения показывает, что различные ее точки испытывают напряженные состояния разных видов. Нейтральный слой работает на чистый сдвиг, наиболее удаленные от него слои — на простое растяжение или сжатие, а в промежуточных слоях наблюдаются всевозможные переходные состояния от растяжения (сжатия) к чистому сдвигу, которые можно изобразить целой серией кругов Мора (рис. 180). Полюсы этих кругов непрерывно перемещаются от левого края круга (растянутая кромка) через центр (нейтральный слой) до правого края (сжатая кромка). Таким образом, при изгибе (в отличие от растяжения или кручения) материал испытывает не одно напряженное состояние, а совокупность различных напряженных состояний.  [c.174]

Балка прямоугольного сечения из упруго-идеально-пластического материала находится под нагрузкой на чистый изгиб.  [c.270]

Рассмотрим далее случай чистого изгиба балки. На рис. 19.6 показаны предельные эпюры нормальных напряжений в прямоугольном сечении балки высотой Л и шириной Ь при ее расчете по методу допускаемых напряжений (рис. 19.6, а) с учетом ди-  [c.550]

Возьмем балку, подвергающуюся чистому изгибу парами сил с моментом М (рис, 7. 9,а),. проведем сечение /—/, делящее ее на две части, и рассмотрим условия равновесия одной из них, например левой. Для простоты чертежа берем балку прямоугольного сечения, хотя ход наших рассуждений совершенно бы не изменился, если бы мы взяли балку, имеющую другую фор.му поперечного сечения, лишь бы она имела одну ось симметрии и пара сил действовала в плоскости симметрии, как указано выше. Ось X направим вдоль нейтрального слоя, тогда ось у будет  [c.167]

Картину деформации бруса при поперечном изгибе удобнее всего наблюдать на резиновой модели с нанесенной на ее боковые поверхности прямоугольной сеткой. Как показывает опыт, при нагружении бруса прямоугольная сетка искажается изменяются как размеры сторон прямоугольников, так и его углы. Причем угловая деформация, вызванная поперечной силой, по высоте сечения распределяется неравномерно достигает наибольшей величины у слоя, совпадающего с осью балки и падает до нуля в наружном слое (рис. 135). Отсюда следует, что гипотеза плоских сечений здесь не выполняется. Однако искривление поперечных сечений не сказывается на законе распределения нормальных напряжений и их величине. Поэтому считают, что нормальные напряжения при поперечном изгибе. меняются по тому же закону, что и при чистом изгибе, и могут быть определены по формуле (17.10)  [c.164]

С помощью эксперимента установлено, что если на боковую поверхность резинового бруска прямоугольного поперечного сечения нанести ортогональную сетку в виде продольных и поперечных прямых (рис. 7.26), то после деформирования на участке чистого изгиба продольные прямые принимают криволинейное очертание, а поперечные — остаются прямыми. При этом сетка остается ортогональной. Отсюда можно сделать вывод, что угловые деформации в плоскости изгиба отсутствуют, и поперечные сечения балки при деформации не искривляются.  [c.131]

ДЛЯ случая чистого изгиба показано пунктиром на рис. 20.17 (в зоне действия растягивающих напряжений ширина сечения уменьшается, а в зоне действия сжимающих напряжений — увеличивается). Отметим, что задача определения перемещений точек поперечного сечения и искажения формы контура прямоугольного сечения балки при чистом изгибе относится к простейшим задачам теории упругости.  [c.433]

М. Наука, 1978), иллюстрирующий зависимость, использованную Корню. На этом рисунке 1 — ось балки (окружность радиуса р), подвергнутой чистому изгибу 2 — испытавшее деформацию первоначально прямоугольное поперечное сечение балки (в опытах Корню отношение высоты поперечного сечения к ширине было намного меньше единицы)  [c.575]

С этой целью были сравнены две балки прямоугольного поперечного сечения обе балки имели ширину 0,5 см и высоту 3,18 см по одну сторону от резкого изменения сечения и 2,502 см по другую нижний контур балки прямая линия, а верхний контур в месте резкого изменения сечения образуется из четверти окружности радиуса / , продолжающейся в виде вертикальной прямой до пересечения с горизонтальной прямой контура, как показано на фиг. 5.23. Обе балки были подвергнуты чистому изгибу с моментом Ж = 71,9 кг. см. При радиусе / —0,555 см, распределение напряжений по контуру, изображенное на фиг. 5.23, обладает некоторыми интересными особенностями. На нижней грани, в точках, достаточно удаленных от места резкого изменения поперечного сечения, величина напряжения оказывается приблизительно такой, какая получается из обычной фор-М  [c.406]

Если бы мы принимали во внимание только вертикальную стенку балки, то предположения предыдущего параграфа были бы выполнены полностью. Но не принимать во внимание горизонтальных полок нельзя, так как они в рассматриваемом явлении играют существенную роль. Мы на основании предыдущего знаем, что при переходе плоской формы равновесия в искривленную кроме изгиба приходится учитывать и кручение. В шестой главе мы уже детально занимались кручением прокатных балок и в 70 нашли удобное приближенное решение для двутавровой балки. Но в задаче об устойчивости плоской формы равновесия при изгибе кручение следует рассматривать совершающимся при других граничных условиях на концах балки, чем в случае чистого кручения. Как и в предыдущем параграфе, мы рассмотрим случай балки, защемленной одним концом.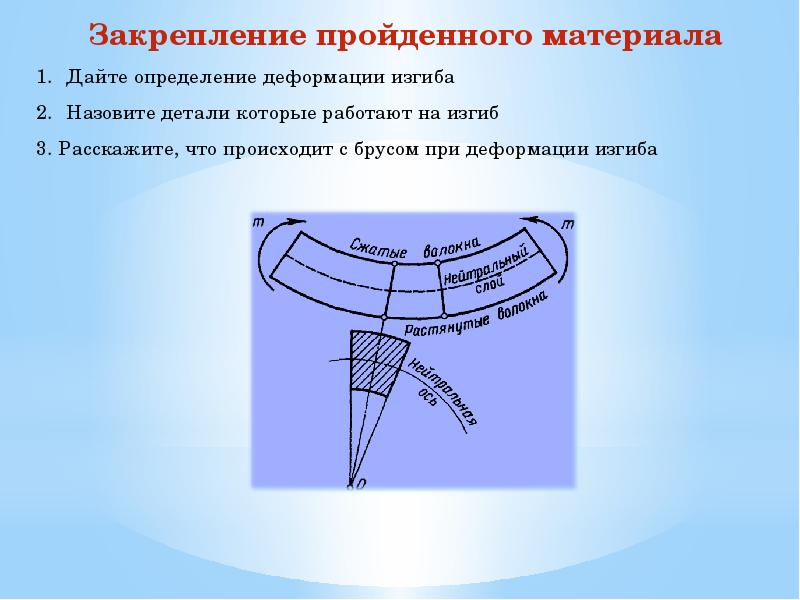 Если бы на свободном конце такой балки действовал крутящий момент, ось которого совпадала бы с осью балки, то мы не получили бы случая чистого кручения, так как на защемленном конце поперечное сечение вынуждено оставаться плоским, в то время как в случае чистого кручения оно перекашивалось бы ). Чтобы осуществить такие граничные условия в точности, можно поступить так воспрепятствовать повороту обоих концов балки около оси ее, а к среднему сечению приложить некоторый момент. Тогда вследствие симметрии среднее поперечное сечение будет оставаться плоским. Само собой разумеется, что сказанное относится к балке любого сечения. В предыдущем параграфе в случае прямоугольного сечения мы это обстоятельство оставляли без внимания, так как там оно большого влияния не оказывало. В случае же двутавровой балки дело обстоит иначе. Сохранение плоской формы концевого сечения имеет здесь потому большее влияние на угол закручивания балки, который получается от действия на свободный конец крутящего момента, что в силу рассматриваемого граничного условия горизонтальные полки, особенно вблизи места защемления, работают на изгиб. Подобный случай кручения стержня эллиптического сечения при  [c.335]

Деформация повлечет за собой некоторое искривление плоских оснований пластинки. Однако вследствие малой толщины пластинки искривление это будет весьма малым. Например, возьмем случай чистого изгиба прямоугольной балки, рассмотренный в 33. Свободные от нагрузки боковые ребра поперечного сечения наклоняются на угол (рис. 44, бу, однако из формулы (5.31) 33 видно, что угол этот пропорционален ширине балки Ь значит,  [c.141]

Резкое изменение сечения прямоугольной балки при чистом изгибе (фиг. 54 )  [c.1106]

Надо заметить, что ввиду отсутствия касательных напряжений в поперечном сечении (чистый изгиб) может показаться, что никакой прочности от склейки вообще не надо требовать. В действительности мы обычно не рассматриваем торцы балки, где приложена внешняя нагрузка. Если же ее распределение отличается от такового для внутренних нормальных напряжений (в неповрежденной балке), то при расслоении, вообще говоря, изменится распределение напряжений в поперечном сечении и это приведет к высвобождению энергии. Если исходить из требования гарантированной прочности (при любых торцевых распределениях нормальных нагрузок), т. е. ставить требование с запасом , то следует считать, что торцевой момент приложен лишь к одной из склеенных балок. Тогда (для балок прямоугольного поперечного сечения) начальная UQ и после отслоения плотности потенциальной энергии деформации следующие  [c.17]

ОНО имеет в точках, определяемых координатами T = th = Когда эллипс очень узок, эти значения весьма велики и точки, в которых они действуют, близки к концам большой оси. Имеются решения для эллиптического отверстия в пластинке, находящейся под действием чистого изгиба в своей плоскостии параболического распределения касательных усилий, которое возникает в тонкой балке прямоугольного сечения ), для эллиптического отверстия с равными и противоположными по знаку сосредоточенными силами, приложенными по концам малой оси ), а также для жесткого и упругого включений, заполняющих отверстие в растянутой пластинке ). Рассматривались и более общие виды решений в форме рядов для действительной функции напряжений ф в эллиптических координатах ). Эквивалентные им комплексные потенциалы можно построить из функций, использованных или упомянутых здесь вместе с аналогом простых функций, приведенных в задачах на стр. 197, если необходимо учесть влияние дислокаций, а также сосредоточенных сил и моментов. Решение для общего случая нагружения эллиптического отверстия дается позже в 67—72.  [c.204]

Трещина в балке прямоугольного сечення. Цусть балка прямоугольного поперечного сечения подвергается знакопеременному чистому изгибу моментом, М, приходящимся на единицу толщины балки (в направлении нормали к плоскости рис. 139), так что Мщах М —Мтах- Пусть трещины длины I развиваются симметрично с краев полосы шириной L (предполагаются выполненными условия плоской задачи теории упругости). Считаем, что при сжатии трещина закрывается. В этом случае коэффициент интенсивности напряжений равен  [c.351]

Балка прямоугольного сечения из упруго-идеальнопластического материала подвергается нагрузке, приводящей к чистому изгибу (рис. 8.21).  [c.275]

Задача 16.30. Дано а , Ъ, Л. Определить максимальные остаточные напряжения после разгрузки балки прямоугольного сечення Ьхку, испытывающей чистый изгиб. До разгрузки балка была доведена до пластического состояния по всему сечению. Использовать теорему А. А. Ильюшина о разгрузке.  [c.346]

В главе XII, посвященной изгибу, будут более точно указаны условия его возникиовеиия. Приведенные здесь условия возникновения изгиба без одновременного кручения справедливы для балки, поперечное сечение которой имеет две оси симметрии. Изгиб обычно сопровождается и сдвигом, различным у разных элементов балки. Исключение составляет изгиб стержня моментами, приложенными к его концам. В этом случае сдвига нет, а изгиб называется чистым (рис. 1.8,з). Чистым сдвигом называется деформация, которую испытывает прямоугольный параллелепипед, по четырем граням которого, перпендикулярным одной и той же плоскости, действуют касательные силы, равномерно распределенные по граням, имеющие одинаковую интенсивность и направленные так, как это показано на рис. 1.8, U.  [c.36]

А. Фёппль интересовался в то время теорией изгиба кривых брусьев и провел большое число испытаний по определению прочности сцепок железнодорожных вагонов. Он полагал, что при вычислении наибольших напряжений в изгибаемом крюке вполне приемлемую точность дает формула простой прямолинейной балки. Профессор К. Бах в Штутгартском политехническом институте был иного мнения и исходил из теории изгиба кривого бруса, построенной Винклером в том предположении, что поперечные сечения кривого бруса остаются при изгибе плоскими. Прандтль получил строгое решение для чистого изгиба кривого бруса узкого прямоугольного поперечного сечения. Оно подтвердило, что поперечные сечения в условиях чистого изгиба остаются действительно  [c.469]

Получить выражение для энергии деформации U,, накопленной в балке при чистом изгибе (рис. 6.21, а), через максимальное нормальное напряжение возникающее в балке. Предполагается, что балка имеет прямоугольное поперечное сечение шириной Ь и высотой h. (Представить энергию U как функцию от максимального напряжения (Тщах модуля упругости Е и размеров балки.)  [c.266]

А. Возьмём балку, подвергающуюся чистому изгибу парами Ж (фиг. 182). Пользуясь методом сечения, разрежем балку сечением 1—/ на 2 части и рассмотрим условия равновесия одной из отсечённых частей, наприйер левой, показанной на фиг. 182 внизу. Для простоты чертежа балка взята прямоугольного сечения. Так как практически искривления балки ничтожны по сравнению с её размерами, то отсечённая часть изображена недеформированной.  [c.261]

На фиг. 23 в координатах т) показаны эпюры напряжений =2у1Й., где у — расстояние от нейтральной оси, /г — высота поперечного сечения Г1 = ст/атах(0), где о — напряжение в момент времени t, а Отаг(О) —максимальное напряжение в начальный момент времени) в поперечном сечении прямоугольной балки, находящейся в условиях чистого изгиба при постоянном  [c.258]

Првмер 16.3. Рассмотрим задачу о ползучести балки прямоугольного поперечного сечения при чистом изгибе (рис, 16.28).  [c.466]

---

Чистый изгиб — балка — Большая Энциклопедия Нефти и Газа, статья, страница 2

Чистый изгиб — балка

Cтраница 2

Формулу для определения нормальных напряжений выводят, яассматдивая чистый изгиб балки.  [16]

Уравнение (V.20) устанавливает связь между хрупкой прочностью при чистом изгибе балки прямоугольного поперечного сечения и кручении круглого стержня.  [17]

Уравнение (5.19), строго говоря, справедливо для случая чистого изгиба балки, т.е. когда изгибающий момент Mx ( z) имеет постоянное значение, а поперечная сила равна нулю. Однако это уравнение используется и в случае поперечного изгиба, что равносильно пренебрежению искривлении поперечных сечений за счет сдвигов, на основании гипотезы плоских сечений.  [18]

Статический аналог рассмотренной задачи ( см. (5.4.31)) соответствует чистому изгибу балки.  [19]

Это и есть искомая формула, дающая возможность вычислять нормальные напряжения при чистом изгибе балки в любой точке ее сечения.  [20]

Это и есть искомая формула, дающая возможность определять нормальные напряжения при чистом изгибе балки в произвольной точке поперечного сечения. Из формулы видно, что нормальные напряжения по сечению распределяются неравномерно.  [21]

На рис. 7.9 приведены экспериментальные зависимости, полученные в Иркутск — НИИхиммаше при чистом изгибе шарнирно-опертых балок.  [22]

Приравнивая критическое напряжение с минимальным коэффициентом защемления стенки поясами, определенное по формуле (7.45), расчетному сопротивлению, получим условную гибкость стенки Ст 5 5, при которой потеря устойчивости стенки от действия только нормальных напряжений ( в зоне чистого изгиба балки) будет происходить одновременно с расчетной потерей прочности балки.  [24]

Приравнивая критическое напряжение с минимальным коэффициентом защемления стенки поясами, определенное по формуле (7.45), расчетному сопротивлению, получим условную гибкость стенки Яст 5 5, при которой потеря устойчивости стенки от действия только нормальных напряжений ( в зоне чистого изгиба балки) будет происходить одновременно с расчетной потерей прочности балки.  [26]

Выявленные на начальном этапе исследований, эти распределения напряжений показали, что использование классических методик проектирования, основанных на использовании таких критериев, как MC / J и VQ / J, может привести к значительным ошибкам даже для столь простого случая, как чистый изгиб балки коробчатого сечения.  [27]

Анализ чистого изгиба балки, выполненный в § 12.5 при помощи аппарата теории упругости, полностью подтвердил правомочность гипотез, принятых в § 12.3, на основе которых была построена элементарная теория чистого изгиба балки. На самом деле то, что постулировались этими гипотезами в случае чистого изгиба представляет собой закон.  [28]

Таким образом, приходим к следующим важным заключениям. При чистом изгибе несимметричной балки плоскость, в которой действует изгибающий момент ( плоскость ху), перпендикулярна нейтральной плоскости ( плоскости xz) только в том случае, когда оси у и z являются главными центральными осями поперечного сечения. Отсюда следует, что если изгибающий момент действует в главной плоскости, то эта плоскость становится плоскостью изгиба, нейтральная ось перпендикулярна к ней и здесь справедлива обычная теория изгиба.  [30]

Страницы:      1    2    3

Чистый изгиб балки в условиях ползучести из разносопротивляющегося материала Текст научной статьи по специальности «Строительство и архитектура»

Механика деформируемого твёрдого тела

УДК 539.376

ЧИСТЫЙ ИЗГИБ БАЛКИ В УСЛОВИЯХ ПОЛЗУЧЕСТИ ИЗ РАЗНОСОПРОТИВЛЯЮЩЕГОСЯ МАТЕРИАЛА

А. М. Локощенко, К. А. Агахи, Л. В. Фомин

Московский государственный университет им. М. В. Ломоносова,

НИИ механики МГУ,

119992, Россия, Москва, Мичуринский пр-т, 1.

E-mails: [email protected], [email protected], [email protected]

Решены задачи о чистом изгибе балок прямоугольного и круглого поперечных сечений при установившейся ползучести с учётом различных характеристик материала при растяжении и сжатии. Определяющие соотношения установившейся ползучести приняты в виде дробно-степенных функций. Приводится сравнение решений задач для балок квадратного и круглого сечений с одинаковыми значениями осевых моментов инерции.

Ключевые слова: балки, изгиб, установившаяся ползучесть, разносопротивляе-мость материала, дробно-степенная модель, квадратное сечение, круглое сечение.

Введение. В настоящее время опубликовано довольно много работ, посвященных изучению чистого изгиба балок в процессе установившейся ползучести. Проведенный обзор некоторых из них [1-13] послужил поводом для дальнейшего исследования этой задачи. Задачи чистого изгиба балок при ползучести для материалов, имеющих одинаковые свойства на растяжение и сжатие, рассмотрены, например, в работах [1, 3-6, 10-13]. В этих работах в качестве определяющих соотношений в основном используются степенные и экспоненциальные функции. В работах [2, 7-9] рассматривается чистый изгиб балок в процессе установившейся и неустановившейся ползучести, в которых учитывается разносопротивляемость материала растяжению и сжатию. При этом для описания ползучести при изгибе авторы используют как степенные [2,7], так и экспоненциальные [9] определяющие соотношения. Во всех перечисленных работах, за исключением работ [12,13], используется феноменологический подход к описанию процесса ползучести. В работах [12,13] предложена методика решения одномерных краевых задач изгиба балки на основе структурной модели среды.

В настоящей статье исследуется чистый изгиб балок с различными формами поперечных сечений в процессе установившейся ползучести. В отличие от рассмотренных работ, для учета разносопротивляемости материала растя-

Александр Михайлович Локощенко (д.ф.-м.н., проф.), зам. директора, НИИ механики МГУ. Камилла Абдул Гусейн кызы Агахи (к.ф.-м.н., доц.), и. о. зав. лаборатории, лаб. прочности и ползучести при высоких температурах НИИ механики МГУ. Леонид Викторович Фомин, ведущий инженер, НИИ механики МГУ.

жению и сжатию принимается сингулярная дробно-степенная модель с различными значениями пределов кратковременной прочности при растяжении и сжатии [14,15].

Проводится сравнение полученных решений для балок круглого и квадратного поперечного сечений с равными значениями их осевых моментов инерции при действии одинакового изгибающего момента.

1. Чистый изгиб балки прямоугольного поперечного сечения. Рассмотрим чистый изгиб балки в условиях высокотемпературной ползучести. Материал балки при соответствующей температуре имеет разные значения пределов кратковременной прочности при растяжении аы > 0 и сжатии <752 < 0 (отношение пределов прочности а = —аь2І(Тьі- Примем, что сечение балки имеет две оси симметрии (Ох и Оу), изгибающий момент М действует в плоскости уОг. Высота сечения балки по оси Оу равна Н, ширина Ь, длина I удовлетворяет неравенствам I » Н, I » Ь.

В этом случае гипотеза плоских сечений имеет вид

Р = Х(У~Уо), (!)

где р = рг — скорость деформации ползучести; Х~ скорость изменения кривизны балки; у — координата, отсчитываемая от срединной линии балки (—0,5Н ^ у ^ 0,5Н)\ уо — координата нейтральной поверхности, на которой отсутствуют напряжения (сг(уо) = <тг(уо) = 0). Смещение нейтральной поверхности от оси симметрии (у = 0) балки при ползучести в рассматриваемой задаче происходит вследствие разносопротивляемости материала растяжению и сжатию.

Определяющие соотношения ползучести в одноосном случае примем в виде, предложенном С. А. Шестериковым и М. А. Юмашевой [14,15], в котором зависимость р от напряжения а имеет дробно-степенной вид:

р = а(—= а У. (2)

V л /(пі,. — п)(ҐТ — пі,- ) /

Таким образом, напряжённо-деформированное состояние изогнутой балки в любой момент времени определяется осевыми напряжениями а = и (у) и осевыми деформациями ползучести р = р(у,і). Мгновенными упруго-пластиче-скими деформациями пренебрегаем.

Уравнения равновесия балки имеют следующий вид:

/уо Г-Н/2 гуо гН/2 ^

{(Т-)(1у + / {(Т+)(1у = 0, / ((Т-)у(1у+ {(Т+)у(1у=—, (3)

-я/2 3уо 7-Я/2 3уо 0

где <т_, (7-1- — напряжения в сжатой и растянутой зонах балки соответственно. Введём следующие безразмерные переменные:

а =—а ь2/&ы, а = а/аы, 1=1А д> = 4М дг = 2ЛГ — _ _ н_<1х — =2У_

ЪН2аЬ1 ’ ЪНаЬ1 ’ Х <Ш 2 АсМ’ У Н’

С учётом введённых безразмерных переменных определяющее соотношение (2) преобразуется к следующему виду:

ф

сії

и

л/(1 — а)(а + а)

(4)

На рис. 1 представлены графики зависимости модуля скорости деформации |ф/(Й| от модуля безразмерного напряжения |<т| (4) при п = 1.

Согласно гипотезе плоских сечений (1) и определяющему соотношению (2) в безразмерных переменных имеем

ф

СІЇ

а2

(1 — а) (а + а)

га/2

= §(5-Л). (5)

Преобразуем последнее выражение: ¡.2

а

Рис. 1. Графики зависимости \с1р/(Щ от \а\ при а = 1,5: 1 — область растяжения; 2 — область сжатия

(1 — а) (а + а)

С& 1,1 — а.

\ 2/га

(у-уо)) =В(у)- (6)

V СІІ

Представим выражение (6) в виде квадратного уравнения относительно безразмерного напряжения а:

(1 + В)а2 + В (а — 1)<т — аВ = 0. (7)

В результате выражение для безразмерных напряжений принимает следующий вид:

-В{а — 1) ± л/В2(а — I)2 + 4(1 + В)аВ

а+’~ ——————2(ГТб)——————• (8)

Система уравнений равновесия (3) в безразмерных переменных приводится к виду

/Уо /•!

[а-)с!у+ / {(т+)(1у = 0; М =

■1 •’УО

ГУО /•!

/ (а-)уйу+ / (а+)уйу- (9)

‘-1 Но

Подставив выражения а_|_ и <т_ из (8) в (9) и учитывая (6), получим систему двух уравнений относительно уо и X-

В таблице в столбцах 1 и 3 приведены результаты решения системы (9) при М = 0,5, а = 1,5 для некоторых значений п. На рис. 2 сплошными линиями изображены вычисленные согласно (6), (8), (9) эпюры напряжений в балке при этих же значениях констант. На рис. 3 приведены зависимости смещения нейтральной оси у о от показателя степени п при а = 1,5.

2. Чистый изгиб балки круглого поперечного сечения. В настоящем пункте рассматривается чистый изгиб при ползучести балки круглого поперечного сечения радиуса К, изготовленной из материала с разными значениями преде-

Результаты численного решения систем уравнений для балок прямоугольного (столбцы 1 и 3) и круглого (столбцы 2 и 4) сечений

те Уо X X

1 2 3 4

1 -0,045 -0,038 0,696 0,803

3 -0,061 -0,049 0,148 0,172

15 -0,077 -0,061 0,00001 0,0000131

Т-, г. нейтральной оси уо от показателя те для

а для балок прямоугольного и круглого се- г

„ 1 n ir 1 г балок прямоугольного 1) и круглого 2)

чении при те = 1, 3, 15 и а = 1,5 4 ‘ „ 4 ‘

поперечных сечении

лов прочности при растяжении <751 и сжатии (Т52 (отношение пределов прочности по-прежнему равно a =

= —vb2/vbi)- Задача решается с учётом гипотезы плоских сечений. Примем, что сечение балки имеет две оси симметрии (Ох и Оу), изгибающий момент действует в плоскости yOz. Высота сечения балки по оси у равна 2R, ширина b = 2Rcos(p,

Lp — угол между радиусом и осью Ох (см. рис. 4), длина I удовлетворяет неравенству I R.

Как и в п. 1, напряжённо-де-формированное состояние изогнутой балки в любой момент времени определяется осевыми напряжениями <7 = и(у) и осевыми деформациями ползучести р = р(у, t). Мгновенными упруго-пластическими деформациями по-прежнему пренебрегаем.

В этом случае, как и в п. 1, гипотеза плоских сечений имеет вид

Рис. 4. Круглое и квадратное поперечное сечение балок с одинаковыми осевыми моментами инерции

Р = х(У~Уо), y = R sm<p, y0 = Rsm<p0. Введём безразмерные переменные

a = — оь2І(Уь\і д’ = о’/о’ы> t = tA;

(10)

При рассмотрении изгиба балок прямоугольного и круглого сечений все уравнения (5), (7), (8) совпадают, различие наблюдается только в уравнениях равновесия:

где сг+;_ выражаются через В (у) по формуле (8), а В (у) с учётом (6), (10) в безразмерных координатах принимает вид

Таким образом, в системе (11) величины и сро являются неизвестными.

3. Сравнение решений задач об изгибе балок круглого и квадратного поперечного сечения. Проведём сравнение решений задач об изгибе балок круглого и квадратного поперечного сечения (как частный случай прямоугольного поперечного сечения при Ъ = Н) при одном и том же изгибающем моменте с учётом равенства осевых моментов инерции. Из равенства осевых моментов инерции следует, что

Отсюда получим соотношение между радиусом К круглого поперечного сечения и стороной Н квадратного поперечного сечения:

Соотношение размеров круглого и квадратного поперечных сечений балок показано на рис. 4. Сравнивая выражения для безразмерных изгибающих моментов в случае квадратного М и круглого М поперечных сечений, получаем

В п. 1 для задачи изгиба при ползучести балки прямоугольного поперечного сечения был произведен расчёт для М = 0,5. Аналогично выполним расчёт для балки круглого сечения, нагруженной моментом М = 0,336.

В таблице в столбцах с номерами 2 и 4 приведены результаты решения

чений п. На рис. 2 штриховыми линиями представлены эпюры распределения напряжений ¿г для балки круглого поперечного сечения.

Из рис. 2 видно, что при п = 1 распределение напряжений близко к линейному. С ростом показателя п наблюдается перераспределение напряжений к характерному для идеально-пластического материала. Наряду с изменением эпюр напряжений в зависимости от показателя степени п наблюдается

/

/

7Г/2

7Г/2

(11)

Я4 тгЯ4

12 4

Я = (Зтг)1/4Я и 1,752Д.

М и 0,672М.

системы уравнений (11) при М = 0,5, М = 0,336, а = 1,5 для некоторых зна-

смещение нейтральной оси (сг(уо) = 0) от оси симметрии балки за счет раз-носопротивляемости материала.

На рис. 3 приведены графики зависимости смещения нейтральной оси уо от показателя степени п для балок круглого и квадратного поперечных сечений.

Сравнение эпюр распределения безразмерных напряжений и при различных значениях п для балок круглого и прямоугольного поперечных сечений (при одинаковых осевых моментах инерции) под действием одного и того же изгибающего момента показало, что величина этих напряжений по абсолютной величине больше для балки круглого поперечного сечения. Это можно объяснить тем, что вследствие гипотезы плоских сечений выдерживать основную часть нагрузки должны волокна, наиболее удаленные от плоскости симметрии, а у балки круглого сечения в этой области ширина меньше.

Из рис. 3 видно, что для любого п смещение нейтральной оси для балки круглого поперечного сечения меньше.

Легко показать, что в частном случае материала балок с одинаковыми свойствами (a = 1) в аналогичной задаче чистого изгиба смещения нейтральной оси не происходит (уо = 0).

Также необходимо отметить, что используемое дробно-степенное определяющее соотношение наиболее адекватно позволяет описывать процесс ползучести, так как оно ограничивает уровень допустимых напряжений пределами кратковременной прочности при растяжении и сжатии.

Заключение. Решены задачи о чистом изгибе балки при ползучести с учётом различия свойства материала при растяжении и сжатии. Определяющее уравнение принято в виде сингулярной дробно-степенной зависимости скорости ползучести от напряжения, мгновенные деформации не принимаются во внимание. Решения получены для прямоугольного и круглого поперечных сечений балок. На основании эпюр распределения напряжений по сечению балок проведено сравнение полученных результатов.

Представленные эпюры напряжений подтверждают гипотезу о смещении нейтральной оси балки при чистом изгибе в случае разносопротивляющегося материала.

Показано влияние показателя п в дробно-степенной зависимости на характер распределения напряжений.

Работа выполнена при поддержке РФФИ (проекты № 11-08-01015, 11-08-00007).

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Качанов Л. М. Теория ползучести. М.: Физматгиз, 1960. 456 с. [Kachanov L. М. Theory

of Creep. Moscow: Fizmatgiz, 1960. 456 pp.]

2. Работное Ю.Н. Сопротивление материалов. М.: Физматгиз, 1962. 456 с.

[Rabotnov Yu. N. Strength of Materials. Moscow: Fizmatgiz, 1962. 456 pp.]

3. Работное Ю. H. Ползучесть элементов конструкций. М.: Наука, 1966. 752 с.

[Rabotnov Yu. N. Creep of Structural Elements. Moscow: Nauka, 1966. 752 pp.]

4. Boyle J. Т., Spence J. Stress Analysis for Creep. London: Buttenworth, 1983. 296 pp.; русск.

пер.: Бойл Дж., Спенс Дж. Анализ напряжений в конструкциях при ползучести. М.:

Мир, 1986. 360 с.

5. Радченко В. П., Еремин Ю. А. Реологическое деформирование материалов и элементов конструкций. М.: Машиностроение-1, 2004. 264 с. [Radchenko V.P., Eremin Yu. А.

Rheological Deformation and Failure of Materials and Structural Elements. Moscow: Mashinostroenie-1, 2004. 264 pp.]

6. Сорокин О. В., Самарин Ю.П., Одинг И. А. К расчёту ползучести балок при изгибе// Докл. АН СССР, 1964. Т. 157, №6. С. 1325-1328; англ. пер.: Sorokin О. V., Samarin Yu. Р., О ding LA. Calculation of the Creep of Beams During Bending// Sov. Phys., Dokl.. Vol. 9. Pp. 728-733.

7. Никитенко А. Ф., Соснин О. В. Изгиб балки из материала с разными характеристиками ползучести при растяжении и сжатии // Проблемы прочности, 1971. №6. С. 67-70; англ. пер.: Nikitenko A. F., Sosnin О. V. Beam flexure for materials possessing different creep characteristics in tension and compression // Strength of Materials, 1971. Vol. 3, no. 6. Pp. 693-697.

8. Горев Б. В. К расчёту на неустановившуюся ползучесть изгибаемого бруса из материала с разными характеристиками на растяжение и сжатие / В сб.: Динамика сплошной среды: Сб. научн. тр. Вып. 14. Новосибирск, 1973. С. 44-51. [Corev В. V. То unsteady creep calculation of a flexible rod made of material with different characteristics for tension and compression / In: Dynamics of Continuous Media: Collected scientific papers. 14. Novosibirsk, 1973. Pp. 44-51].

9. Леллеп Я. Установившаяся ползучесть балок в случае материалов с разными характеристиками на растяжение и сжатие // Тр. Тартус. ун-та (Tartu Ulikooli toimetised), 1975. Т. 355, №15. С. 245-252. [Lellep Ja. Steady-state creep of beams in case of materials with different characteristics at tension and compression// Tr. Tartus. Un-ta., 1975. Vol. 355, no. 15. Pp. 245-252].

10. Еремин Ю. А., Кайдалова Л. В., Радченко В. П. Исследование ползучести балок на основе аналогии структуры уравнения состояния материалов и элементов конструкций // Машиноведение, 1983. №2. С. 67-74. [Eremin Yu. A., Kaydalova L. V., Radchenko V. P. The study of creep of beams based on the analogy of the structure of the equation of state of materials and structural elements // Mashinovedenie, 1983. no. 2. Pp. 67-74].

11. Локощенко А. М., Печенина H. E., Шестериков С. А. Долговечность цилиндрического бруса при чистом изгибе // Изв. вуз. Машиностр., 1988. № 9. С. 9-13. [Lokoshenko А. М., Pechenina N. Е., Shesterikov S. A. The durability of a cylindrical rod under pure bending // Izv. vuz. Mashinostr., 1988. no. 9. Pp. 9-13].

12. Басов М. В. Применение структурной модели стержневого типа для решения задачи изгиба и разрушения балки в условиях ползучести/ В сб.: Актуальные проблемы современной науки. Естественные науки: Тр. 3-й Междунар. конф. молодых учёных и студентов. Часть 1. Математика. Механика (30 сентября — 2 октября 2002 г.). Самара: СамГТУ, 2002. С. 47-48. [Basov М. V. Application of a structural model of rod type to solving the problem of bending and fracture of a beam under creep conditions / In: Actual Problems of Modem Science. Natural Sciences. Part 1. Samara: SamGTU, 2002. Pp. 47-48].

13. Андреева E.A., Агафонов А. А. Решение краевой задачи изгиба балки из пластически разупрочняющегося материала на основании структурной модели / В сб.: Актуальные проблемы современной науки. Естественные науки: Тр. Междунар. форума молодых учёных (9-й Междунар. конф.). Часть 1-3. Математика. Математическое моделирование. Механика (20-23 ноября 2008 г.). Самара: СамГТУ, 2008. С. 168-178. [Andreeva Е. A., Agafonov A. A. The solution of the boundary value problem of rod bending made of plastic softening material on the basis of the structural model / In: Actual Problems of Modern Science. Natural Sciences. Part 1-3. Samara: SamGTU, 2008. Pp. 168-178].

14. Шестериков С. А., Юмашева М. А. Конкретизация уравнения состояния в теории ползучести// Изв. АН СССР. Мех. те. тела, 1984. №1. С. 86-91. [Shesterikov S.A., Yumasheva М. A. Specification of Equation of State in Creep Theory// Izv. AN SSSR. Mekh. Tverd. Tela, 1984. no. 1. Pp. 86-91].

15. Шестериков С.А., Юмашева М. А. Вариант уравнения состояния при ползучести и его приложения/ В сб.: Вопросы долговременной прочности энергетического оборудования/ Труды ЦКТИ. Вып. 246. Ленинград: НПО ЦКТИ, 1988. С. 74-77. [Shesterikov S.A., Yumasheva М. A. Variant of state equations for creep and its

applications / In: Voprosy dolgovremennoiy prochnosti energeticheskogo oborudovaniya/ Trudy TsKTI. 246. Leningrad: NPO TsKTI, 1988. Pp. 74-77].

Поступила в редакцию 07/1/2012; в окончательном варианте — 22/1/2012.

MSC: 74К10; 74С99

PURE BENDING OF BEAMS MADE OF MULTIMODULAR BEHAVIOR MATERIAL UNDER CREEP CONDITIONS

A. M. Lokoschenko, K. A. Agakhi, L. V. Fomin

М. V. Lomonosov Moscow State University,

Research Institute of Mechanics,

1, Michurinsky pr., Moscow, 119192, Russia.

E-mails: [email protected], [email protected], lef [email protected]

The problem of pure bending of beams with rectangular and circular cross-section is solved at steady-state creep, taking into account the different characteristics of the material in tension and compression. Constitutive relations for steady-state creep are taken in the form, of fractional functions. A comparison of solutions of problems for beams with square and circular cross-section with the same values of the axial moments of inertia is given.

Key words: beams, bending, steady-state creep, multimodulus behavior of material, fractional model, square cross-section, circular cross-section.

Original article submitted 07/1/2012; revision submitted 22/1/2012.

Alexander M. Lokoschenko (Dr. Sci. (Phys. & Math.)), Deputy Director, Research Institute of Mechanics. Kamilla A. Agakhi (Ph. D. (Phys. & Math.)), Head of Laboratory, Lab. of Strength and Creep at High Temperatures, Research Institute of Mechanics. Leonid V. Fomin, Leading Engineer, Research Institute of Mechanics.

7. ПЛОСКИЙ ПОПЕРЕЧНЫЙ ИЗГИБ

Изгиб – вид деформации, при котором происходит искривление оси прямого бруса или изменение кривизны кривого бруса. Изгиб плоский (прямой изгиб) – случай изгиба, при котором внешние силы лежат в главной плоскости инерции и являются перпендикулярными к геометрическим осям. Если сечение имеет ось симметрии, то внешние силы располагаются в плоскости симметрии. Главная плоскость инерции – плоскость, проходящая через геометрическую ось бруса и главную ось инерции. Изгиб чистый – вид деформации, при котором из шести внутренних усилий не равно нулю одно – изгибающий момент Mz или My. Изгиб поперечный – случай изгиба, при котором в сечениях бруса наряду с изгибающим моментом М действует и поперечная сила Q. В нагруженном состоянии балка прогибается так, что часть волокон укорачивается, другая часть волокон удлиняется. Нейтральный слой – слой волокон, в котором нормальные напряжения отсутствуют. Нейтральная ось – след пересечения нейтрального слоя с плоскостью поперечного сечения. Балка – конструктивный элемент, с прямолинейной геометрической осью, обычно в виде бруса, работающий главным образом на изгиб. Балка простая – однопролетная балка без консолей, лежащая на двух опорах: шарнирно-подвижной и шарнирно-неподвижной. Расстояние между опорами называют пролетом. Консоль – балка с одним защемленным концом или часть балки, свешивающаяся за опору. Рис. 7.1. Схема взаимного расположения силовой плоскости и плоскостей инерции Силовая плоскость Главные плоскости инерции Опоры и опорные реакции Схемы реальных опорных устройств можно свести к трем типам. Шарнирно-подвижная опора допускает поворот опорного сечения и перемещение его в одном направлении. Опорная реакция перпендикулярно к плоскости опирания катков. Шарнирно-неподвижная опора допускает только поворот опорного сечения балки. Реакция имеет две составляющие: горизонтальную и вертикальную. Жесткая заделка (защемление) не допускает поворота опорного сечения и любых его перемещений. Имеет три реакции: горизонтальную и вертикальную составляющие, а также опорный момент.

Когда стержень подвергается действию чистого изгибающего момента, как показано на рисунке, наблюдается, что осевые линии изгибаются, образуя окружные линии, а поперечные линии остаются прямыми и становятся радиальными линиями.

Чистая гибка

Кинематика чистая гибка:

В процессе гибки появляются осевые линии, которые не продлить или заключить контракт. Поверхность, описываемая набором линий, которые не растяжение или сжатие называется нейтральной поверхностью.Линии на одной стороне нейтральная поверхность расширяется, а другая сжимается, так как длина дуги меньше с одной стороны и больше с другой стороны нейтральной поверхности. В На рисунке показана чистая поверхность как в исходной, так и в изогнутой конфигурации.

Осевая деформация в линейном элементе на расстоянии

y над нейтральной поверхностью определяется как

где r — радиус до нейтральной поверхности.

Стресс распределение в чистом изгибе:

По закону Гука осевое напряжение равно заданный через осевую деформацию соотношением

Следовательно, осевое напряжение равно нулю на нейтральной поверхности и линейно увеличивается как единица удаляется от нейтральной оси.

Осевая нагрузка и расположение нейтральной оси:

Там — нулевая осевая нагрузка в элементе при чистом изгибе.Следовательно, осевая нагрузка создаваемое напряжением должно быть нулевым. Осевая нагрузка , создаваемая напряжение , приложенное к площади поперечного сечения дается приближенным соотношением

полную нагрузку на поперечное сечение можно рассчитать, интегрировав это соотношение по поперечному сечению. Это дает

С осевая нагрузка равна нулю во время чистого изгиба, можно сделать вывод, что для чистого изгиба

читатель напоминает, что положение центра тяжести области рассчитывается по отношение

Следовательно, чтобы осевая нагрузка была равна нулю, нейтральная ось должна проходить через центр тяжести поперечного сечения (т.е.е., y _c = 0). В случае, если осевая нагрузка не равна нулю, положение нейтральной оси относительно центра тяжести поперечного сечения можно рассчитать из отношение

Изгибающий момент и его отношение к радиусу кривизны:

изгибающий момент около нейтрали поверхность, созданная нормальной нагрузкой в результате нормальное напряжение , действующее на площадь поперечного сечения можно рассчитать по

Интеграция по поперечному сечению, чтобы получить полный момент, передаваемый через крест раздел дает

напоминая что интеграл в этом соотношении есть момент площади инерции I относительно нейтральной оси (линия, полученная в результате пересечения креста сечения и нейтральной поверхности), соотношение между изгибающим моментом M и радиусом кривизны r нейтральной оси балки становится

Из этого соотношения можно вычислить выражение для напряжение как функция изгибающего момента, подставив в выражение для осевого напряжения это соотношение для радиуса кривизны.Это дает

Как можно Как видно на рисунке, максимальное и минимальное нормальные напряжения возникают в материал, наиболее удаленный от нейтральной поверхности (вверху или нижняя часть полосы в зависимости от фактического направления момента).

Мехрдад Негахбан и Университет Небраски, 1996-2000 гг.

Все права защищены

Копировать и распространять бесплатно только для личного пользования

Отделение Инженерная механика, Университет Небраски, Линкольн, NE 68588-0526

Вывод уравнения изгиба — важные факторы и методы в деталях

Уравнение изгиба — это подраздел теории изгиба.Эта теория, в свою очередь, в первую очередь предполагает, что балка подвержена деформации, когда сила действует на точку, проходящую через продольную ось балки. Таким образом, теория изгиба относится к изучению осевой деформации, вызванной такими напряжениями, и, следовательно, также известной как теория изгиба.

Что такое уравнение изгибающего напряжения?

Уравнение напряжения изгиба или просто уравнение изгиба подразумевает математическое уравнение, предназначенное для определения величины напряжения в балке.

Однако уравнение изгибающего момента предусматривает набор допущений, которые необходимо принять во внимание, чтобы получить точные данные о напряжениях изгиба.

Таким образом, исчерпывающие допущения уравнения изгиба следующие:

• Рассматриваемая балка должна быть прямой. Кроме того, он должен иметь постоянное поперечное сечение без аберраций.

• Балка должна быть изготовлена ​​из однородного материала. Он также должен иметь симметричную продольную плоскость.

• Вывод уравнения изгибающего момента утверждает, что точка приложенной нагрузки должна лежать в ее продольной плоскости симметрии.

• Одно из наиболее важных допущений в уравнении изгиба состоит в том, что отказ должен быть результатом потери устойчивости, а не изгиба.

• «E» или предел упругости остается постоянным как для растяжения, так и для сжатия.

• Плоское поперечное сечение остается плоскостью на протяжении всего процесса гибки.

Каковы факторы при выводе уравнения изгиба?

Коэффициенты или члены уравнения изгиба, используемые при выводе уравнения изгиба, следующие:

• M = Изгибающий момент.

• I = момент инерции, действующий на ось изгиба.

• σ = напряжение волокна на расстоянии «y» от нейтральной / центральной оси.

• E = Модуль Юнга материала балки.

• R = радиус кривизны этой изогнутой балки.

Однако, если расстояние до самого удаленного элемента c заменяет y, тогда

\ [\ frac {M} {I} = \ frac {{\ sigma \ max}} {c} \]

Следовательно, \ [{\ sigma _ {\ max}} = \ frac {{MC}} {I} = \ frac {M} {Z} \]

Где Z = I / c. Это Z — модуль сечения этой балки.

Как выполняется вывод формулы напряжения изгиба?

При выводе формулы напряжения изгиба в основном вычисляется величина изгибающих напряжений, возникающих в нагруженной балке.

Следовательно, уравнение напряжения изгиба включает следующие шаги —

Деформация в волокне AB = \ [\ frac {{{\ text {изменение длины}}}} {{{\ text {исходная длина}}}} \]

= \ [\ frac {{A’B ‘- AB}} {{AB}} \] [но AB = CD и CD = C’D’]

Следовательно, деформация = \ [\ frac { {A’B ‘- C’D’}} {{C’D ‘}} \]

При наличии CD и C’D’ на нейтральной оси напряжение на нейтральной оси становится равным нулю. Таким образом, эта нейтральная ось лишена какой-либо деформации от приложенной силы.

= \ [\ frac {{\ left ({R + y} \ right) \ theta — R \ theta}} {{R \ theta}} = \ frac {{R \ theta + y \ theta — R \ theta}} {{R \ theta}} = \ frac {y} {R} \]

Тем не менее, \ [\ frac {{{\ text {Stress}}}} {{{\ text {Strain}}} } \] = E (E = модуль упругости Юнга)

Таким образом, уравнение двух деформаций на основе двух соотношений имеет вид \ [\ frac {\ sigma} {y} = \ frac {y} {R} \]

Или \ [\ frac {\ sigma} {y} = \ frac {E} {R} \] ……………………………. (i)

С другой стороны, допустим произвольное сечение балки.2} \ delta A}} \]

Здесь Σy2δA — это свойство материала балки и предполагает второй момент площади поперечного сечения. Его далее обозначает символ I.

В результате

\ [M = \ frac {E} {R} l \] ……………………………. (Ii)

Таким образом, когда мы объединяем уравнение (i) и ( ii), мы приходим к следующему уравнению изгиба —

\ [\ frac {\ sigma} {y} = \ frac {M} {T} = \ frac {E} {R} \]

Таким образом, приведенное выше уравнение относится к выводу уравнения изгиба. Однако это чистый изгиб, потому что изгиб получается, несмотря на отсутствие силы.

За дополнительной информацией по этой теме следите на нашем сайте. Вы также можете скачать наше приложение Vedantu для дополнительного удобства.

Чистое напряжение изгиба — Сопротивление материалов Вопросы и ответы

Этот набор вопросов и ответов с множественным выбором прочности материалов (MCQ) посвящен «чистому напряжению изгиба».

1. В балках с простой опорой распределение напряжений _____ неоднородно.
a) Изгиб
b) Сдвиг
c) Растяжение
d) Сжимающее
Посмотреть ответ

Ответ: a
Пояснение: В балке с простой опорой существует напряжение сжатия выше нейтральной оси и напряжение растяжения ниже нее.Он загибается вогнутостью вверх. Следовательно, распределение изгибающих напряжений по сечению неоднородно.

2. Максимальные напряжения _________ возникают в верхней части волокна свободно опертой балки.
a) Растяжение
b) Сжимающее усилие
c) Сдвиг
d) Изгиб
Просмотр ответа

Ответ: b
Пояснение: Поскольку распределение изгибающего напряжения неравномерно по сечению в балках с простой опорой, максимальное сжимающее напряжение лежит выше нейтрального ось. Очевидно, самое верхнее волокно пучка.Максимальное растягивающее напряжение возникает в нижней части волокна.

3. Напряжение прямо пропорционально _______
a) E
b) u
c) y
d) R
Посмотреть ответ

Ответ: c
Пояснение: двумя уравнениями; мы имеем e = y / R & e = f / E
Приравнивая оба уравнения; мы получаем e = f / E = y / R
Следовательно, напряжение (f) прямо пропорционально расстоянию от нейтральной оси (y).

4. В крайнем волокне напряжение изгиба составляет ______
a) Минимальное
b) Нулевое
c) Постоянное
d) Максимальное
Посмотреть ответ

Ответ: d
Пояснение: Изгибающее напряжение определяется как сопротивление, оказываемое внутренним напряжением на изгиб.В балках напряжения возникают выше или ниже нейтральной оси, то есть в крайних волокнах. Следовательно, напряжение изгиба максимально на крайних волокнах.

5. Кривизна балки равна _____
a) EI / M
b) M / E
c) M / EI
d) E / MI
Посмотреть ответ

Ответ: c
Пояснение: От изгиба уравнение, E / R = M / I = f / y.
Где R называется «радиусом кривизны»
1 / R называется «кривизной балки».
Итак, 1 / R = M / EI.
Итак, кривизна балки прямо пропорциональна изгибающему моменту.

6. Напряжение кожи также называется ______
a) Напряжение сдвига
b) Напряжение изгиба
c) Боковое напряжение
d) Температурное напряжение
Посмотреть ответ

Ответ: b
Пояснение: изгибающий момент приводит к деформации или отклонению балка и внутреннее напряжение устойчивы к изгибу. Сопротивление изгибу, обеспечиваемое внутренним напряжением, называется напряжением изгиба, или «напряжением волокна», или «напряжением кожи», или «продольным напряжением».

7. _________ — полная энергия деформации, запасенная в теле.
a) модуль упругости
b) энергия удара
c) упругость
d) доказательная упругость
Посмотреть ответ

Ответ: c
Объяснение: Когда нагрузка действует на тело, происходит деформация тела, которая вызывает движение приложенная нагрузка. Таким образом, проделанная работа сохраняется в теле в виде энергии, и нагрузка снимается. Эта накопленная энергия, которая возникает из-за напряжения, называется упругостью.

8. В консольных балках напряжение _______ над нейтральной осью.
a) Сжимающий
b) Растягивающий
c) Температура
d) Сдвиг
Посмотреть ответ

Ответ: b
Объяснение: В консольной балке максимальное сжимающее напряжение возникает в нижней части большинства волокон, а максимальное растягивающее напряжение возникает в верхней части волокон ноль на нейтральной оси, следовательно, растягивающие напряжения лежат выше нейтральной оси.

9. Произведение модуля упругости (E) и полярного момента инерции (J) называется жесткостью на кручение.
a) Верно
b) Неверно
Посмотреть ответ

Ответ: b
Пояснение: Произведение модуля жесткости (C) и полярного момента инерции (J) называется жесткостью на кручение и дает поворот на один радиан в вал единичной длины.

10. Рассчитайте максимальное напряжение из-за изгиба стальной полосы толщиной 30 мм и шириной 60 мм, изогнутой вокруг круглого барабана 3.Диаметр 6 м [Возьмем модуль Юнга = 200 кН / м ² ].

a) 2341,76 Н / мм ²
b) 1666,67 Н / мм ²
c) 5411,76 Н / мм ²
d) 4666,67 Н / мм ²
Посмотреть ответ

72 Ответ: b
Пояснение: Толщина стальной полосы = 30 мм; b = 60 мм; d = 3,6 м
R = 3,6 / 2 = 1,8 м
E = 200 кН / м ²
y = 30/2 = 15 мм
E / R = f / y; f = 200000 × 15/1800
= 1666,67 Н / мм ² .

11.Прочность балок зависит только от ________
a) Сечение модуля
b) Момент инерции
c) Жесткость на изгиб
d) Момент сопротивления
Посмотреть ответ

Ответ: a
Пояснение: Отношение момента инерции к расстоянию до крайнее волокно называется модулем сечения. Луч тем сильнее, чем больше модуль сечения. Прочность балки зависит от модуля сечения. Балки с одинаковым модулем среднего сечения прочности одинаковы для балок.

12.Стальная пластина сгибается по круговой траектории радиусом 10 метров. Если сечение пластины имеет ширину 120 мм и толщину 20 мм, рассчитайте максимальное напряжение изгиба. [Рассмотрим модуль Юнга = 200000 Н / мм ² ].
a) 350 Н / мм ²
b) 400 Н / мм ²
c) 200 Н / мм ²
d) 500 Н / мм ²
Посмотреть ответ

Ответ: c
Пояснение : R = 10000 мм; y = 20/2 = 10 мм; E = 200000 Н / мм ²
По уравнению изгиба получаем E / R = f / y
f = 200000 × 10/10000
= 200 Н / мм ² .

Sanfoundry Global Education & Learning Series — Прочность материалов.

Чтобы практиковаться во всех областях сопротивления материалов, — это полный набор из 1000+ вопросов и ответов с несколькими вариантами ответов .

Примите участие в конкурсе сертификации Sanfoundry, чтобы получить бесплатную Почетную грамоту. Присоединяйтесь к нашим социальным сетям ниже и будьте в курсе последних конкурсов, видео, стажировок и вакансий!

(PDF) Аналитическое решение задачи чистого изгиба для оболочечной модели тонкостенной балки прямоугольного сечения

152 I.Кудрявцев В. Гоцелук, А.Е.Митяев, В.Г. Демин

Существующие методы расчета, основанные на гипотезах теории балок

[1] и [2], позволяют оценить работу всей конструкции в целом, но при

при этом нет возможности учитывать напряженно-механические нагрузки. деформированное состояние в локальных

участках тонкостенного поперечного сечения балки, в которых возникают касательные напряжения, вызывающие

деформаций поперечного сечения. Деление сечения зависит также от

других факторов: длины тонкостенной балки, толщины его стенки, условий

нагружения, крепления и т. Д.

Использование упрощенных моделей [1] и [2] в виде одномерных балок

, имеющих эквивалентные геометрические и инерционные характеристики, приводит к их

очень грубой модели, которая не позволяет создавать изделия с минимальными затратами.

массогабаритные параметры и лучшие функциональные и эксплуатационные характеристики-

теристики.

Самым простым решением учета тонкостенного сечения является использование

при расчете таких конструкций теории балок с добавлением эмпирических

поправочных коэффициентов [3].Однако полученные при этом результаты

сильно зависят от выбора значений этих поправочных коэффициентов, которые в справочниках

приведены в зависимости от сочетания определенных размеров поперечного

сечения балки. Выбор промежуточных значений будет неопределенным, так как на

этих интервалах наблюдается сильная нелинейность.

Расчетная методика, созданная на основе фундаментальных работ В.

З. Власов [4], А.Р.Ржаницына [5], Д. В. Бычков [6], являются развитием

теории балок для случая тонкостенных с осесимметричным сечением.

Основным достижением этих работ является оценка и учет

отслоения тонкостенного поперечного сечения в случае действия большого касательного напряжения на

ограниченного кручения или совместного действия изгиба и кручения. Недостатки такого подхода

вытекают из исходной одномерной расчетной схемы конструкции (балки)

, выбранной авторами [4], [5] и [6], поэтому напряженно-деформированное состояние

тонкостенного пучок в целом оценивается, без возможности определить его местное состояние

.

Условия эксплуатации прецизионных стержневых конструкций, таких как волноводы антенно-фидерной системы

, представляющие собой тонкостенные балки с прямоугольным поперечным сечением

Методы расчета потребности в напряженно-деформированном состоянии, позволяющие определить

высокая точность в целом и в любой местности.

Выполнить изложенные выше требования можно только пройдя

при моделировании тонкостенных балок от их одномерных моделей (балки,

балки

) до двумерных расчетных схем (пластины, оболочки) с соответствующими —

зависимостей теории пластин и оболочек [7] и [8].

Расчет тонкостенной балки с неосесимметричным поперечным сечением с использованием теории скорлуп

осложняется наличием складок (табличка справа

Высокотехнологичная крытая ферма в Саут-Бенде надеется откусить с рынка салата | Business

SOUTH BEND — Холодный, влажный и ветреный день — достаточно, чтобы напомнить нам, что зима еще не слишком далеко в зеркале заднего вида.

Но внутри нового здания площадью шесть акров на Уэст-Калверт-стрит в Саут-Бенде Мэтт Гура пристально следит за морем детских растений, которые заполняют теплицу размером с два больших розничных магазина, или 174 000 квадратных футов.

Это похоже на теплый день в начале лета внутри здания, в котором используются компьютеры и мониторы для управления освещением, жидкими питательными веществами, температурой, влажностью и даже углекислым газом, который любит растения.

Гура, директор по операциям Pure Green Farms — закрытой гидропонной фермы на юго-западе города, — называет ее «самой технологически продвинутой листовой теплицей в мире».

«И это в Саут-Бенде», — говорит он.

Хотя строительство крупной крытой фермы в северной Индиане может показаться странным — учитывая холодную погоду и вечные облака, которые, казалось бы, нависают над регионом каждую зиму, — изучали руководство компании Ceres Partners, занимающейся инвестициями в сельское хозяйство, из Саут-Бенд. проекту на долгие годы.

Они считают, что есть возможность подорвать торговлю салатом, в которой преобладают производители в Калифорнии, которые поставляют продукцию на рынки Среднего Запада.

Здесь больше солнечного света, чем многие из нас думают, и тот факт, что летом не слишком жарко, означает, что затраты на поддержание прохлады в здании не будут чрезмерными, сказал Гура.

Комбинация светодиодных ламп и натриевых ламп высокого давления будет дополнять потребности растений в освещении, а также имеется автоматизированная шторка, которую можно использовать для уменьшения количества света, поступающего в теплицу или выходящего из нее, по мере необходимости.

Зимой крытая ферма будет использовать тепло отходов близлежащего завода по производству этанола в Саут-Бенд, и в настоящее время ведутся переговоры о возможном использовании углекислого газа, производимого предприятием, если это будет экономически целесообразно для обоих предприятий.

Церере также понравилось расположение, потому что это недалеко от ее штаб-квартиры недалеко от Университета Нотр-Дам, а также основных транспортных связей, которые будут иметь решающее значение для доставки листовой зелени, производимой Pure Green Farms, в бакалейные лавки, рестораны и другим клиентам по всему региону, сказал Брэндон Зик, главный инвестиционный директор фирмы.

«В радиусе 300 миль проживает 55 миллионов человек, — сказал Джо МакГуайр, опытный руководитель по сбыту продукции, которого пригласили на должность генерального директора Pure Green Farms. «В радиусе 400 миль есть 75 миллионов человек».

Такое расстояние дает Pure Green значительное преимущество при транспортировке по сравнению с традиционными производителями листовой зелени, которые расположены в Калифорнии, Аризоне и других удаленных местах.

К тому времени, когда салат будет собран и переработан в Калифорнии, например, может потребоваться 10 дней, чтобы добраться до полок магазинов на Среднем Западе.И наоборот, ромэн, руккола и листовой салат, выращенные в Pure Green, могут появиться на полках магазинов через пару дней или даже раньше.

«Мы думаем, что на рынке будет большой спрос на более свежие продукты, выращенные на рынке», — сказал МакГуайр.

Первые партии были отправлены в магазины Kroger в Индиане, и скоро Pure Green появится в магазинах Martin’s Super Markets и других бакалейных лавках.

«Человеческие руки никогда не касались»

Помимо фактора свежести, Pure Green считает, что может отделиться от других поставщиков салатов, поскольку не использует пестициды или другие спреи, которые могут потребоваться для борьбы с насекомыми и болезнями растений на открытом воздухе.

Защита растений и устранение вероятности заражения имеют первостепенное значение на предприятии в Саут-Бенде, на котором в настоящее время работает 20 человек.

Сотрудники, входящие в теплицу, проходят через лоток с дезинфицирующим средством для обуви и надевают перчатки, куртки и сетки для волос.

После того, как семена помещены в смесь продезинфицированного торфа и древесного волокна с помощью машины, посадочные лотки перемещаются в теплицу, где им дают питательный напиток, пока они прорастают при менее интенсивном освещении, а затем растут при полном освещении.

В зависимости от сорта потребуется около 25 дней для того, чтобы ромэн, руккола и листовые салаты достигли стадии, когда они будут собраны молниеносными резаками, смешаны, упакованы и упакованы для отправки.

«От посадки до упаковки к ней никогда не прикасаются человеческие руки, пока ее не откроет покупатель», — сказал МакГуайр.

Ничего не пропало. Смесь питательных веществ, которая не потребляется растениями, собирается, очищается, тестируется и используется повторно; Торфяной материал в лотках для выращивания будет компостирован и использован для других сельскохозяйственных целей.

«Мы используем на 90% меньше воды, чем салат-латук, выращиваемый в полевых условиях», — сказал Гура, который до того, как присоединиться к команде Pure Green, занимал должность директора по производству на принадлежащих Ceres фермах Hop Head Farms в Бароде. «Я верю, что это будущее роста».

Хотя действующие законы не позволяют маркировать салат как органический, Зик и МакГуайр указали, что могут возникнуть судебные иски, поскольку по всей стране продолжают появляться предприятия по выращиванию в контролируемой среде.

«Он не классифицируется как органический, потому что мы не закапываем его в землю», — сказал МакГуайр.

Время решает все

Хотя для выращивания томатов и других сельскохозяйственных культур использовались помещения, производство листового салата в значительных объемах является более недавним явлением, вызванным расстояниями доставки, безопасностью пищевых продуктов и стремлением к производству продуктов местного производства.

Помимо фактора свежести, согласно данным Ceres, салат, произведенный на фермах Pure Green Farms, может ежегодно сокращать 500 000 миль грузовиков и до 300 000 фунтов пищевых отходов.

Ариана Торрес, доцент кафедры экономики сельского хозяйства в Университете Пердью, сказала, что сейчас самое подходящее время для таких предприятий, как Pure Green, потому что люди потребляют больше салата и настаивают на более качественной продукции.

«Потребители хотят чего-то местного и свежего», — сказал Торрес. «Люди также больше осведомлены о безопасности пищевых продуктов, и пандемия показала, что в цепочке поставок могут быть сбои».

Несмотря на то, что на рынке есть конкуренты, такие как Gotham Greens в Нью-Йорке и Чикаго и Little Leaf Farms в Массачусетсе, Pure Green все еще находится на переднем крае того, что может стать огромной тенденцией в будущем, сказал Зик. .

«Рынок огромен, и лишь малая его часть выращивается в закрытых помещениях», — сказал Зик, руководитель Ceres. «Хотя мы не будем первыми, кто это сделает, мы все еще рано начинаем заниматься этим и приобретаем важный опыт».

Заглядывая в будущее, бизнесу необходимо повысить эффективность за счет точной настройки высокоавтоматизированных процессов выращивания, сбора урожая и упаковки, сказал Гура.

Будущий рост

На проект уже потрачено около 25 миллионов долларов, но планируется провести до трех дополнительных фаз.В конечном итоге Green Farms может иметь около 16 акров закрытых теплиц и около четырех акров под крышей для посадки, переработки и упаковки.

С 64 акрами, принадлежащими Green Farms, и дополнительными 280 акрами, принадлежащими ее головной организации — Церере, — есть много возможностей для роста, включая возможность привлечения других операторов, имеющих опыт выращивания томатов, клубники и других продуктов.

«Мы были заинтересованы в создании там агротехнологического кампуса», — сказал Зик, добавив, что можно было бы установить партнерские отношения с Purdue, Notre Dame и другими университетами для работы над проблемами, связанными с сельским хозяйством с контролируемой средой.

Мэр Саут-Бенда Джеймс Мюллер был впечатлен тем, что он увидел во время экскурсии по Pure Green Farms в пятницу.

«Многие люди будут удивлены тем, что там происходит, и уровнем технологий», — сказал Мюллер. «Это отчасти лаборатория, отчасти сельское хозяйство, а отчасти передовое производство».

И он сказал, что с нетерпением ждет появления на полках магазинов салата, произведенного в Саут-Бенде.

«Их ферма послужит образцом для устойчивых и передовых методов ведения сельского хозяйства», — сказал он.

Откройте для себя Extreme Wood Bending ™

Pure Timber — это прежде всего производитель гнутых гнутых деревянных деталей, компонентов и изделий из гнутой древесины на заказ, а также продает твердую древесину, изготовленную методом холодного гнутья, для ваших собственных нужд в области гнутья древесины.

Древесина лиственных пород Cold-Bend ™ (Прессованная древесина, Compwood®) чаще всего прессуется в 5 известных североамериканских твердых породах: ясень, красный дуб, белый дуб, вишню и клен.Он также иногда доступен еще для 15 видов лиственных пород умеренной зоны, всего 20 видов, которые мы сжимаем. К этим другим видам относятся бук, вяз, гикори, пекан, черная саранча, медовая саранча, сассафрас, платан, кофейное дерево Кентукки, каркас, красная камедь, дуб живой, апельсин осейдж, малина и грецкий орех. Сжатие древесины не работает с импортными пиломатериалами, сушеными в печи пиломатериалами или любыми хвойными породами.

Это сырье для ваших приложений Extreme Wood Bending ™ использовалось для изготовления студийной и производственной мебели, архитектурного изготовления, реставрации лодок, токарной обработки дерева, скульптуры и производства музыкальных инструментов. Древесина лиственных пород Cold-Bend ™ — это прочная древесина твердых пород, гибкая в холодном состоянии, которая уникально подходит для самых требовательных проектов Extreme Wood Bending ™ . Она неотличима от чистой твердой древесины с прямыми волокнами, потому что она такая. Он только что был подвергнут тщательно контролируемому, но интенсивному продольному термомеханическому сжатию.

Древесина твердых пород была спроектирована так, чтобы быть чрезвычайно гибкой (при условии, что она влажная). Он используется дома в Pure Timber для изготовления изделий или отправляется вам в виде досок, обернутых пластиком, чтобы сохранять влажность в течение длительных периодов времени (от месяцев до лет), чтобы его можно было держать под рукой для текущих и будущих проектов.Его можно повторно распилить и отрегулировать с помощью обычных инструментов, за исключением электрорубанков и фрезерных станков, которые вызывают вырывание волокон при нанесении в направлении волокон. Влажную древесину можно строгать на абразивном станке, шлифовать поперечно, точить на токарном станке, фрезеровать после высыхания, шлифовать или распиливать любым способом, мокрым или сухим. Влажную древесину нельзя строгать или формовать на обычных настольных строгальных станках и промышленных строгальных станках, потому что они рвут и раскалывают волокна. После холодного сгибания вручную (или с помощью приспособлений, зажимов и приспособлений) древесина Cold-Bend ™ высушивается для фиксации формы.

Используйте прессованную древесину для Extreme Wood Bending ™ с радиусом кривизны, равным 5-кратной толщине доски без пара, без нагрева, без подкладных ремней и без упругой отдачи (плита толщиной 1 дюйм, изогнутая до радиуса 5 дюймов — наиболее крупнозернистые породы) (мелкозернистые породы используют соотношение 1: 6). Более узкие радиусы можно согнуть с помощью дуба и ясеня, если нужно немного понять, как дерево ведет себя. Несмотря на то, что это связано с паровой гибкой древесины, гибка с использованием древесины лиственных пород методом Cold-Bend позволяет создавать более экстремальные изгибы древесины и гибку в любой плоскости, даже при поворотах.А дерево гнутое холодным, пара не подаешь. Мы уже обработали его паром и сжали, поэтому, когда вы сгибаете его вручную, он растягивается до новой формы и высыхает в этой форме. В этом разделе еще шесть страниц. См. Вкладки в разделе «Откройте для себя»

Что означают Flying V, Flat Top, Pure Pop Camber или Camber? — Burton Snowboards

Какой изгиб доски мне подходит?

Одним из ключевых элементов того, как доска будет кататься, является ее профиль (форма, когда вы смотрите на нее сбоку) или изгиб.Каждый конкретный изгиб можно найти в разделе «Технические характеристики» на странице продукта каждой платы. Понимание различных изгибов доски может помочь вам определить, какая доска подходит для условий или местности, по которой вы катаетесь.

Мы предлагаем множество различных поворотов: Camber, Flying V, Flat top, Directional Camber, Directional Flying V и Directional Flat Top. Помните, что изгиб доски — лишь один из аспектов выбора доски для катания.

Обычный развал :

Боковой профиль развала похож на радугу.Испытанный и верный, камбер уже почти 40 лет является доминирующим изгибом досок в индустрии сноубордов. Сноуборды с камбером, заимствованные у изгибов горнолыжных лыж, обеспечивают точный поворот и контроль кромок, с подпружиненным щелчком из-за изгиба доски, что обеспечивает лучшие прыжковые характеристики. Опытные райдеры предпочитают этот поворот, особенно для жесткого карвинга и высокоскоростной езды. Даже когда речь идет о более мягких сноубордах для парков, изгибы досок обеспечивают исключительную управляемость и управляемость. Однако они не так снисходительны к ошибкам, и их сложнее научиться или развиваться, чем рокерский или гибридный изгиб.

Pure-Pop Camber :

Мы называем это «Diet Camber», так как его длина составляет около 70% от длины профиля изгиба, который имеет обычная доска изгиба. Зона выпуклости заканчивается сразу за каждым каналом, а плоская зона продолжается на несколько сантиметров длины, пока доска не перейдет в небольшой участок раннего подъема около носа и хвоста. Этот изгиб доски находится где-то между игривым плоским изгибом и точным изгибом изгиба. Он также предлагает увеличенный щелчок, поскольку плоские зоны перед ударами носом и хвостом обеспечивают дополнительную нагрузку и отскок.

Летающий V:

Этот изгиб представляет собой гибрид развала и коромысла, где коромысло — это кривизна, противоположная изгибу. У него есть выпуклость под обеими ступнями и качалка между ступнями, а также снаружи ступней. Носовая часть и хвост приподняты над снегом, что делает езду супер-игривой и плавной, уменьшая способность цепляться за край и позволяя доске лучше гладить в глубоком снегу. Изгиб под стопой дает вам контроль над кромкой и выталкивает там, где вы хотите, не жертвуя игривостью там, где вам это нужно.Flying V может сделать доску мягче, чем ее коллега с камбером. Например, Process Flying V против Process Camber; Flying V будет мягче, даже если они сделаны из тех же материалов. Предназначен для райдеров от новичка до среднего и фристайла, но обеспечивает универсальную платформу для прогресса и исследований.

Плоская вершина :

Эти доски идеально ровные по всей длине доски, с несколькими миллиметрами коромысла раннего подъема на кончике и хвосте.Эта форма — идеальное сочетание стабильности и точности изгиба, а также игривого характера рокера. Из-за отсутствия прогиба, который можно было бы выдавить за доску, для начала поворота требуется очень мало энергии. Плоские доски хорошо работают в любых условиях, от порошковых до плотно упакованных и грумеров. Это отличная форма доски для любого райдера.

Направленный развал:

У этого изгиба доски есть входной рокер, который добавляет подъемную силу носу, в то время как секция изгиба под обеими ногами поддерживает импульс и стабильность в глубоких поворотах и ​​изменчивых условиях.Этот изгиб подходит для тех, кто любит атрибуты традиционного изгиба, но хочет что-то, что будет разгоняться и легче плавать в порошке.