Расчёт балки задачи по сопромату примеры и решения

Содержание:

1. Напряжения в поперечных сечениях
2. Касательные напряжения
3. Пример решения задачи 1.
4. Пример решения задачи 2
5. Расчет на прочность
6. Пример решения задачи 3
7. Пример решения задачи 4

В инженерной практике часто применяются балки с поперечным сечением, имеющим вертикальную ось симметрии. Если внешняя нагрузка и реактивные усилия лежат в одной плоскости, которая совпадает с осью симметрии сечения, то балка будет изгибаться в той же плоскости. Такой изгиб называется плоским (рис.1).

При плоском поперечном изгибе в сечениях балки возникают два внутренних усилия — поперечная сила и изгибающий момент (рис.2).

Напряжения в поперечных сечениях

Поскольку поперечная сила является равнодействующей касательных напряжений (рис.3), а изгибающий момент — равнодействующей нормальных напряжений (рис.4), то, следовательно, в поперечных сечениях балки в общем случае возникают и нормальные напряжения и касательные

Можно показать, что нормальные напряжения распределяются по высоте сечения по линейному закону (рис. 5). Линия, во всех точках которой называется нейтральной линией. В рассматриваемом случае плоского вертикального изгиба нейтральная линия совпадает с осью

По мере удаления от нее напряжения возрастают по модулю, достигая наибольших по модулю значений в крайних точках сечения, наиболее удаленных от нейтральной линии.

Чтобы определить нормальные напряжения в произвольной точке используется следующая формула

где — величина изгибающего момента в рассматриваемом сечении, определяется по эпюре

— осевой момент инерции поперечного сечения, табличная величина;

— координата точки, в которой определяется напряжение.

Возможно вам будут полезны данные страницы:

Задачи на сжатие и растяжение по сопромату примеры и решения

Задачи на кручение по сопромату примеры и решения

Задачи на эпюры по сопромату построение примеры и решения

Задачи с двутавром по сопромату примеры и решения

Знак определяется с помощью эпюры Подробнее это будет рассмотрено при решении конкретных задач.

Преобразуя формулу (1), можно получить формулу для определения максимальных напряжений

где — осевой момент сопротивления сечения, табличная величина.

Касательные напряжения

Касательные напряжения в поперечном сечении балки определяются по формуле Журавского:

где — величина поперечной силы в рассматриваемом сечении, определяется по эпюре

— осевой момент инерции всего сечения, табличная величина;

— статический момент отсеченной части сечения, определяется по формуле:

— координата отсеченной части сечения;

ее площадь; — ширина сечения на уровне отсеченной части. Распределение касательных напряжений по высоте поперечного сечения зависит от формы самого сечения. На рис.6 приведены эпюры касательных напряжений для некоторых часто встречающихся форм поперечных сечений балки.

Как видно из этих рисунков, максимальной величины касательные напряжения достигают на нейтральной линии, а в крайних точках сечения они равны нулю.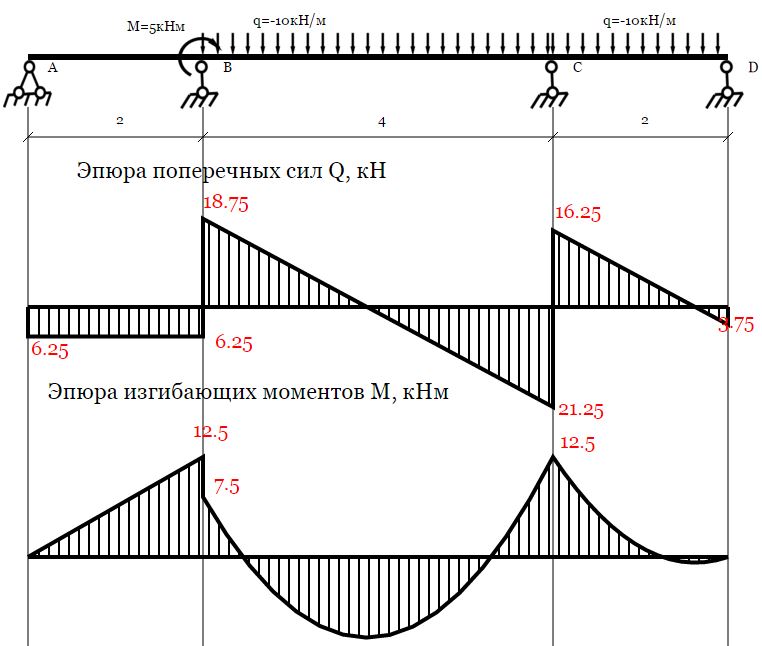 Рассмотрим примеры определения нормальных и касательных напряжений.

Пример решения задачи 1.

1) Пусть в опасном сечении балки, сечение которой изображено на рис.7, возникают изгибающий момент растягивающий нижние волокна и Определить нормальные и касательные напряжения в точке а также наибольшие нормальные и касательные напряжения. Построить эпюру распределения нормальных напряжений по высоте сечения. Решение:

1) Покажем на чертеже сечения положение центра тяжести и проводим оси Это будет система главных центральных осей, так как ось совпадает с осью симметрии сечения.

2) Выпишем из справочника [3, табл.5] формулу для определения момента инерции для треугольного сечения и подставим численные значения

3) Найдем нормальные напряжения в точке используя формулу (1)

Эти напряжения будут отрицательными, так как согласно условию задачи растягиваются нижние волокна сечения, то есть выше нейтральной линии (ось лежит зона сжатия, а ниже — зона растяжения. Точка находится в зоне сжатия, поэтому

4) Найдем наибольшее нормальное напряжение. Поскольку сечение несимметрично относительно оси то целесообразно пользоваться формулой (1). Из чертежа видно, что наибольшие сжимающие напряжения возникают в точке 1, так как эта точка является наиболее удаленной от нейтральной линии в зоне сжатия. Наибольшие растягивающие напряжения возникают в нижних точках сечения

По полученным данным построим эпюру (рис.7).

5) Найдем касательное напряжение в точке Сначала проведем через точку линию, параллельную оси и назовем отсеченной часть сечения, лежащую выше этой линии. Обозначим через точку центр тяжести отсеченной части и вычислим его координату Из чертежа видно

статический момент отсеченной части.

Используем формулу (3):

Здесь ширина основания отсеченной части.

Пример решения задачи 2

Пусть в сечении балки возникают поперечная сила и изгибающий момент растягивающий верхние волокна. Определить наибольшие нормальные и касательные напряжения.

Решение:

1) Покажем положение главной центральной системы координат

2) Найдем осевой момент сопротивления используя справочник

3) Так как сечение симметрично относительно оси и удобнее использовать формулу (2).

Согласно условию задачи растягиваются верхние волокна, поэтому

4) Из рис.6 следует, что наибольшие касательные напряжения возникают в точках, лежащих на нейтральной линии, поэтому проводим линию, совпадающую с осью Отсеченной будет, например, верхняя часть сечения, т. -центр тяжести этой части, т.е. полукруга.

Найдем используя формулу из [3, табл.5]:

Найдем момент инерции всего сечения (т.е. круга) [3, табл.5]:

Используем формулу (3)

Построим эпюры (рис.8).

Расчет на прочность

Расчет на прочность начинается с построения эпюр внутренних усилий балки Сечение, в котором величина достигает наибольшего значения, считается опасным сечением. Именно для такого сечения и делается расчет на прочность.

Если балка выполнена из пластического материала, который одинаково работает на растяжение и сжатие, то условие прочности записывается в виде:

где — расчетное сопротивление, заданная величина .

Если балка выполнена из хрупкого материала, который неодинаково работает на растяжение и сжатие, то используются два условия прочности.

где расчетное сопротивление на растяжение,

расчетное сопротивление на сжатие.

Как правило, расчет балки на прочность производится только по нормальным напряжениям, так как в подавляющем большинстве балок величина нормальных напряжений намного превосходит величину напряжений касательных. Однако в следующих случаях проверяется и условие прочности по касательным напряжениям:

• 1) если рассчитываемая балка выполнена из дерева, так как дерево плохо сопротивляется скалыванию вдоль волокон;
• 2) если балка короткая;
• 3) если на балку действуют большие сосредоточенные силы, приложенные на наибольших расстояниях от опор.

В последних двух случаях поперечные сечения в балке достигают большой величины, в то время как изгибающие моменты за счет малых плеч сравнительно невелики.

Условие прочности по касательным напряжениям записывается в виде:

где расчетное сопротивление на срез.

Пример решения задачи 3

Проверить выполнение условий прочности по нормальным и касательным напряжениям для деревянной балки (рис.9), если

Решение:

1) Строим эпюры Опасным является сечение в заделке, (рис.9).

2) Проверим условие прочности по нормальным напряжениям

Величина была определена в примере 2:

Условие прочности по нормальным напряжениям выполняется.

3) Проверим условие прочности по касательным напряжениям

Величину берем из примера 2:

Условие прочности по касательным напряжениям выполняется. Замечание.

Во всех последующих примерах будем использовать только условие прочности по нормальным напряжениям.