60 кубов это сколько литров: Литры в кубы

Содержание

Периметр, площадь и объем

Данный материал содержит геометрические фигуры с измерениями. Приведённые измерения являются приблизительными и могут не совпадать с измерениями в реальной жизни.

Периметр геометрической фигуры

Периметр геометрической фигуры — это сумма всех её сторон. Чтобы вычислить периметр, нужно измерить каждую сторону и сложить результаты измерений.

Вычислим периметр следующей фигуры:

Это прямоугольник. Детальнее мы поговорим об этой фигуре позже. Сейчас просто вычислим периметр этого прямоугольника. Длина его равна 9 см, а ширина 4 см.

У прямоугольника противоположные стороны равны. Это видно на рисунке. Если длина равна 9 см, а ширина равна 4 см, то противоположные стороны будут равны 9 см и 4 см соответственно:

Найдём периметр. Для этого сложим все стороны. Складывать их можно в любом порядке, поскольку от перестановки мест слагаемых сумма не меняется. Периметр часто обозначается заглавной латинской буквой P (англ. perimeters). Тогда получим:

P = 9 см + 4 см + 9 см + 4 см = 26 см.

Поскольку у прямоугольника противоположные стороны равны, нахождение периметра записывают короче — складывают длину и ширину, и умножают её на 2, что будет означать «повторить длину и ширину два раза»

P = 2 × (9 + 4) = 18 + 8 = 26 см.

Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, найдём периметр квадрата со стороной 5 см. Фразу «со стороной 5 см» нужно понимать как «длина каждой стороны квадрата равна 5 см»

Чтобы вычислить периметр, сложим все стороны:

P = 5 см + 5 см + 5 см + 5 см = 20 см

Но поскольку все стороны равны, вычисление периметра можно записать в виде произведения. Сторона квадрата равна 5 см, и таких сторон 4. Тогда эту сторону, равную 5 см нужно повторить 4 раза

P = 5 см × 4 = 20 см

Площадь геометрической фигуры

Площадь геометрической фигуры — это число, которое характеризует размер данной фигуры.

Следует уточнить, что речь в данном случае идёт о площади на плоскости. Плоскостью в геометрии называют любую плоскую поверхность, например: лист бумаги, земельный участок, поверхность стола.

Площадь измеряется в квадратных единицах. Под квадратными единицами подразумевают квадраты, стороны которых равны единице. Например, 1 квадратный сантиметр, 1 квадратный метр или 1 квадратный километр.

Измерить площадь какой-нибудь фигуры означает выяснить сколько квадратных единиц содержится в данной фигуре.

Например, площадь следующего прямоугольника равна трём квадратным сантиметрам:

Это потому что в данном прямоугольнике содержится три квадрата, каждый из которых имеет сторону, равную одному сантиметру:

Справа представлен квадрат со стороной 1 см (он в данном случае является квадратной единицей). Если посмотреть сколько раз этот квадрат входит в прямоугольник, представленный слева, то обнаружим, что он входит в него три раза.

Следующий прямоугольник имеет площадь, равную шести квадратным сантиметрам:

Это потому что в данном прямоугольнике содержится шесть квадратов, каждый из которых имеет сторону, равную одному сантиметру:

Допустим, потребовалось измерить площадь следующей комнаты:

Определимся в каких квадратах будем измерять площадь. В данном случае площадь удобно измерить в квадратных метрах:

Итак, наша задача состоит в том, чтобы определить сколько таких квадратов со стороной 1 м содержится в исходной комнате. Заполним этим квадратом всю комнату:

Видим, что квадратный метр содержится в комнате 12 раз. Значит, площадь комнаты составляет 12 квадратных метров.

Площадь прямоугольника

В предыдущем примере мы вычислили площадь комнаты, последовательно проверив сколько раз в ней содержится квадрат, сторона которого равна одному метру. Площадь составила 12 квадратных метров.

Комната представляла собой прямоугольник. Площадь прямоугольника можно вычислить перемножив его длину и ширину.

Чтобы вычислить площадь прямоугольника, нужно перемножить его длину и ширину.

Вернёмся к предыдущему примеру. Допустим, мы измерили длину комнаты рулеткой и оказалось, что длина составила 4 метра:

Теперь измерим ширину. Пусть она составила 3 метра:

Умножим длину (4 м) на ширину (3 м).

4 × 3 = 12

Как и в прошлый раз получаем двенадцать квадратных метров. Это объясняется тем, что измерив длину, мы тем самым узнаём сколько раз можно уложить в эту длину квадрат со стороной, равной одному метру. Уложим четыре квадрата в эту длину:

Затем мы определяем сколько раз можно повторить эту длину с уложенными квадратами. Это мы узнаём, измерив ширину прямоугольника:

Площадь квадрата

Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, на следующем рисунке представлен квадрат со стороной 3 см. Фраза «квадрат со стороной 3 см» означает, что все стороны равны 3 см

Площадь квадрата вычисляется таким же образом, как и площадь прямоугольника — длину умножают на ширину.

Вычислим площадь квадрата со стороной 3 см. Умножим длину 3 см на ширину 3 см

3 × 3 = 9

В данном случае требовалось узнать сколько квадратов со стороной 1 см содержится в исходном квадрате. В исходном квадрате содержится девять квадратов со стороной 1 см. Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:

Умножив длину на ширину, мы получили выражение 3 × 3, а это есть произведение двух одинаковых множителей, каждый из которых равен 3. Иными словами выражение 3 × 3 представляет собой вторую степень числа 3. А значит процесс вычисления площади квадрата можно записать в виде степени 3².

Поэтому вторую степень числа называют квадратом числа. При вычислении второй степени числа a, человек тем самым находит площадь квадрата со стороной a. Операцию возведения числа во вторую степень по другому называют возведением в квадрат.

Обозначения

Площадь обозначается заглавной латинской буквой S (англ. Square — квадрат). Тогда площадь квадрата со стороной a см будет вычисляться по следующему правилу

S = a²

где a — длина стороны квадрата. Вторая степень указывает на то, что происходит перемножение двух одинаковых сомножителей, а именно длины и ширины. Ранее было сказано, что у квадрата все стороны равны, а значит равны длина и ширина квадрата, выраженные через букву a.

Если задача состоит в том, чтобы определить сколько квадратов стороной 1 см содержится в исходном квадрате, то в качестве единиц измерения площади нужно указывать см². Это обозначение заменяет словосочетание «квадратный сантиметр».

Например, вычислим площадь квадрат со стороной 2 см.

Значит, квадрат со стороной 2 см, имеет площадь, равную четырём квадратным сантиметрам:

Если задача состоит в том, чтобы определить сколько квадратов со стороной 1 м содержится в исходном квадрате, то в качестве единиц измерения нужно указывать м². Это обозначение заменяет словосочетание «квадратный метр».

Вычислим площадь квадрата со стороной 3 метра

Значит, квадрат со стороной 3 м, имеет площадь равную девяти квадратным метрам:

Аналогичные обозначения используются при вычислении площади прямоугольника. Но длина и ширина прямоугольника могут быть разными, поэтому они обозначаются через разные буквы, например a и b. Тогда площадь прямоугольника, длиной a и шириной b вычисляется по следующему правилу:

S = a × b

Как и в случае с квадратом, единицами измерения площади прямоугольника могут быть см², м², км². Эти обозначения заменяют словосочетания «квадратный сантиметр», «квадратный метр», «квадратный километр» соответственно.

Например, вычислим площадь прямоугольника, длиной 6 см и шириной 3 см

Значит, прямоугольник длиной 6 см и шириной 3 см имеет площадь, равную восемнадцати квадратным сантиметрам:

В качестве единицы измерения допускается использовать словосочетание «квадратных единиц». Например, запись S = 3 кв.ед означает, что площадь квадрата или прямоугольника равна трём квадратам, каждый из которых имеет единичную сторону (1 см, 1 м или 1 км).

Перевод единиц измерения площади

Единицы измерения площади можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:

Пример 1. Выразить 1 квадратный метр в квадратных сантиметрах.

1 квадратный метр это квадрат со стороной 1 м. То есть все четыре стороны имеют длину, равную одному метру.

Но 1 м = 100 см. Тогда все четыре стороны тоже имеют длину, равную 100 см

Вычислим новую площадь этого квадрата. Умножим длину 100 см на ширину 100 см или возведём в квадрат число 100

S = 100² = 10 000 см²

Получается, что на один квадратный метр приходится десять тысяч квадратных сантиметров.

1 м² = 10 000 см²

Это позволяет в будущем умножить любое количество квадратных метров на 10 000 и получить площадь, выраженную в квадратных сантиметрах.

Чтобы перевести квадратные метры в квадратные сантиметры, нужно количество квадратных метров умножить на 10 000.

А чтобы перевести квадратные сантиметры в квадратные метры, нужно наоборот количество квадратных сантиметров разделить на 10 000.

Например, переведём 100 000 см² в квадратные метры. Рассуждать в этом случае можно так: «если 10 000 см² это один квадратный метр, то сколько раз 100 000 см² будут содержать по 10 000 см²»

100 000 см² : 10 000 см² = 10 м²

Другие единицы измерения можно переводить таким же образом. Например, переведём 2 км² в квадратные метры.

Один квадратный километр это квадрат со стороной 1 км. То есть все четыре стороны имеют длину, равную одному километру. Но 1 км = 1000 м. Значит, все четыре стороны квадрата также равны 1000 м. Найдём новую площадь квадрата, выраженную в квадратных метрах. Для этого умножим длину 1000 м на ширину 1000 м или возведём в квадрат число 1000

S = 1000² = 1 000 000 м²

Получается, что на один квадратный километр приходится один миллион квадратных метров:

1 км² = 1 000 000 м²

Это позволяет в будущем умножить любое количество квадратных километров на 1 000 000 и получить площадь, выраженную в квадратных метрах.

Чтобы перевести квадратные километры в квадратные метры, нужно количество квадратных километров умножить на 1 000 000.

Итак, вернёмся к нашей задаче. Требовалось перевести 2 км² в квадратные метры. Умножим 2 км² на 1 000 000

2 км² × 1 000 000 = 2 000 000 м²

А чтобы перевести квадратные метры в квадратные километры, нужно наоборот количество квадратных метров разделить на 1 000 000.

Например, переведём 3 500 000 м² в квадратные километры. Рассуждать в этом случае можно так: «если 1 000 000 м² это один квадратный километр, то сколько раз 3 500 000 м² будут содержать по 1 000 000 м²»

3 500 000 м² : 1 000 000 м² = 3,5 км²

Пример 2. Выразить 7 м² в квадратных сантиметрах.

Умножим 7 м² на 10 000

7 м² = 7 м² × 10 000 = 70 000 см²

Пример 3. Выразить 5 м² 13 см² в квадратных сантиметрах.

5 м² 13 см² = 5 м² × 10 000 + 13 см² = 50 013 см²

Пример 4. Выразить 550 000 см² в квадратных метрах.

Узнаем сколько раз 550 000 см² содержит по 10 000 см². Для этого разделим 550 000 см² на 10 000 см²

550 000 см² : 10 000 см² = 55 м²

Пример 5. Выразить 7 км² в квадратных метрах.

Умножим 7 км² на 1 000 000

7 км² × 1 000 000 = 7 000 000 м²

Пример 6. Выразить 8 500 000 м² в квадратных километрах.

Узнаем сколько раз 8 500 000 м² содержит по 1 000 000 м². Для этого разделим 8 500 000 м² на 1 000 000 м²

8 500 000 м² × 1 000 000 м² = 8,5 км²

Единицы измерения площади земельных участков

Площади небольших земельных участков удобно измерять в квадратных метрах.

Площади более крупных земельных участков измеряются в арах и гектарах.

Ар (сокращённо: a) — это площадь равная ста квадратным метрам (100 м²). В виду частого распространения такой площади (100 м²) она стала использоваться, как отдельная единица измерения.

Например, если сказано что площадь какого-нибудь поля составляет 3 а, то нужно понимать, что это три квадрата площадью 100 м² каждый, то есть:

3 а = 100 м² × 3 = 300 м²

В народе ар часто называют соткой, поскольку ар равен квадрату, площадью 100 м². Примеры:

1 сотка = 100 м²

2 сотки = 200 м²

10 соток = 1000 м²

Гектар (сокращенно: га) — это площадь, равная 10 000 м². Например, если сказано что площадь какого-нибудь леса составляет 20 гектаров, то нужно понимать, что это двадцать квадратов площадью 10 000 м² каждый, то есть:

20 га = 10 000 м² × 20 = 200 000 м²

Прямоугольный параллелепипед и куб

Прямоугольный параллелепипед — это геометрическая фигура, состоящая из грáней, рёбер и вершин.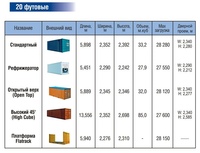 На рисунке показан прямоугольный параллелепипед:

Желтым цветом показаны грáни параллелепипеда, чёрным цветом — рёбра, красным — вершины.

Прямоугольный параллелепипед обладает длиной, шириной и высотой. На рисунке показано где длина, ширина и высота:

Параллелепипед, у которого длина, ширина и высота равны между собой, называется кубом. На рисунке показан куб:

Объём геометрической фигуры

Объём геометрической фигуры — это число, которое характеризует вместимость данной фигуры.

Объём измеряется в кубических единицах. Под кубическими единицами подразумевают кубы длиной 1, шириной 1 и высотой 1. Например, 1 кубический сантиметр или 1 кубический метр.

Измерить объём какой-нибудь фигуры означает выяснить сколько кубических единиц вмещается в данную фигуру.

Например, объём следующего прямоугольного параллелепипеда равен двенадцати кубическим сантиметрам:

Это потому что в данный параллелепипед вмещается двенадцать кубов длиной 1 см, шириной 1 см и высотой 1 см:

Объём обозначается заглавной латинской буквой V.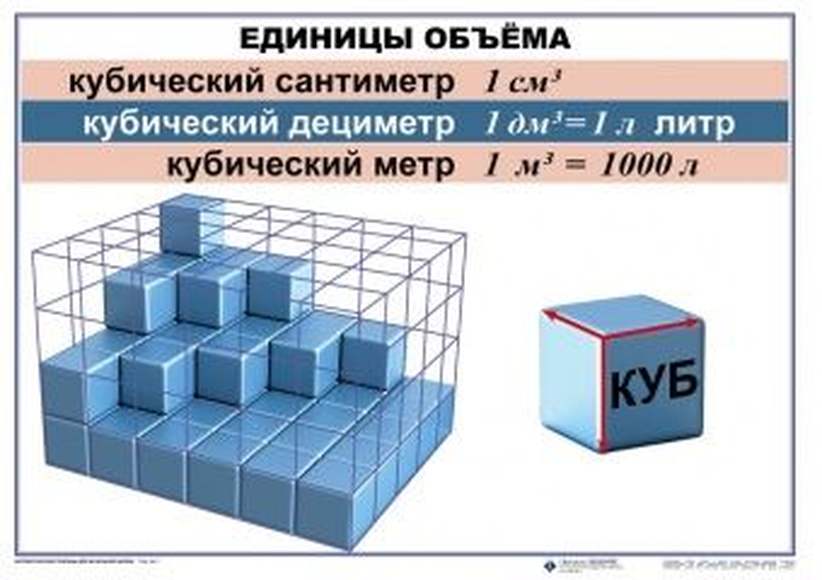 Одна из единиц измерения объема это кубический сантиметр (см³). Тогда объём V рассмотренного нами параллелепипеда равен 12 см³

V = 12 см³

Объём любого параллелепипеда вычисляют следующим образом: перемножают его длину, ширину и высоту .

Объём прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.

V = abc

где, a — длина, b — ширина, c — высота

Так, в предыдущем примере мы визуально определили, что объём параллелепипеда равен 12 см³. Но можно измерить длину, ширину и высоту данного параллелепипеда и перемножить результаты измерений. Мы получим тот же результат

Объём куба вычисляется таким же образом, как и объём прямоугольного параллелепипеда — перемножают длину, ширину и высоту.

Например, вычислим объём куба, длина которого 3 см. У куба длина, ширина и высота равны между собой. Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба:

Перемножаем длину, ширину, высоту и получаем объём, равный двадцати семи кубическим сантиметрам:

V = 3 × 3 × 3 = 27 см³

Действительно, в исходный куб вмещается 27 кубиков длиной 1 см

При вычислении объёма данного куба мы перемножили длину, ширину и высоту. Получилось произведение 3 × 3 × 3. Это есть произведение трёх сомножителей, каждый из которых равен 3. Иными словами, произведение 3 × 3 × 3 является третьей степенью числа 3 и может быть записано в виде 3³.

V = 3³ = 27 см³

Поэтому третью степень числа называют кубом числа. При вычислении третьей степени числа a, человек тем самым находит объём куба, длиной a. Операцию возведения числа в третью степень по другому называют возведением в куб.

Таким образом, объём куба вычисляется по следующему правилу:

V = a³

Где a — длина куба.

Кубический дециметр. Кубический метр

Не все объекты нашего мира удобно измерять в кубических сантиметрах. Например, объём комнаты или дома удобнее измерять в кубических метрах (м³). А объём бака, аквариума или холодильника удобнее измерять в кубических дециметрах (дм³).

Другое название одного кубического дециметра – один литр.

1 дм³ = 1 литр

Перевод единиц измерения объёма

Единицы измерения объёма можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:

Пример 1. Выразить 1 кубический метр в кубических сантиметрах.

Один кубический метр это куб со стороной 1 м. Длина, ширина и высота этого куба равны одному метру.

Но 1 м = 100 см. Значит, длина, ширина и высота тоже равны 100 см

Вычислим новый объём куба, выраженный в кубических сантиметрах. Для этого перемножим его длину, ширину и высоту. Либо возведём число 100 в куб:

V = 100³ = 1 000 000 см³

Получается, что на один кубический метр приходится один миллион кубических сантиметров:

1 м³ = 1 000 000 см³

Это позволяет в будущем умножить любое количество кубических метров на 1 000 000 и получить объём, выраженный в кубических сантиметрах.

Чтобы перевести кубические метры в кубические сантиметры, нужно количество кубических метров умножить на 1 000 000.

А чтобы перевести кубические сантиметры в кубические метры, нужно наоборот количество кубических сантиметров разделить на 1 000 000.

Например, переведём 300 000 000 см³ в кубические метры. Рассуждать в этом случае можно так: «если 1 000 000 см³ это один кубический метр, то сколько раз 300 000 000 см³ будут содержать по 1 000 000 см³»

300 000 000 см³ : 1 000 000 см³ = 300 м³

Пример 2. Выразить 3 м³ в кубических сантиметрах.

Умножим 3 м³ на 1 000 000

3 м³ × 1 000 000 = 3 000 000 см³

Пример 3. Выразить 60 000 000 см³ в кубических метрах.

Узнаем сколько раз 60 000 000 см³ содержит по 1 000 000 см³. Для этого разделим 60 000 000 см³ на 1 000 000 см³

60 000 000 см³ : 1 000 000 см³ = 60 м³

Вместимость бака, банки или канистры измеряют в литрах. Литр это тоже единица измерения объема. Один литр равен одному кубическому дециметру.

1 литр = 1 дм³

Например, если вместимость банки составляет 1 литр, это значит что объём этой банки составляет 1 дм³. При решении некоторых задач может быть полезным умение переводить литры в кубические дециметры и наоборот. Рассмотрим несколько примеров.

Пример 1. Перевести 5 литров в кубические дециметры.

Чтобы перевести 5 литров в кубические дециметры, достаточно умножить 5 на 1

5 л × 1 = 5 дм³

Пример 2. Перевести 6000 литров в кубические метры.

Шесть тысяч литров это шесть тысяч кубических дециметров:

6000 л × 1 = 6000 дм³

Теперь переведём эти 6000 дм³ в кубические метры.

Длина, ширина и высота одного кубического метра равны 10 дм

Если вычислить объём этого куба в дециметрах, то получим 1000 дм³

V = 10³= 1000 дм³

Получается, что одна тысяча кубических дециметров соответствует одному кубическому метру. А чтобы определить сколько кубических метров соответствуют шести тысячамл кубических дециметров, нужно узнать сколько раз 6 000 дм³ содержит по 1 000 дм³

6 000 дм³ : 1 000 дм³ = 6 м³

Значит, 6000 л = 6 м³.

Таблица квадратов

В жизни часто приходиться находить площади различных квадратов. Для этого каждый раз требуется возводить исходное число во вторую степень.

Квадраты первых 99 натуральных чисел уже вычислены и занесены в специальную таблицу, называемую таблицей квадратов.

Первая строка данной таблицы (цифры от 0 до 9) это единицы исходного числа, а первый столбец (цифры от 1 до 9) это десятки исходного числа.

Например, найдём квадрат числа 24 по данной таблице. Число 24 состоит из цифр 2 и 4. Точнее, число 24 состоит из двух десятков и четырёх единиц.

Итак, выбираем цифру 2 в первом столбце таблицы (столбце десятков), а цифру 4 выбираем в первой строке (строке единиц). Затем, двигаясь вправо от цифры 2 и вниз от цифры 4, найдём точку пересечения. В результате окажемся на позиции, где располагается число 576. Значит, квадрат числа 24 есть число 576

24² = 576

Таблица кубов

Как и в ситуации с квадратами, кубы первых 99 натуральных чисел уже вычислены и занесены в таблицу, называемую таблицей кубов.

Куб числа по таблице определяется таким же образом, как и квадрат числа. Например, найдём куб числа 35. Это число состоит из цифр 3 и 5. Выбираем цифру 3 в первом столбце таблицы (столбце десятков), а цифру 5 выбираем в первой строке (строке единиц). Двигаясь вправо от цифры 3 и вниз от цифры 5, найдём точку пересечения. В результате окажемся на позиции, где располагается число 42875. Значит, куб числа 35 есть число 42875.

35³ = 42875

Задания для самостоятельного решения

Задача 1. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите периметр.

Решение

P = 2(a + b)

a = 6, b = 2
P = 2(6 + 2) = 12 + 4 = 16 см

Ответ: периметр прямоугольника равен 16 см.

Показать решение

Задача 2. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите площадь.

Решение

S = ab
a = 6, b = 2
S = 6 × 2 = 12 см²

Ответ: площадь равна 12 см².

Показать решение

Задача 3. Площадь прямоугольника составляет 12 см². Длина составляет 6 см. Найдите ширину прямоугольника.

Решение

S = ab
S = 12, a = 6, b = x
12 = 6 × x
x = 2

Ответ: ширина прямоугольника составляет 2 см.

Показать решение

Задача 4. Вычислите площадь квадрата со стороной 8 см

Решение

S = a²
a = 8
S = 8²= 64 см²
Ответ: площадь квадрата со стороной 8 см равна 64 см²

Показать решение

Задача 5. Вычислите объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см.

Решение

V = abc
a = 6, b = 4, c = 3
V = 6 × 4 × 3 = 72 см³.

Ответ: объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см равен 72 см³

Показать решение

Задача 6. Объем прямоугольного параллелепипеда составляет 200 см³. Найдите высоту параллелепипеда, если его длина равна 10 см, а ширина 5 см

Решение

V = abc
V = 200, a = 10, b = 5, c = x
200 = 10 × 5 × x
200 = 50x
x = 4

Ответ: высота прямоугольного параллелепипеда равна 4 см.

Показать решение

Задача 7. Площади земельного участка, засеянные пшеницей и льном, пропорциональны числам 4 и 5. На какой площади засеяна пшеница, если под льном засеяно 15 га

Решение

Число 4 отражает площадь, засеянную пшеницей. А число 5 отражает площадь, засеянную льном.
Сказано что площади, засеянные пшеницей и льном пропорциональны этим числам.

Проще говоря, во сколько раз изменяются числа 4 или 5, во сколько же раз изменится и площадь, которая засеяна пшеницей или льном. Льном засеяно 15 га. То есть число 5, которое отражает площадь, засеянную льном, изменилось в 3 раза.

Тогда число 4, которое отражает площадь засеянную пшеницей, нужно увеличить в три раза

4 × 3 = 12 га

Ответ: пшеницей засеяно 12 га.

Показать решение

Задача 8. Длина зернохранилища 42 м, ширина составляет длины, а высота – 0,1 длины. Определите сколько тонн зерна вмещает зернохранилище, если 1 м³ его весит 740 кг.

Решение

a — длина
b — ширина
c — высота

a = 42 м
b = м
c = 42 × 0,1 = 4,2 м

Определим объем зернохранилища:

V = abc = 42 × 30 × 4,2 = 5292 м³

Определите сколько тонн зерна вмещает зернохранилище:

5292 × 740 = 3916080 кг

Переведём килограммы в тонны:

Ответ: зернохранилище вмещает 3916,08 тонн зерна.

Показать решение

Задача 9. 12. Бассейн имеет форму прямоугольного параллелепипеда, длина которого равна 5,8 м, а ширина – 3,5 м. Две трубы наполняют его водой в течение 13 ч 32 мин., причём через одну из них вливается 25 л/мин, а через вторую – 0,75 этого количества. Определите высоту (глубину) бассейна.

Решение

Определим сколько литров в минуту вливается через вторую трубу:

25 л/мин × 0,75 = 18,75 л/мин

Определим сколько литров в минуту вливается в бассейн через обе трубы:

25 л/мин + 18,75 л/мин = 43,75 л/мин

Определим сколько литров воды будет залито в бассейн за 13 ч 32 мин

43,75 × 13 ч 32 мин = 43,75 × 812 мин = 35 525 л

1 л = 1 дм³

35 525 л = 35 525 дм³

Переведём кубические дециметры в кубические метры. Это позволит вычислит объем бассейна:

35 525 дм³ : 1000 дм³ = 35,525 м³

Зная объём бассейна можно вычислить высоту бассейна. Подставим в буквенное уравнение V=abc имеющиеся у нас значения. Тогда получим:

V = 35,525
a = 5.8
b = 3.5
c = x

35,525 = 5,8 × 3,5 × x
35,525 = 20,3 × x
x = 1,75 м

с = 1,75

Ответ: высота (глубина) бассейна составляет 1,75 м.

Показать решение

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Опубликовано Автор

Бензиновые квадроциклы для взрослых и детей. Каталог

Сортировка: По умолчаниюНазвание (А — Я)Название (Я — А)Цена (низкая > высокая)Цена (высокая > низкая)Модель (А — Я)Модель (Я — А)

На странице: 25285075100

Квадроцикл IRBIS 150

Тип двигателя: 4х тактный
Объем: 150 куб. см.

Модель С ПСМ

229900 р.

Есть в наличии

Квадроцикл IRBIS 250

Тип двигателя: 4х тактный
Объем: 250 куб. см.

Модель С ПСМ

249900 р.

Есть в наличии

Новый

Под заказ

Новый

Есть в наличии

Новый

Квадроцикл SHERHAN 1000G

Тип двигателя: 4х тактный
Объем: 125 куб. см.
Макс. скорость 60 км/ч

94900 р.

Есть в наличии

Новый

Есть в наличии

Квадроцикл Stalker-110

Тип двигателя: 4х тактный
Объем: 110 куб. см.
Макс. скорость 45 км/ч

59900 р.

Есть в наличии

Квадроцикл Stalker-250

Тип двигателя: 4х тактный
Объем: 250 куб. см.
Макс. скорость 80 км/ч

179000 р.

Есть в наличии

Квадроцикл WELS EVO X 200

Тип двигателя: 4х тактный
Объем: 200 куб. см.
Макс. скорость 70 км/ч

210800 р.

Нет в наличии

Есть в наличии

Новый

Есть в наличии

Квадроцикл Stalker-150

Тип двигателя: 4х тактный
Объем: 150 куб. см.
Макс. скорость 50 км/ч

175000 р.

Нет в наличии

Есть в наличии

Нет в наличии

Есть в наличии

Ожидаются

Нет в наличии

Есть в наличии

Нет в наличии

Есть в наличии

Показано с 1 по 28 из 100 (всего 4 страниц)

Автотранспорт с четырьмя колёсами бывает разным. В России под квадроциклом многие люди понимают четырёхколёсные мотовездеходы, в США — как четырёхколёсные велосипеды. Они также могут во многом отличаться друг от друга. Мы расскажем вам про небольшие копии больших агрегатов. Детские копии японских, немецких и китайских производителей рассчитаны на юных водителей. Наш интернет-магазин предлагает высококачественный транспорт для юных автомобилистов.

Каждому родителю, который тщательно следит за развитием своего ребёнка, нужно внимательно ознакомиться с нашим ассортиментом. Компактный вездеход считается не только игрушкой, но и полезным решением в получении навыков управления автомобилем в юном возрасте. Вы можете купить бензиновый квадроцикл, и ваш ребёнок будет осваивать азы управления на своём собственном автотранспорте. Квадроцикл для детей, который является прототипом взрослой модели, гарантирует юному водителю полную безопасность. Не забудьте заказать и специальную экипировку – красочные шлемы и защитные костюмы, которые будут вдохновлять юного водителя на поездку на своём транспорте. Квадроциклы для детей с атрибутами защиты превратит времяпрепровождения вашего чада в интересную игру на колёсах. Вы убедитесь в том, что полученные в детстве навыки вождения будут полезными для ребенка в будущем.

Где заказать?

Выбрав в каталоге понравившийся детский транспорт, позвоните по телефону или сделайте заказ на сайте магазина. Наши менеджеры окажут необходимую помощь, дадут чёткий ответ на возникшие у вас вопросы. Заказ не придётся долго ожидать, так как мы работаем со всеми регионами России, и ваш заказ будет доставлен точно в срок. Только у нас покупатель найдёт широкий ассортимент транспорта мировых производителей по доступной стоимости. Ваш ребенок запомнит этот подарок на всю жизнь как чудо, и будет очень благодарен за первое своё транспортное средство.

Представляем вашему вниманию широкий выбор популярных вездеходов, заправляемых бензином, от лучших мировых производителей. В нашем магазине имеется богатый выбор мотовездеходов – от простых до более мощных, на топливе или на аккумуляторах. Менеджеры с радостью помогут выбрать именно то, что вам нужно.

Бензиновые квадроциклы имеют некоторые отличия, которыми не похожи на электрические модели:

надёжность конструкции джипа повышается за счёт усиленной рамы;
установлен намного мощней двигатель, а значит развивается большая скорость;
установлена автоматическая коробка передач;
объём бака до пяти литров;
имеют размеры, подходящие для пользования детьми и взрослыми;

улучшено сцепление за счёт резиновых колёс

имеет большую проходимость.

Квадроциклы отличающиеся между собой некоторыми параметрами:

Двигатель – двухтактный или четырёхтактный и мощность;
наличием дополнительных функций;
разные кузова – ATV или UTV;
разные габаритные параметры.

Эти все отличия влияют на стоимость, чем больше дополнительных опций и оснащений, тем выше цена. Какой транспорт лучше заказать остаётся решать клиенту. Вы можете подобрать такой агрегат, на котором будет удобно ездить вам и ребёнку, так как многие мотовездеходы рассчитаны по весу до ста килограмм, а значит могут выдержать взрослого человека.

Как не ошибиться в выборе квадроцикла?

При покупке бензинового квадроцикла необходимо внимание обращать на его размеры, так модель должна быть удобной для сидения в ней ребёнка. Также ребёнок должен легко доставать до приборов управления и сразу надо решить какая должна быть мощность агрегата и его двигателя. Для маленького ребёнка лучшим вариантом будет квадрацикл с двухтактным двигателем. Такие детские транспортные средства производители изготовляют небольшого размера и веса. Двигатель у них имеет намного меньшую мощность. На них установлена функция ограничения скорости, если ребёнок стремится уже к быстрой езде. Если родители сами не прочь проехать на квадроцикле, то в этом случае вам надо обратить внимание на модель с четырёхтактным бензиновым двигателем с объёмом до 150 кубических сантиметров, скоростью до 50 километров и запасом топлива до 5 литров.

Такие модели подойдут для передвижения и взрослому человеку, и вы сможете делить радость с ребёнком от прогулки на лоне природы. Определитесь также с кузовом. Модель кузова ATV чаще все встречается на квадроциклах, она имеет сходство с мотоциклом.

Модели с кузовом UTV напоминают конструкцию автомобиля. Он собой представляет транспорт с сидениями, которые расположены поперёк кузова. Какой выбор будет сделан вами, зависит от предполагаемых условий эксплуатации и решений, возложенными владельцем вездехода на транспортное средство. Производители изготовили их из экологически чистых материалов, поэтому при езде ребёнку ничего не угрожает. Также квадроцикл устойчив, при передвижении на нем невозможно перевернуться. Производители гарантируют полную безопасность при передвижении ребёнку.

Покупайте транспорт для ваших детей на нашем сайте! У нас вы можете найти в продаже популярные электромобили, питбайки, скутеры, мотоциклы, мини кросс, багги и джипы, мотовездеходы, такие как Atv classic mini, Atv h5 mini, Motax Gekkon, Х 16 Big Wheel , Yacota.

Перевести 60 кубических метров в литры

м ³	л
60,00	60 000
60,01	60 010
60,02	60 020
60,03	60 030
60,04	60 040
60,05	60 050
60,06	60 060
60,07	60 070
60,08	60 080
60,09	60 090
60,10	60 100
60,11	60 110
60,12	60 120
60,13	60 130
60,14	60 140
60,15	60 150
60,16	60 160
60,17	60 170
60,18	60 180
60,19	60 190
60,20	60 200
60,21	60 210
60,22	60 220
60,23	60 230
60,24	60 240

м ³	л
60,25	60 250
60,26	60 260
60,27	60 270
60,28	60 280
60,29	60 290
60,30	60 300
60,31	60 310
60,32	60 320
60,33	60 330
60,34	60 340
60,35	60 350
60,36	60 360
60,37	60 370
60,38	60 380
60,39	60 390
60,40	60 400
60,41	60 410
60,42	60 420
60,43	60 430
60,44	60 440
60,45	60 450
60,46	60 460
60,47	60 470
60,48	60 480
60,49	60 490

м ³	л
60,50	60 500
60,51	60 510
60,52	60 520
60,53	60 530
60,54	60 540
60,55	60 550
60,56	60 560
60,57	60 570
60,58	60 580
60,59	60 590
60,60	60 600
60,61	60 610
60,62	60 620
60,63	60 630
60,64	60 640
60,65	60 650
60,66	60 660
60,67	60 670
60,68	60 680
60,69	60 690
60,70	60 700
60,71	60 710
60,72	60 720
60,73	60 730
60,74	60 740

м ³	л
60,75	60 750
60,76	60 760
60,77	60 770
60,78	60 780
60,79	60 790
60,80	60 800
60,81	60 810
60,82	60 820
60,83	60 830
60,84	60 840
60,85	60 850
60,86	60 860
60,87	60 870
60,88	60 880
60,89	60 890
60,90	60 900
60,91	60 910
60,92	60 920
60,93	60 930
60,94	60 940
60,95	60 950
60,96	60 960
60,97	60 970
60,98	60 980
60,99	60 990

60 кубических метров в литры

60 кубических метров равно 60000 литров

Чтобы преобразовать любое значение в кубических метрах в литры, просто умножьте значение в кубических метрах на коэффициент преобразования 1000. , 60 куб. метров умножить на 1000 равно 60000 литров.

Чтобы пересчитать значение кубического метра в соответствующее значение в литрах, просто умножьте количество в кубическом метре на 1000 (коэффициент пересчета). Вот формула :

Значение в литрах = значение в кубических метрах × 1000

Предположим, вы хотите преобразовать 60 кубических метров в литры. Используя приведенную выше формулу преобразования, вы получите:

Значение в литрах = 60 × 1000 = 60000 литров

Этот конвертер может помочь вам получить ответы на такие вопросы, как:

Сколько кубометров в 60 литрах?
60 кубометров сколько литров?
Сколько 60 кубических метров в литрах?
Как перевести кубические метры в литры?
Какой коэффициент пересчета кубических метров в литры?
Как перевести кубические метры в литры?
По какой формуле перевести кубические метры в литры? Среди прочих.

Таблица перевода кубических метров в литры около 60 кубических метров

Таблица перевода кубометров в литры			52 м3	=	52000 литров
53 м3	=	53000 литров
54 куб. м.	=	54000 литров
55 куб.м.	55000 литров
56 м3	=	56000 литров
57 м3	=	57000 литров
58 м3	=	58000 литров
59 м3	=	59000 литров
60 кубических метров	=	60000 литров

9000 3 Кубические метры в литры Таблица перевода 60 м3 = 60000 литров 61 м3 = 61000 литров 62 м3 = 62000 литров 63 м3 = 63000 литров 64 м3 = 64000 литров 65 м3 = 65000 литров 66 м3 = 66000 литров 67 м3 = 67000 литров 68 м3 = 68000 литров 69 м3 = 69000 литров

Примечание: некоторые значения могут быть округлены.