Свая С30.20-3
Забивные железобетонные сваи – стержень определенного сечения, изготовленный из тяжелых марок бетона с предварительным продольным армированием, используемый для строительства фундаментов гражданских и промышленных объектов.
Свайные основания используются для строительства жилых и промышленных зданий на сложных грунтах – подвижных, просадочных, пучинистых и пр. Задача железобетонных забивных свай в передаче несущей нагрузки (веса здания) на прочные грунты, залегающие гораздо ниже слабых слоев.
Вы сможете прямо в Кирове приобрести следующие разновидности железобетонных забивных свай:
- цельные и составные;
- полые и сплошные;
- квадратного и круглого сечения, погружаемые в предварительно подготовленные лидерные скважины;
- с ненапрягаемой продольной арматурой с поперечным армированием;
- предварительно напряженной продольной арматурой, с поперечным армированием и без него.
Весь номенклатурный ряд относится к категории забивных железобетонных свай, которые забивают в грунт под основание.
Большей популярностью пользуются составные, где отдельные секции собираются воедино посредством «стакана» и закрепляются сварным или болтовым соединением после установки первой нижней секции, далее секции набиваются уже на всю длину стержня. Это бюджетный вариант и его проще транспортировать на место, что особенно удобно для города Киров.
Все ЖБ забивные сваи изготавливаются по технологии ГОСТ 19804-2012 и по сравнению с другими типами фундамента имеют ряд преимуществ:
- низкая цена;
- дешевая установка;
- прочность и устойчивость во всех типах грунта;
- нет необходимости в дорогостоящей технике и/или высокой квалификации строителей.
Подавляющее большинство свайных фундаментов в Кирове выполняется именно с использованием ЖБ забивных.
Сваи цельные забивные с ненапрягаемой арматурой
Представляют собой заостренный цельный железобетонный стержень, применяемый в основном на глинистых и песчаных грунтах. Для изготовления используется тяжелый бетон В20 с каркасом из ненапрягаемой арматуры, выполненной из ребристой горячекатаной стали по ГОСТ 5781-82. На верхней – забивной – части выполнена многослойная арматурная сетка для сохранения формы во время установки и строповочные петли.
На верхней – забивной – части выполнена многослойная арматурная сетка для сохранения формы во время установки и строповочные петли.
Сваи составные
Применяются в тех случаях, когда стандартной 12-метровой длины не хватает. Изготовлены из тяжелого бетона В20, состоят из 2-х и более частей, соединяются в месте стыка сваркой или болтами. Армируются ненапрягаемой арматурой класса А-I и А-III (ГОСТ 5781-82). Наконечник дополнительно армируется спиралью, верхняя часть также усилена арматурной многослойной сеткой.
- Объём 0.12м.куб
- Длинна 3000мм
- Ширина 200мм
- Высота 200мм
- Вес
0.
 3тн
3тн
Сваи составные C120.35-НС.3 — Фундаменты ЛЭП
Основные характеристики
- Длина мм: 12000
- Ширина мм: 350
- Высота мм: 350
- Объем бетона, куб.
 м: 1,49
м: 1,49 - Вес изделия, тонн: 3,70
- Класс бетона: B25
- Диаметр и класс продольной арматуры: 14,AIII
Запрос коммерческого предложения
Описание
Сваи составные по серии 1.011.1-10 Железобетонные составные сваи со стаканным и сварным стыками предназначены для свайных фундаментов зданий и сооружений. Составные сваи сечением 300х300 мм бывают общей длиной от 14 до 24 м, сечением 350х350 мм и 400х400 мм длиной от 14 до 28 м при этом состоят из двух секций: верхней и нижней. Составные сваи изготавливаются из тяжелого бетона класса по прочности на сжатие не ниже В25. В качестве крупного заполнителя для бетона применяется щебень из естественного камня и гравия с размером фракций не более 40мм. В качестве продольной арматуры должна применяться горяче-катанная арматурная сталь классов А-II и А-III по ГОСТ5781-82 или Ат-IIIc по ГОСТ 10884-81. Для поперечного армирования следует применять проволоку класса Вр-1 по ГОСТ 6727-80.
Отпускная прочность бетона составных свай в момент отгрузки с предприятия-изготовителя должна быть не ниже 100% от проектной.
Железобетонные составные сваи поставляются в разборном виде, соединение верхней и нижней секции осуществляется в месте строительства.
По типу соединения составные сваи бывают:
В качестве продольной арматуры должна применяться горяче-катанная арматурная сталь классов А-II и А-III по ГОСТ5781-82 или Ат-IIIc по ГОСТ 10884-81. Для поперечного армирования следует применять проволоку класса Вр-1 по ГОСТ 6727-80.
Отпускная прочность бетона составных свай в момент отгрузки с предприятия-изготовителя должна быть не ниже 100% от проектной.
Железобетонные составные сваи поставляются в разборном виде, соединение верхней и нижней секции осуществляется в месте строительства.
По типу соединения составные сваи бывают:
- Со стаканным типом соединения:
 30-ВС.1, С80.30-НС.1
— С — свая сплошного квадратного сечения
— 60/80 — длина сваи в дм
— 30 — сечение сваи в см
— В/Н — верхняя секция сваи/нижняя секция сваи
— С— стаканный стык верхней и нижней секции
— 1 — тип армирования
30-ВС.1, С80.30-НС.1
— С — свая сплошного квадратного сечения
— 60/80 — длина сваи в дм
— 30 — сечение сваи в см
— В/Н — верхняя секция сваи/нижняя секция сваи
— С— стаканный стык верхней и нижней секции
— 1 — тип армирования
- Сварной тип соединения:
- С — свая сплошного квадратного сечения
- 140 — общая (верхняя и нижняя вмесе) длина сваи в дм
- 30 — сечение сваи с см
- Св — сварной стык соединения верхней и нижней секции
 ВП.
Отдельные элементы сваи маркируются — С60.30-ВСв.1, С80.30-НСв.1
ВП.
Отдельные элементы сваи маркируются — С60.30-ВСв.1, С80.30-НСв.1
- С — свая сплошного квадратного сечения
- 60/80 — длина сваи в дм
- 30 — сечение сваи в см
- В/Н — верхняя/нижняя секция
- Св — сварной стык соединения
- 1 — тип армирования
| Тип армирования | Диаметр продольной арматуры |
| 1 | 12АII |
| 2 | 12АIII |
| 3 | 14АIII |
| 4 | 16АIII |
| 5 | 18АIII |
| 6 | 20АIII |
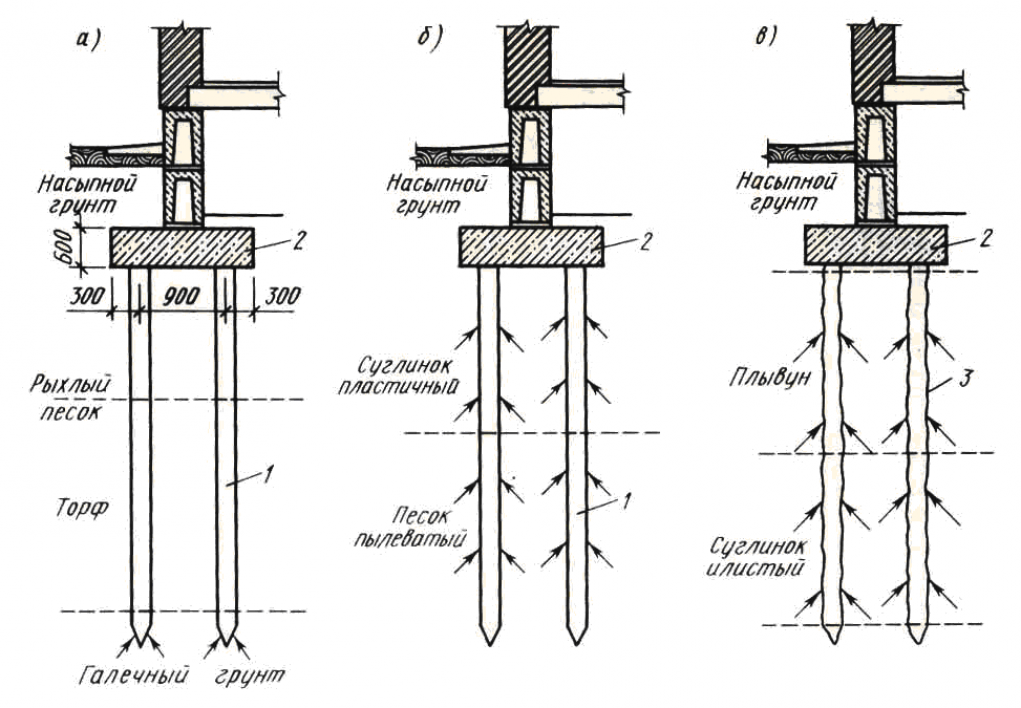 Соединение секций свай со стаканным стыком осуществляется за счёт плотной посадки рифлёного железобетонного выступа верхней секции в цилиндрической полости закладного изделия нижней секции. Соединение секций со сварным стыком осуществляется через накладки из листовой стали, привариваемые к боковым поверхностям закладных изделий секций сваи.
Соединение секций свай со стаканным стыком осуществляется за счёт плотной посадки рифлёного железобетонного выступа верхней секции в цилиндрической полости закладного изделия нижней секции. Соединение секций со сварным стыком осуществляется через накладки из листовой стали, привариваемые к боковым поверхностям закладных изделий секций сваи.
C120.35.НС.3, C.120.35.НС.3, C120,35-НС,3, C120,35,НС,3, C,120,35,НС,3, C12035НС3, C-120.35-НС.3, C-120-35-НС-3, C 120.35-НС.3, C 120 35 НС 3
Доставка
От ближайшего производства
в регионы России:
Развернем производство у Вашего объекта за 3 недели:
Не ждите доставку: наша компания обладает возможностью запуска производственной площадки в любой точке России в течение 3 недель.Консультация по мобильному производству
комбинаторика – Перестановки/Комбинации – Разделение стопки на 3 стопки
Задавать вопрос
спросил
Изменено 5 лет, 1 месяц назад
Просмотрено 431 раз
$\begingroup$Мне задали следующий вопрос:
В мешочке десять шаров, пронумерованных от одного до десяти.

- Сколько различных комбинаций можно составить, вытащив из мешка три шара? (Порядок извлечения шаров не имеет значения.)
- Сколькими различными способами можно разделить шары на три кучки, содержащие соответственно по пять, три и два шара?
Моя попытка решения
- Соотношение перестановки для этой задачи может быть выражено: $$ P(N,k)=\frac{N!}{k!(N-k)!},$$ Где $N$ — общее количество шаров $\left(10\right)$, $k$ — количество выпавших шаров, следовательно, подстановкой получаем: $$P(10,3)=120,$$ Это количество перестановок, но нам сказали, что порядок, в котором вытягиваются шары, не имеет значения, поэтому мы должны рассмотреть отношение комбинации: $$C(N,k)=\frac{P(N,k)}{k!},$$ Следовательно: $$C(10,3)=\frac{120}{6}=20.$$
- Моя проблема со второй частью, я думаю, что могу визуализировать это так же, как я сделал первую часть, как извлечение пяти, трех и двух шаров из 10, поэтому, используя:
$$ P(N,k)=\frac{N!}{k!(N-k)!},$$
$$ P(10,5)=\frac{10!}{5!(10-5)!}=252,$$
$$ P(10,3)=\frac{10!}{3!(10-3)!}=120,$$
$$ P(10,2)=\frac{10!}{2!(10-2)!}=45,$$
$$\text{Всего перестановок}= P(10,5)+P(10,3)+P(10,2)=417.
 2C_2 = 2520$$ $\endgroup$ $\begingroup$
2C_2 = 2520$$ $\endgroup$ $\begingroup$Ваш второй метод правильный.
В первом методе вы предполагаете, что можете использовать одни и те же шары более чем в одной стопке, что явно неверно, поскольку один шар может находиться только в одной стопке за раз.
Также при выполнении второго метода вам придется умножать вместо сложения, потому что вы выполняете операции одну за другой.
$\endgroup$ 2Колода карт по $52$ разделена на четыре стопки по $13$. Какова вероятность того, что в каждой стопке есть один туз?
спросил
Изменено 7 месяцев назад
Просмотрено 12 тысяч раз
$\begingroup$Обычная колода игральных карт по 52$ случайным образом делится на стопки по 4$ по 13$ в каждой.
 Вычислите вероятность того, что в каждой стопке ровно один туз.
Вычислите вероятность того, что в каждой стопке ровно один туз.Приведенный ответ: $(39*26*13)/(51*50*49) \приблизительно 0,105$
Приведенный выше ответ использует условную вероятность, но я хотел бы знать, что не так с моими рассуждениями:
Назовите четыре стопки перегородок $1$, $2$, $3$ и $4$.
- Для раздела $1$ существует ${4 \choose 1}$ способов выбрать, какой туз будет содержать раздел. Затем есть ${48\выбрать 12}$ способов выбрать оставшиеся $12$ карт, так как мы не можем выбрать другие тузы.
- Для раздела $2$ существует ${3\выбрать 1}$ способов выбрать, какой туз будет содержать раздел. Затем есть ${36\выбрать 12}$ способов выбрать оставшиеся $12$ карт, так как осталось только $36$ карт, отличных от туза.
Следуя аналогичным рассуждениям для разбиений $3$ и $4$, мы находим, что существует ${2\выбрать 1}{24 \выбрать 12}$ и ${1\выбрать 1}{12 \выбрать 12} = 1$ способов чтобы сформировать эти руки.
Таким образом, моя вероятность определяется как
$$\frac{4 \cdot {48\выберите 12} + 3\cdot{36\выберите 12} + 2\cdot{24\выберите 12}}{{52\ выберите 13}{39\выбрать 13}{26\выбрать 13}} \не \примерно 0.
 105$$
105$$Знаменатель — это количество способов выбрать карты в каждой руке без каких-либо ограничений.
Я не уверен, что не так с моими вычислениями.
- вероятность
- теория вероятностей
Вы были близки. Вам просто нужно умножить возможности в числителе: $$\frac{4 \cdot {48\выбрать 12} \cdot 3\cdot{36\выбрать 12} \cdot 2\cdot{24\выбрать 12}}{{52\выбрать 13}{39\выбрать 13}{26\выбрать 13}} \приблизительно 0,105$$
$\endgroup$ 1 $\begingroup$Более простой способ: есть 52$ места, куда можно положить туз (13$ мест в каждой из 4$ стопок). Нам все равно, какой туз какой, поэтому мы можем посчитать $\binom{52}{4}$ различных способов выбора четырех мест, куда будут помещены тузы; каждый из этих наборов из четырех мест равновероятен.
94}{\binom{52}{4}} \ приблизительно 0,1055.$$ $\endgroup$ $\begingroup$Мне нравится думать об этой проблеме немного более явно, в терминах условных вероятностей (обусловливающих выборочное пространство).
