Общий порядок построения эпюр Qx и Мх

ТЕМА: «МЕХАНИКА ТВЕРДОГО ТЕЛА. СТАТИКА»
Лекция №5 «Общий порядок построения эпюр Qx и Мх»
5.1 Построение эпюр способом «по участкам»
1. Определяют опорные реакции.
2. Разбивают балки на участки, границами которых являются характерные точки,
и определяют число таких участков.
3. Нумеруют участки. Если нагрузка не сложная, то можно их нумеровать по
порядку слева направо, т.е. от левого до правого конца балки. Если участков много,
то часть их можно пронумеровать начиная от правого конца балки. Благодаря
этому будут проще выглядеть уравнения равновесия.
4. В пределах каждого участка проводят сечения 1-1, 2-2 и т. д. «Привязывают»
каждое сечение к левому или правому концу балки координатами соответственно
х1, х2 и т.д.
5. Определяют граничные значения каждой из координат х1, х2 и т.д.
6. Определяют значения Qх сначала в каждом из сечений в общем виде, затем в
граничных точках, придавая числовые значения координатам х1, х2 и т. д. Строят
эпюру Qх откладывая значения найденных поперечных сил от оси балки в
определенном масштабе и соединяют концы полученных отрезков.
7. Определяют значения Мх сначала в каждом из сечений в общем виде, затем в
граничных точках, придавая числовые значения координатам х1, х2 и т.д. Строят
эпюру Мх откладывая значения найденных изгибающих моментов от оси балки в
определенном масштабе и соединяют концы полученных отрезков.
При наличии распределенной нагрузки необходимо найти экстремальное значение
Мх на этом участке, для чего надо знать, на каком расстоянии от точки начала
действия распределенной нагрузки находится сечение с экстремальным значением
Мх. Определяют это расстояние 2-мя способами:
— находят первую производную от выражения момента и приравнивают ее
нулю: dМх/dх=0;
— определяют по эпюре Qх, рассматривая подобие треугольников.
Пример 5.1 Определить опорные реакции и построить эпюры Qх и Мх для балки,
приведенной на рисунке 5. 1,а, если F=10кН и l=4м.
Решение:
1. Определяем опорные реакции. Поскольку балка
имеет ось симметрии относительно опор, то
очевидно, что опорные реакции:
RA=RВ=F/2=5кН
2. Разбиваем балку на два участка ( и
)
3. Определяем поперечные силы Qх на каждом
участке.
Участок
Участок
(0 х1 l/2)
(l/2 х2 l)
Qх1 = RA = F/2 = 5кН
Qх2 = RA — F = F/2 — F = 5кН
По найденным значениям строим эпюру Qх (рис.5.1,б).
Эпюра Qх
4. Определяем изгибающие моменты Мх на каждом
участке.
Участок
(0 х1 l/2)
Мх1 = RA∙х1 = F/2∙х1
При х1 = 0 → Мх1=0;
При х1 = l /2 → Мх1= F/2∙ l/2= Fl/4=10∙4/4 = 10кН∙м
Эпюра Мх
Участок
(0 х2 l/2)
Мх2 = RВ∙х2 = F/2∙х2
При х2 = 0 → Мх2=0;
При х2 = l/2 → Мх2= F/2∙ l/2= Fl/4=10∙4/4 = 10кН∙м
По найденным значениям строим эпюру Мх (рис.5.1,в).
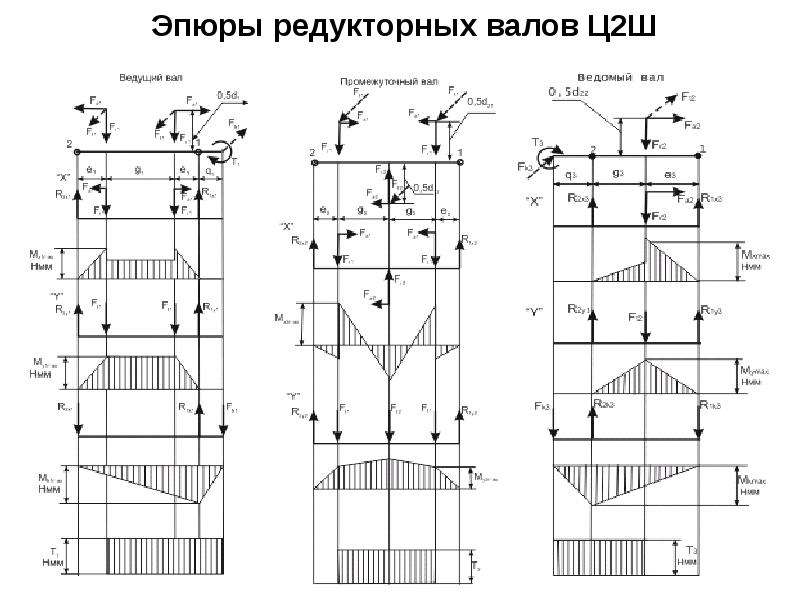
Пример 5.2 Определить опорные реакции и построить эпюры Qх и Мх для балки,
приведенной на рисунке 5.2,а, если F=5кН, l=4м, а=1м
Решение:
1. Определяем опорные реакции:
Проверка:
0≡0. Опорные реакции найдены правильно
2. Разбиваем балку на три участка ( ). Для 3го участка лучше рассматривать правую часть балки.
3. Определяем поперечные силы Qх на каждом
участке.
Участок
Участок
(0 х1 а)
(а х2 а +
Qх1 = -F= -5кН-на всем участке
Qх2 = — F+RA= -5+11,25 = 6,25кН
Qх3 = — RВ= — 3,75кН
Участок
(0 х2
l/2)
По найденным значениям строим эпюру Qх (рис.5.2,б).
4. Определяем изгибающие моменты Мх на каждом
участке.
Участок
(0 х1 а)
Мх1 = -F∙х1
При х1 = 0 → Мх1=0;
При х1 = а → Мх1= -F∙а = -5∙1= -5кН∙м
Участок
(а х2 а + l/2)
Мх2 = -Fх2+ RА(х2-а)
При х2 = а → Мх2=-F∙a + RА(a-а)=-5∙1+11,25∙0 = -5кН∙м;
При х2 = а+l/2 → Мх2= -F(а+l/2) + RА∙l/2=-5(1+2)+11,25∙2 =
-15+22,5=7,5кН∙м
Участок
(0 х3
Мх3 = RВ∙х3
l/2)
При х3 = 0 → Мх3=0;
При х3 = l/2 → Мх3= RВ∙ l/2 = 3,75∙2 = 7,5кН∙м
По найденным значениям строим эпюру Мх (рис. 5.2,в).
Пример 5.3 Определить опорные реакции и построить эпюры Qх и Мх для балки,
приведенной на рисунке 5.3,а, если q=10кН/м, l=3,5м.
Решение:
1. Определяем опорные реакции:
При определении опорных реакций удобнее заменить
распределенную нагрузку сосредоточенной, величина которой
равна произведению интенсивности нагрузки
на длину
участка ее приложения (l/2). Составляем уравнения
равновесия (рис.5.3,а):
Проверка:
0≡0. Опорные реакции найдены правильно
2. Разбиваем балку на три участка ( ).
3. Определяем поперечные силы Qх на каждом
участке.
Участок
(0 х1 l/2)
Qх1 = RA — q∙х1
При х1 = 0 → Qх1 = RА = 13,12кН;
При х1 = l /2 → Qх1 = RА — ql/2 = 13,12 — 10∙1,75= 4,38кН
Qх2 = -RВ = — 4,38кН-на всем участке
Участок
(0 х2
l/2)
По найденным значениям строим эпюру Qх (рис.5.3,б).
Эпюра Qх
Эпюра пересекает нулевую линию в точке С, расстояние до
которой от правой опоры находим из подобия треугольников
АСЕ и АDK:
Это расстояние принято обозначать х0.
4. Определяем изгибающие моменты Мх на каждом
участке.
Участок
(0 х1 l/2)
Мх1 = RA∙х1 — q∙х12
При х1 = 0 → Мх1 = 0;
При х1 = l /2 → Мх1 = RA∙l/2 – q∙(l/2)2 /2 = 13,12∙1,7510∙1,752/2 = 22,96 — 15,31 = 7,65кН∙м
Эпюра Мх
При х1 =х0 =1,31м → Мх1 = RA∙х0 — q∙х02/2 = 13,12∙1,3110∙1,312/2 = 17,19 — 8,58 = 8,61кН∙м;
Участок
(0 х2 l/2)
Мх2 = RВ∙х2
При х2 = 0 → Мх2 = 0;
При х2 = l /2 → Мх2= RВ∙l/2 = 4,38 ∙ 1,75 = 7,66кН∙м
По найденным значениям строим эпюру Мх (рис.5.3,в).
Суммы моментов всех сил слева и справа получились примерно одинаковыми – 7,65 и
7,66кН∙м. Незначительное расхождение произошло из-за округления значений опорных
реакций. Соединяем плавной кривой отложенные значения и получаем на участке AD
параболу выпуклостью вниз (рис.5.3,в).
Проанализировав эпюры Qх и Мх с позиции их изменения по длине балки,
можно сделать выводы
Для самостоятельного решения !
Задача 3. Определить опорные реакции и построить эпюры Qх и Мх для балки, приведенной на
рис. 5.4 при заданных М и l . Исходные данные взять из таблицы 1 по последней цифре
зачетной книжки.
Рисунок 5.4
Величины
М (кН·м)
l (м)
1
7
3,5
2
6
4
3
6
3
4
5
4
Варианты
5
6
8
7
5
4
Таблица 1
7
6
3
8
5
4
9
6
3
0
8
5
Задача 4. Определить опорные реакции и построить эпюры Qх и Мх для балки, приведенной
на рис.5.5 при заданных F и l. . Исходные данные взять из таблицы 2 по последней цифре
зачетной книжки (см. следующий кадр).
Рисунок 5.5
Таблица 2
Величины
Варианты
1
2
3
4
5
6
7
8
9
0
F (кН)
3
4
3
4
5
4
3
4
3
5
l (м)
6
8
9
7
8
6
6
5
6
8
5.2 Построение эпюр способом «по характерным точкам»
1. Определяют опорные реакции.
2. Обозначают характерные точки.
3. Определяют значения Qх и Мх в характерных точках.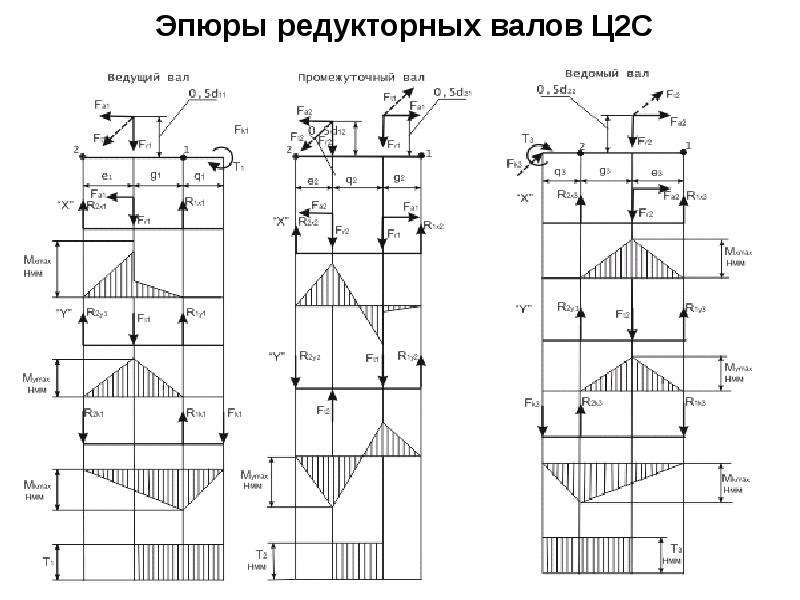
4. Точки, соответствующие полученным значениям, соединяют между собой. При
этом необходимо учитывать следующее. В местах приложения сосредоточенных
сил надо отыскивать два значения поперечной силы Qх (Qлев и Qправ ), которые
отличаются друг от друга на величину сосредоточенной силы. Аналогично при
построении эпюры изгибающих моментов в точке, где приложен внешний
сосредоточенный момент, необходимо находить два значения Мх (Млев и Мправ ),
которые отличаются друг от друга на величину внешнего момента.
5. Оба значения Qх (Qлев и Qправ ) и Мх (Млев и Мправ ) могут быть найдены при
рассмотрении левой части балки, либо одно из значений находят, рассматривая
левую часть балки, а второе – правую.
Для самостоятельного решения !
Задача 5. Для балки, показанной на рис.5.8,а приведены «слепые» (без значений) эпюры
Qх (рис.5.8,б) и Мх (рис.5.8,в). Определите опорные реакции и проставьте значения
поперечных сил и изгибающих моментов в характерных точках.
Рисунок 5.8

Построить несколько графиков в Matplotlib

Улучшить статью

Сохранить статью

Нравится Статья

zawaresumedha

профессиональный

5 опубликованных статей

Читать

Обсудить

Улучшить статью

Сохранить статью

Нравится Статья

Предварительные условия : Matplotlib

В Matplotlib мы можем рисовать несколько графиков на одном графике двумя способами. Один из них — использование функции subplot(), а другой — наложение второго графика на первый, т. е. все графики будут отображаться на одном графике. Мы рассмотрим оба способа один за другим.

Несколько графиков с использованием функции subplot()

Функция subplot() — это функция-оболочка, которая позволяет программисту построить более одного графика на одном рисунке, просто вызвав ее один раз.

Синтаксис: matplotlib.pyplot. subplots(nrows=1, ncols=1, sharex=False, sharey=False, сжатие=True, subplot_kw=None, gridspec_kw=None, **fig_kw)

90 027 Параметры:

1. nrows, ncols: Это количество строк и столбцов соответственно. Также следует отметить, что оба эти параметра являются необязательными и значение по умолчанию равно 1.
2. sharex, sharey:  Эти параметры определяют свойства, общие для осей a и y. Возможные значения для них: row, col, none или значение по умолчанию False.
3. сжатие:  Этот параметр представляет собой указанное логическое значение, которое спрашивает программиста, нужно ли выдавливать, то есть удалять дополнительное измерение из массива. Имеет значение по умолчанию False.
4. subplot_kw: Эти параметры позволяют нам добавлять ключевые слова к каждому подзаголовку, и его значение по умолчанию — None.
5. gridspec_kw: Это позволяет нам добавлять сетки на каждый подграфик и имеет значение по умолчанию None.
6. **fig_kw: Это позволяет нам передать любой другой дополнительный аргумент ключевого слова в вызов функции и имеет значение по умолчанию None.

Пример:

Python3

import matplotlib.pyplot as plt 9 0084 импорт numpy как np импорт математика     X = np.arange( 9008 3 0 , math.pi * 2 , 0,05 )     Y1 = np.sin(X) Y2 = np.cos(X) Y3 = np.tan(X) Y4 = np.tanh(X)     цифра, ось = plt. subplots( 2 , 2 )   ось [ 0 , 0 ].plot(X, Y1) ось [ 900 84 0 , 0 ].set_title( "Синус Функция" )     ось [ 0 , 1 ].plot(X, Y2) ось [ 0 , 1 ]. set_title( "Функция косинуса" )     ось [ 1 , 900 84 0 ].plot(X, Y3) оси[ 1 , 0 ].set_title( "Функция касания" )     ось [ 9008 3 1 , 1 ]. plot(X, Y4) ось [ 1 , 1 ].set_title( "Функция Tanh" )   9 0084   plt.show()

Вывод

Несколько графиков с использованием функции subplot()

В Matplotlib есть еще одна функция, очень похожая на subplot — subplot2grid(). Это почти то же самое, что и функция подзаголовка, но обеспечивает большую гибкость для размещения объектов графика в соответствии с потребностями программиста.

Эта функция записывается следующим образом:

Синтаксис: matplotlib.pyplot.subplot2grid(shape, loc, rowspan=1, colspan=1, fig=None, **kwargs)

Параметр:

1. shape
   Этот параметр представляет собой последовательность двух целочисленных значений, которая указывает форму сетки, для которой нам нужно разместить оси. Первая запись предназначена для строки, а вторая — для столбца.
2. loc
   Подобно параметру формы, даже Ioc представляет собой последовательность из двух целых значений, где первая запись остается для строки, а вторая — для столбца, чтобы поместить ось в сетку.
3. rowspan
   Этот параметр принимает целочисленное значение и число, которое указывает количество строк, на которые ось может простираться или увеличиваться вправо.
4. colspan
   Этот параметр принимает целочисленное значение и число, которое указывает количество столбцов для охвата оси или увеличения длины вниз.
5. рис.
   Это необязательный параметр, который использует фигуру для размещения оси. По умолчанию используется текущая фигура.
6. **kwargs
   Это позволяет нам передать любой другой дополнительный аргумент ключевого слова в вызов функции и имеет значение по умолчанию None.

Пример:

Python3

импорт matplotlib.pyplot as plt импорт 9 0084 numpy as np импорт математика     plot1 = plt.subplot2grid(( 3 , 3 ), ( 0 , 0 ), столбец = 2 ) участок2 = plt.subplot2grid(( 3 , 900 84 3 ), ( 0 , 2 ), междурядье = 3 , colspan = 2 ) plot3 = 90 084 plt. subplot2grid(( 3 , 3 ), ( 1 , 0 ), rowspan = 2 )     90 003 x = np.arange( 1 , 10 )     plot2.plot(x, x * * 0,5 ) 9008 4 plot2.set_title( 'Квадратный корень' ) plot1.plot(x, np.exp(x)) plot1.set_title( 'Экспонент' ) 9000 3     plot3.plot(x, x * x) plot.set_title( 'Квадрат' )     9000 3 plt.tight_layout() plt. show()

Выход

Несколько графиков с использованием функции subplot2grid()

Построение одного графика

Теперь мы узнали о построении нескольких графиков с использованием функций subplot и subplot2grid библиотеки Matplotlib. Как упоминалось ранее, теперь мы рассмотрим построение нескольких кривых путем их наложения. В этом методе мы не используем никаких специальных функций, вместо этого мы напрямую строим кривые одну над другой и пытаемся установить масштаб.

Пример:

Python3

импорт matplotlib.pyplot как plt импорт numpy как np импорт математика     X = np.arange ( 0 , math.pi * 2 , 0,05 ) 9008 2     г = np. sin(X) z = np.cos(X)     9 0083 plt.plot(X, y, цвет = 'r' , метка = 'sin' ) plt.plot(X, z, цвет = 'g' 90 083 , метка = 'cos' )     plt.xlabel( "Угол" ) plt.ylabel( "Величина" ) plt.title( "Синус и функции косинуса" )     plt.legend( )     plt.show()

Вывод

функция синуса и косинуса на одном графике

Последнее обновление: 03 янв, 2021

Нравится статья

Сохранить статью

Как построить несколько графиков в Python?

Python — это язык программирования со множеством функций. Это интерпретируемый язык программирования высокого уровня общего назначения. Созданный Гвидо ван Россумом и впервые выпущенный в 1991 году, Python имеет философию дизайна, которая делает упор на удобочитаемость кода, в частности, используя значительные пробелы. Он предоставляет конструкции, которые позволяют четко программировать как в малых, так и в больших масштабах.

Python — универсальный язык для визуализации. В экосистеме Python есть множество библиотек, которые можно использовать для создания статических, анимированных и интерактивных визуализаций.

В этом посте мы увидим, как использовать некоторые из этих библиотек визуализации Python на практике. Мы рассмотрим, как создавать статические и анимированные визуализации с помощью библиотек Matplotlib и seaborn.

ПОЛУЧИТЕ 15 ДОЛЛАРОВ США НА БЕСПЛАТНОЕ ОБУЧЕНИЕ ПРИ ЗАРЕГИСТРАЦИИ ПО ЭТОЙ ССЫЛКЕ

Как создать несколько графиков Matplotlib в одном рисунке отображать несколько графиков на одном графике.

В следующих параграфах мы более подробно рассмотрим эту функцию и то, как ее можно использовать.

Синтаксис

 matplotlib.pyplot.subplots(numrows, numcols, plot_number)
 

Чтобы построить несколько графиков на одном графике, выполните следующие действия.

1. Установите и импортируйте библиотеки matplotlib и NumPy. Библиотека Matplotlib используется для построения графиков в python, а NumPy занимается всеми математическими операциями.

 импортировать matplotlib.pyplot как plt
импортировать NumPy как np 

2. Создайте массив времени, используя функцию np.arange() NumPy.

 t=np.arange(0, 5, 0.2) 

Здесь 0 — начальная точка, 5 — конечная точка, а 0,2 — интервенция между 0 и 5 (оба включительно).

3. Теперь постройте первый график как

 plt.subplot(121)
plt.plot(t, 'r- -')
plt.xlabel(‘Plot 1) 

4. Аналогичным образом постройте график 2 как …

 plt.subplot(122)
plt.plot(t, 'r- -', t**2, 'b*', t**3, 'g-o')
plt. xlabel(‘Plot 2) 

5. Теперь покажите оба графика на одном графике как…

 plt. subtitle("Построение нескольких графиков")
plt.show() 

Полный синтаксис

 импортировать matplotlib.pyplot как plt
импортировать numpy как np
т=np.arange(0, 5, 0,2)
 
plt.subplot(121)
plt.plot(t, "r--")
plt.xlabel("График 1")
 
plt.subplot(122)
plt.plot(t, "r--", t**2, "b+", t**3, "g-o")
plt.xlabel("График 1")
 
plt.suptitle("Построение нескольких графиков")
plt.show() 

Вывод

Источник: https://www.oraask.com/

Объяснение

• в время построения графиков.
• Затем мы используем функцию subplot(). Функция subplot помогает построить два разных графика на одном рисунке.
• Здесь в этом примере кода функция subplot() имеет параметры 121 и 122; здесь 1 определяет количество строк, а 2 определяет количество столбцов, как мы обсуждали в синтаксисе функции подзаголовка. Третий параметр определяет, какой из них является номером участка, поэтому 1 определяет номер 1-го участка, а 2 определяет номер 2-го участка.
• Затем мы используем функцию plot, внутри которой мы передаем t, который определяется как время и дизайн графика.

здесь 'r- -' означает:
r = красный цвет

– – (двойное тире) = это шаблоны, которые будут напечатаны на экране (см. выходное изображение)

Как построить несколько графиков в python на том же графике

Ранее мы научились строить несколько графиков, используя функцию subplot() библиотеки matplotlib. Теперь мы рассмотрим, как построить несколько графиков на одном графике, наложив их друг на друга. Мы можем сделать это, напрямую построив графики один за другим.

Для примера см. приведенный ниже код.

 импортировать matplotlib.pyplot как plt
импортировать numpy как np
т=np.arange(0, 5, 0,2)
plt.plot(t, "r--")
plt.plot(t**2, "г*")
plt.xlabel("Время")
plt.suptitle("Наложение обоих графиков в один")
plt.show() 

Источник: https://www.oraask.com/

Объяснение
Как мы видим, мы строим графики один за другим, и все графики можно увидеть на одном графике. Это еще один метод, в котором мы накладываем другие графики в один.

Как построить несколько графиков в одной легенде рисунка в Python

Что такое легенда?

Легенды являются ключом к пониманию графиков. Они обеспечивают контекст для различных областей графика. Без легенды график было бы трудно интерпретировать.

Многие временные графики могут быть самоочевидными, но иметь заголовок в метках графика на оси и легенду, которая поясняет больше о графике. В этом разделе вы узнаете, как вставить легенду в график. В основном функция легенды может быть в трех формах.

1. Легенда без этикеток и ручек
2. Легенда только с метками
3. Легенда с этикетками и ручками

Легенда без этикеток и ручек

 import numpy as np
импортировать matplotlib.pyplot как plt
 
т = np.массив ([1,2,3,4])
plt.plot(t**2,t, color='красный',label='квадраты')
plt.plot(t**3,t, color='green',label='cubes')
plt.title("Квадраты и кубы")
plt.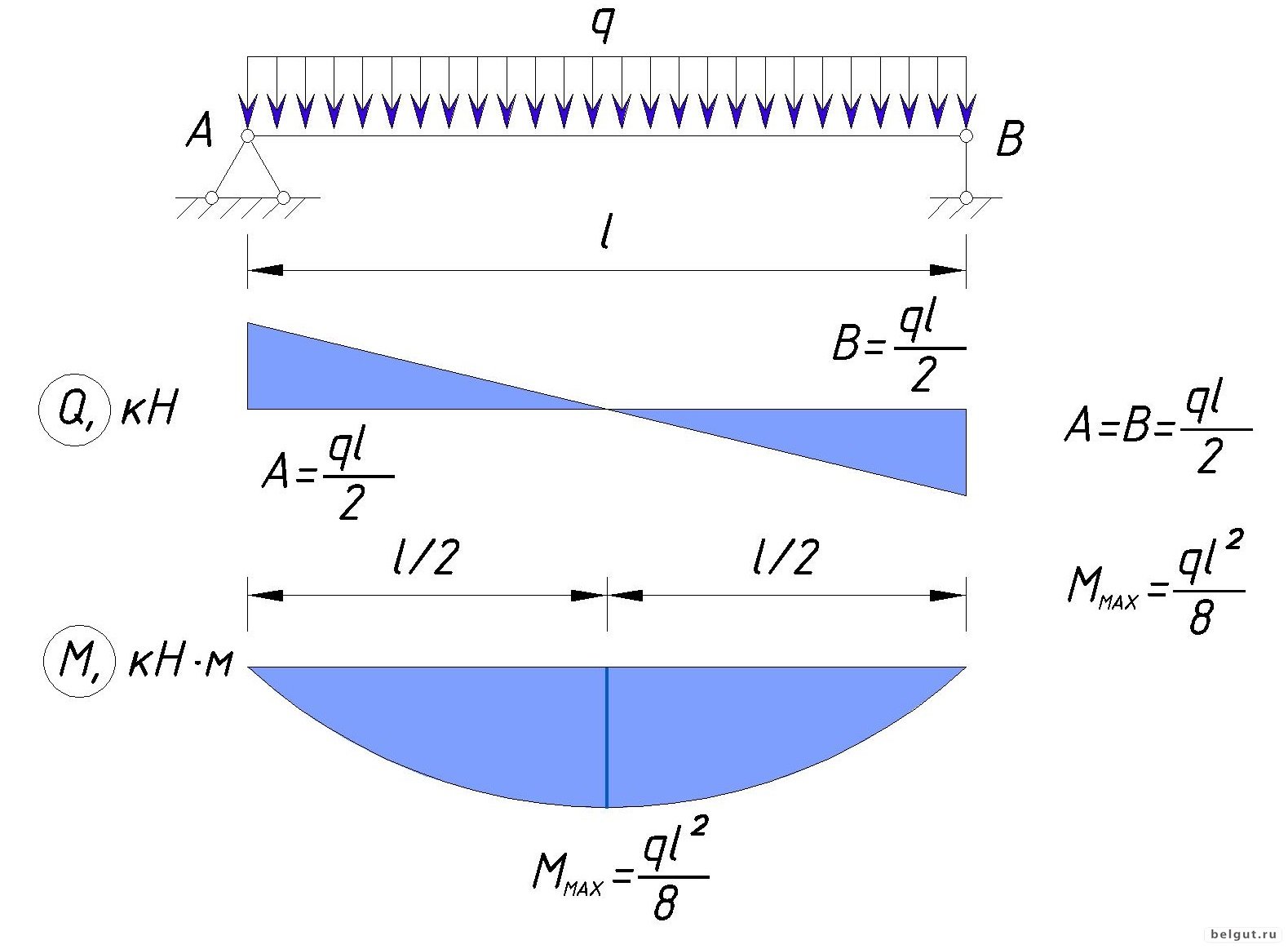 legend()
plt.show() 

Вывод

Источник: https://www.oraask.com/

Объяснение
Метки, включенные в функцию графика, будут автоматически обнаружены функцией легенды, если аргумент не указан. Поэтому, если вы хотите, чтобы легенда работала, вы должны включить метки в функцию графика.

Функция легенды отображает все графики, помеченные ключевыми словами, в том же порядке, в котором они были построены.

Легенда только с метками

Мы можем не маркировать наш график во время построения, игнорируя метки внутри функции plot. Однако мы можем добавить метки, передав их в функцию легенды после построения графиков.

См. пример ниже:

 импортировать numpy как np
импортировать matplotlib.pyplot как plt
 
т = np.массив ([1,2,3,4])
plt.plot(t**2,t, цвет='красный')
plt.plot(t**3,t, цвет='зеленый')
plt.title("Квадраты и кубы")
plt.legend(["квадраты", "кубы"])
plt.show()
 

Вывод

Источник: https://www.