Расчет неразрезной балки по уравнению трех моментов

Как рассчитать неразрезную балку. Уравнение 3-х моментов.

Неразрезная балка нагружена во всех пролетах. Построить эпюры Q и M для неразрезной балки.

Схема неразрезной балки

1. Определяем степень статической неопределимости балки по формуле:

n= Соп -3= 5-3 =2, где Соп – число неизвестных реакций, 3 – число уравнений статики. Для решения данной балки требуется два дополнительных уравнения.

2. Обозначим номера опор с нулевой по порядку (0,1,2,3)

3. Обозначим номера пролетов с первого по порядку (ι_1,ι_2,ι₃)

4. Каждый пролет рассматриваем как простую балку и строим для каждой простой балки эпюры Q и M. То, что относится к простой балке, будем обозначать

с индексом «0», то, что относится к неразрезной балке, будем обозначать без этого индекса. Таким образом,  — это поперечная сила и изгибающий момент для простой  балки.

Рассмотрим балку 1^го пролета

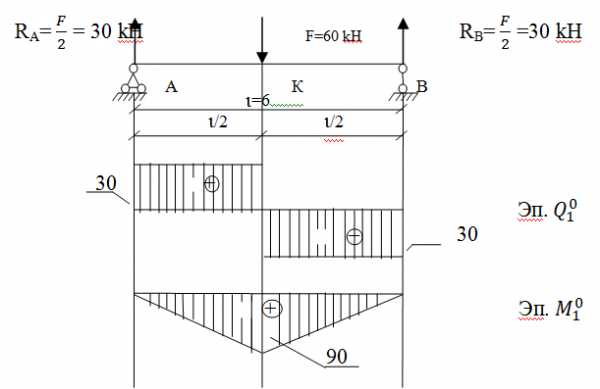
Определим фиктивные реакции для балки первого пролета по табличным формулам (см.таблицу «Фиктивные опорные реакции….»)

Балка 2^го пролета

Балка 3^го пролета

5. Составляем уравнение 3^х моментов для двух точек ­­– промежуточных опор ­– опора 1 и опора 2.  Это и будут

два недостающих уравнения для решения задачи.

Уравнение 3х моментов в общем виде:

Для точки (опоры) 1 (n=1):

Для точки (опоры) 2 (n=2):

Подставляем все известные величины, учитываем, что момент  на нулевой опоре и на третьей опоре равны нулю,  M₀=0; M₃=0

Тогда получим:

Поделим первое уравнение на сомножитель 4 при M₂ 

Второе уравнение поделим на сомножитель 20 при M₂   

Решим эту систему уравнений:

Из первого уравнения вычтем второе, получим:

Подставляем это значение в любое из уравнений и находим M₂

Итак, нашли опорные моменты:

6. Построение эпюры поперечной силы Q для неразрезной балки

Формула для определения Q в любом сечении неразрезной балки:, где

n – пролет

1) Построение эп. Q в первом пролете:

Эта запись означает, что поперечная сила в неразрезной балке в первом пролете будет такая же, как в простой балке с разницей ординат на – 9 . 

На эпюрах должны прослеживаться скачки на величину сил.

2) Построение эп. Q во втором пролете:

Поперечная сила в неразрезной балке во втором пролете будет такая же, как в простой балке с разницей ординат на – 9,5.    

3)Построение эп. Q в третьем пролете:

Поперечная сила в неразрезной балке в третьем пролете будет такая же, как в простой балке с разницей ординат на +15,3.  

Строим эпюру поперечных сил для неразрезной балки.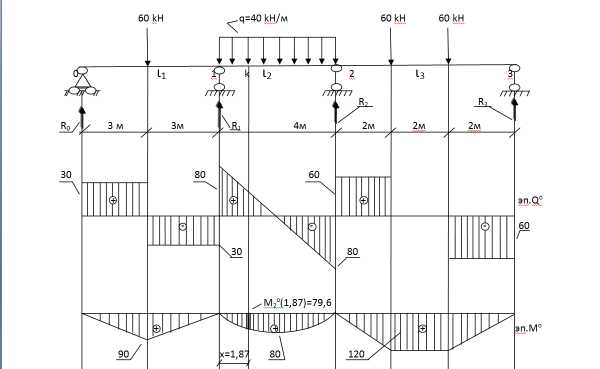 

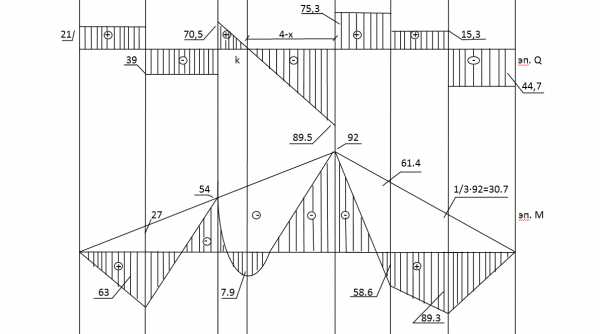
7.  Построение эпюры изгибающего момента для неразрезной балки. Сначала откладываем на опорах значения опорных моментов,   соединяем их линией опорных моментов. Это эпюра опорных моментов.

Эпюру М для неразрезной балки можно построить:

1 вариант – методом «подвешивания».  К эпюре опорных моментов  «подвешиваем»  эпюру M⁰  по разницам ординат. К примеру, в середине первого пролета на эпюре M⁰  ордината равна 90,  а на эпюре опорных моментов -27. В итоге получим 90-27=63. Это значение и откладываем.

2 вариант – формула для определения изгибающего M в любом сечении неразрезной балки:

, где n-пролет , x — расстояние.

Для той же точки первого пролета, которую рассматривали в методе «подвешивания»:

Построение эп. М во 2^ом пролете, загруженном равномерно распределенной нагрузкой

Определим положения т. К. по эпюре Q — это точка экстремума.

Определим М неразрезной балки во 2^ом пролете в этой точке: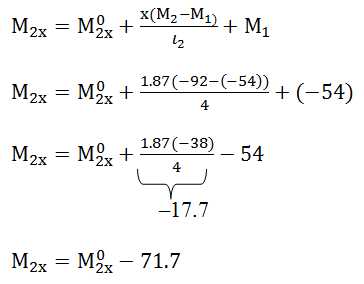 Теперь нужно определить в этой точке К изгибающий момент М в простой балке:

Таким образом, момент в точке К для неразрезной балки:

Строим эпюру М.

8. Выполним проверку опорных реакций. Покажем реакции   на схеме балки на опорах, направив их вверх. Значения этих реакций определим по скачкам эпюры Q. Таким образом получим:

Спроецируем все силы, приложенные к балке, и реакции на вертикальную ось, выполним проверку.

Подставим значения, получим

340-340=0

Проверка верна.

 

 

prosopromat.ru

Последовательность решения задачи на построение эпюр поперечных сил и изгибающих моментов

1. Освобождаем балку от опор, а действие опор заменяем реакциями опор.

2. Определяем реакции опор балки (по двум уравнениям моментов: одно – относительно левой опоры, второе – относительно правой), а затем обязательно проверить правильность решения по уравнению проекций на ось, перпендикулярную балке;

3. Определяем характерные сечения балки (сечения балки, где приложены сосредоточенные силы и моменты, включая опорные сечения).

4. Строим эпюру поперечных сил, для чего вычисляем значения поперечных сил в характерных сечениях.

5. Строим эпюру изгибающих моментов, для чего определяем значение изгибающих моментов в характерных сечениях.

Нормальные напряжения при чистом изгибе.

При деформации изгиба:

• Поперечные прямые линии остаются прямыми, но повернуться навстречу друг другу;

• Продольные прямые линии и ось бруса искривятся;

• Сечения бруса расширятся в поперечном направлении на вогнутой стороне и сузятся на выпуклой стороне.

Линия пересечения нейтрального слоя с плоскостью поперечного сечения называется нейтральной осью.

При чистом изгибе волокна, лежащие на выпуклой стороне, растягиваются, а лежащие на вогнутой стороне – сжимаются, а на границе лежит нейтральный слой, волокна которого только искривляются, не изменяя своей длины. Поэтому при чистом изгибе в поперечном сечении бруса возникают только нормальные

напряжения, неравномерно распределенные по сечению, из-за искривления волокон и оси бруса.

Относительное удлинение при изгибе прямо пропорционально расстоянию до нейтральной оси .

Для вычисления нормальных напряжений при изгибе используем закон Гука: . Эта зависимость определяет линейный закон распределения нормальных напряжений по сечению балки. По ширине балки напряжения постоянны. Наибольшего значения они достигают в точках сечения, наиболее удаленных от нейтральной оси. В точках нейтральной оси напряжения равны нулю.

Нормальные напряжения вычисляются по формуле: , гдеI- осевой момент инерции. Для сечения разных форм есть формула.

Максимальное значение нормальные напряжения возникают с волокнах, наиболее удаленных от нейтральной оси: , гдеW- момент сопротивления изгибу.

Единица измерения .

Определим моменты сопротивления изгибу наиболее распространенных сечений:

сечение	рисунок	формула
Прямоугольник
Прямоугольник
Круг диаметром d
Кольцо

Расчеты на прочность при изгибе.

Проверку прочности и подбор сечений балок обычно проводят исходя из следующего условия: наибольшие нормальные напряжения в поперечных сечениях не должны превышать допускаемые напряжения на растяжение и сжатие.

Для балок из материалов, одинаково сопротивляющихся растяжению и сжатию (сталь и дерево), следует выбирать сечение, симметричное относительно нейтральной оси. В этом случае условие прочности по нормальным напряжениям имеет вид: .

С помощью условия прочности при изгибе можно решить три задачи:

• Проверочный расчет на прочность производится в том случае, если известны размеры поперечного сечения, наибольший изгибающий момент и допускаемое напряжение;

• Проектный расчет на прочность производится в том случае, когда заданы действующие на балку нагрузки и необходимо определить размеры поперечного сечения для определенной формы сечения.

• Определение наибольшей допускаемой нагрузки.

Наиболее выгодные такие сечения, которые дают наибольший момент сопротивления при наименьшей площади.

Последовательность решения задач при расчетах на прочность:

1. Освобождаем балку от опор, а действие опор заменяем реакциями опор.

2. Определяем реакции опор балки (по двум уравнениям моментов: одно – относительно левой опоры, второе – относительно правой), а затем обязательно проверить правильность решения по уравнению проекций на ось, перпендикулярную балке;

3. Определяем характерные сечения балки (сечения балки, где приложены сосредоточенные силы и моменты, включая опорные сечения).

4. Строим эпюру поперечных сил, для чего вычисляем значения поперечных сил в характерных сечениях.

5. Строим эпюру изгибающих моментов, для чего определяем значение изгибающих моментов в характерных сечениях.

6. По эпюре изгибающих моментов определить расчетный (наибольший по абсолютному значению) изгибающий момент, выразив его в Нмм;

7. В выражении условия прочности принять = [] и определить требуемый осевой момент сопротивления поперечного сечения балки;

8. Выразить значение W_x в мм³ (при подстановке в расчетную формулу значенияM_x выражаются в Нмм, а значения [] – в Н/мм², результат получим в мм³) и с помощью таблиц соответствующих ГОСТов по найденному значению W_x подобрать необходимый номер профиля швеллера (ГОСТ 8240-72) или двутавра (ГОСТ 8239-72 «Швеллеры»), или по формулам для определенного сечения вычисляем размеры поперечного сечения балки.

Примеры решения задач.

Задача 1. Для балки построить эпюры поперечных сил и изгибающих моментов, если сосредоточенные силы F₁ = 4 кН и F = 8 кН, момент M = 11 кНм, расстояние a = 2 м, b = 4 м, c = 3 м.

Решение.

1. Определим опорные реакции:

(1)

(2)

Из уравнения (1) кН;

Из уравнения (2) кН.

Проверка:

2. Строим эпюру поперечных сил

В сечении K: кН.

В сечении A: кН;

кН.

В сечении D: кН;

кН.

В сечении B: Q_yB = —R_B = -5 кН.

3. Строим эпюру изгибающих моментов по характерным сечениям K, A, D, В В сечении K: M_xK = 0, так как в этом сечении нет сосредоточенного момента.

В сечении A: кНм.

В сечении B : кНм.

В сечении D: кНм.

Задача 2. Для балки построить эпюры поперечных сил и изгибающих моментов, если сосредоточенные силы как показано на рисунке.

Решение:

1. Строим эпюру поперечных сил по характерным сечениям О,А,В, С.

В сечении O: кН.

В сечении A: кН;

кН.

В сечении B: кН;

кН.

В сечении C: Q_yCлев = —F_{1 +}F₂= -10+20=10 кН.

2. Строим эпюру изгибающих

моментов по характерным сечениям О, A,В,С. В сечении О: M_xО = 0, так как в этом сечении нет сосредоточенного момента.

В сечении A: кНм.

В сечении B : кНм.

кНм

В сечении С: кНм.

Задача 3. По условию задачи 1 из условия прочности подобрать размеры сечения балки в виде прямоугольника с размерами , где , круга с диаметромd и двутавра, если . Определить отношение масс выбранных балок.

Решение:

1. Определяем опасное сечение: это сечение, где возникаем максимальный момент – это сечение В и .

2. Из условия прочности определяем W_х (момент сопротивления изгибу).

3. Вычисляем размеры сечений балки:

двутавр — в соответствии с ГОСТ 8239 выбираем двутавр № (ближайшее большее значение) . W_х = 118см³ — двутавр № 16 А₁ = 21,5см²

• круг —

_{Принимаем d=90 мм.}

_{Принимаем b=47 мм, h=2·47=94 мм.}

4. Отношение масс равно отношению площадей сечений:

Вывод. Балка прямоугольного сечения в 2,7 раза тяжелее двутавровой балки, а балка круглого сечения в 3,8 раз тяжелее двутавровой балки.

studfiles.net

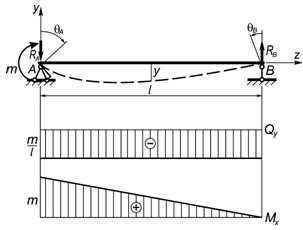
Определение поперечных сил и изгибающих моментов.

Как уже было сказано, при плоском поперечном изгибе в поперечном сечении балки возникают два внутренних силовых фактора и.

Перед определением иопределяют реакции опор балки (рис. 6.3, а), составляя уравнения равновесия статики.

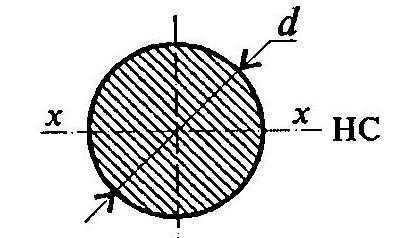Для определения иприменим метод сечений. В интересующем нас месте сделаем мысленный разрез балки, например, на расстоянииот левой опоры. Отбросим одну из частей балки, например правую, и рассмотрим равновесие левой части (рис. 6.3, б). Взаимодействие частей балки заменим внутренними усилиям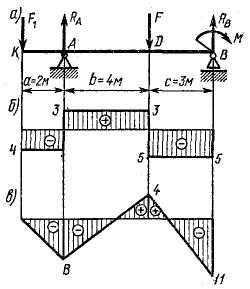ии.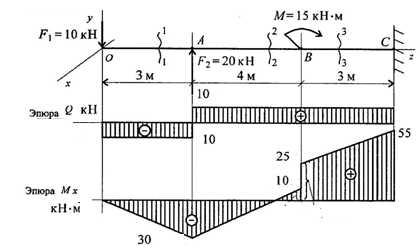

Установим следующие правила знаков для и:

• Поперечная сила в сечении положительна, если ее векторы стремятся вращать рассматриваемое сечение по часовой стрелке;

• Изгибающий момент в сечении положителен, если он вызывает сжатие верхних волокон.

Рис. 6.3

Для определения данных усилий используем два уравнения равновесия:

1. ;;.

2. ;

;

Таким образом,

а) поперечная сила в поперечном сечении балки численно равна алгебраической сумме проекций на поперечную ось сечениявсех внешних сил, действующих по одну сторону от сечения;

б) изгибающий момент в поперечном сечении балки численно равен алгебраической сумме моментов (вычисленных относительно центра тяжести сечения) внешних сил, действующих по одну сторону от данного сечения.

При практическом вычислении руководствуются обычно следующим:

1. Если внешняя нагрузка стремится повернуть балку относительно рассматриваемого сечения по часовой стрелке, (рис. 6.4, б) то в выражении для она дает положительное слагаемое.

2. Если внешняя нагрузка создает относительно рассматриваемого сечения момент, вызывающий сжатие верхних волокон балки (рис. 6.4, а), то в выражении для в этом сечении она дает положительное слагаемое.

Рис. 6.4

Построение эпюр ив балках.

Рассмотрим двухопорную балку (рис. 6.5, а). На балку действует в точкесосредоточенный момент, в точке— сосредоточенная силаи на участке— равномерно распределенная нагрузка интенсивностью.

Определим опорные реакции и(рис. 6.5, б). Равнодействующая распределенной нагрузки равна, а линия действия ее проходит через центр участка. Составим уравнения моментов относительно точеки.

Определим поперечную силу и изгибающий момент в произвольном сечений, расположенном на участке на расстоянииот точки А(рис. 6.5, в). Расстояниеможет изменяться в пределах ().

Значение поперечной силы не зависит от координаты сечения , следовательно, во всех сечениях участкапоперечные силы одинаковы и эпюраимеет вид прямоугольника. Изгибающий момент изменяется по линейному закону Для построения эпюры вычисляем ординаты на границах участка. При : При

Рис. 6.5

Определим поперечную силу и изгибающий момент в произвольном сечений, расположенном на участке на расстоянииот точки(рис. 6.5, г).Расстояниеможет изменяться в пределах ().

Значение поперечной силы не зависит от координаты сечения , следовательно, во всех сечениях участкапоперечные силы одинаковы и эпюраимеет вид прямоугольника. Изгибающий момент

Изгибающий момент изменяется по линейному закону. Определим ординаты эпюры для границ участка.

Определим поперечную силу и изгибающий момент в произвольном сечений, расположенном на участке на расстоянииот точки(рис. 6.5, д).Расстояниеможет изменяться в пределах ().

Поперечная сила изменяется по линейному закону. Определим для границ участка.

Изгибающий момент

.

Эпюра изгибающих моментов на этом участке будет параболической.

Чтобы определить экстремальное значение изгибающего момента, приравниваем к нулю производную от изгибающего момента по абсциссе сечения :

Отсюда

Для сечения с координатой значение изгибающего момента будет составлять

В результате получаем эпюры поперечных сил (рис. 6.5, е) и изгибающих моментов(рис. 6.5, ж).

studfiles.net

2.6. Построение эпюр q и m для балок

Рассмотрим порядок построения эпюр Q u M для наиболее ха­рактерных случаев нагружения балок.

Сосредоточенная сила на свободном конце консоли (рис. 10). Балка имеет лишь один участок. На­чало координат выбираем в крайней левой точкеА балки, ось х направляем вдоль оси балки направо

Вычисляем Q и М в произвольном сечении с абсциссой х.

Справа от рассматриваемого се­чения действует только одна сила P, поэтому

Поперечная сила одинакова во всех сечениях балки, по этому эпюра Q имеет вид прямоугольника. Функция М (х) линейна.

Рис 10 Для построения ее графика достаточно получить две точки — в начале и в конце участка:приX = 0 (сечение А) , при х = l (сечение В) .

Положительные ординаты эпюр Q и М откладываем вверх от базы.

На рис. 10 штриховой линией показана балка в деформиро­ванном состоянии. Как Сжаты нижние волокна балки. Если совместить базисную линию эпюры изгибающих мо­ментов с осью балки, то эпюра М окажется как бы построенной на сжатых волокнах.

Равномерно распределенная нагрузка ин­тенсивностью q кгс/м на консоли (рис. 11). Попе­речную силу и изгибающий момент в произвольном сечении X бу­дем вычислять как результат действия распределенной нагрузки, расположенной слева от сечения:

Поперечная сила Q (х) изменяется по закону пря­мой линии, а изгибающий момент М (х) — по параболическому закону. Для построения эпюры Q вычисляем ординаты в двух точ­ках:

при х = 0 Q_A = 0; при х = l Qb= — gl и проводим прямую.

Эпюра М криволинейна, для ее построения вычисляем ординаты в трех сечениях:

и проводим через полученные три точки кривую.

Нагрузка интенсивностью q н/м, равно­мерно распределенная по всей длине про­лета двухопорной балки (рис. 12).

Вданном случае необходимо сначала определить опорные реакции. Равнодействующая всей распределенной нагрузки равнаgl, и линия действия ее проходит через середину балки. Поэтому

|

Вычисляя поперечную силу и изгибающий момент в произволь­ном сечении x как результат действия сил, расположенных слева от сечения x, (левую часть мысленно отбрасываем) получим

Эпюра Q будет прямоли­нейной, а эпюра М — параболической. Для построения эпюр вычисляем:

Чтобы определить экстремальное значение изгибающего момента, приравниваем нулю производную от изгибающего момента М(х) по абсциссе х сечения:

Так как вторая производная, то в сечении при имеем максимальное значение момента:

Сосредоточенная сила Р, приложенная к двухопорной балке (рис. 13).

Прежде всего найдем опорные реакции:

В данном случае имеем на балке два участка. Вычисляем Q и М в произвольном сечении К₁ на участке АС (0 х а):

Следовательно, во всех сечениях участка поперечные силы одинако­вы и эпюра Q имеет вид прямоугольника.

Изгибающий момент М (х) изменяется по линейному закону:

Для построения эпюры вычисляем ординаты на границах участка:

при х = 0 Ма = 0;

при х = а

В произвольном сечении К₂ на участке СВ (а х l), рас­сматривая действие сил, расположенных справа от него, получим

;

Как и на участке АС, эпюра Q на участке СВ также имеет вид прямоугольника. Для построения эпюры М находим значения ординат в точках С и В

при х; = а M_C =

при х: = / M_B = 0.

Эпюры пред­ставлены на рис. 13. Они показывают, что при х ~ а функция Q (х) терпит раз­рыв и на эпюре Q получается скачок, равный по абсолютной величине внеш­ней силе Р в этом сечении,на эпюре М в этом сечении имеет место излом (угловая точка).

Сосредоточенный момент в пролете двухопорной балки (рис. 14).

Находим опорные реакции, на­правив их вверх:

— отсюда

Меняем направление R_A на обратное. Отметив на участках АС и СВ произвольные сечения х1 и х₂, записываем уравнения для функций О (х) и М (х):

для участка АС (0 х а)

;

для участка СВ (а; х /)

;

На основании этих уравнений строим эпюры Q и М. Эпюра М расположена частично под осью, частично над осью. Поскольку она построена на сжатых волокнах, видим, что на участке АС сжаты нижние волокна балки, а на участке С В — верхние. Этому соответ­ствует изображенная штриховой деформированная ось балки. В том сечении, где изгибающий момент меняет знак, на ней будет точка перегиба.

Там, где приложен внешний момент (сечение С), на эпюре Q изменений нет, а функция М (х) претерпе­вает разрыв и на эпюре М получается скачок, равный по величине внешнему моменту.

Сосредоточенные моменты на опорах однопролетной балки (рис. 15).

Рис 15

Находим опорные реакции:

Тогда для произвольного сечения, находящегося на расстоянии х от левой опоры,

Q(x) =R_A = 0; М(х) = М = const.

Итак, в любом сечении Q = 0, а изгибающий момент постоянен вдоль балки. Такой случай изгиба носит название чистого изгиба.

studfiles.net

БАЛКИ Нагружение сосредоточенными моментами — Эпюры изгибающих моментов

Решение. Брус работает на пространственный изгиб. Определяем реакции в направлениях осей х и у (показаны па рис. 2.141, а) и строим эпюры изгибающих моментов и Му (рис. 2.141, б). Каждая из эпюр строится обычным способом, как для двухопорной балки, нагруженной одной сосредоточенной силой эпюра от действия силы Р, а эпюра УИу от действия силы 0,9 Р. Ординаты первой эпюры откладываем по оси у, а второй — по оси х. При этом получается, что эпюры расположены в тех плоскостях, в которых возникают соответствующие изгибающие моменты.  [c.291]
Построить эпюры поперечных сил и изгибающих моментов для балки, нагруженной сосредоточенным моментом ml и равномерно распределенной моментной нагрузкой интенсивностью т.  [c.100]

На рис. 95, а изображена балка, нагруженная сосредоточенными силами. На рис. 95, б и в приведены эпюры поперечных сил и изгибающих моментов. Вычислите величины ординат этих эпюр в характерных сечениях А, В, С, D, поставьте знаки.  [c.106]

На рис. 96, а изображена консольная балка, нагруженная сосредоточенной силой Р и парой сил, момент которой равен т. Эпюра изгибающих моментов показана на рис. 96, б. Вычислите величины изгибающих моментов в сечении Л, справа и слева отсечения В и в сечении С. Определите величину скачка на эпюре изгибающих моментов в сечении В и постройте эпюру поперечных сил.  [c.107]

На рис. 97, а изображена балка, нагруженная сосредоточенными силами. Определите, какая из приведенных на рисунке эпюр изгибающих моментов соответствует нагружению балки.  [c.107]

Рассмотренный способ расчета балок может использоваться и в случае поперечного изгиба, если учесть, что влияние сдвигов на величину нормальных напряжений незначительно. На рис. 22.4, а показана балка, нагруженная в середине сосредоточенной силой Р. Наибольший изгибающий момент возникает в среднем сечении балки. При достижении моментом величины Мт (эпюра 1) в точках А vl В (рис. 22.4,6) появятся первые пластические деформации. С увеличением силы Р до некоторого значения Pi момент в среднем сечении достигает величины Ml (эпюра 2), а в сечениях D и Е моменты достигнут  [c.499]

Для примера возьмем балку постоянного поперечного сечения, нагруженную в центре сосредоточенной силой W (рис. 58). Эпюра изгибающего момента  [c.233]

При расчете балок обычно важно определить те поперечные сечения, в которых изгибающий момент имеет максимальное или минимальное значение. Для балки, нагруженной сосредоточенными силами подобно рассмотренной в предыдущем примере, максимальный изгибающий момент будет всегда возникать в том поперечном сечении, где приложена одна из сосредоточенных сил. В силу уравнения (4.2), тангенс угла наклона эпюры изгибающего момента в каждой точке равен поперечной силе. Следовательно, изгибающий момент имеет максимальное или минимальное значение в тех поперечных сечениях, где поперечная сила меняет знак.  [c.135]

Для того чтобы продемонстрировать поведение статически неопределимых балок, рассмотрим, например, консольную балку с дополнительной опорой, нагруженную сосредоточенной силой Р, приложенной в середине балки (рис. 9,12, а). Для любой силы, меньшей того значения Р ., при котором начинается пластическая деформация, эпюра изгибающих моментов имеет вид, представленный на рис. 9.12, Ь. Максимальный изгибающий момент имеет место в заделке Л и численно равен ЗPL/16, так что нагрузка, при которой начинают возникать пластические деформации, составляет  [c.359]

Для определения прогиба закрепленного в патроне гладкого валика под воздействием усилия Ру рассмотрим расчетную схему (фиг. 17, а), представляющую балку переменного поперечного сечения, заделанную одним концом и нагруженную сосредоточенным грузом на другом. Эпюра изгибающих моментов для произвольного положения резца по длине I заготовки дана на фиг. 17, б.  [c.40]

На рис. 99, а изображена консольная балка, нагруженная сосредоточенной силой Р и парой сил, момент которой равен М. Эпюра изгибающих  [c.103]

Пример 44. Построить эпюры поперечных сил и изгибающих моментов для балки, нагруженной сосредоточенной парой сил с моментом т— 8 тм, (рис. 120, а).  [c.185]

Нетрудно сообразить, что эпюра изгибающих моментов для всей рамы может быть построена, как для простой балки AD (фиг. 399, а), нагруженной сосредоточенной силой Р. На чертеже дана эта эпюра с учетом характера распределения нагрузки.  [c.396]

На рис. 8.25 приведена схема нагружения главной балки моста крана с четырехколесной тележкой, кабиной крановщика и механизмом передвижения с раздельным приводом, а также эпюры изгибающих моментов от сосредоточенных сил и распределенной нагрузки Ру и Ра — силы давления ходовых кол тележки (принято, что Pi>Pu) Я — распределенная нагрузка ма сы половины про-  [c.237]

На рис. 8.32 и 8.33 показаны схемы нагружения главных балок моста в вертикальной и горизонтальной плоскостях при действии сосредоточенных сил и распределенных нагрузок, эпюры изгибающих моментов для главной балки, а также схемы, изображающие эквивалентные балки и используемые при определении расчетных длин. С целью упрощения силы давления ходовых колес на главные балки заменены их равнодействующими, которые приняты приложенными в середине пролета.  [c.251]

Пример 23.1. Построить эпюры поперечных сил и изгибающих моментов для балки, шарнирно закрепленной двумя концами и нагруженной сосредоточенной силой (рис. 23.8).  [c.240]

Примеры предыдущего параграфа дают определенную зависимость между очертаниями эпюр поперечных сил и изгибающих моментов и внешней нагрузкой. Для установления этих зависимостей рассмотрим балку (рис. 94, а), нагруженную равномерно распределенной нагрузкой интенсивностью q, сосредоточенной силой Р = qa н парой сил т = qa . Для общности выводов все нагрузки мы задали не в численном виде, а в функции интенсивности q равномерно распределенной нагрузки и некоторого расстояния а.  [c.103]

Для построения эпюры динамических изгибающих моментов нужно рассмотреть нагружение скелета балки амплитудными значениями возмущающей силы и сил инерции лш,со , развиваемых сосредоточенными массами (рис. IV.43, б). При этом следует учесть, что инерционные силы находятся в фазе, противоположно.» заданному возмущению (так как со>Р[). Подсчет дает  [c.259]

Рассмотрим ряд типовых примеров, содержащих наиболее часто встречающиеся случаи нагружения. Построим эпюры поперечных сил и изгибающих моментов для балки с защемленным концом, нагруженной на свободном конце сосредоточенной парой сил с моментом М (рис. 92, а).  [c.96]

Усвоив приведенные правила построения эпюр, можно обойтись без составления уравнений изгибающих моментов и поперечных сил для каждого участка балки. Достаточно вычислить ординаты эпюр для характерных сечений и соединить их линиями в соответствии с изложенными выше правилами. Характерными являются сечения балки, где приложены сосредоточенные силы и моменты (включая опорные сечения), а также сечения, ограничивающие участки с равномерно распределенной нагрузкой. Для определения максимальных значений изгибающих моментов дополнительно подсчитываются моменты в сечениях, где поперечные силы равны нулю. Построение эпюр без составления уравнений дает особенно значительный эффект для балок, нагруженных сложной нагрузкой,— имеющих много участков нагружения.  [c.193]

Для расчета крыла на прочность необходимо знать действующие в отдельных его сечениях величины поперечных сил изгибающих моментов М и моментов Мг- Последние определяются относительно оси жесткости крыла. Эпюры Q н М для крыла строятся, как для двухопорной балки с консолями (рис. З.П), нагруженной распределенными и сосредоточенными силами. Опо-  [c.79]

В качестве расчетной схемы поперечины принимаем дпухопорную балку, нагруженную по середине пролета сосредоточенной силой (рис. 1.7, б). Строим эпюру изгибающих моментов (рис. 1.7, б) наибольший изгибающий момент  [c.18]

Расчет балки, лежащей на трех опорах. На рис. 7.8, а изображена балка, лежащая на трех опорах и нагруженная двумя сосредоточенными силами Р. Устранив среднюю опору и приложив на ее месте неизвестную силу X, получим основную систему (рис. 7.8, б). На рис. 7.8, в показана эпюра изгибающего момента, возникающего под действием сил Р. Ордината средней части эпюры М (Р) равна аР. На рис. 7.8, г изображена эпюра изгибающего момента М (X) от действия силы X. Максимальный момент, появляющийся в сечении, лежащем над устраненной средней опорой, равен ЬХ 2. Если положить / = 1, то получим эпюру М (Р) для единичной внешней нагрузки. Если пpJHЯть X = 1, то получим эпюру М (X) от единичной неизвестной силы, приложенной в сечении, расположенном над средней опорой. В дальнейшем пренебрежем упругим перемещением от сдвигающей силы, малым по сравнению с перемещением от изгиба балки. Согласно выражению (7.15), прогиб в среднем сечении 00 от действия нагрузки Р  [c.192]

Пример 43. Для балки, нагруженной на расстоянии а = 4 м от левой опоры сосредоточенным моментом Л1 = 12 тс м (рис. 283), построить эпюры поперечных сил, изгибающих моментов, углов поворота сечений и прогибов, а также подобрать двутавровое сечение из условий прочности и жесткости [а] = 1600 кгс/ Mii  [c.289]

Для балки на двух опорах пролетом / = За, нагруженной равномерно распределенной нагрузкой интенсивностью q, парой сил с моментом M =qa и сосредоточенной силой P — qa (см. рисунок), составить в буквенном виде выражения Q(x) и М х), построить эпюры Q и М и вычислить наибольшие по абсолютному значению величины изгибающего момента и поперечной силы, если q = 2rlM и а = 2 м.  [c.125]

---

mash-xxl.info